Sketching 2D Vessels and Vascular Diseases with Integrated Blood Flow

Patrick Saalfeld

, Alexandra Baer

, Uta Preim

, Bernhard Preim

and Kai Lawonn

Department of Simulation and Graphics, Otto-von-Guericke University, Magdeburg, Germany

Department for Radiology, Municipal Hospital Magdeburg, Magdeburg, Germany

Keywords:

Sketch-based Interface, Vascular Diseases, Computational Fluid Dynamics, Patient Education.

Abstract:

In this paper, we present a sketch-based interface, which allows medical doctors to illustrate different vascu-

lar diseases and treatment methods as well as ﬂuid behavior. With this sketching interface, we provide the

physician with an effective tool to illustrate different medical cases, which is important in the complex ﬁeld

of vascular diseases with respect to patient education. We use techniques from sketch-based interfaces and

GPU-based computational ﬂuid dynamics by considering usability aspects. We provide a concept and a pro-

totypical implementation whose usability is tested with quantitative and qualitative methods. Additionally, we

interviewed a physician to assess the beneﬁts of the tool with respect to patient education.

1 INTRODUCTION

Vascular diseases are a complex ﬁeld with a large

amount of deaths comprising 31% worldwide (see

(Mendis et al., 2011)) and a big impact on economics

about e 196 billion in Europe (see (European Heart

Network, 2012)). The treatment of such a disease

leads to discussion about prevention, diagnosis, and

therapy not only with colleagues, but also with pa-

tients. Most important, the patient education gives the

patient an insight into the complexity and risk of the

possible outcome. An informed patient can beneﬁt in

various aspects from comprehensive patient education

(see (Keulers, 2008)):

• they need less medication,

• the time of treatment may be reduced,

• they are more active in dealing with their diseases

and act more responsible, and

• they are more independent from their treating

physician.

Therefore, a tool that supports physicians to discuss

and communicate vascular diseases is very useful for

patient education. In this paper, we present a program

that helps the physician to easily create different vas-

cular diseases and to show various treatment options

that may help the patient in understanding their dis-

ease. This tool is inspired by the work of Zhu et al.

(Zhu et al., 2011) about sketching tubular shapes and

simulating liquids. Their method has several limita-

tions with respect to sketching vascular structures and

diseases. Furthermore, it is not optimized for tablet

devices, which could be integrated well in the process

of patient education. The physicians need an effec-

tive tool to sketch patient-speciﬁc cases and to illus-

trate the different treatment options for educating the

patient, see Figure 1. Hence, we make the following

contributions:

• We present appropriate methods to sketch vessels,

vascular diseases, and treatment options, which

are usable by medical doctors and understandable

by patients.

• We introduce a plausible representation of blood

ﬂow in real time.

2 MEDICAL BACKGROUND

This work focuses on the vascular diseases of arteries,

which are vessels transporting blood from the heart to

the peripheral capillary of the body. A common rea-

son of those diseases is arteriosclerosis, which leads

to a hardening of vessels by deposition of blood fat,

thrombi, and lime (Kutikhin et al., 2013). This depo-

sition affects vessels in two problematic ways:

1. A weakening of the vessel wall.

2. A narrowing of the vessel (stenosis) up to a com-

plete occlusion.

The weakening can lead to a dilation of the vessels

that may result in an aneurysm. A possible outcome

379

Saalfeld P., Baer A., Preim U., Preim B. and Lawonn K..

Sketching 2D Vessels and Vascular Diseases with Integrated Blood Flow.

DOI: 10.5220/0005196203790390

In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 379-390

ISBN: 978-989-758-087-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

(a) (b) (c)

(d) (e) (f)

Figure 1: Illustration of blood ﬂow before and after a stenting treatment. First, the physician sketches a vessel with an

aneurysm (a). Afterwards, he manipulates and visualizes the underlying ﬂuid simulation to illustrate the blood ﬂow (b-c). The

consequences resulting from the stent treatment (d-e) are illustrated with another color (f).

might be a clot formation inside the aneurysm or a

rupture. A stenosis can lead to an undersupply of in-

volved structures or can cause a clot formation. An-

other dangerous effect is an increased risk of rup-

ture of an aneurysm in cerebral areas (Neugebauer

et al., 2010) with a mortality rate of 40-60% (Bed-

erson et al., 1994). In Figure 2 an aneurysm and

a stenosis are illustrated. For the medical treatment

of such vascular diseases, the physician can use sev-

eral methods, see Wong et al. (Wong et al., 2011)

for an overview. The choice of the treatment depends

on parameters such as location, anatomical access or

pathology. In particular, this work focuses on clipping

as an example of an extravascular treatment method as

well as coiling and stenting as examples of intravas-

cular methods.

The clipping procedure, e.g., for treating a cere-

bral aneurysm, starts with a craniotomy to disclose

the aneurysm. Afterwards, a titanium clip is placed

across the aneurysm neck to stop the blood from en-

tering into the aneurysm (Gasteiger, 2014). Coiling is

performed by entering an artery from the inside. The

coil, a small titanium wire, is used to ﬁll the aneurysm

and to induce a thrombus formation (Teitelbaum et al.,

1994). The stenting method can be used to treat both

stenosis and aneurysms through an intravascular ap-

proach. Similar to the coiling procedure, a catheter is

moved to the affected position from the inside. After-

wards, the stent is expanded and forces the vessel to

expand to treat the stenosis. For treating aneurysms,

stents can help to support the involved vessel during,

e.g., a coiling procedure.

Further descriptions of different forms of vascular

diseases, their treatments, and possibilities for visual-

ization and exploration are mentioned by (Gasteiger,

2014). A historical overview of different treatment

(a) (b)

Figure 2: Illustrations of a saccular aneurysm (a), which

is the most common type, and a stenosis (b) caused by a

narrowed vessel.

options can be found in the work of (Wong et al.,

2011).

3 RELATED WORK

This work involves two main topics: computational

hemodynamics and Sketch-based Interfaces (SBIs), a

form of user interface (UI), which deals with sketch-

ing. The following parts name related work for the

latter topics.

3.1 Computational Hemodynamics

To simulate the behavior of blood, it is necessary to

imitate a non-Newtonian ﬂuid (a ﬂuid with varying

viscosity). Furthermore, in terms of ﬂuid dynamics,

blood is compressible and inhomogeneous. Such a

simulation is not only complicated, but also expensive

regarding the calculation time (Bridson, 2008). We

consider blood as an incompressible, homogeneous

Newtonian ﬂuid to achieve a real time simulation. Ex-

amples for methods to calculate non-Newtonian ﬂuids

can be found in (Ciarlet et al., 2011) and (Ferziger and

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

380

Peri

c, 2002). To describe the state of a ﬂuid, there are

two possibilities: the Lagrangian (a particle-based)

and the Eulerian (a grid-based) description. We use

the Eulerian description because the grid-based char-

acter is well suited to be calculated with fragment

shaders on the GPU. Examples for the Lagrangian de-

scription can be found in (M

uller et al., 2004; Qin

et al., 2010). Both deal with particle-based simula-

tion of blood ﬂow in vessels to support surgeons in

virtual surgery scenarios.

3.2 Sketch-Based Interfaces

The usefulness of SBIs to communicate ideas and

concepts is described among others in (Jorge and

Samavati, 2011). The communication of complex is-

sues is possible without the necessity to draw pre-

cisely and accurately. This advantage, however, is a

disadvantage for the computer, which tries to interpret

the sketch. As a consequence, several works deal with

the interpretation of sketches, see (Jorge and Sama-

vati, 2011) for an overview and examples. The foun-

dations of were laid by Ivan Sutherland (Sutherland,

1963) with the program Sketchpad. Sketch-based in-

terfaces can be seen as a part of post-WIMP (win-

dows, icons, menus, and pointers) UIs because the

sketching is performed with direct input, e.g., a pen or

touch (Preim and Dachselt, pear). So the pointer com-

ponent of the WIMP paradigm is no longer necessary

(van Dam, 1997). (Xu et al., 2002) and (Naya et al.,

2007) showed the advantage of reality-based inter-

faces (such as SBIs) by comparing WIMP-based in-

teraction with reality-based interaction and presented

two ﬁndings: ﬁrst, the users preferred the sketch-

based approach and second they were more efﬁcient

with it. SBIs contain three processing steps: resam-

pling of the input data, beautiﬁcation, and recogni-

tion. This paper only deals with the resampling of the

input data. Examples for the second step (beautiﬁca-

tion) can be found in (Igarashi et al., 1997). There,

line segments were analyzed according to geometric

constraints such as perpendicularity and parallelism.

After that, the program recommends different options

of how to interpret the lines. The user chooses an

option by clicking on it. The processing step recog-

nition describes a procedure where the sketch is com-

pared with an internal representation of symbols. The

similarity is expressed with a parameter. If this pa-

rameter exceeds a value, the sketch is interpreted as

the compared symbol (Jorge and Samavati, 2011). A

simple way to integrate recognition in an application

is described with the 1

Recognizer (Herold and Sta-

hovich, 2012).

An important use case of SBIs is geometric mod-

eling, i.e., the creation of 3D structures. An example

of an SBI for modeling (SBIM) medical structures is

(Pihuit et al., 2010). There, methods are described

to sketch and model branching vessels. To maintain

the sketch-based look of 3D models, it is possible to

visualize them with non-photorealistic rendering. A

comparison of different rendering styles in the med-

ical domain can be found in (Lawonn et al., 2014b).

Contrary to SBIM, the following work addresses the

creation of 2D vessels.

4 METHODS

Our sketch-based interface consists of different con-

cepts to create vessels with interior blood ﬂow based

on intuitive sketch-based gestures. In the following,

we describe the methods and the implementation.

4.1 Blood Flow Simulation

We use the Eulerian ﬂuid simulation, which is de-

scribed in (Stam, 1999; Bridson, 2008; Harris, 2004).

For the ﬂuid simulation, we use the Navier-Stokes

equations for incompressible and homogenous ﬂuid,

which are based on Newton’s second law of ﬂuid mo-

tion:

∂u

∂t

= −(u · ∇)u −

∇p + v∇

u + F, (1)

and

∇ · u = 0. (2)

Equation 1 (momentum equation) describes the be-

havior of the velocity vector ﬁeld u under inﬂu-

ences like advection, diffusion, pressure, and external

forces, which will be described in more detail in the

following. Equation 2 (continuity equation) ensures

the incompressibility by deﬁning u as a divergence-

free vector ﬁeld.

To achieve a real time ﬂuid simulation, the grid

size is an important factor. While a small grid size ac-

celerates the calculation time, details like whirls may

be lost. Another problem are obstacles. To enable the

blood ﬂow to react on these, it is necessary to model

them in the simulation grid. This is achieved by mark-

ing grid cells as occupied. So the grid resolution also

affects the possible level of detail of the obstacles. To

allow a high spatial resolution of grid cells, the sim-

ulation is performed on the GPU. For the GPU-based

calculation, we used the fragment shader similar to

(Harris, 2004).

To solve the equations for the differential oper-

ators, the ﬁnite difference method is used. Further-

more, Equation 1 needs to be split up in single terms,

which are calculated separately.

Sketching2DVesselsandVascularDiseaseswithIntegratedBloodFlow

381

External

Force

External

Force

Advection

Diffusion

Pressure

Calculation

Pressure

Calculation

Pressure Gradient

Subtraction

Pressure Gradient

Subtraction

Fix

Boundary

Fix

Boundary

Fix

Boundary

Fix

Boundary

Fix

Boundary

Fix

Boundary

Fix

Boundary

Fix

Boundary

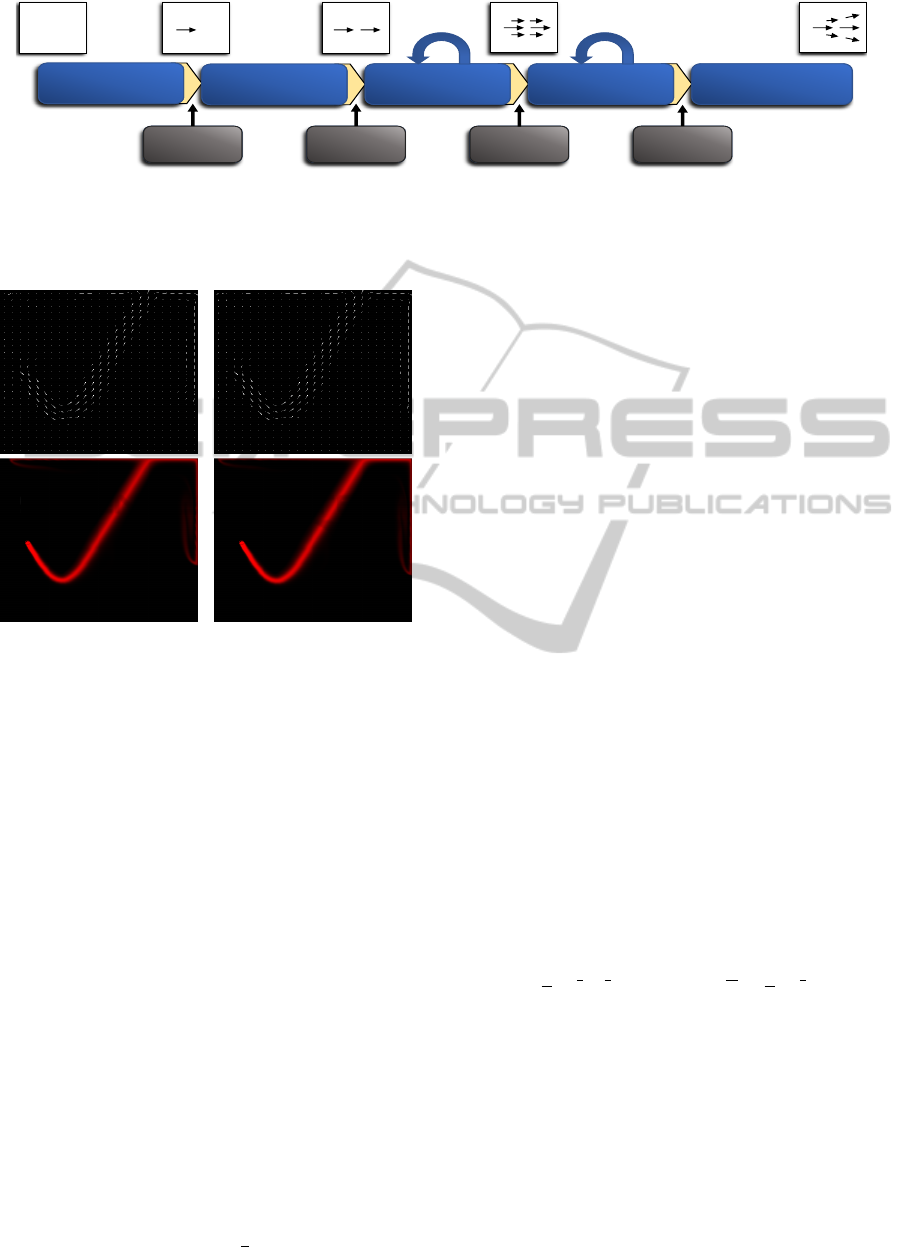
Figure 3: Overview of the calculation pipeline for the ﬂuid simulation including the inﬂuence to the underlying vector ﬁeld.

Each step is realized with a separate fragment shader program. The steps provided with self-referencing arrows show the

steps which are calculated with an adjustable amount of iterations. Here, a trade-off arises between accuracy (high amount of

iterations) and calculation time (low amount of iterations).

(a) (b)

Figure 4: Comparison of the Euler (a) and Runge-Kutta 4

(b) integration methods with a step size of 0.3. Both meth-

ods are visualized with a modiﬁed arrow plot visualization

(top) and a scalar ﬁeld visualization (bottom), which looks

similar to a streakline visualization through the continu-

ous placement of ink during the simulation. Since the dif-

ferences between both methods are small, the faster Euler

method is used.

An overview of the calculation steps is illustrated

in Figure 3. In the following, we describe the mathe-

matical terms and their effects in the ﬂuid simulation.

The ﬁrst term −(u · ∇)u describes the self-

advection of the ﬂuid, which is the process of mov-

ing the velocity itself through the ﬂuid. Here, the

self-advection is realized with semi-Lagrangian ad-

vection (Stam, 1999). Mostly, ﬂuid simulations use

the Runge-Kutta method (Butcher, 1996) for the in-

tegration, which is less error-prone than the simpler

and faster Euler method. Interestingly, as illustrated

in Figure 4, the differences between both methods are

small, due to the small step size used in the applica-

tion. Therefore, we used the Euler method to decrease

the calculation time.

The pressure, a force that gradually spreads from

regions with high to regions with low pressure, is de-

scribed with the second term

∇p. The factor ρ is

a constant to describe the density. Futhermore, this

term also ensures the incompressibility of the veloc-

ity vector ﬁeld, and thus simultaneously ensures the

Equation 2. To achieve this, the term is calculated at

the end. For a description of the derivation, see (Brid-

son, 2008). To calculate this term, it is necessary to

solve a Poisson equation. This is accomplished by the

Jacobi approach because it can be mapped directly

to GPU facilities. For a discussion of different ap-

proaches, see (Kr

uger and Westermann, 2003).

The third term v∇

u expresses the physical pro-

cess of diffusion, i.e., the property of mixing materi-

als without external forces. Here, v is a constant that

describes the viscosity. The calculation of the diffu-

sion also requires the solution of a Poisson equation.

A disadvantage of diffusion is the resulting smoothing

effect on the applied vector ﬁeld, which causes a loss

of details. Therefore, the choice whether diffusion is

applied is left to the user.

The last term F describes external forces, which

allows the user to inﬂuence the simulation dynami-

cally. Normally, such forces are steady, so the inﬂu-

ence of the force to ﬂuid is constant over time. This

approach would not reproduce the pulsating character

caused by the contractions of the heart. This pulsa-

tion can be imitated by applying a factor to the force,

which changes over time. Therefore, we approximate

the function measured by an electrocardiogram with

the following formula:

f (x) = −

−

(−

+x)

+ 1, 12e

−

(1+x)

+ 1.

(3)

This equation was determined by combining three

Gaussian functions with varying heights and widths.

In Figure 5, the difference between a constant and a

pulsating force is illustrated.

Finally, boundary conditions are used to simu-

late the behavior of the ﬂuid at the vessel wall and

the boundary of the draw area. These conditions

are necessary for the velocity vector ﬁeld and for

the scalar ﬁeld, describing the pressure. For the ve-

locity vector ﬁeld, a Dirichlet boundary condition is

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

382

Figure 5: In (a) a constant force is applied to the vector

ﬁeld. In (b) a heartbeat-like function is applied as a factor,

which mimics a more realistic behavior. The corresponding

functions are plotted at the left bottom.

used, which states that the velocity drops to zero at

boundaries. For the scalar ﬁeld, a Neumann con-

dition is used, which states that the derivatives are

zero. To calculate the derivative, the normal of the

boundary is necessary. The normals of the top, right,

bottom, and left image boundaries are deﬁned as

(0, −1), (−1, 0), (0, 1), and (1, 0), respectively. For

determining the normals of arbitrary boundaries, we

use the neighborhood of the obstacle. That means that

for each grid cell, which is an obstacle, eight neigh-

bors are analyzed. Depending on the state of these

neighbors (obstacle or no obstacle) the normal is ap-

proximated to one of eight possible directions. This

approach is described in more detail in (Wu et al.,

2004).

4.2 Blood Flow Visualization

To illustrate the unsteady vector ﬁeld that represents

the blood ﬂow, we implemented two visualization

concepts: (1) a direct and (2) a sparse ﬂow visual-

ization, see Figure 4. The direct visualization is a

modiﬁed line plot on which fans are drawn on an ad-

justable grid. Fans are used because they facilitate a

fast realization of the ﬂow direction for the user.

Especially for patients, a scientiﬁc visualization

method for vector ﬁelds may be inappropriate. Thus,

an additional method is used. It aims to be easily un-

derstandable to visualize the behavior of blood in ar-

eas such as aneurysms and stenoses in a descriptive

way. The used scalar ﬁeld visualization is inspired by

the idea to place colored ink in the vector ﬁeld (also

known as dye injection). By diffusion and advection,

this ink is transported through the vector ﬁeld. The

amount of ink is color-coded with a black-to-hue scale

with different colors. This allows using multiple col-

ors, e.g., to show how blood mixes in an aneurysm

before and after a treatment, see Figure 1.

The colors are taken from the Lab color space,

which allows choosing colors that are roughly per-

ceptually linearized regarding hue and brightness. To

determine different colors, the approach of (Glaßer

et al., 2014) is used. If the ink is placed continu-

ously over time, the visualization technique is similar

to streaklines. In contrast to streaklines, the placed

ink is not connected, but if the amount of placed ink

is high enough, there is the impression of connectiv-

ity. A difﬁcult task by sparse visualization techniques,

namely to identify suitable seed point positions, is left

to the user, i.e., the physician or the patient.

4.3 Sketching

The obtained data from the input device inherits

noise, which is caused by the conversion from the

analog signal to a digital signal (quantization) as well

as the imprecise input from the user. Especially the

quantization, also depending on the sampling rate,

reduces input information during fast input move-

ments from the user. To remove the resulting noise

and obtain equidistant input information, the received

data of the input device is resampled and smoothed.

These steps are commonly applied after the user ﬁn-

ishes drawing, which causes abrupt changes in the

sketch. To avoid these sudden changes, we use on-

the-ﬂy methods that are applied during sketching.

This presents challenges regarding real time capabil-

ity. Ideally, the user did not even realize these steps.

First, the resampling should reduce the obtained sam-

ple points. To achieve this, we use a simple strategy:

we ignore all points that are too close to the last ac-

cepted point. We use the Euclidean distance to mea-

sure the distance of two points, see Figure 6.

A disadvantage of this approach is that it is prone

to draw zigzag lines. This can be neglected, because

vessels, vascular diseases, stents, and coils usually do

not have those shapes. To smooth the accepted sam-

ple points, a local Gaussian ﬁlter similar to (Taubin,

1995) is used. More precisely, the 1-neighborhood of

the accepted points is used to adjust the points with a

Gaussian distribution. The ﬁlter is only applied to the

pre-last point, which was accepted to prevent the line

segments from shrinking, see Figure 6.

5 APPLICATION

The application should be as ﬂexible as possible re-

garding the used direct input device. More precisely,

it should be possible to control the application with

touch and pen-based input. This implies the follow-

ing limitations:

• Special functions from pen-based input devices

like pressure sensitivity or additional buttons are

Sketching2DVesselsandVascularDiseaseswithIntegratedBloodFlow

383

not supported.

• Multitouch input is not supported.

Through these limitations, the used concept is theo-

retically usable for a mouse with a left button only.

Furthermore, the application is designed according

to major usability criteria, such as ”suitability for the

task”, or ”self-descriptiveness”. The evaluation of the

application revealed possibilities for improvements,

which were partially implemented. Improvements

based on the quantitative part, the qualitative part,

or the interview, are marked and discussed. The

application can be downloaded under wwwisg.cs.uni-

magdeburg.de/∼patrick/application/SketchingVessel

s.zip).

5.1 Sketch Vessels and Vascular

Diseases

Mainly, drawing a vessel requires two lines represent-

ing the border of the vessel. Unfortunately, drawing

each line separately leads to strong variations in the

resulting vessel structures. Therefore, we use a cre-

ate tool that creates both lines simultaneously by us-

ing the sketched path as the center line and drawing

the vessel wall around it. The general advantage of

this process is that uniform vessels can be drawn eas-

ier and faster. We ﬁx the width of the vessel to sim-

plify the application. In contrast to (Zhu et al., 2011),

where it is possible to draw vessels under and over al-

ready existing ones through a 2,5D sketching canvas,

this work limits the sketching area to a 2D canvas.

This decision is reasoned by considering what could

happen if the user sketches over an already created

vessel. Besides the possibility to draw the vessel over

or under the existing ones, it is possible to merge the

new vessel with the old ones. This offers the possibil-

ity to create more complex structures like branching

vessels and aneurysms without changing the drawing





(a)

�

(b)

Figure 6: (a) The new point p

has exceeded a speciﬁc dis-

tance to p

and thus, is sampled. The points o

- o

are

too close and thereby omitted. (b) shows the smoothing ap-

proach. In the moment p

is sampled, the pre-last point p

is smoothed. By sampling the pre-last point, a shrinking of

the line is prevented.

Figure 7: As illustrated, the merging behavior can be used to

draw a vessel containing an aneurysm by simply sketching

on top of the previous drawing.

mode. The merge behavior is illustrated in Figure 7

and is realized with an already implemented polyline-

based functionality in the used framework.

Additionally to the possibility to draw aneurysms,

the application offers a possibility to draw stenoses.

A cut tool is used to allow the user to create irregu-

lar non-symmetrical stenoses in a consistent sketch-

based way. To prevent problems during cutting, e.g.,

ambiguity (see (Heckel et al., 2013)), the user does

not only see his sketched contour, which is used for

the cutting process. The start and end point of the

sketched contour are connected, and thus span a cut-

ting area to support the user. This area is substracted

from the existing vessels (see Figure 8).

This tool does not only allow the creation of

stenoses; in combination with the create tool, the user

has a generic sketching tool, which allows the cre-

ation of any 2D structure under the usage of only two

different modes. To support the medical expert dur-

ing the sketching process, it is possible to load im-

ages in the background. The physician can use this

function to load a slice of patient-speciﬁc MRI or CT

data, which contains, e.g., the vessel structures of the

patient. In addition frequently used vessel structures,

such as the Circle of Willis, can be loaded (see Figure

9).

During the evaluation, some participants suggest

a possibility to load vessel structures. This could

Figure 8: The cut tool is used to remove structures from the

already sketched vessel to create a stenosis.

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

384

Figure 9: The medical doctor has loaded a background im-

age of the Circle of Willis which supports the sketching pro-

cess.

help because it allows the physician to not only

load standardized structures, but also patient-speciﬁc

data. The functionality is implemented by loading

a monochrome black-and-white image. Every black

pixel is interpreted as a vessel and every white pixel

as free space, where blood is able to ﬂow. This ap-

proach has, however, a disadvantage. It is only possi-

ble to show bloodﬂow in the loaded vessel structure,

but not to use the other tools, e.g., cutting or treating

the vessel. This disadvantage can be avoided by im-

plementing an object-based save and load mechanism

instead of an image-based, which could be added in

the future.

5.2 Manipulate and Visualize Blood

Flow

As described in Section 4.1, the ﬂow can be manip-

ulated with a force term, which is represented with a

2D vector ﬁeld. To allow the user to inﬂuence this

ﬁeld in a ﬂexible and easy way, a direction tool is

used, which also works in a sketch-based way. Af-

ter the direction tool is selected, the user can sketch

lines, that are represented by arrows directing in the

draw direction. This arrow represents the inﬂuenced

force on the vector ﬁeld.

To transfer the sketched arrow to the vector ﬁeld,

it would be obvious to manipulate only the vectors

directly under the sketched arrow. This behavior is

not desirable, because it only allows to manipulate the

ﬂow in small areas. Instead, the force is applied in

a region around the sketched arrow. The size of this

region is adjustable and is initially set to the width of a

vessel. To achieve a natural effect, the force is slightly

decreased at the border of the region by applying a

Gaussian distribution, resulting in a strong force at

the center and a weak force at the border.

To visualize the ﬂow, the user can use a dye tool

to place ink (blood) in the ﬂuid region. A circle of

ink is placed by just tipping on the canvas or drawing

over an area. The ink is interpreted as a source of in-

ﬁnite amount of ink, which is added in every render

frame. The width of the ink area is adjustable, but set

to the vessel width to allow the user to ﬁll a vessel

with ink in a fast way. Under the assumption that the

physician wants to show the mixing behavior of ﬂuid

by repetitive using of the dye tool, a new color is used

after each usage of the dye tool with the approach ex-

plained in Section 4.2.

5.3 Treating Options

To show the patient how to treat aneurysms and

stenoses, we implemented the following treatment

methods:

• coiling,

• clipping,

• and stenting.

First, we implemented the coiling tool such that the

user should ﬁll out the aneurysm. This coil was illus-

trated with a line, which occurred during the drawing

process. Generating the coil with this approach is not

applicable, since it takes too much effort and is too

time-consuming, which was stated by the participants

in our evaluation. Therefore, we implemented another

approach to improve the coil placement.

First, an area is sketched, e.g., on the vessel wall

of an aneurysm. After the user raises the pen, every

sample point analyzes its neighborhood with a spe-

ciﬁc adjustable distance. This is performed by send-

ing eight rays in a circular manner, starting at ev-

ery sample point. Signiﬁcantly less rays would result

in an inaccurate vessel wall detection and more rays

would not improve the result. We test every ray for

intersecting the vessel wall. If more than one ray col-

lides with the wall, the ray with the shortest distance

is chosen. After that, the corresponding sample point

is placed on the intersection point of the ray. If no

collision occurs, the point keeps the current position.

The underlying grid cells are than treated as obstacles

and thus, the blood ﬂow changes dynamically corre-

sponding to the drawn coil. Figure 10 illustrates this

algorithm.

The clipping method was inspired by the line

drawing method used in Sketchpad (Sutherland,

1963). The point where the user starts drawing rep-

resents the ﬁrst point of the clip. As long as the user

draws with the pen, the current pen position repre-

sents the end point of the clip. These two points are

connected with a dashed line to give the user a pre-

view of the clipping result. After the user ﬁnishes

drawing and raises the pen, the clip is placed and the

blood ﬂow simulation is affected by it.

Sketching2DVesselsandVascularDiseaseswithIntegratedBloodFlow

385

The stent placement algorithm is inspired by the

real treatment. Here, a balloon catheter is inﬂated

to dilate the stent in the vessel. We use this inﬂat-

ing process for providing a stent placement algorithm.

The user draws a line in the center of the vessel with

the stenting tool, which represents the position of the

balloon catheter. After the user ﬁnishes the sketch-

ing process, the application calculates the dilation of

the stent. The difﬁculty to achieve this behavior is to

dilate the stent in the relevant vessel, but not to en-

ter the aneurysm. Since the structure is not differen-

tiated semantically (i.e., in vessels and aneurysms),

the described behavior must be achieved in another

way. To accomplish this, the surrounding region of

the sketched stent is analyzed. The algorithm is de-

scribed in more detail in Figure 11. This method is

more robust according to various input lines. The best

results regarding visual aspects are achieved by draw-

ing a line, which is as close as possible to the center of

the vessel. Inaccurate lines may lead to penetration of

the stent inside the aneurysm. A disadvantage of the

described method is that it depends on four control

points obtained through the start and the end point. If

(a) (b)

(e) (f)

Figure 10: (a) - (f) shows the algorithm to calculate the coil

area. In (a) the physician sketches imprecise over the vessel

wall of the aneurysm. (b) shows the captured sample points

as well as the rays, which are sent in a circular manner from

each sample point. In (c) all rays that collide with the ves-

sel wall are highlighted, from which those with the shortest

distance are chosen (d). The sample points are moved to the

intersection point or remain on their position if no intersec-

tion occurred (e). The adjusted sample points build the new

area for the coil, which lies precisely on the vessel wall.

(a) (b)

(e) (f)

Figure 11: (a) - (f) illustrate the algorithm to calculate the

stent dilation. The user input is illustrated as a sketched

line in (a). After the user ﬁnishes the stent, the normals

of the start and end point are determined (b). The normals

have the length of the vessel width. All four normals are

tested if they intersect the vessel wall. If not, the stent is

discarded. Otherwise, the distance l is determined, which is

the longest length of the normal start point to its intersection

point. Now, for every point of the sketched line, the normals

with length l are determined (c). All of these normals are

tested for intersections with the vessel wall. If they inter-

sect, they are shortened to the intersection point, otherwise

they keep the length l (d). The achieved end points of the

normals are connected (e) and form the border of the stent,

visualized in (f).

not all control points could be determined, e.g., if the

vessel is too wide, not all normals are calculated and

so the stent will not be placed. Similar to the coil-

ing and clipping method, the grid cells under the stent

are marked as occupied and thus, inﬂuence the ﬂuid

simulation.

5.4 Edit, Delete and Copy Objects

The possibility to edit and delete objects such as stents

and coils, is an important aspect regarding the con-

trollability of the application. This is conﬁrmed by

the evaluation (see Section 6.1) in which the partic-

ipants stated that a functionality to delete or edit ob-

jects would be useful. To realize this, it is necessary to

implement a method to select already created objects.

Since a requirement of the application is to control

it with a pen without any further buttons, a suitable

method is necessary. Besides the possibility of ges-

tures or a double tap of the pen, the implemented ap-

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

386

proach is to press and hold the pen on the relevant ob-

ject. Afterwards, the corresponding object is deleted.

The possibility to edit objects, which is currently not

implemented, can be realized with the same approach.

To provide the physician with an easy and fast

possibility to illustrate more treatment options on the

same vessel structures, a copy tool is added to the ap-

plication. It allows to select an area, copy its content

and paste it at another place. With this possibility, the

patient can see different behaviors of the bloodﬂow,

depending on the treatment option. This can help un-

derstanding why a speciﬁc treatment is chosen or why

another is not possible.

5.5 User Interface

The structure of the user interface results from two

considerations:

• The grid used for the ﬂuid simulation is quadratic

and

• adirect input device is used.

The ﬁrst consideration implies that the canvas in

which the user sketches is also quadratic. Through the

horizontal format of current displays this means that

there is potential free space on the sides of the canvas.

This space is used for the menus. In detail, the space

is divided in a left and a right region and used for a se-

mantic differentiation of the functionality. On the left

side, menus and buttons are placed, which are used to

create and manipulate vessels, to sketch treatment op-

tions, and to visualize and control blood ﬂow. On the

right side, there are temporary menus to control simu-

lation parameters such as the number of iterations for

solving or to activate the diffusion process. The sec-

ond consideration (using a direct input device) leads

to the following requirements with respect to interac-

tion. To achieve an easy interaction, all buttons have a

bigger size and there are no sub-menus. Furthermore,

classical WIMP input elements like spin boxes were

omitted, since exact inputs would be hard with, e.g.,

a pen. In Figure 12, a screenshot of the user interface

is shown.

6 EVALUATION

The evaluation is divided into two parts: in the ﬁrst

part, we used qualitative and quantitative methods for

assessing the usability of the prototype. In the second

part, we interviewed a physician to compare the pro-

cedure of typical patient education (with hand drawn

sketches) with the prototype and investigate advan-

tages and disadvantages.

Figure 12: Screenshot of the prototype. Buttons (1-2) are

used to create and edit vessels, (3-4) are used to manipulate

and visualize blood ﬂow, (5-7) are used to sketch treatment

options, (8) is used to select the copy tool, (9) is used to load

a background image to assist the sketching or load vessel

structures out of a monochrome image and (10) is used to

reset the whole canvas. On the right side the functionality

to inﬂuence the ﬂuid simulation in different ways is shown.

6.1 Usability

The qualitative part of the study was performed with

the think aloud method, where the participants com-

ment their activities while solving a problem. It is

helpful to give insights into the misunderstandings of

the participants as well as to understand how the par-

ticipants predict the behavior of the prototype. This

method gives hints for further reﬁnements. The quan-

titative part of the evaluation was conducted with a

questionnaire. The questions are inspired by a ques-

tionnaire for ergonomic principles from ISO 9241-

110 (suitability for learning, suitability for the task,

self-descriptiveness, conformity with user expecta-

tions, controllability, and error tolerance). The single

questions were categorized in the different principles

and could be rated with a 7-point Likert scale.

The evaluation started with a short introduction

of the prototype on a SMARTBoard, a 70” screen

which allows pen interaction. Here, all features were

demonstrated and we asked to think-aloud and noted

the spoken comments of the participants. Initially, the

participants were asked to perform several tasks that

were handed out in written form. For example, they

should draw a vessel with a trifurcation; then, they

should use the cut tool to change the vessel to a bi-

furcation. Furthermore, they were asked to draw an

aneurysm and treat it with the clipping, coiling, and

stenting tool. Finally, they should create and visualize

the blood ﬂow in a speciﬁc direction. Afterwards, the

participants were asked to ﬁll out the questionnaire.

Sketching2DVesselsandVascularDiseaseswithIntegratedBloodFlow

387

+++

-/+

---

Figure 13: This ﬁgure shows the average results of the ques-

tionnaire for each category of the usability principles.

The evaluation was conducted with 14 researchers

with medical visualization knowledge. We had three

female and eleven male participants, aged from 25 to

44 with an average of 31 years. The participants are

experienced computer users with an experience of 20

years on average (minimum: 14, maximum: 30). Ten

participants were experienced with pen interaction. It

took about 15 to 20 minutes to ﬁll out the question-

naire. The statements of the participants are denoted

with [P#].

Think-Aloud Method: Mostly, the participants were

satisﬁed with the prototype: ”it is possible to create

vessels and aneurysms according to my own ideas”

[P13]. Regarding the different tools, the majority of

the participants had no problems using them. For ex-

ample, it was stated that the cut tool ”is more precise

than conventional eraser tools” [P6]. Unfortunately,

the cut tool leads to misunderstandings during the ﬁrst

use. This was caused by different expectations, e.g.,

some participants thought that it can be used as a con-

ventional eraser. After some practice, the functional-

ity was understood and the participants rated this tool

as positive. Another example of a positively rated tool

is the stenting tool. Especially the automatic expand-

ing behavior was noted as useful. In summary, the

participants were satisﬁed with the prototype. Fur-

thermore, they were also pleased with the alignment

of the tools, as it supports the typical workﬂow (gen-

erate vessel, treatment, and visualize blood ﬂow). In

general, they stated that this prototype allows a fast

and easy generation of vessels with simulated blood

ﬂow.

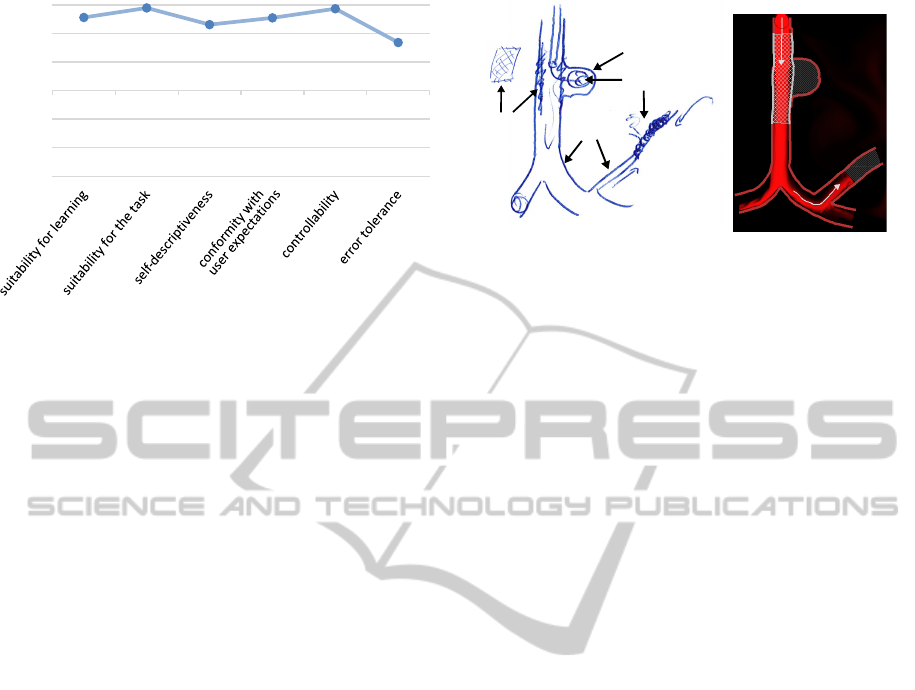
Questionnaire: The results of the questionnaire were

determined by calculating the average of every an-

swer. For this, we assigned the symbols of the 7-Point

Likert scale (- - - to + + +) to the values from -3 to 3.

Figure 13 depicts the average for every category. The

category error tolerance has the lowest rates. Here,

Aneurysm

Vessel

Coil

Stent

(a) (b)

Figure 14: On the left side is the hand sketch of a physi-

cian with additional labels. On the right side are the same

structures made with the application, which the physician

assessed clearer and more understandable.

the users were asked if the effort to correct an inad-

vertently drawn error is signiﬁcantly high. Mostly, the

participants stated that it should be possible to delete

drawn objects and the effort is high to manually cor-

rect them by redrawing. Thus, we added the possibil-

ity to delete drawn objects like stents and coils indi-

vidually, see Section 5.4. However, with an average

of 1.68, this category was rated well. In summary, the

ratings of all categories were positive and the partic-

ipants were satisﬁed with the functional range. For

reﬁnement, we used the results of the evaluation and

improved the prototype according to the suggestions

of the participants.

6.2 Structured Interview

We performed a structured interview of about 20 min-

utes with a physician, which has 12 years of experi-

ence in the ﬁeld of vascular diseases and patient edu-

cation. First, we asked the physician to explain typical

patient education with an example and outline the typ-

ical education procedure. During typical patient edu-

cation, the patient receives textual and image-based

templates with respect to his disease. Additionally,

the physician explains the intervention verbally and

supports this with hand-drawn sketches (see Figure

14). These can help to illustrate speciﬁc medical cases

and answer individual questions from the patient. The

description of the physician revealed the following

disadvantages of the hand-drawn sketches:

• To correct errors, the physician draws over the ex-

isting sketch, which results in a cluttered image.

• The blood ﬂow and the implications of a treatment

are usually not drawn, because it is hard to illus-

trate these and could lead to a confusing image.

• The physician only uses one color to draw all

structures, which makes it difﬁcult to distinguish

between different elements.

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

388

• Some patients have problems to understand the

sketch, because they ﬁnd it difﬁcult to imagine

diseases and treatment options.

After that, we explained the prototype and asked to

perform the patient education again using our appli-

cation. Thereby, we let the physician compare his

hand-drawn images with sketches from the prototype

which showed the following:

• By using different colors, symmetrical, consis-

tent and uniform structures (e.g., for the vessels

or stents), the result is more clear, descriptive and

plastic than the hand sketching, and thereby, the

perception is supported.

• Due to the illustration of blood ﬂow, the ves-

sel structures, the effects of different intervention

methods and possible complications are more un-

derstandable and imaginable.

Furthermore, the physician stated additional advan-

tages of the prototype, e.g., due to the clearer resulting

images, other persons, who were not involved in the

sketching process, are able to understand the sketch.

This is difﬁcult with hand sketches, because of their

cluttering nature. The physician rated the tool as easy

to learn and use, which matches the results of our us-

ability evaluation.

7 CONCLUSIONS AND FUTURE

WORK

This work provided a concept and a prototypical im-

plementation to sketch vessels, vascular diseases, and

treatment methods. It is possible to interactively cre-

ate and manipulate blood ﬂow, which adapts itself in

real time to change the sketch.

The quality and usability of the prototype was

assessed with qualitative and quantitative methods.

The positive feedback of the evaluation indicates that

the proposed concept and prototype are suitable for

sketching vascular structures and treatment options.

The structured interview with the physician revealed

further beneﬁts compared to hand-drawn sketches and

conﬁrmed the idea to improve patient education and

intelligibility by integrating animated blood ﬂow.

A limitation of this work is the representation of

the vessels and blood ﬂow in 2D. The representa-

tion of vessels and ﬂuids in 3D is a challenge with

respect to visualization and interpretation (Lawonn

et al., 2014a). An advantage of the 2D representation

is its easier intelligibility as well as a faster calcula-

tion of details, which is important to achieve a real

time simulation.

For the future, we want to investigate how the de-

scribed concept and prototype can be used for collab-

oration between physicians. This collaboration can

happen at different places where each medical doctor

interacts with an instance of the application. The dif-

ferent instances could be connected and mirror the in-

put from one place to another. Additionally, the com-

munication could be supported with voice chat and

webcams. Another way of collaboration is possible

with only one application, where several physicians

are sketching at the same time in front of a big screen

and discuss a medical case.

Further analysis could investigate the possibility

to lift the whole concept to the third dimension. This

leads to challenges and questions regarding a real time

3D ﬂuid simulation and visualization as well as cre-

ating the vessels. For 3D interaction, there are in-

put and output devices which are more suited than

pen or touch interaction. By lifting the application in

the third dimension, the behavior of blood in vessels

could be simulated more accurately, and thus, make

the application more relevant for scenarios like oper-

ation planning and training.

REFERENCES

Bederson, J. B., Connolly, E. S., Batjer, H. H., Dacey,

R. G., Dion, J. E., Diringer, M. N., Duldner, J. E.,

Harbaugh, R. E., Patel, A. B., and Rosenwasser, R. H.

(1994). Guidelines for the management of aneurys-

mal subarachnoid hemorrhage a statement for health-

care professionals from a special Writing Group of the

Stroke Council, American Heart Association. Stroke,

40(3):994–1025.

Bridson, R. (2008). Fluid Simulation for Computer Graph-

ics. A K Peters/CRC Press.

Butcher, J. C. (1996). A History of Runge-Kutta Methods.

Appl. Numer. Math., 20(3):247–260.

Ciarlet, P., Glowinski, R., and Lions, J. (2011). Numerical

Methods for Non-Newtonian Fluids: Special Volume.

Handbook of Numerical Analysis Handbook of Nu-

merical Analysis. Elsevier.

European Heart Network (2012). European cardiovascu-

lar disease statistics. http://www.ehnheart.org/cvd-

statistics.html. last visited: 18 June 2014.

Ferziger, J. H. and Peri

c, M. (2002). Compressible ﬂow. In

Proc. of Computational Methods for Fluid Dynamics,

pages 309–328. Springer Berlin Heidelberg.

Gasteiger, R. (2014). Visual Exploration of Cardiovascular

Hemodynamics. PhD thesis, Otto-von-Guericke Uni-

versity Magdeburg.

Glaßer, S., Lawonn, K., and Preim, B. (2014). Visualization

of 3D Cluster Results for Medical Tomographic Image

Data. In Proc. of Conference on Computer Graph-

ics Theory and Applications (VISIGRAPP/GRAPP),

pages 169–176.

Sketching2DVesselsandVascularDiseaseswithIntegratedBloodFlow

389

Harris, M. J. (2004). GPU GEMS Chapter 38, Fast Fluid

Dynamics Simulation on the GPU. Pearson Higher

Education.

Heckel, F., Moltz, J. H., Tietjen, C., and Hahn, H. K. (2013).

Sketch-based editing tools for tumour segmentation

in 3d medical images. Computer Graphics Forum,

32(8):144–157.

Herold, J. and Stahovich, T. F. (2012). The 1

; Recognizer:

A Fast, Accurate, and Easy-to-implement Handwrit-

ten Gesture Recognition Technique. In Proc. of the

International Symposium on Sketch-Based Interfaces

and Modeling, SBIM ’12, pages 39–46. Eurographics

Association.

Igarashi, T., Matsuoka, S., Kawachiya, S., and Tanaka, H.

(1997). Interactive beautiﬁcation: A technique for

rapid geometric design. In Proc. of ACM Symposium

on User Interface Software and Technology, pages

105–114.

Jorge, J. and Samavati, F. (2011). Sketch-based Interfaces

and Modeling. Springer London.

Keulers, B. (2008). Computer-based Patient Education: Its

Potential in General and Plastic Surgery. PhD thesis,

University Nijmegen.

uger, J. and Westermann, R. (2003). Linear Algebra Op-

erators for GPU Implementation of Numerical Algo-

rithms. ACM Trans. Graph., 22(3):908–916.

Kutikhin, A., Brusina, E., and Yuzhalin, A. E. (2013).

A Hypothesis of Virus-Driven Atherosclerosis. In

Viruses and Atherosclerosis, volume 4 of Springer-

Briefs in Immunology, pages 1–3. Springer New York.

Lawonn, K., Gasteiger, R., and Preim, B. (2014a). Adaptive

Surface Visualization of Vessels with Animated Blood

Flow. Computer Graphics Forum.

Lawonn, K., Saalfeld, P., and Preim, B. (2014b). Illustra-

tive Visualization of Endoscopic Views. In Bildverar-

beitung f

ur die Medizin (BVM), pages 276–281.

Mendis, S., Puska, P., Norrving, B., Organization, W. H.,

Federation, W. H., and Organization, W. S. (2011).

Global Atlas on Cardiovascular Disease Prevention

and Control. Nonserial Publications Series. World

Health Organization in collaboration with the World

Heart Federation and the World Stroke Organization.

uller, M., Schirm, S., and Teschner, M. (2004). Interac-

tive Blood Simulation for Virtual Surgery Based on

Smoothed Particle Hydrodynamics. Technol. Health

Care, 12(1):25–31.

Naya, F., Contero, M., Aleixos, N., and Company, P. (2007).

ParSketch: A Sketch-based Interface for a 2D Para-

metric Geometry Editor. In Proc. of the 12th Inter-

national Conference on Human-computer Interaction:

Interaction Platforms and Techniques, HCI’07, pages

115–124. Springer-Verlag.

Neugebauer, M., Diehl, V., Skalej, M., and Preim, B.

(2010). Geometric Reconstruction of the Ostium of

Cerebral Aneurysms. In Proc. of VMV 2010 - Vision,

Modeling, Visualization, pages 307–314.

Pihuit, A., Cani, M.-P., and Palombi, O. (2010). Sketch-

based Modeling of Vascular Systems: A First Step

Towards Interactive Teaching of Anatomy. In Proc.

of the Seventh Sketch-Based Interfaces and Modeling

Symposium, SBIM ’10, pages 151–158.

Preim, B. and Dachselt, R. (2015, to appear). Interaktive

Systeme: User Interface Engineering, 3D-Interaktion,

Natural User Interfaces, volume 2. Springer.

Qin, J., Pang, W.-M., Nguyen, B. P., Ni, D., and Chui, C.-K.

(2010). Particle-based Simulation of Blood Flow and

Vessel Wall Interactions in Virtual Surgery. In Proc.

of the Symposium on Information and Communication

Technology, SoICT ’10, pages 128–133.

Stam, J. (1999). Stable ﬂuids. In Proc. of the 26th An-

nual Conference on Computer Graphics and Interac-

tive Techniques, SIGGRAPH ’99, pages 121–128.

Sutherland, I. E. (1963). Sketchpad, A Man-Machine

Graphical Communication System. Outstanding Dis-

sertations in the Computer Sciences. Garland Publish-

ing, New York.

Taubin, G. (1995). Curve and Surface Smoothing Without

Shrinkage. In Proc. of the Fifth International Con-

ference on Computer Vision, ICCV ’95, pages 852–.

IEEE Computer Society.

Teitelbaum, G. P., Higashida, R. T., Halbach, V. V., Larsen,

D. W., McDougall, C. G., Dowd, C. F., and Hieshima,

G. B. (1994). Flow-directed Use of Electrolytically

Detachable Platinum Embolization Coils. Journal

of Vascular and Interventional Radiology, 5(3):453 –

456.

van Dam, A. (1997). Post-WIMP User Interfaces. Commun.

ACM, 40(2):63–67.

Wong, G. K., Tan, H.-B., Kwan, M. C., Ng, R. Y., Yu, S. C.,

Zhu, X.-L., and Poon, W.-S. (2011). Evolution of in-

tracranial aneurysm treatment: From Hunterian liga-

tion to the ﬂow diverter. Surgical Practice, 15(1):16–

20.

Wu, E., Liu, Y., and Liu, X. (2004). An Improved Study

of Real-time Fluid Simulation on GPU: Research Ar-

ticles. Comput. Animat. Virtual Worlds, 15(3-4):139–

146.

Xu, X., Liu, W., Jin, X., and A, Z. S. (2002). Sketch-based

User Interface for Creative Tasks. In Proc. of 5th Asia

Paciﬁc Conference on Computer Human Interaction,

pages 560–570.

Zhu, B., Iwata, M., Haraguchi, R., Ashihara, T., Umetani,

N., Igarashi, T., and Nakazawa, K. (2011). Sketch-

based Dynamic Illustration of Fluid Systems. In Proc.

of the 2011 SIGGRAPH Asia Conference, SA ’11,

pages 134:1–134:8. ACM.

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

390