
Thrombophilia Screening
An Artificial Neural Network Approach
João Vilhena
1
, M. Rosário Martins
2
, Henrique Vicente
3
, Luís Nelas
4
,
José Machado
5
and José Neves
5
1
Departamento de Química, Escola de Ciências e Tecnologia, Universidade de Évora, Évora, Portugal,
2
Departamento de Química, Instituto de Ciências Agrárias e Ambientais Mediterrânicas, Escola de Ciências e Tecnologia,
Universidade de Évora, Évora, Portugal
3
Departamento De Química, Centro De Química de Évora, Escola de Ciências e Tecnologia, Universidade de Évora,
Évora, Portugal
4
Radiconsult.com – Consultoria Informática e Radiologia Lda, Braga, Portugal
5
Cctc, Universidade do Minho, Braga, Portugal
Keywords: Thrombophilia Risk Evaluation, Knowledge Representation and Reasoning, Logic Programming, Artificial
Neural Networks.
Abstract: Thrombotic disorders have severe consequences for the patients and for the society in general, being one of
the main causes of death. These facts reveal that it is extremely important to be preventive; being aware of
how probable is to have that kind of syndrome. Indeed, this work will focus on the development of a
decision support system that will cater for an individual risk evaluation with respect to the surge of
thrombotic complaints. The Knowledge Representation and Reasoning procedures used will be based on an
extension to the Logic Programming language, allowing the handling of incomplete and/or default data. The
computational framework in place will be centered on Artificial Neural Networks.
1 INTRODUCTION
Thrombophilia or Venous ThromboEmbolism (VTE)
may be defined as an increased tendency towards
hypercoagulability and venous thrombosis, i.e., it refers
to a predisposition to thromboembolism (Favaloro et
al. 2009). Thrombophilia is a common clinical condition
with high morbidity and mortality, comprising Deep-
-Vein Thrombosis (DVT) and Pulmonary Embolism
(PE) (Cohen et al. 2007). The incidence of VTE is
estimated at 56-160 per 100,000 people/year (East
and Wakefield, 2010). VTE is a multifactorial disease
and these risks are generally distinguished as either
heritable or acquired, although sometimes this distinc-
tion is unclear (Rosendaal, 1999; Favaloro et al., 2009).
Venous thrombosis could be correlated with
some genetic defects, namely mutations that result in
deficiency of natural coagulation inhibitors, as well as
mutations with increased level/function of coagulation
factors (Reitsma and Rosendaal, 2007). Inherited risk
factors include deficiencies/defects in natural
anticoagulants, such as antithrombin, protein C and
protein S (Mondal et al. 2010; Cafola et al., 2011),
and genetic polymorphisms such as prothrombin
G20210A and factor V Leiden (Reitsma and
Rosendaal, 2007), that lead to a condition designated
as activated protein C resistance (Agrawal et al.
2009). Inherited AntiThrombin (AT) deficiency is an
uncommon autosomal dominant disorder. Most cases
remain heterozygous. Homozygosity for AT
deficiency is rare and is almost always fatal in utero.
Protein C (PC) deficiency is an autosomal dominant
inherited disorder associated with spontaneous and
recurrent thrombotic events. Patients with protein C
and S deficiency are at increased risk for venous
thromboembolic disease, occasional arterial
thrombosis (Mondal et al., 2010). Factor V Leiden
(FVL) increases the risk of thrombosis in PC-deficient
type I families (Cafolla et al. 2011). Other mutations
or polymorphisms associated with increased risk of
thrombosis are methylenetetra-hydrofolate reductase
677C (Rosendaal, 1999).
Acquired thrombophilia risk factors include
antiphospholipid antibodies, detected as lupus
anticoagulants and/or anticardiolipin antibodies and/or
anti-beta-2-glycoprotein-I antibodies. Environmental
51
Vilhena J., Rosário Martins M., Vicente H., Nelas L., Machado J. and Neves J..
Thrombophilia Screening - An Artificial Neural Network Approach.
DOI: 10.5220/0005197500510059
In Proceedings of the International Conference on Health Informatics (HEALTHINF-2015), pages 51-59
ISBN: 978-989-758-068-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

or acquired thrombophilia risk factors include also
previous history or concomitant disease, age,
immobility, surgery, obesity, smoke, cancer hormone
use, and pregnancy or postpartum states (Rosendaal,
1999; Heit et al. 2002; Goldhaber, 2010).
This work reports the founding of a computational
framework that uses knowledge representation and
reasoning techniques to set the structure of the
information and the associate inference mechanisms.
We will centre on a Logic Programming (LP) based
approach to knowledge representation and reasoning
(Neves, 1984; Neves et al. 2007), complemented
with a computational framework based on Artificial
Neural Networks (ANNs) (Cortez et al., 2004).
ANNs are computational tools which attempt to
simulate the architecture and internal operational
features of the human brain and nervous system.
ANNs can be defined as a connected structure of
basic computation units, called artificial neurons or
nodes, with learning capabilities. Multilayered feed-
-forward neural network architecture is one of the
most popular ANNs structure often used for prediction
as well as for classification. This architecture is
molded on three or more layers of artificial neurons,
including an input layer, an output layer and a
number of hidden layers with a certain number of
active neurons connected by modifiable weights. In
addition, there is also a bias, which is only connected
to neurons in the hidden and output layers. The
number of nodes in the input layer sets the number
of independent variables, and the number of nodes in
output layer denotes the number of dependent
variables (Haykin, 2008).
Several studies have shown how ANNs could be
successfully used to model data and capture complex
relationships between inputs and outputs (Caldeira et
al., 2011; Vicente et al., 2012; Salvador et al., 2013).
With this paper we make a start on the development
of a diagnosis assistance system for thrombophilia
risk detection using LP complemented with ANNs.
2 RELATED WORK
Many studies presenting the concept of uncertainty
and/or ”imperfect data” like Hunter (1999) and
Zhang and Goodchild (2002) shows that there is an
emergent interest in the problem of uncertainty as
compared to accuracy or error in data. The notion of
uncertainty is broader than error or accuracy and
includes these more restricted concepts. While
accuracy is the closeness of measurements or
computations to their “true” value or some value
agreed to be the “truth”, uncertainty can be
considered any aspect of the data that results in less
than perfect knowledge about the phenomena being
studied (Hong et al., 2014). On the one hand, it is
consensual that when the data are uncertain, it is need
a different representation and uncertainty can be
reduced by “acquiring additional information or
improving the quality of the information available”
(Hunter, 1999), i.e., in almost all decisions that one
may take, the information is not always exact, but
indeed imperfect, in the sense that we handle
estimated values, probabilistic measures, or degrees
of uncertainty. On the other hand, knowledge and
belief are generally incomplete, contradictory, or even
error sensitive, being desirable to use formal tools to
deal with the problems that arise from the use of
partial, contradictory, ambiguous, imperfect, nebulous,
or missing information (Neves, 1984; Neves et al.,
2007; Hong et al., 2014). Some general models have
been presented where uncertainty is associated to the
application of Probability Theory (Li et al., 2007),
Fuzzy Set Theory (Schneider, 1999), Similarities
(Freire et al., 2002; Liao, 2005). Other approaches
for knowledge representation and reasoning have
been proposed using the Logic Programming
paradigm, namely in the area of Model Theory
(Gelfond and Lifschitz, 1988; Kakas et al., 1998;
Pereira and Anh, 2009) and Proof Theory (Neves,
1984; Neves et al., 2007). The evaluation of knowledge
that stems out from logic programs becomes a point
of research. In this sense, the evaluation of
knowledge that stems out from logic programs
becomes a point of research. Lucas (2003) and
Hommerson (2008) work is a good example of
quality evaluation using logic. The author used
abduction and temporal logic for quality checking of
medical guidelines, proposing a method to diagnose
potential problems in a guideline, regarding the
fulfilment of general medical quality criteria at a
meta-level characterization. They explored an
approach, which uses a relational translation to map
the temporal logic formulas to first-order logic and a
resolution-based theorem prover (Schneider, 1999).
In another research line, the Quality-of-Information
concept (QoI) (Lucas, 2003; Machado et al., 2010)
demonstrated their applicability in dynamic
environments and for decision-making purposes.
The objective is to built a quantification process of
the QoI and an assessment of the argument values of
a given predicate with relation to their domains (here
understood as Degree-of-Confidence (DoC)), that
stems from a logic program or theory during the
evolution process when searching for solutions in
order to solve a problem in environments with default
data. Our main contribution relies on the fact that at
HEALTHINF2015-InternationalConferenceonHealthInformatics
52

the end, the extensions of the predicates that make
the universe of discourse are given in terms of DoCs
predicates that stand for one’s confidence that the
predicates arguments values fit into their respective
domains. This approach potentiate the use of diverse
computational paradigms, like Case Based Reasoning
(Carneiro et al., 2013), Artificial Neural Networks
(Vicente et al., 2012; Salvador et al., 2013), Particle
Swarm (Mendes et al., 2004), just to name a few. It
also incapsulates, in itself, a new vision of Multi-
value Logics, once a proof of a theorem in a
conventional way, is evaluated to the interval [0,1].
Indeed, some interesting results have been obtained,
namely in the fields of Coronary Risk Evaluation
(Rodrigues et al., 2014), Hyperactivity Disorder
(Pereira et al., 2014) and Length of Hospital Stay
(Abelha et al., 2014) among others.
3 KNOWLEDGE
REPRESENTATION AND
REASONING
We follow the proof theoretical approach and an
extension to the Logic Programming (LP) language,
to knowledge representations and reasoning. An
Extended Logic Program (ELP) is a finite set of
clauses in the form:
←
,⋯,
,
,⋯,
1
?
,⋯,
,
,⋯,
,0
2
where ? is a domain atom denoting falsity, the p
i
, q
j
,
and p are classical ground literals, i.e., either positive
atoms or atoms preceded by the classical negation
sign
(Neves, 1984). Under this representation
formalism, every program is associated with a set of
abducibles (Kakas et al. 1998; Pereira and Anh,
2009) given here in the form of exceptions to the
extensions of the predicates that make the program.
With respect to the problem of knowledge
representation and reasoning in LP, a measure of the
Quality-of-Information (QoI) of such programs has
been object of some work with promising results
(Lucas, 2003; Machado et al. 2010). The QoI with
respect to the extension of a predicate i will be given
by a truth-value in the interval [0,1], i.e., if the
information is known (positive) or false (negative)
the QoI for the extension of predicate
i
is 1. For
situations where the information is unknown, the
QoI is given by:
→
1
0
≫0
3
where N denotes the cardinality of the set of terms or
clauses of the extension of predicate
i
that stand for
the incompleteness under consideration. For
situations where the extension of predicate
i
is
unknown but can be taken from a set of values, the
QoI is given by:
1
4
where Card denotes the cardinality of the abducibles
set for i, if the abducibles set is disjoint. If the
abducibles set is not disjoint, the QoI is given by:
1
⋯
5
where
is a card-combination subset, with Card
elements. The next element of the model to be
considered is the relative importance that a predicate
assigns to each of its attributes under observation,
i.e.,
, which stands for the relevance of attribute k
in the extension of
. It is also assumed that
the weights of all the attribute predicates are
normalized, i.e.:
1,∀
6
where
denotes the universal quantifier. It is now
possible to define a predicate’s scoring function
so that, for a value
,⋯,
, defined in
terms of the attributes of
, one may have:
⁄
7
allowing one to set:
,⋯,
∷
8
It is now possible to engender the universe of
discourse, according to the information given in the
logic programs that endorse the information about
the problem under consideration, according to
productions of the type:
,⋯,
∷
∷
9
where
⋃
and m stand, respectively, for “set union”
and the cardinality of the extension of predicate
i
. On
the other hand, DoC
i
denotes one’s confidence on the
attribute`s values of a particular term of the extension
of predicate
i
, whose evaluation will be illustrated
below. In order to advance with a broad-spectrum,
let us suppose that the Universe of Discourse is
described by the extension of the predicates:
⋯
,
⋯
,⋯,
⋯
0
10
Assuming we have a clause that is mapped into a
case, that clause has as argument all the attributes
that make the case. The argument values may be of
ThrombophiliaScreening-AnArtificialNeuralNetworkApproach
53
the type unknown or members of a set, may be in the
scope of a given interval or may qualify a particular
observation. Let us consider the following clause
where the second argument value may fit into the
interval [3,5] with a domain of [0,8], the value of the
third argument is unknown, which is represented by
the symbol
, with a domain that ranges in the
interval [5,15], and the first argument stands for
itself, with a domain that ranges in the interval [0,3].
Let us consider that the case data is given by the
extension of predicate
, given in the form:
:
,
,
→0,1
11
where “{” and “}” is one´s notation for sets, where
“0” and “1” denote, respectively, the truth values
“false” and “true”. One may have:
{
,
,
⟵
,
,
2,
3,5
,
`
,
,
∷1∷
0,3
0,8
5,15
`
,
,
…
}
Once the clauses or terms of the extension of the
predicate are established, the next step is to
transform all the arguments, of each clause, into
continuous intervals. In this phase, it is essential to
consider the domain of the arguments. As the third
argument is unknown, its interval will cover all the
possibilities of the domain. The first argument
speaks for itself. Therefore, one may have:
{
,
,
⟵
,
,
2,2
,
3,5
,
5,15
`
,
,
∷1∷
0,3
0,8
5,15
`
,
,
…
}
Now, one is in position to calculate the Degree of
Confidence for each attribute that makes the term´s
arguments (e.g. for attribute two it denotes one’s
confidence that the attribute under consideration fits
into the interval [3,5]). Next, we set the boundaries of
the arguments intervals to be fitted in the interval [0,1]
according to the normalization procedure given in
the procedural form by
/
,
where the
stand for themselves.
{
,
,
⟵
,
,
20
30
,
20
30
,
30
80
,
50
80
,
55
155
,
155
155
0.67,0.67
,
0.375,0.625
,
0,1
`
,
,
∷1∷
0,1
0,1
0,1
`
,
,
…
}
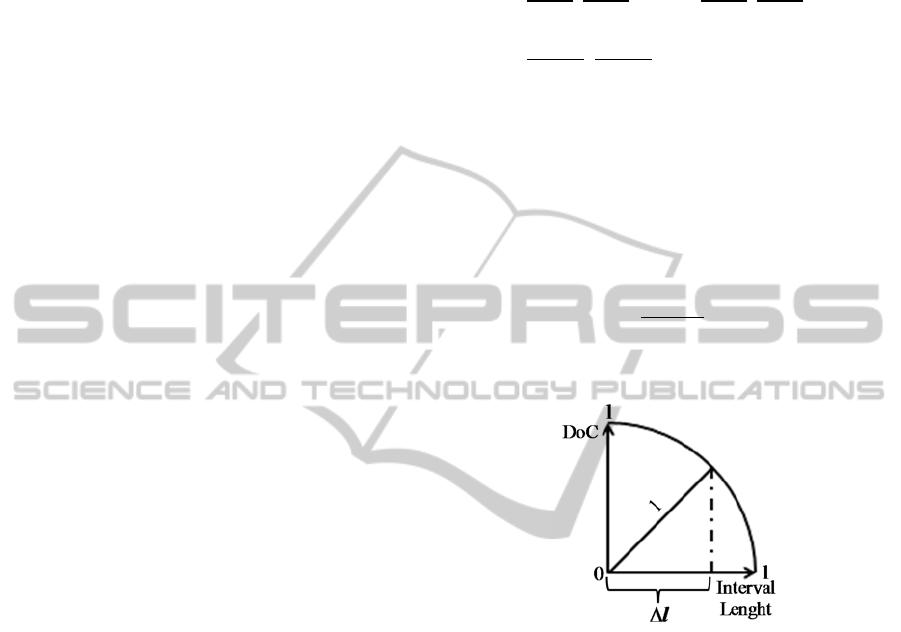
The Degree of Confidence (DoC) is evaluated using
the equation
√
1∆
, as it is illustrated in
Figure 1, where ∆ stands for the length of the
argument´s intervals, once normalized.
Figure 1: Evaluation of the Degree of Confidence.
{
,
,
⟵
,
,
1,0.97,0
`
,
,
∷1∷0.66
0.67,0.67
0.375,0.675
0,1
`
,
,
0,1
0,1
0,1
`
,
,
…
}
4 A CASE STUDY
In order to exemplify the applicability of our model,
HEALTHINF2015-InternationalConferenceonHealthInformatics
54

we will look at the relational database model, since
it provides a basic framework that fits into our
expectations (Liu and Sun, 2007), and is understood
as the genesis of the LP approach to Knowledge
Representation and Reasoning (Neves, 1984).
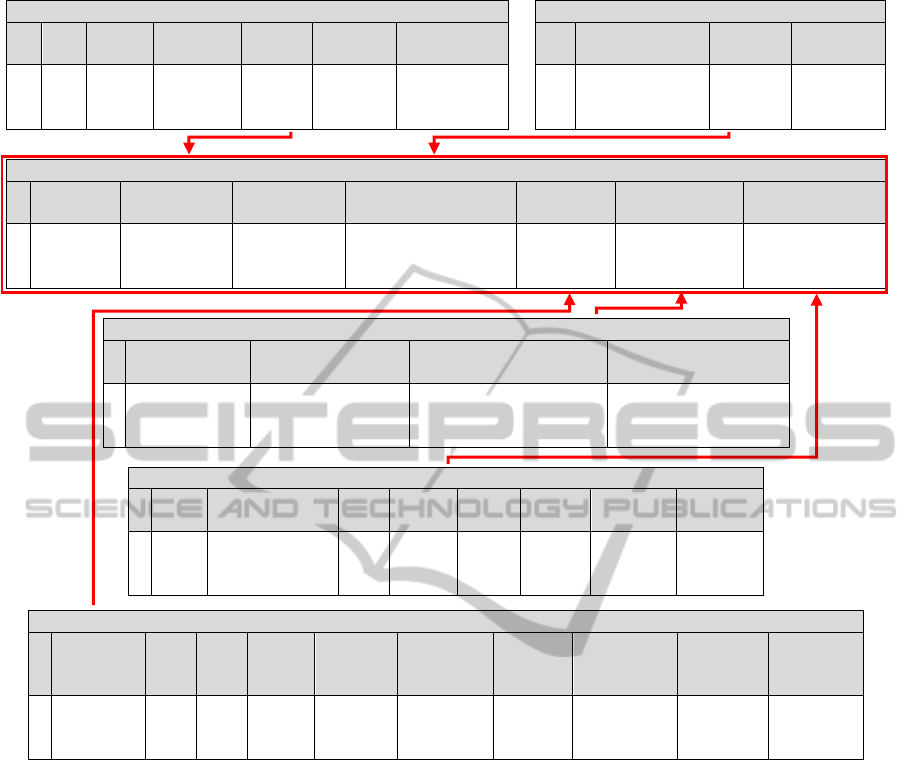
As a case study, consider the scenario where a
relational database is given in terms of the extensions
of the relations depicted in Figure 2, which stands for
a situation where one has to manage information
about thrombophilia risk detection. Under this scenario
some incomplete and/or default data is also available.
For instance, in the Venous Thromboembolism
Predisposing database, the Body Mass Index in case
1 is unknown, while the Blood Group Predisposition
ranges in the interval [0.08,0.14].
In this study, to ensure the scalability of the
method, the extension of the relational database
includes the features, obtained by both objective and
subjective methods, which were pointed relevant by
the research done so far. Thus, physicians will fill
the tables that link to the Venous Thromboembolism
Predisposing one while executing the health check.
The clinics may populate some issues, others may be
perceived by additional exams (e.g. this happens
with the issues of the Thrombophilia Genic Factors
(Major) and Molecular Analysis of Mutations/
/Polymorphisms tables).
The Body Mass Index (BMI) is evaluated using
the equation
⁄
(WHO,
2014). In the Venous Thromboembolism Predisposing
database, the domain of Body Mass Index column is
in the range [0,3], wherein 0 (zero) denotes BMI < 25;
1 (one) stands for a BMI ranging in interval [25,30[;
and 2 (two) denotes a BMI ≥ 30. Age/Heredity
Predisposition column is based on Table 1, adapted
from Sacher (1999). These predisposition values are
clustered by age group and by heredity. Thus, the
value of this parameter for the [0,40[ age group is in
the range [0,0.5] for general population, and in the
range [0.05,5] for population with genetic antecedents.
The blood group predisposition parameter, which is
also evidenced in the Thrombosis Predisposing
database, is based on Table 2 adapted from Spiezia
(Spiezia et al. 2013). Its values are in the range
[0.08,0.14] for O blood group, and in the range
[0.18,0.30] for non-O blood groups.
Table 1: Age/Heredity predisposition (‰), adapted from
(Sacher, 1999).
Age Group General Population Genetic Predisposition
< 40 [0,0.05] [0.05,0.5]
[40,75] [0.05,0.5] [0.5,5]
>75 0.5 5
Table 2: Blood group predisposition (‰), adapted from
(Spiezia et al. 2013).
Blood Group Predisposition
O [0.08,0.14]
non-O [0.18,0.30]
The values presented in the remaining columns are
the sum of the respective databases, ranging between
[0,3], [0,10], [0,4] and [0,8], respectively for
Thrombophilia Genic Factor, Thrombotic Risk
Factors, Mutations/Polymorphisms and Earlier
Secondary Factors columns. Then, one may have:
:
,
,
,
,
,
,
→0,1
where thromb stands for the predicate venous
thromboembolism predisposing, 0 (zero) and 1 (one)
denote, respectively, the truth values false and true.
It is now possible to give the extension of the
predicate thromb, in the form:
{
,,,,,,
←
,,,,,,
,0.5,
0.08,0.14
,0,0,0,2
`
∷1∷
0,3
0,5
0.08,0.30
0,3
0,10
0,4
0,8
`
…
}
In this program, the first clause denotes the closure
of predicate thromb. The next clause corresponds to
patient 1, taken from the extension of the venous
thromboembolism predisposing relation presented in
Figure 2. Moving on, the next step is to transform all
the argument values into continuous intervals and
then normalize the predicate´s arguments in order to
obtain the Degree of Confidence of the thromb
predicate. One may have:
{
,,,,,,
←
,,,,,,
0,3
,
0.5,0.5
,
0.08,0.14
,
0,0
,
0,0
,
0,0
,
2,2
`
∷1∷
0,3
0,5
0.08,0.30
0,3
0,10
0,4
0,8
`
…
}
ThrombophiliaScreening-AnArtificialNeuralNetworkApproach
55
Personal Information
Thrombophilia Genic Factors (Major)
# Age
Gender
Body Mass
(Kg)
Height
(m)
Blood
Group
Strong Family
Story
# Antithrombin III Protein C Protein S
1 77 M 88
O
0
1 0 0 0
n 29 F 65 1,68 A 1 n 0 1 1
Venous Thromboembolism Predisposing
#
Body Mass
Index
Age/Heredity
Predisposition
Blood Group
Predisposition
Thrombophilia Genic
Factors
Thrombotic
Risk Factors
Mutations/
/Polymorphisms
Earlier Secondary
Factors
1
0.5 [0.08,0.14] 0 0 0 2
n 0 [0.05,0.5] [0.18,0.30] 2 2
1
Molecular Analysis of Mutations/Polymorphisms
#
Factor V Leiden
mutation
Prothrombin 20210a
mutation G/A
Methylenetetrahydrofolate
reductase 677C/T
PAI-1 5G/4G Gene
Polymorphism 675G/A
1 0 0 0 0
n
Earlier Secondary Factors Predisposing to Thrombosis
# Smoke
Immobilization/
/Hospitalization
Air
travel
Surgery
Liver
disease
Infection
Oncologic
pathology
Pregnancy
1 1 0 1 0 0 0 0 0
n 0 0 0 0 0 0 0 1
Thrombotic Risk Factors
# Prothrombin
Factor
VII
Factor
VIII
Factor V
Leiden
Fibrinogen Plasminogen
Heparin
cofactor II
Homocysteine
Phopholipid
Antibodies
Previous
Venous
Thrombosis
1 0 0 0 0 0 0 0 0 0 0
n 0 0 1 0 1 0 0 0 0 0
Figure 2: Extension of the Relational Database model. In Molecular Analysis of Mutations/Polymorphisms and Earlier
Secondary Factors Predisposing to Thrombosis databases, 0 (zero) denotes absence and 1 (one) denotes presence. In
Thrombophilia Genic Factors (Major) database, 0 (zero) and 1 (one) denotes, respectively, functional and non-functional
values. In the first eight columns of the Thrombotic Risk Factors database, 0 (zero) and 1 (one) denotes, respectively,
normal and increased values, while in remaining columns denotes, respectively, absence and presence.
The logic program referred to above, is now
presented in the form:
{
,,,,,,
←
,,,,,,
0,1,0.96,1,1,1,1
`
∷1∷0.85
0,1
0.1,0.1
0,0.27
0,0
0,0
0,0
0.25,0.25
`
0,1
0,1
0,1
0,1
0,1
0,1
0,1
`
…
}
where its terms make the training and test sets of the
Artificial Neural Network given in Figure 3.
5 ARTIFICIAL NEURAL
NETWORKS
ANNs could be used to model data and capture
complex relationships. As an example, let us
consider the last case presented in Figure 2, where
one may have a situation in which a venous
thromboembolism predisposition assessment is
needed, given in the form:
HEALTHINF2015-InternationalConferenceonHealthInformatics
56

{
,,,,,,
←
,,,,,,
0,
0.05,0.5
,
0.18,0.30
,2,2,,1
`
∷1∷
0,3
0,5
0.08,0,30
0,3
0,10
0,4
0,8
`
0,0
,
0.05,0.5
,
0.18,0.30
,
2,2
,
2,2
,
0,4
,
1,1
`
∷1∷
0,3
0,5
0.08,0,30
0,3
0,10
0,4
0,8
`
0,0
,
0.01,0.1
,
0.45,1
,
0.67,0.67
,
0.2,0.2
,
0,1
,
0,125,0.125
`
∷1∷
0,1
0,1
0,1
0,1
0,1
0,1
0,1
`
1,0.9960.838,1,1,0,1
`
∷1∷0.83
0,0
0.01,0.1
0.45,1
0.67,0.67
0.2,0.2
0,1
0.125,0.125
`
0,1
0,1
0,1
0,1
0,1
0,1
0,1
`
}
In Figure 3 it is shown how the normalized values of
the interval boundaries and their DoC and QoI
values work as inputs to the ANN. The output
translates the venous thromboembolism predisposition
risk, and DoC the confidence that one has on such a
happening. In addition, it also contributes to build a
database of study cases that may be used to train and
test the ANNs.
In this study were considered 300 patients from
the south of Portugal, with an age average of 52
years, ranging from 27 to 82 years old. The gender
distribution was 46% and 54% for male and female,
respectively. To ensure statistical significance of the
attained results, 20 runs were applied in all tests. In
each simulation, the available data were randomly
divided into two mutually exclusive partitions, i.e.,
the training set with two-thirds of the available data
and, the test set with the remaining one-third of the
cases. The back propagation algorithm was used in
the learning process of the ANN. As the output
function in the pre-processing layer it was used the
identity one. In the others layers we used the
sigmoid function.
The model accuracy was 97.6% for the training
set (203 correctly classified in 208) and 93.5% for
test set (86 correctly classified in 92).
ThrombophiliaScreening-AnArtificialNeuralNetworkApproach
57

6 CONCLUSIONS AND FUTURE
WORK
Diagnosing venous thromboembolism predisposition
risk has shown to be a hard task, as the parameters
that cause the disorder are not fully represented by
objective data. Therefore, it is mandatory to consider
many different conditions with intricate relations
among them. These characteristics put this problem
into the area of problems that may be tackled by
Artificial Intelligence based methodologies and
techniques to problem solving.
Figure 3: The Artificial Neural Network topology.
In this work it is presented the founding of a
computational framework that uses powerful
knowledge representation and reasoning techniques
to set the structure of the information and the
associate inference mechanisms based in ANNs.
This finding has several reasons, namely:
• Data is not equal to information;
• The translation of the raw measurements into
interpretable and actionable read-outs is
challenging; and
• Read-outs can deliver markers and targets
candidates without pre-conception, i.e., knowing
how personal conditions and risk factors may
affect the thrombotic predisposition.
This methodology for problem solving and the
computational techniques used have the advantage
of allowing one to consider incomplete and/or
unknown information, a marker that is not present in
existing systems. Future work may recommend that
the same problem must be approached using others
computational frameworks like Case Based
Reasoning (Carneiro et al. 2013), Genetic
Programming (Neves et al., 2007) or Particle Swarm
(Mendes et al. 2004), just to name a few.
ACKNOWLEDGEMENTS
This work is funded by National Funds through the
FCT – Fundação para a Ciência e a Tecnologia
(Portuguese Foundation for Science and Technology)
within projects PEst-OE/EEI/UI0752/2014 and
PEst-OE/QUI/UI0619/2012.
REFERENCES
Abelha, V., Vicente, H., Machado, J., Neves, J., 2014. An
assessment on the length of hospital stay through artificial
neural networks. In 9th International Conference on
Knowledge, Information and Creativity Support Systems
(to appear).
Agrawal, N., Kumar, S., Puneet, Khanna, R., Shukla, J.,
Khanna, A., 2009. Activated Protein C Resistance in
Deep Venous Thrombosis. Annals of Vascular Surgery,
23: 364-366.
Cafolla, A., D’Andrea, G., Baldacci, E., Margaglione, M.,
Mazzucconi, M.G., Foa, R., 2011. Hereditary protein
C deficiency and thrombosis risk: genotype and
phenotype relation in a large Italian family. European
Journal of Haematology, 88: 336-339.
Caldeira, A.T., Arteiro, J., Roseiro, J. Neves, J., Vicente,
H., 2011. An Artificial Intelligence Approach to
Bacillus amyloliquefaciens CCMI 1051 Cultures:
Application to the Production of Antifungal
Compounds. Bioresource Technology, 102: 1496-1502.
Carneiro, D., Novais, P., Andrade, F., Zeleznikow, J.,
Neves, J., 2013. Using Case-Based Reasoning and
Principled Negotiation to provide decision support for
dispute resolution. Knowledge and Information Systems,
36: 789-826.
Cohen, A., Agnelli, G., Anderson, F., Arcelus, J., Bergqvist
D., Brecht, J., Greer, I., Heit, J., Hutchinson, J., Kakkar,
A., Mottier, D., Oger, E., Samama, M., Spannagl, M.,
2007. Venous thromboembolism (VTE) in Europe.
The number of VTE events and associated morbidity and
mortality. Thrombosis and Haemostasis, 98: 756-764.
Cortez, P., Rocha, M., Neves, J., 2004. Evolving Time Series
Forecasting ARMA Models. Journal of Heuristics, 10:
415-429.
East, A., Wakefield, T., 2010. What is the optimal duration
Pre-processing
Layer
Input
Layer
Hidden
Layer
Output
Layer
0
0
1
BMI
1
1
0.45
0.838
BP
1
0.125
0.125
1
ES
1
BiasBias
0.83
thromb
DoC
No
thrombotic
predisposing
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
HEALTHINF2015-InternationalConferenceonHealthInformatics
58

of treatment for DVT? An update on evidence-based
medicine of treatment for DVT. Seminars in Vascular
Surgery, 23: 182-191.
Favaloro, E., McDonald, D., Lippi, G., 2009. Laboratory
investigations of thrombophilia: the good, the bad and
the ugly. Seminars in Thrombosis and Hemostasis, 35:
695-710.
Freire, L., Roche, A., Mangin, J-F., 2002. What is the best
similarity measure for motion correction in fMRI time
series?. IEEE Transactions on Medical Imaging, 21:
470-484.
Gelfond M., Lifschitz V., 1988. The stable model
semantics for logic programming. In Logic
Programming – Proceedings of the Fifth International
Conference and Symposium, 1070-1080.
Goldhaber, S., 2010. Risk factors for venous
thromboembolism. Journal of the American College of
Cardiology, 56: 1-7.
Haykin, S., 2008. Neural Networks and Learning Machines.
New York: Prentice Hall.
Heit, J., O'Fallon, W., Petterson, T., Lohse, C., Silverstein,
M., Mohr, D., Melton III, L., 2002. Relative impact of
risk factors for deep vein thrombosis and pulmonary
embolism: a population-based study. Archives of
Internal Medicine, 162: 1245-1248.
Hong, T., Hart, K., Soh, L-K, Samal, A., 2014. Using
spatial data support for reducing uncertainty in
geospatial applications. Geoinformatica, 18: 63-92.
Kakas A., Kowalski R. & Toni F., 1998. The role of
abduction in logic programming. In Handbook of
Logic in Artificial Intelligence and Logic
Programming, Volume 5, 235-324.
Hommerson, A., P. Lucas, van Bommel, P., 2008.
Checking the quality of clinical guidelines using
automated reasoning tools. Theory and Practice of
Logic Program, 8: 611-641.
Hunter, G., 1999. Managing uncertainty in GIS. In
Geographical Information Systems, New York: J.
Wiley & Sons, 633-641.
Li, R., Bhanu, B., Ravishankar, C., Kurth, M., Ni, J., 2007.
Uncertain spatial data handling: Modeling, indexing
and query. Computers & Geosciences, 33: 42-61.
Liao, T., 2005. Clustering of time series data - a survey.
Pattern Recognition, 38: 1857-1874.
Liu, Y., Sun, M., 2007. Fuzzy optimization BP neural
network model for pavement performance assessment.
In 2007 IEEE international conference on grey systems
and intelligent services, Nanjing, China, 18-20.
Lucas P., 2003. Quality checking of medical guidelines
through logical abduction. In Proceedings of AI-2003,
Springer: London, 309-321.
Machado J., Abelha A., Novais P., Neves J., 2010. Quality of
service in healthcare units. International Journal of Com-
puter Aided Engineering and Technology, 2: 436-449.
Mendes, R., Kennedy, J., Neves, J., 2004. The Fully Informed
Particle Swarm: Simpler, Maybe Better. IEEE Trans-
actions on Evolutionary Computation, 8: 204-210.
Mondal, R., Nandi, M., Dhibar, T., 2010. Protein C and
Protein S Deficiency Presenting as Deep Venous
Thrombosis. Indian Pediatrics, 47:188-189.
Neves J., 1984. A logic interpreter to handle time and
negation in logic data bases. In Proceedings of the
1984 annual conference of the ACM on the fifth
generation challenge, 50-54.
Neves J., Machado J., Analide C., Abelha A., Brito L.,
2007. The halt condition in genetic programming. In
Progress in Artificial Intelligence – Lecture Notes in
Computer Science, Volume 4874, 160-169.
Pereira L. Anh H., 2009. Evolution prospection. In New
Advances in Intelligent Decision Technologies – Results
of the First KES International Symposium IDT, 51-64.
Pereira, S., Gomes, S., Vicente, H., Ribeiro, J., Abelha, A.,
Novais, P., Machado, J., Neves, J., 2014. An Artificial
Neuronal Network Approach to Diagnosis of Attention
Deficit Hyperactivity Disorder. In Proceedings of 2014
IEEE International Conference on Imaging Systems and
Techniques (IST 2014), Institute of Electrical and
Electronics Engineers, Inc.: New Jersey, 410-415.
Reitsma, P., Rosendaal, F., 2007. Past and future of genetic
research in thrombosis. Journal of Thrombosis and
Haemostasis, 5: 264-269.
Rodrigues, B., Gomes, S., Vicente, H., Abelha, A., Novais, P.,
Machado, J., Neves, J., 2014. Systematic coronary risk
evaluation through artificial neural networks based
systems. In 27th International Conference on Computer
Applications in Industry and Engineering (to appear).
Rosendaal, F., 1999. Venous thrombosis: a multicausal
disease. Lancet, 353: 1167-1173.
Sacher, R. A. 1999. Thrombophilia: a Genetic Predisposition
to Thrombosis. Transactions of the American Clinical
and Climatological Association, 110: 51-61.
Salvador, C., Martins, M.R., Vicente, H., Neves, J.,
Arteiro J., Caldeira, A.T., 2013. Modelling Molecular
and Inorganic Data of Amanita ponderosa Mushrooms
using Artificial Neural Networks. Agroforestry Systems,
87: 295-302.
Schneider, M., 1999. Uncertainty management for spatial
data in databases: Fuzzy spatial data types. In Lecture
Notes in Computer Science, Volume 1651, 330-351.
Spiezia, L., Campello, E., Bom, M., Tison, T., Milan, M.,
Simioni, P., Prandoni, P., 2013. ABO blood groups and
the risk of venous thrombosis in patients with inherited
thrombophilia. Blood Transfusion, 11:250-253.
Vicente, H., Dias, S., Fernandes, A., Abelha, A.,
Machado, J., Neves, J., 2012. Prediction of the Quality
of Public Water Supply using Artificial Neural
Networks. Journal of Water Supply: Research and
Technology – AQUA, 61: 446-459.
WHO, 2014. Obesity and overweight. Fact Sheet Number
311, World Health Organization. Accessed August 10,
2014.
Zhang, J., Goodchild, M., 2002. Uncertainty in geographical
information. New York: CRC press.
ThrombophiliaScreening-AnArtificialNeuralNetworkApproach
59
