Coalition Formation for Simulating and Analyzing Iterative Prisoner’s

Dilemma

Udara Weerakoon

Computer Science Department, Utah State University, Logan, Utah, U.S.A.

Keywords:

Spatial Prisoners Dilemma, Imitator Dynamics, Memetic, Coalition Formation, Game Theory.

Abstract:

In this paper, we analyze the strictly competitive iterative version of the non-zero-sum two player game, the

Prisoner’s Dilemma. This was accomplished by simulating the players in a memetic framework. Our pri-

mary motivation involves solving the tragedy of the commons problem, a dilemma in which individuals acting

selﬁshly destroy the shared resources of the population. In solving this problem, we identify strategies for

applying coalition formation to the spatial distribution of cooperative or defective agents. We use two rein-

forcement learning methods, temporal difference learning and Q-learning, on the agents in the environment.

This overcomes the negative impact of random selection without cooperation between neighbors. Agents

of the memetic framework form coalitions in which the leaders make the decisions as a way of improving

performance. By imposing a reward and cost schema to the multiagent system, we are able to measure the

performance of the individual leader as well as the performance of the organization.

1 INTRODUCTION

Game theory originated as a branch of applied math-

ematics, and found applications in the social sci-

ences, such as economics, political science, social

studies, and international relations (Axelrod, 1995;

Aunger, 2000). Currently, game theory is expand-

ing its horizon into other realms like computer sci-

ence, biology, engineering, and philosophy. In com-

puter science, game theory concepts are used to un-

derstand the competition between agents where indi-

vidual agents perform better when they impose penal-

ties on other individual agents. If one agent does bet-

ter, another does proportionally worse. Game theory

also shows them how they impact society as a whole

(Smith and Prince, 1973). Prisoner’s Dilemma (PD)

is a well-studied problem (Burguillo-Rial, 2009; Grif-

ﬁths, 2008; Nowak and Sigmund, 1998; Riolo et al.,

2001) that handles the above mentioned competition

which is referred to as social dilemma.

Hardin (Hardin, 1968) describes society’s

dilemma. In society, each individual acts indepen-

dently based on his or her self-interest, using the

rational decision making process. Even when it

is clear that these decisions are not conducive to

achieving its long-term goals, it is not surprising

to see that such decisions eventually lead to the

destruction of the shared resources of the society.

This scenario illustrates a concept usually referred to

as the tragedy of commons (Hardin, 1968). Tragedy

of commons can be observed in many ﬁelds including

multiagent systems (Gotts et al., 2003) and those

related to environmental issues such as sustainability

and competing behavior of parasites (Smith and

Prince, 1973). The commons dilemma stands as a

model for various types of resource consumption

problems in society. Some examples of these scarce

natural resources are water, land, and non-renewables

such as oil and coal. It is advisable to simulate

this model in a multiagent environment so that we

may experiment with techniques and strategies that

overcome or ameliorate the effect of the tragedy of

commons.

In this paper, we employ evolutionary game the-

ory and focus on a simulation using a memetic frame-

work of an organized society of replicate agents in

which an agent acts as either a defector or a coop-

erator. When an agent acts as a cooperator, it un-

selﬁshly interacts with an opponent in a fair manner

towards the consumption of shared resources. On the

other hand, the agent in the role of defector acts self-

ishly towards an opponent. Under the rules and con-

straints of PD, our experiment investigates the validity

of the fundamental behavior of agents called primi-

tive actions, and the effects of two reinforcement ma-

chine learning strategies: temporal difference learn-

Weerakoon U..

Coalition Formation for Simulating and Analyzing Iterative Prisoner’s Dilemma.

DOI: 10.5220/0005199000220031

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence (ICAART-2015), pages 22-31

ISBN: 978-989-758-073-4

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

ing (TDL) (Leng et al., 2008) and Q-learning (QL)

(Watkins and Dayan, 1992). This experimental in-

vestigation is used to identify the effect of TDL and

QL in motivating agents to cooperate with each other

for sharing the societal beneﬁts (utilities/rewards) in a

manner that is as fair as possible to reduce the devas-

tation of tragedy of commons.

We consider a multiagent system that is populated

on a grid with each cell representing an individual

agent. Each agent deploys its learning model which

helps the agent analyze its knowledge gained through

lessons learned from a limited number of previous

iterations of the game. This helps the agent to se-

lect the most successful behavior (in terms of utili-

ties earned), and then the agent uses the most suc-

cessful behavior for the current situation. To do that,

the agent uses previously gained knowledge. The as-

sumption of limited memory enables us to model the

social dilemma with in computational limitations in

terms of resources and time.

The following illustrates some capabilities of an

agent in this environment. An agent may remain iso-

lated rather than join a coalition. In line with ratio-

nal agents’ society, an individual will not be willing

to join a coalition that is considered weak or a coali-

tion whose potential success in the future is equally

weak. Hence, it is rational that individuals act inde-

pendently. An agent may also act as a cooperator or

a defector as a result of its most recent game iteration

experiences.

In the scenario where an agent decides to join a

coalition, it pays a one-time joining fee to the leader

and then collaborates with the other coalition mem-

bers. A coalition member decides to cooperate or de-

fect with a member from another coalition by utiliz-

ing the lessons learned from the past interactions with

the corresponding coalition. As a coalition member,

if the agent realizes that the remuneration in its util-

ity is not worthwhile after evaluating its neighbors’

utilities, the agent does not engage with the coalition.

There is a social tendency to form a coalition around

a successful leader in terms of power, capital, and

strength to secure success in future endeavors, either

as an individual or as a group, by contributing money,

effort, or ideas. In reality, being a member of a com-

munity guarantees an individual’s fair consumption of

shared resources, and the protection of earned utilities

against threats of violence from other communities.

We analyze the utility that the agent’s society

earns as a consequence of cooperation or defection

by comparing the utility with ideal best cases. Perfor-

mance of the leader is analyzed according to its coali-

tion size and its individual utility. We investigate the

societal structure with the objective of minimizing the

consequence of the tragedy of commons, and herein

present our ﬁndings. QL experimentally outperforms

TDL in minimizing the negative impact of defection,

by facilitating agents to cooperate as coalition mem-

bers.

In a society that has reached stability, or equi-

librium, the cooperative agent society forms a lower

number of stable coalitions than might exist in a soci-

ety of non-cooperators. But even so, the approximate

number of members in each stable coalition remains

the same.

2 RELATED WORK

Riolo, Cohen and Axelrod (Riolo et al., 2001) (RCA)

describe a tag-based approach to cooperation in which

an agent’s decision to cooperate is based on whether

arbitrary tags of both agents are sufﬁciently similar to

each other. Tag-based cooperation is independent of

past or future interactions within the current genera-

tion. Situations in which the environment is dynamic

and agents reproduce, the value of the tag is typically

dependent on the parent’s action, not the action within

the current generation. In their model, each agent is

initially randomly assigned a tag value and a tolerance

level with a uniform distribution [0, 1]. An agent co-

operates with a recipient agent if the recipient’s tag

value is within the agent’s tolerance level. Thus, the

agent with a higher tolerance value cooperates with

agents that have a wide range of tags, while others

with a low tolerance level cooperate with an agent that

has a very similar tag. In their simulation, each agent

acts as a potential cooperator in P interaction pairs,

after which the population of the agents is reproduced

in proportion to their relative score as determined by

the game matrix of PD. During reproduction, each

offspring’s tag and tolerance value are subjected to

potential mutations such that new tags and tolerance

values are produced according to a probability distri-

bution. Ultimately, they found that this approach en-

ables a higher cooperation rate within the simulation

without reciprocity. Our model differs from this in

that, we use coalition formation, rather than tag val-

ues, to achieve a higher cooperation level by consid-

ering similar behavior of ethical and political groups

in the society.

Grifﬁths (Grifﬁths, 2008) demonstrates an ap-

proach to remedy the tragedy of commons that com-

bines the tag-based approach of the RCA model

and the image-scoring approach of Nowak and Sig-

mund (Nowak and Sigmund, 1998). Grifﬁths’ simu-

lation differs from the RCA approach as he introduces

cheater agents who refuse to cooperate even though

CoalitionFormationforSimulatingandAnalyzingIterativePrisoner'sDilemma

the rules of the system require them to do so. Al-

though Grifﬁths introduced cheater agents, his model

enabled an agent to identify cheaters to avoid interac-

tion with them, and corporate with other agents who

are trustworthy. However the author extended the

image-scoring approach to reduce the requirement for

indirect reciprocity. In particular, an agent uses an

estimate of the combined image score of its neigh-

bors’ to reduce the impact of cheaters. Agents use

what they have learned in the reproduction phase,

such that each agent compares itself to another and

adopts the other’s tag and tolerance if the other’s score

is higher. There are two ways to determine reproduc-

tion: 1) Interval-based reproduction - An agent re-

produces after a ﬁxed number P of interactions and

2) Rate-based reproduction - They specify a repro-

duction probability that represents the probability that

an agent will reproduce after each interaction. In

our model, in an effort to overcome the problem of

abysmal cooperation present as a result of the PD,

we will analyze the effect of coalition formation with

TDL and QL. However, historical records of an agent

provide some accurate evidence in deciding the best

action to play because the reproduction of agents is

not considered in our model.

Burguillo-Rial (Burguillo-Rial, 2009) (BR) exper-

imented with a multiagent organization in which each

agent has two options: cooperate or defect. BR pre-

sented a model using a memetic framework and evo-

lutionary game theory to simulate a spatial and iter-

ated PD. Each agent has local knowledge of the en-

vironment, and the individual’s knowledge is limited

to the number of neighbors within a predeﬁned ra-

dius. In his model, the agent population is placed on

a square lattice (40 × 40), where each cell is consid-

ered an agent. Isolated agents can apply algorithms

probabilistic tit-for-tat or learning automata for se-

lecting a cooperative or defective strategy. Agents

have the ability to form a coalition that has a leader

agent which decides the coalition’s strategy. In our

model, using the same framework, we have extended

the simulation boundaries by introducing the use of

TDL and QL. Then we analyze the consequences of

those learning methods on individuals, and as well as

on the agents’ society.

3 EVOLUTIONARY GAME

THEORY AND MEMETICS

This section introduces two important concepts that

are related to the simulation and framework of our

experiment: 1) evolutionary game theory (Smith and

Prince, 1973) and 2) memetics (Aunger, 2000). Game

theory describes the feasibility of applying multia-

gent system strategies to ﬁnd an approach to solve

the well-known and difﬁcult problem of PD. Follow-

ing, memetics and its framework are discussed with

respect to each agent’s behavior in a multiagent sys-

tem.

3.1 Evolutionary Game Theory

Maynard-Smith and Price (Smith and Prince, 1973)

introduced the formalization of evolutionarily stable

strategies as an application of a mathematical the-

ory to enable the formal study of games. Ultimately,

that formal study enabled researchers to apply con-

clusions and observations from Evolutionary Game

Theory (EGT) (Smith and Prince, 1973) to other re-

search areas like artiﬁcial intelligent, economics and

sociology. Currently, EGT seems to be the predomi-

nant theoretical tool in use for the analysis of multi-

agent systems, especially when considering coopera-

tion and negotiation.

Many of the solution concepts of EGT remain at

a descriptive level, meaning the solution concepts de-

scribe the properties of appropriate and optimal so-

lutions, without explaining how to compute the solu-

tions. Moreover, the complexity of computing such

solutions remains very hard at the level of NP-hard

or worse. Multiagent systems signiﬁcantly points out

these problems which facilitates a researcher’s ability

to develop tools to address them.

Evolutionary Stable Strategy (ESS) (Smith and

Prince, 1973) plays an important role in EGT. The

term ESS means an agent cannot beneﬁt by changing

the current strategy while the others keep their strate-

gies unchanged. Nash equilibrium is a type of ESS

and well known in game-theory literature. It is also

one of the most important concepts in analyzing mul-

tiagent systems. The difﬁculty with this concept is

that not every interaction scenario has a Nash equilib-

rium, and that some interaction scenarios have more

than one.

3.2 Memetics

By deﬁnition, memetics (Aunger, 2000) is the theoret-

ical and empirical science that studies the replication,

spread, and evolution of memes. A meme is an infor-

mation pattern held in an individual’s memory that is

capable of being copied to another individual’s mem-

ory. A meme can be considered as a behavioral pat-

tern that can be transferred from one to another. This

transmission can be interpreted as imitator dynamics

in the multiagent system domain.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

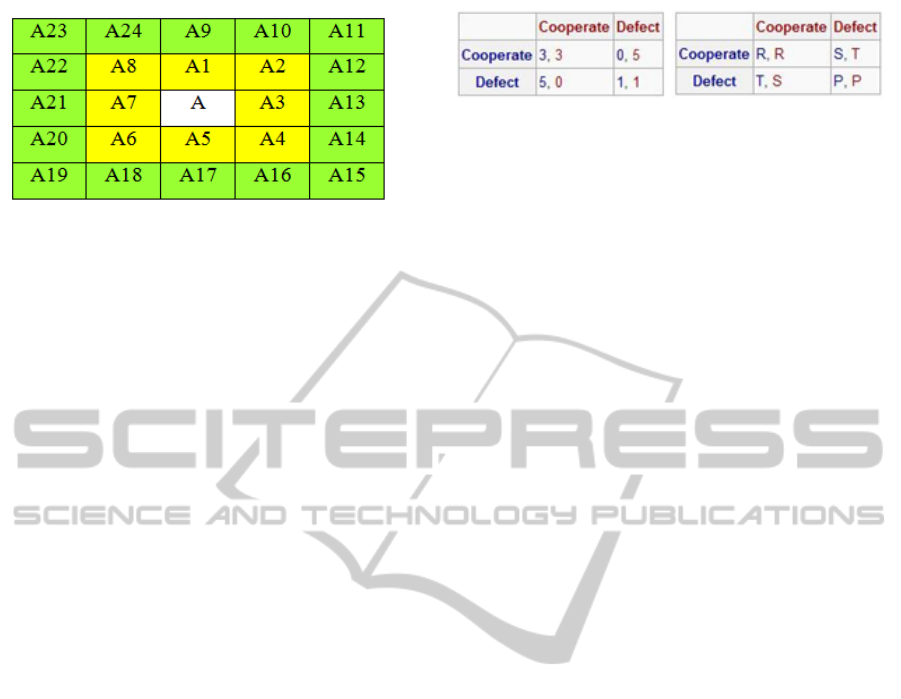
Figure 1: Cell agent A and two neighborhood radius 1 (yel-

low) and 2 (both yellow and green).

In this experiment, we model the memetics frame-

work by considering two characteristics of any suc-

cessful replicator: 1) Copying-ﬁdelity: Copies of the

original pattern will remain after several rounds and

2) Longevity: the longer any instance of the replicat-

ing pattern survives, the more copies can be made of

it. The imitator characteristic of the memetics model

adds the behavior of imitation to agents, so the agent

can bring the most successful strategy to the next

round.

The memetics framework is the most suitable

model with regards to our agent society, because

the implementation of memetics simulates a society

wherein each individual agent has the option of two

primitive actions: cooperate or defect. Each individ-

ual agent has the same capability as the other agents

yet they may behave differently.

4 MULTIAGENT SYSTEM

The proposed approach we follow in this paper is ex-

plored using spatial games in which players (agents)

are either a pure cooperator or pure defector. They in-

teract with their neighbors in a two-dimensional array

of space, which enables them to analyze their neigh-

bors’ strategy from iteration to iteration.

4.1 Spatial Game

In our simulation, which is similar to BR, we place

the individual agent in a cell of a grid (i.e. a two-

dimensional spatial array). The individual agent plays

the game with a predeﬁned set of neighbors that are

bounded by the neighborhood radius. In each round,

each agent ﬁrst decides its status as an independent

agent, a deserter agent, or a member agent depend-

ing on the role of the agent and its opponent’s role

in the interaction. Second, the agent decides whether

to cooperate/defect with/to the opponent. We elabo-

rate each agent’s role and criteria of decision making

in Section 5. In this simulation, all the agents exist

Figure 2: Prisoner’s dilemma game matrix.

through the entire iteration, till the end. They are

static. The simulation version of this experiment is

designed for a discrete time, in the sense that the total

utility to each cell is evaluated, and then all cells are

updated simultaneously. This corresponds to the com-

mon biological situation wherein an interaction phase

is followed by a reproduction phase. For example, an

agent evaluates its neighbors’ utilities earned from the

previous iteration, but not the current iteration.

4.2 Basic Game Rules

Prisoner’s dilemma is a famous game matrix in game

theory and multiagent system. The concept is as fol-

lows: Two criminals have been arrested for a crime

and are being interrogated separately. On the one

hand, each knows that if neither of them talks, they

will be convicted and punished for lesser charges,

leading to each getting two years in prison. On the

other hand, if both confess they each will get ten years

in prison. If only one confesses and testiﬁes against

the other, the one who did not cooperate with the po-

lice will get a life sentence and the one who did co-

operate will get parole. The utility function of each

agent is shown in Figure 2.

In Figure 2, T stands for the temptation to de-

fect, R for the reward for mutual cooperation, P for

the punishment of mutual defection, and S for the

sucker’s payoff. To be deﬁned as the iterative PD,

the following two inequalities must hold:

T > R > P > S (1)

2R > T + S (2)

The ﬁrst inequality (i.e. Equation 1) ensures Nash

equilibrium is defection, but the cooperation Pareto

dominates Nash equilibrium. If the second inequality

(i.e., Equation 2) does not hold, then full cooperation

is not necessarily Pareto optimal, if the game is re-

peatedly played by two players.

5 AGENT ROLES

Based on the idea that a society of humans can be

simulated in our agent based memetic framework,

CoalitionFormationforSimulatingandAnalyzingIterativePrisoner'sDilemma

we model different social groups as formed agent-

coalitions of this multiagent system. Even though so-

cial groups evolve, as is their nature, with hierarchical

roles which increase in number over time, for simplic-

ity, our model simulates only two roles, the leader and

the members of the coalition.

As a leader, an agent considers an interesting

trade-off between the size and the joining-fee of its

coalition. On the one hand, the size of a coalition

inﬂuences the strength of the leader proportionally,

meaning that if the size of the coalition is expand-

ing, the power of the leader is gradually increasing.

On the other hand, members of the coalition utilize

their resources, such as money, effort, or ideas on be-

half of the coalition. To represent these dual inﬂuence

factors of the coalition, we introduce a joining-fee, as

shown in Equation 3. With a joining-fee, the agent

who is willing to join a coalition is forced make a

one-time payment deﬁned by the leader, but a higher

joining-fee motivates agents to consider some other

coalition with a lower joining-fee, ultimately weaken-

ing the leader of the coalition on a higher joining-fee.

joining-fee

= X −ln(

coalition(l

)

) (3)

In Equation 3, the joining-fee of a coalition that

is headed by leader agent l

is deﬁned as the differ-

ence between a predeﬁned value X and the natural

logarithm of the coalition’s size. In our model, the

joining-fee decreases with the increase in the number

of members in stable coalitions, and when the society

reaches equilibrium, the difference in the fees to join

these coalitions is negligible.

To represent the dual inﬂuence stated above, BR

imposes a fee on the members of a coalition for the

leader as a portion of their utilities in each iteration. In

contrast, the individual agent, who is willing to join a

coalition, does not consider the fee to join a coalition.

Instead the agent rewards the best neighbor agent in

the coalition. This is determined by analyzing the

earnings of the neighbor agent, in terms of the util-

ities paid so far in the iteration. The more the agent

earns, the better a neighbor it is.

In our simulation, irrespective of the agent’s role,

each agent selects its best neighbor according to the

following preference: 1) the best neighboring leader

(

) in terms of its coalition’s joining-fee and earned

utilities; 2) the best neighbor ( ˆn

) that is selected

by utilizing the learning model and 2 heuristics: a

higher average and a higher rise of utilities in past few

rounds

. In the case of selecting the best neighboring

agent (

or ˆn

), the learning model is utilized by agent

In our model, the number of considered past interac-

tions is a predeﬁned limit for all agents.

i if it does not deploy the 2 heuristics described above

due to inadequate neighborhood interactions. After

selecting the best neighboring agent, each agent’s be-

havior is categorized according to its role.

1. Independent Agent: Leader

invites agent i to

join with the coalition. In our model, agent i ac-

cepts the invitation to join the coalition by paying

the coalition’s joining-fee. However, if the best

neighbor ˆn

of agent i does not belong to the coali-

tion led by leader

, then the agent will remain in-

dependent, and not join the coalition at this junc-

ture. If in the future it’s best neighbor and the

majority neighbors

of agent i join the coalition

led by leader

, then agent i may also join at this

later time. In an interaction between each neigh-

bor, agent i decides to cooperate or defect based

on the outcome of its learning strategy. The de-

cision of agent i is independent of its neighbors’

current activities, but it depends on previous ex-

periences and learning practices with neighbors.

2. Member of a Coalition: Agent i may decide to ac-

cept or reject an invitation to join a different coali-

tion of leader

based on the coalition’s size as a

heuristic. When the heuristic is false (i.e., size of

agent i’s coalition is large), agent i not only re-

fuses the invitation but also defects with leader

If the heuristic is true agent i accepts the invita-

tion and joins a new coalition. Agent i joins a

coalition proposed by best neighbor ˆn

, when the

heuristic is true

and the value from the learning

model is optimistic. The optimistic value from the

learning model has a higher probability of coop-

eration with neighbors, and so earns higher utili-

ties in the future. If best neighbor ˆn

is an inde-

pendent agent and has positive interactions in the

past (according to the learning model) then agent

i invites ˆn

to join with its coalition. Positive in-

teractions express the level of cooperation in the

past. As mentioned above, agent i always coop-

erates with other members of the same coalition,

and follows the decision from the learning model

for other neighbors.

3. Leader of a Coalition: After determining the

under-performance of its coalition members (i.e.,

their utilities are negative), leader l dissolve the

coalition and all its members become independent

agents. In the case of interacting with best neigh-

boring leader

, leader l merges with the coali-

tion proposed by

based on 2 heuristics: 1) if

the size of the proposed coalition is sufﬁciently

The threshold value of selecting the majority prefer-

ence is predeﬁned in the simulation.

coalition (i)

coalition (ˆn

)

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

larger

than the current one and 2) if neighboring

leader

’s utility is higher than l’s. The other alter-

native is leader l defects with neighboring leader

and coalition members of

. By considering

the heuristic of coalition sizes

and the optimistic

value from the learning model as described above,

leader l gives up its leadership role to accept an in-

vitation to join neighbor ˆn

’s coalition and become

an agent. The next best member of the coalition

in terms of utilities then leads the coalition that

leader l left. Moreover, leader l defects with any

independent agents and members of other coali-

tions.

5.1 Learning from Experiences

Reinforcement learning is a mechanism in machine

learning that assumes that an agent perceives the cur-

rent state of the dynamic environment, and maps the

situation to an action in order to maximize the reward.

The next two sections discuss two main reinforcement

machine learning algorithms: TDL and QL.

5.1.1 Temporal Difference Learning

The agent learns how to achieve a given goal by a

trial-and-error approach. It then tags actions that gen-

erate higher rewards as successful actions that are safe

to use in future interactions, and tags others as failure

actions that it should avoid performing in the future.

In this manner, the agent learns to apply the best past

solution to new situations using a learning function

that is derived from TDL.

new

= R

old

+ β ·

{

[Rew(a

) · ρ] − R

old

}

(4)

In the equation 4, the term R

new

is the record of

the reward that will be updated to the knowledge base

and reused to select the action as described in Section

5. Rew(a

) is the reward of the action a

ρ = # cooperate neighbors ÷ #total neighbors (5)

In the equation 5, the parameter ρ is used to ex-

tract the reward made by cooperative neighbors in the

neighborhood. The learning rate β (0 ≤ β ≤ 1) indi-

cates the tendency of an agent to explore. A higher

learning rate indicates the agent is less likely to ex-

plore. Finally, the agent stores this result into the

knowledge base with the action. Instead of storing the

action and the total reward that is gained from games

played with all its neighbors directly to the knowl-

edge base, the agent should pick up a portion of the

The proportion of the coalition size should exceed a

predeﬁned threshold.

coalition (l)

coalition ( ˆn

)

total reward that is inﬂuenced by cooperative agents

among all its neighbors. In this way, if the majority of

its neighbors are defectors, the agent tends to be a de-

fector. This is the dominant strategy of these games.

5.1.2 Q-Learning

Q-learning (Watkins and Dayan, 1992) is a

reinforcement-based learning process. The agent

in the game environment learns from feedback.

When it earns high utility from its actions, it tends

to repeat those actions. Since agents interact with

each other, and consequently learn from each other,

they do not need to construct an explicit model of the

environment.

The basic idea is that the agent acts according to

action a

∈ A to achieve a given goal. It receives feed-

back based on an individual reward that is calculated

after each action. The goal is for the agent to learn a

control policy (π) that maps the set of states (S) to a

set of actions (A) as follows:

π : S → A (6)

Equation 6 deﬁnes the policy of an agent. An

agent chooses an action a

that maximizes the accu-

mulative reward. The accumulative reward can be de-

ﬁned as the sum of the rewards.

In Q-learning, an agent keeps a table with a lim-

ited capacity of action reward pairs,

, r

that con-

tain the value of taking a

and its reward r

. Every

time an agent performs an action, it can update its Q-

value. This information can then be used by the agent

to help decide which action to perform. Q-value is

updated by the following:

) = Q

(k−1)

) + β ·



− ρ · max

ˆa

(k−1)

( ˆa

) − Q

)



(7)

In equation 7, Q

) is the Q-value of the action

of the k

trial and max

ˆa

(k−1)

( ˆa

) is the action ˆa

that gives the maximum Q-value of the (k − 1)

trial.

If a low learning rate is used, the agent is slow to

react to changes in the environment, whereas a high

learning rate means that the agent reacts quickly to

changes without exploring other possibilities.

5.2 Coalition Formation

In our simulation, we appoint leaders for the initial

set of coalitions created. From this point forward, the

coalitions are maintained as follows.

When a leader of a coalition leaves (as mentioned

above), the next agent with the highest rewards be-

comes the new leader of that coalition.

CoalitionFormationforSimulatingandAnalyzingIterativePrisoner'sDilemma

A leader agent can dissolve its coalition if the

coalition is too weak to make any positive progress, or

it can merge its coalition with a larger, stronger coali-

tion, but the leader will lose its position as a leader.

An agent identiﬁes the best neighbor by utilizing

the learning model and 2 heuristics as follows:

• By considering the average of utilities in the past

few rounds;

• By considering the increase of utilities in the last

few rounds.

If the best neighbor agent is a member or a leader of

a coalition, the current agent may join that coalition,

as described previously, during the start of each itera-

tion.

5.3 Game Matrix

Coercion and extortion can be observed in any soci-

ety, especially when observed over the centuries as

strong ethical or political groups form. For this rea-

son, we present our memetic simulation framework

as the simple dynamic of pay or else (Axelrod, 1995).

Any agent (aggressor agent) can demand cooperation

from a neighbor agent, with the threat that if payment

is not forthcoming, there will be retaliation in the

form of increased payment. To represent this interest-

ing idea, the agent that initiates the demand needs to

raise weapons (threats) that consequently cost more.

So, we deﬁne the punishment as the damage caused

by the opponent: the war is the reason for armament

on both sides. Deﬁnitions are as follows:

= P − ln





coalition(A

)





(8)

= P − ln(

coalition(A

)

) (9)

Here, P

and P

are the punishment payoff of

agents A

and A

, respectively. The decision to de-

fect can be symbolized the raising of arms to de-

clare a war, so preparation for the war requires re-

sources for military research/trainings and manufac-

turing weapons. In a situation in which the oppo-

nent decides to unconditionally surrender (by cooper-

ating); the aggressor agent has no further additional

expenses. Since the aggressor agent receives more

payoff than its opponent, there is a higher probabil-

ity of expanding the coalition of the aggressor agent.

Hence, it can be considered as a net wealth-gain in

consequence of the threat.

As shown in Equation 8 and 9, the decision of both

agents to declare retaliation results in costs to both

sides, but more so to the weaker and smaller coalition

(as expressed by a percentage of the total expense).

Thus, the model is a rational one in which an agent

can impose more damage to the retaliated agent via

an alliance of other member agents in the same coali-

tion. Also, a higher number of member agents can

cause more damage to the opponent when both are

defecting.

Unlike in our model, suckers (i.e., agents who

cooperate while opponents are defecting) of the BR

model were penalized using the same criteria as men-

tioned above. So, in his model, a negative payoff for

an agent who cooperates, irrespective of the decision

to defect by the opponent, is guaranteed a penalty

without a rational decision. The decision of penal-

ized cooperative agents to ultimately join the coali-

tion, even though they had initially defected (espe-

cially when the coalition of the opponent is compara-

tive larger than the other agent) helps to form a coali-

tion so large that all the agents in the simulation be-

come a member, in the end.

6 SIMULATION RESULTS

This section describes the underlying implementation

of the simulation, experiment design, and outcomes in

light of the above discussed concepts and theories. As

discussed previously, the memetic framework is de-

signed using a grid with the same square dimensions,

and each cell is considered as an agent of the society.

Each cell is smart enough to determine its own role in

the simulation. When it acts independently, an agent

can deploy strategies to inﬂuence the action of the cur-

rent round. An agent can join a coalition or even lead

a coalition, because the framework simulation facili-

tates such an agent to work collaboratively with other

members of the coalition in an autonomous manner.

Moreover, the simulation provides the following ser-

vices:

1. Automated tests to minimize errors in the statisti-

cal analysis;

2. Easier to tune or change simulation parameters;

3. Automated data analysis and graphical represen-

tation of it.

The grid of the simulation consists of 50 × 50 =

2500 cells. Throughout our experiments, we use the

same grid size. Initially in our experiments, agents

are not allowed to form coalitions. In other words,

each agent is considered to be independent. After sev-

eral rounds, the agents are allowed to form coalitions

by utilizing the learning model and heuristics as de-

scribed above. In the interaction between neighbors

of any agent, an agent chooses to cooperate or defect

with the probability of 50%. The purpose of the initial

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

rounds is to allow agents to gain experience that even-

tually will help them to deploy their learning model

successfully.

Colors can be changed according to their role in

the simulation such as 1) Black: a leader of a coali-

tion; 2) White: an independent agent; 3) Other: color

of the coalition, as shown in Figure 3.

Initial parameter values of the simulation are de-

scribed in Table 1, and the initial simulation is shown

in Figure 3.

Table 1: Initial Parameter Values of the Simulation.

Parameter Value Description

Neighborhood

radius

1 An agent can play with

its immediate eight

neighboring agents.

Memory slots 10 An agent stores 10 re-

cent incidents happed

in the past with a neigh-

bor.

Learning rate

(β)

0.3 Learning rate of TDL

and QL.

Q-value range [5, 10] Range of initial Q-

values

Random play

rounds

5 During ﬁrst ﬁve rounds,

agents play randomly.

Majority 0.8 80% of neighbors are

members of a same

coalition

Proportional

Threshold

0.7 The proportion of

current and proposed

coalition’s size is less

than 0.7

Figure 3: Memetic framework - Java applet.

6.1 Learning

Our experiments for the scenario are as described in

Section 5.1. As mentioned, initially all agents start

the game as independent agents. We compare our

results with two solutions proposed by (Burguillo-

Rial, 2009): Learning Automata (LA) and Probabilis-

tic Tit-For-Tat (PTFT).

6.1.1 Agent Role Distribution

Figure 4 shows the Agent’s Role Distribution

throughout the simulation, wherein independent co-

operators soon join a coalition and disappear, as in-

dependent agents, from the system. Moreover, the

number of coalition members increases with the num-

ber of rounds, and the number of independent defec-

tors decrease within the system. It is well to recall

that there is always a set number, 2, 500, of agents in

the system, but that coalition size varies. Once agents

have enough information and training for their perfor-

mance enhancement, TD Learning agents outperform

LA agents and Q-Learning agents outperform PTFT

agents.

Figure 4: Agent’s role distribution.

6.1.2 Agent Reward

In this section, we have collected and analyzed the

rewards collected by coalition members and leaders

over the life of the experiment.

Figure 5 depicts the percentage of the total reward

to the society, each agent type received. As shown in

the graph, the reward of leaders decreases due to the

decline in the number of coalitions, which in turn re-

duces the number of leaders in the society. Reward

percentages of member and independent agents in-

crease and decrease respectively, due to the respec-

tive rise and decline in their number. This ﬁgure also

conﬁrms the results acquired for the previous Figure

CoalitionFormationforSimulatingandAnalyzingIterativePrisoner'sDilemma

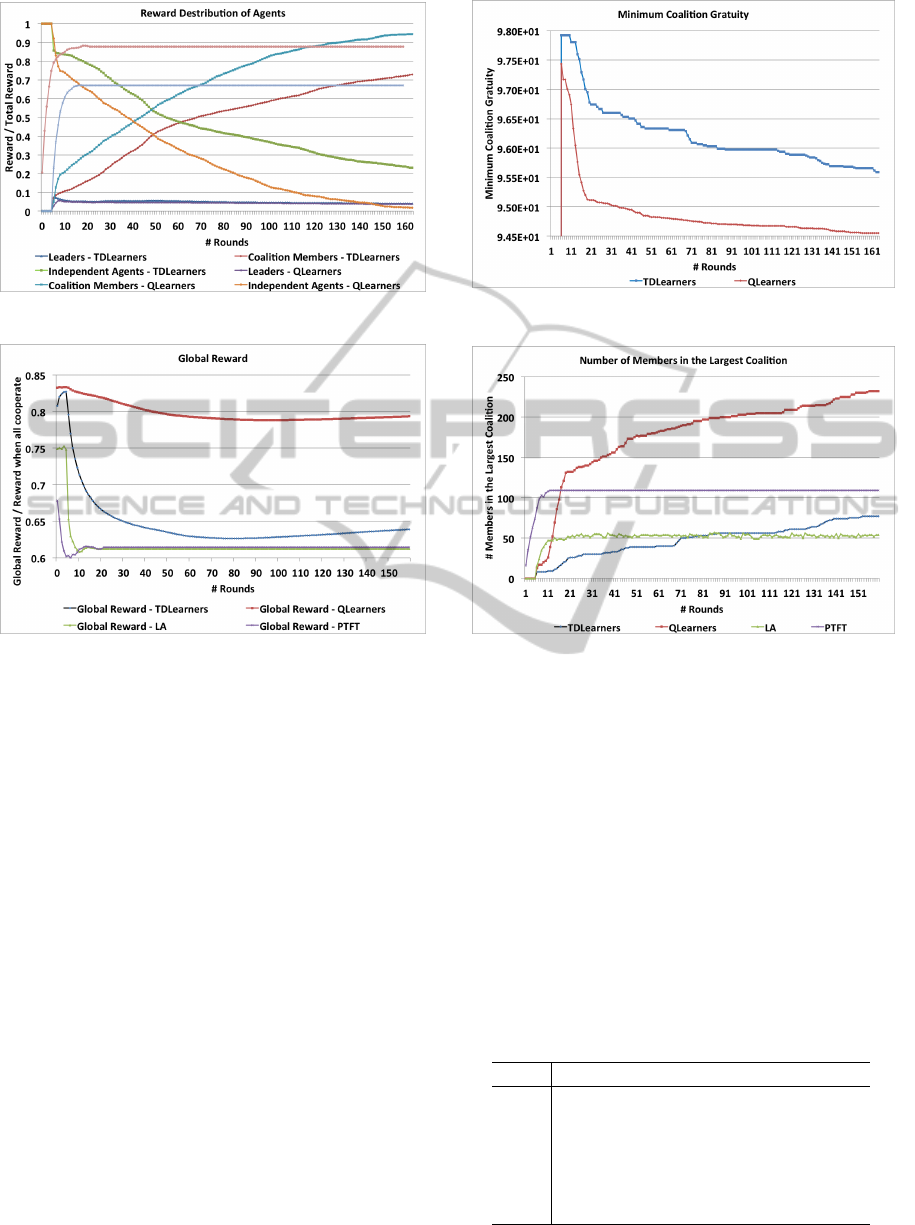
Figure 5: Reward distribution of agents.

Figure 6: Global reward.

Figure 6 shows what happens when the number of

agents in a coalition increases. The Global Reward

deceases initially due to the domination of indepen-

dent defectors and later increases due to the increase

in the number of member agents. Global reward is the

total number of rewards of all the agents in compari-

son to the maximum rewards gained if all the agents

cooperate with each other. As depicted, solutions LA

and PTFT need to be improved in order to cope with

a complex simulation that has several uncertainty fac-

tors: coalition join fee, power against others and se-

lection of the best coalition, that needs to be decided

based on agent’s local knowledge.

6.1.3 Coalition

Figure 7 shows that the joining-fee, paid by agents to

the leader of a coalition, decreases with each succes-

sive round because as the size of a coalition grows, it

can charge less to join. Minimum coalition joining-

fee helps the leader to expand its coalition size and

increases the chances of invasion by other coalitions

(i.e. force to merge). We did not include LA and

PTFT as joining-fee is not presented in (Burguillo-

Rial, 2009).

Figure 7: Minimum coalition joining-fee.

Figure 8: Number of members in the largest coalition.

Figure 8 shows that the number of members in-

side the largest coalition increases with the number

of rounds. This shows that over time, we have de-

creasing numbers of coalitions emerging as domi-

nant coalitions. Interestingly enough, dominant coali-

tions consist of an equal number of members. A

higher number of members in the coalition increase

its strength, there-by helping it to face defections suc-

cessfully. Both LA and PTFT reach their stability

level sooner, but those solutions are not able to im-

prove over the time for a better solution.

Table 2: Cooperators (C), Defectors (D), No. of Coalition

Members (CM), No. of Coalitions (NC), and No. of Mem-

bers in the Largest Coalition (NMLC) Vs. Neighborhood

Radius (NR).

NR C D CM NC NMLC

0.5 104 1554 818 24 71

1 5 49 2398 48 139

1.25 4 5 2446 45 171

1.75 0 4 2446 45 364

2 0 0 2459 41 377

3 0 0 2466 34 228

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

Since, the agents who deploy the QL model out-

perform the agents who deploy TDL model, we fur-

ther analyze Q-learners by changing the neighbor-

hood radius and setting the learning rate to half (i.e.

β = 0.5). The results are shown as Table 2. As shown

in the table, agents (including leaders) prefer to act as

independent agents at the lower neighborhood radius

(NR = 0.5). Conversely, coalitions are much more sta-

ble (i.e. each coalition consists of the large number of

members) at the higher neighborhood radius (NR = 3)

although the number of coalitions is less.

7 CONCLUSION AND FUTURE

WORK

From the experiments performed, we conclude that

the heuristics applied in the simulation help in solving

the problem of the tragedy of commons (prisoner’s

dilemma) to some extent. With the increase in the

number of rounds, we identiﬁed an increase in the

number of member agents, and a corresponding de-

crease in the number of defector agents and indepen-

dent agents. Also, the coalitions with high performing

agents were more likely to survive during the execu-

tion of the game play.

The decrease in the joining fee of each coali-

tion through rounds increases the chances of coalition

growth (attracting more agents to join this coalition).

The temporal difference learning component helps in-

dividual agents join a stronger coalition and stay with

it.

Although, the temporal difference learning and

the Q-learning components applied here help in de-

termining the best possible strategy for an agent, Q-

learning outperforms temporal difference learning.

There are several opportunities for future work.

That of highest priority is to continue our experimen-

tal evaluation to understand the trust and reputation

models that change the agent’s behavior more realis-

tically. Also, studying and applying other reinforce-

ment learning techniques, like function approxima-

tion would be interesting. A comparative analysis of

these different learning models could prove fruitful.

Our secondary concern is to explore the effect of a

dynamic environment, in which the agent is not con-

sidered as static. It can disappear and reappear from

the system during the execution. We would like to

come up with techniques and algorithms that make

the agent organization robust against failures after be-

ing introduced to the dynamic environment.

Our third concern is to integrate the ideas of

cheaters and indirect reciprocity to our simulation for

a better understanding of the coalition formation and

overall behavior of the agent society.

The author expresses gratitude toward Kalyan

Mekala and Vicki Allan for cooperative work along

the years. Additionally, the author thanks anonymous

reviews for their helpful comments.

REFERENCES

Aunger, R. (2000). Darwinzing Culture: The Status of

Memetics as a Science. Oxford University Press.

Axelrod, R. (1995). Building New Political Actors: A model

for the Emergence of New Political Actors. Artiﬁcial

Societies: The Computer Simulation of Social Life.

London: University College Press.

Burguillo-Rial, J. C. (2009). A memetic framework for

describing and simulating spatial prisoner’s dilemma

with coalition formation. In The 8th International

Conference on Autonomous Agents and Multiagent

Systems, Budapest, Hungary.

Gotts, N. M., Polhill, J. G., and Law, A. N. R. (2003).

Agent-based simulation in the study of social dilem-

mas. Artif. Intell. Rev., 19(1):3–92.

Grifﬁths, N. (2008). Tags and image scoring for robust co-

operation. In Padgham, Parkes, Mller, and Parsons,

editors, Proc. of 7th Int. Conf. on Autonomous Agents

and Multiagent Systems (AAMAS 2008), pages 575–

582, Estoril, Portugal.

Hardin, G. (1968). The tragedy of the commons. Science,

162:1243–1248.

Leng, J., Sathyaraj, B., and Jain, L. (2008). Temporal dif-

ference learning and simulated annealing for optimal

control: A case study. In Agent and Multi-Agent Sys-

tems: Technologies and Applications, volume 4953,

pages 495–504.

Nowak, M. A. and Sigmund, K. (1998). Evolution of indi-

rect reciprocity by image scoring. Nature, 393:573–

577.

Riolo, R. L., Cohen, M. D., and Axelrod, R. (2001). Evo-

lution of cooperation without reciprocity. Nature,

414:441–443.

Smith, J. M. and Prince, G. R. (1973). The logic of animal

conﬂict. Nature, 246:15–18.

Watkins, C. and Dayan, P. (1992). Technical note: Q-

learning. Machine Learning, 8(3-4):279–292.

CoalitionFormationforSimulatingandAnalyzingIterativePrisoner'sDilemma