
Refracted Acoustic Communications in Wireless Underwater Sensor
Networks with Mobility
S. Blouin
1
, M. Barbeau
2
and E. Kranakis
2
1
Underwater Sensing, DRDC Atlantic Research Centre, Nova Scotia, Canada
2
School of Computer Science, Carleton University, Ottawa, Ontario, Canada
Keywords:
Routing, Refraction, Sensor Networks, Mobile Nodes.
Abstract:
Routing is a fundamental function of any wireless network. For battery-powered underwater sensors us-
ing acoustic waves, routing is even more challenging due to an ever changing and communication-opaque
ocean. Herein, we propose a shallow-water routing scheme that adapts to a unique physical phenomena of the
medium. In particular, the proposed routing exploits downward and upward refractions for underwater net-
works comprising mobile nodes. Solutions for node-to-node links are developed before extending the concept
to network routing. In particular, necessary and sufficient conditions guaranteeing the existence of a single-hop
link through acoustic refraction are derived. Simulations convey results followed by concluding remarks.
1 INTRODUCTION
Routing is a fundamental function of any wireless net-
work because rarely all nodes are within the trans-
mission range of one another. This is especially true
for battery-powered underwater network nodes with
a barrier-type topology meant to monitor coastlines,
track migrating marine mammals, or protect habitats.
The main challenge of routing is to identify the chain
of nodes used to transfer data from a source to a des-
tination in the most efficient manner.
Underwater acoustic waves propagate further than
electromagnetic or optical waves (Heard et al., 2009).
Thus, the primary medium for wireless underwa-
ter communications is acoustic waves. Unfortu-
nately, underwater acoustic communications are un-
predictable due to frequency-dependent attenuation,
time-varying multipath effects, large Doppler/delay
spreads, and limited bandwidth (Stojanovic and
Preisig, 2009). Underwater acoustics are such that
significant losses occur due to absorption and spread-
ing (Urick, 1983). In certain underwater environ-
ments, the acoustic channel suffers from rapid vari-
ations (Blouin and Inglis, 2013). Certain links may
be unidirectional. Besides, acoustic paths bend due
to varying sound speed in the water column. Those
conditions make the selection of the most appropriate
underwater route a non-trivial task. Mobility through
the underwatermedium whose properties change both
in time and space exacerbate the problems.
Most underwater routing schemes are derived
from terrestrial radio communications. They are
rarely optimized for the underwater communication-
opaque environment and almost never tailored to
the limitations of the medium (Otnes et al., 2012).
Among such routing protocols, one finds both
proactive (SEAWEB (Rice and Ong, 2010), DSDV
(Perkins and Bhagwat, 1994)) and reactive (DSR
(Johnson and Maltz, 1996)) schemes. Proactive pro-
tocols actively maintain a routing table by period-
ically exchanging topology information. Reactive
protocols search for a topological route only when
there exists data to transmit. For battery-powered
sensors, reactive protocols are usually preferred from
an energy-conservation standpoint, but they do result
in additional delays. Many approaches perform ge-
ographic routing(Karp and Kung, 2000) where data
packets are progressively brought closer to the desti-
nation at every step. However, with such an approach
there is no guarantee of finding a path, thus possibly
leading to a communication void.
Geographic routing further breaks down in two
categories, i.e., location-awareor location-free,based
on the knowledge of the location of the destination
node. Most geographic routing protocols in fact re-
quire that each node knows its own location, which
in turn necessitates a sensor position estimation tech-
nique (Li et al., 2010) and its associated hardware and
software. Even though multihop transmissions may
reduce power consumption (Porto and Stojanovic,
113
Blouin S., Barbeau M. and Kranakis E..
Refracted Acoustic Communications in Wireless Underwater Sensor Networks with Mobility.
DOI: 10.5220/0005199501130121
In Proceedings of the 4th International Conference on Sensor Networks (SENSORNETS-2015), pages 113-121
ISBN: 978-989-758-086-4
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2007), there exists an optimal hop length between
routers for a given set of transmission parameters
(Zorzi et al., 2008).
We propose a routing scheme exploiting down-
ward and upward refracting phenomena for under-
water networks with mobility. The contributions re-
late to theoretical results defining the existence of re-
fracted paths between two underwater nodes and con-
ditions leading to interference with the ocean surface
and bottom. These results constitute the initial steps
in addressing a challenging routing problem that min-
imizes power losses for improving underwater com-
munications.
Section 2 reviews background material. Section 3
presents an approach to exploit refracted paths to es-
tablish point-to-point links. Section 4 generalizes the
approach to sensor networks with mobile nodes. Sim-
ulation results and concluding remarks are provided
in Sections 5 and 6. Additional material and proofs
are found in appendices.
2 BACKGROUND
2.1 Problem Definition
A generic underwater sensor network configuration,
made of both static and mobile nodes, is illustrated in
Figure 1. The left-most static node 1 intends to send
a message to the right-most mobile node 6. In addi-
tion to variable separation distances between sensors,
energy losses due to underwater sound propagation
should be considered to efficiently solve the routing
problem.
Figure 1: Underwater sensor network.
Shallow-water acoustics are such that routing is
extremely challenging due to the multi-path effects,
often accompanied by frequency and delay spread
(van Walree, 2013). The various acoustic paths link-
ing source 1 to sink 6 can approximately be grouped
as occurring through either refraction (curved paths
due to the varying speed of sound through the water
column) or reflection (acoustic waves bouncing off
the bottom or the surface). Here, we focus on re-
fracted acoustic paths that do not encounter the sur-
face or bottom of the underwater environment. Such
paths are called direct paths.
Overspread occurs when both frequency and de-
lay spreads disable the demodulation of the received
signal (Otnes et al., 2012). Reflected paths tend to
lead to larger overspread than refracted paths, espe-
cially when multiple reflections occur with a moving
sea surface. Moreover, every reflection transfers en-
ergy to the boundary it encounters, resulting in addi-
tional attenuation. Consequently, usage of refracted
paths should be preferred as they may provide sav-
ings in terms of power consumption, which is critical
for underwater battery-powered wireless sensors.
The prior arguments highlight the importance of
exploiting refracted paths as much as possible in the
underwater environment. Therefore, the main ques-
tion of interest is:
How does one exploit refracted paths to route
a message from node 1 to node 6 through
an underwater sensor network made of both
static and mobile nodes?
A unique feature of the aforementioned problem
pertains to the fact that the routing strategy needs
to adapt to the ever-changing network topology in-
duced by the presence of mobile nodes and also to the
varying sound speed profile resulting from a dynamic
ocean.
The sound speed profile describes the variation
of the speed of sound, c(z), as a function of depth,
z. Such profile originates from variations in water
temperature, pressure and conductivity (thus salin-
ity) with depth. The sound speed value c(z) usually
ranges between 1400m/s and 1600m/s (Erbe, 2011),
but changes over both time and space. We define the
slope of the sound speed profile as
g =
d c(z)
dz
, (1)
with c(z) in (m/s), z in (m), and g in (1/s or second
−1
).
2.2 Assumptions
We assume the presence of the following features:
• First-order, i.e., linear, sound speed profiles.
• Flat bottom and surface oceanic boundaries.
• Sensory node with an acoustic transducer having a
relatively narrow beamwidth β and a controllable
directionality −π/2 < φ < π/2 with respect to the
horizon.
• Nodes equipped with pressure sensors providing
a depth measurement.
SENSORNETS2015-4thInternationalConferenceonSensorNetworks
114

• Global knowledge of relative distances separating
nodes.
Even though not always present in practice, the
first-order sound speed profile assumption is a com-
mon initial hypothesis in the shallow-water acoustic
literature (Katsnelson et al., 2012). Its main impact
is that the resulting sound speed profiles reduce to the
three categories shown in Figure 2: isovelocity (null
slope or g = 0), downward refracting (negative slope
or g < 0), and upward refracting (positive slope or
g > 0), where c
0
(m/s) denotes the sound speed at the
sea surface and g the sound speed profile slope de-
fined in Equation 1. The narrow beamwidth assump-
tion is similar to the focus-beam concept presented
in (Nicolaou et al., 2007). Depth measurement ca-
pability is assumed in depth-based routing schemes
(Hasannezhad et al., 2014). Awareness of relative dis-
tances is often assumed in location-aware approaches.
Figure 2: First-order sound speed profiles.
Given the first-order sound speed profile assump-
tion, the sound speed has a slope belonging to one of
these categories:
d c(z)
dz
= 0, isovelocity,
< 0, downward refracting, or
> 0, upward refracting.
(2)
Given a sea surface sound speed c
0
(at depth z =
0), the linear evolution of sound speed with respect to
depth is expressed as
c(z) = c
0
+ gz, (3)
with the slope g as defined in Equation 1. We denote
node i’s depth as z
i
and associate a sound speed c
i
defined as
c
i
= c(z
i
) = c
0
+ gz
i
, (4)
such that c
i
> 0 for all i’s.
3 POINT-TO-POINT LINK
We derive conditions indicating the existence of an
acoustic refracted path between any two nodes. In
Section 4, this point-to-point link solution is extended
by searching all potential paths through the network
and selecting the path leading to the lowest transmis-
sion loss.
3.1 Straight and Curved Acoustic Rays
We leverage notions from the Acoustic Ray theory
and thus assumes that appropriate communication fre-
quencies apply (Urick, 1983). An isovelocity sound
speed profile leads to straight acoustic rays whereas
non-isovelocity cases (upward and downward refract-
ing) generate curved acoustic rays.
We focus on curved acoustic rays. More specifi-
cally, the up-coming solution applies to the downward
refracting situation, as it is often encountered in shal-
low waters (Katsnelson et al., 2012).
An important result originating from Snell’s Law
stipulates that in the presence of a linearly varying
sound speed profile of constant slope g, any acoustic
ray departing from a source node describes an arc of
a circle (Urick, 1983). Given an underwater source
node i, the center of all circles resulting from dif-
ferent departure angles resides on a line of centers
whose vertical distance from the source node location
is computed as
R
i
= −
c
i
g
. (5)
According to Equation (5), an isovelocitysound speed
profile (g = 0) generates arcs of an infinite radius,
thus straight rays, whereas downward (respectively,
upward) refraction, i.e., g < 0 (resp., g > 0) locates
the line of centers under (resp., above) the sea surface.
3.2 Potential Refracting Scenarios
Figure 3 shows the concepts of the line of centers as
well as a generic case with two underwater nodes, i
and j. Node i is the source and node j the sink. Note
that the water depth is represented by D. The sep-
aration distance between nodes i and j is d
ij
. Such
a configuration leads to four potential and mutually-
exclusive cases when an acoustic ray departs from
node i:
• Case 1: The acoustic ray hits the sea surface be-
fore reaching node j.
• Case 2: The acoutic ray overshoots node j.
• Case 3: The acoutic ray directly hits node j.
• Case 4: The acoustic ray undershoots node j, or
hits the sea bottom before reaching node j.
RefractedAcousticCommunicationsinWirelessUnderwaterSensorNetworkswithMobility
115
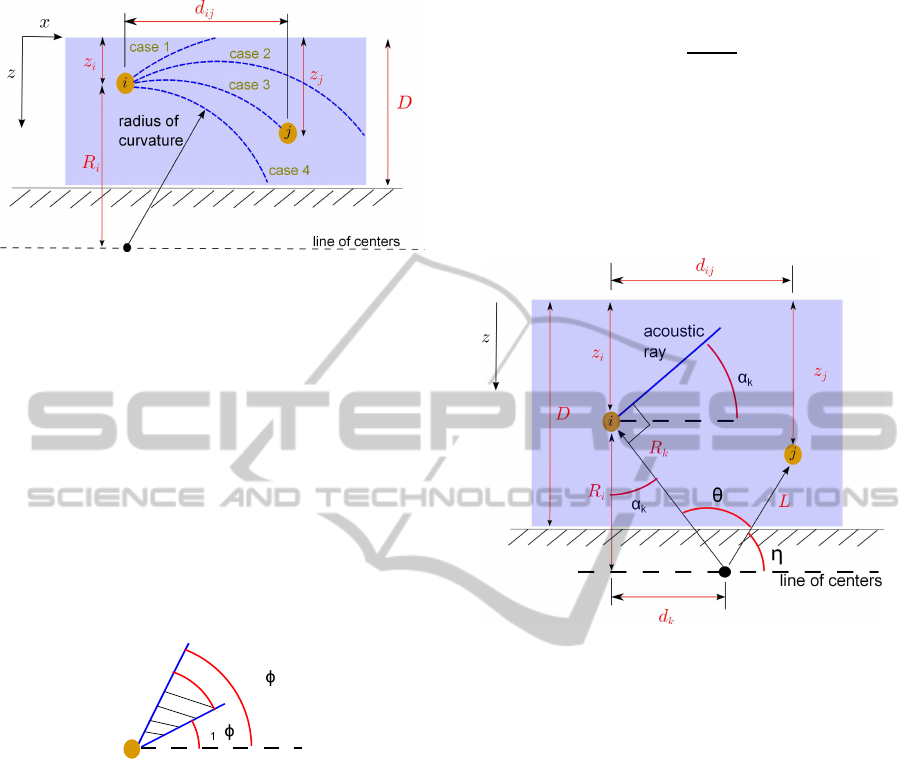
Figure 3: Potential downward-refracted acoustic paths.
3.3 Geometric Solution for Cases 1-to-4
Figure 4 shows (in blue) the two rays acting as the
outer envelope for all acoustic rays departing from
node i. Given a beamwidth β and a direction φ (with
respect to the horizon), the envelope determines the
angles α
1
and α
2
where
α
1
= φ, (6)
α
2
= φ+ β, (7)
such that −π/2 < α
1
,α
2
< π/2 which means that
acoustic rays are prevented from traveling along the
vertical axis and solely interacting with boundaries.
α =
α
2
= +β
β
i
Figure 4: Acoustic rays departing from node i.
The rationale here is that if both value α
1
,α
2
fall
in the same case, 1, 2, or 4, of Figure 3, then no in-
termediate directionality angle α
k
contained between
α
1
and α
2
results in an acoustic ray departing from
node i and reaching node j by a refracted path. Simi-
larly, if α
1
coincides with case 4 and α
2
matches case
2, then there exists an intermediate directionality an-
gle α
1
≤ α
k
≤ α
2
for which an acoustic ray departing
from node i reaches node j by a refracted path.
Assuming an acoustic ray departing from node i
at an angle α
k
where α
1
≤ α
k
≤ α
2
, it is possible to
compute the exact location of the corresponding cir-
cle center with simple geometry as illustrated in Fig-
ure 5. Given that the acoustic ray departing from node
i forms a right angle with the line joining node i and
its circle center, we can derive R
k
, the radius of curva-
ture, and d
k
, the horizontal distance separating node i
from the center of the circle describing the curved
acoustic ray as follows
R
k
=
|R
i
|
cosα
k
, (8)
d
k
= R
i
tanα
k
, (9)
where R
i
originates from Equation (5). Note that the
absolute value of R
i
in Equation (8) is taken so that
the radius of curvature remains positive and to recon-
cile equations in references (Urick, 1983) and (Lur-
ton, 2010) for downward and upward refracting sce-
narios.
α
k
i
line of centers
R
i
acoustic
ray
R
k
d
k
α
k
Figure 5: Center of curvature of an acoustic ray.
We next solve the geometry problem and identify
conditions leading to Cases 1 through 4.
3.3.1 Case 1
Using node i’s location as the center of an (x,z) co-
ordinate system, it can be seen from Figure 5 that if
the top of the circle centered at (d
k
,R
i
) and of radius
R
k
is above or at sea level then the acoustic ray hits
the sea surface, otherwise it does not. Consequently,
if R
i
+ z
i
, the depth of the circle center, exceeds the
length of the curvature radius R
k
, i.e.,
z
i
+ R
i
> R
k
, (10)
then the refracted acoustic ray avoids the sea surface.
Using the previous argument and the development
found in Appendix, we obtain the following result.
Proposition 1
Assume an underwater node
i
at depth
z
i
in the pres-
ence of a linear sound speed variation as defined in
Equation (4). A refracted acoustic ray departing from
node
i
at an angle
|α
i
| < π/2
avoids the sea surface if
and only if
α
i
< α
max
i
, (11)
SENSORNETS2015-4thInternationalConferenceonSensorNetworks
116

where
α
max
i
= arccos
−
sign
(g)
c
i
c
0
. (12)
The angle α
max
i
of Proposition 1 represents the
largest departing angle that an acoustic ray can have
to avoid the sea surface.
Example 1. The network configuration of Figure 1 is
specified through a node depth array Z = {z
1
,... ,z
6
}
and a node-to-node horizontal separation distance ar-
ray d = {d
12
,... ,d
16
} with values
Z = {150, 135,147,125,150,143} − λ,
d = {400, 1000,1600,1900,2600+ δ},
where λ is a depth offset for all sensors, while δ is
a range offset for the mobile node only. Environ-
mental conditions are D = 200 m, c
0
= 1500 m/s,
and g = −0.25 1/s. All acoustic transducers have a
beamwidth of β = 10
o
and their directionality angle
φ takes different values through the following three
scenarios.
Scenario 1:
With λ = 0, δ = 0, φ = −β/2, Equations
(6) and (7) give α
1
= −α
2
= −5
o
and α
max
i
of Equa-
tion (12) is (in degrees)
Node i
1 2 3 4 5 6
α
max
i
12.8 12.2 12.7 11.7 12.8 12.5
As α
max
i
> max(α
1
,α
2
) = 5
o
for all i’s, Proposition 1
implies that none of the acoustic rays departing from
any node will reach the sea surface.
Scenario 2:
By making the environment shallower
with λ = 121, Equation (12) now gives
Node i
1 2 3 4 5 6
α
max
i
(degrees) 5.6 3.9 5.3 2.1 5.6 4.9
so that some acoustic rays departing from nodes 2, 4
and 6 violate the condition of Proposition 1.
Scenario 3: For this scenario, the λ = 121 value still
applies. Slightly changing the directionality angle to
φ = −β/2− 3
o
on all nodes alters α
1
and α
2
such that
α
1
= −8
o
and α
2
= 2
o
. Given that α
max
i
values of
Equation (12) remain unchanged from the previous
scenario, max(α
1
,α
2
) < α
max
i
and no acoustic rays
departing from any node hits the sea surface as per
Proposition 1.
Example 1 is instructive in that (a) controlling the
directionality angle φ can help ensure that no acoustic
ray disperses its energy by interacting with the sea
surface, and (b) there exists a technique for altering φ
as captured in the next result.
Corollary 2
Assume an underwater node
i
at depth
z
i
in the pres-
ence of a linear sound speed variation as defined in
Equation (4). Given a fixed beamwidth
β
, Equation
(11) of Proposition 1 holds if the directionality angle
φ
satisfies
φ < α
max
i
− β (13)
The proof of Corollary 2 follows from the fact
that Equation (13) is equivalent to φ+ β = α
2
< α
max
i
based on Equation (7).
3.3.2 Cases 2, 3, and 4
Assuming that Equation (11) holds, Cases 2, 3, and 4
can be solved using a similar development. Denoting
node j’s depth as z
j
, Figure 5 displays the geome-
try involved in identifying the distance L separating
node j’s location from the center of the circle associ-
ated with an acoustic ray leaving node i at an angle
α
k
. Note that Figure 5 represents the particular case
where d
ij
> d
k
.
Expressing the distance L mathematically gives
L =
q
(d
ij
− d
k
)
2
+ (z
i
+ R
i
− z
j
)
2
. (14)
From Figure 3 and Equation (14), the remaining cases
correspond to
L < R
k
, ray overshoots node j (Case 2),
L = R
k
, ray reaches node j (Case 3),
L > R
k
, ray undershoots node j (Case 4).
(15)
For Case 3, the following result holds.
Proposition 3
Assume two underwater nodes
i, j
at depths
z
i
,z
j
in
the presence of a linear sound speed variation as de-
fined in Equation (4). A refracted acoustic ray depart-
ing from node
i
at an angle
|α
k
| < π/2
and reaching
node
j
exists if and only if
L = R
k
, (16)
which is equivalent to an acoustic ray departing angle
α
k
= arctan
1
2d
ij
R
i
d
2
ij
+ (∆z
ij
)
2
+ 2∆z
ij
R
i
. (17)
The proof for Proposition 3 can be found in Ap-
pendix. Equation (17) is a closed-form solution indi-
cating which angle α
k
results in a refracted path be-
tween node i and node j. Using the geometry shown
in Figure 5, it is possible to compute the arc length S
ij
of the refracted acoustic path linking node i to node j
through
S
ij
= R
k
θ, (18)
RefractedAcousticCommunicationsinWirelessUnderwaterSensorNetworkswithMobility
117
where R
k
is derived as per Equation (8) and the arc
angle span θ (rad) shown in Figure 5 is given by
if d
ij
> d
k
θ = α
k
+ 0.5π− η
η = arctan
z
i
+ R
i
− z
j
d
ij
− d
k
,
if d
ij
< d
k
θ = α
k
− 0.5π+ η
η = arctan
z
i
+ R
i
− z
j
d
k
− d
ij
,
(19)
with α
k
from Equation (17) and η shown in Figure 5.
4 NETWORK ROUTING
A refracted acoustic route between a source node 1
and a destination node 6 exists if there is a sequence
of refracted paths linking node 1 to node 6.
Underwater transmission loss, TL, is a measure
of the rate at which the sound energy is lost (Urick,
1983) and a common computation is
TL = N log
10
r− a · r, (20)
where N is the coefficient of geometric spreading, r
the range or straight-line distance (in meters) from the
acoustic source to the destination, and a the absorp-
tion coefficient. Given the relatively close proximity
between network nodes, it can be assumed that spher-
ical spreading dominates and is captured by inject-
ing N = 20 in Equation (20). Frequency-dependent
values for a, the absorption coefficient, are shown in
Appendix for atmospheric pressure and a temperature
of 5
o
Celsius (Kinsler et al., 1982) (Kinsler et al.,
2000). For commercial acoustic modems operating
in the 10-30 kHz frequency band (Hasannezhad et al.,
2014), the absorption coefficient a varies linearly in
the 0.0008 − 0.0076 db/m range.
We modify Equation (20) to compute transmission
loss along a refracted path from node i to j, with arc
length given by Equation (18), as follows
TL
∗
i→ j
= N log
10
S
ij
− a· S
ij
. (21)
Based on Equation (18) for S
ij
, Equation (8) for R
k
,
Equation (5) for R
i
, Equation (19) for θ, and Equation
(4) for c
i
, TL
∗
i→ j
is a nonlinear function h(·) with the
following input variables
TL
∗
i→ j
= h(a,c
0
,d
ij
,g,N, z
i
,z
j
,α
k
) (22)
with α
k
from Equation (17) and where all other vari-
ables are measured quantities or constants.
5 SIMULATION RESULTS
We apply the previous results of Section 3 to the un-
derwater network configuration of Figure 1.
Example 2. Similar to Example 1, environmental
conditions are D = 200 (m), c
0
= 1500 (m/s), and
g = −0.25 (1/s). In Equation (21), N = 10 given
the shallow water context and a = 0.0043 as acous-
tic communications are assumed to occur around 25
kHz. The network configuration is specified by a node
depth array Z = {z
1
,... ,z
6
} and a separation distance
array d = {d
12
,... ,d
16
} defined as
Z = {150, 135,147,125,150,143} − λ,
d = {400, 1000,1600,1900,2600+ δ},
where λ = 0 and δ = 0. From the distance array given
above, any node-to-node distance d
ij
can be derived
as shown in Appendix. All sensors have a beamwidth
of β = 10
o
and directionality angle φ = −0.5β. Table
1 lists all sixteen different configurations of forward
routes departing from node 1 and reaching node 6.
Table 1: Possible forward routes between node 1 and 6.
# Route
1 1 → 6
2 1 → 2 → 6
3 1 → 3 → 6
4 1 → 4 → 6
5 1 → 5 → 6
6 1 → 2 → 3 → 6
7 1 → 2 → 4 → 6
8 1 → 2 → 5 → 6
9 1 → 3 → 4 → 6
10 1 → 3 → 5 → 6
11 1 → 4 → 5 → 6
12 1 → 2 → 3 → 4 → 6
13 1 → 2 → 3 → 5 → 6
14 1 → 2 → 4 → 5 → 6
15 1 → 3 → 4 → 5 → 6
16 1 → 2 → 3 → 4 → 5 → 6
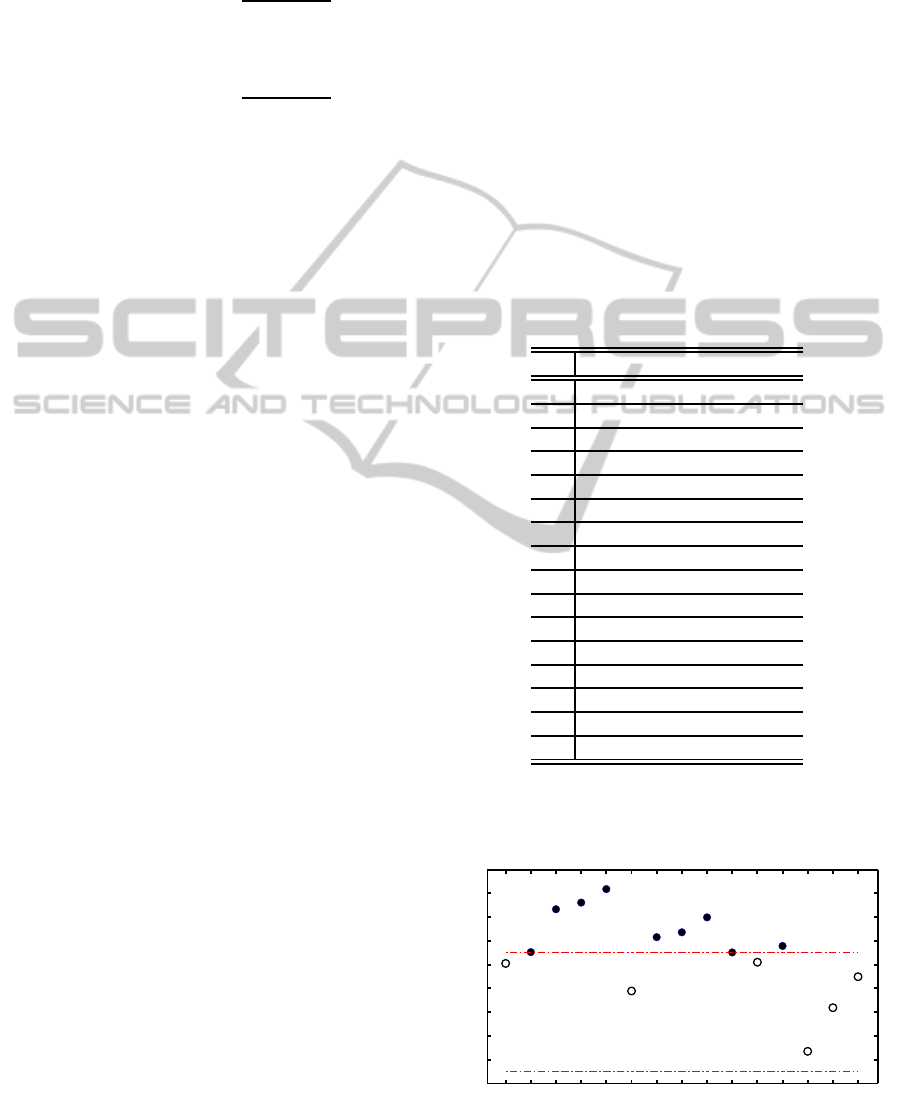
Figure 6 shows the α
k
values of Proposition 3
insuring a direct refracted path between two nodes
whose numbers are given on the horizontal axis.
1−2 1−3 1−4 1−5 1−6 2−3 2−4 2−5 2−6 3−4 3−5 3−6 4−5 4−6 5−6
−6
−4
−2
0
2
4
6
8
10
12
Single−hop link (Departing node # − Receiving node #)
Acoustic ray departing angle (degree)
Figure 6: Angles ensuring a refracted path between nodes.
SENSORNETS2015-4thInternationalConferenceonSensorNetworks
118
Given that acoustic rays are restricted to depart at
angles between +5
o
and −5
o
(indicated by red dashed
lines in Figure 6), only links 1 → 2, 2 → 3, 3 → 5,
4 → 5, 4 → 6, and 5 → 6 satisfy this constraint and are
indicated by hollow circular markers. Consequently,
only route # 13 of Table 1 is actually feasible given
the present constraints.
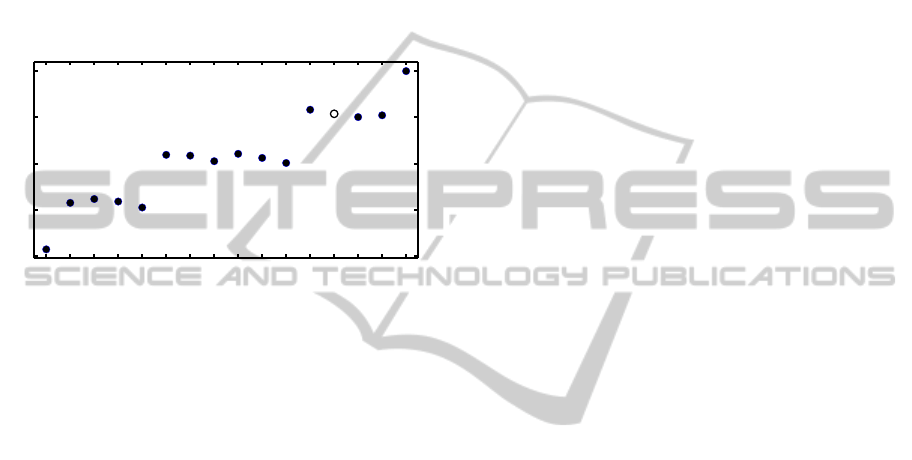
Figure 7 shows the summation of individual trans-
mission loss along the routes of Table 1 using Equa-
tion (21) for each individual single-hop link. Route #
13, the only feasible one, has an overall transmission
loss of 204 dB, which is significant.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
50
100
150
200
250
Route number
Total transmission loss (dB)
Figure 7: Overall transmission loss over all routes.
From Figure 6, it can be seen that augmenting the
beamwidth β from 10
o
to 12
o
would incorporate links
1 → 3, 3 → 4 and 3 → 6 which in turn, enables route
# 3, i.e., 1 → 3 → 6, whose overall transmission loss
is 112 dB, a gain of 92 dB due to a 2
o
increase in
beamwidth.
6 CONCLUSION
This publication proposes a routing scheme exploit-
ing downward and upward refracting phenomena for
underwater networks with mobile nodes.
The proposed technique presents an approach us-
ing refracted paths to establish node-to-nodelinks and
extends those results to a routing problem in a sen-
sor network with mobile nodes. Both theoretical and
practical results are derived. In particular, necessary
and sufficient conditions guaranteeing the existence
of a single-hop link through an acoustic refracted path
are derived.
Examples and simulations illustrate how impor-
tant are the network configuration and the available
steering capability of the acoustic energy.
REFERENCES
Blouin, S. and Inglis, G. (2013). Toward distributed noise-
source localization for underwater sensor network. In
Proceedings of the IET Intelligent Signal Processing
(ISP) conference, pages 1–6, London, UK.
Erbe, C. (2011). Underwater Acoustics: Noise and the Ef-
fects on Marine Mammals, A Pocket Handbook. Jasco
Applied Science, 3rd edition. —www.jasco.com—.
Hasannezhad, B., Barbeau, M., Blouin., S., Cervera, G.,
Garcia-Alfaro, J., and Kranakis, E. (2014). Sim-
ulation of underwater communications with colored
noise approximation and mobility. submitted to the
28th annual IEEE Canadian Conference on Electrical
and Computer Engineering (CCECE2015).
Heard, G., Desharnais, F., Ebbeson, G., Fleming, R., and
Schattschneider, G. (2009). The use of underwater
communication networks in fixed and mobile sens-
ing systems. In Underwater Acoustic Measurements,
pages 597–604, Nafpilon, Greece.
Johnson, D. and Maltz, A. (1996). Mobile Computing.
Kluwer Academics Publishers.
Karp, B. and Kung, H. (2000). GPSR: greedy perimeter
stateless routing for wireless networks. In Proceed-
ings of the 6th annual international conference on
Mobile computing and networking (MobiCom), pages
243–254.
Katsnelson, B., Petnikov, V., and Lynch, J. (2012). Funda-
mentals of Shallow-water Acoustics. Springer.
Kinsler, L., Frey, A., Coppens, A., and Sanders, J. (1982).
Fundamentals of Acoustics. John Wiley & Sons, Inc.,
third edition. pages 158-160 (model from Fisher and
Simmons, J. Acoust. Soc. Am., 62, 558, 1977).
Kinsler, L., Frey, A., Coppens, A., and Sanders, J. (2000).
Fundamentals of Acoustics. John Wiley & Sons, Inc.,
fourth edition. pages 226-228.
Li, Z., Li, R., Wei, Y., and Pei, T. (2010). A survey of lo-
calization techniques in wireless sensor networks. In-
formation Technology Journal, 9(8):1754–1757.
Lurton, X. (2010). An Introduction to Underwater Acous-
tics. Springer-Verlag, Berlin, 2nd edition.
Nicolaou, N., See, A., Cui, J., and Maggiorini, D. (2007).
Improving the robustness of location-based routing
for underwater sensor networks. In Proceedings of
the MTS/IEEE Oceans, pages 1–6, Vancouver (B.C.),
Canada.
Otnes, R., Asterjadhi, A., Casari, P., Goetz, M., Husoy, T.,
Nissen, I., Rimstad, K., van Walree, P., and Zorzi, M.
(2012). Underwater Acoustic Networking Techniques.
Springer.
Perkins, C. and Bhagwat, P. (1994). Highly dy-
namic destination-sequenced distance-vector routing
(DSDV) for mobile computers. ACM SIGCOMM
Comput. Cummun. Rev., 24(4):234–244.
Porto, A. and Stojanovic, M. (2007). Optimizing the trans-
mission range in an underwater acoustic network. In
Proceedings of the MTS/IEEE Oceans. Vancouver
(B.C.), Canada.
Rice, J. and Ong, C. (2010). A discovery process for ini-
tializing underwater acoustic networks. In Proceed-
ings of the Fourth International conference on Sensor
Technologies and Applications, pages 408–415.
Stojanovic, M. and Preisig, J. (2009). Underwater acous-
tic communication channels: Propagation models and
RefractedAcousticCommunicationsinWirelessUnderwaterSensorNetworkswithMobility
119

statistical characterization. IEEE Communication
Magazine, 47:84–89.
Urick, R. J. (1983). Principles of Underwater Sound. Mc-
Graw Hill, 3rd edition.
van Walree, P. (2013). Propagation effects in underwater
acoustic communication channel. IEEE Journal of
Oceanic Engineering, 38(4):614–631.
Zorzi, M., Casari, P., Baldo, N., and Harris, A. (2008).
Energy-efficient routing schemes for underwater
acoustic networks. IEEE J. Selected Areas in Comm.,
26(9):1754–1766.
APPENDIX
Proof of Proposition 1
z
i
+ R
i
> R
k
⇒ α
i
< α
max
i
: Using Equations (4) and
(5), the left-hand side of Equation (10) becomes
z
i
+ R
i
= z
i
−
c
i
g
= z
i
−
c
0
+ gz
i
g
= −
c
0
g
.
Given that c
i
> 0 for all i’s, that −π/2 < α = α
k
< π/2
or cosα > 0, and Equation (8), the right-hand side of
Equation (10) expands as
R
k
=
|R
i
|
cosα
=
c
i
|g|
·
1
cosα
=
c
0
+ gz
i
|g|
·
1
cosα
R
k
=
c
0
|g|
+ z
i
sign(g)
1
cosα
=
c
0
|g|cosα
+
z
i
sign(g)
cosα
so that Equation (10) can be re-written as
−
c
0
g
>
c
0
|g|cosα
+
z
i
sign(g)
cosα
which after manipulations becomes
−
c
0
g
−
c
0
|g|cosα
>
z
i
sign(g)
cosα
,
−
c
0
g
1+
1
sign(g)cosα
>
z
i
sign(g)
cosα
,
−
c
0
g sign(g)
[sign(g)cosα + 1] > z
i
sign(g),
sign(g)cosα + 1 <
gz
i
sign
2
(g)
−c
0
=
gz
i
−c
0
,
cosα <
1
sign(g)
gz
i
−c
0
− 1
= −
1
sign(g)
c
i
c
0
.
z
i
+ R
i
> R
k
⇐ α
i
< α
max
i
: Through contradiction,
we show that z
i
+ R
i
≤ R
k
⇒ α
i
≥ α
max
i
. Using the
previous development, it follows that
−
c
0
g
≤
c
0
|g|cosα
+
z
i
sign(g)
cosα
which through manipulations becomes
cosα ≥ −
1
sign(g)
c
i
c
0
.
thus
α ≥ arccos
−
1
sign(g)
c
i
c
0
= α
max
i
.
Proof of Proposition 3
(⇒) Assume that nodes i, j are linked through an
acoustic ray departing at angle |α
k
| < 0.5π from node
i. From Equation (8), the radius of curvature of the
acoustic ray departing from node i is R
k
. From Snell’s
Law and the constant slope g, the acoustic ray de-
scribes an arc of a circle meaning that the radius of
curvature for the entire arc remains equal to R
k
, thus
L = R
k
.
(⇐) If L = R
k
, then both nodes i, j are located on the
perimeter of a circle of radius R
k
. Consequently, both
nodes are linked by an acoustic ray given Snell’s Law
and the constant slope g. The departing angle α
k
fol-
lows from the relationship between R
k
and α
k
through
Equation (8) and the fact that |α
k
| < 0.5π.
Replacing L by R
k
in Equation (14) and putting it
to the square gives
(R
k
)
2
= (d
ij
− d
k
)
2
+ (z
i
+ R
i
− z
j
)
2
,
which after replacing R
K
and d
k
by their respective
expression in (8) and (9) leads to
R
i
cosα
k
2
= (d
ij
− R
i
tanα
k
)
2
+ (z
i
+ R
i
− z
j
)
2
.
Re-labeling z
i
− z
j
in the previous Equation by ∆z
ij
and expanding the right-hand side results in
R
i
cosα
k
2
= (d
ij
− R
i
tanα
k
)
2
+ (∆z
ij
+ R
i
)
2
R
2
i
cos
2
α
k
= d
2
ij
− 2d
ij
R
i
tanα
k
+ R
2
i
tan
2
α
k
+ ...
(∆z
ij
)
2
+ 2∆z
ij
R
i
+ R
2
i
Grouping all R
2
i
terms on the left-hand side gives
R
2
i
1
cos
2
α
k
− 1− tan
2
α
k
= d
2
ij
− 2d
ij
R
i
tanα
k
+ ...
(∆z
ij
)
2
+ 2∆z
ij
R
i
so that the new left-hand term equals zero thus leaving
the following expression
0 = d
2
ij
− 2d
ij
R
i
tanα
k
+ (∆z
ij
)
2
+ 2∆z
ij
R
i
which if re-arranged so as to extract α
k
leads to Equa-
tion (17).
SENSORNETS2015-4thInternationalConferenceonSensorNetworks
120
Node-to-node Distances
Node-to-node distances can be derived as follows
d
23
= d
13
− d
12
, d
35
= d
15
− d
13
,
d
24
= d
14
− d
12
, d
36
= d
16
− d
13
,
d
25
= d
15
− d
12
, d
45
= d
15
− d
14
,
d
26
= d
16
− d
12
, d
46
= d
16
− d
14
,
d
34
= d
14
− d
13
, d
56
= d
16
− d
15
.
Absorption Coefficient
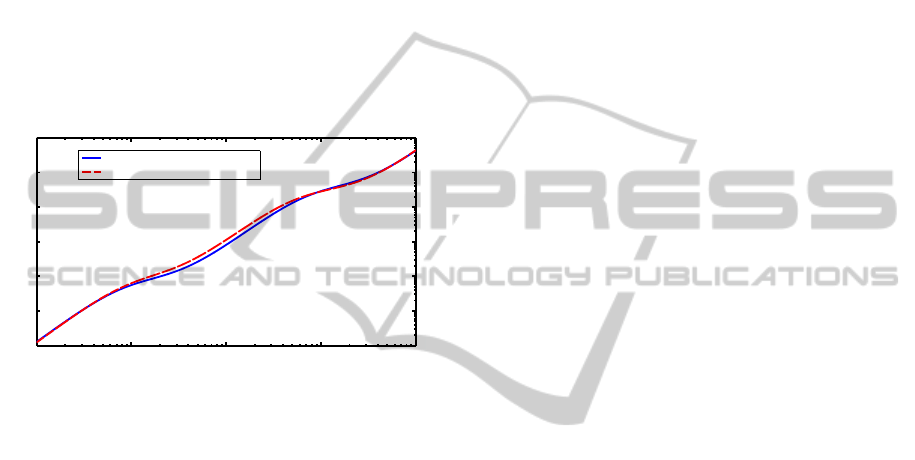
Figure 8 displays the absorption coefficient for one
atmosphere and a temperature of 5 degrees Celsius.
10
2
10
3
10
4
10
5
10
6
10
−6
10
−5
10
−4
10
−3
10
−2
10
−1
10
0
Frequency (Hz)
Absorption Coefficient (dB/m)
Kinsler, et al., Fourth Edition [19]
Kinsler, et al., Third Edition [18]
Figure 8: Absorption coefficient (1 atm., 5
o
C).
RefractedAcousticCommunicationsinWirelessUnderwaterSensorNetworkswithMobility
121
