
Simple Temporal Networks with Partially Shrinkable Uncertainty
∗
Andreas Lanz
1
, Roberto Posenato
2
, Carlo Combi
2
and Manfred Reichert
1
1
Institute of Databases and Information Systems, University of Ulm, Ulm, Germany
2
Department of Computer Science, University of Verona, Verona, Italy
Keywords:
Simple Temporal Constraint Network with Uncertainty, STNU, Controllability, Guarded Constraints.
Abstract:
The Simple Temporal Network with Uncertainty (STNU) model focuses on the representation and evaluation
of temporal constraints on time-pointvariables (timepoints), of which some (i.e., contingent timepoints) cannot
be assigned (i.e., executed by the system), but only be observed. Moreover, a temporal constraint is expressed
as an admissible range of delays between two timepoints. Regarding the STNU model, it is interesting to
determine whether it is possible to execute all the timepoints under the control of the system, while still
satisfying all given constraints, no matter when the contingent timepoints happen within the given time ranges
(controllability check). Existing approaches assume that the original contingent time range cannot be modified
during execution. In real world, however, the allowed time range may change within certain boundaries, but
cannot be completely shrunk. To represent such possibility more properly, we propose Simple Temporal
Network with Partially Shrinkable Uncertainty (STNPSU) as an extension of STNU. In particular, STNPSUs
allow representing a contingent range in a way that can be shrunk during run time as long as shrinking does
not go beyond a given threshold. We further show that STNPSUs allow representing STNUs as a special case,
while maintaining the same efficiency for both controllability checks and execution.
1 INTRODUCTION
For more than a decade, the temporal constraint com-
munity has focused on the concept of controllabil-
ity (Morris et al., 2001). Given a set of temporal
constraints, of which each is expressed as an admissi-
ble range of delays between two time-point variables
(timepoints for short), we distinguish two types of
constraints: contingent and requirement constraints.
The latter represent the standard temporal constraints,
where both timepoints are under control of the sys-
tem that “executes” the timepoints according to the
assigned constraints (i.e., the system fixes the time-
points on the time line). This means that, during
execution, the range admissible for some timepoints
could be restricted by the system as it depends on
the execution of already executed timepoints. In turn,
contingent constraints are related to pairs of time-
points of which one (i.e., the contingent timepoint)
is not under control of the system. Contingent time-
points are either given by the environment (Morris
et al., 2001), i.e., they are related to uncontrollable,
but expected, events, or by an external agent (i.e.,
human or software) who may decide autonomously
when to execute the contingent timepoint. Consider-
ing this scenario, the attention of the temporal con-
∗
This paper is a short version. A more complete version
is described in a technical report (Lanz et al., 2014).
straint community has moved from the problem of
consistency, which consists of determining whether
there exists an execution of all timepoints satisfying
all given constraints (Dechter et al., 1991), to the prob-
lem of controllability; i.e., to determine whether it is
possible to execute all timepoints under the control of
the system, while satisfying all given constraints, no
matter when the contingent timepoints happen within
their given time ranges (Morris et al., 2001).
Most contributions from literature assume that the
original time range of a contingent constraint cannot
be modified during execution. Thus there is no differ-
ence between contingent timepoints given by the en-
vironment and the ones executed by external agents.
In the real world, however, it is quite common that
during execution the allowed time range may change,
although it cannot be completely shrunk. To represent
the behavior of external agents more properly, we may
assume that an agent accepts certain reductions (i.e.,
modifications) of the initial execution range, as long
as these do not go beyond a given threshold. In other
words, there is an unshrinkable range of execution
time the agent can always use. Further, this range is in-
cluded into a larger one, the system may shrink during
execution. The basic idea of our approach is to repre-
sent the fact that both the agent and the system are
aware that some timepoints of the larger time range
may be removed before starting the agent’s activity.
370
Lanz A., Posenato R., Combi C. and Reichert M..
Simple Temporal Networks with Partially Shrinkable Uncertainty.
DOI: 10.5220/0005200903700381
In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART-2015), pages 370-381
ISBN: 978-989-758-074-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

T1 Biking
[5,20]
T2 Stretching
[10,40]
[1,5]
[25,50]
(a) Rigid temporal ranges
T1 Biking
[5,20]
T2 Stretching
[10,[15,20],40]
[1,5]
[25,50]
(b) Flexible temporal ranges
Figure 1: A simple physiotherapy. Range [x,y] represents
the minimum and maximum allowed duration (in minutes)
for the corresponding activity.
For example, consider a physiotherapy (cf. Fig. 1)
consisting of two subsequent activities, namely Biking
and Stretching, with one overall temporal constraint.
The first activity has an allowed duration range, while
its actual duration is decided by the physiotherapist
according to the patient’s state. The second activ-
ity, i.e., the stretching exercise, is performed by the
patient over a time period, which is decided by an-
other therapist who considers both the state of the
patient and the goal of the therapy. Let us assume
that the given ranges are as depicted in Fig. 1 (a):
activities are visualized as rounded boxes and subse-
quent activities are linked to their predecessor through
a directed arc. Temporal constraints are represented
through arcs together with their related ranges. Ac-
tivities Biking and Stretching have possible durations
within ranges [5, 20] and [10,40], respectively, which
are autonomously decided by therapists. However,
the overall therapy must be within range [25,50], as-
suming that it may take between 1 and 5 time units to
start Stretching after ending Biking. Note that for this
scenario it can be easily verified that the correspond-
ing temporal network is not controllable, as there is
no way to ask the second activity to have a duration
depending on the actual duration of the first activity.
As more realistic representation of this scenario,
the second therapist may accept that the allowed du-
ration range may be shrunk during execution, while
guaranteeing that the “core” range [15, 20] can be al-
ways applied when executing Stretching. This sce-
nario is depicted in Fig. 1 (b) where the range is
represented as [10,[15, 20],40], highlighting the non-
shrinkable part. One can easily observe that in this
case the network can be executed in a way satisfy-
ing all constraints, while still allowing the therapists
to autonomously choose the durations of the involved
activities.
This paper discusses how to represent and deal
with the described extension of contingent constraints
in simple temporal constraint networks with uncer-
tainty (STNUs), i.e., temporal networks that allow
representing both requirement and contingent con-
straints (Morris et al., 2001). In addition to dynamic
controllability, we discuss that there are no alterna-
tive representations of such shrinkable contingent con-
straints based on compositions of standard require-
ment and contingent constraints. Moreover, we gen-
eralize shrinkable constraints to represent time ranges
having certain “guards” on their possible lower and
upper bounds.
2 BACKGROUND AND RELATED
WORK
A Simple Temporal Network (STN) (Dechter et al.,
1991) is a directed weighted graph where a node rep-
resents a time-point variable (timepoint), usually cor-
respondingto the start or end of activities, and an edge
represents a lower and an upper bound constraint on
the distance between the two timepoints it connects.
Each STN is associated with a distance graph, derived
from the upper and lower bound constraints, where a
constraint between a pair of timepoints X and Y is
represented as two edges: X
v
→ Y, representing the
constraint Y ≤ X + v, and X
−u
← Y, which stands for
Y ≥ X + u, u,v ∈ R. An STN is denoted as consistent
if it is possible to execute each node, i.e., to assign a
real value to each timepoint such that all temporal con-
straints are satisfied. The consistency property can be
verified by searching for negative loops in the graph.
It is well known that consistency checking as well as
determining the earliest/latest value of each timepoint
can be done in polynomial time (Dechter et al., 1991).
To represent events that cannot be executed,
but only observed, (Morris et al., 2001) intro-
duced Simple Temporal Networks with Uncertainty
(STNUs). STNUs augment Simple Temporal Net-
works (STN) (Dechter et al., 1991) with contingent
timepoints representing timepoints whose value is de-
cided by the environment. Each contingent timepoint
has one incoming edge, called contingent link, which
is labeled by a time range. Therefore, any contin-
gent timepoint may assume a value from a bounded
range, but the exact value is decided by the environ-
ment at run time. (Morris et al., 2001) provided a for-
mal semantics for the dynamic controllability, which
is discussed in detail in Sect. 2.1. Moreover, (Mor-
ris et al., 2001) presented a pseudo-polynomial-time
algorithm, called DC-checking algorithm, that deter-
mines whether a given STNU is dynamically control-
lable (DC). Further, (Morris and Muscettola, 2005)
SimpleTemporalNetworkswithPartiallyShrinkableUncertainty
371

proposed the first polynomial DC-checking algorithm,
which operates in O(n
5
) time, where n is the number
of timepoints. In this paper, we denote this algorithm
as MM5. In turn, (Morris, 2006) and (Morris, 2014)
presented two interesting optimizations of the MM5
algorithm not further discussed in this paper.
(Lanz et al., 2013) showed how Conditional Sim-
ple Temporal Networks with Uncertainty (CSTNUs),
an extension of STNU considering alternative execu-
tion paths, can be applied in the context of time-aware
business processes in order to verify their controllabil-
ity at both design and run time. Concerning temporal
aspects of a business process, it is emphasized that ac-
tivity durations usually represent worst case estimates,
which are either based on the experience of a domain
expert or extracted from process logs; further, the ex-
ecution times of most activities can be shortened if
required. Accordingly, one may assume that an ac-
tivity has a flexible maximum duration MaxD
F
that
may be restricted up to a contingent minimum and
maximum duration range [MinD
C
,MaxD
C
]. In other
words, they proposedand analyzed a mapping of time-
aware business processes to CSTNU in which activity
durations are expressed in terms of shrinkable time
intervals [[MinD
C
,MaxD
C
]MaxD
F
].
For a more extensive discussion of the related
work please refer to our technical report (Lanz et al.,
2014).
2.1 Dynamic Controllability of STNUs
As proposed by (Morris et al., 2001), an STNU is
a set of time-point variables (timepoints) and tempo-
ral constraints together with a set of contingent links.
Each contingent link has the form (A, x, y,C), where
A and C are timepoints and 0 < x < y < ∞ holds. A
is called the activation timepoint and C the contingent
timepoint. Once A is executed, C is guaranteed to be
executed such that C− A ∈ [x, y] holds. However, the
particular time at which C is executed is uncontrol-
lable since it is decided by the environment; i.e., it
can be only observed when it happens.
Let S = (T , C,L) be an STNU, with T being a
set of timepoints, C a set of constraints, and L a set of
contingent links. The corresponding graph for S has
the form (T ,E, E
ℓ
,E
u
). Thereby, each timepoint in
T serves as a node in the graph; E is a set of ordinary
edges; E
ℓ
is a set of lower-case and E
u
a set of upper-
case edges (Morris and Muscettola, 2005):
• Each ordinary edge has the form X
v
Y, repre-
senting the constraint Y − X ≤ v.
• Each lower-case edge has the form A
c : x
C, repre-
senting the possibility that the contingent duration,
C− A, might take on its minimum value x.
• Each upper-case edge C
C:−y
A, represents the
possibility that the contingent duration, C − A,
might take on its maximum value y.
An STNU is dynamically controllable if there ex-
ists a strategy for executing its timepoints, in a way
guaranteeing that all constraints in the network can
be satisfied, no matter how the durations of the contin-
gent links actually turn out. The strategy is dynamic
since its execution decisions can react to observations
of contingent links that have already been completed,
while excluding those not completed yet.
This section presents preliminary notions and in-
troduces the dynamic controllability of an STNU as
defined in (Morris et al., 2001) and subsequently fixed
in (Hunsberger, 2009).
For an STNU, a situation specifies fixed durations
for all contingent links.
Definition 1 (Situations). Let S be an STNU
comprising k contingent links, (A
1
,x
1
,y
1
,C
1
),. . .,
(A
k
,x
k
,y
k
,C
k
), with corresponding duration ranges
[x
1
,y
1
],. . .,[x
k
,y
k
]. Then: Ω
S
= [x
1
,y
1
] ×. .. ×[x
k
,y
k
]
is called the space of situations for S. Any ω =
(d
1
,. . .,d
k
) ∈ Ω
S
is called a situation. Where possi-
ble, we may write Ω instead of Ω
S
.
The concept of schedule formalizes the execution
of timepoints.
Definition 2 (Schedule). A schedule for an STNU is
a mapping ψ : T → R that assigns a real number to
each timepoint in T .
Given a situation ω for an STNU, the replacement
of its contingent links by the durations specified in ω
determines a projection of the STNU onto situation ω.
Definition 3 (Situation Projection for an STNU). Sup-
pose S = (T , C ,L) is an STNU and ω = (d
1
,. . .,d
k
)
a situation. The projection of S onto ω—denoted as
sitPrj(S, ω)—is the STN (T , C
′
) with:
C
′
= C ∪ {(d
i
≤ C
i
− A
i
≤ d
i
) | 1 ≤ i ≤ k}
Given an STNU, multiple schedules may exist.
We are interested in finding a strategy that determines
schedules that satisfy all constraints in any situation.
Definition 4 (Execution Strategy for an STNU). Let
S = (T ,C ,L) be an STNU. An execution strategy for
S is a mapping σ : Ω → ψ such that for each situa-
tion ω ∈ Ω, σ(ω) is a (complete) schedule for the
timepoints in T . Furthermore, if for each situation ω
schedule σ(ω) is a solution for the situation projec-
tion sitPrj(S ,ω), then σ is called viable. In any case,
the execution time of timepoint X in schedule σ(ω) is
denoted as [σ(ω)]
X
.
A situation history for an STNU specifies the du-
rations of all contingent links that have finished their
execution prior to a time t in schedule σ(ω).
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
372
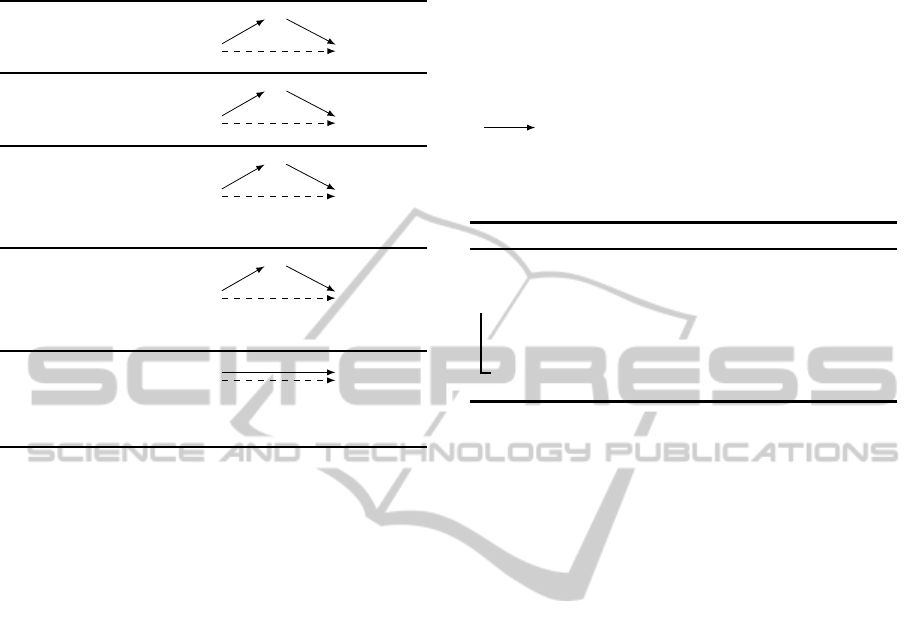
Table 1: Edge-generation rules of the MM5 algorithm.
Dashed edges are the generated ones.
No Case:
Q
T
S
u
v
u+ v
Upper Case:
Q
T
S
u
R : v
R : u+ v
Lower Case:
Q
T
S
s : u
v
u+ v
Applicable if: v < 0 ∨ (v = 0 ∧ S 6≡ T)
Cross Case:
Q
T
S
s : u
R : v
R : u+ v
Applicable if: R 6≡ S ∧ (v < 0∨ (v = 0 ∧ S 6≡ T))
Label Removal:
S
T
R : v
v
Applicable if: v ≥ −x, x is the lower
bound for the contingent link from T to R
Definition 5 (Situation History for an STNU). Let
S = (T , C, L) be any STNU, σ any execution strat-
egy for S, ω any situation, and t any real number. The
history of t in situation ω for strategy σ—denoted as
sitHst(t,ω, σ)—is defined as follows:
sitHst(t,ω, σ) = {(A,C, [σ(ω)]
C
− [σ(ω)]
A
) |
∃x,y such that (A, x, y,C) ∈ L ∧ [σ(ω)]
C
< t}
Definition 6 (Dynamic Execution Strategy for an
STNU). An execution strategy σ for an STNU is
called dynamic if for any situations, ω
1
and ω
2
, and
any non-contingent timepoint X, it holds:
sitHst([σ(ω
1
)]
X
,ω
1
,σ) = sitHst([σ(ω
1
)]
X
,ω
2
,σ)
⇒ [σ(ω
1
)]
X
= [σ(ω
2
)]
X
.
Definition 7 (Dynamic Controllability of an STNU).
An STNU S is called dynamically controllable (DC)
if there exists an execution strategy for S that is both
viable and dynamic.
In order to determine whether an STNU is dynami-
cally controllable, (Morris and Muscettola, 2005) pro-
posed a polynomial-time checking algorithm, MM5,
which works by recursively generating new edges in
the STNU graph according to the rules from Table 1
and checking whether newly added edges determine
negative loops in the graph. For each rule, existing
edges are represented as solid arrows and newly ones
as dashed arrows. Each of the first four rules takes two
existing edges as input and generates a single edge as
output. Finally, notation R 6≡ S expresses that R and
S must be distinct time-point variables, and does not
represent a constraint on the values of those variables.
We observe that the edge-generation rules from
Table 1 only generate ordinary or upper-case edges.
The upper-case edges generated by respective rules
represent conditional constraints, called waits (Mor-
ris et al., 2001). In particular, an upper-case edge
B
C:−v
A represents the following constraint: as long
as contingent timepoint C remains unexecuted, time-
point B must wait at least v units after the execution
of A, the activation timepoint for C.
Procedure: MM5-DC-Check(G).
Input: G = (T , C ,L): STNU graph instance to analyze.
Output: the controllability of G.
for 1 to |T |
2
+ |T ||L| +|L| do
if (AllMax matrix inconsistent) then return false;
Generate new edges using rules from Table 1;
if (no edges generated) then return true;
return false;
Procedure MM5-DC-Check shows the pseu-
docode of the MM5 DC-checking algorithm. Its time
complexity is O(n
5
) (Morris and Muscettola, 2005).
2.2 Alternative Characterization of an
Execution Strategy
As observed in (Hunsberger, 2009), the original defi-
nition of dynamic execution strategy (DES) obscures
the real-time features of typical execution scenarios
and the kinds of execution decisions an execution sys-
tem may make. Therefore, (Hunsberger, 2009) pro-
posed an alternative characterization of a DES to not
only represent the conditions under which a system
must make real-time execution decisions, but also
the outcomes of those decisions. Two kinds of real-
time execution decisions (RTEDs) are defined: WAIT
and (τ,χ), which can be described as: “Wait until
some contingent duration completes” or “If nothing
happens before τ, then execute the (executable) time-
points in χ.” The outcome of a RTED depends on
the situation and is represented by a partial sched-
ule that specifies the execution of one or more addi-
tional timepoints. The outcome of a WAIT decision
solely involves the execution of contingent timepoints,
whereas the outcome of a (τ,χ) decision may involve
the execution of contingent as well as non-contingent
timepoints. An RTED-based strategy is defined as
a mapping from partial schedules to real-time execu-
tion decisions. (Hunsberger, 2009) proved that RTED-
based strategies correspond one-to-one to DESs.
In more detail, givenan STNU and a partial sched-
ule ψ : T → R (i.e., the domain of ψ may be a subset
of T ), we denote by µ(ψ) = max{ψ(t) | t ∈ Dom(ψ)}
SimpleTemporalNetworkswithPartiallyShrinkableUncertainty
373

the maximum execution time of timepoints appearing
in ψ, by U(ψ) = {x | x 6∈ Dom(ψ)} the set of unex-
ecuted timepoints in ψ, by U
x
(ψ) ⊆ U(ψ) the set of
non-contingent unexecuted timepoints, by U
c
(ψ) ⊆
U(ψ) the set of contingent unexecuted timepoints,
and by U
a
(ψ) ⊆ U
c
(ψ) the set of contingent activated
unexecuted timepoints, respectively.
Let ψ be a partial schedule for an STNU S and
ω = (ω
1
,. . .,ω
q
) a situation for S. ψ respects ω if for
each contingent link (A
i
,x, y,C
i
) one of the following
conditions holds: (1) neither A
i
nor C
i
appear in ψ;
(2) only A
i
appears in ψ, and ψ(A
i
) + ω
i
> µ(ψ); or
(3) both A
i
andC
i
appear in ψ, and ψ(A
i
)+ω
i
= ψ(C
i
).
ψ is called respectful if it respects at least one situa-
tion. If ψ is both respectful and partial, it is called
a respectful, partial schedule (RPS). A strategy σ is
respectful if for each ω, σ(ω) respects ω.
Let us recall the definition of WAIT and (τ, χ) de-
cisions.
WAIT Decision. Let ψ be some RPS for S such that
U
a
(ψ) is non-empty. Then WAIT is an admissible
RTED.
Outcome of a WAIT Decision. If U
a
(ψ) 6=
/
0 and ω
is a situation respected by ψ, then the time at which
the next contingent timepoint will execute is defined
as tnc(ψ, ω) = min{ψ(A
i
) + ω
i
| C
i
∈ U
a
(ψ)}. With
χ
a
(ψ,ω) = {C
i
∈ U
a
(ψ) | ψ(A
i
) + ω
i
= tnc(ψ,ω)},
we denote the non-empty set of contingent timepoints
that will be executed at time tnc(ψ, ω). Then, the out-
come of the WAIT decision for ψ in situation ω is de-
fined to be the execution of contingent timepoints at
time tnc(ψ,ω): ψ ∪ {(C
i
,tnc(ψ, ω)) | C
i
∈ χ
a
(ψ,ω)}.
(τ,χ) Decision. Let ψ be some RPS for S such that
U
x
(ψ) 6=
/
0. If τ > µ(ψ) and χ is a non-empty subset
of U
x
(ψ), then (τ,χ) is an admissible RTED for ψ.
Outcome of a (τ, χ) Decision. Let ω be a situation
respected by ψ. The outcome of a (τ,χ) decision de-
pends on the relationship between tnc(ψ, ω) and in-
stant τ. For the sake of simplicity, let τ
c
= tnc(ψ,ω)
and χ
a
= χ
a
(ψ,ω) ifU
a
(ψ) 6=
/
0; otherwise, let τ
c
= ∞.
If τ
c
< τ, the outcome solely involves the execution
of the contingent timepoints in χ
a
. In turn, if τ < τ
c
,
the outcome solely involves the execution of the non-
contingent timepoints in χ. Finally, for τ
c
= τ, the
outcome involves the execution of the timepoints in
both χ
a
and χ.
(Hunsberger, 2009) proved that the original
dynamic execution strategy can be described
in terms of RTEDs as shown in procedure
RTEDExecutionStrategy. Thereby, function
RTExecutionDecision is used to determine the
the next RTED. For the sake of brevity, the RTED
WAIT is represented as (τ, χ) decision with τ := ∞
and χ :=
/
0 in the given context.
Function: RTExecutionDecision(S , ψ).
Input: S : STNU. ψ; partial schedule
Output: δ(ψ): real-time execution decision
if (U
x
(ψ) =
/
0) then // WAIT RTED!
δ(ψ) := (τ
x
,χ), where τ
x
:= ∞ and χ :=
/
0;
else // (τ, χ) RTED!
foreach (x ∈ U
x
(ψ)) do
[m(x), M(x)] = current time-window for x;
W(x) := −∞;
foreach ((A
i
,C
i
) | C
i
∈ U
a
(ψ) ∧ x
C
i
:−w
i
−→ A
i
) do
W(x) := max{W(x),ψ(A
i
) + w
i
};
floor(x) := max{m(x),W(x)};
go(x) := min{ floor(x), M(x)};
δ(ψ) := (τ
x
,χ), where τ
x
:= min{go(x) | x ∈ U
x
(ψ)}
and χ := {x ∈ U
x
(ψ) | τ
x
= go(x)};
return δ(ψ);
Procedure: RTEDExecutionStrategy(S).
Input: S : STNU.
ψ = {(Z, 0)}; // initial partial schedule
while (U(ψ) 6=
/
0) do
(τ
x
,χ) = RTExecutionDecision(S ,ψ);
if (nothing happens before time τ
x
) then
Execute the timepoints in χ;
else
Observe the contingent timepoints executed at
some τ
c
< τ
x
;
Update ψ to include the executed events;
Update S to include the corresponding constraints;
Starting with a partial schedule ψ = {(Z,0)},
which only fixes the initial timepoint Z, proce-
dure RTEDExecutionStrategy iteratively determines
an RTED δ(ψ), considering two possibilities (cf.
function RTExecutionDecision). If all executable
timepoints have already been executed, δ(ψ) = (∞,
/
0)
holds (i.e., RTED WAIT); otherwise, δ(ψ) = (τ
x
,χ)
with the values of τ
x
and χ being computed by con-
sidering all unexecuted timepoints and using an all-
pairs, shortest-path algorithm. floor(x) corresponds
to the earliest time, timepoint x may be executed with-
out violating its lower bound m(x) or any of its rele-
vant waits. go(x) is the same, except that it enforces
the constraint that x does not violate its upper bound
M(x). It is noteworthy that Morris and Muscettola
showed that a conflict between floor(x) and M(x)
is not possible for an STNU accepted by their algo-
rithm. After determining the RTED δ(ψ) = (τ
x
,χ),
procedure RTEDExecutionStrategy waits for the out-
come of δ(ψ) and then updates ψ and S accordingly.
If there are still unexecuted timepoints, the procedure
iterates, otherwise it terminates.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
374

3 GUARDED TEMPORAL
CONSTRAINTS
Regarding an STNU, the execution of a contingent
timepoint can be thought of as being completely out
of the control of the system that executes the network.
Typically, a system activates a contingent link (A, x,
y,C) by executing its activation timepoint A. After-
wards, the execution of C is out of the system’s con-
trol. However, the contingent timepoint C is guaran-
teed to execute such that C− A ∈ [x,y] holds.
As motivated in Sect. 1, for real-world problems
this is often too strict. In many cases, the system may
exercise some control over the execution of the con-
tingent timepoint. As example consider a case where,
at an activation timepoint, the system transfers control
to an external agent. The agent is then responsible for
executing the corresponding contingent timepoint. In
turn, the system waits for the agent to complete its
task (i.e., to execute the contingent timepoint). When
transferring the control to the agent, the system may
inform the agent about the temporal constraints to be
met. The agent then adapts its plan in order to com-
ply with the additional constraints. At the same time,
the system must guarantee that it is able to meet the
commitment made, i.e., it needs to ensure that it can
deal with any decision the agent makes for executing
timepoint C based on the given constraints.
In many cases, the agent responsible for executing
timepoint C cannot completely control the execution
of C either (e.g., in case the agent is executing a net-
work itself). Particularly, he might only be able to pro-
vide a preferred duration range [x, y] as well as bounds
x
max
and y
min
to which x may be increased or y may
be decreased (i.e., x ≤ x
max
and y ≥ y
min
). In turn, the
system executing the network must ensure that, when
executing timepoint A (i.e., when activating the con-
straint between A and C), the agent responsible for
executing timepoint C has at least y
min
time units and
is not required to take more than x
max
time units to
execute C. We denote x
max
(y
min
) as the guard of x
(y).
Note that this example addresses a common sce-
nario, i.e., to transfer execution control at run time
to another agent, which is responsible for executing a
complex task (e.g., another network).
The need to model constraints of this type requires
an extension of the STNU formalism, we denote as
Simple Temporal Network with Partially Shrinkable
Uncertainty (STNPSU). In particular, STNPSU ex-
tends contingent links of STNU to guarded links.
Definition 8 (STNPSU). A Simple Temporal Net-
work with Partially Shrinkable Uncertainty (STNPSU)
is a triple (T ,C ,G), where:
• T is a set of timepoints;
• C is a set of requirement constraints X
[u,v]
−→ Y (i.e.,
STN constraints); and
• G is a set of guarded links each having the form
(A,[x, x
max
],[y
min
,y],C) where A and C are time-
points, and 0 ≤ x ≤ y < ∞, x ≤ x
max
, 0 ≤ y
min
≤ y.
• If (A
1
,[x
1
,x
1
max
],[y
1
min
,y
1
],C
1
) as well as (A
2
,
[x
2
,x
2
max
],[y
2
min
,y
2
],C
2
) are distinct guarded
links in G, then C
1
and C
2
are distinct timepoints.
Informally, we denote an STNPSU as dynamically
controllable if it is possible to execute it such that, no
matter how the execution of any guarded link turns
out, for any other guarded link (A,[x,x
max
],[y
min
,y],
C) the lower bound x never must be increased beyond
its guard x
max
and the upper bound y never must be
decreased below its guard y
min
in order to ensure con-
trollability of the network.
The execution semantics of STNPSU can be sum-
marized as follows: The basic execution semantics is
the same as for an STNU. However, when executing
an STNPSU, the outer bounds [x, y] of a guarded link
(A,[x, x
max
],[y
min
,y],C) may be restricted to [x
′
,y
′
]
with x ≤ x
′
≤ x
max
, y
min
≤ y
′
≤ y, and x
′
≤ y
′
in or-
der to ensure controllability of the remaining network.
In turn, when executing the activation timepoint A of
a guarded link (A, [x, x
max
],[y
min
,y],C), the latter is ac-
tivated and its current bounds [x
′
,y
′
] are fixed. Partic-
ularly, the guarded link (A,[x, x
max
],[y
min
,y],C) is re-
placed by the strict guarded link (A,[x
′
,x
′
],[y
′
,y
′
],C).
The latter is equivalent to a contingent link of STNU.
As we will show in Sect. 3.3, this change does not
affect controllability of the network.
It is noteworthy that guarded links of STNPSU
may be used to represent two different types of con-
straints
1
:
Type 1: If x
max
< y
min
holds, a guarded link repre-
sents a partially contingent constraint. Particu-
larly, the guarded link represents a temporal con-
straint x ≤ C − A ≤ y with a contingent (i.e., un-
shrinkable) core [x
max
,y
min
] ⊆ [x,y]. This repre-
sents an extension of the classical contingent links
of STNU. Moreover, if x = x
max
∧ y = y
min
hold,
the guarded link is equivalent to a contingent link
of STNU. We call this a strict guarded link.
Type 2: If x
max
≥ y
min
holds, a guarded link rep-
resents a partially shrinkable constraint with a
guarded core [y
min
,x
max
]. In detail, this repre-
sents a temporal constraint x ≤ C − A ≤ y whose
bounds cannot be shrunk beyond a certain point
(i.e., x
max
and y
min
, respectively). As opposed to a
contingent link, x may be restricted to be greater
1
Please refer to our technical report (Lanz et al., 2014)
for a more detailed discussion.
SimpleTemporalNetworkswithPartiallyShrinkableUncertainty
375

than y
min
and y to be lower than x
max
. This rep-
resents an extension of the classical requirement
constraints.
As example of a Type 1 guarded link consider
guarded link (A,[10, 15],[20, 40],C), which repre-
sents the duration of activityStretching (cf. Fig. 1 (b)).
During execution, the outer bounds [10, 40] of this
guarded link may be shrunk in order to ensure con-
trollability of the remaining network. In the given
case, for example, they may be shrunk to (A,[7,15],
[20, 23],C) or (A, [5, 15],[20, 20],C). However, the
outer bounds may at most be shrunk to the contingent
core of the guarded link, i.e., the above guarded link
may at most be shrunk to (A,[15, 15],[20, 20],C).
In turn, an example of a Type 2 guarded link
is given by (A, [5,20], [10, 25],C). In this case, the
lower bound of the guarded link may at most be
increased to 20 and the upper bound may at most
be decreased to 10. Thus, (A,[15, 20],[10, 20],C),
(A,[20, 20],[10, 23],C), and (A,[5, 20], [10, 10],C) are
possible values this guarded link may be shrunk to.
Note that a Type 2 guarded link may also be shrunk
to a single value, e.g., (A,[15, 20],[10, 15],C). How-
ever, a Type 2 guarded link must always allow for
at least one value within its guarded core [y
min
,x
max
]
(i.e., [10, 20]).
During execution, when activating a guarded link
of Type 1 or 2 (i.e., when executing its activation time-
point), the current outer bounds of the guarded link
are fixed. This is to ensure that the outer bounds of
the guarded link cannot be modified while it is active.
Therefore, the current outer bounds of the guarded
link are set to be strict. For example, when execut-
ing timepoint A, the Type 2 guarded link (A,[15, 20],
[10, 20],C) is replaced by a strict guarded link (A,
[15, 15], [20, 20],C). The latter is equivalent to a con-
tingent link (A, 15,20,C) of STNU and ensures that
the agent responsible for executing timepoint C may
now choose any time in range [15, 20] to execute time-
point C.
3.1 Dynamic Controllability of STNPSU
This section presents preliminary definitions of basic
concepts required for the definition of dynamic con-
trollability of a STNPSU.
The set of core situations specifies the contingent
core of all guarded links of Type 1 (partially contin-
gent guarded links), while the set of core settings spec-
ifies the guarded core of all guarded links of Type 2
(partially shrinkable guarded links).
Definition 9 (Core Situations and Core Settings).
Suppose S = (T , C ,G) is an STNPSU. Let G
c
= {g ∈
G|g = (A, [x,x
max
],[y
min
,y],C) ∧ x
max
< y
min
} be the
set of guarded links for which the guard x
max
of the
lower bound is lower than the guard y
min
of the upper
bound (i.e., Type 1). Further, let G
r
= G \ G
c
be the
set of guarded links for which y
min
≤ x
max
holds (i.e.,
Type 2).
If G
c
contains k guarded links, (A
1
,[x
1
,x
1
max
],
[y
1
min
,y
1
],C
1
),. . .,(A
k
,[x
k
,x
k
max
],[y
k
min
,y
k
],C
k
), then
Ω
c
S
= [x
1
max
,y
1
min
] × .. . × [x
k
max
,y
k
min
] is called the
space of core situations for S. Any ω
c
= (d
1
,. . .d
k
) ∈
Ω
c
S
is called a core situation.
Further, if G
r
contains m guarded links, (A
1
,
[x
1
,x
1
max
],[y
1
min
,y
1
],C
1
),. . .,(A
m
,[x
m
,x
m
max
],
[y
m
min
,y
m
],C
m
), then Ω
r
S
= [y
1
min
,x
1
max
] × .. . ×
[y
m
min
,x
m
max
] is called the space of core settings
for S.
Given the space of core situations Ω
c
and the
space of core settings Ω
r
of an STNPSU, a projection
of the STNPSU onto an STNU can be obtained as fol-
lows: First, each guarded link in G
c
is replaced by a
contingent link for the range specified in Ω
c
. Second,
each guarded link in G
r
is replaced by a requirement
constraint for the range in Ω
r
.
Definition 10 (Core STNU of an STNPSU). Let S =
(T , C, G) be an STNPSU.
Then: The projection of S onto its space of
core situations Ω
c
and its space of core settings Ω
r
—denoted as stnuPrj(S, Ω
c
,Ω
r
)—corresponds to an
STNU (T , C
′′
,L
′′
) with:
C
′′
= C ∪ {(y
i
min
≤ C
i
− A
i
≤ x
i
max
) | 1 ≤ i ≤ m,
Ω
r
=[y
1
min
,x
1
max
] × .. . × [y
m
min
,x
m
max
]}
L
′′
= {(A
i
,x
i
max
,y
i
min
,C
i
) | 1 ≤ i ≤ k,
Ω
c
=[x
1
max
,y
1
min
] × .. . × [x
k
max
,y
k
min
]}
We denote the respective STNU as the core STNU of
STNPSU S.
Finally, this leads us to the dynamic controllabil-
ity of an STNPSU. We provide a formalization of the
dynamic controllability of an STNPSU based on the
dynamic controllability of an STNU. We choose this
approach since the formalization of dynamic control-
lability of STNU is robust and verified in literature.
Theorem 1 (Dynamic Controllability of STNPSU).
An STNPSU S = (T ,C ,G) is dynamically control-
lable (DC), if the core STNU that results from the
STNU Projection stnuPrj(S, Ω
c
,Ω
r
) of the STNPSU
is dynamically controllable.
Proof. ⇒ It is a matter of definitions to show that, if
the core STNU is DC (cf. Sect. 2.1), the correspond-
ing STNPSU is DC as well: each schedule being a
solution of the core STNU is also a solution of the
STNPSU. Indeed, it is always possible to restrict the
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
376
STNPSU to its core situations. Thus, for each core sit-
uation of the STNPSU, a dynamic execution strategy
(DES), which is a viable DES for the STNU, is also a
viable DES for the STNPSU regarding its core situa-
tions. Hence, if the core STNU is DC, the STNPSU
will be DC as well.
⇐ If the core STNU is not DC (i.e., no viable DES
exists), at least one core situation ω
c
of the STNPSU
exists for which no DES exists within the core set-
tings. Hence, for core situation ω
c
, one of the partially
shrinkable guarded links must be restricted beyond its
guards to find a DES which returns a solution. As this
is not possible, the STNPSU is not DC either.
3.2 DC-Checking for Guarded
Constraints
This section shows how the dynamic controllability
of an STNPSU may be checked without need to re-
strict the respective STNPSU to its core STNU. First,
we emphasize the close relationship between dynamic
controllability of STNU and the one of STNPSU (cf.
Theorem 1). In turn, this fosters the following graph-
based representation of an STNPSU, which is similar
to the one of an STNU.
Definition 11 (Graph of a STNPSU). The graph for
an STNPSU S has the form (T , E, E
ℓ
,E
u
), where
each timepoint in T corresponds to a node in the
graph; E is a set of ordinary edges, E
ℓ
is a set of
lower-case edges, and E
u
is a set of upper-case edges:
• Each requirement constraint X
[u,v]
−→ Y is repre-
sented by two ordinary edges X
v
−→ Y and Y
−u
−→
X.
• Each guarded link (A, [x, x
max
],[y
min
,y],C) is rep-
resented by
– two ordinary edges A
y
−→ C and C
−x
−→ A,
– one lower-case edge A
c:x
max
−→ C, and
– one upper-case edge C
C:−y
min
−→ A.
As example of this graph-based representation of
an STNPSU, consider the graph depicted in Fig. 2. It
shows the STNPSU corresponding to the activity se-
quence depicted in Fig. 1 (b). If multiple edges exist
between two nodes (e.g., an ordinary and an upper-
case edge), for the sake of readability, we draw only
one arrow between the nodes and annotate it with the
values of the respective edges. Further, we use bold
arrows to highlight edges representing a guarded link.
At this point, we want to emphasize important dif-
ferences between the graph of an STNU and the one
of an STNPSU:
• In an STNU, the value of any lower-case edge
A
c:x
max
−→ C always corresponds to the negativevalue
B
S
B
E
S
S
S
E
20; b
E
:5
−5; B
E
:−20
5
−1
40; b
E
:15
−10; B
E
:−20
50
−25
B
S
= Start of Biking; B
E
= End of Biking;
S
S
= Start of Stretching; S
E
= End of Stretching
Figure 2: STNPSU corresponding to the activity sequences
from Fig. 1 (b).
Q
S
y; s:x
max
−x; S:−y
min
Figure 3: Guarded Link.
of the ordinary edge C
−x
−→ A pointing in the op-
posite direction (i.e., x = x
max
). Similarly, the
value of any upper-case edge C
C:−y
min
−→ A always
corresponds to the negativevalue of ordinary edge
A
y
−→C (i.e., y = y
min
). For an STNPSU, this does
not apply. Particularly, we only require x ≤ x
max
and y ≥ y
min
.
• In an STNU, the value of a lower-case edge
A
c:x
max
−→ C always is lower than the negative value
of the upper-case edge C
C:−y
min
−→ A pointing in the
opposite direction (i.e., x
max
< y
min
). Note that for
an STNPSU this is not required.
In our technical report (Lanz et al., 2014), we
show that, except one minor change regarding one
of the edge generation rules (cf. Table 1), proce-
dure MM5-DC-Check may be reused in order to
check dynamic controllability of a STNPSU. Partic-
ularly, we analyze all possible combinations of edges
between three nodes of an STNPSU graph (i.e., all
possible triangles). Based on this, it can be shown
that the resulting distance graph of the STNPSU has
no negative loops if and only if the distance graph of
the core STNU has no negative loops as well.
Consider the single guarded link depicted in Fig. 3.
It comprises two triangles S-Q-S and Q-S-Q. Note
that it is a matter of applying the edge-generation
rules to these two triangles (i.e., the No Case rule
to S-Q-S and the No Case, Upper Case, Lower Case,
and Label Removal rules to Q-S-Q) to ascertain that
a valid guarded link does not contain a negative loop.
In case of a partially shrinkable guarded link (Type 2),
in addition, the Label Removal (cf. Table 1) rule may
be applied to the upper-case edge between S and Q,
replacing it with a requirement edge. This poses no
problem for checking dynamic controllability, but it
is undesired as it obscures some of the properties of
the guarded link. Thus, we restrict the Label Removal
SimpleTemporalNetworkswithPartiallyShrinkableUncertainty
377

rule to R 6≡ S to prevent this. Note that this change
does not influence the applicability of the rule to an
STNU. Regarding an STNU, for R ≡ S it holds that
v < −x (i.e., x
max
< y
min
; cf. Table 1), i.e., for an
STNU, the rule will never be applied if R ≡ S holds.
3.3 Executing STNPSUs
This section shows how an STNPSU may be exe-
cuted by means of an appropriate extension of pro-
cedure RTEDExecutionStrategy (cf. Sect. 2.2).
Consider procedure ExRTEDExecutionStrategy.
The first part of the procedure executes the same
actions as procedure RTEDExecutionStrategy (cf.
Sect. 2.2). The second part activates all guarded links
(A
i
,[x, x
max
],[y
min
,y],C
i
) whose activation timepoint
A
i
has just been executed. The guarded link seman-
tics requires to allow each of them, once it is acti-
vated, to use any possible value in the range defined
by the current outer bounds, i.e., [x, y]. By construc-
tion and due to the fact that the network is DC, for a
Type 1 guarded link the possibility of using any pos-
sible value in the range is guaranteed only for the
core range [x
max
,y
min
], while for a Type 2 guarded
link only the possibility of using at least one value in
the range [y
min
,x
max
] is guaranteed. Particularly, the
execution of some other timepoints before the occur-
rence of C
i
may modify the bounds of these guarded
links making the network not controllable. Therefore,
the procedure has to suitably update the bounds of the
guarded links (lines 14–20) before transforming them
into strict ones (lines 21–27). Finally, the execution
goes back to the first part until there are no more un-
executed timepoints.
The key point of the procedure consists in the ex-
ecution of timepoints subjected to guarded links as
contingent timepoints with suitable ranges; this al-
lows for the exploitation of the correctness proof of
RTEDExecutionStrategy (Hunsberger, 2009). In or-
der to show that this transformation preserves the con-
trollability of the network, it is sufficient to show
that the transformation of any guarded link—during
runtime—into a strict one with a suitable range is al-
ways possible and preserves the dynamic controllabil-
ity of the rest of network (i.e., the unexecuted subnet-
work).
Theorem 2. Suppose S is a dynamically controllable
STNPSU, ψ is a respectful, partial schedule, and (A,
[x,x
max
],[y
min
,y],C) is a guarded link of S. Let us
assume that A has just been executed and that the
outer bounds x and y of the guarded link AC have
been updated as described in lines 13–25 of proce-
dure RTEDExecutionStrategy to the values x
′
and y
′
.
Then: The new values x
′
and y
′
satisfy x
′
≤ x
max
and
Procedure: ExRTEDExecutionStrategy(S ).
Input: S: STNPSU.
1 ψ = {(Z,0)}; // initial partial schedule
2 while (U(ψ) 6=
/
0) do
3 (τ
x
,χ) = RTExecutionDecision(S ,ψ);
4 if (nothing happens before time τ
x
) then
5 execute the time-points in χ;
6 else
7 observe the contingent timepoints executed at
some τ
c
< τ
x
;
8 χ = set of executed contingent timepoints;
9 Update ψ to include the execution events in χ;
10 Update S to include the corresponding
constraints;
11 foreach (A
i
∈ χ) do // Activate guarded links
12 foreach ((A
i
,[x, x
max
], [y
min
,y],C
i
) ∈ G) do
13 [x
′
,y
′
] = current outer bounds of guarded
A
i
C
i
;
14 repeat // Prepare the guarded link for execution
// Determine its maximum controllable range
15 range(A
i
,C
i
) = min{v− u | a ∈
U(ψ)!∧a
v
−→ C
i
∧v ≥ 0∧(C
i
−u
−→
a∨C
i
C
j
:−u
−→ a)};
// Update its bounds to observe max. controll.
range
16 y
′
=min{y
′
,max{y
min
,x
′
+
range(A
i
,C
i
)}};
// x
′
is update only if the update y
′
is not
sufficient
17 x
′
= max{x
′
,y
′
− range(A
i
,C
i
)};
18 if x
′
or y
′
is modified then
19 Update S to include the
modified outer bounds of the
guarded link;
20 until neither x
′
nor y
′
is modified;
// Consider the max possible wait constraint for C
i
21 W(A
i
,C
i
) := −∞;
22 foreach
((A
i
,C
j
)|C
j
∈ U
a
(ψ)∧C
i
C
j
:−w
j
−→ A
i
)do
23 W(A
i
,C
i
) := max{W(A
i
,C
i
),w
j
};
24 floor(A
i
,C
i
) := max{x
′
,W(A
i
,C
i
)};
25 x
′
:= min{ f loor(A
i
,C
i
),y
′
};
26 Transform the guarded link to the strict
guarded link (A
i
,[x
′
,x
′
], [y
′
,y
′
],C
i
);
27 Update S to include the new constraint;
y
min
≤ y
′
and the STNPSU S
′
resulting after the trans-
formation of the guarded link (A, [x
′
,x
max
],[y
min
,y
′
],
C) into the strict one (A, [x
′
,x
′
],[y
′
,y
′
],C) is dynami-
cally controllable as well.
Sketch of the proof. Due to the lack of space, we only
give a outline of the complete proof.
Let us assume that, before the execution of lines
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
378

13–25, the guarded link AC is given as (A,[x, x
max
],
[y
min
,y],C). Instructions of lines 13–25 update the
outer bounds [x,y] to [x
′
,y
′
]. Let us assume that the
guarded link is of Type 1.
2
Since the network is
DC before line 13 and the core range [x
max
,y
min
] is
a contingent range, the update made in lines 13–25
cannot reduce [x,y] to [x
′
,y
′
] such that x
′
> x
max
or
y
′
< y
min
holds. Hence, the updated range [x
′
,y
′
] con-
tains (possibly in a weak way) the core range of (A,
[x,x
max
],[y
min
,y],C). Thus, there are 4 possible cases:
(1) x
′
= x
max
∧ y
′
= y
min
, (2) x
′
= x
max
∧ y
′
> y
min
, (3)
x
′
< x
max
∧ y
′
= y
min
, and (4) x
′
< x
max
∧ y
′
> y
min
. In
case (1) the guarded link is already strict and, hence,
it is not changed by the procedure. Case (4) is a com-
bination of cases (2) and (3).
Hence, let us consider case (2) and (3). In
case (2), by contradiction, suppose that the changing
of the guarded link (A, [x
max
,x
max
],[y
min
,y
′
],C) into
the strict one (A, [x
max
,x
max
],[y
′
,y
′
],C) makes the re-
maining network not dynamically controllable. This
means that there exists at least one negative loop in-
volving timepoints A, C, and some B, where B has
not yet executed (i.e., it has to occur after A), but has
to be executed before C. All other timepoints, i.e.,
unexecuted ones that have to be executed after C, can-
not contribute to form a negative loop since each of
them—by definition of controllability—must have at
least one possible execution time for each possible ex-
ecution time of C in the range [ψ(A) + x
max
,ψ(A) +
y
′
].
Now, instead of considering the distance graph and
negative loops in it, let us reason in term of ranges
and their spans
3
. Given the dynamic controllabil-
ity of the network before the transformation, it is a
fact that B has at least one possible execution time
for each possible execution time of C in the range
[ψ(A) + x
max
,ψ(A) + y
min
], i.e., with such range there
is no negative loop involving A, B, and C. Equiva-
lently, the span of the constraint between B and C
is greater or equal to the span y
min
− x
max
+ 1 of the
contingent core of the guarded link between A and C.
Therefore, a negative loop can only emerge when the
new bound y
′
is considered, or, equivalent, when the
span of the constraint between B and C is less than the
span y
′
− x
max
+ 1 of the outer bounds of the guarded
link between A and C.
However, when preparing the guarded link for ex-
ecution, y
′
is determined such that the span of range
[x
max
,y
′
] of the link between A and C is lower than or
equal to the span of the constraint between B and C.
Thus, there cannot exist any negative loop involving
2
The case of a guarded link of Type 2 can be discussed
in a similar way.
3
The span of a range [a,b] is b−a+ 1.
A
S
A
C
A
E
y
C
;a
c
:x
C
−x
C
;A
C
:− y
C
f
y
F
−x
F
0
Figure 4: STNU pattern representing a shrinkable duration
range [x
F
,[x
C
+ f,y
C
], y
F
] (0 ≤ x
C
≤ x
F
≤ x
C
+ f ∧ x
C
≤ y
C
≤ y
F
≤
y
C
+ f).
A, B, and C.
Case (3) can be shown in a similar way taking also
into account any possible wait constraint that may in-
crease the value of x
′
.
4 ON THE EXPRESSIVENESS OF
GUARDED CONSTRAINTS
This section informally discusses the expressiveness
of STNPSUs. Further, we show that most guarded
links cannot be represented in STNUs by other solu-
tions.
Consider again the physiotherapy session scenario
from Fig. 1 (b): Activity Stretching has a duration
range of [10, 40], which may be shrunk to a core du-
ration range of [15,20] during run time according to
the actual duration of activity Biking. Fig. 2 depicts
the temporal aspects of the session in terms of an
STNPSU: each of the two activities is represented
through a pair of timepoints, of which one represents
the starting instant of the activity and the other one
the ending instant. The allowed duration of activity
Stretching is represented as guarded link (S
S
,[10, 15],
[20, 40], S
E
) while the contingent duration of activity
Biking is represented as strict guarded link (B
S
,[5, 5],
[20, 20], B
E
). Based on the results from Sect. 3 one
can easily verify that the STNPSU is dynamically con-
trollable, i.e., for each possible execution time of ac-
tivity Biking, the system is able to determine a suit-
able duration range for activity Stretching containing
the core range [15, 20] such that each possible execu-
tion time in this range satisfies the overall duration
constraint [25, 50].
Let us discuss some of the limitations that arise
when representing the temporal aspects of the physio-
therapy session in terms of an STNU. The main prob-
lem is how to represent the temporal constraints of
activity Stretching. One option to be considered is
the pattern depicted in Fig. 4. It constitutes a general-
ization of the pattern proposed by (Lanz et al., 2013).
This pattern is composed of three timepoints A
S
, A
C
,
and A
E
connected by a contingent link and two re-
quirement constraints. More precisely, timepoints A
S
and A
E
represent the starting and ending timepoint of
the respective activity. In turn, A
C
is an internal time-
SimpleTemporalNetworkswithPartiallyShrinkableUncertainty
379

point that is only used for checking dynamic control-
lability of the STNU, but is not considered when exe-
cuting the activity. The values of the three constraints
guarantee that the overall duration range of the pat-
tern lies in range [x
F
,y
F
] and the upper bound y
F
can
be shrunk to y
C
at run time. Moreover, the lower
bound x
F
may be shrunk to x
C
+ f as well. Hence,
the overall constraint represented by this pattern is
similar to guarded link (A
S
,[x
F
,x
C
+ f],[y
C
,y
F
],A
E
)
(0 ≤ x
C
≤ x
F
≤ x
C
+ f ∧ x
C
≤ y
C
≤ y
F
≤ y
C
+ f).
This pattern can be used to represent some settings
of both types of guarded links. However, for example,
it can not be used to represent the duration of activity
Stretching (cf. Fig. 1 (b)).
Particularly note that, the pattern contains a strict
dependency between the value of the guard for the
lower bound, x
C
+ f, and the distance between the
guard for the upper bound y
C
and the upper bound y
F
itself. In detail, for the contingent constraint between
A
S
and A
C
(cf. Fig. 4) it holds 0 ≤ x
C
. Thus, for the
guard of the lower bound x
C
+ f ≥ f holds as well.
Moreover, y
F
≤ y
C
+ f holds and thus y
F
− y
C
≤ f.
As a result, y
F
− y
C
≤ f ≤ x
C
+ f must hold, i.e., the
distance between the upper bound y
F
and the guard
for the upper bound y
C
must be lower or equal to the
value of the guard for the lower bound x
C
+ f. Note
that, it is not possible to extend the pattern to cover
arbitrary guarded constraints as it is not possible to
resolve this dependency between the constraints com-
prising the pattern. Thus, STNPSU is more expressive
than STNU.
5 CONCLUSION
The main contribution of this paper is to present an ex-
tension of STNU that allows for the definition and ef-
ficient management of a novel kind of constraints, i.e.,
guarded links. A guarded link represents an admissi-
ble range of delays between two timepoints, where
each bound of the range can be shrunk during run
time, but not beyond a given threshold. A guarded
link constitutes a generalization of the two kinds of
STNU constraints, i.e., requirement and contingent
constraints, in the sense that a contingent link may be
represented as a simple form of a guarded one and that
a guarded link may represent a requirement constraint.
An STNU where it is possible to define guarded links
is denoted as Simple Temporal Network with Partially
Shrinkable Uncertainty (STNPSU). In particular, the
dynamic-controllability check and the execution of a
STNPSU can be done in polynomial time.
Networks such as STNU can be used as temporal
foundation for a broad class of Process-Aware Infor-
mation Systems currently being developed (Reichert
and Weber, 2012). In this context, the extension pro-
posed in this paper may be used to better represent
the temporal properties of sub processes (i.e., com-
plex tasks). It is quite common to have sub processes
whose allowed durations can be restricted in a limited
way prior to their execution. In turn, once a sub pro-
cess starts to execute, it is necessary to guarantee that
the allowed duration range can be used without any
further interference.
There are different avenues for future work. First,
we want to study the applicability of our approach to
CSTNU, for which the presence of labeled constraints
and links requires to consider further and different
propagation rules that have to be extended to take ac-
count of guarded constraints. Second, the application
of STNPSU as temporal foundation of Process-Aware
Information Systems could be interesting. Particu-
larly, STNPSU might serve as a tool for an appropri-
ate and scalable analysis of the temporal properties of
the business processes.
ACKNOWLEDGEMENTS
The authors would like to thank Luke Hunsberger for
his valuable feedback and suggestions.
REFERENCES
Dechter, R., Meiri, I., and Pearl, J. (1991). Temporal con-
straint networks. Artificial Intelligence, 49(1-3):61–
95.
Hunsberger, L. (2009). Fixing the semantics for dynamic
controllability and providing a more practical char-
acterization of dynamic execution strategies. In Intl
Symp. on Temporal Repres. and Reasoning (TIME’09),
pages 155–162. IEEE CPS.
Lanz, A., Posenato, R., Combi, C., and Reichert, M. (2013).
Controllability of time-aware processes at run time. In
On the Move to Meaningful Internet Systems: Proc.
CoopsIS’13, pages 39–56. Springer.
Lanz, A., Posenato, R., Combi, C., and Reichert, M. (2014).
Simple temporal networks with partially shrinkable
uncertainty (extended version). Technical Report UIB-
2014-05, Ulm University.
Morris, P. (2006). A structural characterization of temporal
dynamic controllability. In Benhamou, F., editor, Intl
Conf on Principles and Practices of Constraint Pro-
gramming (CP’06), pages 375–389. Springer.
Morris, P. (2014). Dynamic controllability and dispatcha-
bility relationships. In Simonis, H., editor, Intl Conf
on Integration of AI and OR Techniques in Constraint
Programming (CPAIOR’14), volume 8451 of LNCS,
pages 464–479. Springer.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
380

Morris, P. H. and Muscettola, N. (2005). Temporal dynamic
controllability revisited. In Veloso, M. M. and Kamb-
hampati, S., editors, National Conf on Artificial Intel-
ligence (AAAI’05), pages 1193–1198. AAAI Press.
Morris, P. H., Muscettola, N., and Vidal, T. (2001). Dy-
namic control of plans with temporal uncertainty. In
Intl Joint Conf on Artificial Intelligence (IJCAI’01),
pages 494–502. Morgan Kaufmann.
Reichert, M. and Weber, B. (2012). Enabling Flexibility
in Process-aware Information Systems: Challenges,
Methods, Technologies. Springer.
SimpleTemporalNetworkswithPartiallyShrinkableUncertainty
381
