
An Interactive Model for Structural Pattern Recognition based on the
Bayes Classifier
Xavier Cortés, Francesc Serratosa
and Carlos Francisco Moreno-García
Universitat Rovira i Virgili, Tarragona, Spain
Keywords: Bayes Classifier, Structural Pattern Recognition, Interactive Pattern Recognition, Graph Matching.
Abstract: This paper presents an interactive model for structural pattern recognition based on a naïve Bayes classifier.
In some applications, the automatically computed correlation between local parts of two images is not good
enough. Moreover, humans are very good at locating and mapping local parts of images although any kind
of global transformations had been applied to these images. In our model, the user interacts on the
automatically obtained correlation (or correspondences between local parts) and helps the system to find the
best correspondence while the global transformation parameters are automatically recomputed. The model is
based on a Bayes classifier in which the human interaction is properly modelled and embedded in the
model. We show that with little human interaction, the quality of the returned correspondences and global
transformation parameters drastically increases.
1 INTRODUCTION
There are lots of applications for image verification
or comparison that the whole process is completely
automatic with high accuracy ratios. One of the most
common applications is the Automatic Fingerprint
Identification System (AFIS) (Maltoni, 2009) or
image retrieval based on graphs (Jouili, 2012;
Lebrun, 2011; Park, 1999; Toselli, 2011; Solé, 2011;
Sanromà, 2012; Serratosa, 2013). Nevertheless, in
some cases, in which the ratio between noise and
signal is very high in the input image, these
completely automatic applications fail. In these
cases, it is useful to use the semi-automatic
approaches (Solé, 2013), in which a specialist can
edit the automatically extracted local features to
modify them (erase, create or update). Then, with
the updated features, the automatic matching or
query process is performed obtaining a result with
higher quality. In the case of AFIS, it is usual that
the specialist verifies and modifies the extracted
minutiae of the fingerprint to be queried.
The idea of interaction between humans and
machines is no new. Most of machines have been
developed with the aim of assisting human beings in
their work instead of substituting them. With the
introduction of computer machinery, however, this
idea changed, since some systems where developed
to completely substitute humans in certain types of
tasks. An early vision of interactive human-machine
technologies appeared in 1974 (Jarvis, 1974). Then
the medical applications rapidly took those ideas to
detect illnesses in a semiautomatic way. For
instance, interactivity was used to detect blood cells
in images in 1981 (Landeweerd, 1981). Nowadays,
this interest has increased substantially (Solé, 2013)
and (Sanchís, 2012). Moreover, it can be applied to
other applications such as human tracking
(Serratosa, 2012).
The aim of classical pattern recognition is to
automatically solve recognition problems. However,
in many real applications, the needed recognition
rate is higher than the one reached by the automatic
pattern recognition system. In these cases, some sort
of post-processing is applied where humans correct
the error committed by machine. It turns out,
however, that very often this post-processing phase
is the bottleneck of a recognition system, causing
most of its operational costs. To solve this problem,
some visual interactive systems have been presented
that allow expert to interact and modify the
automatically extracted features of the objects (Zou,
2007).
In the model we present, the human interaction
not only is considered in the extraction of the local
features but also in the matching or comparison
process. Thus, the obtained result is closer to the
ideal one. This approach is characterized by human
240
Cortés X., Serratosa F. and Moreno-García C..
An Interactive Model for Structural Pattern Recognition based on the Bayes Classifier.
DOI: 10.5220/0005201602400247
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 240-247
ISBN: 978-989-758-076-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

and machine being tied up in a much close loop than
usually. That is, the human gets involved not only in
the first step of the recognition process (where the
local features are extracted) or at the end, (where he
decides that the automatically obtained decision is
correct or not), but during the recognition process. In
this way, many errors can be avoided beforehand
and correction costs can be reduced.
Humans (or human specialists) are very good at
finding the correspondences (also called labelling or
matching between local parts) between local parts of
an object (for instance, minutiae of two fingerprints,
regions in segmented images or corners in
skeletonised images) but this is the most difficult
task for an automatic system. In the model we
present, the specialist can recursively interact in the
matching process until he considers it has obtained a
good-enough match. In each interaction, the
automatic process considers the hypothesis imposed
by the user and, considering the model, obtains the
best correspondence between local parts of both
images. Note that, in each hypothesis, the user is not
forced to interact on all the mappings that he
considers not correct. But he can interact in a small
part of the incorrect ones. Usually, imposing a small
part of the labellings, other wrong labellings are
amended. On the contrary, it is difficult for the
specialist to decide which are the values of the
global parameters between images (scale, rotation,
translation, colour modifications,…) that is, the
matrix values that transform an image into the other
using some transformation model (affine or others).
In this model, the user does not interact in the global
parameters.
In this paper, we present a new model that shifts
from the concept of fully automatic structural pattern
recognition to a model where the obtained
correspondence is conditioned by the human
feedback. This shift is caused by the fact that the
correspondence obtained by the full automation
system often turns out to be non-natural. In the next
section, we formalise the classical image registration
based on structural pattern recognition. In section 3,
we present our new model in which we incorporate
the human interactivity and in section 4, we
empirically evaluate it. Section 5 concludes the
paper.
2 CLASSICAL IMAGE
REGISTRATION MODEL
Let
and
be two input images to be compared.
Both images
and
are represented by any kind
of representation that explore the local parts of the
image
and
. In this
framework, the aim of classical image
correspondence is to obtain a labelling between the
outstanding parts of these images represented by
points (for instance Harris corners (Harris, 1988),
SIFTs (Lowe, 1999) and others (Mikolajczyk,
2005)) or graph nodes (for instance shock graphs
(Sebastian, 2004))
,
and a final distance
value
,
(for instance the Euclidean distance
between two vector points or the Edit distance
between graphs (Sanfeliu, 1983)). Sometimes,
instead of a distance function, the system returns a
similarity
,
or a probability that both
structures are the same. Nevertheless, to find this
labelling or correspondence, it is crucial to find the
deformation applied to one of the images to obtain
the other. In image retrieval, these global parameters
are called alignment parameters and several
approaches have been presented that obtains the best
correspondence together with the alignment Φ
such as Iterative Closest Point (ICP) (Zhabg, 1992),
Robust Point Matching (RPM) (Rangarajan, 1997),
Dual-Step EM (Andrew,1998), Graph
Transformation Matching (GTM) (Aguilar, 2009) or
Smooth Structural Graph Matching (Sanromà,
2012). Moreover, some methods have explicitly
been developed to reject points that are considered
outliers since they appear only in one of the two
images such as RANSAC (Fischler, 1981). In the
model we present, Φ represents a set of global
parameters that globally deform one of the images;
no necessary Φ has to be the alignment parameters.
Figure 1 shows the basic scheme of the classical
image correspondence process. There is a first step
in which the local parts
and
of the images
and
are obtained using methods such as (Harris,
1988), (Lowe, 1999) and (Mikolajczyk, 2005). Then,
in the semi-automatic methods, there is a second
step in which the user edits these local parts (erase,
create or modify their positions or values). We note
this editing user feedback as
and
. Note that
the user not only has access to the obtained structure
(or object representation) but also to the original
image. The last step obtains the correspondences
and a similarity measure
,
in a completely
automatic way through methods such as (Zhabg,
1992), (Rangarajan, 1997), (Andrew, 1998),
(Aguilar, 2009), (Sanromà, 2012), (Serratosa, 2014)
and (Solé, 2012). Note that the global parameters Φ
are needed to compute the correspondences and
the similarity
,
but usually Φ is not a returned
parameter of the system.
AnInteractiveModelforStructuralPatternRecognitionbasedontheBayesClassifier
241
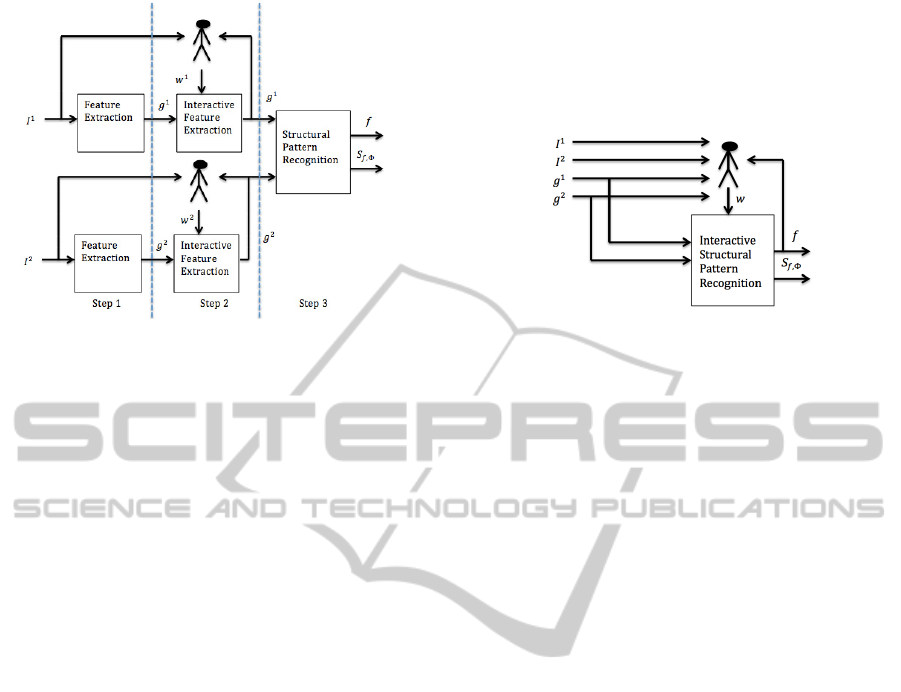
Figure 1: Image Correspondence Process with human
interaction in the local parts extraction.
In the next section, we present a classical
structural pattern recognition method that can be
applied at step 3 of the classical image registration
process (figure 1). It is not the aim of this paper to
talk about the first and second step of this process.
3 INTERACTIVE IMAGE
REGISTRATION MODEL
In the interactive model we present, we have adapted
the third step depicted in figure 1 to add more
human interactivity (Cortés, 2015). The interaction
is applied on the correspondences between local
parts of objects but not on the global parameters.
This is because finding the best correspondence
between a set of parts is an easy and natural task for
humans. Placing structural pattern recognition
within the human-interaction framework requires
changes in the way we model the problem at hand.
We have to take direct advantage of the feedback
information provided by the user in each iteration
step to improve “raw performance”. Figure 2 shows
a schematic view of the third step of the image
registration process (figure 1). Similarly to the first
step, the user has access to the original images
because they are the most informative input for the
natural intelligence. Moreover, the user has access to
both structures and the correspondence
automatically obtained. The output of the module is
the same as the classical one: the automatically
obtained labelling
,
and the similarity
function
,
,
.
In the next sub-sections we comment the
following aspects. First, we explain how to model
the feedback of the user applied on the labelling.
Second, we comment how to model the similarity
between the user feedback and the current labelling.
Finally, we explain an interactive and structural
pattern recognition model based on the maximum
posterior probability.
Figure 2: Semiautomatic Pattern Recognition as the third
step in the interactive registration process. The first and
second steps are similar to the ones shown in figure 1.
3.1 Human Interaction on the
Correspondences
We have defined a model to capture the users
feedback that makes easy the users tasks. For
humans, it is easy to detect a correct or wrong
labelling and also to define a new one when they see
both images together with the current labelling. We
represent the human actions through the following
expression User_feedback
,
,
,
,
.
These actions are represented as a vector
,…,
that each position represents a simple
user action. In each iterative step of the algorithm,
the user can interact with a different number of
possible simple actions. These actions are inserted to
the vector , in each human interaction, thus,
increasing the number of elements of . The current
number of actions is .
Using a graphical application, the user can only
perform the following different actions. The human
action
or
means that the q
th
simple action of the user is to confirm that the
labelling
is correct. It is represented as
,
. On the contrary, the human
action
or
means that the
labelling
is not correct. It is represented
as
,
. The human action
,
, means that the user imposes a possibly
new labelling
→
.Itisrepresentedas
,
. Note that
and
have to be
original nodes (non-extended) since the graphical
application does not show extended nodes.
Moreover, the first four actions are applied on only
one node and the fifth action is applied to a pair of
nodes. Finally, the human action
means
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
242

that the user accepts the current labelling for all the
nodes,
→
∀
1,…,
.
Figure 3 shows an example of a current labelling
in black and the imposed human actions in red. The
original graphs
and
have 6 nodes.
Nevertheless, these graphs have been extended to 8
nodes to assure outliers can be considered. Thus,
nodes
,
,
and
are null nodes that have to
be labelled to outliers of the other graph.
Figure 3: Graphical representation of the current labelling
in black and the humans’ feedback in red. The graphical
application has some easy-to-use tools to receive the
human feedback related to actions , and .
Moreover, there is a special tool to label a node to a null
node.
The current labelling (in black) is
,
,
,
,
,
,
and
. The user
considers (in red) that labellings
and
are correct. Moreover, the user imposes the
labelling
. Therefore, the result of the
current human actions are
,
,
,
and
,
.
3.2 Human Interaction and
Correspondences
Closer is the labelling (or node correspondences) the
user desires to the automatically obtained labelling
(or automatically obtained correspondences
correspondences), better is considered the
performance of the system. For this reason, it is
important to define a similarity measure between the
human actions (that is, the human labelling) and the
automatic labelling. This similarity is defined as
follows,
∑
1
∀
|
,
∀
,
|
∑
1
∀
|
,
∀
,
|
(1)
The
∈
0,1
is the fraction of
mappings imposed by the human that coincide with
the current labelling . Note that the nodes that the
user has not imposed the labelling do not affect the
similarity value. In the situation where the user has
not interacted yet, the ambiguity is solved as
1. This is because, when
there is no human feedback, then the interactive
model has to perform in the same way than the
classical model.
3.3 Interactive and Structural Pattern
Recognition
We have modelled the interactive and structural
pattern recognition problem similarly to the classical
structural pattern recognition. Nevertheless, we have
to take into consideration the feedback of the
specialist, . Therefore, we aim to find the best
labelling and transformation parameters such that
the posterior probability conditioned to both graphs
and also the human feedback is maximised.
,Φ
argmax
∀∈
∀∈
,Φ
|
,
,
(2)
Applying the Bayes rule, we obtain,
,Φ
argmax
∀∈
∀
∈
,
,
|
,Φ
,Φ
,
,
(3)
The likelihood
,
,
|
,Φ
can be
decomposed in two other probabilities using the
conditional probability definition as follows
,
,
|
,Φ
,
|
,,Φ
|
,Φ
.
The prior probability on the graphs together with
the hypothesis generated by the user,
,
,
,
does not depend on , therefore, it is constant
through the maximisation process and can be
dropped off.
And the joint probability of the current labelling
together with the global parameters
,Φ
are
modelled as
,Φ
Φ
since we
consider they are independent events due to the
labelling does not to be affected by the global
parameters. We can deduct few information about
the probability on the correspondence P
f
. We
merely impose that the function has to be bijective
and so, this probability is zero if this is not the case.
We assume an equal probability for the bijective
functions.
P
f
0i
f
∃ij
1/n! otherwise
(4)
Where f
v
fv
;1i,jn
We assume that P
Φ
is constant for all values of
Φ. In fact, we could assume, depending on the
application, that some global parameters are less
possible to appear, for instance, in the case of
AnInteractiveModelforStructuralPatternRecognitionbasedontheBayesClassifier
243

alignment parameters, the ones with large rotation
angles or very large (or small) scale transformations.
Thus, due to this probability becomes constant
through the maximisation process; we do not take
into consideration.
The probability P
g
,g
|
w,f,Φ
conditioned by
the user hypothesis w, the current correspondence
function and the global parameters Φ is modelled
assuming independence between local parts
,
|
,,Φ
∏
,
|
,,Φ
·
∏
,
|
,,Φ
,
and imposing that
and
. This model is
similarly to the non-interactive one and the Naïve
Bayes classifier (Richar, 1995).
Moreover, we propose the following model for
the node local probability
,
|
,,Φ
becomes the following where 1,
,
|
,
,Φ
0∃
,
1∃
,
,
|
,Φ
(5)
In the same way, the model for the edge local
probability
,
|
,,Φ becomes the
following where 1,,
,
|
,
,Φ
0
∃
,
⋁
∃
,
1
∃
,
∧
∃
,
,
|
,Φ
(6)
The interpretation of this model is the following.
When the user says the labelling is true or imposes a
labelling, then, we assume the probability is 1. On
the contrary, if the user says the labelling is not
correct, then the probability of this labelling is null.
Otherwise, the user does not inform about the
labelling and we assume the automatically obtained
one is the correct and so, the probability is estimated
through this labelling
,
|
,Φ
or
,
|
,Φ. The usual interpretation of these
probabilities is through a distance function such as,
,
|
,Φ
,
.
To assure the model optimises a bijective
labelling, we also impose the following
probabilities,
,
|
,,Φ
0∃
,
where 1;∀.
,
|
,,Φ0∃
,
where 1;∀.
(7)
And similarly for the arcs,
,
|
,,Φ
0
∃
,
∧
∃
,
where 1,;∀
′
′
.
,
|
,,Φ
0
∃
,
∧
∃
,
where 1,;∀
′
′
. (8)
The conditional probability
|
,Φ
of the
human interaction with respect to the current
correspondence and the transformation parameters is
interpreted as the influence of the feedback or how
much we believe on this feedback. Similar to the
probabilities on the nodes and arcs, we suppose
independence on each local action,
|
,Φ
∏
|
,Φ
∀
. This assumption seems to be
logical if we assume the user acts in the same way
through the whole process. In the model we describe
here, the human only acts on the correspondence
but not on the global parameters Φ although they
influence in the decision that the user takes, since
the user views the effect of Φ on the images.
We define the degree of confidence in the user as
∈0,1. It represents the probability of a correct
interactivity and it is an application dependent
parameter of the model. If
is high, we have a high
confidence in the user and it is almost sure that at the
next algorithm iteration, the new automatically
obtained labelling will consider the human feedback.
On the contrary, if
is low, although the user
imposes some mappings between nodes, the optimal
new labelling could not include some of these
mappings.
The effect of the two human actions ( and
) on the local confidence probabilities is
defined as follows.
,
|
,Φ
,
|
,Φ
; ∀ (9)
,
|
,Φ
1
1
Considering all the assumptions and probability
estimations, the final expression is,
,Φ
≅argmax
∀∈
∀∈
∏
|
,Φ
∀
,..,
∏
,
|
,,Φ
∀
,..,
(10)
∏
,
|
,,Φ
∀,
,..,
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
244
Note that the maximum value is reached when the
obtained labelling
is the same than the human
imposes through .
4 PRACTICAL VALIDATION
For our experiments, we consider the CMU “house”
and “castle” sequences. There are two datasets
consisting of 111 frames of a toy house and a castle
(CMU, 2009). Each frame in these sequences has
been hand-labelled, with the same 30 landmarks
identified in each frame (Caetano, 2006). The ideal
labelling imposed by the human in its interactive
actions is going to be these hand-made labellings.
From each landmark, we have only considered their
bidirectional position in the image. The cost
,Φ
between landmarks is the Euclidean
distance of their image positions.
We explore the performance of our method
considering the separation between frames (as it is
done in (Caetano, 2006)). Experiments marked with
are performed through all pair of images that the
distance between frames is . The final result values
are the average of these experiments.
The interaction of the user is modelled as
follows. The user interacts in each step with only
one action . There are not contradictory orders
with previous iterations and this action is always
done to modify the current labelling. That is, it is
performed on node labellings that the user considers
wrong (the ideal labelling is different from the
current labelling). With the aim of performing
automatically the experiments, we generate the
actions as follows. In each iteration, the system
compares the ideal labelling with the current
labelling, from the first point to the 30
th
point. If
is the first point such that
is different from the
ideal labelling, then, we generate the action
,
, being
the receiving node of the ideal
labelling.
We assess the quality of the current labelling
with the Hamming distance between the current
labelling and the ideal labelling.
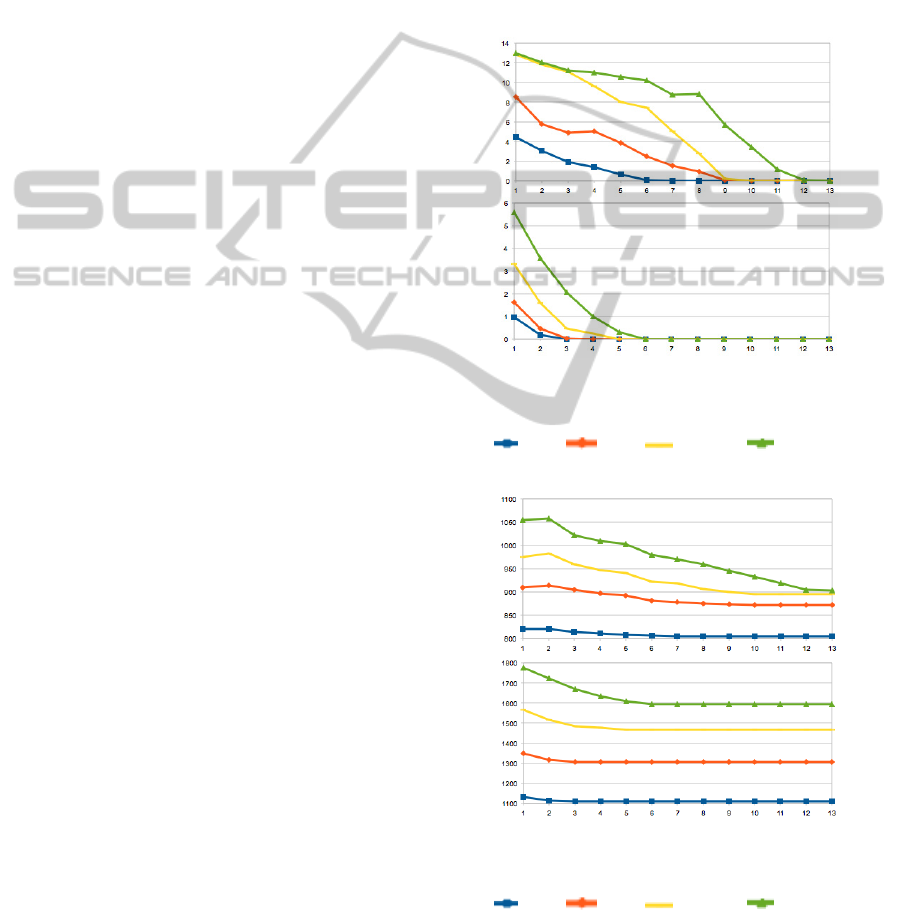
Figure 4 and Figure 5 show the Hamming
distance between the ideal labelling and the current
labelling and the Cost
,
. Note that not all the
experiments get the maximum number of iterations
since when the Hamming distance is zero; it is
supposed that the user introduces an and the
iterative algorism stops. The registration algorithm
in these experiments is the Hungarian method
(Munkres, 1957). We have performed other
experiments using ICP (Zhabg, 1992), but, due to
there is not an important difference between images,
the automatic labelling was almost perfect without
the need of human interaction.
We realise that when the hamming distance
decreases, also does the cost in almost all the tests.
This means that the ideal labelling of the user is in
conjunction with the representation of the objects
and the cost function. This fact can be used as a
measure of quality of the representation of the
objects given a specific application.
Figure 4: Hamming distance respect of the number of
iterations on the Hotel and House dataset.
F50: , F60: , F70: and F80: . Fi means that
the distance between frames is i.
Figure 5: Cost function respect of the number of iterations
on the Hotel and House dataset.
F50: , F60: , F70: and F80: . Fi means that
the distance between frames is i.
Table 1 shows the ratio between the initial hamming
distance with respect to the maximum number of
iterations. For instance, in the case of Hotel and F50,
AnInteractiveModelforStructuralPatternRecognitionbasedontheBayesClassifier
245

initial hamming distance = 4.5, number of iterations
= 6, so 4.5/6 = 0.75. This value represents the
decrease of the hamming distance in each iteration.
The case that the value is higher than 1 appears
when, in each iteration, not only the manually
imposed labelling is amended but also other ones.
Note that this situation appears in the cases when
there is an important reduction of the cost, and so,
the “human distance” is consistent with the “model
distance”.
Table 1: Cost function respect of the number of iterations
of the Hotel and House dataset.
F50 F60 F70 F80
Hotel
0.75 0.94 1.44 1.08
House
0.33 0.50 0.70 0.91
5 CONCLUSIONS
We have presented an interactive and structural
pattern recognition model based on the Bayes
classifier for image registration. Some fully
automatic systems for image registration do not
achieve the desirable quality due to high distortion
on the images, bad quality of these images or simply
that the systems do not capture the main local
features of the objects to be compared. The main
idea of this model is that a specialist is very good at
finding some correspondences between local parts.
Then, we have designed a very easy-to-use model
that with some interactions, the possibly wrong and
automatically obtained labellings are amended.
Experiments show that with few user interactions the
system obtains the ideal labelling.
This is the first time that an interactive model has
been presented and modelled through the Bayes
theorem that explicitly modifies the labelling
between local parts. We believe that the task of
finding a labelling between images based on local
parts is costless for humans although it has been
shown to be a very difficult task for machines. This
model can be used in a great amount of applications
in which there is a specialist that verifies the final
result such as medical diagnosis or fingerprint
identification.
ACKNOWLEDGEMENTS
This research is supported by the CICYT project
DPI2013-42458-P and TIN2013-47245-C2-2-R.
REFERENCES
Davide Maltoni, Dario Maio, Anil K. Jain & Salil
Prabhakar, “Handbook of Fingerprint Recognition”,
Springer, (2009).
Salim Jouili & Salvatore Tabbone, “Hypergraph-based
image retrieval for graph-based representation”,
Pattern Recognition, Available online 28 April (2012).
Justine Lebrun, Philippe-Henri Gosselin & Sylvie Philipp-
Foliguet, “Inexact graph matching based on kernels for
object retrieval in image databases”, Image and Vision
Computing, 29 (11), pp: 716-729, (2011).
In Kyu Park, Il Dong Yun & Sang Uk Lee, “Colour image
retrieval using hybrid graph representation”, Image
and Vision Computing, 17 (7), pp: 465-474, (1999).
Toselli, A. H., Vidal E. & Casacuberta, F. “Multimodal
interactive pattern recognition and applications”,
Springer (2011).
A. Solé & F. Serratosa, Models and Algorithms for
computing the Common Labelling of a set of
Attributed Graphs, Computer Vision and Image
Understanding 115 (7), pp: 929-945, 2011.
G. Sanromà, R. Alquézar, F. Serratosa & B. Herrera,
Smooth Point-set Registration using Neighbouring
Constraints, Pattern Recognition Letters 33, pp: 2029-
2037, 2012.
F. Serratosa, X. Cortés & A. Solé, Component Retrieval
based on a Database of Graphs for Hand-Written
Electronic-Scheme Digitalisation, Expert Systems
With Applications 40, pp: 2493 -2502, 2013.
A. Solé & F. Serratosa, Graduated Assignment Algorithm
for Multiple Graph Matching based on a Common
Labelling, International Journal of Pattern Recognition
and Artificial Intelligence 27 (1), pp: 1 - 27 2013.
Jarvis, R. A. “An interactive minicomputer laboratory for
graphics, image processing and pattern recognition”,
Computer 7 (10), pp: 49-60, (1974).
G. H Landeweerd, E. S Gelsema, M Bins, M. R Halie,
“Interactive pattern recognition of blood cells in
malignant lymphomas”, Pattern Recognition, 14, (1–
6), pp: 239-244, (1981).
Alberto Sanchís, Alfons Juan, Enrique Vidal: “A Word-
Based Naïve Bayes Classifier for Confidence
Estimation in Speech Recognition”. IEEE
Transactions on Audio, Speech & Language
Processing 20(2): 565-574, (2012).
F. Serratosa, R. Alquézar & N. Amézquita, A Probabilistic
Integrated Object Recognition and Tracking
Framework, Expert Systems With Applications 39, pp:
7302-7318, 2012.
Jie Zou, George Nagy, “Visible models for interactive
pattern recognition”, Pattern Recognition Letters, 28,
(16), pp: 2335-2342, (2007).
Harris, C. & Stephens, M. “A combined corner and edge
detector”, Proceedings of the 4th Alvey Vision
Conference. pp. 147–151, (1988).
Lowe, D. G., “Object recognition from local scale-
invariant features”. Proceedings of the International
Conference on Computer Vision. 2. pp. 1150–1157,
(1999).
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
246

Mikolajczyk, K. & Schmid, C. “A performance evaluation
of local descriptors”. IEEE Transactions on Pattern
Analysis & Machine Intelligence, 27(10): 1615–1630
(2005).
Sebastian, T., Klein, P. & Kimia, B. “Recognition of
shapes by editing their shock graphs”. IEEE Trans. on
Pattern Analysis & Machine Intelligence 26(5): 550–
571 (2004).
Sanfeliu, A. & Fu, K. “A distance measure between
attributed relational graphs for pattern recognition”.
IEEE Transactions on Systems, Man and Cybernetics
13, 353–362. (1983).
Zhabg, Z. “Iterative Point Matching for Registration of
Free-form Curves”, International Journal of Computer
Vision 13(2): 119-152. (1992).
Rangarajan, A., H. Chui, et al. The softassign procrustes
matching algorithm. International Conference on
Information Processing in Medical Imaging. (1997).
Andrew D. J. Cross, Edwin R. Hancock: “Graph Matching
With a Dual-Step EM Algorithm” IEEE Trans. Pattern
Analysis & Machine Intellig., 20(11): 1236-1253
(1998).
Aguilar, W., Frauel, Y., Escolano, F. & Martinez-Perez,
M. E. “A robust graph transformation matching for
non-rigid registration”. Image and Vision Computing
27, 897–910. (2009).
G. Sanromà, R. Alquézar, & F. Serratosa, “A New Graph
Matching Method for Point-Set Correspondence using
the EM Algorithm and Softassign”, Computer Vision
and Image Understanding CVIU, 116(2), pp: 292-304,
(2012).
Fischler, M. and R. Bolles “Random sample consensus: a
paradigm for model fitting with applications to image
analysis and automated cartography”,
Communications of the ACM 24(6): 381-395 (1981).
F. Serratosa, “Fast Computation of Bipartite Graph
Matching”, Pattern Recognition Letters, PRL 45, pp:
244–250, 2014.
A. Solé, F. Serratosa & A. Sanfeliu, “On the Graph Edit
Distance cost: Properties and Applications”,
International Journal of Pattern Recognition and
Artificial Intelligence, IJPRAI 26, (5), pp:, 2012.
X. Cortés & F. Serratosa, “An Interactive Method for the
Image Alignment problem based on Partially
Supervised Correspondence”, Expert Systems With
Applications, 42 (1), pp: 179 – 192, 2015.
Richard O. Duda & Peter E. Hart, “Pattern Classification
and Scene Analysis”, John Wiley, 1995.
CMU “house” data set, http://vasc.ri.cmu.edu
/idb/html/motion/house/index.html, 2009.
T. S. Caetano, T. Caelli, D. Schuurmans & D. A. C.
Barone, “Graphical Models and Point Pattern
Matching,” IEEE Trans. Pattern Analysis and Machine
Intelligence, vol. 28, no. 10, pp. 1646-1663, (2006).
Munkres, J. “Algorithms for the assignment and
transportation problems”. Journal of the Society for
Industrial and Applied Mathematics 5(1), 32–38,
(1957).
AnInteractiveModelforStructuralPatternRecognitionbasedontheBayesClassifier
247
