
Unconstrained Speech Segmentation using Deep Neural Networks
Van Zyl van Vuuren
1
, Louis ten Bosch
2
and Thomas Niesler
1
1
Department of Electrical and Electronic Engineering, University of Stellenbosch, Stellenbosch, South Africa
2
Department of Linguistics, Radboud University, Nijmegen, The Netherlands
Keywords:
Unconstrained Automatic Speech Segmentation, Deep Neural Networks, Generative Pre-training.
Abstract:
We propose a method for improving the unconstrained segmentation of speech into phoneme-like units using
deep neural networks. The proposed approach is not dependent on acoustic models or forced alignment, but
operates using the acoustic features directly. Previous solutions of this type were plagued by the tendency to
hypothesise additional incorrect phoneme boundaries near the phoneme transitions. We show that the appli-
cation of deep neural networks is able to reduce this over-segmentation substantially, and achieve improved
segmentation accuracies. Furthermore, we find that generative pre-training offers an additional benefit.
1 INTRODUCTION
Speech can be segmented into phonemes manually
by phonetic specialists, but this is known to be te-
dious, expensive and subjective. The use of accu-
rate and reliable automatic segmentation algorithms
is a desirable alternative. Especially when little or no
transcribed phonetic material is available, such algo-
rithms can facilitate the development of pronunciation
dictionaries, and can be used to obtain suitable boot-
strapping acoustic training data, thereby substantially
accelerating the development of automatic speech
recognition (ASR) systems. Automatic segmentation
algorithms are also useful outside ASR, such as for
the study of pronunciation variation, the development
of coherent large-scale dictionaries, and in text-to-
speech (TTS) applications (Sharma and Mammone,
1996; Wang et al., 2003; Adell et al., 2005).
A distinction can be made between segmenta-
tion approaches that require phone or orthographic
transcripts, and those that do not. These two ap-
proaches are often referred to as constrained and un-
constrained respectively (Keri and Prahallad, 2010).
Constrained speech segmentation algorithms are
usually based on a forced alignment between phone-
based hidden Markov models (HMMs) and the acous-
tic feature (Adell et al., 2005; Keri and Prahallad,
2010; Hoffmann and Pfister, 2010). In a severely
under-resourced setting, it may not be possible to ob-
tain suitable phone models. Indeed, the phone inven-
tory itself may not yet be fully known.
Unconstrained speech segmentation algorithms
detect segment boundaries using only the acoustic
features. Because this approach does not require
acoustic models, it can for example be applied in sit-
uations where the phone inventory has not yet been
established. Popular past approaches to this problem
are based on finding peaks in vector distance func-
tions that respond to the dynamics of the acoustic fea-
tures (Aversano et al., 2001; Sarkar and Sreenivas,
2005; Estevan et al., 2007; ten Bosch and Cranen,
2007; R
¨
as
¨
anen et al., 2011). The focus of this paper
is specifically on unconstrained speech segmentation.
Artificial neural networks (ANNs) have been ap-
plied to both constrained and unconstrained speech
segmentation. In the former case, use is usually made
of hybrid HMM/ANN systems in which multilayer
perceptrons (MLPs) act either as phone probability
estimators (Finster, 1992; Malfrere et al., 1998), or
are used to detect phoneme transitions in order to
refine the boundaries produced by an HMM align-
ment (Toledano, 2000; Lee, 2006). In the latter case,
the ANN’s are trained to estimate a local score, which
is a value that indicates rapid changes in the features
extracted from the audio signal, and therefore gives
an indication of when a phoneme boundary is likely
to be present (Suh and Lee, 1996; Keri and Prahal-
lad, 2010). Maxima in the local score that are above
a certain threshold are taken to correspond to a hy-
pothesised segment boundary. This family of algo-
rithms can deliver excellent performance but also suf-
fers from the insertion of surplus boundaries (over-
segmentation). These are due to clusters of maxima
in the local score, not all of which correspond to true
248
Zyl van Vuuren V., ten Bosch L. and Niesler T..
Unconstrained Speech Segmentation using Deep Neural Networks.
DOI: 10.5220/0005201802480254
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 248-254
ISBN: 978-989-758-076-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

boundaries. Recently, we have addressed this by em-
bedding an ANN local score estimator within a dy-
namic programming (DP) framework, and were able
to show reduced over-segmentation and improved
performance (van Vuuren et al., 2013). In the cur-
rent paper we build on this work by employing deep
neural network architectures as local score estimators.
The remainder of this paper is structured as fol-
lows. Sections 2 and 3 describe the application of
deep belief networks to the unconstrained segmenta-
tion problem, Section 4 describes the way in which
we assess the accuracy of competing systems, and
Sections 5 and 6 respectively describe the experimen-
tal set-up and results. Finally, Section 7 concludes.
2 RESTRICTED BOLTZMANN
MACHINES
Restricted Boltzmann machines (RBMs) have proved
to be useful building blocks in the creation of deep
neural architectures, and have recently achieved high
accuracies in phone classification experiments (Mo-
hamed et al., 2012). We hoped to emulate this success
for the unconstrained speech segmentation task by us-
ing RBMs to achieve a more accurate local score.
An RBM is an energy-based stochastic generative
model that can learn a probability distribution from
observations by training the parameters of an undi-
rected bipartite graph, also known as a Markov ran-
dom field (MRF) (Fischer and Igel, 2012). The vis-
ible nodes v = (v
1
, ..., v
m
) and hidden nodes (latent
variables) h = (h
1
, ..., h
n
) are illustrated in Figure 1,
where each node represents a random variable.
h
1
h
2
h
3
h
4
h
n
v
1
v
2
v
3
v
m
c
1
c
2
c
3
c
4
c
n
b
1
b
2
b
3
b
m
b
3
w
mn
w
1n
w
3n
w
11
Figure 1: A restricted Boltzmann machine (RBM).
Each node has an associated real-valued bias in-
dicated by b
i
and c
j
for the ith visible and jth hidden
node respectively. Furthermore, each undirected con-
nection (edge) between a visible node v
i
∈ {1, ..., m}
and hidden node h
j
∈{1, ..., n}has an associated real-
valued weight w
i j
. The joint probability distribution
over visible and hidden nodes is the Boltzmann dis-
tribution (Bishop et al., 2006), and is given by Equa-
tion 1,
p(v, h) =
1
Z
e
−E(v, h)
(1)
where Z is the partition function given by Equation 2.
Z =
∑
v, h
e
−E(v, h)
(2)
Associated with each configuration of values for
the visible v and hidden h nodes of the RBM is a
scalar value E(v, h) called the energy as given by
Equation 3.
E(v, h) = −
m
∑
i=1
n
∑
j=1
w
i j
v
i
h
j
−
m
∑
i=1
b
i
v
i
−
n
∑
j=1
c
j
h
j
(3)
Binary RBMs have binary stochastic nodes for
which the visible and hidden nodes have associated
binary values, i.e. (v, h) ∈ {0, 1}
m+n
. Furthermore,
the probability of a 1 being associated with a visi-
ble or hidden node, given the hidden or visible vec-
tors respectively, can be shown to be a sigmoid func-
tion. To increase the probability of an observed or
training vector the weights are adjusted by gradient
ascent in order to maximise the log-likelihood of the
training sample. Since this is exponentially computa-
tionally expensive, an approximate training procedure
known as contrastive divergence (CD) is used instead
of the exact maximum likelihood learning (Bengio,
2009; Krizhevsky and Hinton, 2009; Fischer and Igel,
2012). CD employs Gibbs sampling to sample from
the model’s distribution. The resulting weight update
is given by Equation 4, where ε is the learning rate
and v
k
is the k
th
Gibbs sample. The update equation
for the biases is similar.
∆w
i j
= ε(p(h
j
= 1|v
0
)v
0
i
−p(h
j
= 1|v
k
)v
k
i
)
(4)
In the literature it is common to use 1 step CD (Er-
han et al., 2010), and this approach was followed in
our experiments.
Because the input will be real-valued, the visible
nodes of the RBM at the bottom of the stack of RBMs
will be modelled as Gaussian instead of binary. An
RBM with Gaussian visible nodes and binary hidden
nodes is referred to as a Gaussian-Bernoulli RBM
(GBRBM), and has the energy function shown in
Equation 5 (Krizhevsky and Hinton, 2009), where σ
i
is the standard deviation of the i
th
visible Gaussian
variable.
E(v, h) =
m
∑
i=1
(v
i
−b
i
)
2
2σ
2
i
−
n
∑
j=1
c
j
h
j
−
m
∑
i=1
n
∑
j=1
v
i
σ
i
h
j
w
i j
(5)
UnconstrainedSpeechSegmentationusingDeepNeuralNetworks
249

To simplify learning, some authors (Cho et al.,
2011) advise the use of a fixed variance, commonly
σ
i
= 1. The conditional probability for the visible
nodes given the hidden nodes is then given by Equa-
tion 6,
p(v
i
= v|h) = N
v
b
i
+ σ
i
∑
j
h
j
w
i j
, 1
!
(6)
where N (·|µ, σ
2
) is a Gaussian distribution with
mean µ and variance σ
2
. Another simplification is to
use the means (µ
i
) of the visible nodes (Equation 6)
as the samples instead of sampling from the Gaus-
sian distribution during Gibbs sampling. This is done
because the standard deviations are not updated and
therefore samples from the Gaussian distribution will
be either dominated by noise or are only slightly af-
fected by the standard deviation. These restrictions
were applied in the experiments that follow, and there-
fore all the features in the training data were prepro-
cessed to have zero mean and unit variance before
training the GBRBM. In this way the contrastive di-
vergence algorithm can remain unchanged.
3 PRE-TRAINING OF DEEP
NETWORKS
To generatively pre-train a deep network, RBMs are
stacked in layers. The first RBM is a GBRBM trained
to generate the input data. After this, the proba-
bility of activation for the hidden nodes, generated
from the training data, is used as the training data for
next RBM layer. This procedure is known as greedy
layer-wise learning (Hinton et al., 2006; Bengio et al.,
2007). As the RBMs are stacked, more abstract fea-
tures are detected by the higher RBMs. Finally a layer
of neurons corresponding to the labels of the classifi-
cation problem is added to the top of the the network.
The parameters of the network can then be fine-tuned
by backpropagation. We will conduct experiments
both with and without generative pre-training of the
networks in order to establish its benefits for the un-
constrained speech segmentation task.
4 ASSESSMENT OF
SEGMENTATION ACCURACY
The R-value is a scalar value between 0 and 1 that
has been proposed for the assessment of segmentation
accuracy (R
¨
as
¨
anen et al., 2009). Equations 7 and 8
define two quantities known as the hit rate (HR) and
over-segmentation (OS) respectively in terms of the
number of hits (N
hit
), the number of hypothesised
boundaries (N
f
), and the number of reference bound-
aries (N
re f
) in an utterance. The number of hits is the
number of hypothesised boundaries within 20ms of a
true boundary.
HR =
N
hit
N
re f
(7)
OS =
N
f
N
re f
−1 (8)
The R-value is defined as the average of two dis-
tances r
1
and r
2
which are themselves defined on a
plane whose axes are HR and OS. The distances r
1
and r
2
are determined by using Equations 9 and 10
respectively, and subsequently the R-value by Equa-
tion 11.
r
1
=
q
(1 −HR)
2
+ OS
2
(9)
r
2
=
−OS + HR −1
√
2
(10)
R = 1 −
abs(r
1
) + abs(r
2
)
2
(11)
The larger r
1
or r
2
, the smaller the R-value will
become. Hence, the larger the R-value, the better
the segmentation performance. Informal testing re-
vealed that when the number of hypothesised bound-
aries becomes substantially more than the number of
true phoneme boundaries, it is likely that the neural
network is overfitting. The R-value strongly penalises
over-segmentation, and is therefore effective at com-
bating overfitting when using early stopping during
training, as described later in Section 5.3. Other per-
formance measures found in the literature do not ex-
plicitly penalise over-segmentation.
5 EXPERIMENTAL SET-UP
5.1 Data
Our experimental evaluations are based on the TIMIT
database (Fisher et al., 1986), which has also been
employed by several other authors for the evalu-
ation of unconstrained speech segmentation algo-
rithms (Aversano et al., 2001; Sarkar and Sreenivas,
2005; Estevan et al., 2007; Keri and Prahallad, 2010;
R
¨
as
¨
anen et al., 2011). The TIMIT data offers a pho-
netic segmentation (i.e. the locations of phone bound-
aries) that has been produced by human phonetic ex-
perts. Such a carefully prepared manual segmentation
is not found in other, more recent, speech databases.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
250

The standard TIMIT 462-speaker training set will
be used to train the segmentation algorithms. The
development set consists of 50 speakers drawn from
the full 168-speaker test set, and is used to optimise
high-level parameters of the algorithms (Halberstadt,
1998). The standard TIMIT 24-speaker core test set is
used exclusively for final testing. There is no speaker
overlap between any of these three sets.
In all experiments, a frame length of 10ms with
a frame skip of 5ms was used during feature extrac-
tion. Each frame of speech was represented by a 39-
dimensional feature vector consisting of 12 MFCCs,
log energy, and appended first and second derivatives.
5.2 Baseline Systems
For purposes of comparison, two unconstrained seg-
mentation systems were included as baselines for our
proposed approach. These baseline systems have
been described previously by (Keri and Prahallad,
2010) and by (van Vuuren et al., 2013).
5.2.1 MLP-based Segmentation
A multi-layer perceptron (MLP) can be used to com-
pute a local score on the basis of a group of consec-
utive feature vectors by training an output neuron to
produce a 1 when the evidence in the input feature
vectors supports the presence of a boundary, and a
value of 0 when the evidence supports the absence of
a boundary. This approach has been shown by (Keri
and Prahallad, 2010) to lead to state-of-the-art perfor-
mance. This system has therefore been included as a
baseline for our experiments.
A segment boundary is hypothesised at the frame
at which the local score is at a maximum within a
search region, as demonstrated by Equation 12.
[
ˆ
B
R
] = argmax
t∈{S
R
...E
R
}
{LS(i
t
)} (12)
Here i
t
is the i
th
frame, S
R
and E
R
are the start and
end of the search region respectively, LS(i
t
) is the lo-
cal score at frame i
t
, and B
R
is the hypothesised seg-
ment boundary. The search region is defined as an
interval within which the local score exceeds a value
of 0.5.
As proposed by (Keri and Prahallad, 2010), our
baseline MLP-based segmentation system used a net-
work with single hidden layer and 30 hidden neurons.
Training data consisted of feature vector groups lo-
cated around phoneme boundaries in the TIMIT train-
ing set and feature vector groups midway between
two boundaries. The network was trained using back-
propagation without pre-training, with groups of 11
feature vectors centred about the point of interest.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.005
0.01
0.015
0.02
0.025
0.03
Local score
Probability
Boundary
No boundary
Figure 2: Probability distribution of MLP-based local score
values at, and away from, phoneme boundaries, estimated
from TIMIT.
Figure 2 shows the distribution of the local score
values computed on the TIMIT corpus by the result-
ing MLP. The limited overlap of these two distribu-
tions indicates that the local score can achieve good
discrimination between locations at which a bound-
ary is present, and location where it is not.
5.2.2 Dynamic Programming
The local score can be embedded in a dynamic pro-
gramming (DP) framework that includes an explicit
probabilistic model for the length of a segment. The
segmentation of a speech utterance is then formulated
as a Markov model, where each frame corresponds
to a state. The transition probabilities correspond
to the probability of the corresponding hypothesised
segment length, as established from a corpus such as
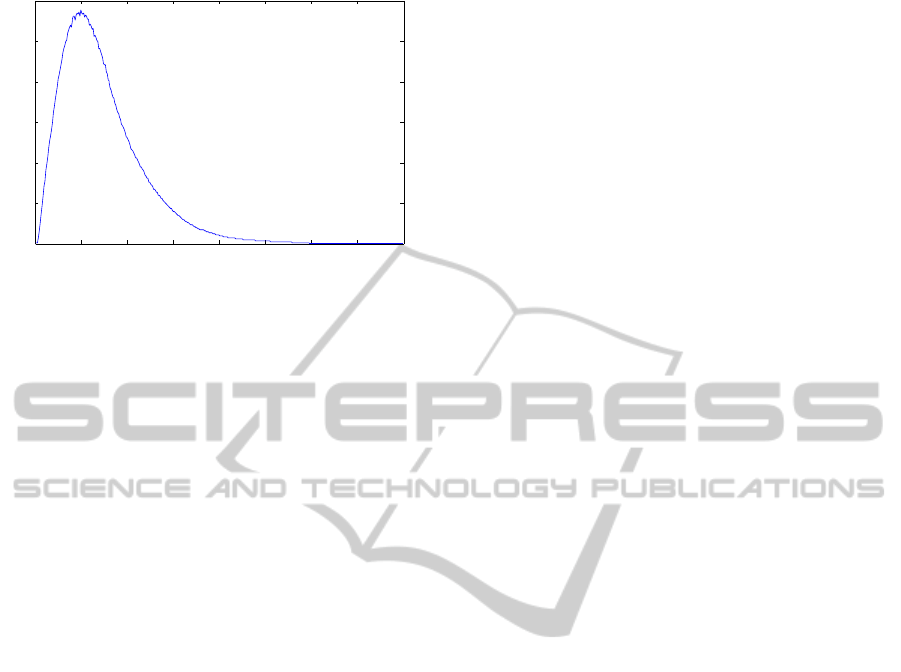
TIMIT and shown in Figure 3. The Markov emis-
sion probabilities are calculated from the distribution
of the local score values LS(i
t
), which were shown in
Figure 2.
Using these distributions, the probability of a
boundary given the local score at a particular frame
can be calculated and this serves as the basis of the DP
search. We have shown recently that this embedding
of a MLP-based local score in a DP framework can re-
duce the insertion incorrect boundaries when the local
score exhibits multiple closely-spaced maxima (van
Vuuren et al., 2013). We have therefore included such
a system as a second baseline for our experiments.
5.3 RBM-based Systems
All RBM-based systems used in our experiments have
logistic sigmoid neurons, since sigmoid functions are
also used to sample values from an RBM. We will
consider networks with between 1 and 5 hidden lay-
ers, with each hidden layer having the same number
UnconstrainedSpeechSegmentationusingDeepNeuralNetworks
251
0 50 100 150 200 250 300 350 400
0
0.002
0.004
0.006
0.008
0.01
0.012
Probability
Segment length (ms)
Figure 3: Probability distribution of phoneme lengths in the
TIMIT training set.
of neurons (256, 512 or 1024). For each network ar-
chitecture, a network is prepared with and without
pre-training. The subsequent supervised training by
backpropagation employs early stopping to find the
best performing network on the development set, af-
ter which the network’s performance was tested on
the TIMIT core test set.
Early stopping is a technique used to avoid
overfitting during supervised training of neural net-
works (Erhan et al., 2010). After each training epoch
the network’s development set performance is com-
pared to the previous epoch’s performance. When the
performance deteriorates, the learning rate is halved.
Training then continues from the previous epoch’s
weight values. We found that the networks’s perfor-
mance tends to alternate slightly between epochs, al-
though improving in the longer term. For this reason
we chose to halve the learning rate only when the per-
formance drops consistently over 5 trial epochs.
For generative pre-training each RBM was sub-
jected to 50 training epochs, i.e. 50 epochs of un-
supervised training per layer of the DBN, at a learn-
ing rate of 0.005 for the Gaussian Bernoulli RBM
and 0.05 for the binary RBMs, and with a momen-
tum of 0.9. These values were chosen to be similar
to those used to train RBM-based acoustic models for
phone classification (Mohamed et al., 2012). Early
stop training starts with a learning rate of 0.1 and mo-
mentum of 0.9, and continues until the learning rate is
smaller than 0.01. Stochastic gradient descent and un-
supervised pre-training used mini-batches consisting
of 128 training samples.
An input vector to the neural network consisted
of the features associated with 11 consecutive frames
centred on the test frame. Since the feature vector
extracted from each frame was 39-dimensional, each
input vector had a total of 429 components.
6 EXPERIMENTAL RESULTS
Every network architecture was subjected to three
early stop training sessions, from which a mean per-
formance was calculated. This average is taken to in-
dicate typical performance. Figure 4 shows this per-
formance on the TIMIT core test set for 256, 512, and
1024 hidden neurons per hidden layer.
When the number of hidden layers is increased
from 1 to 2, there is in all cases a notable performance
improvement. However, when 3 or more hidden lay-
ers are used, further gains are not reliably achieved.
There is gradual improvement in performance as the
number of neurons per hidden layer is increased.
The core test set performance of the networks with
best performance on the development set, with and
without pre-training are shown in Table 1. The net-
works with and without pre-training contained 5 and
3 hidden layers respectively, both with 1024 neurons
per layer (Figure 4). The performance of the pre-
trained network when embedded in the DP algorithm
as described in Section 5.2.2 is also shown.
Hypothesised boundaries falling outside a 20ms
region around the true phoneme boundaries are re-
garded as insertions, and missed phoneme bound-
aries as deletions. The average percentage insertions
and deletions per reference phoneme boundary are in-
cluded in the table. Both deep networks achieve sub-
stantial improvements in segmentation performance.
Best performance is achieved when pre-training is ap-
plied. It is interesting to see that the incorporation
of dynamic programming leads to deteriorated per-
formance in our DNN experiments. Since the chief
motivation for the dynamic programming framework
was to reduce over-segmentation, this indicates that
the local scores estimated by the deep networks are
less prone to these insertion errors, and therefore the
incorporation of DP is unnecessary and even counter-
productive.
7 DISCUSSION AND
CONCLUSION
Our experiments show that a deep neural network is
able to provide a substantially better local score for
use in unconstrained speech segmentation than previ-
ously proposed alternatives. Pre-training provides a
performance benefit, as does a larger number of neu-
rons per hidden layer. Furthermore, the local scores
estimated by deep networks appear to reduce the ten-
dency to over-segment that has been associated with
this class of algorithms in the past. Other means of re-
ducing over-segmentation, such as the introduction of
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
252

1 2 3 4 5
0.865
0.87
0.875
0.88
0.885
0.89
0.895
Hidden layers
R−value
256 neurons with no pre−training
256 neurons with pre−training
512 neurons with no pre−training
512 neurons with pre−training
1024 neurons with no pre−training
1024 neurons with pre−training
Figure 4: Segmentation performance on the TIMIT core test set for networks with 256, 512, and 1024 hidden neurons per
layer, and with between 1 and 5 hidden layers.
Table 1: Comparison of segmentation performance, measured on the TIMIT core test set, of systems with best performance
on the development set.
System
Ins(%) Del(%) R-value
MLP benchmark from (Keri and Prahallad, 2010) 12.74 17.00 0.857
MLP with DP benchmark from (van Vuuren et al., 2013) 13.06 15.72 0.863
DNN without pre-training 11.17 12.73 0.887
DNN with pre-training 10.14 12.66 0.891
DNN with DP and pre-training 13.12 14.05 0.868
probabilistic models for segment length and dynamic
programming, therefore no longer lead to any perfor-
mance benefit. This simplifies the segmentation algo-
rithm.
In the future we plan to investigate whether the
performance benefit of our proposed algorithm per-
sists when applied to data substantially different from
the TIMIT training material. We are particularly in-
terested to know the behaviour of unconstrained seg-
mentation algorithms trained on TIMIT but applied
to entirely different languages. Eventually, we would
like to determine whether such cross-domain segmen-
tation can be used to facilitate the development of
ASR systems for under-resourced languages.
ACKNOWLEDGEMENTS
This research was supported by the National Research
Foundation of South Africa under grant UID 71926.
Opinions expressed and conclusions arrived at are
those of the authors and are not necessarily to be at-
tributed to the NRF.
REFERENCES
Adell, J., Bonafonte, A., Gomez, J., and Castro, M. (2005).
Comparative study of automatic phone segmentation
methods for TTS. In Proceedings of the IEEE Inter-
national Conference on Acoustics, Speech, and Signal
Processing (ICASSP).
Aversano, G., Esposito, A., Esposito, A., and Marinaro, M.
(2001). A new text-independent method for phoneme
UnconstrainedSpeechSegmentationusingDeepNeuralNetworks
253

segmentation. In Proceedings of the 44th IEEE Mid-
west Symposium on Circuits and Systems.
Bengio, Y. (2009). Learning deep architectures for AI.
Foundations and Trends in Machine Learning, 2(1):1–
127.
Bengio, Y., Lamblin, P., Popovici, D., and Larochelle, H.
(2007). Greedy layer-wise training of deep networks.
Advances in neural information processing systems,
19:153.
Bishop, C. M. et al. (2006). Pattern recognition and ma-
chine learning, volume 1. Springer.
Cho, K. et al. (2011). Improved learning algorithms for re-
stricted Boltzmann machines. Master’s thesis, School
of science, Aalto University.
Erhan, D., Bengio, Y., Courville, A., Manzagol, P.-A., Vin-
cent, P., and Bengio, S. (2010). Why does unsuper-
vised pre-training help deep learning? The Journal of
Machine Learning Research, 11:625–660.
Estevan, Y. P., Wan, V., and Scharenborg, O. (2007). Find-
ing maximum margin segments in speech. In Proceed-
ings of the IEEE International Conference on Acous-
tics, Speech, and Signal Processing (ICASSP).
Finster, H. (1992). Automatic speech segmentation us-
ing neural network and phonetic transcription. In
Proceedings of the International Joint Conference on
Neural Networks (IJCNN).
Fischer, A. and Igel, C. (2012). An introduction to restricted
Boltzmann machines. In Progress in Pattern Recogni-
tion, Image Analysis, Computer Vision, and Applica-
tions, pages 14–36. Springer.
Fisher, W. M., Doddington, G. R., and Goudie-Marshall,
K. M. (1986). The DARPA speech recognition re-
search database: specifications and status. In Proceed-
ings of the DARPA Workshop on Speech Recognition.
Halberstadt, A. K. (1998). Heterogeneous Acoustic Mea-
surements and Multiple Classifiers for Speech Recog-
nition. PhD thesis, Massachusetts Institute of Tech-
nology, MIT.
Hinton, G. E., Osindero, S., and Teh, Y.-W. (2006). A fast
learning algorithm for deep belief nets. Neural com-
putation, 18(7):1527–1554.
Hoffmann, S. and Pfister, B. (2010). Fully automatic seg-
mentation for prosodic speech corpora. In Proceed-
ings of Interspeech.
Keri, V. and Prahallad, K. (2010). A comparative study
of constrained and unconstrained approaches for seg-
mentation of speech signal. In Proceedings of the In-
ternational Conference on Spoken Language Process-
ing (ICSLP).
Krizhevsky, A. and Hinton, G. (2009). Learning multiple
layers of features from tiny images. Master’s the-
sis, Department of Computer Science, University of
Toronto.
Lee, K.-S. (2006). MLP-based phone boundary refining for
a TTS database. IEEE Transactions on Audio, Speech
and Language Processing, 14(3):981–989.
Malfrere, F., Deroo, O., and Dutoit, T. (1998). Pho-
netic alignment : Speech synthesis based vs. hybrid
HMM/ANN. In Proceedings of the International Con-
ference on Spoken Language Processing (ICSLP).
Mohamed, A.-r., Dahl, G. E., and Hinton, G. (2012).
Acoustic modeling using deep belief networks. IEEE
Transactions on Audio, Speech, and Language Pro-
cessing, 20(1):14–22.
R
¨
as
¨
anen, O., Laine, U., and Altosaar, T. (2011). Blind seg-
mentation of speech using non-linear filtering meth-
ods. Speech Technologies, pages 105–124.
R
¨
as
¨
anen, O. J., Laine, U. K., and Altosaar, T. (2009). An
improved speech segmentation quality measure: the
R-value. In Proceedings of Interspeech).
Sarkar, A. and Sreenivas, T. (2005). Automatic speech seg-
mentation using average level crossing rate informa-
tion. In Proceedings of the IEEE International Con-
ference on Acoustics, Speech, and Signal Processing
(ICASSP).
Sharma, M. and Mammone, R. (1996). ‘Blind’ speech seg-
mentation: automatic segmentation of speech without
linguistic knowledge. In Proceedings of the Fourth In-
ternational Conference on Spoken Language Process-
ing (ICSLP).
Suh, Y. and Lee, Y. (1996). Phoneme segmentation of con-
tinuous speech using multi-layer perceptron. In Pro-
ceedings of the Fourth International Conference on
Spoken Language (ICSLP).
ten Bosch, L. and Cranen, B. (2007). A computational
model for unsupervised word discovery. In Proceed-
ings of Interspeech.
Toledano, D. (2000). Neural network boundary refining for
automatic speech segmentation. In Proceedings of the
IEEE International Conference on Acoustics, Speech,
and Signal Processing (ICASSP).
van Vuuren, V. Z., ten Bosch, L., and Niesler, T. (2013). A
dynamic programming framework for neural network-
based automatic speech segmentation. In Proceedings
of Interspeech.
Wang, D., Lu, L., and Zhang, H.-J. (2003). Speech segmen-
tation without speech recognition. In Proceedings of
theInternational Conference on Multimedia and Expo,
ICME.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
254
