Why Robots Failed

Demonstrating the Superiority of Multiple-order Trading Agents in Experimental

Human-agent Financial Markets

Marco De Luca

Department of Computer Science, University of Bristol,

Merchant Venturers Building, Woodland Road, Bristol BS8 1UB, U.K.

Keywords:

Agent-based Computational Economics, Continuous Double Auction, Experimental Economics, Trading

Agents.

Abstract:

In the past decade there has been a rapid growth of the use of adaptive automated trading systems, commonly

referred to in the ﬁnance industry as “robot traders”: AI applications replacing highly-paid human traders in

the global ﬁnancial markets. The academic roots of this industry-changing deployment of AI technologies can

be traced back to research published by a team of researchers at IBM at IJCAI 2001, which was subsequently

replicated and extended by De Luca and Cliff at IJCAI 2011 and ICAART 2011. Here, we focus on the

order management policy enforced by Open Exchange (OpEx), the open source algorithmic trading system

simultaneously, robots only deal with one order at the time. We hypothesise that such unbalance may have

strongly inﬂuenced the victory of human traders over robot traders, reported in past studies by De Luca et

al., and by Cartlidge and Cliff. We employed OpEx to implement a multiple-order policy for robots as well

as humans, and ran several human vs. robot trading experiments. Using aggregated market metrics and

time analysis, we reached two important conclusions. First, we demonstrated that, in mixed human-robot

markets, robots dealing multiple simultaneous orders consistently outperform robots dealing one order at a

time. And second, we showed that while human traders outperform single-order robot traders under speciﬁc

circumstances, multiple-order robot traders are never outperformed by human traders. We thus conclude

that the performance of robot traders in a human-robot mixed market is strongly inﬂuenced by the order

management policy they employ.

1 INTRODUCTION

At IJCAI 2001 (Das et al., 2001), a team of re-

searchers from IBM demonstrated that software au-

tomated trading agents could consistently outperform

human traders in a real-time asynchronous continuous

double auction (CDA) market.

The CDA is the market mechanism widely

adopted by the majority of modern ﬁnancial elec-

tronic exchanges; in a CDA, traders can asyn-

chronously post bids and offers that are usually pub-

licly visible by every other trader, and a trade is made

whenever the outstanding bid price is greater than or

equal to the outstanding ask price.

Relevant to real world ﬁnancial markets, IBM’s

stunning results triggered worldwide media coverage

and in the 13 years since then, such automated trad-

ing systems have become commonplace in the world’s

major ﬁnancial markets, where they are colloquially

known as “trading robots” or “robot traders”.

At ICAART 2011 (De Luca and Cliff, 2011a) and

IJCAI 2011 (De Luca and Cliff, 2011b) De Luca and

Cliff replicated and extended IBM’s results for the

ﬁrst time since they were presented in 2001: they

found that Vytelingum’s “Adaptive Aggressive” (AA)

trading robot (Vytelingum et al., 2008; Vytelingum,

2006) dominated both Cliff’s “Zero Intelligence Plus”

(ZIP) (Cliff, 1996), and IBM’s GDX, designed by

Tesauro and Bredin (Tesauro and Bredin, 2002);

and they conﬁrmed that the three robot traders, AA,

GDX and ZIP, perform consistently better than human

agents.

The human vs. robot experiments conducted by

De Luca and Cliff adopt a methodology that resem-

bles closely the one described in the IBM study.

An asynchronous real-time electronic trading system

De Luca M..

Why Robots Failed - Demonstrating the Superiority of Multiple-order Trading Agents in Experimental Human-agent Financial Markets.

DOI: 10.5220/0005203100440053

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence (ICAART-2015), pages 44-53

ISBN: 978-989-758-073-4

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

featuring a centralised exchange and remote graph-

ical trading terminals was employed. Each experi-

ment had a ﬁxed duration, and pitted 6 robot traders

against 6 human traders; both robots and humans

were equally split into 3 buyers and 3 sellers. Ex-

periments simulated sales trading: real world sales

traders aim at maximising their own proﬁt, which is

the sum of the commission they charge their clients

for every sale or purchase they execute, on their be-

half, of a speciﬁc amount of a certain commodity

at a given price. In the simulated sales trading ses-

sions, a deﬁnite part of the automated experimental

economics system simulated the agents’ clients, and

communicated to the agents (both human and robot)

the clients’ will of buying or selling the virtual com-

modity, and the numeric values of quantity and price;

De Luca and Cliff refer to such instructions as assign-

ments, and to the predetermined sequence of assign-

ments distributed to each agent in the course of an

experiment as the schedule of that agent. At the start

of the experiment, the system released the ﬁrst assign-

ment in the agent’s schedule; the agent will start trad-

ing such assignment; when (and if) the assignment is

traded, the system distributes the second assignment

to the agent, and so on, until there are no more as-

signments left for that agent, or the experiment time

is up.

De Luca et al. (De Luca et al., 2011) subsequently

ran further human vs. robot (ZIP, AA) experiments on

a more realistic market previously explored by Cliff

and Preist (Cliff and Preist, 2001): in it, the sched-

ule of each agent still consisted of a ﬁxed number of

clients’ instructions, but the instructions were period-

ically released at predetermined times, until the mar-

ket simulator was stopped. To use Cliff and Preist’s

nomenclature, we will call such timed instructions

permits, and we will refer to markets operating on

a permit schedule as continuous-replenishment, or

simply continuous markets. Crucially, unlike assign-

ments, permits are released regardless of whether or

not the agent has ﬁnished trading the previous per-

mit: they are triggered solely by time. Yet, the re-

sults De Luca et al. found were strongly contrasting

with those obtained previously: indeed, humans out-

performed robots in the continuous market simulated

in (De Luca et al., 2011), although the victory was not

as manifest as that shown in (Das et al., 2001).

The ﬁnding of such a trading performance unbal-

ance in favour of humans was as controversial as un-

expected: ﬁrst, because the preceding two human vs.

robot trading agents studies showed the undisputed

victory of robots; second, because with the realism

added by the novel continuous-replenishment mech-

anism, one would anticipate a scenario closer to the

real-world, where the use of automated traders is wide

spread because of their excellent performance; and

third, because, based on common sense, one would

generally expect machines to be better than humans

at numerical tasks such as trading.

The matter was later studied by Cartlidge and Cliff

(Cartlidge and Cliff, 2012; Cartlidge and Cliff, 2013),

who conﬁrmed that, in a market continuously replen-

ished of currency and stock, human traders perform

better than robot traders (AA).

Also, Cartlidge and Cliff revealed an undesired

behaviour in OpEx’s AA implementation, for which

AA robot buyers (sellers) would systematically trade

with the seller (buyer) offering (bidding) the best

price, whenever the difference between the two out-

standing bid and ask prices, divided by the mean of

the two outstanding prices, dropped below a ﬁxed

threshold. In this context, it is useful to recall that

in a CDA the outstanding bid price and ask price are

often referred to as best bid and best ask; the differ-

ence between the best ask and the best bid is what is

commonly called spread; and we refer to the spread

divided by the mean of the best prices as relative

spread. AA’s behaviour is then usually referred to as

crossing the spread or jumping the spread.

Thus, in further experiments, Cartlidge and Cliff

pitted human traders against robot traders implement-

ing a revised version of the AA strategy: one that

was free of the unwanted spread-jumping behaviour

They found that, under those conditions, robots per-

formed better than humans, thus concluded that the

spread-jumping bug caused the robot traders to per-

form worse, both in their experiments, and in De Luca

et al.’s previous work (De Luca et al., 2011). Indeed,

the reassuring victory of robot traders over human

traders that they obtained in their experiments was the

most recent ﬁnding on mixed human/robot agents ex-

perimental ﬁnancial markets at the time we wrote this

paper.

We have seen how, in continuous markets, all

players receive permits to buy or sell continuously

throughout the simulation. We will call orders the

instructions sent by the trading agents (human and

robot) to the market; agents send orders to the market

to trade the permits they receive from their clients: a

new order is ﬁrst sent to the market, and can then be

amended (i.e. its quantity and price can be modiﬁed),

or canceled (i.e., removed from the market). Here, we

In reality, the AA strategy would still jump the spread

methodically, but the minimum value of the relative spread

that triggered the aggressive behaviour had been reduced

considerably, with respect to the value previously used. For

more details on the spread-crossing behaviour of the AA

robot, refer to section 3.

WhyRobotsFailed-DemonstratingtheSuperiorityofMultiple-orderTradingAgentsinExperimentalHuman-agent

FinancialMarkets

focus on the order management policy robots and hu-

mans adopt within the continuous replenishment mar-

ket paradigm: while permits are distributed to them

in the same way, humans and robots manage their or-

ders differently. Humans employ the cash and stock

received through permits to send orders to the mar-

ket without further restrictions: noticeably, humans

can send a new order even though orders that they

previously sent are still open, that is, not completely

traded; in particular, human traders can keep mul-

tiple (open) orders on the market at the same time.

Robots, instead, process one order at a time: they

only send a new order to the market upon either suc-

cessful completion or intentional cancellation of the

previous order they sent. Therefore robots manage (at

most) one order at a time, whereas humans can (and

do) keep several orders simultaneously. We will re-

fer to the former order management policy as “single-

order”, and to the latter as “multiple-order”. Also,

for shortness, we will thereafter refer to robots em-

ploying a single-order policy as “single-order robots”,

and to robots employing a multiple-order policy as

“multiple-order robots”.

Our intuition is that the enforcement of the single-

order policy deteriorates the performance of robot

traders; we believe that this holds independently from

the particular trading strategy robots implement. In-

spired by that, we used OpEx to explore how chang-

ing the robots’ order management policy from single-

order to multiple-order affected their performance.

We studied the effect of changing from single-order

to multiple order in two experiment conditions: one

where the AA spread-jumping behaviour was unde-

sirably strong (i.e., within 15%, as in (De Luca et al.,

2011)) and the other where the spread-jumping be-

haviour was much weaker at 1%, as originally in-

tended (as in (Cartlidge and Cliff, 2013)).

The next section explains the basic features of

CDA-based markets and deﬁnes the metrics we will

use to compute the performance of the traders, in

order to determine the outcome of our experiments.

Section 3 describes the changes we made to the ex-

perimental conditions used in previous studies, to im-

plement the multiple-order policy for the robots. We

report the results we obtained in our simulations in

section 4 and we discuss them in section 5; ﬁnally,

we present our conclusions in section 6.

2 BACKGROUND

Vernon Smith’s Nobel-prize-winning experimental

work (Smith, 1962) demonstrated that a CDA-based

market made up of human traders can reach close-to-

optimal efﬁciency. Furthermore, Smith proved that

the competitive market dynamics will cause the con-

vergence of the transaction prices towards the theo-

retical market equilibrium price p

∗

. In his seminal

study, Smith distributed one unit to sell (buy) at no

less (more) than a speciﬁc price to each trader; such

price is known as cost price c of a seller, or limit price

l of a buyer. If p is the price of a speciﬁc transaction,

the proﬁt made by the buyer is thus l − p, while the

proﬁt made by the seller is p − c.

Formally, let I be the set of buyers and J the set

of sellers in the market. Let L

= {l

i,1

, l

i,2

, . . . , l

i,N

} be

the set of limit prices of the N

units owned by buyer

i, and C

= {c

j,1

, c

j,2

, . . . , c

j,M

} the set of cost prices

of the C

units owned by seller j. The market equilib-

rium price is given by:

∗

= argmax

(

∑

i∈I

∑

n=1

max(0, l

i,n

− p)

∑

j∈J

∑

m=1

max(0, p − c

j,m

)

(1)

To compare the performance of the traders, Smith

measured their allocative efﬁciency, which is the total

proﬁt earned by the trader divided by the maximum

theoretical proﬁt of that trader, expressed as a per-

centage.

Deﬁned as the proﬁt that a trader could have made

if all the market participants would have traded their

(tradable) units at price p

∗

, the maximum theoretical

proﬁt π

∗

of buyer b

is given by:

∗

∑

n=1

max(0, l

i,n

− p

∗

) (2)

Denoting with p

i,n

the price at which buyer i ac-

tually trades the unit with limit price l

i,n

, the actual

proﬁt π

earned by buyer i is:

∑

n=1

max(0, l

i,n

− p

i,n

) (3)

Therefore, the allocative efﬁciency E

of buyer i

is:

∗

(4)

The allocative efﬁciency of a group of N traders is

thus:

E =

∑

j=1

∗

(5)

Equations 5 and 4 also hold for sellers; however,

the formula of the proﬁt of a seller must be used in-

stead of that of the proﬁt of a buyer in Equation 2

and Equation 3, in order to evaluate the allocative ef-

ﬁciency of sellers.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

In this work, we will also use the following met-

rics to establish the performance of a market in terms

of how far from the theoretical equilibrium it trades.

Used to calculate the difference between the total

proﬁt made by two groups, X and Y , divided by the

mean of those two proﬁts, delta proﬁt is deﬁned as:

∆P(X −Y ) =

2(π

− π

)

+ π

(6)

The delta proﬁt of an ideal market, where the two

groups match identically, should be zero.

Smith’s alpha (Vernon Smith, (Smith, 1962)) cap-

tures the standard deviation of trade prices about the

theoretical equilibrium price; lower values of α are

desirable, indicating trading around p

∗

. In the follow-

ing deﬁnition, we also normalise α by p

∗

, and express

its value as a percentage by multiplying by 100:

α =

100

∗

∑

i=1

− p

∗

)

(7)

A measure of how the proﬁt generated by each

trader in a group differs from the value it would be

expected of them if all transactions took place at the

equilibrium price p

∗

, is the proﬁt dispersion. For a

group of N traders, proﬁt dispersion is calculated as

the root mean square difference between the proﬁt

achieved π

by each trader, i, and the maximum theo-

retical proﬁt available to that trader, π

∗

disp

∑

i=1

(π

− π

∗

)

(8)

3 EXPERIMENT

METHODOLOGY

3.1 OpEx

We ran our human vs. robot experiments on Open

Exchange (OpEx). OpEx is the open source algorith-

mic trading system developed in 2009-2010 by Marco

De Luca at University of Bristol. Since there was no

de facto standard experimental economics platform

to simulate human-agent asynchronous CDA markets

when he started his doctoral research in 2009, De

Luca created OpEx to offer a free, open source so-

lution. Since its inception, and excluding this study,

OpEx has hosted over 70 human-agent trading ses-

sions, which were the empirical basis for six peer-

reviewed publications (De Luca and Cliff, 2011a; De

Luca and Cliff, 2011b; De Luca et al., 2011; Cartlidge

et al., 2012; Cartlidge and Cliff, 2012; Cartlidge and

Cliff, 2013). OpEx is available for download from

Sourceforge (De Luca, 2012); on 10 November 2014,

OpEx had been downloaded 935 times since it was

ﬁrst distributed in February 2012. A complete de-

scription of OpEx can be found in (De Luca et al.,

2011).

3.2 Experiment Design

We used OpEx to perform a total of 24 human vs.

robot trading experiments that took place from Mon-

day 3rd to Thursday 6th February 2014, at Algo-

rithmic Trading Consulting’s premises in Boadilla

del Monte, Madrid, Spain. All human participants

were registered full-time undergraduate economics

students at several universities

in Spain; none of

the subjects had previous (professional) experience in

electronic trading.

Each experiment involved 6 human traders and 6

robot traders, both equally divided into 3 buyers and

3 sellers. We split the 24 participants into 4 groups

of six; we then used each of those groups in an ex-

perimental session consisting of six consecutive but

distinct experiments: this way, we were able to run 24

experiments using only 24 participants.

The premises were laid out so that human partic-

ipants would sit at the two long sides of a large con-

ference room table, three by each side. Each of the

seats was set up with a netbook displaying the OpEx

GUI; an external mouse and numerical keypad were

plugged to the netbook for convenience. Each net-

book corresponded to a speciﬁc market role: the three

netbooks on one side to Buyer1, Buyer2, Buyer3; and

the three netbooks on the opposite side to Seller1,

Seller2, Seller3 (in this order). The experiment ad-

ministrator would sit at one of the short ends of the

table and use a laptop to control and supervise both

the market and the experiment.

At the start of each session humans were randomly

allocated to a seat (market role); the subjects were

briefed about the rules of the experiment; and they

were given some time to familiarise with the OpEx

GUI. During the tutorial robot traders were switched

off, thus allowing human participants to trade among

themselves and get accustomed to the market. Brief-

ing and tutorial took about 10 minutes.

Then the actual experiment was run for six times

in a row, each one lasting 10 minutes. At the end

of each run, and before the following one, we intro-

duced a 2 minutes break during which the adminis-

trator could set the new experimental conﬁguration,

and the participants rotated seats anti-clockwise

thus

Universidad Complutense de Madrid. Universidad

Carlos III de Madrid. Univeridad Rey Juan Carlos.

We purposely mixed human roles between experi-

WhyRobotsFailed-DemonstratingtheSuperiorityofMultiple-orderTradingAgentsinExperimentalHuman-agent

FinancialMarkets

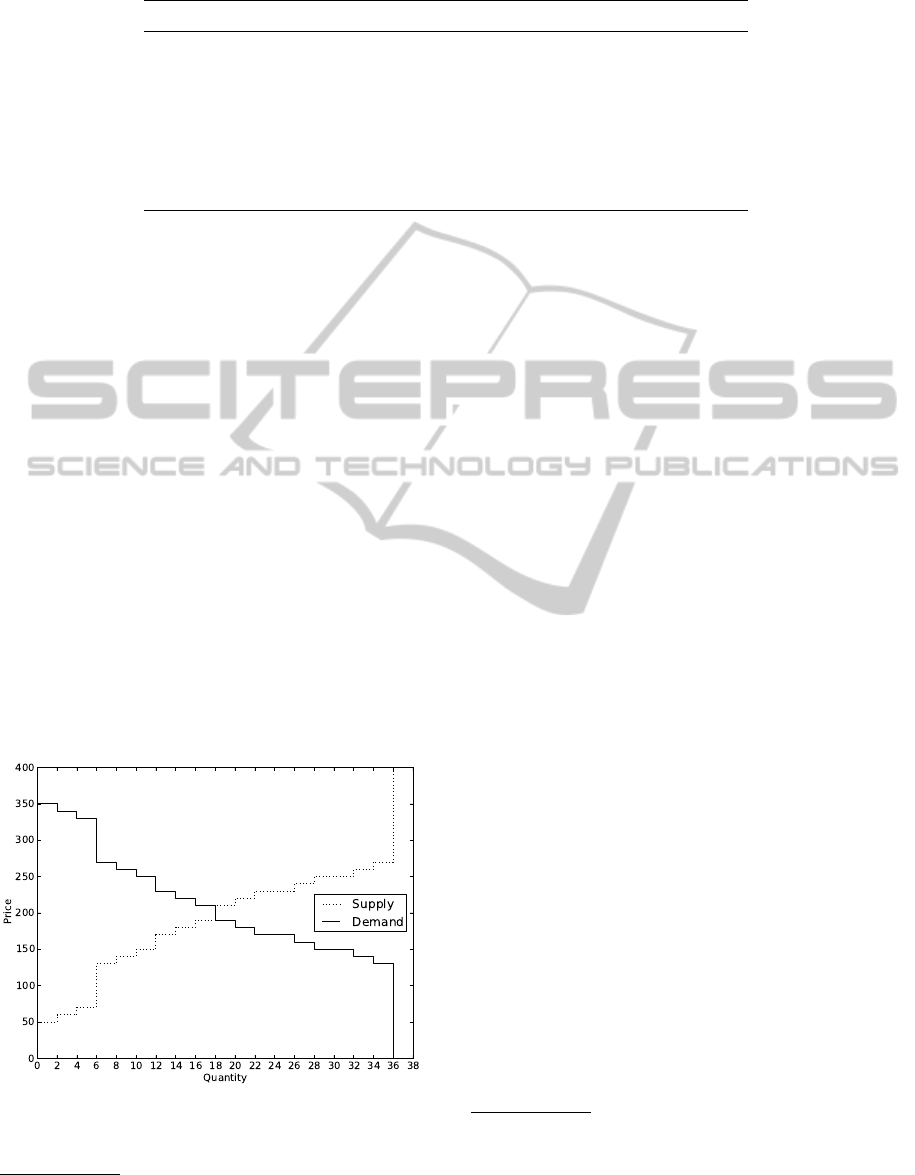
Table 1: Permit schedule employed in the 24 simulations.

1 2 3 4 5 6

Buyer1 350 (0) 250 (5) 220 (7) 190 (9) 150 (14) 140 (16)

Buyer2 340 (1) 270 (3) 210 (8) 180 (10) 170 (12) 130 (17)

Buyer3 330 (2) 260 (4) 230 (6) 170 (11) 160 (13) 150 (15)

Seller1 50 (0) 150 (5) 180 (7) 210 (9) 250 (14) 260 (16)

Seller2 60 (1) 130 (3) 190 (8) 220 (10) 230 (12) 270 (17)

Seller3 70 (2) 140 (4) 170 (6) 230 (11) 240 (13) 250 (15)

playing a different market role each time. Overall, an

experimental session lasted less than 90 minutes, with

60 minutes of experiment time.

Finally, we motivated all participants by paying

each of them e25, plus, to incentivise traders to make

proﬁt, the human trader scoring the highest alloca-

tive efﬁciency (as deﬁned in Section 2, Equation 4)

on each experimental session was rewarded with an

additional e250 prize. Since one prize was given at

the end of each experimental session, and the human

participants to each session were 6, participants had a

1-in-6 chance of winning the prize. The total cost of

the experiments was e25*24 + e250*4 = e1600.

3.3 Supply and Demand

We employed the schedule of permits used in (De

Luca et al., 2011; Cartlidge et al., 2012). The limit

prices are shown in Table 1, arranged by trader and

permit type; the time step at which each permit is sent

is shown in brackets. Figure 1 displays the supply and

demand curves that originate from such schedule.

Figure 1: Supply and demand.

ments, to reduce the opportunity for collusion and coun-

teract any bias in market role.

3.4 Robot Conﬁguration

In (Cartlidge and Cliff, 2012), Cartlidge and Cliff

noted that the implementation of AA found in version

1.0 of OpEx displayed an undesired behaviour, not

documented in Vytelingum’s original description of

the trading strategy (Vytelingum, 2006; Vytelingum

et al., 2008), for which the robot would cross the

spread every time its relative value fell below a pre-

determined percentage threshold. While they re-

ported that the idea of systematically crossing the

spread can be reasonable and beneﬁcial to conver-

gence, Cartlidge and Cliff pointed out that the ﬁxed

value of 0.15 (i.e., 15%) used for the threshold was

much too high

. Indeed, they demonstrated that when

the threshold was set to the 1% value originally spec-

iﬁed by Vytelingum (Vytelingum, 2006), robots out-

performed human traders, but when the threshold was

set to 15% the humans outperformed the robots. In-

spired by their results, in this work we will experiment

with both settings of the threshold: 1%, and 15%.

3.5 Order Management Policies

We have seen in Section 1 how permits are the in-

structions sent by (simulated) clients to agents, while

orders are the instructions that agents send to the mar-

ket. The relationship between permits and orders is

not necessarily one to one. In fact, importantly, one

permit for one unit can give origin to many orders.

This is possible because orders can be cancelled: once

an order for one unit has been cancelled, that unit is

no longer advertised on the market, therefore a new

order can (and should) be sent to the market, to newly

implement the client’s instruction. Once a unit has

been received by a trader as a permit, we will refer to

the process of sending, amending, and cancelling or-

Contextually, De Luca was informed of the bug, and

released a new version of OpEx in which the value of the

threshold that triggered spread-crossing was conﬁgurable.

The new version, OpEx 1.1, was released on 25 March

2012.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

ders that the trader executes in order to trade that unit,

as working that permit.

The order management policy to apply for hu-

mans and robots was a design choice that was faced

when permits were distributed on a periodic regular

schedule (continuous market, as studied in (Cliff and

Preist, 2001; De Luca et al., 2011; Cartlidge et al.,

2012; Cartlidge and Cliff, 2012; Cartlidge and Cliff,

2013)), rather than sequentially and only upon com-

pletion of the preceding one (cyclical market, as stud-

ied in (Das et al., 2001; De Luca and Cliff, 2011a; De

Luca and Cliff, 2011b)). By order management pol-

icy, we mean the set of rules that apply to a group of

traders for what concerns the creation and handling of

orders.

We say that a group of traders follows a multiple-

order policy, if an order for one unit with a certain

limit price l can be sent to the market, provided that

a permit for one unit with limit price l has been re-

ceived, and no further orders are on the market for

that particular unit. In particular, this allows a trader

to submit a new order for a new unit even though an

order of hers for a previously received unit was still

on the market.

Instead, the following applies to traders following

a single-order policy:

1. when a new permit is received:

(a) if the trader is not working any permit, then the

trader will immediately start working the new

permit;

(b) if the trader is working a more proﬁtable permit

than the newly arrived, then the trader will ig-

nore the newly arrived permit and push it to the

“deferred permits queue”;

than the newly arrived, then the trader will can-

cel the current order, push the associated permit

to the “deferred permits queue”, and start work-

ing the newly arrived permit;

2. when a trader completes the order related to the

current permit:

(a) if the “deferred permits queue” is not empty, the

trader retrieves the most proﬁtable permit from

it, and starts working it;

(b) if the “deferred permits queue” is empty, the

trader does nothing.

In order to change the order management policy

implemented by OpEx robots from single-order to

multiple-order, we leveraged the existing infrastruc-

ture and implemented the following multiple-order

policy (similar rules apply to sellers):

1. when a new permit to buy at limit price l is re-

ceived by a trader:

(a) if the trader is not working any permits at limit

price l, then the trader will send a new order

with limit price l;

(b) if the trader is already working permits at limit

price l, then the trader will amend the existing

order at limit price l to include the quantity just

requested in the last permit;

2. when a trader completes the order related to the

current permit, the trader becomes idle and waits

to receive the next permit.

4 EXPERIMENTAL RESULTS

In this paper, we tested both the single-order and the

multiple-order policy across 24 simulations: 12 sim-

ulations for each policy. And for each of the two

policies, we explored the effects of two values of the

minimum relative spread threshold crossed by the AA

trading strategy: 15%, and 1%. We will refer to this

threshold as MaxSpread, after the name of the OpEx

variable that represents it.

We tested the four resulting combinations in four

sets of six 10 minutes’ simulations.

We will ﬁrst focus on the group efﬁciency of

robots and humans, as deﬁned by Equation 5: Table 2

summarises the results we obtained under the four dif-

ferent experimental conditions employed. Each cell

in the table represents an experiment and contains: the

symbolic name we gave to the experiment; an indica-

tion of the allocative efﬁciency of the robots, com-

pared to that of the humans; and the level of signif-

icance of the result, according to Fligner and Polli-

cello’s robust rank order (RRO) test

Table 2: Group allocative efﬁciency of robots and humans

compared.

MaxSpread=15% MaxSpread=1%

MP15

R = H

p > 10.4%

MP01

R > H

1.1% < p < 2.2%

SP15

H > R

0.11% < p < 0.54%

SP01

R > H

5.1% < p < 10.4%

Fligner and Pollicello ﬁrst reported on the robust rank

order (RRO) test in 1981 (Fligner and Pollicello, 1981). The

RRO test is a non-parametric test of difference in medians,

which Feltovich showed in (Feltovich, 2003) to apply well

to the domain of small sample statistics (in which we deﬁ-

nitely are), and to perform better than the more commonly-

used Wilcoxon-Mann-Whitney ’U’ test.

WhyRobotsFailed-DemonstratingtheSuperiorityofMultiple-orderTradingAgentsinExperimentalHuman-agent

FinancialMarkets

The bottom section of the table shows that,

if robots enforce a single-order policy: when

MaxSpread=1%, robots outperform humans (experi-

ment SP01, R > H); and when MaxSpread=15%, hu-

mans outperform robots (experiment SP15, H > R).

The results of the RRO test to the raw group alloca-

tive efﬁciency data of robots and humans in the two

experiments show that: in experiment SP01 the differ-

ence between the two group efﬁciencies is signiﬁcant

at the 10.4% level (that is, 5.1% < p < 10.4%); and

in experiment SP15 the difference is signiﬁcant at the

0.54% level (0.11% < p < 0.54%).

Our novel ﬁndings resulting from using a

multiple-order policy for the robots are shown in

the top row of Table 2. In experiment MP01, with

MaxSpread=1%, robots outperform humans with a

level of signiﬁcance of 2.2% (1.1% < p < 2.2%); and

in experiment MP15, with MaxSpread set to 15%,

the difference between the efﬁciency of robots and

humans is not signiﬁcant at 10.4% or less (i.e., p >

0.104).

Moreover, we compared the performance of

robots in all experiments employing a multiple-order

policy (MP01 and MP15) to that of their single-order

policy counterpart (SP01 and SP15). The RRO test

showed that the ﬁrst group performed better than

the second group with a level of signiﬁcance of 1%

(0.5% < p < 1%).

To extract further comparative information related

to the performance of robots conditional to the four

experimental conditions, we isolated the raw data of

the group allocative efﬁciency of robots in our four

experiments, and thus applied the RRO test to the two

series of 6 points (one per each 10-minutes simula-

tion in the 60 minutes experiment) identiﬁed by each

pair of adjacent cells in Table 2. Table 3 contains the

results.

The two groups of robots under comparison are la-

belled R1 and R2. For each of the four comparisons,

the table shows: the experimental conditions under

which each of the two groups of robots traded and the

signiﬁcance level according to the RRO test. The ex-

perimental conditions include the name of the experi-

ment, the order-management policy, and the value of

MaxSpread. The robots in the group labelled R1 are

those with the resulting higher group efﬁciency, as de-

ﬁned in Equation 5.

Looking at market efﬁciency, that is the group al-

locative efﬁciency of all traders, the ranking of the

most efﬁcient markets is MP01, MP15, SP01 and

SP15 in this order, displaying efﬁciencies of 0.818,

0.785, 0.780 and 0.773 respectively. Further, for each

experiment we calculated the delta proﬁt between the

two groups, robots and humans (as per Equation 6);

Table 3: Group allocative efﬁciency of robots compared

across different experimental conditions.

R1 R2 RRO

MP01

Multiple

SP01

Single

0.54% < p < 1.1%

MP01

Multiple

MP15

Multiple

15%

0.11% < p < 0.54%

SP01

Single

SP15

Single

15%

0.11% < p < 0.54%

MP15

Multiple

15%

SP15

Single

15%

0.11% < p < 0.54%

Table 4: Aggregated market statistics. For each experiment,

the table shows: market efﬁciency; relative proﬁt difference

between robots and humans; proﬁt dispersion; and Smith’s

α.

Experiment E ∆P π

disp

MP01 0.818 3.6% 901 9.3%

MP15 0.785 -1.8% 1079 12.7%

SP01 0.780 3.4% 1155 17.3%

SP15 0.773 -18.4% 1206 6.4%

the proﬁt dispersion, shown in Equation 8; and ﬁnally

Smith’s alpha (Equation 7). Table 4 summarises our

ﬁndings with respect to such statistics.

While the metrics employed so far explain mea-

surements that apply to the experiment as a whole,

we introduce here a novel analysis that reveals com-

ponents of the human-agent interaction that are re-

lated to time. In the course of the simulations, per-

mits are regularly distributed to the traders, following

the schedule in Table 1. Once a permit has been dis-

tributed to a trader (either human or robot), the trader

decides how to employ that permit, compatibly with

the order-management policy that is being enforced.

Thus, considering both the present market conditions

and the past evolution, the trader decides whether to

send an order immediately, or delay execution of the

order until he estimates there are better market con-

ditions to send the order. The order, in turn, may im-

mediately ﬁll if it’s an aggressive order, or it may sit

in the order book, perhaps its price may be modiﬁed

a few times, and then it may eventually ﬁll.

By scanning the time series of order instructions

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

stored OpEx’s database with sub-second time resolu-

tion, we analysed the Time-To-Complete of the per-

mits, deﬁned as the time elapsed from the moment a

permit is received by a trader, to the moment the order

that trader sent to work that permit ﬁlls. After mea-

suring this time for all trades, we grouped the results

by trader group, human or robot, and subsequently

by proﬁtability of the permit, intra-marginal or extra-

marginal. We thus obtained, for each of our exper-

iments, four populations of Time-To-Complete. Ta-

ble 5 shows the median of each of the four populations

in the different experiments; we labelled each popu-

lation so that, for example, R-IM stands for “robots,

intra-marginal permits”, and H-EM stands for “hu-

mans, extra-marginal permits”.

Table 5: Time-To-Complete for each experiment. The table

shows the median (in seconds) of the Time-To-Complete of

intra-marginal and extra-marginal permits, for both human

and robot traders.

Experiment R-IM H-IM R-EM H-EM

MP01 0.8 20 119 325

MP15 0.1 10 106 125

SP01 1.7 12 112 140

SP15 0.3 20 110 135

5 DISCUSSION

The results in the bottom line of Table 2 agree with the

ﬁndings presented in (De Luca et al., 2011; Cartlidge

and Cliff, 2012; Cartlidge and Cliff, 2013), that is:

if the order-management policy enforced by robots is

single-order, humans perform better than robots when

MaxSpread is 15%, while robots outperform humans

when MaxSpread is 1%. The innovative multiple-

order policy we employed for robots revealed the re-

sults displayed in the top row of the table. When

MaxSpread is 1%, switching from single-order to

multiple-order still reveals a victory of robots: we

found that the RRO test gives a stricter result for

MP01 than it does for SP01, and we interpret this ﬁnd-

ing as the fact that the switch to a multiple-order pol-

icy beneﬁted the robots, as a group. We found though

that there is no statistically signiﬁcant difference be-

tween the efﬁciency of robots and humans in experi-

ment MP15; by visually inspecting Table 2, we notice

that, when MaxSpread is 15%, switching from single-

order to multiple-order turns the distinct victory of

humans in experiment SP15, into what the RRO test

signalled as an indecisive case. However, the com-

parison of all the results obtained for multiple-order

robots with those obtained for single-order robots in-

dicate a sharp result (RRO 0.5% < p < 1%): multiple-

order robots perform better than single-order robots,

regardless of whether MaxSpread is 15% or 1%.

We then studied the relationship that holds be-

tween the efﬁciency of robots across our experiments

(see Table 3), and found that indeed the effects of

switching the robots policy to multiple-order are ex-

plained. All the RRO test results have a level of sig-

niﬁcance of p=0.54%, except for MP01 vs. SP01

which has a level of signiﬁcance of p=1.1%: overall,

very sharp results. In detail:

• the performance of robots was signiﬁcantly bet-

ter in MP01 than it was in SP01: this conﬁrms

our previous interpretation of the different level

of signiﬁcance in the two cases;

• robots employing a multiple-order policy perform

better when MaxSpread=1% (MP01) than when

MaxSpread=15% (MP15);

• even though MaxSpread is 15% (that is, AA is

crossing the spread excessively), switching to a

multiple-order policy beneﬁts the performance of

robots, declaring their efﬁciency signiﬁcantly bet-

ter at the 0.54% level;

• ﬁnally, we conﬁrmed that robots that em-

ploy a single-order policy perform better when

MaxSpread is 1% (SP01 vs. SP15).

Furthermore, we interpreted the metrics sum-

marised in Table 4 as follows. Sorting the experi-

ments by descending value of market efﬁciency, is in-

deed equivalent to sorting them by ascending value of

proﬁt dispersion

, and result into the sequence MP01,

MP15, SP01, SP15. In both cases, the indication

is that markets where the multiple-order policy is in

place are better.

The ranking deriving from Smith’s α still places

MP01 and MP15 before SP01, but it puts SP15 in

the ﬁrst place; to explain this, we speculate that the

combination of less simultaneous orders by robots,

and AA aggressively accepting more offers, made the

trade price time series more stable around p

∗

in SP15.

The values of ∆P are mixed; however, qualita-

tively, we can see how the magnitude of ∆P is much

higher in SP15, than it is in every other experiment.

In particular, we point out how the absolute value of

∆P in MP15 is about one tenth of the value in SP15:

we interpret this as a further conﬁrmation that switch-

ing to a multiple-order policy boosts the quality of the

market.

Higher values of market efﬁciency, and lower values of

proﬁt dispersion are better.

WhyRobotsFailed-DemonstratingtheSuperiorityofMultiple-orderTradingAgentsinExperimentalHuman-agent

FinancialMarkets

Figure 2: Box plot of Time-To-Complete. The charts of the four sets of experiments MP15, MP01, SP15, SP01 are displayed

in the sub-ﬁgures, respectively from left to right, and from top to bottom. The time axis is logarithmic.

Figure 2 offers a graphical representation of our

time analysis, in the form of a box plot. The bot-

tom, middle, and top of the box are respectively the

ﬁrst, second (median) and third quartiles of each set

of data. The whiskers of the plot extend to the low-

est datum still within 1.5 IQR of the lower quartile,

and the highest datum still within 1.5 IQR of the up-

per quartile; by IQR we mean the interquartile range,

that is the difference between the third and the ﬁrst

quartile.

We will mainly focus on the statistics of Time-

To-Complete for the group R-IM: that is, the val-

ues we collected for the intra-marginal permits traded

by robots in each experiment. With MaxSpread=1%,

switching the policy to multiple-order consistently re-

duces the values of ﬁrst, second and third quartiles

(SP01 vs. MP01); the same effect applies to SP15

vs. MP15. In practise, this means that the robots

of MP01 and MP15 send to the market orders that

take less time to complete than their counterparts of

SP01 and SP15, respectively. Together with the re-

sults we found for the group allocative efﬁciency, this

evidences the superior pricing employed by the robots

that manage multiple orders simultaneously. Once

again, this illustrates how adopting a multiple-order

policy is beneﬁcial in both cases: MaxSpread=1%,

and MaxSpread=15%.

6 CONCLUSIONS

We resumed the investigation on human vs. robot ex-

perimental trading simulations from the last major

ﬁnding published by Cartlidge and Cliff (Cartlidge

and Cliff, 2012; Cartlidge and Cliff, 2013): lower

values of the minimum relative spread to cross

(MaxSpread) result in better group allocative efﬁ-

ciency for AA robots.

We introduced a new dimension in the analysis,

time to complete, that is orthogonal to the one deﬁned

by MaxSpread; and we generated data in the newly

deﬁned 2-dimensional space of experimental condi-

tions. We evaluated the resulting markets using both

aggregated metrics (i.e. allocative efﬁciency, group

efﬁciency, Smith’s α, delta proﬁt, proﬁt dispersion),

and time analysis.

First, we proved that we could successfully repro-

duce Cartlidge and Cliff’s results.

Second, we demonstrated that robots that manage

simultaneous multiple orders display a superior per-

formance to that of robots that manage one order at

a time, separately in the two cases: MaxSpread=1%,

and MaxSpread=15%.

Third, we extended our comparison across the

MaxSpread axis and proved that the superiority of

multiple-order policy on single-order policy holds re-

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

gardless of the value of MaxSpread. This is a strong

result: prior to this study, to the best of our knowl-

edge, the only explanation given to the supremacy

of humans over robots reported in (De Luca et al.,

2011) was that found by Cartlidge and Cliff (Cartlidge

and Cliff, 2012), claiming that this phenomenon was

due to a malfunctioning of the AA robots. Indeed,

here we proved that multiple-order robots outperform

single-order robots. Therefore, the poor performance

of robots in (De Luca et al., 2011) may as well be

explained by the disadvantage that robots employing

a single-order policy have, when they challenge hu-

mans allowed to deal multiple simultaneous orders.

Finally, presuming that no commercial algorithm

would manage only one order at a time, we argue that

we moved a step towards a more realistic model of

sales-trading behaviour in real-world ﬁnancial mar-

kets.

ACKNOWLEDGEMENTS

We are indebted to Dave Cliff for his many help-

ful suggestions on the style and the structure of this

paper. Marco De Luca’s PhD research was par-

tially supported by funds from the University of

Bristol Merchant Venturers’ School of Engineering.

Equipment costs for constructing De Luca’s Open

Exchange (OpEx) system were met by a research

grant from EPSRC made to Dave Cliff, number

EP/I001603/1. Thanks to Algorithmic Trading Con-

sulting, S.L. (http://www.algotradingconsulting.com)

for funding the rewards we used as incentives in

our experiments, ﬁnancing the registration costs to

ICAART 2015, and providing the venues where the

experiments were run. We are very grateful to all

the participants to our experiments at Algorithmic

Trading Consulting’s premises in Boadilla del Monte,

Madrid (Spain).

REFERENCES

Cartlidge, J. and Cliff, D. (2012). Foresight project, Driver

Review DR25. Exploring the “robot phase transition”

in experimental human-algorithmic markets. Techni-

cal report, UK Government’s Ofﬁce for Science.

Cartlidge, J. and Cliff, D. (2013). Evidencing the “robot

phase transition” in human-agent experimental ﬁnan-

cial markets. In Proceedings of ICAART 2013.

Cartlidge, J., Szostek, C., De Luca, M., and Cliff, D. (2012).

Too fast too furious. Faster Financial-Market Trading

Agents Can Give Less Efﬁcient Markets. In Proceed-

ings of ICAART 2012.

Cliff, D. (1996). Minimal-intelligence agents for bargaining

behaviors in market-based environments. Technical

report, Hewlett Packard Laboratories.

Cliff, D. and Preist, C. (2001). Days without end: On

the stability of experimental single-period continuous

double auction markets. Technical report, Hewlett

Packard Laboratories.

Das, R., Hanson, J., Kephart, J., and Tesauro, G. (2001).

Agent-human interactions in the continuous double

auction. In Proceedings of IJCAI 2001.

De Luca, M. (2012). Open Exchange (OpEx) - The open

source Algorithmic Trading System, SourceForge.

De Luca, M. and Cliff, D. (2011a). Agent-Human Interac-

tions in the Continuous Double Auction, Redux. Us-

ing the OpEx Lab-in-a-Box to explore ZIP and GDX.

In Proceedings of ICAART 2011.

De Luca, M. and Cliff, D. (2011b). Human-agent auction

interactions: Adaptive-aggressive agents dominate. In

Proceedings of IJCAI 2011.

De Luca, M., Szostek, C., Cartlidge, J., and Cliff, D. (2011).

Foresight project, Driver Review DR13. Studies on

interactions between human traders and Algorithmic

Trading Systems. Technical report, UK Government’s

Ofﬁce for Science.

Feltovich, N. (2003). Nonparametric tests of differences

in medians: comparison of the Wilcoxon-Mann-

Whitney and robust rank-order tests. Experimental

Economics.

Fligner, M. and Pollicello, G. (1981). Robust Rank Proce-

dures for the Behrens-Fisher Problem. Journal of the

American Statistical Association, (76):162–168.

Smith, V. (1962). An experimental study of compara-

tive market behavior. Journal of Political Economics,

70:111–137.

Tesauro, G. and Bredin, J. (2002). Strategic sequential bid-

ding in auctions using dynamic programming. In Pro-

ceedings of AAMAS 2002.

Vytelingum, P. (2006). The Structure and Behaviour of the

Continuous Double Auction. PhD thesis.

Vytelingum, P., Cliff, D., and Jennings, N. (2008). Strate-

gic bidding in continuous double auctions. Artiﬁcial

Intelligence, 172(14):1700–1729.

WhyRobotsFailed-DemonstratingtheSuperiorityofMultiple-orderTradingAgentsinExperimentalHuman-agent

FinancialMarkets