
Schedule Two-machine Flow-shop with Controllable Processing Times
Using Tabu-search
Kailiang Xu and Gang Zheng
School of Automation and Information Engineering, Xi’an University of Technology, Xi’an, Shaanxi, China
Keywords:
Two-machine flow-shop, Controllable processing times, Heuristic, Tabu-search.
Abstract:
A two-machine flow-shop scheduling problem with controllable processing times modeled by a non-linear
convex resource consumption function is considered in this paper. The objective is to minimize the resource
consumption that is needed to control the makespan not to exceed the given deadline. The problem is proved to
be strongly N P -hard. An optimalresource allocation algorithm is designed to calculate the optimal processing
times of the jobs, while the optimal or near-optimal processing sequence of the jobs is determined by aheuristic
or a tabu-search algorithm.
1 INTRODUCTION
In this paper, we consider a two-machine flow-shop
scheduling problem with controllable job-processing
times. The problem is stated as follows: A set of jobs
J = {1,2,...,n} are to be processed in a two-machine
flow-shop. Each job j contains two operations, O
1, j
and O
2, j
, processed on machine 1 and machine 2 with
preemption not allowed. The processing time of each
operation is a non-linear convex decreasing function
with respect to the allocated resource, described as
follows:
p
i, j
(u
i, j
) =
ω
i, j
u
i, j
k
, p
i, j
> 0 (1)
i = 1,2
j = 1,2,...,n
where ω
i, j
is the processing parameter (a positive
value which represents the workload of the opera-
tions), u
i, j
is the amount of the resource allocated
to operation O
i, j
and k is a constant positive param-
eter. The objective is to determine the processing se-
quence of the jobs, and the processing time of the op-
erations, such that the makespan will not exceed the
given deadline K, while the total resource consump-
tion is minimized. Because processing times can be
extended arbitrarily, in the optimal schedule opera-
tions must be processed continually without idle time
between them. Therefore, the problem can be formu-
lated as follows:
(P)
min U =
2
∑
i=1
n
∑
j=1
u
i, j
s.t. p
1,σ(1)
+
n
∑
j=1
p
2,σ( j)
≤ K
j
∑
l=2
p
1,σ(l)
≤
j−1
∑
l=1
p
2,σ(l)
j = 2,3,...,n
p
i, j
=
ω
i, j
u
i, j
k
,u
i, j
> 0 i = 1,2
j = 1,2,...,n
where σ = {σ(1),σ(2),...,σ(n)} is the processing
sequence of the jobs. Using the three field problem
classification introduced by Graham(Graham et al.,
1979) and extended by Shabtay(Shabtay and Steiner,
2007), the problem can be denoted as F
2
|conv,C
max
≤
K|
∑
2
i=1
∑
n
j=1
u
i, j
.
Scheduling problems with controllable processing
times have been on literature for nearly 30 years. In
most early work (e.g. Janiak(Janiak, 1989), (Janiak,
1986), (Janiak, 1998), (Janiak et al., 2007), (Now-
icki, 1993) and Biskup(D. Biskup, 2001), etc.), it
is supposed that processing times are linear decreas-
ing functions with respect to resource consumption.
Shabtay(Shabtay and Steiner, 2007) pointed out this
assumption does not obey the law of diminishing
marginal returns, which states that productivity in-
creases to the amount of resource at a decreasing rate.
Therefore, the non-linear convex resource consump-
14
Xu K. and Zheng G..
Schedule Two-machine Flow-shop with Controllable Processing Times Using Tabu-search.
DOI: 10.5220/0005204300140022
In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 14-22
ISBN: 978-989-758-075-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

tion function formulated by Eq.2 is adopted. Monma
et al.(Monma et al., 1990) pointed out this function
has many applications in the actual government activ-
ities and industrial operations. A number of related
research work has been on literature, including mini-
mizing the makespan(M.Kaspi, 2006) on a single ma-
chine, parallel machine scheduling problems(Shabtay
and Kaspi, 2006), and other scheduling problems as
well. Xu et al.(Xu et al., 2010)(Xu and Feng, 2010)
studied scheduling jobs with arbitrary release dates
and due dates in a single machine. For a detailed de-
scription of the recent work in this field, reader may
refer to the survey((Shabtay and Steiner, 2007)).
Two-machine flow-shop is a special case of the
flow-shop scheduling problems. Nowicki and Zdrza-
lka(Nowicki, 1993) and Janiak(Janiak, 1998), (Janiak
et al., 2007) studied a series of two machine flow-
shop problems, where processing times of the oper-
ations are linearly related with the resource consump-
tion. Shabtay et al.(Shabtay et al., 2007) studied a no-
wait two-machine flow-shop problem, where process-
ing times are convex functions of the resource con-
sumption, and jobs are restricted that they cannot wait
between the two machines. The problem is proved
to be strongly N P -hard, and two heuristic algorithms
are designed to obtain near optimal solutions for large
scaled problems. In this paper, the ”no-wait” assump-
tion is removed, but the problem is still strongly N P -
hard.
Property 1. Problem P is strongly N P -hard.
Proof. Let the less than or equal to condition in the
second set of the constraints replaced by equal to. Ob-
viously, the new problem is a special case of prob-
lem P. Since the second operation of every job is
restricted to start immediately after the first opera-
tion completes, the problem is thus degenerated to the
”no-wait” two-machine flow-shop problem, which is
proved to be strongly N P -hard. Therefore, problem
P is also strongly N P -hard.
In order to solve the problem, a two-step strategy
is adopted. In the first step, a tabu-search or a heuris-
tic algorithm searches for the optimal or near optimal
job-processing sequence of the problem. In the sec-
ond step, when a processing sequence is adopted, the
processing times as well as the resource consumption
of the operations are calculated by a polynomial time
resource allocation algorithm. By the cooperation of
the two steps, an optimal or near optimal solution can
be obtained within acceptable computing time.
The rest of this paper is organized as follows. In
Section 2, the optimal resource allocation algorithm
is presented. In Section 3 and Section 4, a heuris-
tic algorithm and a tabu-search algorithm for the job-
processing sequence are presented. In Section 5, a
set of numerical experiments are conducted to test the
performance of the scheduling algorithms. Finally, a
conclusion is presented in Section 6.
2 OPTIMAL RESOURCE
ALLOCATION
Consider in this section the problem of optimally al-
locating resource to operations under an arbitrary job-
processing sequence σ. The problem is first decom-
posed into a set of sub-problems solved by the equiv-
alent workload method. After that, a dynamic pro-
gram method is applied to search for the optimal so-
lution among them. For convenience, it is assumed
that σ = {σ(1), σ(2),...,σ(n)} = {1,2,...,n}.
According to the equivalent workload method de-
fined by Monma et al.(Monma et al., 1990), when n
operationsare to be processed in serial with makespan
no larger than deadline K, the optimal solution is
p
j
=
ω
k
k+1
j
∑
n
i=1
ω
k
k+1
i
K j = 1,2,. .. , n
u
j
= ω
k
k+1
j
∑
n
i=1
ω
k
k+1
i
1
k
K
−
1
k
j = 1,2,. .. , n
U =
∑
n
j=1
ω
k
k+1
j
k+1
k
K
−
1
k
(2)
and operations can be regarded as a single one with
equivalent workload Ω
s
=
∑
n
i=1
ω
k
k+1
i
k+1
k
. When n
operations are to be processed in parallel, the optimal
solution is
p
j
= K j = 1,2,..., n
u
j
= ω
j
K
−
1
k
j = 1,2,..., n
U =
∑
n
i=1
ω
i
K
−
1
k
(3)
and operations can also be regarded as a single oper-
ation with equivalent workload Ω
p
=
∑
n
i=1
ω
i
.
Consider the two-machine flow-shop resource al-
location problem. In a schedule, precedence con-
straints can be classified into two types. The first type
is critical precedence constraint, which occurs when
the second operation of a job starts immediately af-
ter its predecessor completes. Other precedence con-
straints are slack constraints, because they have no
influence to the resource allocation when they are re-
laxed.
In an optimal schedule, the precedence constraints
of job 1 and job n are always critical. Beside them,
ScheduleTwo-machineFlow-shopwithControllableProcessingTimesUsingTabu-search
15

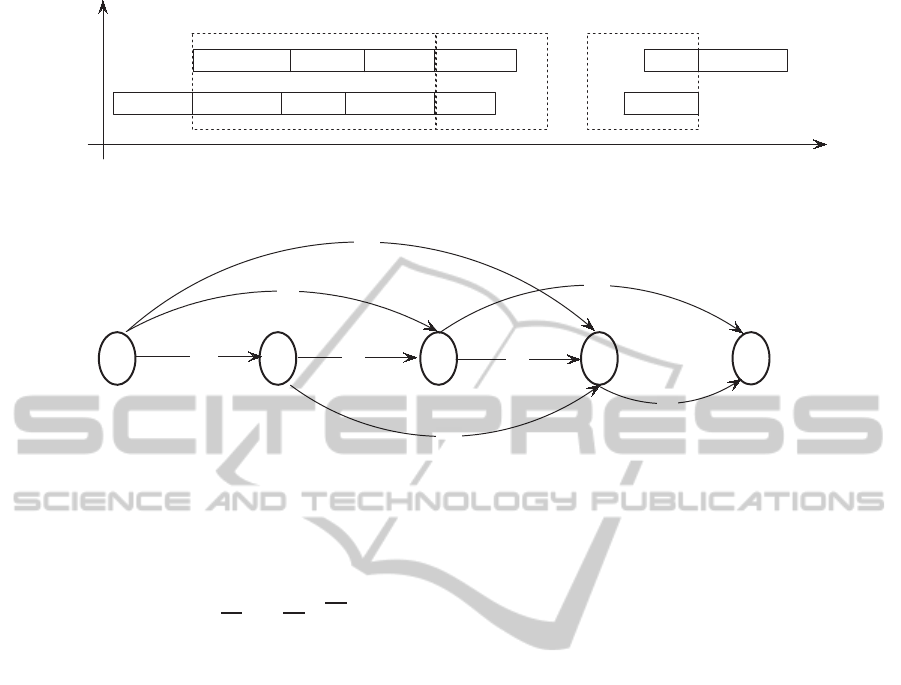
there are usually other critical precedence constraints,
which divide operations on machine 1 and machine 2
into sections Λ = {Λ
1
,Λ
2
,. .. , Λ
m
}, shown by Fig.1.
For example, let Λ
h
be a section with operations
O
1,i+1
,O
1,i+2
,. .. , O
1, j
processed on machine 1, and
operations O
2,i
,O
2,i+1
,. .. , O
2, j−1
processed on ma-
chine 2. Inside the section, since slack precedence
constraints have no influence to the resource alloca-
tion, it can be calculated by solving the following
problem:
(P1)
min U =
j
∑
l=i+1
u
1,l
+
j−1
∑
l=i
u
2,l
s.t.
j
∑
l=i+1
p
1,l
≤ p
Λ
h
, p
1,l
> 0
j−1
∑
l=i
p
2,l
≤ p
Λ
h
, p
2,l
> 0
where p
Λ
h
is the total processing time of section Λ
h
,
and is not known yet.
According to the equivalentworkload method, op-
erations within Λ
h
can be regarded as a single opera-
tion with workload
Ω
Λ
h
= Ω
1,Λ
h
+ Ω
2,Λ
h
(4)
Ω
1,Λ
h
=
j
∑
l=i+1
ω
k
k+1
1,l
!
k+1
k
(5)
Ω
2,Λ
h
=
j−1
∑
l=i
ω
k
k+1
2,l
!
k+1
k
(6)
Because sections in Λ are in serial, their equivalent
workload equals
Ω
Λ
=
Ω
k
k+1
Λ
1
+ ·· · + Ω
k
k+1
Λ
m
k+1
k
(7)
and the equivalent workload of all the jobs is
Ω
σ
=
ω
k
k+1
1,1
+ Ω
k
k+1
Λ
+ ω
k
k+1
2,n
k+1
k
(8)
So given the deadline K, the processing time of
the operations O
1,1
and operation O
2,n
are
p
1,1
=
ω
1,1
Ω
σ
k
k+1
K (9)
p
2,n
=
ω
2,n
Ω
σ
k
k+1
K (10)
while the total processing time of each section is
p
Λ
h
=
Ω
Λ
h
Ω
σ
k
k+1
K (11)
and the processing time of the operations in section
Λ
h
is
p
1,l
=
ω
1,l
Ω
1,Λ
h
k
k+1
p
Λ
h
=
ω
1,l
Ω
Λ
h
Ω
1,Λ
h
Ω
σ
k
k+1
K, i+ 1 ≤ l ≤ j(12)
p
2,l
=
ω
2,l
Ω
2,Λ
h
k
k+1
p
Λ
h
=
ω
2,l
Ω
Λ
h
Ω
2,Λ
h
Ω
σ
k
k+1
K, i ≤ l ≤ j − 1(13)
Consider dividing operations into sections to yield
the optimal solution. The problem need be trans-
formed into a directed graph G = (V,A) as follows:
Let nodes V = (v
1
,v
2
,. .. , v
n
) represent precedence
constraints of the jobs. Draw arcs between every
pair of nodes, where each arc represents a section
of operations. For example, arc A
i, j
between node
v
i
and v
j
represents the section that contains opera-
tions O
1,i+1
,O
1,i+2
.. . O
1, j
and O
2,i
,O
2,i+1
.. . O
2, j−1
.
Assume the total processing time of the section is T,
and calculate the processing time of the operations by
solving problem P2. Because precedence constraints
are relaxed in P1, the solution may not be feasible.
Therefore, it is necessary to check whether or not the
following condition is satisfied
l
∑
r=i+1
p
1,r
≤
l−1
∑
r=i
p
2,r
, ∀l = i+ 1,i+ 2,. . ., j− 1
(14)
If the check fails, the section represented by A
i, j
is
infeasible, and A
i, j
will be removed from the graph. If
the check succeeds, the arc will be kept on the graph,
and the equivalent workload of the section, denoted
as Ω
i, j
, will be calculated and marked as the length of
the arc.
After all the feasible arcs are enumerated, and
their length calculated, a graph as Fig.2 shows is
formed. On the graph, each path from node 1 to
node n represents a feasible solution to the resource
allocation problem, and the length of the path equals
the equivalent workload of the sections on the path.
Therefore, the optimal resource allocation problem is
transformed to searching for the shortest path on the
graph. Since the graph is acyclic, the path can be
found by a simple dynamic programming method as
follows:
Let Ω
j
represent the minimum equivalent work-
load of the operations O
1,2
,. .. , O
1, j+1
and operations
O
2,1
,. ..,O
2, j
. Let A
j
be the set of the feasible arcs
that sink to node v
j
. Ω
j
as well as Ω
Λ
can be calcu-
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
16
1,1 2,1 3,1 4,1
1,2 2,2 3,2
5,1
4,2
n,1
n-1,2 n,2
... ... ... ...
... ... ... ...
Processing time
Machine 1
Machine 2
Figure 1: Operations on two machines are divided into a series of sections.
1 2 3
n
... ... ... ...
4
A
1,3
A
1,4
A
2,4
A
3,n
A
4,n
A
1,2
A
2,3
A
3,4
Figure 2: The directed graph with feasible arcs.
lated recursively as follows:
Ω
1
= 0
Ω
j
= min
A
i, j
∈A
j
Ω
k
k+1
i
+ Ω
k
k+1
i, j
k+1
k
Ω
Λ
= Ω
n
(15)
Obviously, the shortest path can be found by tracing
back from node n to node 1, so the resource allocation
and processing times of the operations can be calcu-
lated according to Eq.9-13.
Based on the above discussion, the optimal re-
source allocation algorithm can be formally stated in
the follows:
Algorithm 1. Optimal Resource Allocation
1. For a problem with n jobs, list node 1,2,.. . ,n for
the directed graph;
2. For each i = 1,2,... , n− 1, generate sections Λ
i, j
for j = i + 1, i + 2, . .. ,n. Calculate the resource
allocation of the operations in each section, and
check their feasibility. If section Λ
i, j
is feasible,
draw an arc from node i to node j, let the equiva-
lent workload of the section, Ω
i, j
, be the length of
the arc;
3. For each j = 1,2,. . .,n, calculate Ω
j
using recur-
sive equations Eq.15;
4. Search for the shortest path from node 1 to node
n. Calculate processing time of the operations ac-
cording to Eq.9-Eq.13.
3 HEURISTIC ALGORITHM
SPT-LPT rule minimizes the makespan for the two-
machine flow-shop problem with constant processing
times. According to this rule, jobs are partitioned
into two sets: Set I contains jobs with p
1, j
≤ p
2, j
,
Set II jobs with p
1, j
> p
2, j
. Jobs in Set I are sorted
by p
1, j
according to SPT (Shortest Processing Time
first) rule, and are scheduled first. Jobs in Set II are
sorted by p
2, j
according to LPT (Longest Processing
Time first) rule, and are scheduled afterward. Based
on this rule, a heuristic algorithm for the two-machine
flow-shop problem with controllable processing times
is presented as follows:
Algorithm 2. Heuristic Algorithm
Step 1. Select the job whose first operation has the
smallest workload. When there are more than
one such jobs, select among them the one
whose second operation has the largest work-
load. Let the job be processed as the first one,
and denote it as σ(1);
Step 2. Select among left jobs the one whose second
operation has the smallest workload. When
there are more than one such jobs, select
among them the one whose first operation has
the largest workload. Let the job be processed
as the last one, and denote it as σ(n);
Step 3. Calculate processing times of the operations
by solving following relaxed problem:
ScheduleTwo-machineFlow-shopwithControllableProcessingTimesUsingTabu-search
17

(P2)
min U =
∑
j∈J /σ(1)
u
1, j
+
∑
j∈J /σ(n)
u
2, j
s.t.
∑
j∈J /σ(1)
p
1, j
≤ 1
∑
j∈J /σ(n)
p
2, j
≤ 1
p
i, j
=
ω
i, j
u
i, j
k
, u
i, j
> 0
i = 1,2
j = 1,2,..., n
Step 4. Sort and classify unscheduled jobs by the
SPT-LPT rule. Let jobs in Set I be processed
after job σ(1), and jobs in set II be processed
before job σ(n);
Step 5. Calculate the optimal resource allocation of
the operations.
Because the problem we study is strongly N P -
hard, a heuristic algorithm cannot guarantee the opti-
mality. Therefore, a tabu-search algorithm is designed
to further improve the heuristic solution.
4 TABU-SEARCH ALGORITHM
Tabu-search is essentially a meta-heuristic method
that guides a heuristic local search procedure to
explore the solution space beyond local optimal-
ity(Glover, 1989). Tabu-search features responsive
exploration and adaptive memory. Responsive ex-
ploration allows detailed analysis to be performed on
the scheduling result at each iteration, while adaptive
memory prevents the searching procedure trapped in
the local optimality by recording the recent behav-
ior of the searching procedure. By the incorporation
of these two features, tabu-search guarantees intelli-
gent problem solving. As a result, a large number
of successful tabu-search algorithms for scheduling
problems can be found in literature. For example,
Bilge et al.(Bilge et al., 2004) presented a tabu-search
algorithm for parallel machine scheduling with total
tardiness, Xu et al.(Xu et al., 2010) solved a single
machine scheduling problem with controllable job-
processing times and arbitrary release dates and due
dates.
4.1 The Objective Function
The scope of this paper is to minimize the resource
consumption that is needed to control the makespan
within deadline K. Since resource consumption is di-
rectly related to the equivalent workload of the job-
processing sequences, it is more convenient to eval-
uate scheduling results by their equivalent workload.
Therefore, equivalent workload of the job-processing
sequences, rather than their actual resource consump-
tion, is adopted as the objective function of the tabu-
search algorithm.
4.2 The Initial Solution
Local search algorithms, such as simulated annealing
and tabu-search, always start from an initial solution
that is normally generated by a heuristic algorithm.
For our problem, the initial solution is obtained by the
heuristic algorithm presented in Section 3. Because
the problem is strongly N P -hard, the tabu-search al-
gorithm need be applied to further improve the solu-
tion.
4.3 Generate Neighboring Schedules
Insert move and swap move are two frequently used
moves that generate neighboring schedules by mod-
ifying the current schedule. An insert move takes a
job away from its current processing position, and in-
serts it to another position. A swap move, on the other
hand, exchanges the processing sequence of two adja-
cent jobs. Since jobs are all processed in serial in the
flow-shop, a swap move can always be replaced by an
insert move. Therefore, only insert moves will be per-
formed in the tabu-search algorithm. Because jobs are
processed without precedence constraints, they can
be processed on any processing position. Therefore,
neighboring schedules are generated by inserting jobs
to every processing position.
4.4 The Tabu Mechanism
Tabu mechanism helps the searching procedure avoid
becoming trapped in the cycle state of the local min-
imum. Typically, a list of mutations, which the pro-
cedure is not allow to make, is kept at any stage of
the searching. Every time a mutation is made in the
current schedule, the reversed mutation is entered at
the top of tabu-list, while all other entries are pushed
down one position and the bottom entry is deleted.
For this problem, the tabu-list is made up of en-
tries of the form {i, j}, where j is the job that moves,
and i is its direct predecessor before the move. Any
neighboring schedule that contains the pair of adja-
cent jobs {i, j}, unless it is better than the best sched-
ule obtained so far, will be forbidden. In this way,
the tabu-mechanism prohibits a recently moved job
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
18

j from becoming the direct successor of job i again
within the tabu durance.
At the beginning of the searching procedure, it is
usually not difficult to jump off the local minimum.
However, as the solution improves, the local mini-
mum space grows larger, making it much more dif-
ficult to avoid. Therefore, if the solution keeps nei-
ther improved nor degenerated after a number of iter-
ations, the searching procedure must be trapped in a
wide local minimum space. In this case, the objective
function value of the selected schedule will be pushed
into the tabu-list, and neighboring schedules with the
same value will be tabued in the following iterations.
In this way, the searching procedure can be forced to
move away from the local minimum more effectively.
If an improvement is achieved, this strategy will be
canceled, until next time the searching procedure is
once again trapped in a wide local minimum space.
4.5 The Searching Procedure
Based on the above discussion, the tabu-search algo-
rithm that searches for the optimal or near optimal
job-processing sequence is presented in the follows.
There are two input parameters that needs to be spec-
ified by the user:
• TabuDepth: The depth of the tabu-list, which is
normally set between [6,10]. Experience shows
difference TabuDepth values normally has no sig-
nificant influence to the scheduling result.
• TabuStop: The searching procedure stops if the
solution cannot be further improved after Ta-
buStop times of iterations.
Below is the tabu-search algorithm:
Algorithm 3. The Tabu-search Algorithm
Step 1. Generate initial solution using Algorithm 2.
Let IterCnt = 0.
Step 2. For each job j = 1,2,.. . ,n, generate neigh-
boring schedules by inserting job j to ev-
ery possible processing position. Calculate
the equivalent workload of the neighboring
schedules, and sort them by the equivalent
workload in ascending order.
Step 3. Take the first neighboring schedule from the
candidate list. If the equivalent workload of
the schedule is smaller than that of the best
schedule obtained so far, or the schedule is
not tabued, then replace the current schedule
by the selected neighboring schedule. Other-
wise, discard the schedule, and repeat Step 3.
Step 4. If the current schedule is improved, let
IterCnt = 0; Otherwise, let IterCnt =
IterCnt + 1. If IterCnt < IterStop, then go
to Step 2; Otherwise, let the best schedule be
the scheduling result and exit.
One significant advantage of the tabu-search al-
gorithm is its easy implementation of parallel com-
puting. For our problem, neighboring schedules are
generated for every job independently, therefore, it is
possible to decompose the neighborhood generation
procedure into n sub-procedures, and perform them
in parallel. In this way, in a multi-core computer with
m independent threads, the computing speed can be
improved, roughly speaking, m times.
5 COMPUTATIONAL
EXPERIMENT
In order to evaluate the performance of the schedul-
ing algorithm presented in this paper, a set of compu-
tational experiments were conducted in this section.
The experiments were performed on a personal com-
puter with an Intel i7-2600 CPU that features 4 cores
and 8 independent threads. The algorithm was im-
plemented in C++ and was capable for parallel com-
puting, such that the computing power of the com-
puter can be fully employed. All the problem in-
stances were generated at random, where the work-
load ω
j,1
and ω
j,2
obey the discrete uniform distri-
bution between [10,100]. Problem instances are or-
ganized in groups, each group contains 50 instances
that have the same number of the jobs. Through-
out the experiment, the input parameters of the tabu-
search algorithm were fixed to be TabuDepth = 8 and
TabuStop = 30. According to the discussion in Sec-
tion 2 and 3, equivalent workload can be calculated
for every job-processing sequence, which decides the
resource consumption directly. Therefore, in the ex-
periment solutions were evaluated by their equivalent
workload, rather than their actual resource consump-
tion.
The experiment was performed in two steps: First,
it was carried out on small-scaled problem instances,
such that the the scheduling results can be compared
with the optimal solutions obtained by an enumerative
searching procedure; Second, the experiment was car-
ried out on large-scaled problem instances to test the
efficiency of the searching procedure.
5.1 Experiment for Solution Quality
In this part, a simple enumerative searching proce-
dure was implemented to obtain optimal solutions
for every problem instance. Because the problem
ScheduleTwo-machineFlow-shopwithControllableProcessingTimesUsingTabu-search
19

is strongly N P -hard, only small-scaled problem in-
stances can be solved by this procedure. Based on
the optimal solution, the quality of the scheduling re-
sults is evaluated by calculating their relative differ-
ence from the optimal solutions using the following
equation:
RD =
Ω
σ
Ω
σ
⋆
∗ 100% (16)
where σ
⋆
is the optimal job-processing sequence, σ is
the processing sequence obtained by the scheduling
algorithm. The experimental results are listed in Table
1, which contains following columns:
• n: The number of the jobs in each problem in-
stance. Because only the optimal solution of
small-scaled problem instances can be obtained
by the enumerative algorithm within acceptable
computing time, we have n = 10,11,12 in the test.
• k: The coefficient of the resource consumption
function. Three typical values, k = 0.5, 1, 2, are
tested.
• Heuristic: The tabu-search procedure starts from
the initial solutions generated by the heuristic al-
gorithm (Algo.2), so the quality of the heuristic
solutions are also evaluated in the table. For each
group of problem instances, the average and max-
imum relative difference from the optimal solu-
tions are listed in the table.
• Tabu-search: The quality of the solutions obtained
by the tabu-search algorithm. They are evaluated
in the same way as heuristic solutions.
It can be seen from the experimental result, that
the heuristic solutions are normally already close to
the optimum. Starting from the initial solutions, that
tabu-search algorithm is able to able to find optimal
solution for most of the problem instances. For in-
stances that the algorithm fails to achieve optimum,
the scheduling results are also very close to the op-
timal solution. Therefore, the algorithm presented in
this paper is capable for generating optimal or near-
optimal solutions for the scheduling problem.
5.2 Experiment for Large-scaled
Problems
In this part, a set of computational experiments were
carried out to evaluate the capability of the algorithm
solving large-scaled problems. Unless P = N P , it is
impossible to obtain optimal solutions within accept-
able computing time for such problems. Therefore,
the scheduling results are evaluated by how much im-
provement the tabu-search algorithm achieves from
the initial heuristic solutions, which is calculated as
follows:
RD =
Ω
σ
0
Ω
σ
∗ 100% (17)
where σ
0
is the initial processing sequence generated
by the heuristic algorithm, and σ that by the tabu-
search algorithm. The experimental results are listed
in Table 2, which contains following columns:
• n, k: The same as those in Table 1.
• Solution: The quality of the scheduling results.
For each group of problem instances, it is evalu-
ated by the average relative difference (AvgRD),
minimum relative difference (MinRD) and max-
imum relative difference (MaxRD) between the
tabu-search and heuristic solutions.
• Computing time: The computing time that the
searching procedure consumes to obtain the
scheduling results. It is evaluated by the aver-
age computing time (AvgTime), maximum com-
puting time (MaxTime) and minimum computing
time (MinTime).
According to the experimental results, the tabu-
search algorithm is able to solve almost all the prob-
lem instances with 150 jobs, and a large number of
instances with 200 jobs within one hour. It can also
be seen, that the average computing time of the tabu-
search algorithm grows polynomially as the number
of the jobs grows. Therefore, for even larger prob-
lem instances, the computing can easily be controlled
within acceptable time by using more powerful com-
puter with more CPUs.
6 CONCLUSION
A two-machine flow-shop scheduling problem is
studied in this paper, where the processing times of
the operations can be compressed and controlled by
allocating extra resource to them. The relationship
between resource consumption and processing time
is described by a non-linear convex resource con-
sumption function. The scope of the study is to
determine the processing sequence of the jobs, and
the processing times of the the operations, such that
the makespan can be controlled not to exceed the
given deadline K, while the total resource consump-
tion could be minimized. The problem is proved to be
strongly N P -hard. An optimal resource allocation al-
gorithm as well as a heuristic and a tabu-search algo-
rithm are designed to solve the problem. Experiment
shows, by the cooperation of the resource allocation
and job sequencing algorithms, the optimal or near
optimal solutions can be obtained within acceptable
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
20

Table 1: Experimental results for small-sized problems.
n k Heuristic Tabu-search
AvgRD(%) MaxRD(%) AvgRD(%) MaxRD(%)
10 0.5 100.350 102.100 100.001 100.015
1.0 100.300 101.814 100.000 100.001
2.0 100.131 101.137 100.000 100.003
11 0.5 100.566 102.984 100.003 100.086
1.0 100.333 101.576 100.003 100.004
2.0 100.158 101.145 100.000 100.004
12 0.5 100.507 101.528 100.000 100.002
1.0 100.431 101.370 100.000 100.002
2.0 100.194 101.038 100.000 100.016
Table 2: Experimental results for large-sized problems.
n k Solution Computing time
AvgRD(%) MinRD(%) MaxRD(%) AvgTime(s) MinTime(s) MaxTime(s)
100 0.5 103.087 100.600 104.075 535 147 917
1.0 103.704 100.756 106.219 549 191 1492
2.0 102.133 101.165 103.097 418 174 783
150 0.5 103.501 101.974 105.519 1537 526 4303
1.0 102.833 101.764 103.797 1792 555 3135
2.0 101.914 101.534 102.447 1813 713 3577
200 0.5 103.498 102.813 104.457 3869 1275 7264
1.0 102.444 101.964 102.861 4043 1529 10081
2.0 101.587 101.223 101.987 3421 1479 7706
computing time for medium- and large-scaled prob-
lems.
ACKNOWLEDGEMENTS
This paper is supported by the National Natural Sci-
ence Foundation of China (No. 61203183) and
Shaanxi Province Education Department Natural Sci-
ence Research Item (11JK0918).
REFERENCES
Bilge, U., Kirac, F., Kurtulan, M., and Pekgun, P. (2004). A
tabu search algorithm for parallel machine total tardi-
ness problem. 31(3):397–414.
D. Biskup, H. J. (2001). Common due date assignment
for scheduling on a single machine with jointly re-
ducible processing times. Int. J. Production Eco-
nomics, 69(3):317–322.
Glover, F. (1989). Tabu search. part i. ORSA Journal of
Computing, 1(1):190–206.
Graham, R., Lawler, E., Lenstra, J., and Rinnooy, A. K.
(1979). Optimization and approximation in determin-
istic sequencing and scheduling: a survey. Annals of
Discrete Mathematics, 5(1):287–326.
Janiak, A. (1986). One-machine scheduling problems with
resource constraints. Lecture Notes in Computer Sci-
ence, 84(1):358–364.
Janiak, A. (1989). Minimization of the blooming mill stand-
stills - mathematical model, suboptimal algorithms.
Mechanika, 8(2):37–49.
Janiak, A. (1998). Minimization of the makespan in
a two-machine problem under given resource con-
straints. European Journal of Operations Research,
107(1):325C337.
Janiak, A., Kozan, E., Lichtenstein, M., and Oguz, C.
(2007). Metaheuristic approaches to the hybrid flow
shop scheduling problem with a cost-related crite-
rion. International Journal of Production Economics,
105(2):407–424.
M. Kaspi, D. S. (2006). A bicriterion approach to time
cost trade-offs in scheduling with convex resource-
dependent job processing times and release dates.
33(1):3015–3033.
Monma, C., Schrijver, A., Todd, M., and Wei, V. (1990).
Convex resource allocation problems on directed
acyclic graphs: duality,complexity,special cases and
extensions. Mathematics of Operations Research,
15(4):736–748.
Nowicki, E. (1993). An approximation algorithm for the m-
machine permutation flow shop scheduling problem
ScheduleTwo-machineFlow-shopwithControllableProcessingTimesUsingTabu-search
21

with controllable processing times. European Journal
of Operations Research, 70(3):342C349.
Shabtay, D. and Kaspi, M. (2006). Parallel machine
scheduling with a convex resource consumption func-
tion. European Journal of Operations Research,
173(1):92–107.
Shabtay, D., Kaspi, M., and Steiner, G. (2007). The no-wait
two-machine flow-shop scheduling problem with con-
vex resource-dependent processing times. IIE Trans,
39(5):539C557.
Shabtay, D. and Steiner, G. (2007). A survey of scheduling
with controllable processing times. Discrete Applied
Mathematics, 155.
Xu, K. and Feng, Z. (2010). A branch and bound algorithm
for scheduling jobs with controllable processing times
on a single machine to met due dates. Annals of Op-
erations Research, 181(1):303–324.
Xu, K., Feng, Z., and Jun, K. (2010). A tabu-search
algorithm for scheduling jobs with controllable pro-
cessing times on a single machine to meet due-dates.
37(11):1924–1938.
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
22
