
Airline Disruption Management
Dynamic Aircraft Scheduling with Ant Colony Optimization
Henrique Sousa
1
, Ricardo Teixeira
1
, Henrique Lopes Cardoso
1,2
and Eugénio Oliveira
1,2
1
DEI/FEUP, Faculdade de Engenharia, Universidade do Porto, Porto, Portugal
2
LIACC, Laboratório de Inteligência Artificial e Ciência de Computadores, Porto, Portugal
Keywords: Aircraft Scheduling, Disruption Management, Ant Colony Optimization.
Abstract: Disruption management is one of the main concerns of any airline company, as it can influence its annual
revenue by upwards of 3%. Most of medium to large airlines have specialized teams which focus on
recovering disrupted schedules with very little automation. This paper presents a new automated approach
to solve both the Aircraft Assignment Problem (AAP) and the Aircraft Recovering Problem (ARP), where
the solutions are responsive to unforeseen events. The developed algorithm, based on Ant Colony
Optimization, aims to minimize the operational costs involved and is designed to schedule and reschedule
flights dynamically by using a sliding window. Test results tend to indicate that this approach is feasible,
both in terms of time and quality of the proposed solutions.
1 INTRODUCTION
The aviation sector is surely a key component in any
thriving economy, as it supports $2.4 trillion of the
world’s gross domestic product (GDP) and creates
an estimated 58.1 million jobs (International Air
Transport Association, 2011). Depending on its
scale, when an event disrupts the normal flow of an
airline company, the consequences can be massive;
for instance, the eruption of the Icelandic volcano
Eyjafjallajokull in April 2010 was responsible for
worldwide economic and social setbacks. Therefore,
the need for solutions that improve airline
disruptions management is a legitimate concern not
only for airline companies, that aim to increase
profits by reducing operational costs, but also for the
general public, due to its economic and social
impact.
When a disruption occurs, the airlines try to find
a solution with a minimum impact to the airline’s
schedule and with lowest added cost. Usually, the
first problem to be tackled is the Aircraft Recovery
Problem (ARP) which aims to recover the flight
schedule by applying a set of operations to the
disrupted plan so that a new aircraft can be assign to
the disrupted flight. After solving the ARP the
Airline Operations Control Centres (AOCC) have to
deal with the Crew Rescheduling Problem (CRP)
and the Passenger Rescheduling Problem (PRP).
These three problems differ on the function they
optimize; for instance, while the ARP minimizes the
airline’s costs, the PRP minimizes the total
travelling time each passenger takes to reach its
destination.
In order to recover from a disruption, four
different operations can be applied: aircraft
reassignment, flight delay, flight cancellation, and
flight rerouting. Most of the AOCCs rely on human
experts’ effort to minimize the impact of the
disruption by means of these operations. In a large
scale setup, this is a difficult task because the total
cost of each operation include many dependent
factors, e.g., to cancel a flight one must take into
account the cost of parking in a specific airport, the
hotel charges for both passengers and crew and the
cost for alternative transportation for passengers.
Therefore, the need for an automated system to solve
these problems has been increasing in the past few
years. One might think that the current setup for
most airlines should be enough to handle a few
unpredictable events but, in an ever growing
industry, flight delays may be caused by simple
events such as abnormal fuel consumption or even
missing luggage.
This paper proposes a new approach to deal with
a subset of airline disruption management problem,
the ARP. Section 2 contains information about the
relevant literature addressing this area. Section 3
398
Sousa H., Teixeira R., Lopes Cardoso H. and Oliveira E..
Airline Disruption Management - Dynamic Aircraft Scheduling with Ant Colony Optimization.
DOI: 10.5220/0005205303980405
In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART-2015), pages 398-405
ISBN: 978-989-758-074-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

formally describes the problem at hand. Section 4
presents the ant colony optimization approach we
have developed. Section 5 includes an experimental
evaluation of the approach when fed with a real
dataset from the major Portuguese airline, TAP.
Finally, Section 6 summarizes the main
contributions of the paper, discusses limitations of
the approach and proposes lines for improvement.
2 STATE OF THE ART
Previous studies about the ARP can be categorized
into two large groups defined by the methods used to
find the solution, i.e., Operations Research (OR) and
Meta-heuristics.
2.1 Exact Methods
Although most of AOCCs are still human
dependent, they are not fully manual. Usually, these
teams use software that provides options regarding a
specific disruption from which the operator must
choose accordingly. This kind of software is often
equipped with Operational Research-based methods
since these are well known and reliable algorithms
giving measurable solutions in acceptable time.
One of the first articles about ARP appeared in
the mid-1980s with the works of Teodorovic
(Teodorovic and Guberinic, 1984). His objective
was to find a new daily schedule when some
aircrafts became unavailable; later on he also
explored some integration with crew and passenger
constraints in an attempt to develop a more cohesive
solution. The first relevant computational
breakthrough came by the works of Jarrah (Jarrah et
al., 1993); using network flow models, his method
should reduce costs between 20% and 90%
compared with an un-optimized schedule recovery
problem. His tests included real flights from United
Airlines, during October 1993 and March 1994, and
resulted in an estimate $540,000 in delay costs.
There are also many solutions that solve the ARP
using integer programming, the most relevant work
being from Thengvall (Thengvall et al., 2001). His
implementation was tested with real data from
Continental Airlines and results show that optimal or
near-optimal solutions are often obtained; the
downside is that his model is very restricted as it
only considers delaying and cancelling flights.
The latest work, to our knowledge, belongs to
Wu and Le (Wu and Le, 2012), where the authors
model the ARP as a time-space network and several
real restrictions were taken into account, e.g.,
aircraft maintenance costs. Their implementation
was tested with data provided from a major Chinese
airline and results reveal that a feasible solution is
found twice as fast as an exact algorithm. Although
encouraging, this kind of performance is still too
weak when the problem is scaled to higher
dimensions.
2.2 Meta-heuristic Methods
With the increasing need for better automated
solutions to solve the ARP, several meta-heuristic
methods have been applied to this domain. Perhaps
the first relevant study in this field was conducted by
Løve (Løve et al., 2005) -- using a local search
method, his solutions are developed considering
delays, cancellations and reassignments and the goal
is to maximize the profit. Although the study’s
results reveal that good solutions are achieved in less
than 10 seconds, by maximizing the profit instead of
reducing costs, some restrictions, e.g., passenger
satisfaction, are not taken into account.
Liu (Liu et al., 2006) developed a model using a
Multi-Objective Genetic Algorithm (Konak et al.,
2006) to construct new feasible aircraft reschedules.
This model already considers several objectives that
simulate different roles in the ARP. The study was
limited only by the fact that it was tested with a
small dataset of 7 aircrafts and 70 flights.
Perhaps the most interesting article to our work
was written by Zegordi and Jafari (Zegordi and
Jafari, 2010) who used the Ant Colony Algorithm
(Colorni et al., 1991) heuristic to solve the ARP.
Their approach is very complete regarding real
domain constraints, such as maintenance
requirements and other restrictions and regulations.
Test experiments reveal that the algorithm is able to
construct a feasible revised schedule in less than 5
seconds and, according to the authors, such method
was successfully applied to an airline. Despite its
robustness, this approach does not consider
scenarios where aircrafts from different flight
rotations recover each other.
Finally we would like to mention the work of
Castro (Castro et al., 2014) who developed a new
approach to Airline Disruption Management, where
a multi-agent system approach is used, including
specialist agents for different dimensions of the
disruption management problem. Despite this
innovative approach, this work focuses on handling
disruptions in a pre-scheduled plan, not combining
the AAP and ARP problems. This is something we
address in our own work.
All these proposals have brought improvements
AirlineDisruptionManagement-DynamicAircraftSchedulingwithAntColonyOptimization
399

to the classical Operations Research approach.
Nonetheless we believe that a more cohesive
solution, capable of a higher automation and better
optimization is still missing.
3 PROBLEM DEFINITION
In the solution proposed in this paper, we will strive
to solve two different but complementary
dimensions of the problem at hand: the Aircraft
Assignment Problem (AAP) (Gabteni and
Gronkvist, 2009) and the ARP. The AAP may be
described as the problem of assigning flights to
aircrafts in such a way that some operational
constraints are satisfied and possibly that some
objective function is optimized. In our approach
these consist on aircraft’s capacity vs. number of
passengers and average aircraft maintenance cost
(both mechanical and fuel). This way an efficient
allocation takes place because aircrafts are tailored
to each flight, resulting in cost savings.
The AAP original solution will provide a first
optimized schedule for the set of flights and
aircrafts. This schedule will be affected in case of a
disruption, i.e., an event that stops a flight to keep its
schedule. When such a disruption occurs, the
objective is to recover the affected flight(s) reusing
the original plan as much as possible, minimizing
the total cost. To recover a flight one must choose
the best suited action that implies the lowest cost. In
order to achieve this, flights can be delayed or
cancelled.
Delays can result in different outcomes in terms
of the assigned aircraft, i.e., simple aircraft delay;
aircraft swaps, both between a fleet of aircrafts as
well as different aircraft types; or flight rerouting,
where passengers reach their destination having a
midway stop. On the other hand, cancellations entail
a cost computed with the measure of passenger
discontent and the cost of local hotel charges.
Therefore, within the scope of this paper, solving
the combination of both the AAP and the ARP
translates into minimizing the following function:
.
∈∈
.1
∈
.
∈
.
∈
(1)
Subject to:
.
.
(2)
.
(3)
.
.
(4)
.
(5)
∈
∈∈
(6)
∀
(7)
∀
(8)
∀
⇒
,
,
0
(9)
∀
⇒
,
,
0,1
(10)
∀,
,
,
,
∈
0,1
(11)
The decision variables in the model are
described in Table 1.
Table 1: Model variables description.
Var Meaning
Flag indicating if flight
is assigned to aircraft .
Flag indicating if flight
is delayed.
Flag indicating if flight
is cancelled.
Flag indicating if flight
is rerouted or leased to
another airline.
Actual time of departure of flight
.
Scheduled time of departure of flight
.
Cost of passenger discontent.
Set of all aircrafts.
Set of all flights.
Cost of assigning aircraft to flight
.
Cost of delaying flight
.
Cost of cancelling flight
.
Cost of rerouting passengers from flight
.
Cost of rerouting passengers from flight
using
a
different airline.
N
umber of passengers on flight
.
N
umber of passengers on flight
that have bee
n
re-routed internally.
N
umber of passengers on flight
that have bee
n
leased to other airlines.
Cost of 1 minute of delay.
Cost of rerouting 1 passenger from flight
using
a
different airline.
Cost of hotel charges for 1 passenger from fligh
t
.
Total number of flights to be scheduled.
This model is based on the one presented in
(Zegordi and Jafari, 2010), with some changes.
Function (1) to be minimized represents the total
cost associated to scheduling and/or recovering all
flights, aircrafts and passengers. Therefore, the ARP
is slightly altered due to the introduction of
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
400

passenger related costs. Function (1) includes cost of
aircraft assignment, total delay, cancellation and
disrupted passengers. Minimizing the first term aims
at efficiently assigning aircrafts to flights, i.e.,
providing the most cost effective aircraft given a
certain flight. The second and third terms promote
reliable operations by minimizing flight delay and
cancellation, respectively. The last term recovers
disrupted passengers either through reassigning them
to another flight route to the same destination (with
midway stops), or by transporting them using
another airline or means of transportation.
Constraints in (2) to (5) detail how to compute
each of the costs described in the objective function
(1). Constraint (6) ensures that the sum of active
flags equals the number of flights, so that no flight is
left without an aircraft. Constraint (7) guarantees
that in case of rerouting the sum of passengers re-
routed internally with the passengers leased to other
airlines equals the original number of passengers
from flight f. Finally, constraints (8) through (10)
ensure both that the atod is at least the same of tod,
i.e., the atod is a reflection of any delay a flight may
have; and that delaying, cancelling and rerouting
flags are only active if a flight has different tod and
atod. Constraint (11) is a domain restriction for all
bit flags.
4 ONLINE SCHEDULING WITH
ANT COLONY OPTIMIZATION
The Ant Colony Optimization (ACO) firstly
described by Dorigo (Colorni et al., 1991) is a local
search optimization algorithm that mimics the
behaviour of ants as a sociable species. In Dorigo’s
adaptation, an ant is a conceptual unit performing a
random construction of a solution. This solution is
the set of nodes visited by the ant; in nature, these
are geographic points in the field on which they are
looking for food. The convergence to optimization
occurs because ants communicate with each other
through stigmergy, i.e., they give feedback about a
specific solution through the so-called pheromones.
Therefore, when an ant is on the verge of choosing
the next node, the ones with the highest pheromone
levels are more likely to be chosen.
Lately ACO has been applied to a vast range of
problems (Dorigo and Stutzle, 2004) with a relative
amount of success. However, unlike genetic
algorithms or simulated annealing, the application of
ACO is usually better than other meta-heuristics
when the problem can be described by highly
constrained graphs. Thus, this approach is expected
to be especially appropriate for solving the problem
as modelled in Section 3.
Our approach is split in two distinct parts that are
related with the different problems the algorithm
solves: the Aircraft Assignment Problem and the
Aircraft Recovering Problem. Although both
problems are bounded to optimize the same
expression, the practical outcome results in different
behaviours. When the algorithm first runs it receives
information about which routes are needed to assign
aircrafts, as well as where and how many airplanes
are available. Therefore, its first objective is to
create a valid aircraft assignment such that all flights
are feasible while minimizing the cost. On the other
hand, the algorithm keeps running in order to adapt
its schedule in case of a sudden disruption, where
the original solution is modified so that all flights
remain feasible with the lowest cost raise.
4.1 Illustrating Example
In order to illustrate how we have applied ACO to
the AAP/ARP problem, in this section we provide an
example where we graphically represent all
outcomes for both AAP and ARP solutions. Our
directed graph representation consists of two sets of
nodes: one representing aircrafts and the other all
flights within the scheduling scope (see Figure 1).
Figure 1: Model representation (circle nodes represent
flights, triangle nodes represent aircrafts).
Every flight/aircraft node is connected to every
aircraft node. Furthermore, each aircraft has
connections to possible flights assignments (e.g.
aircraft CSTOJ has an edge to flight 815 but not to
flight 803 because the aircraft is not located at the
flight’s origin airport or/and does not have the
required passenger seats). A flight node can be
AirlineDisruptionManagement-DynamicAircraftSchedulingwithAntColonyOptimization
401
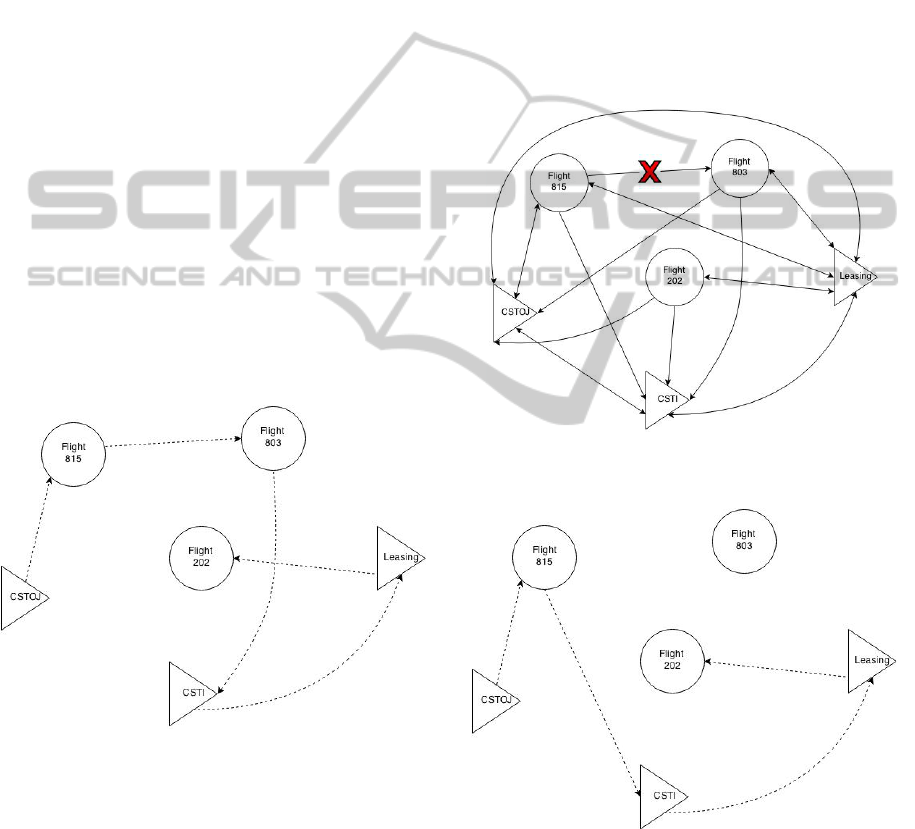
connected to another flight node if it respects a
spatial and time constraint: the second flight’s origin
has to be the same as the first flight’s destination,
and the second flight must depart after the scheduled
arrival of the first flight plus some rotation time, so
that the aircraft can be properly set up (refuelling,
transportation between gates, inspection, etc.). The
leasing node is a special aircraft node that is
connected to every flight, allowing flights to be
leased to other airlines whenever an internal solution
is not viable and the cost of leasing is lower than
cancelling the flight.
In order to build a solution, an ant must first
choose an aircraft, followed by a series of flight
nodes representing the flights assigned to that
aircraft. When the next node to be visited represents
an aircraft this means that subsequent flights are
linked to it (the last visited aircraft is assigned to the
flights). Flight nodes visited after the leasing node
will have a leased aircraft assigned. Flights not
included in the path are cancelled. This process
continues until all aircraft nodes are visited. The
objective is to find the minimum cost path in the
directed graph. In Figure 2 we can see a possible
solution: aircraft CSTOJ is assigned to flights 815
and 803; aircraft CSTI has no flights; flight 202 will
use a leased aircraft.
Figure 2: Possible solution.
When the system is notified with a disruption,
the solution graph is updated (see Figure 3) and the
ants will try to optimize a new path given those
constraints with new actions on flight nodes. Delays
may also be accepted, thus demanding no changes in
the previous solution path. A possible solution to the
disruption event is shown in Figure 4, where it can
be seen that flight 803 has been cancelled.
This representation allows optimization of both
AAP and ARP regarding the objective function
defined in Equation (1). On the other hand, the
ability to respond to disruptions on the go allows the
algorithm to adapt to environmental constraints with
minimum human interaction. This approach is online
rescheduling: the algorithm is constantly renewing
and updating the best solution. In theory, this
approach could result in a perpetually running
algorithm that would assign aircrafts and deal with
disruptions continuously. The algorithm would have
a sliding window, e.g., a month, where all flights
within that window would be taken into account
while optimizing. As the time window moves
forward, past flights are discarded and new ones are
taken into consideration.
Figure 3: Disruption event (flight 815 is delayed, breaking
connection with flight 803).
Figure 4: Solving the disruption.
4.2 Algorithm Implementation
In this section we include details of our implemented
algorithm. A pheromone matrix keeps track of all
the pheromone values of every edge in the problem
graph, which are initialized to 1.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
402

Every ant chooses probabilistically its next node
depending on the relative amount of pheromone in
the edge connecting the current node and the next
one (see Eq. 12, where
is the pheromone value
for edge ).
/
(12)
When an ant finishes its graph traversal task (as
described in Section 4.1), pheromones are laid out
(i.e., the pheromone matrix is updated through
addition) for each selected edge according to:
1
∗
(13)
where is the solution’s fitness, according to
function (1), and is a constant which normalizes
the amount of pheromone deposited, so that it is not
negligible when the fitness value is too big
1
.
In each iteration, the algorithm updates the
pheromone matrix with a decay factor. This mimics
the evaporation of natural pheromones, preventing
the overflow of pheromone values and allowing the
colony to respond to changes in the fitness
landscape: when a good path stops being viable, ants
stop depositing or deposit less pheromones, which
results in ants progressively abandoning this
previously good path. This constant updating creates
a reactive algorithm that responds to changes in the
environment. A pheromone evaporation rate must be
found so that the colony achieves a good balance
between quick response to new and better paths and
enough persistence to not give up on potentially
good solutions. This means that the lower the
evaporation rate, the more lasting is the “memory”
of the colony regarding older paths. The pheromone
evaporation rule is:
max1,
∗
(14)
where is the pheromone evaporation rate, which
for the experiments presented in Section 5 we have
set to 0.85.
5 EXPERIMENTS AND RESULTS
Our ACO algorithm was tested on a real dataset
obtained from (Castro et al., 2014). This dataset
contains actual flight information from Portuguese
airline TAP relative to all 5722 flights in September
2009 and a fleet of 72 aircrafts. In order to conduct
1
Note that we want to minimize function (1), thus the
fitness value is actually a cost.
our experiments, we had to parse TAP’s dataset and
extract information about flight routes, i.e.,
departure, arrival, origin, destination, total distance
and number of tickets sold; how many and where
aircrafts were initially positioned; information
regarding the aircrafts, maintenance costs per mile
and total capacity; and hotel charges per
passenger/night. The given dataset did not contain
any information about the cost of leasing, therefore,
those values where extrapolated to be 50% higher
than internal costs.
Two different experiments, regarding both AAP
and ARP, were conducted. All tests were conducted
under a machine with an Intel I5 650 and 4.00 GB of
RAM and all implementations were coded in Java.
On the first experiment we were trying to
evaluate the algorithm’s ability to solve de AAP
considering both the time it took to solve the
problem and the quality of the final assignment
schedule. These tests consisted on a time
comparison between our ACO approach and a
branch and bound (BB) optimization algorithm
(Lawler and Wood, 1966); when BB became
unresponsive due to memory overflows, a depth first
search (DFS) (Tarjan, 1972) was used to compare
the ACO’s solution with DFS’s first feasible
solution. This experiment also contains information
regarding the best known solution (BKS), i.e., the
actual assignment carried by TAP on September
2009. The BKS’s schedule operational costs served
as a reference measure to evaluate the quality of a
solution. Results regarding this experiment,
summarized in Table 2, show that our ACO
approach, although not always the fastest algorithm,
consistently returns good solutions. This experiment
also proves that an exact approach, such as branch
and bound, is infeasible when a higher number of
flights are taken into account. Overall, as the
problem size grows, it is obvious that ACO’s
approach provides much better solutions than its
competitors.
A second experiment was conducted in order to
evaluate the algorithm’s capacity to overcome
unforeseen aircraft disruptions (ARP). In order to
compare ACO’s results with BB and DFS, a set of
predefined disruptions was created so that the
overload was the same across all algorithms. The set
of disruptions contained situations where aircrafts
were unavailable for a short or long period of time
due to minor or major aircraft failure/ impediment.
Disrupted aircrafts targeted both flights with and
without future dependencies, that is, likely to cause a
“snowball effect” of consecutive delays. The scope
of this experiment only considered the ARP;
AirlineDisruptionManagement-DynamicAircraftSchedulingwithAntColonyOptimization
403

therefore, each algorithm execution time excludes
the AAP; moreover, the initial flight schedule was
similar across all implementations so that only the
recovery capability would be evaluated. There was
no useful information from TAP’s dataset that we
could use to evaluate the performance on this
instance of the algorithm. For that reason, the BKS
is considered to be the solution returned by the
ACO, since it consistently outperformed its
competitors. Table 3 summarizes the results
obtained from this experiment. As expected, ACO’s
performance is much better in terms of solutions
quality, although it takes, on average, 40% more
time than other approaches. The trade-off between
time and quality will probably be an issue to take
into account when applying our approach in larger
datasets.
Table 2: Experiment results regarding AAP experiment.
Algorithm
Number of
Flights
Total
Time
Difference
to BKS
ACO
20
2.35 s
0%
BB 0.90 s
0%
DFS 0.58 s
-1,1%
ACO
50
8.60 s
0%
BB -
-
DFS 2.95 s
-6.4%
ACO
100
32.43 s
-0.4%
BB -
-
DFS 7.05 s
-13.4%
Table 3: Experiment results regarding ARP experiment.
Algorithm
Number of
Flights
Total
Time
Difference
to BKS
ACO
20
3.13 s
0%
BB 1.20 s
0%
DFS 1.18 s
-2,3%
ACO
50
15.33 s
0%
BB -
-
DFS 8.68 s
-9.7%
ACO
100
25.10 s
0%
BB -
-
DFS 18.41 s
-20.2%
6 CONCLUSIONS
This paper focused on studying the AAP and ARP
with a detailed introduction of several approaches in
the literature upon this topic. Most of the analysed
models lack a consideration of passenger
disruptions, a problem that can influence both the
airline’s maintenance costs and passenger
satisfaction. We have developed an ACO algorithm
to solve the AAP and ARP while considering
disrupted passengers as part of the cost function. The
objective function that is defined in our problem
considers aircraft assignment costs and, in case of
unforeseen events, it allows flights to be delayed,
cancelled or rerouted. Ants will always try to
combine these actions so that total costs are kept to
the minimum and disruptions are not propagated to
other flights.
Conducted experiments reveal that our online
ACO rescheduling approach is able to solve
different sets of AAP/ARP within reasonable time
and with very good final solutions. We believe that
this time overhead is largely compensated by the
quality of the solutions produced. This approach is a
step towards a full automation of AOCC’s because
the developed algorithm is ready to run in a
continuous fashion, where a sliding window through
time considers future flights and discards past ones,
constantly optimizing the current schedule and
always ready to adapt to a new environment. An
AOCC equipped with such a system would save the
airline not only on operational costs, due to a better
flight recovery, but also from having less employees
dedicated to flight recovery. On the other hand, we
realize that real flight management is not, at the
moment, ready to cope with a dynamic approach
such as our ACO-based method, because the
constant change in aircraft assignments could
compromise security protocols and long term flight
planning. Nevertheless, our approach can be seen as
a starting point towards a more realistic responsive
system.
A possible improvement to our approach could
be a different representation that aggregates flights
from the same route. This improvement would allow
a faster optimization because flights would be
compressed by routes, thus generating fewer nodes
in the system. Some methods from operations
research could also be introduced, especially on the
AAP as an initial solution to the ACO. On the other
hand, the algorithm could be expanded with the
introduction of new constraints from crew
rescheduling problem resulting in a broader
algorithm.
Finally, although we have made preliminary tests
to the performance of ACO applied to this problem,
we need to perform a comparative evaluation of our
implementation with other meta-heuristic
approaches.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
404

ACKNOWLEDGEMENTS
The authors would like to thank António Castro for
his help on understanding the AAP/ARP problems
and for providing the dataset on which experiments
have been run.
REFERENCES
International Air Transport Association, 2011. Benefits of
Aviation Homepage. [online] Available at:
http://www.benefitsofaviation.aero [Accessed 4 June
2014].
Castro, A. J. M., Rocha, A. P., Oliveira, E., 2014. A New
Approach for Disruption Management in Airline
Operations Control. Studies in Computational
Intelligence, Vol. 562, Springer, ISBN 978-3-662-
43372-0.
Colorni, A., Dorigo, M., Maniezzo, V., 1991. Distributed
optimization by ant colonies. European Conference on
Artificial Life, Paris, France, pp.134-142, Elsevier
Publishing.
Dorigo, M., Stutzle, T., 2004. Ant Colony Optimization.
MIT Press, Cambridge, MA.
Gabteni, S., Gronkvist, M., 2009. Combining column
generation and constraint programming to solve the
tail assignment problem. Annals of Operations
Research, 171(1), pp. 61-76.
Jarrah, A., Yu, G., Krishnamurthy, N., Rakshit, A., 1993.
A decision support framework for airline flight
cancellations and delays, Transportation Science,
27(3), pp. 266-280.
Konak, A., Coit, D., Smith, A., 2006. Multi-objective
optimization using genetic algorithms: A tutorial,
Reliability Engineering & System Safety, 91(9), pp.
992-1007.
Lawler, E. L. and Wood, D. E., 1966. Branch-and-bound
methods: A survey. Operations research, 14(4), pp.
699-719.
Liu, T., Jeng, C., Liu, Y., Tzeng, J., 2006. Applications of
multi-objective evolutionary algorithm to airline
disruption management, IEEE Int. Conf. on Systems,
Man and Cybernetics (SMC '06), Volume 5, pp. 4130-
4135.
Løve, M., Sørensen, K. R., Larsen, J., Clausen, J., 2005.
Using Heuristics to Solve the Dedicated Aircraft
Recovery Problem. Central European Journal of
Operations Research, 13(2), 189–207.
Tarjan R., 1972. Depth-first search and linear algorithms.
SIAM journal on computing, 1(2), pp. 146-160.
Teodorovic, D., Guberinic, S., 1984. Optimal dispatching
strategy on an airline network after a schedule
perturbation. European Journal of Operational
Research, 15(2), pp. 178-182.
Thengvall, B., Yu, G., Bard, J., 2001. Multiple fleet
aircraft schedule recovery following hub closures,
Transportation Research Part A: Policy and Practice,
35(4), pp. 289-308.
Wu, C., Le, M., 2012. A New Approach to Solve Aircraft
Recovery Problem, The Second Int. Conf. on
Advanced Communications and Computation
(INFOCOMP 2012), pp. 148-154.
Zegordi, S., Jafari, N., 2010. Solving the airline recovery
problem by using ant colony optimization.
International Journal of Industrial Engineering, 21(3).
AirlineDisruptionManagement-DynamicAircraftSchedulingwithAntColonyOptimization
405
