Improvement of Recovering Shape from Endoscope Images Using RBF

Neural Network

Yuji Iwahori

, Seiya Tsuda

, Robert J. Woodham

, M. K. Bhuyan

and Kunio Kasugai

Dept. of Computer Science, Chubu University, Kasugai 487-8501, Japan

Dept. of Computer Science, University of British Columbia, Vancouver V6T 1Z4, Canada

Dept. of Electronics and Electrical Engineering, Indian Institute of Technology Guwahati, Guwahati 781039, India

Dept. of Gastroenterology, Aichi Medical University, Nagakute 480-1195, Japan

Keywords:

Endoscope Image, VBW Model, RBF-NN, Shape Modiﬁcation, Reﬂection Factor.

Abstract:

The VBW (Vogel-Breuß-Weickert) model is proposed as a method to recover 3-D shape under point light

source illumination and perspective projection. However, the VBW model recovers relative, not absolute,

shape. Here, shape modiﬁcation is introduced to recover the exact shape. Modiﬁcation is applied to the output

of the VBW model. First, a local brightest point is used to estimate the reﬂectance parameter from two images

obtained with movement of the endoscope camera in depth. After the reﬂectance parameter is estimated, a

sphere image is generated and used for Radial Basis Function Neural Network (RBF-NN) learning. The NN

implements the shape modiﬁcation. NN input is the gradient parameters produced by the VBW model for

the generated sphere. NN output is the true gradient parameters for the true values of the generated sphere.

Depth can then be recovered using the modiﬁed gradient parameters. Performance of the proposed approach

is conﬁrmed via computer simulation and real experiment.

1 INTRODUCTION

Endoscopy allows medical practitioners to observe

the interior of hollow organs and other body cavi-

ties in a minimally invasive way. Sometimes, diag-

nosis requires assessment of the 3-D shape of the ob-

served tissue. For example, the pathologicalcondition

of a polyp often is related to its geometrical shape.

Medicine is an important area of application of com-

puter vision technology. Specialized endoscopes with

a laser light beam head (Nakatani et al., 2007) or with

two cameras mounted in the head (Mourgues et al.,

2001) have been developed. Many approaches are

based on stereo vision (Thormaehlen et al., 2001).

However, the size of the endoscope becomes large

and this imposes a burden on the patient. Here, we

consider a general purpose endoscope, of the sort still

most widely used in medical practice.

Shape recovery from endoscope images is consid-

ered. Shape from shading (SFS) (Horn, 1975) and

Fast Marching Method (FMM) (Sethian, 1996) based

SFS approach (Kimmel and Sethian, 2001) are pro-

posed. These approaches assume orthographic pro-

jection. An extension of FMM to perspective projec-

tion is proposed in (Yuen et al., 2007). Further ex-

tension of FMM to both point light source illumina-

tion and perspective projection is proposed in (Iwa-

hori et al., 2010). Recent extensions include gener-

ating a Lambertian image from the original multiple

color images (Ding et al., 2010), (Neog et al., 2011).

Application of FMM includes solution (Iwahori et al.,

2014) under oblique illumination using neural net-

work learning (Ding et al., 2009). Most of the pre-

vious approaches treat the reﬂectance parameter as a

known constant. The problem is that it is impossible

to estimate the reﬂectance parameter from only one

image. Further, it is also difﬁcult to apply point light

source based photometric stereo (Iwahori et al., 1990)

in the context of endoscopy.

Iwahori et al. (Iwahori et al., 1997) developed Ra-

dial Basis Function Neural Network (RBF-NN) pho-

tometric stereo, exploiting the fact that an RBF-NN

is a powerful technique for multi-dimensional non-

parametric functional approximation.

Recently, the Vogel-Breuß-Weickert (VBW)

model (Vogel et al., 2007), based on solving the

Hamilton-Jacobi equation, has been proposed to re-

cover shape from an image taken under the conditions

of point light source illumination and perspective

Iwahori Y., Tsuda S., Woodham R., Bhuyan M. and Kasugai K..

Improvement of Recovering Shape from Endoscope Images Using RBF Neural Network.

DOI: 10.5220/0005206800620070

In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 62-70

ISBN: 978-989-758-077-2

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

projecction. However, the result recovered by the

VBW model is relative. VBW gives smaller values

for surface gradient and height distribution compared

to the true values. That is, it is not possible to apply

the VBW model directly to obtain exact shape and

size.

This paper proposes a new approach to improve

the accuracy of polyp shape determination as absolute

size. The proposed approach estimates the reﬂectance

parameter from two images with small camera move-

ment in the depth direction. A Lambertian sphere

model is synthesized using the estimated reﬂectance

parameter. The VBW model is applied to the synthe-

sized sphere and shape then is recovered. An RBF-

NN is used to improve the accuracy of the recovered

shape, where the input to the NN is the surface gradi-

ent parameters obtained with the VBW model and the

output is the corresponding, corrected true values.

The proposed approach is evaluated via computer

simulation and real experiments and it is conﬁrmed

that the obtained shape is improved.

2 VBW MODEL

The VBW model (Vogel et al., 2007) is proposed as a

method to calculate depth (distance from the viewer)

under point light source illumination and perspective

projection. The method solves the Hamilton-Jacobi

equations (Benton, 1977) associated with the models

of Faugeras and Prados (Prados and Faugeras, 2004)

(Prados and Faugeras, 2003). Lambertian reﬂectance

is assumed.

The following processing is applied to each point

of the image. First, the initial value for the depth

default

is given using Eq.(1) as in (Prados and

Faugeras, 2005).

default

= −0.5log(I f

) (1)

where I represents the normalized image intensity and

f is the focal length of the lens.

Next, the combination of gradient parameters

which gives the minimum gradient is selected from

the difference of depths for neighboring points. The

depth, Z, is calculated from Eq.(2) and the process

is repeated until the Z values converge. Here, (x, y)

are the image coordinates, ∆t is the change in time,

(m, n) is the minimum gradient for (x, y) directions,

and Q =

√

+ f

is the coefﬁcient of the perspec-

tive projection.

Z(x, y) = Z(x, y) + ∆t exp(−2Z(x, y))

−∆t



I f

√

(m(x)

+n(y)

)+(xm(x)+yn(y))



(2)

Here, it is noted that the shape obtained with the

VBW model is given in a relative scale, not an abso-

lute one. The obtained result gives smaller values for

surface gradients than the actual gradient values.

3 PROPOSED APPROACH

3.1 Estimating Reﬂectance Parameter

When uniform Lambertian reﬂectance and point light

source are assumed, image intensity depends on the

dot product of surface normal vector and the light

source direction vector subject to the inverse square

law for illuminance.

Measured intensity at each surface point is deter-

mined by Eq.(3).

E = C

(s·n)

(3)

where E is image intensity, s is a unit vector towards

the point light source, n is a unit surface normal vec-

tor, and r is the distance between the light source and

surface point.

The proposed approach estimates the value of the

reﬂectance parameter, C, using two images acquired

with a small camera movement in the depth direc-

tion. It is assumed that C is constant for all points

on the Lambertian surface. Regarding geometry, it is

assumed that both the point light source and the op-

tical center of lens are co-located at the origin of the

(X, Y, Z) world coordinate system. Perspective pro-

jection is assumed.

The actual endoscope image has the color textures

and specular reﬂectance. Using the approach pro-

posed by (Shimasaki et al., 2013) the original input

endoscope image is converted into one that satisﬁes

the assumptions of a uniform Lambertian gray scale

image.

The procedure to estimate C is as follows.

Step 1. If the value of C is given, depth Z is uniquely

calculated and determined at the point with the lo-

cal maximum intensity (Tatematsu et al., 2013).

At this point, the surface normal vector and the

light source direction vector are aligned and pro-

duce the local maximum intensity for that value

of C.

Step 2. For camera movement, ∆Z, in the Z direction,

two images are used and the difference in Z, Z

dif f

at the local maximum intensity points in each im-

age is calculated. Here the camera movement, ∆Z,

is assumed to be known.

ImprovementofRecoveringShapefromEndoscopeImagesUsingRBFNeuralNetwork

Step 3. Let f(C) be the error between ∆Z and Z

dif f

f(C) represents an objective function to be min-

imized to estimate the correct value of C. That

is, the value of C is the one that minimizes f (C)

given in Eq.(4).

f(C) = (∆Z −Z

dif f

(x, y))

(4)

3.2 NN Learning for Modiﬁcation of

Surface Gradient

The size and shape recovered by the VBW model are

relative. VBW gives smaller values for surface gra-

dient and depth compared to the true values. Here,

modiﬁcation of surface gradient and improvement of

the recovered shape are considered. First, the sur-

face gradient at each point is modiﬁed by a neural

network. Then the depth is modiﬁed using the esti-

mated reﬂectance parameter,C, and the modiﬁed sur-

face gradient, (p, q) = (

∂Z

∂X

∂Z

∂Y

). A Radial Basis Func-

tion Neural Network (RBF-NN) (Ding et al., 2009) is

used to learn the modiﬁcation of the surface gradient

obtained by the VBW model.

Using the estimated C, a sphere image is synthe-

sized with uniform Lambertian reﬂectance.

The VBW model is applied to this synthesized

sphere. Surface gradients, (p, q), are obtained using

forward difference of the Z values obtained from the

VBW model.

The estimated gradients, (p, q), and the corre-

sponding true gradients for the synthesized sphere,

(p, q), are given respectively as input vectors and out-

put vectors to the RBF-NN. NN learning is applied.

After NN learning, the RBF-NN can be used to

modify the recovered shape for other images.

Two endoscope images, (a) and (b), and the im-

ages assuming Lambertian reﬂectance, (c) and (d),

generated using (Shimasaki et al., 2013), are shown

(a) Orginal1 (b) Orginal2

Figure 1: Endoscope Image and Lambertian Image.

in Fig.1.

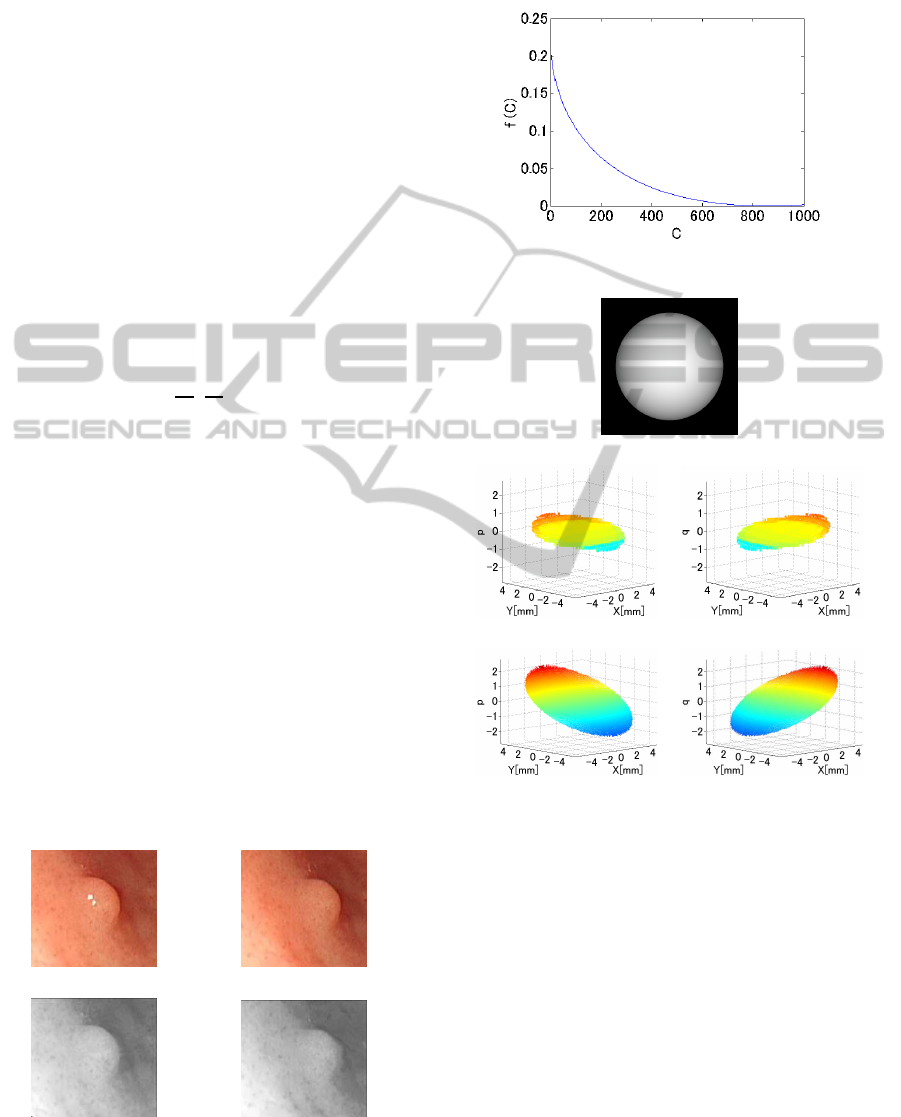
An example of the objective function, f(C), is

shown in Fig.2.

Figure 2: Objective Function f(C).

(a) Sphere

(b) p by VBW (c) q by VBW

(d) True p (e) True q

Figure 3: Synthesized Sphere for NN Learning.

The synthesized sphere image used in NN learn-

ing is shown in Fig.3(a). Surface gradients obtained

by the VBW model are shown in Fig.3(b)(c) and the

correspondingtrue gradients for this sphere are shown

in Fig.3(d)(e). Points are sampled from the sphere as

input for NN learning, except for points with large

values of (p, q). The procedure for NN learning is

shown in Fig.4.

3.3 NN Generalization and

Modiﬁcation of Z

The trained RBF-NN allows generalization to other

test objects. Modiﬁcation of estimated gradients,

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

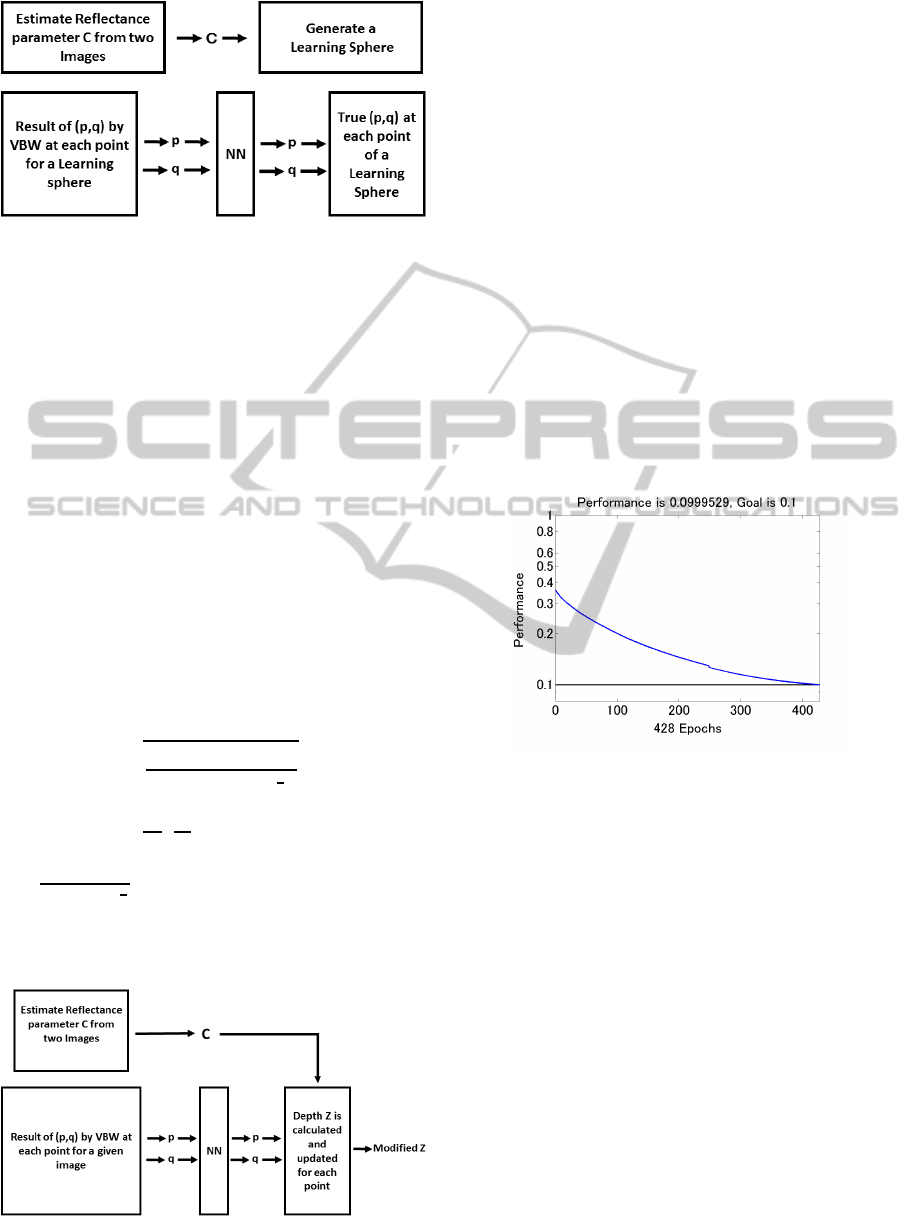
Figure 4: Learning Flow.

(p, q), is applied to the test object and its depth, Z, is

calculated and updated using the modiﬁed gradients,

(p, q).

In the case of endoscope images, preprocessing is

used to remove specularities and to generate a uni-

form Lambertian image based on (Shimasaki et al.,

2013).

Next, the VBW model is applied to the this Lam-

bertian image and the gradients, (p, q), are estimated

from the obtained Z distribution.

The estimated gradients, (p, q), are input to the

NN and modiﬁed estimates of (p, q) are obtained as

output from the NN.

Recall that the reﬂectance parameter, C, is esti-

mated from f(C), based on two images obtained by

small movement of endoscope in the Z direction.

The depth, Z, is calculated and updated by Eq.(5)

using the modiﬁed gradients, (p, q), and the estimated

C, where Eq.(5) also is the original equation devel-

oped in (Iwahori et al., 2010).

Z =

CV(−px−qy+ f)

E(p

+ q

+ 1)

(5)

Again, (p, q) = (

∂Z

∂X

∂Z

∂Y

), E represents image inten-

sity, f represents the focal length of the lens and

V =

+ f

)

A ﬂow diagram of the processing described above

is shown in Fig.5.

Figure 5: Flow of NN Generalization.

4 EXPERIMENTAL RESULTS

4.1 NN Learning

A sphere was synthesized with radius 5mm and with

center located at (0, 0, 15). The focal length of the

lens was 10mm. The image size was 9mm×9mm

with pixel size 256×256 pixels.

The VBW model was used to recover the shape of

this sphere. The resulting gradient estimates, (p, q),

are shown in Fig.3(b) and (c), respectively.

These estimated gradients, (p, q), are used as NN

input and the corresponding true gradients, (p, q),

output from the NN, are shown in Fig.3(d) and (e).

Learning was done under the conditions: error goal

1.0e-1, spread constant of the radial basis function

0.00001, and maximum number of learning epochs

500. Learning was complete by about 400 epochs

with stable status.

The results of learning is shown in Fig.6.

Figure 6: Learning Result.

The reﬂectance parameter, C, was estimated as

854 from f (C). The difference in depth, Z, was 0.5

[mm] for the known camera movement.

As shown in Fig.6, NN learning was complete at

428 epochs. The square error goal reached the spec-

iﬁed value. Processing time for NN learning was

around 30 seconds.

A sphere has a variety of surface gradients and it

is used for the NN learning. After a sphere is used for

NN learning, not only a sphere object but also other

object with another shape including convex or con-

cave surfaces is also available in the generalization

process. This is because surface gradient for each

point is modiﬁed by NN and this modiﬁcation does

not depend on the shape of target object.

4.2 Computer Simulation

Computer simulation was performed for a second pair

of synthesized images to conﬁrm the performance of

ImprovementofRecoveringShapefromEndoscopeImagesUsingRBFNeuralNetwork

NN generalization. Synthesized cosine curved sur-

faces were used, one with center located at coordi-

nates (0, 0, 12) and the other with center at (0, 0, 15).

Common to both, the reﬂectance parameter,C, is 120,

the focal length, f, is 10mm and the waveform cycle

is 4mm and the ± amplitude is 1mm. Image size is

5mm×5mm and pixel size is 256×256 pixels.

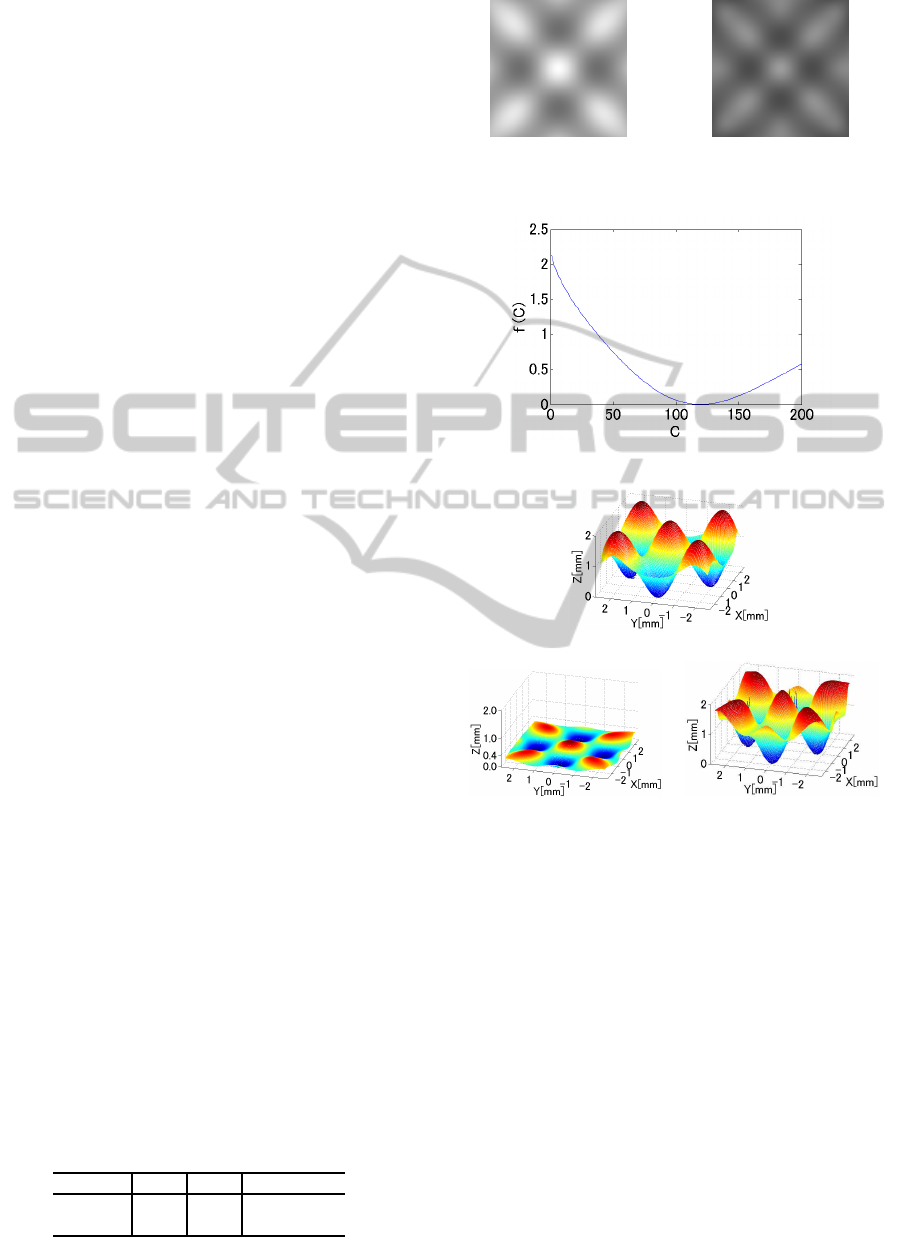
The synthesized image whose center is located at

(0, 0, 12) is shown in Fig.7(a) and the one with center

located at (0, 0, 15) is shown in Fig.7(b).

The reﬂectance parameter, C, was estimated ac-

cording to the proposed method. Using the learned

NN, the gradients, (p, q), obtained from the VBW

model were input and generalized. The gradients,

(p, q), were modiﬁed and the depths, Z, were updated

using Eq.(5).

The graph of the objective function, f(C), is

shown in Fig.8 and the true depth is shown in Fig.9(a).

The estimated C was 119 (compared to the true value

of 120). The estimagtd Z

dif f

was 2.9953 (compared

to the true value of 3).

The result recovered by VBW for Fig.7(a) is

shown in Fig.9(b). The modiﬁed values of depth, us-

ing the NN and Eq.(5), are shown in Fig.9(c).

Table.1 gives the mean errors in surface gradient

and depth estimation. The percentages given in the

Z column represent the error relative to the amplitude

of maximum−minimum depth (=4mm) of the cosine

synthesized function. In Table 1, the original VBW

results have a mean error of around 3.8 degrees for the

surface gradient while the proposed approach reduced

the mean error to about 0.1 degree. Depth estimation

also improved to a mean error of 8.3% from 43.1%.

NN generalization improved estimation of shape for

an object with different size and shape. It took 9 sec-

onds to recover the shape while it took 61 seconds for

NN learning with 428 learning epochs, that is, it took

70 seconds in total.

Computer simulation was performed for a sec-

ond pair of synthesized images to conﬁrm the per-

formance of NN generalization. Synthesized cosine

curved surfaces were used, one with center located at

coordinates (0, 0, 12) and the other with center at (0,

0, 15). Common to both, the reﬂectance parameter,C,

is 120, the focal length, f, is 10mm and the waveform

cycle is 4mm and the ± amplitude is 1mm.

Another experiment was performed under the fol-

lowing assumptions. The reﬂectance factor,C, is 590,

Table 1: Mean Error.

p q Z[mm]

VBW 23.04 23.04 0.86 (43.1%)

Proposed 0.32 0.32 0.25 ( 8.3%)

(a) Center:(0,0,12) (b) Center:(0,0,15)

Figure 7: Cosine Model.

Figure 8: Objective Function f(C).

(a) True Z

(b) Z by VBW (c) Modiﬁed Z

Figure 9: Results.

the focal length, f, is 10mm and the object is a sphere

with radius 5mm. The centers for two positions of the

sphere were set at (0, 0,15) and (0, 0, 17) respectively,

as shown in Fig.10. The image size was 9mm× 9mm

with pixel size 360×360 pixels. Here, 4% Gaus-

sian noise (mean 0, variance 0.02, standard deviation

0.14142) is added to each of the two input images.

The graph of the objective function, f(C), is shown in

Fig.11 and the true depth is shown in Fig.12(a). The

result recovered by VBW is shown in Fig.12(b). The

improved result is shown in Fig.12(c). The mean er-

rors in surface gradient and depth are shown in Table

2. Evaluations for 6% (mean 0, variance 0.03, stan-

dard deviation 0.17320) and 10% (mean 0, variance

0.03, standard deviation 0.17320) Gaussian noise in-

cluded in Table 3, as well.

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

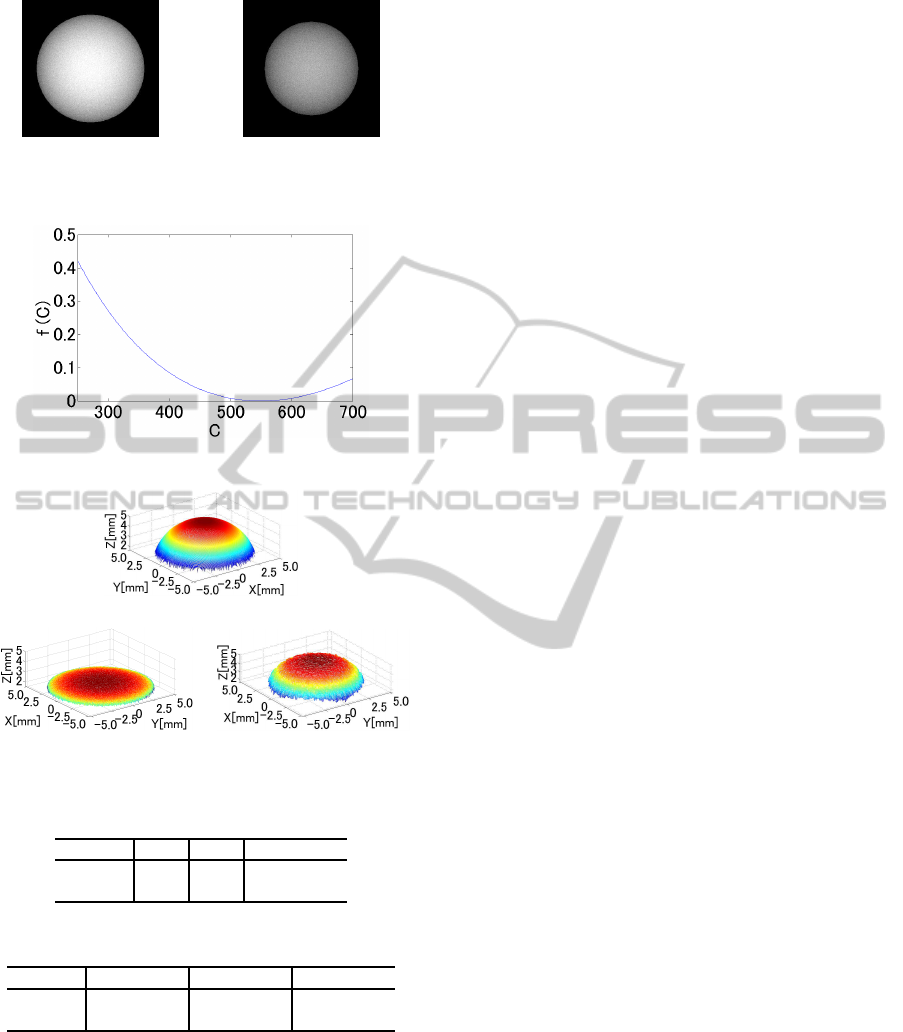
(a) Center:(0,0,15) (b) Center:(0,0,17)

Figure 10: Sphere Images with Gaussian Noise.

Figure 11: Objective Function f (C).

(a) True Z

(b) Z by VBW (c) Modiﬁed Z

Figure 12: Results.

Table 2: Mean Error.

p q Z[mm]

VBW 17.04 17.45 3.36 (67.2%)

Proposed

0.45 0.45 0.36 ( 7.2%)

Table 3: Mean Error of Z for Different Gaussian Noise.

4% 6% 10%

VBW 3.36 (67.2%) 3.25 (65.1%) 2.82 (56.6%)

Proposed

0.36 ( 7.2%) 0.36 ( 7.2%) 0.36 ( 7.3%)

Learning epochs for Gaussian noise 4%, 6% and

10% were 212, 212 and 210. Processing time was

around 40 seconds for every case of different Gaus-

sian noises.

The reﬂectance parameter, C, estimated from

Fig.11, was 591. Improvement in the estimated re-

sults is shown in Fig.12(a)(b)(c) and Table 2.

In all three cases, Gaussian noise of 4%, 6% and

10%, the proposed approach reduced the mean er-

ror in Z signiﬁcantly compared to the original VBW

model.

This suggests generalization using the RBF-NN is

robust to noise and is applicable to real imaging sit-

uations, including endoscopy. Result of VBW model

gives less errors with noises butthis is based on the re-

sult that the recovered shape is relative scale and sen-

sitive to the original intensity of each point according

to Gaussian noise, while the proposed approach gives

much better shape with the absolute size. Although

the error increases a little bit according to Gaussian

noise, the approach is still robust and stable result is

obtained.

4.3 Real Image Experiments

Two endoscope images obtained with camera move-

ment in the Z direction are used in the experiments.

The reﬂectance parameter,C, was estimated and a

RBF-NN was learned using a sphere synthesized with

the estimated C. VBW was applied to one of the im-

ages which was ﬁrst converted to a uniform Lamber-

tian image.

Surface gradients, (p, q), were modiﬁed with the

NN then depth, Z, was calculated and updated at each

image point. The focal length, f=10mm, the image

size 5mm×5mm, and camera movement, ∆Z=3mm,

were assigned to the same known values as those in

the computer simulation. The error goal was set to be

0.1.

The two endoscope images are shown in Fig.13(a)

and (b). The generated Lambertian images are shown

in Fig.13(c) and (d), respectively.

The objective function, f(C), is shown in Fig.14.

The result from the VBW model is shown

in Fig.15(a) and the modiﬁed result is shown in

Fig.15(b).

The estimated value of the reﬂectance parameter,

C, was 1141. The difference in depth, Z, at the local

maximum point was 1 [mm] for the camera move-

ment Z

dif f

between two images. In Fig.13(c)(d),

specularities were removed compared to Fig.13(a)(b).

The converted images are gray scale with the appear-

ance of uniform reﬂectance. Fig.15(b) gives a larger

depth range than Fig.15(a). This suggests depth esti-

mation is improved. The size of the polyp was 1cm

and the processing time for shape modiﬁcation was 9

seconds. As it took 117 seconds for NN learning with

540 epochs, a total processing time was 126 seconds.

Although quantitative evaluation is difﬁcult, med-

ical doctors with experience in endoscopy qualita-

tively evaluated the result to conﬁrm its correct-

ness. Different values of the reﬂectance parameter,

ImprovementofRecoveringShapefromEndoscopeImagesUsingRBFNeuralNetwork

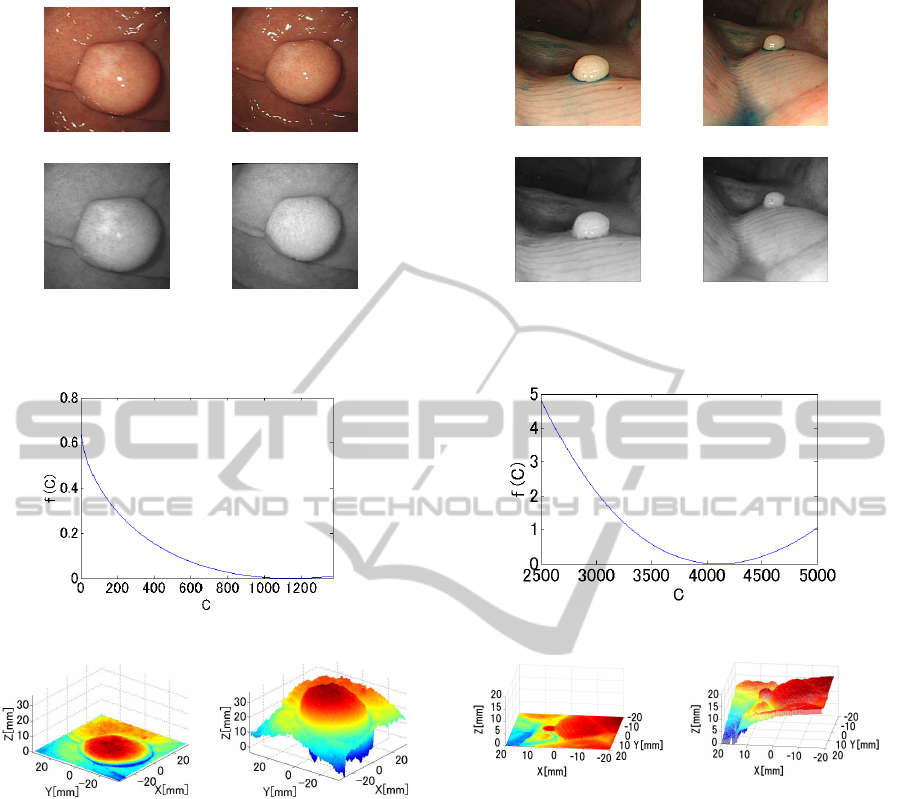
(a) Endoscope 1 (b) Endoscope 2

Figure 13: Endoscope Image and Generating Lambert Im-

age.

Figure 14: Objective Function f (C).

(a) Z by VBW (b) Modiﬁed Z

Figure 15: Result for Endoscope Images.

C, were estimated in different experimental environ-

ments. The absolute size of a polyp is estimated based

on the estimated value ofC. Accurate values of C lead

to accurate estimation of the size of the polyp. The

estimated polyp sizes were seen as reasonable by the

medical doctor. This qualitatively conﬁrms that the

proposed approach is effective in real endoscopy.

Another experiment was done for the endoscope

images shown in Fig.16(a)(b). The generated gray

scale Lambertian images are shown in Fig.16(c)(d),

respectively. Here the focal length is 10mm, image

size is 5mm×5mm, pixel size is 256×256 and ∆Z was

set to be 10mm.

The graph of f (C) is shown in Fig.17. The VBW

result for Fig.16(d) is shown in Fig.18(a), while that

for the proposed approach is shown in Fig.18(b).

(a) Endoscope 1 (b) Endoscope 2

Figure 16: Endoscope Image and Generating Lambert Im-

age.

Figure 17: Objective Function f (C).

(a) Z by VBW (b) Modiﬁed Z

Figure 18: Result for Endoscope Images.

C was estimated as 4108 from Fig.17. Fig.18(b)

shows greater depth amplitude compared to Fig.18(a).

The estimated size of the polyp was about 5mm.

This corresponds to the convex and concave shape es-

timation based on a stain solution. It took 60 seconds

for NN learning with 420 epochs and a total process-

ing time was 70 seconds.

4% Gaussian noise was added to a real image

and the corresponding results are shown in Fig.19(a).

Shape was estimated from the generated Lambertian

image, shown in Fig.19(b). The corresponding results

are shown in Fig.19(c) and Fig.19(d). Here the focal

length is 10mm, image size is 5mm×5mm, pixel size

is 256×256 and ∆Z was 3mm.

In this paper, it is assumed that movement of the

endoscope is constrained to be in the depth, Z, direc-

tion only. Here, it is seen that the result is acceptable

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

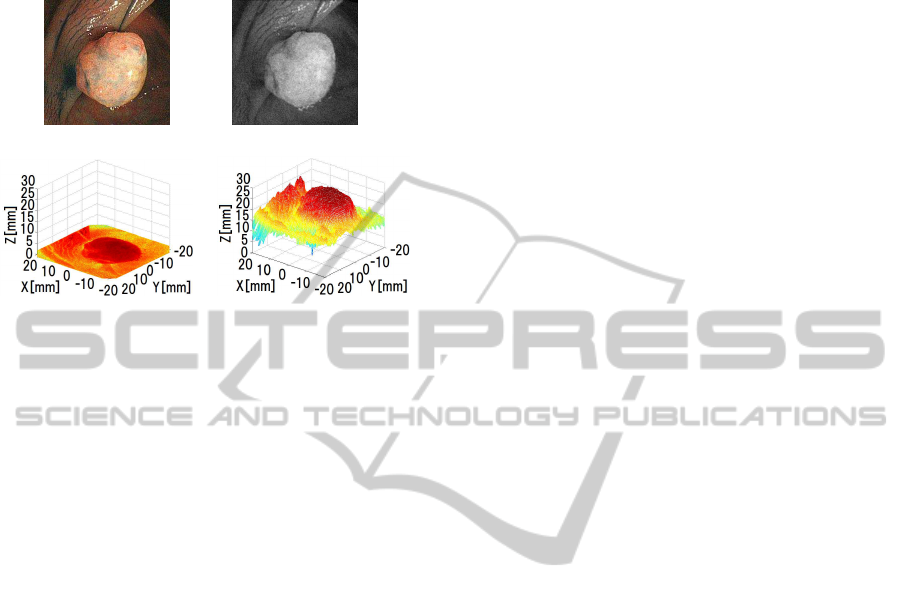
even when camera movement is in another direction,

provided rotation is minimal and the overall camera

movement is still small.

(a) Endoscope (b) Lambert

Figure 19: Result with Gaussian Noise.

The reﬂectance parameter, C, was estimated as

13244 and Fig.19(b) shows the ﬁnal estimated shape.

Total of processing time was 90 seconds including 80

seconds for NN learning with 480 epochs.

The estimated size of this polyp was about 1cm.

Although Gaussian noise was added, shape recovery

remained robust.

5 CONCLUSION

This paper proposed a new approach to improve the

accuracy of absolute size and shape determination of

polyps observed in endoscope images.

An RBF-NN was used to modify surface gradi-

ent estimation based on training with data from a syn-

thesized sphere. The VBW model was used to esti-

mate a baseline shape. Modiﬁcation of gradients with

the RBF-NN improved the accuracy of that baseline

shape estimation. Estimation of the reﬂectance pa-

rameter, C, was achieved under the assumption that

two images are acquired via small camera movement

in the depth, Z, direction. The RBF-NN is non-

parametric in that no parametric functional form has

been assumed for gradient modiﬁcation. The ap-

proach was evaluated both in computer simulation

and with real endoscope images. Results conﬁrm

that the approach improves the accuracy of recov-

ered shape to within error ranges that are practical for

polyp analysis in endoscopy.

ACKNOWLEDGEMENT

Iwahori’s research is supported by Japan Society for

the Promotion of Science (JSPS) Grant-in-Aid for

Scientiﬁc Research (C) (26330210) and Chubu Uni-

versity Grant. Woodham’s research is supported

by the Natural Sciences and Engineering Research

Council (NSERC). The authors would like to thank

Kodai Inaba for his experimental help and the related

member for useful discussions in this paper.

REFERENCES

Benton, S. H. (1977). The Hamilton- Jacobi Equation: A

Global Approach. In Academic Press, Volume 131.

Ding, Y., Iwahori, Y., Nakamura, T., He, L., Woodham,

R. J., and Itoh, H. (2010). Shape Recovery of Color

Textured Object Using Fast Marching Method via

Self-Caribration. In EUVIP 2010, pp. 92-96.

Ding, Y., Iwahori, Y., Nakamura, T., Woodham, R. J., He,

L., and Itoh, H. (2009). Self-calibration and Image

Rendering Using RBF Neural Network. In KES 2009,

Volume 5712, pp. 705-712.

Horn, B. K. P. (1975). Obtaining Shape from Shading In-

formation. In The Psychology of Computer Vision,

Winston, P. H. (Ed.), Mc Graw- Hill, pp. 115-155. Mc

Graw- Hill.

Iwahori, Y., Iwai, K., Woodham, R. J., Kawanaka, H.,

Fukui, S., and Kasugai, K. (2010). Extending Fast

Marching Method under Point Light Source Illumi-

nation and Perspective Projection. In ICPR2010, pp.

1650-1653.

Iwahori, Y., Shibata, K., Kawanaka, H., Funahashi, K.,

Woodham, R. J., and Adachi, Y. (2014). Shape from

SEM Image Using Fast Marching Method and Inten-

sity Modiﬁcation by Neural Network. In Recent Ad-

vances in Knowledge-based Paradigms and Applica-

tions, Advances in Intelligent Systems and Computing

234, Springer, Chapter 5, pp.73-86.

Iwahori, Y., Sugie, H., and Ishii, N. (1990). Reconstructing

Shape from Shading Images under Point Light Source

Illumination. In ICPR 1990, Vol.1, pp. 83-87.

Iwahori, Y., Woodham, R. J., Ozaki, M., Tanaka, H., and

Ishii, N. (1997). Neural Network based Photomet-

ric Stereo with a Nearby Rotational Moving Light

Source. In IEICE Trans. Info. and Syst., Vol. E80-D,

No. 9, pp. 948-957.

Kimmel, R. and Sethian, J. A. (2001). Optimal Algorithm

for Shape from Shading and Path Planning. In Jour-

nal of Mathematical Imaging and Vision (JMIV) 2001,

Vol. 14, No. 3, pp. 237-244.

Mourgues, F., Devernay, F., and Coste-Maniere, E. (2001).

3D reconstruction of the operating ﬁeld for image

overlay in 3D-endoscopic surgery. In Proceedings of

the IEEE and ACM International Symposium on Aug-

mented Reality (ISAR), pp. 191-192.

ImprovementofRecoveringShapefromEndoscopeImagesUsingRBFNeuralNetwork

Nakatani, H., Abe, K., Miyakawa, A., and Terakawa, S.

(2007). Three-dimensional measuremen endoscope

system with virtual rulers. In Journal of Biomedical

Optics, 12(5):051803.

Neog, D. R., Iwahori, Y., Bhuyan, M. K., Woodham, R. J.,

and Kasugai, K. (2011). Shape from an Endoscope

Image Using Extended Fast Marching Method. In

Proc. of IICAI-11, pp. 1006-1015.

Prados, E. and Faugeras, O. (2003). A mathematical and

algorithmic study of the Lambertian SFS problem for

orthographic and pinhole cameras. In Technical Re-

port 5005, INRIA 2003.

Prados, E. and Faugeras, O. (2005). Shape From Shading:

a well-posed problem? In CVPR 2005, pp. 870-877.

Prados, E. and Faugeras, O. D. (2004). Unifying Ap-

proaches and Removing Unrealistic Assumptions in

Shape from Shading: Mathematics Can Help. In

ECCV04.

Sethian, J. A. (1996). A Fast Marching Level Set Method

for Monotonically Advancing Fronts. In Proceedings

of the National Academy of Sciences of the United

States of America (PNAS U.S.), Vol. 93, No. 4, pp.

1591-1593.

Shimasaki, Y., Iwahori, Y., Neog, D. R., Woodham, R. J.,

and Bhuyan, M. K. (2013). Generating Lambertian

Image with Uniform Reﬂectance for Endoscope Im-

age. In IWAIT2013, 1C-2 (Computer Vision 1), pp.

60-65.

Tatematsu, K., Iwahori, Y., Nakamura, T., Fukui, S., Wood-

ham, R. J., and Kasugai, K. (2013). Shape from En-

doscope Image based on Photometric and Geometric

Constraints. In KES 2013, Procedia Computer Sci-

ence, Elsevier, Vol.22, pp. 1285-1293.

Thormaehlen, T., Broszio, H., and Meier, P. N. (2001).

Three-Dimensional Endoscopy. In Falk Symposium,

pp. 199-212.

Vogel, O., Breuß, M., and Weickert, J. (2007). A Di-

rect Numerical Approach to Perspective Shape-from-

Shading. In Vision Modeling and Visualiz-ation(VMV)

2007, pp. 91-100.

Yuen, S. Y., Tsui, Y. Y., and Chow, C. K. (2007). A fast

marching formulation of perspective shape from shad-

ing under frontal illumination. In Pattern Recognition

Letters, Vol. 28, No.7, pp. 806-824.

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods