
Cooperative Gesture Recognition
Learning Characteristics of Classifiers and Navigating the User to an Ideal
Situation
Hiromasa Yoshimoto and Yuichi Nakamura
Academic Center for Computing and Media Studies, Kyoto University, Sakyo-ku, Kyoto 606–8501, Japan
Keywords:
Cooperative Recognition, Gesture Interface, and Usability.
Abstract:
This paper introduces a novel scheme of gesture interface that guides the user toward obtaining better perfor-
mance and usability. The accuracy of gesture recognition is heavily affected by how the user makes postures
and moves, as well as environmental conditions such as lighting. The usability of the gesture interface can
potentially be improved by notifying the user of when and how better accuracy is obtained. For this purpose,
we propose a method for estimating the performance of gesture recognition in its current condition, and a
method for suggesting possible ways to improve performance to the user. In performance estimation, accu-
racy in the current condition is estimated based on supervised learning with a large number of samples and
corresponding ground truths. If the estimated accuracy is insufficient, the module searches for better condi-
tions that can be reached with the user’s cooperation. If a good improvement is possible, the way to improve
is communicated to the user in terms of visual feedback, which shows how to avoid or how to recover from
the undesirable condition. In this way, users benefit, i.e., better accuracy and usability, by cooperating with
the gesture interface.
1 INTRODUCTION
As the success of Microsoft’s Kinect sensor shows,
a gesture-based interface is one of practical solu-
tion for a natural user interface(Shotton and Sharp,
2011; OpenNI organization, 2010; PrimeSense Inc.,
2010). Its fundamental technologies, such as mo-
tion tracking and gesture classification, however, still
face many difficulties and challenges (Pavlovic et al.,
1997; Moeslund et al., 2006; Ren et al., 2013), be-
cause of the ambiguities of human’s behavior, self-
occlusion, and the sensor’s measurement noise, etc.
Moreover, a gesture-based interface has additional us-
ability requirements. It must not only maintain good
recognition performance, but also needs to indicate
its internal status, to give easy ways to recover from
failures(Nielsen, 2009; Jacko and Sears, 2003).
In this paper, we focus on a framework for deal-
ing with both of the above goals: to improve the per-
formance of gesture recognition, and to improve the
usability of the gesture interface. For these two goals,
we propose a cooperative gesture recognition scheme,
which navigates the user into changing their behavior
so that both performance and usability are improved
at the same time.
For this navigation, we introduce a condition vec-
tor and a condition space to represent how the gesture
is easily recognized by the gesture recognition mod-
ule. The condition vector is defined by the parameters
measured by sensors, such as the user’s standing po-
sition, posture of upper body, and movement speed of
the user’s hands.
We then use recall and precision as a measure of
recognition performance, and calculates the distribu-
tion in condition space. Here, we can assume that
if the condition space has enough dimensions, i.e.,
enough parameters, performances around neighbor-
ing positions are similar. If the recognition perfor-
mance is satisfactory for one condition vector, it is
expected to be satisfactory in its neighborhood. For
covering over the condition space, we assume it can
be separated into two portions: a portion in which the
recognition performance is satisfactory and another
portion with unsatisfactory performance.
With the above assumptions, our cooperative
recognition scheme is composed by adding two mod-
ules to a common gesture interface scheme: a per-
formance estimation module and a feedback module.
These two modules work as follows. The perfor-
mance estimation module estimates recall and preci-
210
Yoshimoto H. and Nakamura Y..
Cooperative Gesture Recognition - Learning Characteristics of Classifiers and Navigating the User to an Ideal Situation.
DOI: 10.5220/0005206902100218
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 210-218
ISBN: 978-989-758-077-2
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

sion from the current condition vector, and the feed-
back module advises the user to change his/her be-
havior to a more desirable condition, where the recall
and precision become higher.
We modeled this performance estimation module
as functions that map condition vectors into recall
and precision. If enough labeled training samples
are available, these functions are constructed by su-
pervised machine learning. With these functions, the
module can not only estimate the performance of cur-
rent conditions, but also predict performance for any
condition.
The feedback module uses estimate functions to
search for more suitable conditions around the cur-
rent condition, where the predicted performance in-
creases. If a suitable condition is found, then the feed-
back module synthesizes visual hints to navigate the
user into the suitable condition. For example, if the
left position is predicted to have more suitable condi-
tions for the gesture recognition, the feedback module
draws an arrow-shaped computer graphic (CG) object
that induces the user to move a little to the left.
The main contribution of this scheme proposes not
a specialized application but a practical and general-
ized scheme. Our scheme can improve the perfor-
mance of the existing gesture interface by just adding
two modules. No modification of existing gesture
classifiers is required.
This paper is structured as follows. In Section 2,
an overview of related works is given. The proposed
scheme is described in Section 3. In Section 4, we
present the experimental evaluation, and we conclude
in Section 5.
2 RELATED WORK
In the fields of amusement or entertainment, a
gesture-based interface is a practical technology.
There are many commercial products, such as Mi-
crosoft’s Kinect sensors(Ren et al., 2013), Nintendo
Wii, and Eye cam Sony, etc. However, despite these
latest technologies, there are still challenging prob-
lems in gesture recognition.
From the viewpoint of computer vision (CV) and
pattern recognition (PR), gesture recognition still has
challenges in accuracy and the robustness of measure-
ment and recognition. For example, in hand gesture
recognition, the difficulties arise from the complex
structure of hands and the wide variations in their
appearances. Moreover, the ambiguities of the sen-
sor’s observation make further difficulties for gesture
recognition; e.g., when we use an RGB–D camera as
the sensor, the pixel’s noise and occlusions on the cap-
Figure 1: Example of ”easy” and “difficult” images for
gesture/sign recognition; the difficulties arise from image
noise, occlusions, motion blurs, etc.
Table 1: Four categories of the classifier’s output.
Ground truth is:
X
¯
X
Output
X
TP: True positive FP: False positive
of (Correct) (Type I error)
classifier
¯
X
FN: False negative TN: True negative
is: (Type II error) (Correct)
tured color and depth image cause ambiguities in im-
age analysis. Figure 1 shows actual hand depth im-
ages captured by a Kinect sensor; there are various
images ranging from “easy” to “difficult” recognition.
Although various approaches have been proposed to
overcome these difficulties in terms of CV or PR, ro-
bust and accurate gesture recognition remains a dif-
ficult task(Pavlovic et al., 1997; ?). In other words,
there is no approach that can guarantee 100% accu-
racy in gesture recognition.
However, from the viewpoint of the usability en-
gineering, the user interface should be designed to be
efficient to use and easy to learn. Nielsen’s(Nielsen,
2009) guidelines in usability engineering appeal for
a gesture-based user interface to provide some func-
tions that help the user to diagnose how accurate the
recognized result is, and to rectify the error when ges-
ture recognition fails. These features have already
been proposed in many studies and are used in many
commercial products. However, the pattern of appli-
cation design is not yet well discussed and formalized.
3 COOPERATIVE GESTURE
RECOGNITION
In general, each algorithm in gesture recognition,
such as a feature detector or a gesture classifier, uses
CooperativeGestureRecognition-LearningCharacteristicsofClassifiersandNavigatingtheUsertoanIdealSituation
211

TP
TN
FN
TN
FN
TP
FP
“easy” condition
for classifier
“difficult” condition
for classifier
(a) Condition space
TP
TN
FN
TN
FN
TP
FP
Navigate
(b) User navigation
Figure 2: Overview of cooperative gesture recognition: (a)
we propose condition space to learn the characteristics func-
tion of the classifier. (b) This space is also used to navigate
the user to change the user’s behavior or the environments
where the performance of classification will be improved.
its own assumptions on the human behaviors and en-
vironment, e.g., a user is standing in a certain area.
Recognition performance is directly related to how far
those assumptions are satisfied.
In a case where the assumptions are well satisfied,
we can expect good recognition accuracy. However,
it is difficult to estimate directly how far the assump-
tions are satisfied because the process of a feature de-
tector or a classifier usually includes non-linear, high-
dimensional computation, and human behavior and
the environments that are hard to model.
Instead of dealing with direct estimation, we con-
sider a substitute measure that represents the “appro-
priateness” of a current gesture and environment as
a recognition target. For this purpose, we introduce
a condition vector , and the space where the vector
lies is the condition space. Our key idea is that, if
we take a sufficient number and variety of dimensions
for the condition space, the “appropriateness” can be
well approximated and we work similarly to the de-
gree of how far assumptions are satisfied. Compo-
nents of the condition vector, for example, would be
the user’s standing position, velocity, or the color of
clothes. Moreover, some indices about jitters or the
signal-to-noise ratio of the pixels’ values on captured
images can also be used.
Theoretically, as we consider greater numbers and
variations of dimensions, the appropriateness is more
accurately approximated. However, we have compu-
tational problems in handling high-dimensional fea-
tures, e.g., the curse of dimensionality; therefore, we
need to design the instances of condition vectors care-
fully.
3.1 Predicting Gesture Recognition
Performance
Once the condition space is composed, the next prob-
lem is to decide what kind of measure is appropriate
for “appropriateness”. Our suggestion is that the use
of recognition accuracy is simple and sufficient.
Let us consider the gesture recognition process
as a multi-class classifier of an input gesture. More
specifically, we assume an one-versus-the-rest config-
uration of binary classifiers; for each gesture class C
X
,
the gesture recognition works as a binary-class clas-
sifier F
X
that outputs X or
¯
X, indicating whether the
input belongs to gesture C
X
or not. Next, we catego-
rize the combinations of recognition results and ac-
tual classes, as Table 1. For each category, we use the
following four labels: true positive (TP), true negative
(TN), false positive (FP), and false negative (FN). The
terms “positive” and “negatives” refer to the predicted
gesture class, and the other terms “true” and “false”
refer to the correctness of the recognition result.
Using these labels, the overview of condition
space can be shown in Figure 2a. Our framework pre-
dicts the performance of F
X
at a given query condition
vector s as precision P
X
(s) and recall R
X
(s), which are
defined as
P
X
(s) :=
#T P
X
(s)
#T P
X
(s) + #FP
X
(s)
(1)
R
X
(s) :=
#T P
X
(s)
#T P
X
(s) + #FN
X
(s)
(2)
P
¯
X
(s) :=
#T N
X
(s)
#FN
X
(s) + #T N
X
(s)
(3)
R
¯
X
(s) :=
#T N
X
(s)
#FP
X
(s) + #T N
X
(s)
, (4)
where # means the number of neighbors, e.g.,
#T P
X
(s) means the number of samples labeled T P
X
around s. Note that these recall and precision are
functions of s. In the pattern recognition field, the
recall and precision are usually used as indices for av-
erage performance over all possible conditions. How-
ever, our proposed functions calculate recall and pre-
cision around s. Using these functions of s, we can
predict and compare the actual performances of the
two conditions.
The final problem is how to calculate the func-
tions: #T P(s), #T N(s), #FP(s), and #FN(s). These
functions count the number of samples around any
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
212

given query point s in condition space. One of possi-
ble way is learning by example; we can collect gesture
recognition results as training samples where each
sample is a set of predicted gesture class, the actual
gesture, and its condition vector. Once a sufficient
number of training samples are collected, we have
several methods to estimate the values of these func-
tions at each position in the condition space. The de-
tails of the algorithm that we used in our experiments
are described in Section 4.1.
3.2 Navigating the User to an Ideal
Condition
It is widely recognized that the usability of an in-
terface will be increased by giving any appropriate
feedback to the user within a reasonable time(Nielsen,
2009). Many gesture interfaces already give supple-
mental information as feedback, such as the confi-
dence or likelihood of the recognition result. This
internal information helps the user to diagnose what
is going on, and to find the reasons for the errors.
Our cooperative recognition framework proposes
the following two additional feedbacks:
1. Feedback to show “appropriateness” of current
condition, which informs the user whether the
current condition is desirable for gesture classi-
fiers.
2. Feedback to show the method to improve ap-
propriateness, which is synthesized by a gesture
recognition system for the purpose of leading the
user towards changing his/her behaviors, or envi-
ronment so that sufficient gesture recognition ac-
curacy is obtained.
Feedback is achieved by showing the estimated
performance for the current condition vector by using
our recall and precision function. For example, we
often use a kind of a cursor or an avatar to show the
results of gesture recognition. In these cases, we can
obtain feedback of the appropriateness of the current
condition by changing the color or size of the cursor
or the avatar.
Figure 2b shows the overview of the second feed-
back. This feedback is achieved by two tasks: a
search task to find a better condition s
2
than the cur-
rent condition s
1
and an inform task to navigate the
user on the way to change the condition. There can
be several strategies for these tasks, and their imple-
mentation strongly depends on the specific applica-
tion requirements.
However, the design of these two tasks is formu-
lated as follows. For the search task, a possible strat-
egy is as follows. First, we prepare the goal condition
Figure 3: Overview of experimental system.
candidates, e.g., move to the left by one step, move
a hand downward by 20 degrees. Then, we compare
these candidate conditions with the current condition
and choose the best one. This comparison can be eas-
ily achieved by referring the values of estimated re-
call and precision. For the inform task, we propose
the following two visual approaches:
Symbol-based Feedback. This feedback uses sym-
bols, such as an arrow-shaped CG. For example,
to encourage the user to move to the left by one
step, this feedback displays an arrow-shaped CG
that gives the user the distance and direction to
move.
Example-based Feedback. This feedback uses a
previously captured image or video as a prece-
dent. The image or video can give a concrete ex-
planation of how the previous user improved its
condition.
4 EXPERIMENT WITH
EXPERIMENTAL GESTURE
INTERFACE
We built a prototype gesture system to verify our
framework.
Although the characteristics of the gesture clas-
sifiers and system usability heavily depend on their
application, we think this example is commonly ap-
plicable to other gesture interfaces.
Figure 3 shows the overview of the prototype sys-
tem design that provides a drawing application with
the following two functions: drawing a line by using
a “pointing hand” gesture, and erasing lines by the
“opened hand” gesture. This interface uses the dis-
play to show the virtual canvas for drawing, and also
to show the silhouette of the user. The user can look
at this display as a mirror and can draw something
naturally with his/her gestures.
This gesture interface recognizes the user’s ges-
ture from a combination of their upper body posture
and hand shape. For this recognition process, we use
a Kinect sensor to measure the user as color and depth
images. For posture recognition, we use the skeleton
tracker implemented by OpenNI library(OpenNI or-
CooperativeGestureRecognition-LearningCharacteristicsofClassifiersandNavigatingtheUsertoanIdealSituation
213

(a) Input 3D depth data (b) Result of plane fitting
Figure 4: Example of hand fitting.
ganization, 2010). For hand shape recognition, we
implemented the following four–step algorithm:
1. Find the hand regions on color and depth im-
ages by using the skeleton information obtained
by OpenNI library.
2. Convert the 3D points of the hand into a normal-
ized 2D image. To remove the wrist area, and also
to analyze the hand shape, we find a plane that
corresponds to the palm of the hand. We use the
RANSAC algorithm(Fischler and Bolles, 1981) to
find this plane. Figure 4 shows an example of the
input 3D points around the hand region, and the
obtained hand plane. We also use principal com-
ponent analysis for the points onto the plane to
find the hand orientation and its size. Using these
orientation and size parameters, we projected 3D
points to the normalized 2D image plane.
3. Count the number of fingertips. This is done by
a simple template matching algorithm on the nor-
malized 2D image.
4. Classify the hand shape. This process is achieved
by using the number of the fingertips and the dis-
tribution of the 3D points.
As mentioned in Section 3, our scheme can help to
improve the recognition performance if the condition
space contains “easy” and “difficult” regions. The im-
provement does not depend on the performance of a
recognition algorithm. Therefore, a simple algorithm
such as our prototype system is sufficient for the eval-
uation of our proposed idea.
4.1 Estimators for Precision and Recall
We built estimators of precision and recall, as we
mentioned in Section 3.1. For simplicity, this study
focuses on recognition of hand shape only.
First, we categorized possible gestures into three
classes according to the hand’s shape: “opened hand”
shape as C
A
, “pointing hand” shape as C
B
, and other
shapes as C
Z
. Simultaneously, we assumed that target
gestures interface uses three binary classifiers: F
A
, F
B
,
and F
Z
.
Then, we defined the condition vector with the fol-
lowing parameters: user’s forearm direction, 3D po-
sition of hands, 3D position of feet, speed of hand
Table 2: Training dataset.
Outputs of
classifiers
Number of training samples
#A 8033 #B 8086 #Z 8799
F
A
(s)
A #T P
A
6717 #FP
A
180 #FP
A
702
¯
A #FN
A
1316 #T N
A
7906 #T N
A
8097
F
B
(s)
B #FP
B
200 #T P
B
4812 #FP
B
697
¯
B #T N
B
7833 #FN
B
3274 #T N
B
8102
movement, and depth image quality. For the last
parameter, we estimated the image quality from the
number of pixels where the distance is not acquired
by the Kinect sensor. For other parameters, we use
the skeleton information obtained by OpenNI library.
Using this condition vector and corresponding
condition space, we captured in a total of 15 min data
sequences from four participants. Then, we collected
about 24,000 training samples, which consisted of a
pair of condition vectors, label of gesture, and out-
puts of classifiers. Table 2 shows the details of them.
Note that to acquire the samples is not an onerous
task. For example, to acquire the samples labeled ges-
ture C
A
, we just asked the participants to use the tar-
get gesture-interface freely while keeping an “opened
hand”. Then, we recorded a pair of condition vec-
tors of the participants and output of the classifiers at
the same time, e.g., when the classifier F
A
outputs A,
we automatically assign T P
A
for its sample. Using
this method, we can easily prepare a huge number of
training-sets and labels. No tedious tasks, like anno-
tations by human hand, are required.
Then, we built the estimators for precision and re-
call. To reduce the computational cost for real-time
processing, we used a support vector machine (SVM)
for approximation. First, suppose you have a classi-
fier F
A
. The goal is to decompose the condition space
into two areas: where F
A
works accurately, and where
F
A
works inaccurately. When the actual gesture is A,
the outputs of F
A
are grouped into two categories: TP
or FN, where TP means recognized as A correctly, and
TN means the gesture is misrecognized as C
B
or C
Z
.
We use the SVM to find the hyperplane that separates
these TP and FN categories for C
A
when the actual
gesture is A. Using this hyperplane, we assume that
if the condition vector is more on the TP side, the ra-
tio of
#T P
#FN+#TP
will increase. In other words, we can
substitute the signed distance from the hyper-plane as
the recall R
A
of F
A
. Similarly, we can build a total
of four hyper-planes for F
A
: TP–FN and TP–FN for
actual gesture A, and TN–FP and TN–FN for actual
gesture
¯
A. These correspond to four estimators: R
A
and R
¯
A
for recall, and P
A
and P
¯
A
for precision.
As an evaluation of this approximation, we mea-
sured the histograms of TP, TN, FP, and FN in-
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
214

0
50
100
150
200
-3 -2 -1 0 1 2 3
0
0.2
0.4
0.6
0.8
1
Frequency
P
A
Distance
FP
A
TP
A
P
A
(a) P
A
0
50
100
150
200
-3 -2 -1 0 1 2 3
0
0.2
0.4
0.6
0.8
1
Frequency
P
A
-
Distance
FN
A
TN
A
P
A
-
(b) P
¯
A
0
50
100
150
200
-3 -2 -1 0 1 2 3
0
0.2
0.4
0.6
0.8
1
Frequency
R
A
Distance
FP
A
TP
A
R
A
(c) R
A
0
50
100
150
200
-3 -2 -1 0 1 2 3
0
0.2
0.4
0.6
0.8
1
Frequency
R
A
-
Distance
FN
A
TN
A
R
A
-
(d) R
¯
A
Figure 5: Learning results of gesture A: each graph shows
the relation between P or R and the histogram of TP, FP,
TN, and FN.
0
50
100
150
200
-3 -2 -1 0 1 2 3
0
0.2
0.4
0.6
0.8
1
Frequency
P
B
Distance
FP
B
TP
B
P
B
(a) P
B
0
50
100
150
200
-3 -2 -1 0 1 2 3
0
0.2
0.4
0.6
0.8
1
Frequency
P
B
-
Distance
FN
B
TN
B
P
B
-
(b) P
¯
B
0
50
100
150
200
-3 -2 -1 0 1 2 3
0
0.2
0.4
0.6
0.8
1
Frequency
R
B
Distance
FP
B
TP
B
R
B
(c) R
B
0
50
100
150
200
-3 -2 -1 0 1 2 3
0
0.2
0.4
0.6
0.8
1
Frequency
R
B
-
Distance
FN
B
TN
B
R
B
-
(d) R
¯
B
Figure 6: Learning results of gesture B: each graph shows
the relation between P or R and the histogram of TP, FP,
TN, and FN.
stances and corresponding estimated recall and pre-
cision. Figure 5 shows the result of F
A
and Figure 6
shows the result of F
B
. In these figures, the x-axis is
a signed distance between the SVM’s hyperplane and
data sample. In the figure 5a, the red bar shows a his-
togram of #FP
A
, and the green bar shows a histogram
of #T P
A
, while the blue line is the ratio of each pair of
red and green bars. This ratio means P
A
at the signed
distance. As the figure 5a shows, the SVM separates
the condition space into FP
A
and TP
A
regions, and P
A
becomes higher as the signed distance becomes big-
ger. The same relationships are confirmed in the other
categories
¯
A, B, and
¯
B, and other classifiers F
B
.
Using these relationships, we confirm that we can
estimate P and R only from the signed distance of the
condition vector. As an additional evaluation result,
Figure 7 shows the relationship between the estimated
recall and its input depth images. It shows that as
the estimated recall decreases, the undesirable factors,
such as noise and self-occlusion, appears frequently.
These results show that our approximation ap-
proach is practicable and valid.
4.2 Visual Feedback to the User
As feedback for navigating the user to a desirable
condition, we implement a symbol-based feedback.
First, we prepare feedback candidates; each candi-
date is a pair of user’s actions to improve the con-
dition, and corresponding symbols that can navigate
the user to do the action. Figure 8 shows some sam-
ples of the symbols. Frame #2822 of Figure 8 shows
a feedback that navigates the user to change the ori-
entation of his/her fingertips. Frame #3096 of Figure
8 shows another feedback that navigates the user to
move to his/her right side. These arrow-shaped object
R
A
≈ 0.1 R
A
≈ 0.3 R
A
≈ 0.5 R
A
≈ 0.7 R
A
≈ 0.9
R
B
≈ 0.1 R
B
≈ 0.3 R
B
≈ 0.5 R
B
≈ 0.7 R
B
≈ 0.9
Figure 7: Example of recall estimation: this figure shows captured depth images sorted by R
A
(top) and R
B
(bottom). As the
R
A
or R
B
increases, the image errors, such as pixel noise and self-occlusions, drastically reduce.
CooperativeGestureRecognition-LearningCharacteristicsofClassifiersandNavigatingtheUsertoanIdealSituation
215
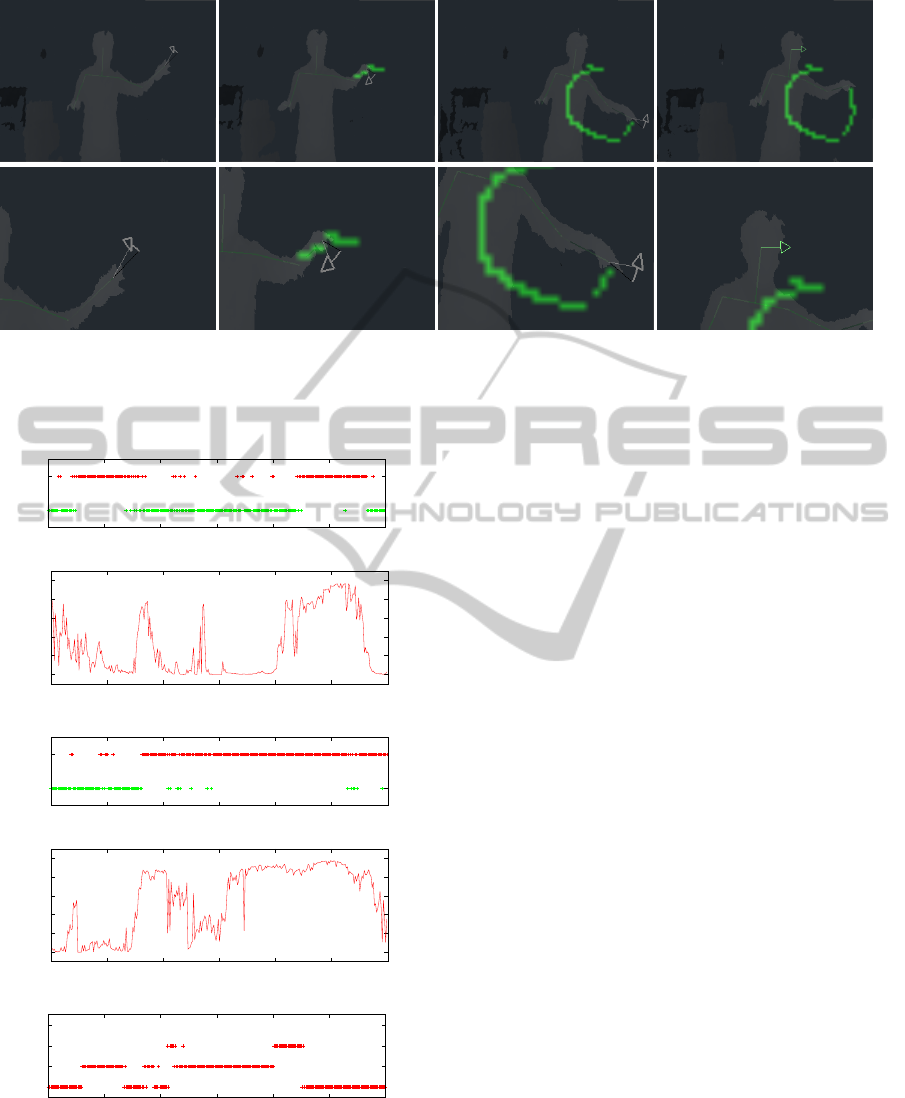
Frame #2822 Frame #2937 Frame #3070 Frame #3096
Figure 8: Screen-shots of experiment system: (top) screen-shots; (bottom) zoom-up images round the feedback.
are overlaid on the silhouette of the user in real-time.
FN
TP
500 550 600 650 700 750 800
Output of F
A
(s)
Frame
0
0.2
0.4
0.6
0.8
1
500 550 600 650 700 750 800
R
A
(s)
Frame
(a) No feedback
FN
TP
500 550 600 650 700 750 800
Output of F
A
(s)
Frame
0
0.2
0.4
0.6
0.8
1
500 550 600 650 700 750 800
R
A
(s)
Frame
(b) With feedback (proposed)
Up hand
Down hand
Move left
Move right
500 550 600 650 700 750 800
Frame
(c) Displayed symbols for feedback
Figure 9: Estimated recall and the classified results: (a)
without the feedback, the situation sometimes falls into a
“bad” condition, where the estimated recall R
A
becomes
low, and the classifier outputs wrong results. (b) with the
feedback, our navigation can retain a “good” condition,
where the classifier outputs correct results.
The user can look at this interface as a mirror;
seeing himself/herself naturally from this silhouette,
and easily understand that the meaning of the arrow-
shaped object is the direction and amount of required
action.
4.3 Evaluation of Recognition
Performance and Usability
In experiments, we focused on the interval during
which the participant uses gesture A, and recorded the
estimated recall R
A
(s) and precision P
A
(s), and the ac-
tual accuracy of the classifier’s output F
A
(s).
We prepared four symbol-based feedbacks for the
navigation: move a hand upward/downward, and take
one step to the left/right. These feedbacks are synthe-
sized as the arrow-shaped objects, as shown in Figure
8. We asked three participants to use our experimen-
tal gesture interface and recorded the data sequences
for approximately 15 min.
First, we compared the influence of our feedback
on these values. Figure 9a shows the recorded se-
quence in the case without feedback. This is 300
frames (10 seconds) sequence. The above red-graph
shows the time sequence of R
A
(s). As this graph
shows, the value of R
A
(s) changes dynamically. This
means that the condition vector s is drastically varying
between ideal and undesirable conditions. As a result,
the recognition result of F
A
also varies between accu-
rate (labeled as TP) and inaccurate (labeled as FN). In
contrast, with our visual feedback, the performance
was improved. Figure 9b shows the case with feed-
back, and Figure 9c shows the displayed symbols for
the feedback. The graph shows that the estimated re-
call R
A
(s) with feedback is higher than without feed-
back, and the recognition result F
A
(s) retains an accu-
rate (TP) output.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
216

0
100
200
300
400
500
600
700
800
900
0 0.2 0.4 0.6 0.8 1
Frequency
R
A
, P
A
P
A
R
A
Figure 10: Histogram of R
A
and P
A
, without user naviga-
tion.
0
200
400
600
800
1000
1200
1400
0 0.2 0.4 0.6 0.8 1
Frequency
R
A
, P
A
P
A
R
A
Figure 11: Histogram of R
A
and P
A
, with user navigation.
Table 3: Performance of F
A
.
Precision Recall
No feedback 0.59 0.70
With feedback (proposed) 0.61 0.88
We compared the histograms of R
A
and P
A
dur-
ing the experiments. Figures 10 and 11 show the
cases without and with feedback, respectively. Com-
paring those two histograms, these results show that
our feedback scheme can improve situation in terms
of R
A
(s).
We also evaluated how our approach can improve
the actual performance. Table 3 shows the actual re-
call and precision through the experiments. In this
experiment, we use visual feedback to navigate the
participant mainly for increasing the estimated recall.
As a result, the recall is improved from 0.70 to 0.88,
while precision remains unchanged. This means that
our proposed scheme can predict the ideal situation
in terms of recall and navigate the user to the ideal
situation.
From these results, we demonstrate that our coop-
erative recognition scheme is practicable and efficient
in increasing the accuracy of gesture recognition.
4.4 Discussion
The above experiments support our assumption men-
tioned in Section 3: the system performance in the
neighbor of a ”condition” is similar to the system per-
formance of the ”condition”. By the symbol-based
feedback method, we get better performance when
getting further in the direction of the ”easy” condi-
tion.
As far as the above assumption holds, our scheme
can be applied to a wide variety of recognition sys-
tems, because we do not need to change the inside of
a system. Our scheme also gives the users the know-
how for using a system, i.e., how to use a system with
good performance, and it also saves the user’s time
of trial and error for learning how to use the system.
We believe that this scheme can greatly increase the
usability of the gesture interface.
5 CONCLUSION
This paper proposed a cooperative gesture recogni-
tion scheme for a gesture-based user interface, which
navigates the user towards making gesture recogni-
tion more accurate. Our experiments showed its prac-
ticability and effectiveness.
We plan to apply and evaluate our gesture recogni-
tion scheme with different types of gesture interfaces
in the future.
ACKNOWLEDGMENTS
This work was supported in part by the JST-CREST
project “Creation of Human-Harmonized Information
Technology for Convivial Society.”
REFERENCES
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: a paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Commun. ACM, 24(6):381–395.
Jacko, J. A. and Sears, A., editors (2003). The
Human-computer Interaction Handbook: Fundamen-
tals, Evolving Technologies and Emerging Applica-
tions. L. Erlbaum Associates Inc., Hillsdale, NJ, USA.
Moeslund, T. B. and Granum, E. (2001). A survey of com-
puter vision–based human motion capture. Computer
Vision and Image Understanding: CVIU, 81(3):231–
268.
Moeslund, T. B., Hilton, A., and Kr
¨
uger, V. (2006). A
survey of advances in vision-based human motion
capture and analysis. Comput. Vis. Image Underst.,
104(2):90–126.
Nielsen, J. (2009). Ten usability heuristics. http://
www.nngroup.com/articles/ten-usability-heuristics/.
OpenNI organization (2010). OpenNI User Guide. OpenNI
organization.
Pavlovic, V. I., Sharma, R., and Huang, T. S. (1997). Visual
interpretation of hand gestures for human-computer
CooperativeGestureRecognition-LearningCharacteristicsofClassifiersandNavigatingtheUsertoanIdealSituation
217

interaction: A review. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 19:677–695.
PrimeSense Inc. (2010). Prime Sensor
TM
NITE 1.3 Algo-
rithms notes. PrimeSense Inc.
Ren, Z., Yuan, J., Meng, J., and Zhang, Z. (2013). Robust
part-based hand gesture recognition using kinect sen-
sor. Multimedia, IEEE Transactions on, 15(5):1110–
1120.
Shotton, J. and Sharp, T. (2011). Real-time human pose
recognition in parts from single depth images. IEEE
Conference on Computer Vision and Pattern Recogni-
tion (2011), 2(3):1297–1304.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
218
