
Two-way Multimodal Online Matrix Factorization for Multi-label
Annotation
Jorge A. Vanegas, Viviana Beltran and Fabio A. Gonz´alez
MindLab Research Group, Universidad Nacional de Colombia, Avenida Carrera 30 # 45, Bogot´a, Colombia
Keywords:
Machine Learning, Multi-label Annotation, Semantic Embedding, Online Learning.
Abstract:
This paper presents a matrix factorization algorithm for multi-label annotation. The multi-label annotation
problem arises in situations such as object recognition in images where we want to automatically find the
objects present in a given image. The solution consists in learning a classification model able to assign one
or many labels to a particular sample. The method presented in this paper learns a mapping between the
features of the input sample and the labels, which is later used to predict labels for unannotated instances.
The mapping between the feature representation and the labels is found by learning a common semantic
representation using matrix factorization. An important characteristic of the proposed algorithm is its online
formulation based on stochastic gradient descent which can scale to deal with large datasets. According to the
experimental evaluation, which compares the method with state-of-the-art space embedding algorithms, the
proposed method presents a competitive performance improving, in some cases, previously reported results.
1 INTRODUCTION
Multi-label annotation has been an active research
area in the last years due to its potential impact in an
increasing number of new applications such as music
categorization (Trohidis et al., 2008), functional ge-
nomics (Zhang and Zhou, 2006), video content anal-
ysis (Wang et al., 2008), noise detection (Qi et al.,
2012), image understanding (Wu et al., 2010) and
image search (Siddiquie et al., 2011), among oth-
ers (Tsoumakas and Katakis, 2007). The problem
of multi-label annotation (or classification) refers to
the problem where a single instance can be simul-
taneously assigned to multiple classes. This differs
from multi-class classification where each sample is
assigned to only one class. It means that, in multi-
class classification, classes are assumed mutually ex-
clusive, but in multi-label classification classes are of-
ten correlated.
A common approach to address multi-label an-
notation is to handle this problem as a conventional
classification problem, i.e., multiples classifiers are
trained, and only one binary classifier is used per la-
bel. In this way a new instance is annotated by in-
dependently applying the set of classifiers. Due to
the fact that one classifier is required for each label,
this approach may not scale well when there is a large
number of labels.
An alternative to dealing with large number of la-
bels is to find a compact representation of them using
a dimensionality reduction method. This approach is
followed by multi-label latent space embedding meth-
ods which have shown competitive results.
In this paper we describe a method for multi-label
annotation based on semantic embedding. The pro-
posed method finds a common semantic space for the
original features representation of an instance and its
corresponding labels to model a direct mapping be-
tween the feature representation and annotation la-
bels. An important characteristic of the proposed
method is its formulation as an online learning algo-
rithm based on stochastic gradient decent, which al-
lows it to deal with large collections of data, achiev-
ing a significantly reduction in memory requirements
and computational load.
The rest of this paper is organized as follows: Sec-
tion 2 discusses the related work; Section 3 presents
the details of the proposed multi-label annotation
method; Section 4 presents the experimental evalua-
tion; and, finally, Section 5 presents some concluding
remarks.
2 RELATED WORK
An alternativeapproach to solve the problem of multi-
279
Vanegas J., Beltran V. and A. González F..
Two-way Multimodal Online Matrix Factorization for Multi-label Annotation.
DOI: 10.5220/0005209602790285
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 279-285
ISBN: 978-989-758-076-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

label annotation is known as multi-label latent space
embedding (MLLSE) which finds a transformation
that maps labels into a reduced label space. The pur-
pose of this embedding is to find correlated informa-
tion in the original data, that helps to remove irrel-
evant, redundant or noisy features, and at the same
time to reduce the computational complexity of the
learning algorithms. The problem of finding a latent
space have been approached by following different
strategies like Canonical Correlation Analysis (CCA)
(Sun et al., 2011), Principal Label Space Transform
(PLST) (Tai and Lin, 2012), Compressed Sensing
(CS)(Hsu et al., 2009) and Nonnegative Matrix Fac-
torization (NMF) (Caicedo et al., 2012; Akata et al.,
2011).
There are several methods based on NMF. For in-
stance, Caicedo et al. propose two alternatives to con-
struct a common semantic space: asymmetric NMF
(ANMF) and mixed NMF (MNMF) which differ in
that in the asymmetric version the construction of
the semantic space is reinforced by the most reliable
modality. As another example, Akata et al. (Akata
et al., 2011) proposed a joint non-negativematrix fac-
torization to find common latent components.
Unfortunately most of the methods based on latent
space embedding have been designed without taking
into account scalability considerations for handling
large-scale data. There are some works that consider
a large-scale setup in the formulation of the models:
for instance, Hsan et al. (Tsai et al., 2011) propose
a reformulation of the basic algorithm called MCR
(Multi-stage Convex Relaxation) to make it suitable
for large scale collections, in a way that makes it
possible to achieve a significant reduction in learning
time and in the amount of required storage by reduc-
ing the dimensionality of some intermediate matrices.
There are other works that seek to achieve scal-
ability by using an online formulation. For in-
stance, Weston et al. (Weston et al., 2010) that
learns to represent images and annotations jointly in
a low-dimensional embedding space, using stochas-
tic gradient descent (SGD). In a similar way, Otalora-
Montenegro et al. (Ot´alora-Montenegro et al., 2013)
proposed a multi-label method based on an online
multimodal matrix factorization (OMMF) algorithm
based on SGD.
The algorithm presented in this paper, called Two-
way Multimodal Matrix Factorization (TWMMF) is a
multi-label latent space embedding method based on
a stochastic gradient descent approach, which makes
the algorithm suitable for large scale learning prob-
lems. An important characteristic of the method is
that, unlike other general matrix factorization meth-
ods which only learn the transformation from the
semantic space to the original data, the proposed
method also learns a mapping from the original rep-
resentation space to the semantic space. Other matrix
factorization methods require an extra effort to find
the projection to the semantic space.
3 TWO-WAY MULTIMODAL
MATRIX FACTORIZATION
If we describe the feature representation of an in-
stance as an n−dimensional vector, we can represent
the entire collection by a matrix X
v
∈ R
n×l
, where l is
the number of elements. In the same way we can rep-
resent the labels associated to an specific instance by
an m−dimensional binary indicator vector, where m
is the total number of possible labels, and in the j−th
position in the vector we have a value of 1 if the j−th
label is assigned to the image or 0 otherwise. So, we
can construct a label indicator matrix X
t
∈ R
m×l
.
In this paper we propose a model that finds a
mapping F : R
n
→ R
r
, from the sample representa-
tion space to a semantic space, and simultaneously
finds a back-projection from the semantic space to
the original space G : R
r
→ R
n
, where n ≫ r. So we
want to find two linear transformations what allows
to project the original data representation to a lower-
dimensional space (semantic representation) and at
the same time learns to reconstruct from this lower-
dimensional representation the original data.
If we assume that both F and G are linear map-
pings with coefficients W
v
and W
′
v
respectively, for an
entire collection we want to find a reconstruction of
the original feature representation as follows:
X
v
≈ W
′
v
W
v
X
v
(1)
where W
v
∈ R
r×n
is an encoder matrix that
projects the original representation to a lower-
dimensional semantic space and W
′
v
∈ R
n×r
is a de-
coder matrix that reconstructs the original data. In the
same way for the label information, we have:
X
t
≈ W
′
t
W
t
X
t
(2)
where W
t
∈ R
r×m
, W
′
t
∈ R
m×r
are the encoder
and decoder matrices for the label information respec-
tively.
Our main purpose is to learn a mapping between
the original features and label information. Therefore,
we also seek that the previoustransformation matrices
also satisfy the following condition:
X
t
≈ W
′
t
W
v
X
v
(3)
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
280

This condition forces both the original represen-
tation and the label representation to share the same
semantic space and defines a mapping between both
representations.
Finally, we can formulate this problem as an op-
timization problem by minimizing the following loss
function:
L
X
v
, X
t
,W
v
,W
′
v
,W
t
,W
′
t
= α
X
v
−W
′
v
W
v
X
v
2
F
+(1−α)
X
t
−W
′
t
W
t
X
t
2
F
+δ
X
t
−W
′
t
W
v
X
v
2
F
+β
kW
v
k
2
F
+
W
′
v
2
F
+ kW
t
k
2
F
+
W
′
t
2
F
(4)
where α controls the relative importance between
the reconstruction of the instance representation and
the label representation, δ controls the relative im-
portance of the mapping between instance features
and label information and β controls the relative im-
portance of the regularization terms, which penalizes
large values for the Frobenius norm of the transfor-
mation matrices.
3.1 Gradient Descent Solution
The problem above has a non-convex objective func-
tion (eq. 4). However, this function is differentiable
for all the unknown parameters and the solution can
be computed using a gradient descent approach:
θ
(τ+1)
= θ
(τ)
− γ
(τ)
∇L
θ
(τ)
(5)
where γ
τ
is the step-size in the τ-th iteration used
to update each parameter θ and the gradients of the
loss function for each parameter in the model are as
follows:
∇
W
′
v
L = −2α
X
v
−W
′
v
W
v
X
v
X
T
v
W
T
v
+2βW
′
v
(6)
∇
W
v
L = −2αW
′
v
X
v
−W
′
v
W
v
X
v
X
T
v
−2δW
′
t
X
t
−W
′
t
W
v
X
v
X
T
v
+ 2βW
v
(7)
∇
W
′
t
L = −2(1− α)
X
t
−W
′
t
W
t
X
t
X
T
t
W
T
t
−2δ
X
t
−W
′
t
W
v
X
v
X
T
v
W
T
v
+ 2βW
′
t
(8)
∇
W
t
L = −2(1− α)W
′
t
X
t
−W
′
t
W
t
X
t
X
T
t
+2βW
t
(9)
3.2 Online Formulation
The previous subsection presents a strategy to find the
coding and decoding matrices by using a gradient de-
scent approach. Unfortunately, this strategy by itself
is not suitable for large scale data sets, due to the fact
that its formulation has high memory requirements,
since all training samples in the dataset are required
in each iteration. For this reason, we want to refor-
mulate the problem using an online learning approach
based on stochastic approximations. The main idea of
online learning based on a stochastic approximationis
to update the solution using a single training sample
at a time. In this way, we can scan the whole dataset
with low memory requirements. Following this ap-
proach, the final updating rules only depend on the
τ-th sample (x
(τ)
v
, x
(τ)
t
, visual and text features for the
τ-th image) an the corresponding gradient functions
are as follows.
∇
W
′
v
L
(τ)
= −2α
x
(τ)
v
−W
′
(τ)
v
W
(τ)
v
x
(τ)
v
x
(τ)T
v
W
(τ)T
v
+2βW
′
(τ)
v
(10)
∇
W
v
L
(τ)
= −2αW
′
(τ)
v
x
(τ)
v
−W
′
(τ)
v
W
(τ)
v
x
(τ)
v
x
(τ)T
v
−2δW
′
(τ)
t
x
(τ)
t
−W
′
(τ)
t
W
(τ)
v
x
(τ)
v
x
(τ)T
v
+2βW
(τ)
v
(11)
∇
W
′
t
L
(τ)
= −2(1− α)
x
(τ)
t
−W
′
(τ)
t
W
(τ)
t
x
t
x
T
t
W
T
t
−2δ
x
t
−W
′
t
W
v
x
v
x
(τ)T
v
W
T
v
+ 2βW
′
t
(12)
∇
W
v
L
(τ)
= −2(1− α)W
′
(τ)
t
x
(τ)
t
−W
′
(τ)
t
W
(τ)
t
x
t
x
(τ)T
t
+2βW
(τ)
t
(13)
where x
(τ)
v
and x
(τ)
t
are vectors of features and la-
bel representation, respectively, for one instance. But
also, this method can be generalized by using several
samples grouped in mini-batches, this helps to a faster
execution and numerical stability (Cotter et al., 2011).
3.2.1 Adaptive Step-size
A potential problem with gradient descent is that it
might get stuck in a local minima. We can alleviate
this problem by the inclusion of a momentum term
(Rumelhart et al., 1986). The main idea about us-
ing momentum is to stabilize the parameter change
by making non-radical updates using a combination
Two-wayMultimodalOnlineMatrixFactorizationforMulti-labelAnnotation
281

of the previous update and the gradient. So in this
way the original update term:
△W
(τ)
= −γ
(τ)
∇
W
L
θ
(τ)
(14)
takes the form:
△W
(τ)
= −γ
(τ)
∇
W
L
θ
(τ)
+ p△W
(τ−1)
(15)
where p is the momentum parameter which tries
to preserve a portion of the previous update.
3.2.2 Online Learning Algorithm
The final algorithm for learning process (Algorithm 1)
is as follows: starts by a random initialization of the
transformation matrices, and for each iteration a mini-
batch of instances with its corresponding features and
label representation are randomly sampled from the
training set, then, the gradients of the lost function are
calculated for each transformation matrix (the gradi-
ent of the lost functions is calculated by taking into
account only the current observations), and the new
transformation matrices are calculated by using the
update terms based on momentum. Finally, the al-
gorithm ends when a predefined maximum number of
epochs is reached.
3.3 Prediction
Once the parameters have been learned (coding and
decoding matrices) we can use this model to predict
the label representation ˜x
t
from de feature representa-
tion x
v
of a new unannotated sample, as follows:
˜x
t
= W
′
t
W
v
x
v
(16)
The transformation of the input features generates an
m−dimensional vector with an smoothed label rep-
resentation, which can be interpreted as a probabil-
ity distribution which denotes the probability that the
j − th label is assigned to an instance. The final
decision to assign a label would be taken by defin-
ing a threshold, so we assign 1 to the j − th label if
˜x
t, j
≧ threshold, or we can assign 1 to the top−k la-
bels with the highest values in the vector.
3.4 Implementation Details
We used the Pylearn2 library (Goodfellow et al.,
2013) the proposed method. This is a machine learn-
ing research library built on top of Theano (Bergstra
et al., 2010) that facilitates the use of the GPU in a
transparent way. Its emphasis on modularity allows
us the reuse of code components and there is almost
no restrictions on their use. Furthermore, it provides
Algorithm 1: Two-way multimodal online matrix factor-
ization algorithm for learning state.
input r:latent space size, γ
0
: initial step size, epochs: num-
ber of epochs, X
v
∈ R
n×l
, X
t
∈ R
m×l
, α, δ, β
Random initialization of transformation matrices:
W
′
(0)
v
= random
matrix(r, n)
W
(0)
v
= random
matrix(n, r)
W
′
(0)
t
= random
matrix(r, m)
W
(0)
t
= random
matrix(m,r)
for i = 1 to epochs do
for j = 1 to l do
τ = i× j
x
(τ)
v
, x
(τ)
t
← sample
without replacement(X
v
, X
t
)
Compute gradients:
g
(τ)
W
′
v
= ∇
W
′
v
L
x
(τ)
v
, x
(τ)
t
,W
(τ)
v
,W
′
(τ)
v
,W
(τ)
t
,W
′
(τ)
t
g
(τ)
W
v
= ∇
W
v
L
x
(τ)
v
, x
(τ)
t
,W
(τ)
v
,W
′
(τ)
v
,W
(τ)
t
,W
′
(τ)
t
g
(τ)
W
′
t
= ∇
W
′
t
L
x
(τ)
v
, x
(τ)
t
,W
(τ)
v
,W
′
(τ)
v
,W
(τ)
t
,W
′
(τ)
t
g
(τ)
W
t
= ∇
W
t
L
x
(τ)
v
, x
(τ)
t
,W
(τ)
v
,W
′
(τ)
v
,W
(τ)
t
,W
′
(τ)
t
Update term calculation using momentum:
△W
′
(τ)
v
= −γ
(τ)
g
(τ)
W
′
v
+ p△W
′
(τ−1)
v
△W
(τ)
v
= −γ
(τ)
g
(τ)
W
v
+ p△W
(τ−1)
v
△W
′
(τ)
t
= −γ
(τ)
g
(τ)
W
′
t
+ p△W
′
(τ−1)
t
△W
(τ)
t
= −γ
(τ)
g
(τ)
W
t
+ p△W
(τ−1)
t
Update transformation matrices:
W
′
(τ+1)
v
= W
′
(τ)
v
+ △W
′
(τ)
v
W
(τ+1)
v
= W
(τ)
v
+ △W
(τ)
v
W
′
(τ+1)
t
= W
′
(τ)
t
+ ∆W
′
(τ)
t
W
(τ+1)
t
= W
(τ)
t
+ ∆W
(τ)
t
end for
end for
returnW
′
(N)
v
,W
(N)
v
,W
′
(N)
t
,W
(N)
t
a way of specifying all parameters for a specific and
complete experiment without exposing any specific
implementation details. It can be done by using the
YAML language. Two of the main advantages of us-
ing Theano and pylearn2 are: first, it allows to spec-
ify our models symbolically and the library optimizes
the code for both CPU and GPU. Second, that we can
change the objective function anytime we want and
compute the gradients in an easy way.
Due to these facilities, this is a convenient library
to test our method, mainly, due to the improvement
in resource management in GPU and CPU, but also,
to the fact that our method is trained with gradient
descent algorithm. This help us to test our method in
a large scale context.
As it was mentioned above, we use the library
pylearn2 to take advantage of the computation and
use of resources using a GPU. Table 1 shows the to-
tal execution time for some parameter configurations
using the GPU and the CPU. The reported time in-
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
282
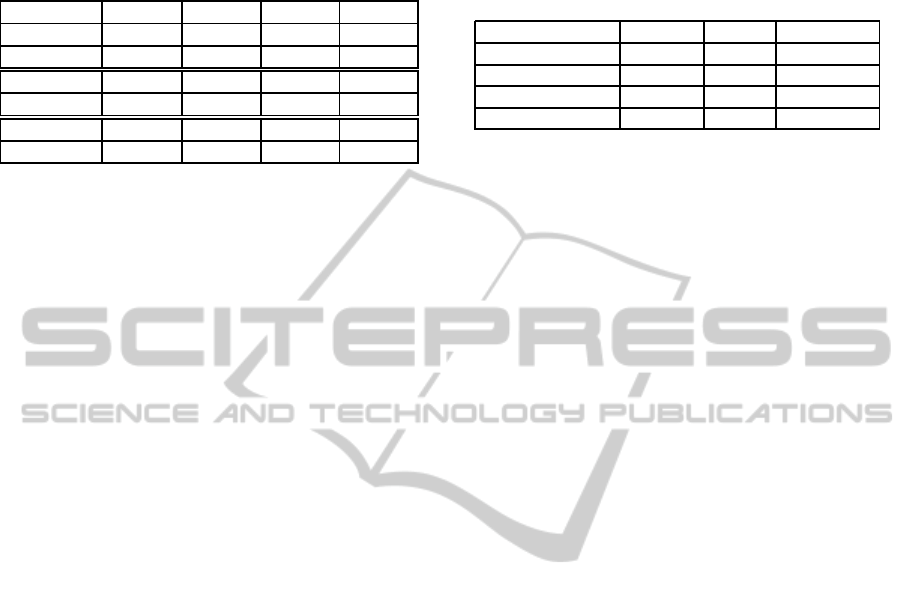
Table 1: Execution time using GPU and CPU to run 120, 15
and 1 epochs using the library pylearn2. Execution time ex-
ecution includes loading time for the dataset, training time
and evaluation of the performance with f-score measure.
Dataset Epochs 120 15 1
Corel GPU 0:19:40 0:01:15 0:00:45
CPU 0:42:47 0:02:43 0:00:47
Bibtex GPU 0:40:56 0:01:40 0:01:22
CPU 2:08:47 0:06:39 0:01:45
MediaMill GPU 0:54:58 0:07:06 0:03:21
CPU 4:33:19 0:18:18 0:04:20
cludes loading time for the dataset, training time and
evaluation of the performance with f-score measure.
The time reported shows that even when running
few epochs, the total execution time is less using
GPU than CPU. When running much more epochs
and when the dataset gets bigger, the reduction in time
becomes much more significant. To perform the pa-
rameter exploration,this is very useful, due to the fact,
that we have to explore more than seven parameters to
obtain the best results.
4 EXPERIMENTS AND RESULTS
The objective of this section is to evaluate the perfor-
mance of the proposed algorithm in different multi-
label annotation task. The performance of the pro-
posed algorithm is compared with several baselines
using 3 standard multi-label datasets with different
sizes and different dimension for features represen-
tation.
4.1 Experimental setup
In order to compare our method, we used the same
experimental setup as in (Ot´alora-Montenegro et al.,
2013), i.e. we use 80% of the images for training and
the remaining 20% for test. Results were compared
against 8 MLLSE algorithms (OVA, CCA, CS, PLST,
MME, ANMF, MNMF, OMMF).
The proposed method has a set of parameters that
impact the quality of the resulting model. These pa-
rameters were experimentally tuned by using a ran-
dom 5-fold cross validation in the training set. We
have two parameters that control the importance of
the two different modalities in our method and a third
parameter that controls the relative importance of the
regularization terms. These first two parameters are
α and δ. The parameter α controls the relative im-
portance of the modalities in an independent way. It
showed to have low values for the visual modality and
high values for the textual modality. The parameter δ
Table 2: Selected datasets to evaluate our method. The char-
acteristics described in the table are: total number of possi-
ble labels (Labels), features dimensionality (Features), av-
erage number of labels per instance (Label cardinality) and
total number of instances in the dataset (Examples).
Dataset Corel5k Bibtex MediaMill
Labels 374 159 101
Features 500 1,836 120
Label cardinality 3,522 2,402 4.376
Examples 5,000 7,395 43,907
controls the relative importance of the mapping be-
tween instance features and label information and it
showed to have high values. This setup, shows how
the annotation task is favored, by one hand, giving
more importance to the textual modality (label repre-
sentation) and second, by imposing a strong indepen-
dence between the modalities.
4.2 Datasets
The method was evaluated in three standard multi-
label and publicly available datasets with different
sizes (Corel5k, Bibtex and MediaMill) that have been
used in previous works using F1 score to evaluate the
annotation performance. The datasets are distributed
by the Mulan framework authors (Tsoumakas et al.,
2011). Table 2 summarizes the main characteristics
of these datasets.
Corel 5k is widely used in keyword based im-
age retrieval and image annotation tasks. It contains
around 5000 images manually annotated with 1 to 5
keywords. A standard set of 499 images are used as
test, and the rest is used for training. The vocabulary
contains 374 words.
Bibtex contains 7395 bibtex entries that have been
tagged by users of a social network using 159 tags.
Each bibtex entry contains a small set of textual ele-
ments representing the author, the title, and the con-
ference or journal name. The text is represented as
bag-of-words, with a feature space with dimensional-
ity equal to 1836.
MediaMill consists of patterns about multimedia
files. It dataset includes 43907 sub-shots with 101
classes, where each image is characterized by a 120-
dimensional vector.
4.3 Annotation Performance
We used a threshold strategy to evaluate the per-
formance of our method in the same way as is de-
scribed in (Ot´alora-Montenegro et al., 2013). This
is, we assign 1 to the label j of the instance x
n
if
x
nj
> threshold.
Two-wayMultimodalOnlineMatrixFactorizationforMulti-labelAnnotation
283

Table 3: F-Measure for each method. The best performance
for each dataset, is presented in bold. values in parentheses
are the dimension of the generated embedding space.
Method Corel5k Bibtex MediaMill
OVA 0.112 0.372
CCA 0.150 0.404
CS 0.086 (50) 0.332 (50)
PLST 0.074 (50) 0.283 (50)
MME 0.178 (50) 0.403 (50) 0.199 (350)
ANMF 0.210 (30) 0.297 (140) 0.496 (350)
MNMF 0.240 (35) 0.376 (140) 0.510 (350)
OMMF 0.263 (40) 0.436 (140) 0.503 (350)
Our Method 0.283 (100) 0.422 (300) 0.540 (300)
Table 4: Convergence time for the algorithm Online Ma-
trix Factorization for Space Embedding (OMMF) and our
method Two Way Online Matrix Factorization (TWOMF).
Algorithm OMMF TWOMF
Corel 00.02.30 00.09.29
Bibtex 06.02.00 00.16.60
MediaMill 88.37.55 01:08.11
We evaluated the performance of our method in
each one of the datasets, calculating the F-Measure.
Table 3 shows the results for each baseline method
and the dimension of the embedding space. In
Corel5k and MediaMill datasets, we got the best re-
sults in comparison with the other methods and in
Bibtex we got a competitive result, being surpassed
only by OMMF method.
Table 4 shows the convergence times of the al-
gorithms Online Matrix Factorization for Space Em-
bedding (OMMF) and our method in each one of the
datasets.
By Comparing our algorithm against the OMMF,
we can see gains when dealing with larger datasets. In
Corel5k that contains only 5.000 examples, the gain
in time is not better. In the case of Bibtex and Medi-
aMill, which are larger,it is evident the improvements
in time execution using our implementation, i.e., us-
ing the pylearn2 library which makes use of the GPU.
5 CONCLUSIONS AND FUTURE
WORK
In this paper we presented a novel multi-label an-
notation method which learns a mapping between
the original sample representation and labels by find-
ing a common semantic representation. The method
was compared against state-of-art latent space embed-
ding methods showing competitive results. An im-
portant characteristic of this method is that, unlike
the method proposed by Otalora-Montenegro et al.
(Ot´alora-Montenegro et al., 2013) based on OMMF,
the transformation from the semantic representation
to the label space is learned directly in the training
phase, making the annotation process very simple, re-
quiring a simple multiplication by a transformation
matrix. Finally, Another important characteristic of
this method is its ability to deal with large collections
of data, thanks to its formulation as an online learn-
ing algorithm, achieving a significantly reduction in
memory requirements and computational load.
A major limitation in this method as well as in
other multi-label latent space embedding methods is
that it is a linear model which imposes significant re-
strictions that limit its flexibility. Therefore, as a fu-
ture work it would be interesting to explore non-linear
alternatives, which allow to model more complex re-
lationships what could improve the performance in
annotation task.
ACKNOWLEDGEMENTS
This work was partially funded by project Multi-
modal Image Retrieval to Support Medical Case-
Based Scientific Literature Search, ID R1212LAC006
by Microsoft Research LACCIR and Jorge A. Vane-
gas also thanks for doctoral grant support Colciencias.
617/2013.
REFERENCES
Akata, Z., Thurau, C., and Bauckhage, C. (2011). Non-
negative matrix factorization in multimodality data for
segmentation and label prediction. In 16th Computer
Vision Winter Workshop.
Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu,
R., Desjardins, G., Turian, J., Warde-Farley, D., and
Bengio, Y. (2010). Theano: a CPU and GPU math
expression compiler. In Proceedings of the Python for
Scientific Computing Conference (SciPy). Oral Pre-
sentation.
Caicedo, J. C., BenAbdallah, J., Gonz´alez, F. A., and Nas-
raoui, O. (2012). Multimodal representation, index-
ing, automated annotation and retrieval of image col-
lections via non-negative matrix factorization. Neuro-
computing, 76(1):50–60.
Cotter, A., Shamir, O., Srebro, N., and Sridharan, K. (2011).
Better mini-batch algorithms via accelerated gradient
methods. CoRR, abs/1106.4574.
Goodfellow, I. J., Warde-Farley, D., Lamblin, P., Dumoulin,
V., Mirza, M., Pascanu, R., Bergstra, J., Bastien, F.,
and Bengio, Y. (2013). Pylearn2: a machine learning
research library. CoRR, abs/1308.4214.
Hsu, D., Kakade, S. M., Langford, J., and Zhang, T. (2009).
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
284

Multi-label prediction via compressed sensing. CoRR,
abs/0902.1284.
Ot´alora-Montenegro, S., P´erez-Rubiano, S. A., and
Gonz´alez, F. A. (2013). Online matrix factorization
for space embedding multilabel annotation. In Ruiz-
Shulcloper, J. and di Baja, G. S., editors, CIARP (1),
volume 8258 of Lecture Notes in Computer Science,
pages 343–350. Springer.
Qi, Z., Yang, M., Zhang, Z. M., and Zhang, Z. (2012). Min-
ing noisy tagging from multi-label space. In Proceed-
ings of the 21st ACM International Conference on In-
formation and Knowledge Management, CIKM ’12,
pages 1925–1929, New York, NY, USA. ACM.
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986).
Parallel distributed processing: Explorations in the
microstructure of cognition, vol. 1. In Rumelhart,
D. E., McClelland, J. L., and PDP Research Group, C.,
editors, Parallel Distributed Processing: Explorations
in the Microstructure of Cognition, Vol. 1, chapter
Learning Internal Representations by Error Propaga-
tion, pages 318–362. MIT Press, Cambridge, MA,
USA.
Siddiquie, B., Feris, R. S., and Davis, L. S. (2011). Image
ranking and retrieval based on multi-attribute queries.
In Proceedings of the 2011 IEEE Conference on Com-
puter Vision and Pattern Recognition, CVPR ’11,
pages 801–808, Washington, DC, USA. IEEE Com-
puter Society.
Sun, L., Ji, S., and Ye, J. (2011). Canonical correlation
analysis for multilabel classification: A least-squares
formulation, extensions, and analysis. IEEE Trans.
Pattern Anal. Mach. Intell., 33(1):194–200.
Tai, F. and Lin, H.-T. (2012). Multilabel classification with
principal label space transformation. Neural Comput.,
24(9):2508–2542.
Trohidis, K., Tsoumakas, G., Kalliris, G., and Vlahavas,
I. P. (2008). Multi-label classification of music into
emotions. In Bello, J. P., Chew, E., and Turnbull, D.,
editors, ISMIR, pages 325–330.
Tsai, M.-H., Wang, J., Zhang, T., Gong, Y., and Huang, T. S.
(2011). Learning semantic embedding at a large scale.
In ICIP, pages 2497–2500.
Tsoumakas, G. and Katakis, I. (2007). Multi label classi-
fication: An overview. International Journal of Data
Warehouse and Mining, 3(3):1–13.
Tsoumakas, G., Spyromitros-Xioufis, E., Vilcek, J., and
Vlahavas, I. (2011). Mulan: A java library for multi-
label learning. Journal of Machine Learning Re-
search, 12:2411–2414.
Wang, J., Zhao, Y., Wu, X., and Hua, X.-S. (2008).
Transductive multi-label learning for video concept
detection. In Proceedings of the 1st ACM Inter-
national Conference on Multimedia Information Re-
trieval, MIR ’08, pages 298–304, New York, NY,
USA. ACM.
Weston, J., Bengio, S., and Usunier, N. (2010). Large scale
image annotation: Learning to rank with joint word-
image embeddings. In ECML.
Wu, F., Han, Y., Tian, Q., and Zhuang, Y. (2010). Multi-
label boosting for image annotation by structural
grouping sparsity. In ACM Multimedia, pages 15–24.
Zhang, M.-L. and Zhou, Z.-H. (2006). Multilabel neu-
ral networks with applications to functional genomics
and text categorization. IEEE Transactions on Knowl-
edge and Data Engineering, 18(10):1338–1351.
Two-wayMultimodalOnlineMatrixFactorizationforMulti-labelAnnotation
285
