
Discriminative Kernel Feature Extraction and Learning for Object
Recognition and Detection
Hong Pan
1,2
, Søren Ingvor Olsen
1
and Yaping Zhu
1
1
Department of Computer Science, Univeristy of Copenhagen, 2100 Copenhagen Ø, Denmark
2
School of Automation, Southeast University, Nanjing, 210096, China
Keywords: Context Kernel Descriptors, Cauchy-Schwarz Quadratic Mutual Information, Feature Extraction and
Learning, Object Recognition and Detection.
Abstract: Feature extraction and learning is critical for object recognition and detection. By embedding context cue of
image attributes into the kernel descriptors, we propose a set of novel kernel descriptors called context
kernel descriptors (CKD). The motivation of CKD is to use the spatial consistency of image attributes or
features defined within a neighboring region to improve the robustness of descriptor matching in kernel
space. For feature learning, we develop a novel codebook learning method, based on the Cauchy-Schwarz
Quadratic Mutual Information (CSQMI) measure, to learn a compact and discriminative CKD codebook
from a rich and redundant CKD dictionary. Projecting the original full-dimensional CKD onto the
codebook, we reduce the dimensionality of CKD without losing its discriminability. CSQMI derived from
Rényi quadratic entropy can be efficiently estimated using a Parzen window estimator even in high-
dimensional space. In addition, the latent connection between Rényi quadratic entropy and the mapping data
in kernel feature space further facilitates us to capture the geometric structure as well as the information
about the underlying labels of the CKD using CSQMI. Thus the resulting codebook and reduced CKD are
discriminative. We report superior performance of our algorithm for object recognition on benchmark
datasets like Caltech-101 and CIFAR-10, as well as for detection on a challenging chicken feet dataset.
1 INTRODUCTION
Recognition and detection of real-world objects is
challenging. Currently local-based image models
(Bo et al. 2010, Bo et al. 2011, Bo et al. 2009, Wang
et al. 2013, Jégou et al. 2009, Cao et al. 2010,
Lazebnik et al. 2006, Lowe 2004, Bay et al. 2008,
Ojala et al. 2002, Dalal and Triggs 2005, Pedersen et
al. 2013, Alcantarilla et al. 2012, Alcantarilla et al.
2013) dominate the state-of-the-art object
recognition and detection methods. These
representations follow the bag-of-features model
(Jégou et al. 2009, Cao et al. 2010) that firstly
extracts low-level patch descriptors over a dense
grid or salient points, then encodes them into
middle-level features unsupervised, and finally
derives the image-level representation using spatial
pooling schemes (Jégou et al. 2009, Cao et al. 2010,
Lazebnik et al. 2006). Usually, carefully designed
descriptors such as SIFT (Lowe 2004) and HOG
(Dalal and Triggs 2005) are used as the low-level
descriptor to gather statistics of pixel attributes
within local patches. However, design of hand-
crafted descriptors is non-trivial as it require
sufficient prior knowledge and well-tuned
parameters to achieve a good performance. Besides,
we still lack a deep understanding on the design
rules behind them. Recently, Bo et al. (Bo et al.
2010, Bo et al. 2011) tried to answer how SIFT and
HOG measure the similarity between image patches
and interpret the design philosophy behind them
from a kernel’s view. They showed that the inner
product of orientation histogram applied in SIFT and
HOG is a particular match kernel over image
patches. Based on that, they provided a general way
to turn pixel-level attributes into patch-level features
and designed a set of low-level descriptors called
kernel descriptors (KDES). To reduce the
dimensionality of KDES, they applied Kernel
Principal Component Analysis (KPCA). However,
KPCA only captures second-order statistics of
KDES and cannot preserve its high-order statistics.
It inevitably degrades the distinctiveness of KDES
for nonlinear clustering and recognition where high-
99
Pan H., Olsen S. and Zhu Y..
Discriminative Kernel Feature Extraction and Learning for Object Recognition and Detection.
DOI: 10.5220/0005212900990109
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 99-109
ISBN: 978-989-758-076-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

order statistics are needed. Wang et al. (Wang et al.
2013) merged the image label into the design of
patch-level KDES and derived a variant KDES
called supervised kernel descriptors (SKDES).
Guiding KDES under a supervised framework with
the large margin nearest neighbor criterion and low-
rank regularization, SKDES reported an improved
performance on object recognition.
In this work, we focus on improving the KDES
by embedding extra context cues and further
learning a compact and discriminative CKD
codebook for object representation using
information theoretic learning techniques. In
particular, for feature extraction, we develop a set of
CKD that enhance the KDES with embedded spatial
context. Context cues enforce some degree of spatial
consistency which improves the robustness of CKD.
For feature learning, we adopt the Rényi entropy-
based CSQMI as an information theoretic measure
to learn a compact and discriminative codebook
from a rich and redundant CKD dictionary. Our
codebook learning involves two steps including the
codebook selection and refinement. In the first step,
a group of compact and discriminative basis vectors
are selected from all available basis vectors to
construct the codebook. By maximizing the CSQMI
between the selected basis vectors in the codebook
and the remaining basis vectors in the dictionary, we
obtain a compact CKD codebook. By maximizing
the CSQMI between the low-dimensional CKD
generated from the codebook and their class labels,
we also boost the discriminability of the learned
codebook. In the second step, we further refine the
codebook for improved discriminability and low
approximation error with a gradient ascent method
that maximizes the CSQMI between the low-
dimensional CKD and their class labels, given the
constraint on a sufficient approximation accuracy.
Projecting the full-dimensional CKD onto the
learned CKD codebook, we derive the final low-
dimensional discriminative CKD for feature
representation. Evaluation results on standard
recognition benchmark, and a challenging chicken
feet dataset show that our proposed CKD model
outperforms the original KDES as well as carefully
tuned SIFT descriptor.
2 FEATURE EXTRACTION
USING CKD
We enhance the original match kernel (Bo et al.
2010) by embedding extra neighborhood constraints
into it. As neighborhood defines an adjacent set of
pixels surrounding the center pixel, these
neighborhood information can be regarded as spatial
context of the center pixel. So we refer to this
enhanced match kernel as Context Match Kernel
(CMK) and the resulting descriptors as Context
Kernel Descriptors. Intuition behind CMK is that
pixels with similar attributes from two patches
should have a high probability to have neighboring
pixels whose attributes are also similar. Considering
the spatial co-occurrence constraint, our CMK
significantly improve the matching accuracy. CMK
can be conveniently applied to develop a set of local
descriptors from any pixel attributes, such as
gradient, color, texture, and shape, etc.
2.1 Formulation of CMK
An image patch can be modelled as a set of pixels
1
n
i
i
x
X
, where x
i
is the coordinate of the ith
pixel. Let a
i
be attribute vector at the ith pixel x
i
. The
k-neighborhood N
k
i
of pixel x
i
in X is defined as a
group of pixels (including itself) that are closest to
it. Mathematically, N
k
i
= {x
j
∈X | ∥x
i
x
j
∥≤k; k≥1}. To
eliminate the image noise, we smooth the image
using a Haar wavelet filter and compute the local
gradient in the k-neighborhood. For the k-
neighborhood centered at x
p
, we first normalize the
neighborhood’s attribute by voting the pixel’s
attribute in N
k
p
with its gradient magnitude weighted
by a Gaussian function centered at x
p
. The width of
Gaussian function, which normalizes the attributes
contributed from off-center pixels, is controlled by
the neighborhood size k. Similarly, we can also
normalize the attribute in the k-neighborhood
centered at x
q
. With the normalized attribute in N
k
p
and N
k
q
, we then define the context kernel of
attributes a between x
p
and x
q
2
2
2
2
[(,),(,)] (,)
8
1
exp
8
1
exp
p
u
k
q
v
k
p p qq pq
up
puu
p
xN
k
vq
qvv
q
xN
k
xa xa aa
xx
aam
k
N
xx
aam
k
N
con a
κκ
(1)
where m
u
and m
v
are the gradient magnitudes at
pixels x
u
and x
v
, respectively;
p
a
and
q
a
are the
normalized image attributes in k-neighborhoods
centered at x
p
and x
q
, respectively;
2
(,)exp( || ||)
pq a p q
aa a a
a
κ
T
() ()
ap aq
aa
is a
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
100

Gaussian kernel measuring the similarity of
normalized attributes
p
a
and
q
a
. The context kernel
κ
con
provides a normalized measure of the attribute
similarity between two k-neighborhoods centered at
pixels x
p
and x
q
. Merging κ
con
into match kernels (Bo
et al. 2010) and replacing the attribute a in Eq.(1)
with specific attributes, we can derive a set of ad hoc
attribute-based CMKs.
For example, let θ'
p
and m'
p
be normalized
orientation and normalized magnitude of the image
gradient at pixel x
p
, such that θ'
p
= (sinθ
p
, cosθ
p
) and
2
pp p
pP
mm m
, with τ being a small
positive number. To compare the similarity of
gradients between patches P and Q from two
different images, the gradient CMK K
gck
can be
defined as
(, ) ( , ) ( , )
[( , ), ( , )]
p
qpq pq
pPqQ
pp qq
PQ mm x x
xx
gck o s
con
K κκ
κ
(2)
where
κ
o
(θ'
p
, θ'
q
) = exp(-γ
o
∥θ'
p
−θ'
q
∥
2
) =
o
(θ'
p
)
T
o
(θ'
q
)
is the orientation kernel measuring the similarity of
normalized orientations at two pixels x
p
and x
q
;
κ
s
(x
p
, x
q
) = exp(-γ
s
∥x
p
−x
q
∥
2
) =
s
(x
p
)
T
s
(x
q
) is the
spatial kernel measuring how close two pixels are
spatially; and κ
con
[(x
p
, θ'
p
), (x
q
, θ'
q
)] is given by
Eq.(1). Similarly, to measure the similarity of color
attributes between P and Q, color CMK K
cck
can be
defined as
(, ) ( , ) ( , )
[( , ), ( , )]
pq pq
pPqQ
pp qq
P
Qccxx
x
cxc
cck c s
con
K κκ
κ
(3)
where κ
c
(c
p
, c
q
)=exp(-γ
c
∥c
p
−c
q
∥
2
)=
c
(c
p
)
T
c
(c
q
) is
the color kernel measuring the similarity of color
values c
p
and c
q
. For color images, we use
normalized rgb vector as color value, whereas
intensity value is used for grayscale images.
For the texture attribute, the texture CMK, K
lbpck
,
is derived based on Local Binary Patterns (lbp)
(Ojala et al. 2002)
(,) ( , )(,)
[( , ),( , )]
pq p q p q
pPqQ
ppqq
P
Qlbplbpxx
x lbp x lbp
lbpck lbp s
con
K κκ
κ
(4)
where
3
2
pp p
pN
is the normalized
standard deviation of pixel values within a 3×3
window around x
p
; κ
lbp
(lbp
p
, lbp
q
) = exp(-γ
lbp
∥lbp
p
−lbp
q
∥
2
) is a Gaussian match kernel for lbp
operator.
As shown in Eq.(2)-(4), each attribute-based
CMK consists of four terms: 1) normalized linear
kernel, e.g. m'
p
m'
q
for K
gck
;
1 for K
cck
and '
p
'
q
for
K
lbpck
, weighting the contribution of each pixel to the
final attribute-based CMK; 2) attribute kernel
evaluating the similarity of pixel attributes; 3) spatial
kernel κ
s
measuring the relative distance between
two pixels; 4) context kernel κ
con
comparing the
spatial co-occurrence of pixel attributes. In this
sense, we formulate these attribute CMKs, defined
in Eq.(2)-(4), in a unified way as
(, ) ( , ) ( , )
[( , ), ( , )]
pq p q p q
pPqQ
pp qq
P
Qwwaaxx
xa xa
as
con
K κκ
κ
(5)
where w
p
w
q
and κ
a
correspond to normalized linear
weighting kernel and attribute kernel, respectively.
2.2 Approximation of CMK
Using the inner product representation, we rewrite K
as K(P,Q) = <ψ(Q), ψ(P)> = ψ(P)
T
ψ(Q), with
()
ψ
() () (,)
ascon
wa x xa
, where ⨂ is the
tensor product; ψ(·) gives the mapping features in
kernel space, namely the CKD. To obtain an
accurate approximation of the match kernel matrix K,
we have to uniformly sample on a dense grid along
sufficient basis vectors. In particular, for
a
and
con
,
we discretize a into G bins and approximate them
with their projections onto subspaces spanned by the
G basis vectors
1
{()}
gG
ag
a
. For space vector x, we
discretize spatial basis vectors into L bins and
sample along the L basis vectors spatially. Finally,
ψ(·) can be approximated by projections onto the
G×L×G joint basis vectors: {ϕ
l
} = {
a
(a
1
)⨂
s
(x
1
)⨂
con
(a
1
),…,
a
(a
G
)⨂
s
(x
L
)⨂
con
(a
G
)}(l=1,⋯,GLG), i.e.
1
()
GLG
ll
l
f
ψ
(6)
where f
l
is the projection coefficient onto the lth joint
basis vector ϕ
l
. Thus, dimensionality of the resulting
CKD ψ is G×L×G. Uniform sampling provides a set
of representative joint basis vectors, but does not
guarantee their compactness. Projections onto the
basis vectors usually yield a group of redundant
CKD. Next, we show how to learn a compact and
discriminative CKD codebook using a CSQMI-
based information theoretic feature learning scheme.
Projecting the original CKD ψ onto the codebook
reduces the redundancy of ψ and gives a low-
dimensional discriminative CKD representation.
DiscriminativeKernelFeatureExtractionandLearningforObjectRecognitionandDetection
101

3 FEATURE LEARNING USING
CSQMI
Shannon entropy and its related measures, such as
mutual information and Kullback-Leibler divergence
(KLD) are widely used in feature learning (Battiti
1994, Peng et al. 2005, Yang and Moody 1999,
Kwak and Choi 2002, Zhang and Hancock 2011, Liu
and Shum 2003, Qiu et al. 2014, Brown et al. 2012,
Leiva-Murillo and Artes-Rodriguez 2012, Hild II et
al. 2006, Hild II and Torkkola et al. 2006). However,
Shannon entropy-based feature learning methods
share the common weakness of high evaluation
complexity involved in the estimation of probability
density function (pdf) in Shannon entropy (Battiti
1994). Recently, Rényi entropy (Rényi 1961,
Principe 2010) has attracted more attentions in
information theoretic learning. The most impressive
advantage of Rényi entropy is its moderate
computational complexity because the estimate of
Rényi entropy can be efficiently implemented by the
kernel density estimation (Parzen 1962) (e.g. the
Parzen windowing). Several novel information
theoretic metrics derived from Rényi entropy are
introduced in feature learning (Jenssen 2010,
Jenssen 2008, Gómez -Chova et al. 2012, Zhong and
Hancock 2012).
3.1 Rényi Entropy and CSQMI
Given a data set S = {s} (s∈
d
) generated from a pdf
of p(s), then its Rényi entropy (Principe 2010) is
defined as
2
() 1(1 )log ()
H
pd
S
ss
. Standard
Shannon entropy can be treated as a special case of
Rényi entropy as α→1. Rényi entropy of order α = 2,
given in Eq.(7), is called Rényi quadratic entropy
H
2
(S) (Principe 2010)
2
22
() log ()
H
pd
S
ss
(7)
Similar to KLD defined using Shannon entropy,
Cauchy-Schwarz divergence (CSD) based on Rényi
quadratic entropy also defines a measure of
divergence between different pdfs. Given two data
set S
1
and S
2,
with S
1
having M
1
samples generated
from a pdf of p
1
(s) and S
2
having M
2
samples
generated from a pdf of p
2
(s), the CSD (Principe
2010, Jenssen 2008) of p
1
and p
2
is given by
2
12
12 2
22
12
222
() ()
(; ) log
() ()
2 ( , ) ( ) ( )
ppd
CSD p p
pdpd
HHH
12 1 2
sss
ss ss
S
SSS
(8)
where
2212
(, ) log ()()Hppd
12
S
Ssss measuring
the similarity between two pdfs can be considered as
the Rényi quadratic cross entropy. We can interpret
H
2
(S
1
, S
2
) as the information gain from
observing one density with respect to the “true”
other density. Hence, the CSD derived from Rényi
quadratic entropy is semantically similar to
Shannon’s mutual information. Based on CSD (p
1
;
p
2
), the CSQMI between S
1
and S
2
is defined as
(Principe 2010)
12 1 2
222
212 21 2
212 1 2
(; ) ( (,);()())
log ( , ) log ( ) ( )
2log ( , ) ( ) ( )
CSD
ICSDppp
p
dd p p dd
pppdd
12 12 1 2
12 12 1 2 12
12 1 2 12
SS ss s s
ss ss s s ss
ss s s ss
(9)
where p
12
(s
1
, s
2
) is the joint pdf of (S
1
, S
2
), and p
1
(s
1
)
and p
2
(s
2
) are marginal pdf of S
1
and S
2
. I
CSD
(S
1
; S
2
)
≥ 0 meets the equality if and only if S
1
and S
2
are
independent. So I
CSD
(S
1
; S
2
) is a measure of
independence that reflects the information shared
between S
1
and S
2
. In other words, it measures how
much knowing S
1
reduces the uncertainty about S
2
,
and vice versa.
Principe (Principe 2010) showed that, using a
Parzen window estimator (Parzen 1962), Rényi
quadratic entropy and its induced measures like CSD
and I
CSD
can be efficiently and accurately estimated
with a sample-based estimator involving no
approximations or assumptions besides the density
estimation itself, even in high-dimensional feature
space like our CKD. Whereas, it is not possible for
Shannon entropy (Principe 2010). This explains why
we choose Rényi quadratic entropy based CSQMI,
instead of Shannon entropy based mutual
information, as the feature learning criterion in our
algorithm. Principe (Principe 2010) provided the
approximation of CSQMI using a Gaussian Parzen
window estimator.
In addition, Jenssen (Jenssen 2010) illustrated
that, when applying a Gaussian Parzen window
estimator, Rényi quadratic entropy estimator relates
to the squared Euclidean length of mean vector of
the mapping data in kernel feature space. Whereas,
CSD estimator relates to the angle between the mean
vectors of mapping data clusters, associated with
p
1
(s) and p
2
(s), in kernel feature space. Thus CSQMI,
measuring the CSD between a joint pdf and the
product of two marginal pdfs, also relates to the
cluster structure in kernel feature space. The
relationships between Rényi quadratic entropy,
CSD/CSQMI and the mean vector of mapped
features in kernel space provide us the geometric
interpretation behind H
2
(S) and CSD/ CSQMI. It
means that the Rényi quadratic entropy-based
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
102

measures are very suitable to analyze nonlinear data
(even in high-dimensional space) and capture the
geometric structure of the data. In contrast, the
Shannon entropy and KLD do not have such good
properties.
3.2 Codebook Selection and
Refinement using CSQMI
As mentioned in Sec.2.2, we approximate the
original CKD ψ with a redundant group of joint
basis vectors
1
{}
GLG
ll
.We define these joint basis
vectors as dictionary, and represent it as
Φ (Φ has a
cardinality of G×L×G). Assuming we are given
CKD,
= [ψ
1
,⋯, ψ
M
], of M samples from C
classes, for each class c (c = 1,
⋯,C), it has M
c
samples and their CKD are denoted as
c
= [ψ
c
1
,⋯,
ψ
c
Mc
]. We rewrite CKD of all samples as
1
{}
C
cc
ΨΨ
.
Similarly, we denote
F
1
{}
C
cc
F , where F
c
=
[F
c
1
,⋯,F
c
Mc
] =
11T
1
[( , , ) ,
ccGLG
ff
T
1
,( , , ) ]
cc
MM
ccGLG
ff
. Then, Eq.(6) can be
represented as
= F, where = [ϕ
1
,⋯, ϕ
G×L×G
]
and
1
11 1
1
1
C
C
M
C
M
GLG CGLG
ff
ff
F
is the projection
coefficients matrix. Given a CKD ψ from a random
sample, we measure the uncertainty of its class label
L in terms of class prior probability by H
2
(L), given
in Eq.(7). Whereas, CSQMI I
CSD
(ψ; L) defined in
Eq.(9) measures the decrease in uncertainty of the
pattern ψ due to the knowledge of the underlying
class label L.
Given and an initial dictionary Φ, we aim to
learn a compact and discriminative subset of joint
basis vectors
Φ
*
from Φ, such that cardinality (Φ
*
)
< cardinality (
Φ). We refer to Φ
*
as codebook.
Projecting the original CKD
onto the codebook
*
gives a low-dimensional CKD,
*
=
*
F
*
. We
expect
*
should be compact and discriminative. To
learn a compact codebook, we maximize the CSQMI
between
*
and the unselected basis vectors −
*
in
, i.e. I
CSD
(
*
; −
*
). As I
CSD
(
*
; −
*
)
signifies how compact the codebook
Φ
*
is, a higher
value of I
CSD
(
*
; −
*
) means a more compact
codebook. However, that codebook may not be
discriminative, because it does not give any
information regarding the new CKD
*
from their
class label L. Therefore, we also need to maximize
the CSQMI between
*
and L, i.e. I
CSD
(
*
; L),
which provides the discriminability of the new CKD
generated from the codebook
*
. To this end, the
codebook learning problem can be mathematically
formulated as
(; ) (;)
arg max
CSD CSD
I
IL
*
** *
Φ
ΦΦ Φ Ψ
(10)
where λ
is the weight parameter to make a tradeoff
between the compactness and discriminability terms.
We use a two-step strategy to optimize the
compactness and discriminability of the codebook
simultaneously. In the first step (Codebook
Selection), the codebook that maximizes Eq.(10) is
selected from the initial dictionary in a greedy
search manner. In the second step (Codebook
Refinement), the selected codebook is refined via a
gradient ascent method to further maximize the
discriminability term I
CSD
(
*
; L) while keeping the
approximation error as low as possible.
3.2.1 Codebook Selection
The first term in Eq.(10), i.e. I
CSD
(
*
; −
*
), is a
compactness term which measures the the
compactness of the codebook
*
. The second term,
i.e. I
CSD
(
*
; L), measures the discriminability of the
codebook
*
. Based on [33], the probability of
Bayes classification error resulted from the final
CKD
*
, i.e. P(e
*
), has its upper bound given by
2
1
() () (;)
2
CSD
eHLILP
*
Ψ *
Ψ
. Thus, the selected
discriminative codebook
*
corresponding to the
minimal Bayes classification error bound should
maximize the I
CSD
(
*
; L). During the codebook
selection, we start with an empty set of
*
and
iteratively select the next best basis vector ϕ
*
from
the remaining set
−
*
, such that the mutual
information gain between the new codebook
*
∪ ϕ
*
and the remaining set, as well as the mutual
information gain between the CKD derived from
new codebook and the class label, are maximized
*
(;())(;)
arg max
(;)(;)
CSD CSD
CSD CSD
II
ILIL
**
*
** **
ΦΦ
ΦΦ
ΦΦΦ ΦΦΦ
ΨΨ
*
**
(11)
3.2.2 Codebook Refinement
We refine the codebook
*
to further enhance its
discriminability by maximizing the discriminability
term in Eq.(10), i.e.
max ;
CSD
I
L
*
*
Φ
Ψ
. To
guarantee a compact codebook, we assume that
cardinality (
*
) ≪ cardinality (). Under such an
assumption, the projection coefficient is solved by
F
*
=
†
which minimizes the approximation error
e =
∥−
*
F
*
∥
2
, where
†
= pinv(
*
) = (
*T
*
)
-
DiscriminativeKernelFeatureExtractionandLearningforObjectRecognitionandDetection
103

1
*T
is a pseudo-inverse of
*
. Thus, the problem of
refining
*
for improving the discriminability of
codebook while keeping its approximation accuracy
is converted to search for
*
that maximizes I
CSD
(
*
;
L), subject to F
*
=
†
. Since I
CSD
(·;·) is a quadratic
symmetric measure, the objective function I
CSD
(
*
;
L) is differentiable. We use the gradient ascend
method to iteratively refine
*
such that I
CSD
(
*
; L)
is maximized. In each iteration,
*
is updated with a
step size υ. After k-th iteration,
*
k
becomes
1
1
11 11
(;)
(;) (;) (;)
k
c c
CSD
kk
i
MM
CC
T
i
CSD CSD c CSD
c
ii
ci ci
cc
IL
IL IL IL
**
*
**
*
ΦΦ
** *
**
Ψ
ΦΦ
Φ
ΨΨ Ψ
ΦΦ
*
**
ψ
F
ψψ
(12)
Once
*
is refined, we update the projection
coefficients F
*
and the low-dimensional
discriminative CKD
*
according to F
*
=
†
and
*
=
*
F
*
, respectively.
4 EXPERIMENTS
We test our method on Caltech-101(Li et al. 2006)
and CIFAR-10 (Torralba et al. 2008) for recognition
and on our own chicken feet dataset for detection.
We also compare our result with the original KDES
(Bo et al. 2010), SKDES (Wang et al. 2013), and
dense SIFT features (Lazebnik et al. 2006, Lowe
2004). We adopt the code from
www.cs.washington.edu/ robotics/projects/kdes/ to
implement the original KDES. To make a fair
comparison, in all experiments, except for the final
feature dimensionality, we follow the setting of (Bo
et al. 2010) for common parameters used in our
model. Namely, basis vectors for κ
o
, κ
c,
and κ
s
are
sampled using 25, 5×5×5, and 5×5 uniform grids,
respectively.
For κ
lbp
, we choose all 256 basis
vectors. κ
con
share the same basis vectors with their
attribute kernels κ
a
. We use a three-level spatial
pyramid for pooling CKD at different levels. The
pyramid level is set as 1×1, 2×2 and 4×4. Gaussian
Parzen window is used to approximate CSQMI, and
the width parameter σ is tuned following a grid
search in the range [0.01σ
d
, 100σ
d
], where σ
d
is the
median distance of all training samples. The best
window width is selected by cross-validation. The
optimal neighborhood distance parameter, k, is
decided via a grid search between 1 and 8. The
weight parameter λ in Eq.(10) is decided by cross-
validation. To select CKD codebook with a desirable
codebook size, we try different parameters and
select the best codebook in a cross-validation
manner such that its size is no higher than the
expected codebook size. Linear SVM classifiers
implemented with the LIBlinear (www.csie.ntu.edu.
tw/~cjlin/liblinear/) are used in all experiments.
4.1 Evaluation of Object Recognition
Caltech-101: It collects 9144 images from 101
object categories and a background category. Each
category has 31 to 800 images with significant color,
pose and lighting variations. We use this dataset for
a comprehensive comparison on the recognition
performance of KDES, SKDES and our CKD. A 4-
neighborhood which achieves the best performance
is used to evaluate the context information for CKD.
For each category, we train one-vs-all linear SVM
classifiers on 30 images and test on no more than 80
images for KDES and our method. We run five
rounds of testing for a confident evaluation. Results
of SKDES are obtained from (Wang et al. 2013).
Table 1 lists the average recognition accuracy and
standard deviation of different options of kernel
descriptors. Some recently reported results are also
provided for comparison.
From table 1, we observe that our CKD
consistently outperforms KDES and SKDES, for
both individual and combined version. Except for
the gradient CKD (G_CKD), both color CKD
(C_CKD) and texture CKD (LBP_CKD) are
significantly better than their original KDES. In
particular, compared with the original color and
texture KDES, the recognition accuracy of C_CKD
and LBP_CKD is increased by 62.97% and 5.69%,
respectively. For the combined version, the accuracy
of combined CKD is 83.3%, which is 6.90% higher
than the original KDES combination and 4.10%
higher than the SKDES combination. We notice the
smaller standard errors of our results compared with
SKDES. It means CKD is more robust than SKDES,
thanks to the extra embedded spatial co-occurrence
constraints.
To investigate the impact of codebook size on
the recognition performance, we train classifiers
using different codebook sizes and compare the
recognition accuracy of the combined CKD
(COM_CKD) and combined KDES (COM_KDES)
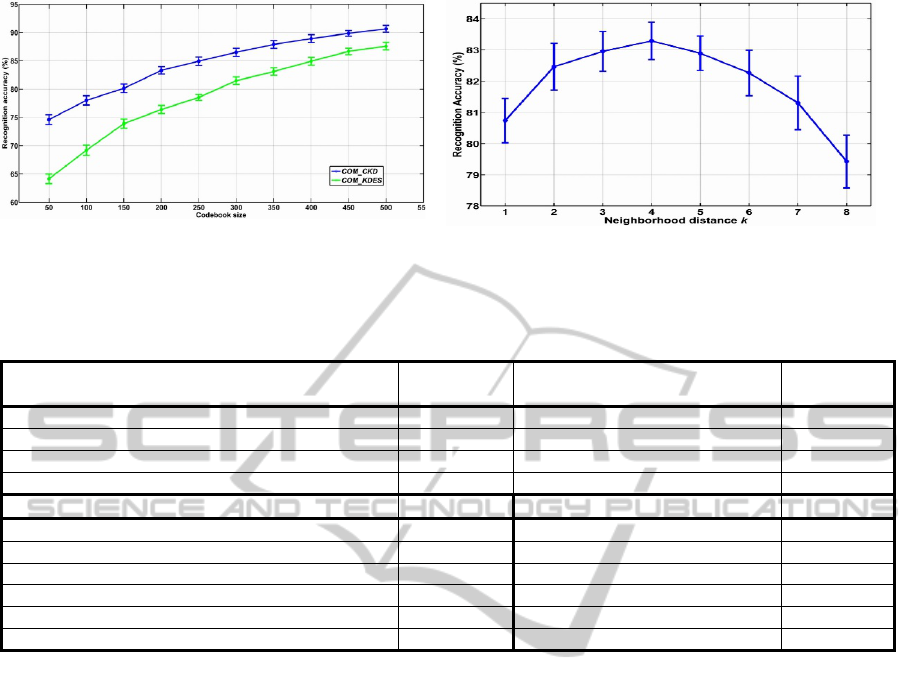
in Fig.1(a). As expected, COM_CKD outperforms
COM_KDES consistently over all codebook sizes.
We also note a relative small performance drop
(14%) of COM_ CKD when codebook size
decreases from 500 to 50, whereas for COM_KDES
the accuracy drop is 26%. This verifies the
effectiveness of our codebook learning model, which
can select discriminative CKD codebook even in
low-dimensional cases. We also compare the
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
104
(a) recognition performance at different codebook sizes (b) recognition performance at different neighborhood distances
Figure 1: Performance comparison at different codebook sizes and neighborhood distances on Caltech-101.
Table 1: Comparison of mean recognition accuracy (%) and standard deviation of KDES, SKDES and CKD on Caltech-
101.
Features
KDES(Bo et
al. 2010)
SKDES (Wang et al. 2013) CKD
gradient 75.2±0.4 77.3±0.7 77.8±0.6
color 42.4±0.5 68.4±1.4 69.1±0.9
texture(lbp) 70.3±0.6 71.6±1.3 74.3±0.8
combination 76.4±0.7 79.2±0.6 83.3±0.6
Method Accuracy Method Accuracy
Jia et al. 2012 75.3±0.7 Feng et al. 2011 82.60
SLC (McCann and Lowe 2012) 81±0.2 SDL (Jiang et al. 2012) 75.3±0.4
Adaptive deconvolutional net (Zeiler et al. 2011) 71.0±1.0 SSC (Oliveira et al. 2012) 80.02±0.36
Boureau et al. 2011 77.3±0.6 M-HMP (Bo et al. 2013) 82.5±0.5
LSAQ (Liu et al. 2011) 74.21±0.8 SPM_SIFT(Lazebnik et al. 2006) 64.6±0.8
Pyramid SIFT (P-SIFT) (Seidenari et al. 2014) 80.13 PHOW(Bosch et al. 2007) 81.3±0.8
recognition performance of CKD yielded under
different neighborhood distances. As shown in
Fig.1(b), neighborhoods with medium distances
perform better than neighborhoods with small
distances, and recognition accuracy tends to drop for
neighborhoods with large distances. This can be
understood by the fact that the discriminability of
descriptors defined within a local patch tends to be
smoothed as more noises and outlier data included
when the neighborhood distance becomes larger.
CIFAR-10: This dataset consists of 60000 tiny
images with 32×32 pixels. It has 10 categories, with
5000 training images and 1000 test images per
category. We choose this dataset to test the
performance of our method on recognition of tiny
objects. Similar to [1], we calculate CKD around 8 ×
8 image patches on a dense grid with a spacing of 2
pixels. A 3-neighborhood which gives the best
performance is applied to calculate CKD. The whole
training images are split into 10,000/40,000
training/validation set, and the validation set is used
to optimize the kernel parameters of γ
s
, γ
o
, γ
c
, and γ
lbp
using a grid search. Finally, a linear SVM classifier
is trained on the whole training set using the
optimized kernel parameters.
We compare the performance of COM_CKD with
several recent feature learning approaches using deep
learning (stochastic pooling based Deep
Convolutional Neural Network−spDCNN (Zeiler and
Fergus, 2013), tiled Convolutional Neural
Networks−tCNN (Le et al. 2010), Multi-column
Deep Neural Networks−MDNN (Ciresan et al.
2012)), sparse coding (improved local Coordinate
Coding−iLCC (Yu and Zhang, 2010), spike-and-slab
Sparse Coding− ssSC (Goodfellow et al. 2011),
hierarchical kernel descriptor (HKDES) (Bo et al.
2011) and spatial pyramid dense SIFT (SPM_SIFT)
(Lazebnik et al. 2006). For SPM_SIFT, we use a 3-
layer spatial pyramid structure and calculate dense
SIFT feature in an 8×8 patch over a regular grid with
a spacing of 2 pixels. Table 2 reports the recognition
accuracy of various methods. As we see, COM_CKD
and MDNN defeat other methods by a large margin.
Compared with MDNN, COM_CKD achieves a
comparable performance with only a 0.37% deficit in
classification rate. However, our method is much
more simple and efficient than MDNN model. For
example, for a 32×32 pixel image, our method takes
0.224s to calculate the full-dimensional 3-
neighborhood COM_CKD and 320.21s to learn a
DiscriminativeKernelFeatureExtractionandLearningforObjectRecognitionandDetection
105

200-dimensional discriminative codebook using
CSQMI on average on a platform with Intel Core i7
2.7GHz CPU and 16G RAM. Merging different
pixel attributes in the kernel space, CKD tune low-
level complementary cues into image-level
discriminative descriptors. Even coupled with simple
linear SVM classifier, our method still achieves
superior performance compared with other
sophisticated models.
Table 2: Comparison of recognition accuracy (%) of
various methods on CIFAR-10.
Method Accuracy Method Accuracy
spDCNN 84.88 SPM_SIFT 65.60
tCNN 73.10 HKDES 80.00
iLCC 74.50 MDNN
88.79
ssSC 78.80 COM_CKD 88.42
4.2 Evaluation of Object Detection
To adapt our method for object detection, we train a
two-class linear SVM classifier as the detector using
COM_CKD features. For an instance image, we
decompose it into several scales and detect possible
locations of all candidate objects using a sliding
window at each scale. Finally, we merge detection
results at different scales and remove the duplicate
detections at the same location. We test our detector
on a chicken feet dataset collected in a chicken
slaughter house. The aim of our detector is to find
and localize chicken feet. As illustrated in Fig.3, this
chicken feet dataset is very challenging due to the
following facts: chicken feet are very small
compared with other parts of the body, usually more
than forty chickens are squeezed in a box, multiple
chicken feet may appear in one image, in many cases
feet are severely occluded (most part of feet are
hidden under feather), the appearance of feet changes
drastically due to different poses, and finally the
color of the feet is very similar to feather and chest.
We crop a total of 717 image patches containing
chicken feet as positive training examples, and 2000
patches without chicken feet as negative training
examples. Another set of 318 images containing
chicken feet patches never occurred in the training
set are used as test set. Since chicken feet are also
tiny, we use the same patch size and sampling grid
for the CIFAR-10 dataset to evaluate CKD. The
parameters of CKD and SVM are tuned by the 10-
fold cross-validation on training set. To judge the
correctness of detections, we adopt standards of the
PASCAL Challenge criterion (Everingham et al.
2010), i.e. a detection is considered as correct only if
the predicted bounding box overlaps at least half area
with the ground-truth bounding box. All other
detections of the same object are counted as false
positives. We compare the detection performance of
our model with the HKDES model (Bo et al. 2011)
and a 3-level SPM _SIFT (Lazebnik et al. 2006) in
terms of the Equal Error Rate (EER) on the
Precision-Recall (PR) curves, i.e. PR-EER. PR-EER
defines the point on the PR curve, where the recall
rate equals the precision rate.
Fig.2 plots the Precision-Recall curves for all
methods. As we see, among all tested models,
COM_CKD achieves the best overall performance
(EER=78.53%), followed by the HKDES model
(EER=75.61%) that combines gradient, color and
shape cues into KDES. This further confirms that
merging different visual cues into object
representation can significantly boost the
performance of the classifier. One interesting
observation is that, expect for C_CKD, results from
our single CKD models are better than the
sophisticated SIFT method. In particular, EERs of
LBP_CKD and G_CKD model are 71.23% and
69.55%, respectively, whereas EER of SPM_SIFT is
only 59.41%. Considering individual CKD, C_CKD
gives the worst result with EER=44.10%. Both
LBP_CKD and G_CKD perform well, with LBP_
CKD achieving a slightly better average accuracy.
This is not surprising. Color difference between
chicken feet and other parts (feather and chest) is
marginal (refer to Fig.3). Color distributions of
chicken feet and other parts overlap quite much. In
particular, the color distribution of feet and chest can
hardly allow an acceptable separation based on color
cue alone. In contrast, feet show a moderate
difference in texture structures from feature and
chest. Hence, texture based LBP_CKD outperforms
other single feature for this dataset. Fig.3 shows
some detection examples resulting from the best
COM_CKD feature. Due to the influence of shadow
caused by the box boundary and severe occlusions,
some small chicken feet under the box shadow (in
left images) or hidden by the feather (in right
images) are missed by the detector, which give the
false negative detections. But for these images no
false positive detections appear.
5 CONCLUSIONS
Based on the context cue and Rényi quadratic
entropy based CSQMI, we propose a set of novel
kernel descriptors called context kernel descriptors
and an information theoretic feature learning method
to select a compact and discriminative codebook for
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
106
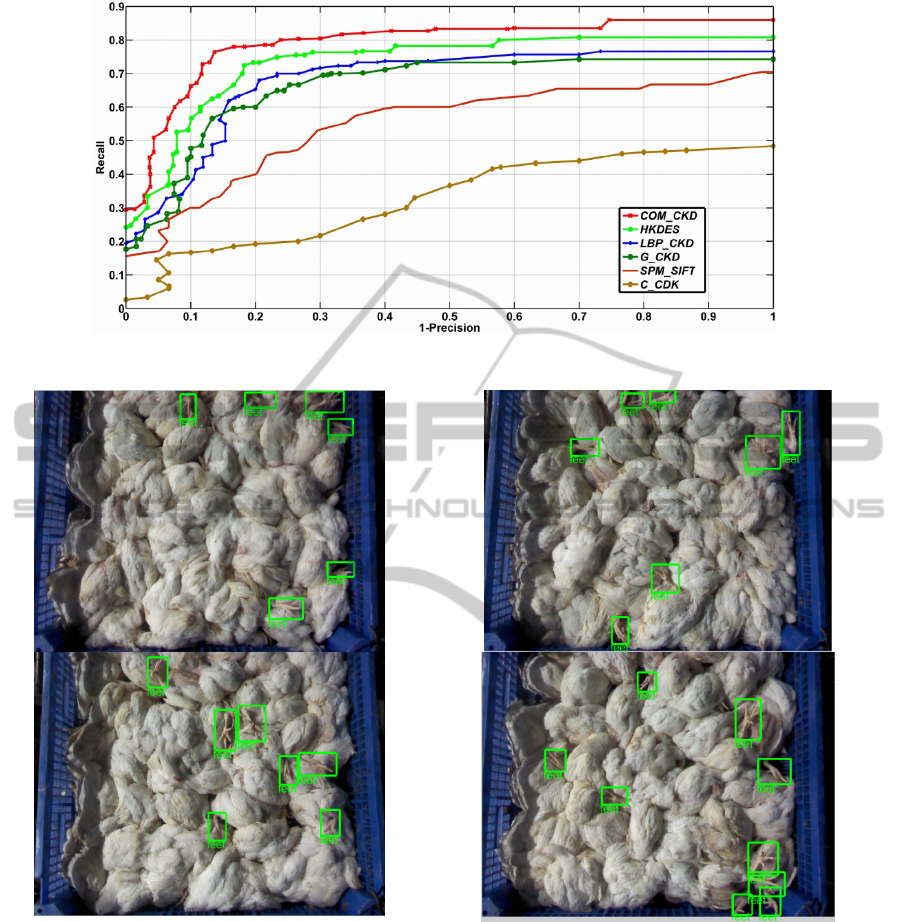
Figure 2: Precision-Recall curves of all methods tested on the chicken feet dataset.
Figure 3: Detection examples resulting from COM_CKD feature.
object representation. We evaluate our method in
object recognition and detection applications. The
contributions of our work lie in 1) the new CKD
enhances the original KDES by adding extra spatial
co-occurrence constraints to reduce the mismatch of
image attributes (features) in kernel space; 2) instead
of using traditional KPCA for feature reduction, we
apply CSQMI criterion to learn a subset of compact
and discriminative CKD codebook that captures the
cluster structure of input samples as well as the
information about their underlying labels. Evaluation
results on both popular benchmark and our own
datasets show the effectiveness of our method for
generic (especially tiny) object recognition and
detection.
ACKNOWLEDGEMENTS
This work is supported by The Danish Agency for
Science, Technology and Innovation, project “Real-
time controlled robots for the meat industry”, and
partly supported by NSF of Jiangsu Province, China
DiscriminativeKernelFeatureExtractionandLearningforObjectRecognitionandDetection
107

under Grant BK20131296, Grant BK20130639 and
NSFC under Grant 61005051. The authors thank
Lantmännen Danpo A/S for providing the chicken
images.
REFERENCES
Alcantarilla, P., Bartoli, A. and A.Davison. KAZE
Features. Proc. of ECCV, 214-227, 2012.
Alcantarilla, P., Nuevo, J., Bartoli, A., Fast explicit
diffusion for accelerated features in nonlinear scale
spaces. Proc. of BMVC, 13.1-13.11, 2013.
Battiti, R., Using Mutual Information for Selecting
Features in Supervised Neural Net Learning. IEEE
Trans. Neural Networks, 5(4):537-550, 1994.
Bay, H., Ess, A., Tuytelaars, T, Van Gool, L., SURF:
Speeded Up Robust Features. Computer Vision and
Image Understanding, 110(3):346-359, 2008.
Bo, L., Lai, K., Ren, X., Fox, D., Object Recognition with
Hierarchical Kernel Descriptors. Proc. of CVPR,
1:1729-1736, 2011.
Bo, L., Ren, X., Fox, D., Kernel Descriptors for Visual
Recognition. Proc. of NIPS, 244-252, 2010.
Bo, L., Ren, X., Fox, D., Multipath sparse coding using
hierarchical matching pursuit. Proc. of CVPR, 1:660-
667, 2013.
Bo, L., Sminchisescu, C., Efficient Match Kernel between
Sets of Features for Visual Recognition. Proc. of NIPS.
1:135-143, 2009.
Bosch, A., Zisserman, A., and Munoz, X., Image
Classification using Random Forests and Ferns. Proc.
of ICCV, 1:1-8, 2007.
Boureau, Y.-L., Roux, N. L., Bach, F., Ponce, J., LeCun,
Y., Ask the locals: Multi-way local pooling for image
recognition. Proc. of ICCV, 1:2651–2658, 2011.
Brown, G., Pocock, A., Zhao, M., Luján, M., Conditional
likelihood maximisation: a unifying framework for
information theoretic feature selection. The Journal of
Machine Learning Research, 13(1):27-66, 2012.
Cao, Y., Wang, C., Li, Z., Zhang, L., Spatial -bag-of-
features. Proc. of CVPR, 1:3352-3359, 2010.
Ciresan, D., Meier, U., Schmidhuber, J., Multi-column
Deep Neural Networks for Image Classification. Proc.
of CVPR, 3642-3649, 2012.
Dalal, N., Triggs, B., Histograms of oriented gradients for
human detection. Proc. of CVPR, 1:886 -893, 2005.
Everingham, M. L, Van Gool, C., Williams, K. I., Winn,
J., and Zisserman, A., The pascal visual object classes
(VOC) challenge. International Journal of Computer
Vision, 88(2): 303–338, 2010.
Feng, J., Ni, B., Tian, Q., Yan, S., Geometric p-norm
feature pooling for image classification. Proc. of
CVPR, 1:2697–2704, 2011.
Gómez-Chova, L., Jenssen, R., Camps-Valls, G., Kernel
Entropy Component Analysis for Remote Sensing
Image Clustering. IEEE Geoscience and Remote
Sensing Letters, 9(2):312-316, 2012.
Goodfellow, I., Courville, A., Bengio, Y., Spike-and-Slab
Sparse Coding for Unsupervised Feature Discovery, in
NIPS Workshop on Challenges in Learning
Hierarchical Models, 2011.
Hellman, M.E., Raviv, J., Probability of error,
equivocation, and the Chernoff bound. IEEE Trans. on
Information Theory, 16:368–372, 1979.
Hild II, K.E., Erdogmus, D., Principe, J.C., An Analysis of
Entropy Estimators for Blind Source Separation.
Signal Processing, 86(1):182-194, 2006.
Hild II, K., Erdogmus, D., Torkkola, K., Principe, J.,
Feature Extraction Using Information-Theoretic
Learning. IEEE Trans. Pattern Analysis and Machine
Intelligence, 28(9):1385-1392, 2006.
Jégou, H., Douze, M., Schmid, C., Packing bag-of-
features. Proc. of ICCV, 1:2357-2364, 2009.
Jenssen, R., Kernel entropy component analysis. IEEE
Trans. Pattern Analysis and Machine Intelligence,
32(5):847–860, 2010.
Jenssen, R., Eltoft, T., A new information theoretic
analysis of sum-of-squared-error kernel clustering.
Neurocomputing, 72(1-3):23-31, 2008.
Jia, Y., Huang, C., Darrell, T., Beyond spatial pyramids:
Receptive field learning for pooled image features.
Proc. of CVPR, 1:3370–3377, 2012.
Jiang, Z., Zhang, G., and Davis, L. S., Submodular
dictionary learning for sparse coding. Proc. of CVPR,
1:3418–3425, 2012.
Kwak, N., Choi, C., Input Feature Selection by Mutual
Information Based on Parzen Window. IEEE Trans.
Pattern Analysis and Machine Intelligence,
24(12):1667-1671, 2002.
Lazebnik, S., Schmid, C., Ponce, J., Beyond bags of
features: Spatial pyramid matching for recognizing
natural scene categories. Proc. of CVPR, 1:2169-2178,
2006.
Le, Q., Ngiam, J., Chia, Z.C., Koh, P., Ng, A., Tiled
convolutional neural networks. Proc. of NIPS, 1:1279-
1287, 2010.
Leiva-Murillo, J., and Artes-Rodriguez, A., Information-
Theoretic Linear Feature Extraction based on Kernel
Density Estimators: A Review. IEEE Trans. Systems,
Man, and Cybernetics, Part C: Applications and
Reviews, 42(6):1180-1189, 2012.
Li, F., Fergus, R., and Perona, P., One-shot learning of
object categories. IEEE Trans. Pattern Analysis and
Machine Intelligence, 28(4):594–611, 2006.
Liu, C., Shum, H., Kullback-Leibler boosting. Proc. of
CVPR, 1:587-594, 2003.
Liu, L., Wang, L., and Liu, X., In defense of soft-
assignment coding. Proc. of ICCV, 1:2486–2493,
2011.
Lowe, D., Distinctive image features from scale-invariant
keypoints. International Journal of Computer Vision,
60(2):91-110, 2004.
McCann, S., Lowe, D., Spatially local coding for object
recognition. Proc. of ACCV, 2012.
Ojala, T., Pietikäinen, M., Mäenpää, T., Multiresolution
gray-scale and rotation invariant texture classification
with local binary patterns. IEEE Trans. Pattern
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
108

Analysis and Machine Intelligence, 24(7):971-987,
2002.
Oliveira, G., Nascimento, E., Vieira, A., Sparse spatial
coding: a novel approach for efficient and accurate
object recognition. Proc. of ICRA, 2592–2598, 2012.
Parzen, E., On the estimation of a probability density
function and the mode. Ann. Math. Statist.,
33(3):1065–1076, 1962.
Pedersen, K., Smidt, K., Ziem, A., Igel, C., Shape index
descriptors applied to texture-based galaxy analysis.
Proc. of ICCV, 1:2240-2447, 2013.
Peng, H., Long F., Ding C., Feature Selection Based on
Mutual Information: Criteria of Max-Dependency,
Max-Relevance, and Min-Redundancy. IEEE Trans.
Pattern Analysis and Machine Intelligence,
27(8):1226-1238, 2005.
Principe, J., Information theoretic learning: Renyi’s
entropy and kernel perspectives. Springer, 2010.
Qiu, Q., Patel, V., Chellappa, R., Information-theoretic
Dictionary Learning for Image Classification. IEEE
Trans. Pattern Analysis and Machine Intelligence,
April, 2014.
Rényi, A., On measures of entropy and information.
Fourth Berkeley Symposium on Mathematical
Statistics and Probability, 547-561, 1961.
Seidenari, L., Serra, G., Bagdanov, A., Del Bimbo, A.,
Local Pyramidal Descriptors for Image Recognition.
IEEE Trans. Pattern Analysis and Machine
Intelligence, 36(5):1033–1040, 2014.
Torralba, A., Fergus, R., Freeman, W., 80 million tiny
images: A large data set for nonparametric object and
scene recognition. IEEE Trans. Pattern Analysis and
Machine Intelligence, 30(11):1958–1970, 2008.
Wang, P., Wang, J., Zeng, G., Xu, W., Zha, H., Li, S.,
Supervised Kernel Descriptor for Visual Recognition.
Proc. of CVPR, 1:2858-2865, 2013.
Yang, H., Moody, J., Feature Selection Based on Joint
Mutual Information. Proc. of International ICSC
Symposium on Advances in Intelligent Data Analysis,
1:22-25, 1999.
Yu, K., Zhang, T., Improved local coordinate coding using
local tangents. Proc. of ICML, 1:1215–1222, 2010.
Zeiler, M., Fergus, R., Stochastic Pooling for
Regularization of Deep Convolutional Neural
Networks. Proc. of ICLR, 2013.
Zeiler, M. D., Taylor, G. W., Fergus, R., Adaptive
deconvolutional networks for mid and high level
feature learning. Proc. of ICCV, 1:2018–2025, 2011.
Zhang, Z., Hancock, E., A graph-based approach to feature
selection. Graph-Based Representations in Pattern
Recognition, 205-214, 2011.
Zhong, Z., Hancock, E., Kernel entropy-based
unsupervised spectral feature selection. International
Journal of Pattern Recognition and Artificial
Intelligence, 26(5):126002-1-18, 2012.
DiscriminativeKernelFeatureExtractionandLearningforObjectRecognitionandDetection
109
