Biomechanical Effects of the Geometry of Ball-and-Socket

Intervertebral Prosthesis on Lumbar Spine Using Finite Element

Method

Jisu Choi

, Dong Ah Shin

and Sohee Kim

Department of medical system engineering, Gwangju Institute of Science and Technology, Cheomdan-gwagiro,

Gwangju, South Korea

Department of Neurosurgery, Yonsei University College of Medicine, Seoul, South Korea

Keywords: Lumbar Artificial Disc, Total Disc Replacement, Finite Element Method (FEM).

Abstract: The purpose of this study was to analyze the biomechanical effects of three different types of ball-and-

socket geometry of a lumbar artificial disc using finite element method. A three dimensional linear finite

element (FE) model was developed, and the lumbar artificial disc was inserted at L3-L4 level. The height of

implant was fixed and location of implant was also center-fixed. Three different curvatures of ball-and-

socket geometry were modeled (radius of curvature: 50.5mm for C1, 26mm for C2, 18.17mm for C3). The

biomechanical effects including range of motion (ROM), stress of intervertebral disc, facet contact force

and stress on implant were compared among different geometries. As the radius of curvature decreased, the

result shows that ROM increased at the surgical level and the stress on implant decreased. The change in

stress within intervertebral disc was not significant. The facet contact force at surgical level was maximum

with C2 while C1 and C3 had similar facet contact force. We confirmed that the geometry of artificial disc

can cause remarkable biomechanical changes at surgical level.

1 INTRODUCTION

Total disc replacement (TDR) has been accepted as

a better treatment due to its various advantages over

spinal fusion methods in degenerative disc disease

(Mayer and Korge, 2002). TDR preserves disc

height and inter-segmental range of motion. In

addition, adjacent level effect is lower than

conventional fusion methods (Panjabi et al., 2007).

Although TDR has many advantages, complications

have been reported (Bertagnoli et al., 2006). The

system can cause facet arthrosis and excessive

motion at surgical level, and it also has potential to

generate subsidence of metallic endplate of the

implant. In order to understand the reasons for

complications, many of previous studies have used

finite element analysis (Rohlmann et al., 2005),

(Rundell et al., 2008). The surgical methods such as

preserving the annulus fibrous, positioning the

implant, and re-suturing the anterior longitudinal

ligament could affect the motion biomechanically. In

addition, the size of facet joint gap leads different

biomechanical changes such as facet contact force at

surgical level. Although various factors were

investigated, the effect of implant geometry has not

been analysed. In the present study, the artificial disc

is based on ball-and-socket type, but the curvature of

ball-and-socket can vary. Accordingly, we aim to

investigate the effect of the curvature of ball-and-

socket implant and compare the biomechanical

effects at the adjacent and surgical levels of lumbar

spine using finite element method (FEM).

2 METHODS

A three dimensional linear finite element model was

developed and validated based on the study by

Yamamoto et al. The surgical finite element model

was constructed based on this validated model. The

height and location of implant were fixed and only

the curvature of ball-and-socket geometry was

varied. Three surgical FE models with different

implant geometries were constructed and compared.

116

Choi J., Shin D. and Kim S..

Biomechanical Effects of the Geometry of Ball-and-Socket Intervertebral Prosthesis on Lumbar Spine Using Finite Element Method.

DOI: 10.5220/0005213001160120

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2015), pages 116-120

ISBN: 978-989-758-070-3

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

2.1 Finite Element Model

The computed tomographic scan data of a healthy

24-year-old male was taken and reconstructed to

three dimensional geometry using Mimics software

(Materialise Inc., Leuven, Belgium). The 3D

geometry was imported to Hypermesh software

(Altair Engineering, Inc., Troy, MI, USA) and

converted from surface to solid type. Then, it was

meshed with finite elements. The cortical bone was

obtained from cancellous bone’s surface and

cartilage endplate was extracted from the surface of

intervertebral disc. The final FE model has five

vertebras (L1-L5), four intervertebral discs, and

ligaments. The total number of nodes and elements

were 398,260 and 945,960, respectively.

2.2 Material Properties

The material properties of each component were

obtained from previous literatures (Table1). Nucleus

pulposus has nearly incompressible property.

Annulus fibrous ground was modeled to be linear

elastic, and annulus fibers were not modeled in this

study. Ligaments were modeled to be linear elastic,

in which only tension can occur.

Table 1: Material properties of the used FE model.

Components

Young’s

Modulus

(MPa)

Poisson’s

ration

Reference

Cortical bone 5000 0.3

Rohlmann et

al. 2006b

Cancellous bone 50 0.2

Rohlmann et

al. 2006a

Posterior bone 3500 0.25

Rohlmann et

al. 2005

Nucleus Pulposus 1 0.499

Chen et al

Goel et al

Annulus fibrous 2 0.45

Lavaste et al.

1992

Cartilage

endplate

24 0.4

Goel et

al.1995a

Ligaments

ALL

PLL

ITL

ISL

SSL

32.9

58.7

11.6

0.45

Goel et al.

1995a

Metallic endplate 210000 0.3 Liau JJ

Polyethylene

inlay

(UHMWPE)

1016 0.46 Liau JJ

Figure 1: The surgical FE model with artificial disc at

L3/4 level and different curvatures of ball-and-socket

geometry. (C1: 50.5mm, C2: 26mm, C3: 18.17mm).

The FE model was exported to Abaqus software

(ABAQUS 6.13.; Hibbitt, Karlsson&Sorenson, Inc.,

Providence, RI, USA) after the material properties

were applied to each component of lumbar spine in

the model.

2.3 Surgical FE Model

The artificial disc was modeled to be 34.5mm,

27mm, and 2mm in width, length, and thickness,

respectively. The implant height was designed to be

8.7mm to fit the FE model. The implant was

modeled to have three different radii of curvature

(50.5mm for C1, 26mm for C2, 18.17mm for C3)

and inserted at L3-L4 level. Following the standard

surgical method, anterior longitudinal ligament and

Nucleus pulposus were removed and only lateral

Annulus fibrous was remained. The implant was

located at the center of vertebral body. The

coefficient of sliding contact between ball-and-

socket was 0.07 (Godest et al., 2002). The tie

interaction was applied to the endplates of implant

and vertebrae for complete fusion. The surgical FE

model is shown in Figure 1.

2.4 Boundary and Loading Condition

For validation of the intact FE model, we followed

the same protocol used in the study of Yamamoto et

al. The moment of 10 Nm was applied to the

superior surface of L1, and the inferior surface of L5

was fixed in all directions. The same boundary and

loading conditions were also applied to the surgical

models.

BiomechanicalEffectsoftheGeometryofBall-and-SocketIntervertebralProsthesisonLumbarSpineUsingFiniteElement

Method

117

3 RESULTS

3.1 Model Validation

To validate the FE model, the range of motion of FE

model was compared with the results of the study by

Yamamoto et al (Yamamoto et al., 1989). The

results were within ±1 standard deviation of the

average of Yamamoto et al’s study in all motion

(Figure 2).

3.2 Range of Motion

There was no significant difference among all

groups at the adjacent level (L2/3, L4/5). However,

at surgical level, the ROM in C1, C2 and C3 models

was changed by +38.5%, +46.2%, and +57.7% in

extension, -33.3%, -22.2%, and -12.7% in flexion, -

5%, +30%, and +35% in bending, +191%, +4.3%,

and +30.4% in torsion, respectively compared to the

intact model. The results are shown in Figure 3.

3.3 The Stress of Intervertebral Disc

The stress of intervertebral disc at adjacent level

(L2/3, L4/5) was within +2.4% of that of the intact

model (Figure 4).

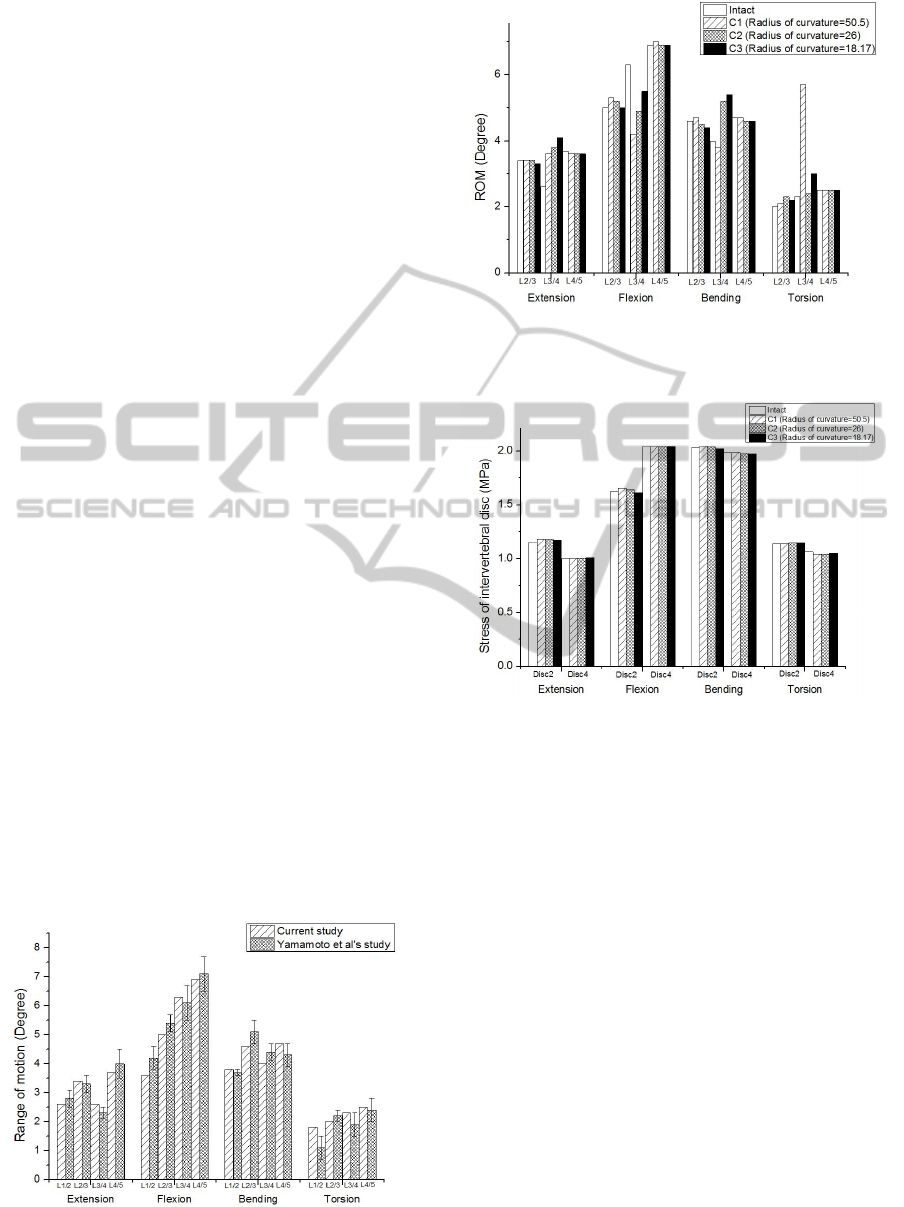
3.4 The Facet Contact Force

The facet contact force at the adjacent level (L4/5)

was not significantly changed. At the surgical level,

the facet contact force in C1, C2 and C3 models was

changed by -4.2%, +5.9%, and -19% in extension,

+81.9%, +172.3%, and +76.9% in lateral bending,

+116.2%, +140.5%, and +107.9% in axial torsion,

respectively compared to the intact model. The facet

contact force was maximum in C2, and minimum in

C3 (Figure 5).

Figure 2: Comparison of range of motion between current

study and Yamamoto et al’s study.

Figure 3: The range of motion with the different

curvatures of implant in extension, flexion, bending and

torsion at adjacent and surgical level.

Figure 4: The stress of intervertebral disc with the

different curvatures of implant in extension, flexion,

bending and torsion at adjacent level.

3.5 The Stress on Implant

The stress on implant decreased with the higher

degree of curvature in extension, flexion, and lateral

bending. In axial torsion, intact and surgical models

had relatively similar level of the stress on implant

(Figure 6).

4 DISCUSSION

In this study, we investigated the biomechanical

changes according to different curvatures of ball-

and-socket implant. Other factors that may affect the

result, such as the surgical method, location and

height of implant were fixed and only the curvature

of ball- and-socket was varied.

BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

118

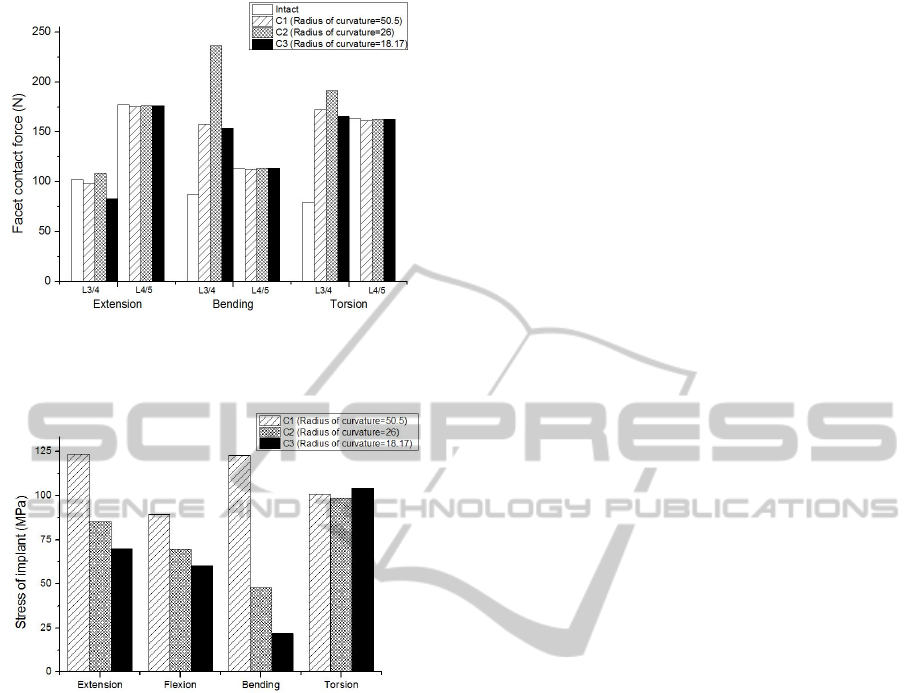
Figure 5: The facet contact force with the different

curvatures of implant in extension, bending and torsion at

L3/4 and L4/5level.

Figure 6: The stress on implant with the different

curvatures of implant in extension, flexion, bending and

torsion.

The range of motion, stress of intervertebral disc,

facet contact force, and stress on implant were

investigated with different curvatures.

The results show that the geometry of ball-and-

socket artificial disc caused remarkable

biomechanical changes at surgical level.

The general effects after inserting artificial disc

such as increase in ROM and facet contact force at

surgical level were similar to previous FE model

study (Chen et al., 2009). In this study, the range of

motion increased in extension, bending, and torsion

after TDR. However, the ROM decreased in flexion

after TDR. The reason for decreasing ROM in

flexion can be attributed to the location of implant.

A previous study related to TDR and intersegmental

rotation reported that even slightly anterior position

can cause significant ROM decrease in flexion

(Rundell et al., 2008). Accordingly, the location of

implant in this study could be slightly anterior rather

than center location. This issue, however, was not

critical because we focused on the geometry of

implant with fixed location. Also, the results were in

agreement with the previous study except for flexion.

In addition, the facet contact force increased after

inserting artificial disc as was reported by previous

studies (Kim et al., 2010).

The biomechanical effects according to the

geometry of implant at surgical level, such as the

ROM, facet contact force were significantly affected.

In addition, the stress on implant was also affected

by geometry of implant.

The entire ROM increased with decreasing

radius of curvature in extension, flexion, and lateral

bending. In axial torsion, ROM was maximum with

the largest radius of curvature. It was speculated that

the smaller radius of curvature enables the wider

range of motion, but the central point of rotation axis

misplaces in axial rotation.

The geometry of implant significantly affects the

facet contact force (FCF). The FCF was maximum

in C2, while C1 and C3 had similar values. It was

assumed that the FCF increased due to the

translation of vertebral body through the small

curvature and decreased with large curvature

because vertebral body rotates rather than translates.

The adjacent intervertebral disc stress was

similar among surgical models. The disc stress was

independent from geometry of implant.

Lastly, the implant stress tended to increase with

increasing radius of curvature in extension, flexion

and bending.

From these results, it turned out that the

translation or rotation of the artificial disc depends

on the curvature of ball-and-socket geometry. In the

case with smaller curvature, the artificial disc

translates through the curvature rather than rotates.

Therefore, the facet contact force increases and the

stress on implant also increases. Accordingly, the

facet arthrosis at surgical level and subsidence of

implant can be occurred. In addition, excessive

motion could be generated in axial torsion.

On the other hand, in the case with larger

curvature, the artificial disc rotates through the

curvature rather than translates. Therefore, the facet

contact force decreases and stress on implant also

decreases compared to the values with small

curvature. However, excessive motion can be

occurred in all motion.

Therefore, the curvature of implant should be

carefully considered to prevent undesired

complications in the future clinical application.

In this study, the follower load which represents the

intersegmental muscle force was not applied to the

FE model. Therefore, physiologic condition

BiomechanicalEffectsoftheGeometryofBall-and-SocketIntervertebralProsthesisonLumbarSpineUsingFiniteElement

Method

119

containing partial body weight and muscle force

should be included in future study.

5 CONCLUSIONS

In this study, we investigated that the geometry of

ball-and-socket implant can cause significant

biomechanical changes including ROM, facet

contact force at the surgical level. In addition, the

geometry of implant affects the stress on implant

itself. It is anticipated that this study can increase the

understanding of different biomechanical effects

with different curvature of implant at surgical level,

and contribute to designing improved ball-and-

socket artificial disc.

ACKNOWLEDGEMENTS

This work was supported by the grant from the

institute of Medical System Engineering (iMSE) at

GIST.

REFERENCES

Bertagnoli, R., Yue, J. J., Nanieva, R., Fenk-Mayer, A.,

Husted, D. S., Shah, R. V., Emerson, J. W., 2006. J.

Neurosurg. Spine 4, 85–90.

Chen, S.-H., Zhong, Z.-C., Chen, C.-S., Chen, W.-J.,

Hung, C., 2009. Med. Eng. Phys. 31, 244–253.

Godest, A. C., Beaugonin, M., Haug, E., Taylor, M.,

Gregson, P. J., 2002. J. Biomech. 35, 267–275.

Kim, K.-T., Lee, S.-H., Suk, K.-S., Lee, J.-H., Jeong, B.-

O., 2010. J. Korean Neurosurg. Soc. 47, 446–453.

Mayer, M. H., Korge, A., 2002. Eur. Spine J. 11, S85–

S91.

Panjabi, M., Henderson, G., Abjornson, C., Yue, J., 2007.

Spine 32, 1311–1319.

Rohlmann, A., Zander, T., Bergmann, G., 2005. Spine 30,

738–743.

Rundell, S. A., Auerbach, J. D., Balderston, R. A., Kurtz,

S. M., 2008. Spine 33, 2510–2517.

Yamamoto, I., Panjabi, M.M., Crisco, T., Oxland, T.,

1989. Spine 14, 1256–1260.

BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

120