Detection of Ruptures in Spatial Relationships in Video Sequences

Abdalbassir Abou-Elailah

, Valerie Gouet-Brunet

and Isabelle Bloch

Universit´e Paris-Est, IGN, SRIG, MATIS, 73 avenue de Paris, 94160 Saint Mand´e, France

Institut Mines-Telecom, Telecom ParisTech, CNRS LTCI, Paris, France

Keywords:

Spatial Relationships, Angle Histogram, Distances, Fuzzy Object Representation, Detection of ruptures.

Abstract:

The purpose of this work is to detect strong changes in spatial relationships between objects in video se-

quences, with a limited knowledge on the objects. First, a fuzzy representation of the objects is proposed

based on low-level generic primitives. Furthermore, angle and distance histograms are used as examples to

model the spatial relationships between two objects. Then, we estimate the distances between different angle

or distance histograms during time. By analyzing the evolution of the spatial relationships during time, rup-

tures are detected in this evolution. Experimental results show that the proposed method can efﬁciently detect

the ruptures in the spatial relationships, exploiting only low-level primitives. This constitutes a promising step

towards event detection in videos, with few a priori models on the objects.

1 INTRODUCTION

In the literature, there are many intelligent video

surveillance systems, and each system is dedicated

to a speciﬁc application, such as sport match analy-

sis, people counting, analysis of personal movements

in public shops, behavior recognition in urban en-

vironments, drowning detection in swimming pools,

etc.

The VSAM project (Visam, 1997) was probably

one of the ﬁrst projects dedicated to surveillance from

video sequences. The goal of ICONS project (Icons,

2000) was to recognize the incidents in video surveil-

lance sequences. The goal of the three projects AD-

VISOR (Advisor, 2000), ETISEO (Etiseo, 2004) and

CareTracker (Caretaker, 2006) was to analyze record

streaming video, in order to recognize events in urban

areas and to evaluate scene understanding. The AVI-

TRACK project (Avitrackr, 2004) was applied to the

monitoring of airport runways, while the BEWARE

project (Beware, 2007) aimed to use dense camera

networks for monitoring transport areas (railway sta-

tions, metro).

In this context, an increasing attention is paid to

“event” detection. In (Piciarelli et al., 2008), an ap-

proach is proposed to detect anomalous events based

on learning 2-D trajectories. In (Saleemi et al., 2009),

a probabilistic model of scene dynamics is proposed

See http://www.cs.ubc.ca/∼lowe/vision.html for exam-

ples of companies and projects on these topics.

for applications such as anomaly detection and im-

provement of foreground detection. For crowded

scenes, tracking moving objects becomes very dif-

ﬁcult due to the large number of persons and back-

ground clutter. There are many approaches proposed

in the literature for abnormal event detection, based

on spatio-temporal features. In (Jiang et al., 2009),

an unsupervised approach is proposed based on mo-

tion contextual anomaly of crowd scenes. In (Mehran

et al., 2009), a social force model is used for abnormal

crowd behavior detection. In (Cong et al., 2013b),

an abnormal event detection framework in crowded

scenes is proposed based on spatial and temporal con-

texts. The same authors proposed in (Cong et al.,

2013a) a similar approach based on sparse represen-

tations over normal bases. Recently, Hu et al. (Hu

et al., 2014) proposed a local nearest neighbor dis-

tance descriptor to detect anomaly regions in video

sequences. More recently, the authors in (Tran et al.,

2014) haveproposeda video event detection approach

based on spatio-temporal path search. It is also ap-

plied for walking and running detection.

In this paper, we adopt a different point of

view. We address the question of detecting struc-

tural changes or ruptures, which can be seen as a ﬁrst

step for event detection. We propose to use low-level

generic primitives and their spatial relationships, and

we do not assume a known set of normal situations or

behaviors. To our knowledge, the proposed approach

is the ﬁrst one that exploits low-level primitives and

110

Abou-Elailah A., Gouet-Brunet V. and Bloch I..

Detection of Ruptures in Spatial Relationships in Video Sequences.

DOI: 10.5220/0005213501100120

In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 110-120

ISBN: 978-989-758-076-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

spatial relationships in an unsupervised manner to de-

tect ruptures in video. In order to illustrate the interest

of spatial relationships, let us consider a car passing

another car on a road. For human beings, it is easy to

detect and recognize this kind of event. To learn an

intelligent system to detect and recognize this event,

one solution is to break down this event into the spa-

tial relationships between the objects (the two cars in

this case) at many points in time. For example, the

car A is behind the car B at the beginning. If the car

A wants to pass the car B, the spatial relationships be-

tween the two cars rapidly changes from behind state

to beside state and then to ahead state. Thus, detect-

ing ruptures in spatial relationships can be important

in detecting and recognizing actions or events in video

sequences.

We propose to detect in an unsupervised way

strong changes (or ruptures) in spatial relationships in

video sequences. This rules out supervised learning-

based algorithms which require speciﬁc training data.

This is useful in all situations where an action or

an event can be detected based on such changes or

ruptures. Here, we use Harris detector (Harris and

Stephens, 1988), and/or SIFT detector (Lowe, 2004)

to extract low-level primitives, which are suitable to

efﬁciently detect and track moving objects during

time in video sequences (Tissainayagam and Suter,

2005; Zhou et al., 2009). In order to associate fea-

tures points to objects (to compute the fuzzy repre-

sentation), the algorithm proposed in (Tissainayagam

and Suter, 2005; Zhou et al., 2009) can be used. The

work presented in this paper is considered as a further

analysis step after tracking the objects using feature

points. Furthermore, we propose a fuzzy represen-

tation of the objects, based on their feature points,

to improve the representation of the objects and of

the spatial relationships. Then, the structure of the

scene is modeled by spatial relationships between dif-

ferent objects using their fuzzy representation. There

are several types of spatial relationships: topological

relations, metric relations, directional relations, etc.

In this paper, we use directional and metric relation-

ships as an example. More speciﬁcally, we consider

the angle histogram (Miyajima and Ralescu, 1994)

for its simplicity and reliability, and similarly the dis-

tance histogram. In order to study the evolution of

the spatial relationships over time and to detect strong

changes in the video sequences, we need to measure

the changes in the angle or distance histograms dur-

ing time. Note that this approach differs from meth-

ods based on motion detection and analysis, since it

considers structural information and the evolving spa-

tial arrangement of the objects in the observed scene.

In the literature, many measures have been proposed

to measure the distance between two normalized his-

tograms. Here, we propose to adapt these measures to

angle histograms, in order to use them in our method.

Finally, a criterion is proposed to detect ruptures in

the spatial relationships based on distances between

angle or distance histograms over time.

The proposed methods for the fuzzy representa-

tion and detection of ruptures in the spatial relation-

ships are described in Section 2. Experimental results

are shown in Section 3 in order to evaluate the perfor-

mance of the proposed approach. Finally, conclusions

and future work are presented in Section 4.

2 RUPTURE DETECTION

APPROACH

The proposed approach is divided into two main parts.

In the ﬁrst part, our goal is to estimate a fuzzy repre-

sentation of the objects exploiting only feature points.

In the second one, spatial relationships between ob-

jects are investigated, using this representation of the

objects. Based on the evolution of the spatial relation-

ships during time, strong changes in video sequences

are detected.

The fuzzy representation of the objects using the

features points is described in Section 2.1. Speciﬁ-

cally, we study the spatial distribution of the feature

points that are extracted using a detector such as Har-

ris or SIFT, for a given object. Feature points can be

used to isolate and track objects in video sequences

(Tissainayagam and Suter, 2005; Zhou et al., 2009).

Thus, we suppose that each moving object is repre-

sented by a set of interest points isolated from oth-

ers with the help of such techniques. Here, we pro-

pose two different criteria to represent the objects as

regions, exploiting only the feature points. The ﬁrst

one is based on the depth of the feature points, by as-

signing a value to each point based on its centrality

with respect to the feature points. The second one as-

signs a value to each point depending on the density

of its closest feature points. Finally, the depth and

density estimations are combined together, to form

a fuzzy representation of the object, where the com-

bined value at each pixel represents the membership

degree of this pixel to the object. This allows reason-

ing on the feature points or on the fuzzy regions de-

rived from them, without needing a precise segmen-

tation of the onjects.

In Section 2.2, the computation of the spatial rela-

tionships is discussed based on the fuzzy representa-

tion of the objects. As an example, we illustrate the

concept with the computation of the angle and dis-

tance histograms. Then, the existing distances be-

DetectionofRupturesinSpatialRelationshipsinVideoSequences

111

tween two normalized histograms are detailed, and

the adaptation of these distances to angle histograms

is also discussed. Finally, a criterion is deﬁned as

the distance between the angle or distance histograms

during time, in order to detect ruptures in the spatial

relationships.

2.1 Fuzzy Object Representation

In this section, we detail the estimation of the fuzzy

representation based on the feature points.

Figure 1: Feature point distribution for a given object.

Feature Detection: For a given object, let x

(k = 1,2,...,n) be the detected feature points. For a

given pixel p of the object, let px

denote the line con-

necting the pixel p and x

(i ∈[1...n]), d

the distance

between p and x

, and θ

the angle between

−→

and

the horizontal line as shown in Fig. 1 (θ

∈ [0,2π]).

Distances d

and angles θ

are used to estimate

depth and density weights for each object based on

the x

. The depth weight is computed using the an-

gles θ

, and is denoted by dh. The second weight is

computed using the distances d

, and is denoted by dy.

Hereafter, their estimations are described, as well as

their fusion.

Depth Estimation: In the depth estimation (i.e.

centrality), all the feature points are taken into ac-

count. Several approaches have been proposed in the

literature for depth measures (Hugg et al., 2006), such

as simplicial estimation (Liu, 1990), half-space esti-

mation (Tukey, 1975), convex-hull peeling estimation

(Eddy, 1982), L1-depth (Vardi and Zhang, 2000), etc.

In this paper, we propose a new depth measure which

is based on the entropy. For each pixel p, the com-

puted angles θ

are sorted in ascending order as shown

in Fig 2. Let

(

≥

if j > i) be the sorted angles.

We deﬁne ∆

as follows:

∆



(2π+

) −

if i = 1

−

i−1

if i ∈ [2...n]

(1)

∆

n−1

2π

Figure 2: Sorted angles.

Let p

∆

2π

, p

has two properties: 0 ≤ p

≤ 1

and

∑

i=1

= 1. Thus, p

can be seen as a discrete

probability distribution of the angles. Then, the depth

weight is deﬁned as the entropy of this probability dis-

tribution:

dh(p) =

∑

i=1

−p

log

(2)

This depth measure can be explained as follows:

let us consider a point q inside the object with feature

points distributed equitably around it in terms of di-

rections. In this case, we obtain p

= p

= ... = p

and the depth weight of point q is equal to 1 (the high-

est weight). Otherwise, if the point q is outside the ob-

ject, the depth weight depends on the angle view (∆

can represent the angle view) and the distribution of

the feature points inside the object (p

, p

,..., p

). If

the angle view becomes smaller and smaller (e.g. the

point q is moving away from the object), the depth

weight of the point q becomes also smaller accord-

ingly.

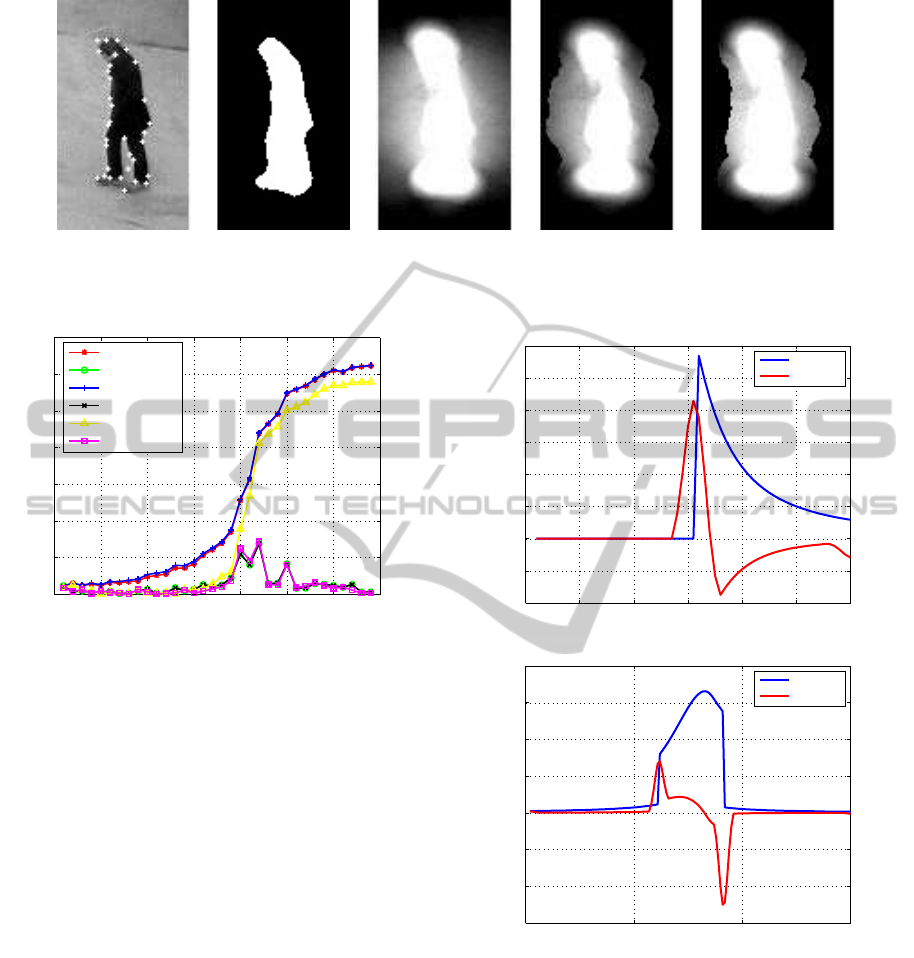
Fig. 3 shows the representation of several state of

the art depth estimations for an object, including our

proposal. As we can see, the entropy depth can bet-

ter represent the shape of the object than the existing

depth measures. In terms of computation time, the

L1-depth and the proposed depth are the most efﬁ-

cient ones compared to other measures. Our exper-

imental tests showed that the choice of a particular

depth measure has a limited impact on the detection

of the rupture. However, the entropy depth measure

may present a signiﬁcant enhancement compared to

other depth measures, in the applications that need

a precise shape estimation, to describe ﬁne relation-

ships, for example when objects meet.

Density Estimation: For density estimation, for

a given pixel inside the object, only the neighbor fea-

ture points are taken into consideration (feature points

within a certain distance r, or k closest feature points).

Thus, the distances d

that are lower than a certain dis-

tance r are taken into account to compute the density

weight for the pixel p as follows:

dy(p) =

∑

i=1

(1−

), where d

≤ r (3)

where M is the number of points inside the circle of

radius r. This radius can be estimated automatically

and online, based on statistics on the distances be-

tween points, in order to be adapted to the scale of

the object. Fig. 4 (c) shows a representation of the

density estimation.

Fusion of Depth and Density Estimations: We

present a combination approach to fuse the two esti-

mations obtained from depth and density of the fea-

ture points. For the sake of optimization, the pixels

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

112

(a) (b) (c) (d) (e) (f)

Figure 3: Depth measures: original object with feature points (a), simplicial estimation (Liu, 1990) (b), half-space estimation

(Tukey, 1975) (c), convex-hull peeling estimation (Eddy, 1982) (d), L1-depth (Vardi and Zhang, 2000) (e), and the proposed

depth (f) (image from PETS 2009 database (PETS, 2009)).

q that are taken into consideration for the fusion are

deﬁned as follows: dy(q) > 0 or dh(q) > th, where th

is a given threshold. The obtained estimation of the

object is referred to as “fuzzy representation”.

Here, the z-score (Carroll and Carroll, 2002) is ap-

plied on the two estimations, in order to make them

comparable. The z-score is the most commonly used

normalization process. It converts all estimations

to a common scale with an average of zero and a

standard deviation of one. It is deﬁned as follows:

Z = (X −

M)/(σ), where M and σ represent the av-

erage and the standard deviation of the X estimation,

respectively. Let Z

and Z

be the depth and density

estimations respectively, after applying the z-score

normalization.

The obtained fuzzy representation, using different

fusion operators, are compared with a Ground Truth

(GT) where the objects are segmented precisely (see

Section 3 for details, and an example in Fig. 4 (g)).

The combination approach which gives the best per-

formance consists in using the two operators min and

max together as deﬁned in the following expression:

F(p) = min



max



(p),Z

(p)



(4)

where

σ =

2th

. Then, F is normalized using Min-Max

scaling (Han et al., 2006) to obtain the membership

function µ

which varies in [0,1]. This fusion can be

explained as follows: when Z

(or Z

) is greater

than

σ, the membership value µ

(p) is equal to 1.

Otherwise, µ

(p) is less than 1 according to the max-

imum between them. As an example, Fig. 4 shows

different fuzzy representations of the object using min

operator, max operator, and Eq. 4 for the fusion. As

we can see, the last fusion approach shows the best

fuzzy representation of the object according to the

ground truth. The obtained fuzzy representations are

used to compute the spatial relationships.

2.2 Spatial Relationships and Rupture

Detection

Here, the goal is to estimate the spatial relationships

between two objects based on their fuzzy represen-

tation. The angle (Miyajima and Ralescu, 1994) and

distance histograms are selected as examplesto model

the spatial relationships. It is important to note that

the proposed method also applies to other types of

spatial relationships.

Angle Histogram: Given two fuzzy regions A =

{(a

,µ

)),i = 1,...,n} and B = {(b

,µ

)), j =

1,...,m}, where a

and b

are the elements of A and

B, and µ

and µ

represent their membership func-

tions respectively, for all possible pairs {(a

),a

∈

A and b

∈B}, the angle θ

between a

and b

is com-

puted, and a coefﬁcient µ

(θ

) = µ

) ×µ

) is

derived. For a given direction α, all the coefﬁcients

of the angles that are equal to α are accumulated as

follows:

∑

=α,i=1,..,n, j=1,..,m

(θ

) (5)

Finally, h = {(α,h

),α ∈ [0, 2π]} is the angle his-

togram. In our case, the histogram can be seen as an

estimate of the probability distribution of the angles.

Thus, the obtained histogram is normalized to display

frequencies of the existed angles with the total area

equaling 1. It is normalized by dividing each value

by the sum R

∑

α∈[0,2π]

, instead of normalizing

by the maximum value (which would correspond to a

possibilistic interpretation).

When the objects are represented sparsely by fea-

ture points, then µ

) = 1 and µ

) = 1 (where a

and b

represent the feature points on the objects A

and B respectively), and the same approach is used to

compute the angle histogram between the two sparse

objects A and B.

DetectionofRupturesinSpatialRelationshipsinVideoSequences

113

(a) (b) (c) (d) (e) (f) (g)

Figure 4: Original object with the feature points (a), depth estimation (b), density estimation (c), fusion using min operator

(d), fusion using max operator (e), fusion using Eq. 4 (f), and the object segmented precisely GT (g).

Distance Histogram: In this case, all the dis-

tances d

between a

(i = 1,...,n) and b

(j = 1, ...,

m) are computed. Based on these distances, the dis-

tance histogram is formulated in the same way as the

angle histogram:

∑

=l,i=1,..,n, j=1,..,m

) (6)

where µ

) = µ

) ×µ

) and l represents a

given distance value. The obtained histogram is nor-

malized such that the sum of all bins is equal to 1.

Comparison of Spatial Relationships: There are

two main approaches to estimate distances between

histograms. The ﬁrst approach is known as bin-to-

bin distances such as L

and L

norms. The sec-

ond one is called cross-bin distances; it is more ro-

bust and discriminative since it takes the distance on

the support of the distributions into account. Note

that the bin-to-bin distances may be seen as particu-

lar cases of the cross-bin distances. Several distances

based on cross-bin distances, such as Quadratic-Form

(QF) distance (Hafner et al., 1995), Earth Mover’s

Distance (EMD) (Rubner et al., 2000), Quadratic-Chi

(QC) histogram distance (Pele and Werman, 2010),

have been proposed in the literature. We have tested

these three distances on different examples, and ex-

periments showed that they were well adapted to an-

gle histograms. Finally, the QF distance was used in

our experiments to assess the distance between the

angle or distance histograms during time, because of

its simplicity. It is deﬁned as follows: d(h

) =

√

ZSZ

, where Z = h

−h

and S = {s

} is the bin-

similarity matrix. This distance is commonly used for

normalized histograms (the distance histogram for ex-

ample). Here, we propose an approach to adapt it to

the case of angle histograms just by adjusting the el-

ements of the similarity matrix S. We consider that

the two histograms h

and h

deﬁned on [0,2π] con-

sist of k bins B

. Usually, for a distribution on the

real line, the distance between B

and B

is deﬁned

as follows: x

= |B

−B

|, where 1 ≤ i ≤ k and 1 ≤

j ≤ k. However, in the case of angle histograms,

the distance between B

and B

is deﬁned as follows:

= min(x

,2π −x

) to account for the periodicity

on [0,2π]. Thus, the elements of the matrix S are sim-

ply deﬁned, in the case of angle histograms, using x

instead of x

as follows:

= 1 −

max

i, j

)

(7)

Criterion for Rupture Detection: Based on the

fuzzy representation of the objects exploiting only

the feature points, the angle or distance histogram h

between two different objects is computed. Let f

(i = 0, 1,...,N −1) be the frames of the video se-

quences, and h

be the computed angle or distance

histogram between the objects A and B in frame f

In this paper, we deﬁne y(i) = d(h

i+1

) for each

i = 0, 1,...,N −1. This function describes the evo-

lution of the angle or distance histograms over time.

If a strong change in the spatial relationships occurs at

instant R (R < N), where R denotes the instant of rup-

ture, this means that the angle or distance histogram

effectively changes compared to previous angle or

distance histograms (h

,i < R). A rupture is detected

according to the following criterion W: ∀i < R −1,

y(R−1) −y(i) > t, and t is a threshold value. Thus,

the instant of rupture R can be effectively detected

from the analysis the function y.

Here, in order to clearly show the instant of rup-

tures in the spatial relationships and removenoise, we

also show the evolution of the function y ﬁltered by a

Gaussian derivative, denoted by g, instead of a simple

ﬁnite difference. This ﬁlter can remove noise and the

function g effectively exhibits the instant of the strong

changes in the spatial relationships using a threshold

approach. This approach is particularly well suited

for abrupt changes, leading to clear peaks in the func-

tion g, that are then easy to detect (a simple threshold

can be sufﬁcient). For slower changes, a multiscale

approach can be useful to detect more spread peaks.

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

114

(a) Frames number 1, 30, and 50 of SE 1. (b) Frames number 45, 55, 74, 95, and 105 of SE 2.

RE 1 selected from PETS 2009.

(d) Frames number 595, 630, 670, and 700 of RE 2 selected from

PETS 2009.

Figure 5: Events SE 1 (a), SE 2 (b), RE 1 (c) and RE 2 (d).

(a) Frames number 1, 5, 10, and 50 of SE 3.

(b) Frames number 1955, 2010, 2060, and 2100 of RE 3 selected from PETS 2006 (PETS, 2006).

Figure 6: Events SE 3 (a) and RE 3 (b).

3 EXPERIMENTS AND

EVALUATIONS

To evaluate the performance of the proposed ap-

proach, we created some synthetic events (illustrated

in Fig. 5, (a) and (b)), and also used a variety of

events selected from the PETS 2009 datasets (PETS,

2009) (illustrated in Fig. 5, (c) and (d)). Here, we

call “event”, some frames that contain a rupture in the

spatial behavior. The results of the proposed fuzzy

representation are also compared to classical segmen-

tation approaches: a binary segmentation approach

(Comanicu and Meer, 2002) and an approach using

differences between the background and the actual

frame. Then, morphological operations are carried

out to remove small objects and ﬁll holes. The last

one is used as ground truth (GT) because it produces

very precise segmentations.

A synthetic event and an event selected from

PETS 2006 dataset (PETS, 2006), displayed in Fig. 6,

are used to illustrate the proposed approach using the

distance histogram.

To associate feature points to objects, here we

simply consider the points included in the bounding

boxes associated with objects available in the PETS

2009 dataset.

3.1 Parameters Tuning

In this section, some results are detailed concerning

the tuning of the parameters that are used in the pro-

posed approach. Speciﬁcally, we discuss the estima-

DetectionofRupturesinSpatialRelationshipsinVideoSequences

115

tion of the radius r, which is used in the computa-

tion of the density estimation. Then, some results are

shown for different values of the threshold th, which

is used in the combination of depth and density esti-

mations. Finally, we show the effect of the number of

bins on the computation of the distance between two

angle histograms.

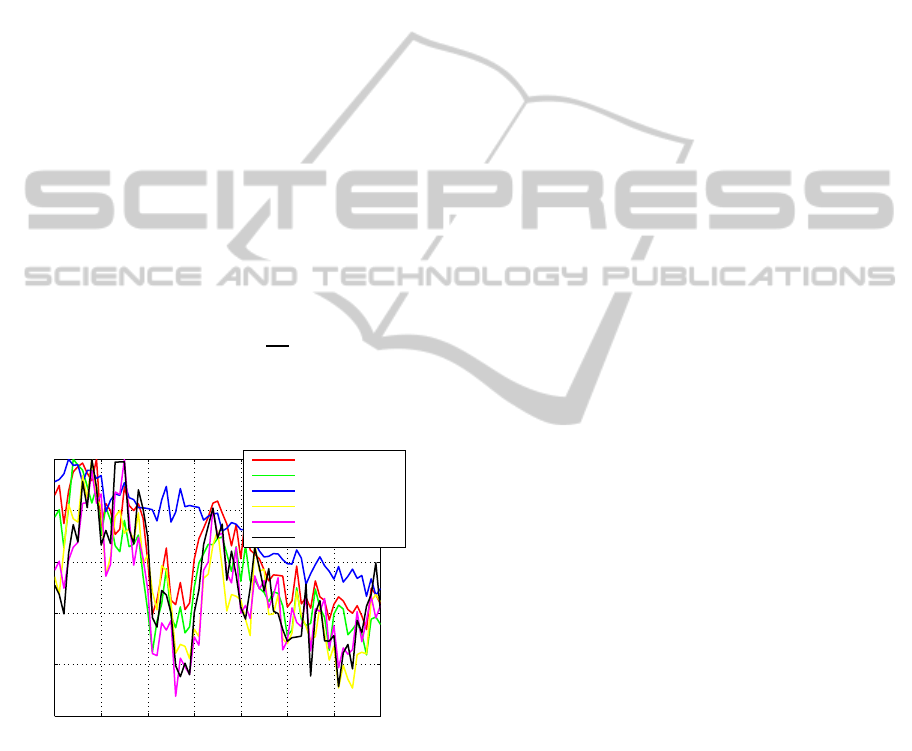
r Parameter: Fig. 7 shows different estimations

of the radius r (normalized) during time. First, all

the possible distances d

among the feature points are

computed. The mean, median, and maximum of these

distances are computed, as shown in the ﬁgure (three

ﬁrst curves). Then, Delaunay triangulation is applied

on the feature points, and two other estimations of

the radius r are computed, as the mean and median

of the lengths of the triangle edges (fourth and ﬁfth

curves). Finally, as in (Lom´enie and Stamon, 2008),

the median of all radius of the circumscribed circle

around the Delaunay triangles provides the last esti-

mation (last curve). As we can see, the maximum of

the distances (third curve) gives the most robust and

stable estimation during time. Other experiments on

different objects show the same result. Thus, the ex-

pression

r = max

i=1,..,n, j=i,..,m

(8)

is adopted to estimate the radius r for the density es-

timation.

540 550 560 570 580 590 600 610

0.5

0.6

0.7

0.8

0.9

Frame number

Mean distances

Median distances

Max distances

Mean Delaunay

Median Delaunay

Median radius Delaunay

Figure 7: Different estimations of the radius r based on the

feature points.

th Parameter: In the fusion of depth and den-

sity estimations, a threshold th is used. Fig. 8 shows

the original object with the feature points, the ground

truth (GT) of the object, and the fuzzy representation

(FR) of the object for different values of th. As we

can see, the proposed fusion approach is quite robust

to the variation of the used threshold th. In the paper,

a value of th equal to 0.5 is used in the combination

of depth and density estimations.

Number of Bins: In this section, we study the

effect of the number of bins (quantiﬁcation) on the

distance between two angle histograms. We deﬁned

the function y as the distance between two successive

angle histograms in frames f

and f

i+1

. Here, we also

deﬁne z(i) = d(h

) for i = 0, 1,...,N −1, i.e. the

distance to the histogram in the initial frame, to con-

sider strong changes in the angle histograms. Fig. 9

shows the evolution of the two functions y and z, for

numbers of bins of 360, 18, and 6. As we can see,

there is almost no difference between 360 and 18 bins,

for the two functions. For a number of bins equal to

6, there is a difference compared to 360 and 16 bins

for the function z. For the function y, the three curves

are almost the same. Thus, the used distance between

two angle histograms is robust to the variation of the

number of bins.

3.2 Ruptures in Spatial Relationships

We now illustrate how the analysis of the distances

between histograms allows us to detect ruptures in

spatial relations, both for orientation and distances.

3.2.1 Angle Histogram

Three snapshots of the ﬁrst synthetic event (SE) are

shown in Fig. 5 (a) (two objects moving together and

then separately). In this case, there is a rupture in the

directional spatial relationships, when the two objects

diverge. Fig. 5 (b) shows ﬁve snapshots of the sec-

ond SE. In this event, the object B moves towards the

object A (ﬁxed) from the left to the right. Then, the

object B changes of direction (frame 74), and when

the object B becomes above the object A, it goes to-

wards the top. Fig. 10 shows the functions y and g

during time for the two events SE 1 and 2. For the

event SE 1, the function y shows a strong variation

at frame number 31. At this instant, there is the rup-

ture in the spatial relationships (the two objects begin

to separate). Using the evolution of g over time, the

instant of the rupture can be detected by applying a

threshold (a threshold of 0.02 can be used to detect the

instants of rupture for the SE). For the second SE, we

can see two strong variations in the function y; the ﬁrst

strong variation (frame 60) occurs when B changes of

direction with respect to A, the second strong varia-

tion (frame 90) occurs when B becomes above A and

changes its direction towards the top. The function

g clearly shows the two strong variations. Thus, the

proposed method can efﬁciently detect the instants of

ruptures in the spatial relationships. Other SE were

created and tested using the proposed approach, and

similar results were obtained.

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

116

Original object GT FR - th = 0.2 FR - th = 0.5 FR - th = 0.8

Figure 8: Original object with the feature points, GT of the object, and fuzzy representations of the object for th equal to 0.2,

0.5, and 0.8 respectively.

440 445 450 455 460 465 470 475

0.2

0.4

0.6

0.8

1.2

1.4

Frame number

Distance

y - 360 bins

y - 18 bins

y - 6 bins

z - 360 bins

z - 18 bins

z - 6 bins

Figure 9: The functions y and z over time using various

number of bins.

Let us now evaluate the proposed detection of rup-

tures in the spatial relationships in the presence of

noise (deformation of objects, etc.) in real events. For

the real event (RE) 1 (Fig. 5 (c)), the two persons con-

verge then diverge. Fig. 11 (top) shows the functions

y and g over time using the proposed fuzzy represen-

tation, for the event RE 1. Two ruptures in the di-

rectional spatial relationships exist in this event. The

ﬁrst one is when the two persons meet, and the second

rupture when the two persons separate. It is clear that

the two instants of the ruptures can be efﬁciently de-

tected using the evolution of g (a threshold of 0.2 can

be used to detect the instants of ruptures for the RE).

In the event RE 2 (Fig. 5 (d)), the two persons (sur-

rounded by white and blue bounding boxes) converge

and diverge several times. In Fig. 11 (bottom), we

show the functions y and g over time, using the fuzzy

representation of the objects, for the event RE 2. All

the ruptures in the directional spatial relationships can

be efﬁciently detected using the function g.

3.2.2 Distance Histogram

Four snapshots of the third synthetic event are shown

in Fig. 6 (a). At the beginning of this event, the two

0 10 20 30 40 50 60

−0.02

−0.01

0.01

0.02

0.03

0.04

0.05

0.06

S. Event 1

Distance

Frame number

0 50 100 150

−0.06

−0.04

−0.02

0.02

0.04

0.06

0.08

S. Event 2

Distance

Frame number

Figure 10: Functions y and g for events SE 1 (top) and 2

(bottom), computed from angle histograms.

objects diverge at a speed of 5 pixels/frame, and at

a given instant (precisely at frame 10), the speed of

the two objects becomes 10 pixels/frame. Thus, the

velocity of the objects is suddenly increased. Fig. 6

(b) shows four snapshots of the third real event se-

lected from PETS 2006. In this event, the luggage is

attended to by the owner for a moment, and then the

person leaves the place and goes away.

In Fig. 12, the functions y and g during time for

DetectionofRupturesinSpatialRelationshipsinVideoSequences

117

440 445 450 455 460 465 470 475

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

Real event 1

Distance

Frame number

550 600 650 700 750 800

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

Real event 2

Distance

Frame number

Figure 11: Functions y and g over time, using the proposed

fuzzy representation, for the events RE 1 (top) and RE 2

(down), computed from angle histograms.

0 5 10 15 20

−0.02

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

Synthetic event 3

Distance

Frame number

Figure 12: Functions y and g over time, using the proposed

fuzzy representation, for the event SE 3, computed from

distance histograms.

the event SE 3 are shown. As we can see, the function

y shows a strong variation at frame number 10, when

the velocity of the objects changes. At this instant, a

rupture in the metric spatial relationships is detected,

1950 2000 2050 2100 2150

−0.08

−0.06

−0.04

−0.02

0.02

0.04

0.06

0.08

Real event 3

Distance

Frame number

Figure 13: Functions y and g over time, using the proposed

fuzzy representation, for the event RE 3, computed from

distance histograms.

using the evolution of g over time.

In the presence of noise, we show in Fig. 13 the

functions y and g during time for the third real event.

When the person leaves the place and goes away, we

can see a strong change in the function y. By nalyz-

ing the obtained results, the instant of rupture in the

metric spatial relationships can be detected. These re-

sults can be used to indicate events occurring in the

video sequences, such as escaping in Fig. 6 (a) and

Left-Luggage in Fig. 6 (b).

3.3 Impact of Object Representation

Here, we show the importance of the fuzzy represen-

tation based on a simple feature points representation.

Two feature detectors, Harris and SIFT, are tested.

Fig. 14 illustrates the function y during time (com-

puted here from angle histograms) for different rep-

resentations of the objects, for RE 1. The Harris and

SIFT features are directly used to estimate the spatial

relationships between the two objects and to compute

the function y (red and green curves in the ﬁgure).

In addition, we show in the same ﬁgure the evolution

of the function y computed on the fuzzy representa-

tion of the objects using the Harris and SIFT features

(blue and black curves in the ﬁgure). As we can see,

the evolution of the function y obtained from the fuzzy

representation of the objects using the SIFT features

(black curve) can signiﬁcantly reduce the variation of

the distance (i.e. less amplitude of the curve) on ar-

eas when there is no rupture in the spatial relation-

ships (see Fig. 14, frames 440 to 456) with respect to

the SIFT features without computing the fuzzy rep-

resentation. Thus, the proposed fuzzy representation

of the objects before computing the spatial relation-

ships can improve the robustness of the detection of

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

118

Table 1: Estimated variance of the noise (×10

−4

) (Garcia, 2010) in the function y, for different object representations, for RE

1 and 2.

Event Harris FR Harris SIFT FR SIFT Mean-Shift GT

RE 1 13 12 27 10 31 12

RE 2 7.7 5.48 8.9 7 31 5.4

440 445 450 455 460 465 470 475

0.05

0.1

0.15

0.2

0.25

0.3

0.35

SIFT points

FR SIFT

Real event 1

Distance

Frame number

Harris points

FR Harris

Figure 14: Function y over time, computed from angle his-

tograms, for different estimations of the objects: Harris fea-

tures, SIFT features, fuzzy representation (FR) of the ob-

jects using Harris features (FR Harris) and SIFT features

(FR SIFT), for RE 1.

ruptures, based on the observation that SIFT features

are more noisy across frames than Harris features in

this sequence. However, noise is present in the func-

tion y for all object representations. Assuming that

the function y has additive Gaussian noise, the algo-

rithm proposed by Garcia (Garcia, 2010) is used to es-

timate the variance of the noise of the function y, for

the different object representations: Harris features,

fuzzy representation of the objects using Harris fea-

tures (FR Harris), SIFT features, fuzzy representation

of the objects using SIFT features (FR SIFT), the bi-

nary segmentation using Mean-Shift algorithm (Co-

manicu and Meer, 2002) and GT.

Tab. 1 shows the variance of the noise in the func-

tion y, for the different object representations, for

the two events RE 1 and 2. It is clear that the pro-

posed fuzzy representation signiﬁcantly reduces the

variance of the noise, which becomes close to the one

of the GT. Especially, for SIFT features, the variance

of the noise reduces from 27 to 10 for RE 1, and from

8.9 to 7 for RE 2. In addition, the variance of the

noise of the proposed object representation is signif-

icantly less than the one of the binary segmentation

using Mean-Shift algorithm.

4 CONCLUSION

In this paper, a new method was proposed to de-

tect strong changes in spatial relationships in video

sequences. Speciﬁcally, new approaches have been

proposed to compute depth and density estimations,

based on feature points, as well as fuzzy represen-

tations of the objects by combining depth and den-

sity estimations. Exploiting the fuzzy representations

of the objects, the angle and distance histograms are

computed. Then, the distance between the angle or

distance histograms is estimated during time. Based

on these distances, a criterion is deﬁned in order

to detect the signiﬁcant changes in the spatial rela-

tionships. The proposed method shows good perfor-

mances in detecting ruptures in the spatial relation-

ships for both synthetic and real video sequences.

Future work will focus on further improvement of

the proposed method in order to detect other kinds of

ruptures, and investigating the use of spatio-temporal

relationships. Besides, we will investigate multi-time

scale analysis, in order to better detect events that

take more time to happen. In addition, proposing a

complete event detection framework based on spatial

relationships as discriminative features seems to be

promising.

ACKNOWLEDGEMENTS

This research is part of French ANR project DE-

SCRIBE “Online event detection in video sequences

using structural and Bayesian approaches”.

REFERENCES

Advisor (2000). http://www-sop.inria.fr/orion/ADVISOR/.

Advisor Project.

Avitrackr (2004). http://www-sop.inria.fr/members/ Fran-

cois.Bremond/topics Text/avitrackProject.html. Avit-

rackr Project.

Beware (2007). http://www.eecs.qmul.ac.uk/∼sgg/BEWA

RE/ Beware Project.

Caretaker (2006). http://www-sop.inria.fr/members/

Francois. Bremond/topics Text/caretakerProject.htm.

Caretaker Project.

DetectionofRupturesinSpatialRelationshipsinVideoSequences

119

Carroll, S. and Carroll, D. (2002). Statistics made simple for

school leaders: data-driven decision making. R&L

Education.

Comanicu, D. and Meer, P. (2002). Mean shift: A robust

approach toward feature space analysis. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

24(5):603–619.

Cong, Y., Yuan, J., and Liu, J. (2013a). Abnormal event de-

tection in crowded scenes using sparse representation.

Pattern Recognition, 46(7):1851 – 1864.

Cong, Y., Yuan, J., and Tang, Y. (2013b). Video anomaly

search in crowded scenes via spatio-temporal motion

context. IEEE Transactions on Information Forensics

and Security, 8(10):1590 – 1599.

Eddy, W. (1982). Convex hull peeling. In COMPSTAT,

pages 42–47.

Etiseo (2004). http://www-sop.inria.fr/orion/ETISEO/.

Garcia, D. (2010). Robust smoothing of gridded data in

one and higher dimensions with missing values. Com-

putational Statistics and Data Analysis, 54(4):1167 –

1178.

Hafner, J., Sawhney, H., Equitz, W., Flickner, M., and

Niblack, W. (1995). Efﬁcient color histogram in-

dexing for quadratic form distance functions. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 17(7):729 – 736.

Han, J., Kamber, M., and Pei, J. (2006). Data mining: con-

cepts and techniques. Morgan Kaufmann.

Harris, C. and Stephens, M. (1988). A combined corner

and edge detector. In Fourth Alvey Vision Conference,

pages 147–151.

Hu, X., Hu, S., Zhang, X., Zhang, H., and Luo, L. (2014).

Anomaly detection based on local nearest neighbor

distance descriptor in crowded scenes. The Scientiﬁc

World Journal, 2014.

Hugg, J., Rafalin, E., Seyboth, K., and Souvaine, D. (2006).

An experimental study of old and new depth mea-

sures. In Workshop on Algorithm Engineering and

Experiments (ALENEX), pages 51–64.

Icons (2000). http://www.dcs.qmul.ac.uk/research/ vi-

sion/projects/ICONS/. Icons Project.

Jiang, F., Wu, Y., and K.Katsaggelos, A. (2009). Detecting

contextual anomalies of crowd motion in surveillance

video. In 16th IEEE International Conference on Im-

age Processing, pages 1117 – 1120.

Liu, R. (1990). On a notion of data depth based on random

simplices. The Annals of Statistics, 18(1):405–414.

Lom´enie, N. and Stamon, G. (2008). Morphological mesh

ﬁltering and α-objects. Pattern Recognition Letters,

29(10):1571 – 1579.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60(2):91 – 110.

Mehran, R., Oyama, A., and Shah, M. (2009). Abnormal

crowd behavior detection using social force model.

In IEEE Conference on Computer Vision and Pattern

Recognition, pages 935 – 942.

Miyajima, K. and Ralescu, A. (1994). Spatial organization

in 2D images. In Third IEEE Conference on Fuzzy

Systems, pages 100–105.

Pele, O. and Werman, M. (2010). The quadratic-chi his-

togram distance family. In European Conference on

Computer Vision (ECCV), pages 749 – 762.

PETS (2006). http://www.cvg.rdg.ac.uk/PETS2006/data.

html.

PETS (2009). http://www.cvg.rdg.ac.uk/PETS2009/a.html

Piciarelli, C., Micheloni, C., and Foresti, G. (2008).

Trajectory-based anomalous event detection. IEEE

Transactions on Circuits and Systems for Video Tech-

nology, 18(11):1544 – 1554.

Rubner, Y., Tomasi, C., and Guibas, L. (2000). The earth

mover’s distance as a metric for image retrieval. Inter-

national Journal of Computer Vision, 40(2):99–121.

Saleemi, I., Shaﬁque, K., and Shah, M. (2009). Probabilistic

modeling of scene dynamics for applications in visual

surveillance. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 31(8):1472 – 1485.

Tissainayagam, P. and Suter, D. (2005). Object tracking in

image sequences using point features. Pattern Recog-

nition, 38(1):105 – 113.

Tran, D., Yuan, J., and Forsyth, D. (2014). Video event

detection: From subvolume localization to spatio-

temporal path search. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 36(2):404 – 416.

Tukey, J. W. (1975). Mathematics and the picturing of

data. In International Congress of Mathematicians,

volume 2, pages 523–531.

Vardi, Y. and Zhang, C.-H. (2000). The multivariate l1-

median and associated data depth. National Academy

of Sciences, 97(4):1423–1426.

Visam (1997). http://www.cs.cmu.edu/∼vsam/. Visam

Project.

Zhou, H., Yuan, Y., and Shi, C. (2009). Object tracking

using SIFT features and mean shift. Computer Vision

and Image Understanding, 113(3):345 – 352.

ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods

120