
Non Emergency Patients Transport
A Mixed Integer Linear Programming
José A. Oliveira, João Ferreira, Luis Dias, Manuel Figueiredo and Guilherme Pereira
Algoritmi Research Centre, University of Minho, Guimarães, Portugal
Keywords: Non Emergency Patients Transport, Team Orienteering Problem, Mixed Integer Linear Programming,
AMPL, NEOS Server.
Abstract: This work presents a model and a heuristic to solve the non-emergency patients transport (NEPT) service
issues given the new rules recently established in Portugal. The model follows the same principle of the
Team Orienteering Problem by selecting the patients to be included in the routes attending the maximum
reduction in costs when compared with individual transportation. This model establishes the best sets of
patients to be transported together. The model was implemented in AMPL and a compact formulation was
solved using NEOS Server. A heuristic procedure based on iteratively solving problems with one vehicle
was presented, and this heuristic provides good results in terms of accuracy and computation time.
1 INTRODUCTION
In 2012, Portugal published several official
documents about the non-emergency patient
transport (NEPT) service in “Diário da República”
(DRE). The legislative motivation was based on a
requirement laid down in the Memorandum of
Understanding signed between the Portuguese
Government and the International Monetary Fund,
the European Central Bank and the European Union
to reduce the cost of NEPT services (DRE, 2011).
This legislation mandates the minimum
requirements for the quality and safety of care
delivered to patients by NEPT services, (DRE,
2012a).
In 2011, the Northern Department of Health
(ARSN, 2011) reported the implementation of a
computer system to optimize the management of
NEPT services. The published documents state that
the computer system "will allow greater accuracy in
terms of prescription and simultaneously ensures
your organization rationally, promoting the transport
of multiple users whenever appropriate and
possible." The Northern Department of Health
expected to achieve a reduction of transport costs in
the region of €3 million related to a reduction of
20% of costs.
The current paper is composed of five sections.
After the introduction, Section 2 presents a
description of the problem, the main topics referred
by the law, and a brief literature review. Section 3
describes the model and presents the mathematical
formulation. Section 4 includes a discussion of the
heuristic and its results. Section 5 summarizes the
main conclusions of this work.
2 TRANSPORT PROBLEM
2.1 NEPT Definition
In light of the legislation in 2014 in Portugal (DRE,
2012b-h), and with regard to access by the users to
the services of the National Health Service (NHS),
NEPT is considered the associated transport system
for the health care system, where the origin or
destination are the medical centres and services
within the NHS, private entities or social entities
with a contract or agreement for the provision of
health care under the following conditions:
consultations for inpatient or outpatient surgery,
diagnostic procedures and therapeutic treatments,
transporting the patient after discharge from hospital
(with prior prescription) and transporting the patient
after discharge from the emergency room (with prior
prescription).
2.2 Transport Prescription
Prescription of transportation is solely the
262
A. Oliveira J., Ferreira J., Dias L., Figueiredo M. and Pereira G..
Non Emergency Patients Transport - A Mixed Integer Linear Programming.
DOI: 10.5220/0005214902620269
In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 262-269
ISBN: 978-989-758-075-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

responsibility of the attending physician, who shall
record the following information in the support
doctor system or equivalent system: the clinical
justification, or reasons for needing transport, and
verification of the economic condition. Where there
is a need to make the ambulance transport, the
following is required: the justification of the mode
of transport; the conditions under which the
transport should occur, particularly if the patient
requires ventilation, oxygen, wheelchair or is sick in
bed or isolated, the justification of the need for a
companion, and the justification of the need for
monitoring a health professional. After the shipping
prescription by the physician is completed, a
member of the administrative services staff validates
the economic condition of the patient and proceeds
to request transportation.
The requisition of transport satisfies the criteria
of minimizing the distance between the place of
origin, which must match the address from which
the transportation is effected, and the place of
destination, which must take into account the
location of the nearest place of origin. The NEPT is
performed by ambulance or by ambulette (simple
vehicle for patient transport - SVPT), which is a
passenger car, with a maximum capacity of five or
nine people, for the NEPT service whose clinical
condition does not impose the need for health care
during the transport.
The non-emergency patient transport is carried
out, where possible, in SVPT, taking into account
the need to optimize the capacity of the vehicle
against the following criteria: a) Grouping of clients,
regardless of origin, within the same route; b)
intended for health facility and preferably in the
same county or geographical area; c) users for the
same time period for consultation or treatment.
The attending physician shall justify the use of
individual transport ambulances, in a reasoned
manner. To further the grouping of users, the NEPT
may allow deviations of less than 10 km or 30
minutes journey, considering the travelling of the
first patient. The first patient assumes a critical
importance to define the route and to define the cost
of the transportation service. The first patient should
be the most distant patient to destination. A transport
on SVPT may carry a single patient in cases where
there are no other patients in the same time period or
along the same route, but this is an exception, and an
effort must be made to carry additional patients
where possible.
2.3 Transport Organization
Transportation must be ordered and scheduled at
least 48 hours before the journey. In individual
situations of an exceptional nature where this time
limit cannot be observed since no agreement has
been authorized between the requesting entity and
the carrier, the time limit of tacit acceptance and
approval of daily transportation requests is
determined by the computer system, at 15 hours and
30 minutes.
Requests for transportation are grouped
according to the schedules of supply of care to
which patients are intended, according to the
following guidelines:
• If the destination is within the geographic
boundaries of the patient’s county of origin or within
a radius of 10 km, these requests are grouped at one
hour intervals between delivery of the first and the
last patient;
• If the destination is outside the patient’s county of
origin, the interval between the delivery of the first
patient and the last can be two or four hours,
depending on the distance which, according to
geographical features, can be a range of 100 km to
130 km. This time is to be determined by the entity
responsible for organizing the transport.
The law states that the rule of the maximum
deviation should be applied to the "Optimization of
routes". Patients can be grouped for a journey,
regardless of parish or municipality, provided that
there is no deviation more than 10 km or 30 minutes,
provided the previous guidelines are observed.
The costs resulting from NEPT are the
responsibility of the requesting entity. Thus it
becomes important for the requesting entity to
optimize and streamline the process of transporting
non-emergency patients. It is not known how the
requesting entity must make the optimization of
NEPT, so this study hopes to be an important and
timely contribution.
2.4 Literature Review
The health care industry is rife with problems of
management and organization which have been
studied over the past several decades (Stiver et al.,
1982, Begur, Miller and Weaver, 1997). The
research attention to such problems is increasing
and, in the Western world, results from increased
demand for health care and the need to keep the
social cost of health care as low as possible. The
increased demand for health care has two vectors
justifying its growth: the democratization of access
to healthcare in developed societies and an aging
population. The increased demand for health care
causes transporting patients an important problem in
NonEmergencyPatientsTransport-AMixedIntegerLinearProgramming
263

the logistics of the health systems, since it is a
significant portion of operating costs. As far as
health logistic problems are concerned, an effective
transport service is now becoming an extremely
complex problem that has to be solved efficiently, so
it requires the best solution methodologies. Bellamy
et al. (2003) defines non-emergency transport needs
including ordinary situations in which a patient
simply cannot get to and from a healthcare facility
under their own power.
According to Wilken et al. (2005), patient
transportation is a critical part in providing
healthcare services. The authors discuss non-
emergency transportation in rural southern Illinois,
and they point out the importance of this issue.
Many individuals do not have the funds to pay for
public transportation and often public transportation
is not available or easily accessible to them so they
may miss regular doctor’s appointments, treatments,
and so on. As a consequence, the patient may
become more ill and then must be transported to a
medical facility by emergency transportation. Safei
(2011) studied the non-emergency medical
transportation services available in rural British
Columbia, and he reported the success of the
"Connections service" in enhancing rural and
northern communities’ access to healthcare services,
in particular among those with limited means and
resources.
Health authorities and health managers rely on
knowledge and state of the art technology to address
the logistic of health systems. Today, information
systems provide support for making the decision,
allowing gains in effectiveness and efficiency.
Transport in health care is a subject which has been
studied in the literature of optimization of logistic
processes for many years. Vaisblat and Albert
(2013) carried out one study which focused on the
scheduling of a special fleet serving the needs of
patients. Hains et al. (2011) addressed the issue of
safety and quality in NEPT. Recently Díaz-Parra et
al. (2014) published a state of the art review on the
problem of transport which included several variants
of problems, mathematical formulas, and techniques
used in problem solving.
One of the most studied routing problems is the
vehicle routing problem (VRP), which basically
aims to define a set of vehicle routes which are
optimized to visit a series of well-defined locations.
This problem presents a large number of variants
which address more specific situations. Berbeglia et
al. (2010) refer to the static or dynamic nature of
routing problems. In the static case, all the
information is known in advance and does not
change during the construction and implementation
phases. In the dynamic case, the available
information is updated (changed) during both the
construction phase and the implementation phase, by
virtue of new user requests. In these problems, the
proposed solution is a solution strategy that can be
changed with the passage of time. Typically,
dynamic situations of this kind occur in transport at
the request of users with special needs, which need
to be sent to the car which will transport them to
their destination. The dynamic aspect of this
problem stems from the fact that transportation
requests sometimes arise on the same day they need
to be met: this type of problem is called a DARP
(Dial-A-Ride Problem).
Both the static and dynamic versions of DARP
have received significant contributions, such as a
review of Cordeau and Laporte (2007) about models
and algorithms. Psaraftis (1988) examined a single
route of this problem in which clients request a
service to be made available as soon as possible.
Whenever a new order is entered, the system updates
the proceedings and attempts to accommodate the
new request on an existing, but only partially
complete, route. Meanwhile, Madsen et al. (1995)
presented an algorithm to a real case of the dynamic
DARP with multiple vehicles that met up to 300
requests daily to transport people with special needs.
One VRP variant is the “Vehicle routing
problems with profits” (Archetti et al., 2013). In this
type of problem, two different decisions have to be
made simultaneously—which which customers to
serve and how to sequence them in one or several
routes. In general, a profit is associated with each
customer that makes the customer more or less
attractive. The majority of real-world applications
require systems that are more flexible in order to
overcome some imposed constraints that may lead to
the selection of customers. To deal with the selection
of customers, the Team Orienteering Problem (TOP)
models can be used. The main difference between
the TOP and the VRP is related to the fact that not
all the TOP vertices of the graph (clients) must be
visited, as in the VRP. In the TOP, each customer
has an associated profit, and the routes have
maximum durations or distances. The choice of
customers is made by balancing their profits and
their contributions to the route duration or distance.
The objective is to maximize the total reward
collected by all routes while satisfying the time
limit.
The TOP is a fairly recent concept, first
suggested by Butt and Cavalier (1994) under the
name Multiple Tour Maximum Collection Problem.
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
264

Later, Chao et al. (1996) formally introduced the
problem and designed one of the most frequently
used sets of benchmark instances. TOP has recieved
significant attention from the scientific community
(Vansteenwegen, Souffriau, Oudheusden, 2011;
Archetti, Speranza and Vigo, 2013) either in
presenting exact solution methodology (Archetti,
Bianchessi and Speranza, 2013) or in approximate
solution methodology (Hu and Lim, 2014).
Vansteenwegen and his team maintain a repository
of public instances (The Orienteering Problem: Test
Instances, 2014).
Gutiérrez-Jarpa et al. (2009) studied the problem
with fixed delivery and optional collections, utilizing
a mixed solution which uses VRP for delivery and
TOP for collection. The authors studied the
particular case of a single vehicle and presented a
new branch-and-cut method that allows the system
to solve larger instances. The method can solve
instances which include up to 90 vertices. The
authors refer to the need to extend the investigation
to cases with multiple vehicles and the development
of heuristics to solve large scale instances. Despite
the great practical interest that this modelling system
has for reverse logistics, the authors report they
found only study, Gribkovskaia et al. (2008) that
have applied tabu search to the single vehicle pickup
and delivery problem with selective pickups.
3 THE MODEL
The real problem studied in this article concerns the
non-emergency transport of patients from their
homes to the hospital and from the hospital back to
their homes. Currently, in Portugal the shuttle
typically collects patients from their homes to the
hospital for treatment and back again. This system
creates the situation – “many (origins)-to-one
(target)-to-many (destinations).” The way to
organize this transport is not clearly established in
law, which means that money is being wasted on the
waiting time of the vehicle, and patients often waste
time waiting for their transportation.
We decided by modelling the NEPT problem
with the TOP point of view. What will happen is that
given a list of non-urgent patients for whom
transportation was requested and given a fleet of
vehicles available with a capacity of eight seats, it is
the allocation of transport services to maximize the
occupancy of the vehicle and minimizing the
distance travelled. Patients who can not be included
in the routes of these vehicles will be transported in
specially requested for this ambulances service.
3.1 Mathematical Model
Since the group of patients is a severely constrained
situation, it is our choice to model the real problem
presented by the NHS as a Team Orienteering
Problem, solving for the set of available vehicles.
Vertices not included in the routes of the problem
are the users who will make the path by individual
transport.
Our model is based on the Team Orienteering
Problem and we follow the mathematical model
presented by Labadie et al (2012). We define the
search of different paths from a common start point
(i=1) to a common ending point (i=n). If we want
the start point to be the same ending point, we use
the same coordinates for both points.
We have established the following variables:
k
ij
x
- set of binary variables that is equal to 1 if arc
(i, j) is selected in the path k and 0 otherwise.
k
j
y
- set of binary variables that is equal to 1 if
vertex j is in path k and 0 otherwise.
k
j
w - set of binary variables that is equal to 1 if
vertex j is the first vertex in the path after the start
point.
k
W - is the maximum value for the length of the
path that is a function of the distance of the first
vertex to terminal vertex and an allowed increase.
j
X
- a variable the controls a sequential number for
the vertices in the path.
k
ij
TPS - is an auxiliary variable to linearize the
product of
kk
ij
wy
.
To define the objective function we define three
parcels.
TIC is the Total Individual Cost, equivalent
to transporting each patient individually.
CIP is the
Cost of Individual Transport for patients who are
transported together with some other patient. This
parcel is the main savings when a patient is not
transported individually.
A
PC is Additional Patient
Cost (incremental cost) related to patients who are
transported together in same vehicle with the first
patient. This parcel is to pay the additional
deviations to collect patients in the route of the first
patient. By law, this cost is nowadays 20% of the
cost of the first patient in the route. In a solution
with an individual transport for all patients, CIP and
APC are equal to zero.
1
1
2
n
iin
i
TIC c c
11
1,
22
()
mn n
k
j
jn ij
kj i
CIP c c x
NonEmergencyPatientsTransport-AMixedIntegerLinearProgramming
265

1
1
121
mnn
k
iin ij
kji
A
PC s c c TPS
Figure 1 explains these calculations considering
the transportation of two patients: A and B. COST1
is the solution cost using two vehicles/routes, both
starting at S and ending at E; COST2 is the solution
cost using only one vehicle, where A is first patient
in the route; while COST3 is the solution cost using
one vehicle, where B is the first patient in the route.
It is possible to establish the following relations:
COST1=TIC;
CIP(A)=a1+a2; CIP(B)=b1+b2;
COST2=TIC-CIP(B)+APC(B);
COST2=TIC-CIP(B)+20%CIP(A);
COST3=TIC-CIP(A)+APC(A);
COST3=TIC-CIP(B)+20%CIP(B).
Obviously, APC(A) and APC(B) depends on
which is the first patient in the route where they are
included.
Figure 1: Cost parcelles.
The mathematical formulation of the Mixed
Integer Linear Programming (MILP) is presented
next:
min TIC CIP APC
(1)
subject to:
1
2
1, , 1; 1, ,
n
kk
ij j
i
x
yj nk m
(2)
1
12
2, , ; 1, ,
nn
kk
ij ji
ii
x
xj nk m
(3)
1
1
21
11,,
nn
kk
jin
ji
x
xk m
(4)
1
11
12,,1
mn
k
ij
ki
x
jn
(5)
1
1, ,
kk
jj
wxk m
(6)
1
1
2
1, ,
n
kk
jn j
j
WcxdMaxk m
(7)
1
22
1, ,
nn
kk
ij ij
ij
cx W k m
(8)
1
1X
(9)
1, , 1;
12,,;
1, ,
kk
j i ij ij
in
X
XxM x j n
km
(10)
11
max
22
1, ,
nn
kk
ii
ii
wyLk m
(11)
2, , 1
2, , 1
1, ,
1
kk
ij i
kk
ij j
kkk
ij i j
TPS w
in
TPS y j n
km
TPS w y
(12)
Expression (1) represents the objective function
to be minimized. It is intended to diminish the total
transport cost removing individual transportation as
much as possible, paying the necessary deviations to
collect patients in shared routes.
In terms of constraints, expression (2) assign
visited patients to only one route, and in expression
(5) patients could be visited by only one route.
Expression (3) ensures the flow conservation in each
node. Expression (4) ensures that a vehicle starts the
route from node 1. Expressions (6) (7) and (8)
establish the first patient in the route and calculate
the maximum length for the route according to the
distance from the first patient to the destination. The
law allows an increase in the length of the route to
collect additional patients, but this is currently
limited (
dMax ) to 10 km or 30 minutes.
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
266
Expressions (9) and (10) eliminate sub tours, and the
capacity of vehicle is verified in expression (11).
Expression (12) linearizes the objective function.
3.2 NEOS Server Experiments
The model was implemented in AMPL language and
submitted to the NEOS Server to evaluate the
quality of solutions provided by this compact
formulation. Sixty-four Euclidean instances were
randomly created to perform the computational
experiments. The instances are divided into two sets,
based on the capacity of the vehicle: four places and
eight places available to transport the patients. The
size of the instances varies from twenty to one
hundred patients, and from three to ten vehicles.
Table 1: Experimental results (capacity = 4).
vehicles x capacity
nodes 3x4 4x4 7x4 10x4
20
1272.65 1184.0 1055.93 1055.93
30
1840.37 1693.42 1383.03
gap 5.43%
1299.10
gap 34.16%
40
2671.87 2498.09 2048.70
gap 20.73%
1776.02
gap 70.69%
50
3478.46 3248.65 2709.00
gap 17.63%
2362.49
gap 47.45%
60
4311.22 4074.27
gap 3.42%
3455.71
gap 17.67%
2987.28
gap 36.01%
70
5043.11 4802.52
gap 3.29%
4131.28
gap 12.73%
3718.51
gap 31.35%
80
5818.70 ----
mem_error
4931.43
gap 12.31%
4507.76
gap 30.52%
100
----
mem_error
7155.63
gap 4.55%
----
mem_error
8198.99
gap 77.61%
Table 2: Experimental results (capacity = 8).
vehicles x capacity
nodes 3x8 4x8 7x8 10x8
20
1245.22 1156.65 1048.91 1048.91
30
1812.94 1665.99 1376.02 1299.10
gap 30.13%
40
2561.95 2362.82 1915.61
gap 23. 26%
1706.82
gap 66.38%
50
3238.03 2974.04 2362.52
gap 31. 87%
2075.69
gap 68.38%
60
4003.97 3702.97 2932.47
gap 34. 77%
2523.03
gap 83.67%
70
4693.05 4389.54
gap 6.88%
3682.41
gap 36. 55%
3135.39
gap 81.95%
80
5450.52 ----
mem_error
4332.84
gap 32. 28%
3686.95
gap 70.91%
100
6785.59 6505.46
gap 13.98%
----
mem_error
----
mem_error
Using the NEOS Server with AMPL/
Gurobi/MINTO/scip/XpressMP, the MILP could not
find a solution for all instances. Experiments with
instances of different sizes were performed to find
the maximum number of vertices that it is possible
to solve optimally. Memory errors (“mem_error”)
were reported when the solution exceed 3GB of
memory limit. Also, it is only possible to dispose a
maximum of eight hours of computation with the
NEOS Server. When the maximum time was
achieved, it reported the best solution founded and
the correspondent gap. Tables 1-2 present these
results.
Apparently solving instances with vehicles with
larger capacity becomes easier and it was possible to
solve an instance with one hundred patients and
three vehicles.
4 HEURISTIC PROCEDURE
As expected, the compact model could not be used
to solve for large instances using the NEOS Server.
However, the NEOS Server can solve the large
instance’s terms of vertices using only one vehicle
(Orienteering Problem - OP). Considering this
situation, we developed a heuristic procedure to
solve the TOP that is based in successive OP
solutions. Iteratively, to the remaining unvisited
vertices, we solve the problem using the compact
formulation with one vehicle.
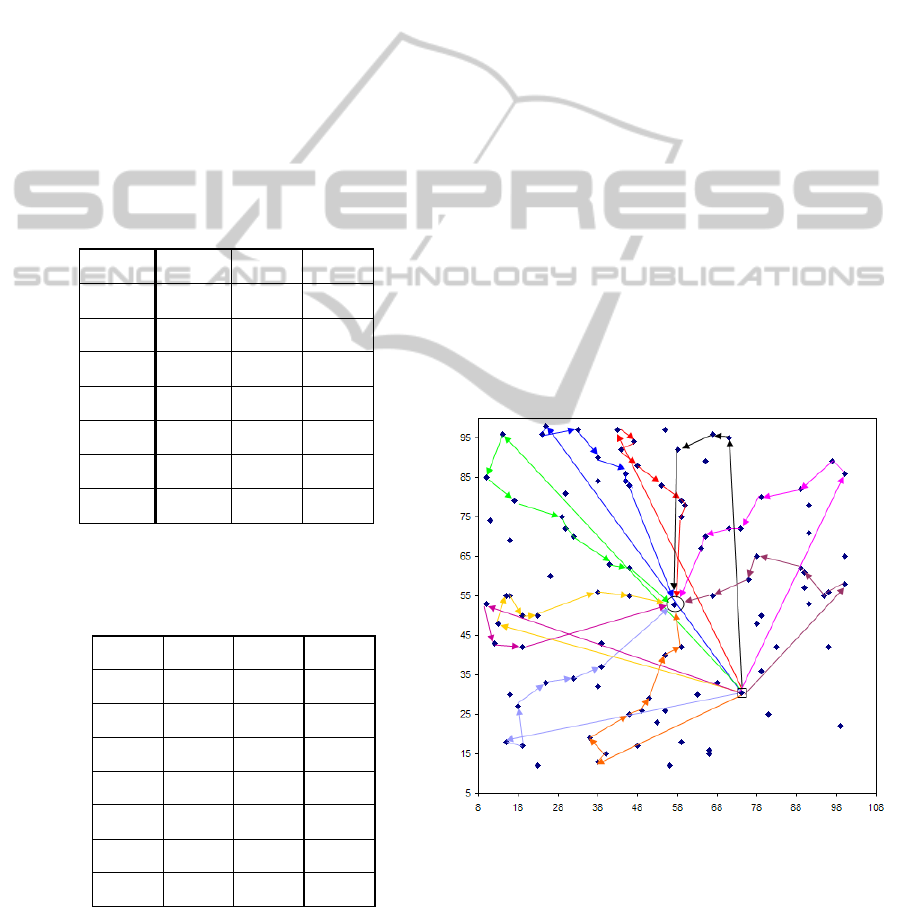
Figure 2: Heuristic Solution (100 nodes_10x8).
Figure 2 presents the solution obtained with
heuristic procedure to solve the large instance (one
hundred patients with ten vehicles each with
capacity of eight patients). The patients not included
in these ten routes must be transported individually.
In terms of computational time, 198 seconds was
NonEmergencyPatientsTransport-AMixedIntegerLinearProgramming
267

required to produce the 10 routes.
To confirm the results obtained with this
heuristic, we solved the 32 instances with capacity
equal 8. Table 3 compares the results obtained with
NEOS Server (“NeosS” line) and heuristic (“heur”
line) in this set of instances.
Table 3: Experimental results (capacity = 8).
vehicles x capacity
nodes 3x8 4x8 7x8 10x8
20
NeosS
heur
1245.22
1245.22
1156.65
1156.65
1048.91
1048.91
1048.91
1048.91
30
NeosS
heur
1812.94
1812.94
1665.99
1665.99
1376.02
1376.02
1299.10*
1311,43
40
NeosS
heur
2561.95
2561.95
2362.82
2362.82
1915.61*
1930,27
1706.82*
1748,65
50
NeosS
heur
3238.03
3240.36
2974.04
2994.45
2362.52*
2382.93
2075.69*
2118,02
60
NeosS
heur
4003.97
4003.97
3702.97
3707.29
2932.47*
2917.65
2523.03*
2478.83
70
NeosS
heur
4693.05
4693.05
4389.54*
4389.54
3682.41*
3624.17
3135.39*
3163.34
80
NeosS
heur
5450.52
5450.52
----
5141.44
4332.84*
4240,82
3686.95*
3627,75
100
NeosS
heur
6785.59
6785.59
6505.46*
6403.38
----
5398.40
----
4801.58
The heuristic obtained the optimal solution in 13
instances, and obtained better or equal result than
NEOS Server in 23 of 32 instances, representing
around 70%. We recall that for some instances we
present the values obtained by the NEOS Server at
the end of available computation time. These
instances are signalized with an asterisk “*” .
5 CONCLUSIONS
This work presents a model and a heuristic to solve
the problems posed by the non-emergency patient
transport in Portugal, given the new rules recently
established. The model follows the same principle of
the Team Orienteering Problem to select the patients
to be included and the routes providing the
maximum reduction in the costs. This approach is
different from VRP strategies because some vertices
are not visited. Particularly in this problem a patient
that it is not visited by the routes means that the
patient must be transported individually. Indeed, this
model establishes the best sets of patients that
should be transported jointly.
In this study, several Euclidean instances were
generated to test our approach. The model was
implemented in AMPL and our compact formulation
was used to solve the instances using the NEOS
Server. Instances with one hundred patients and ten
vehicles with a capacity for eight patients each could
not be solved within available computation time
provided by the NEOS Server.
A heuristic procedure based on iteratively
solving problems with one vehicle was presented,
and this heuristic provides good results in terms of
accuracy and computation time. Taking into account
the knowledge provided by this study, a greedy
heuristic and a genetic algorithm will be developed
to solve this problem.
In this work, it is assumed the transport is the
type “1 to many to 1”, meaning the all patients have
the same destination. For further work, we will study
the situation of several destinations. Also, this study
assumes an equal due date for all patients, but future
work will consider different due dates for patients.
Finally, our model was tested with real instances
with distances provide by Google Maps and
generates promising preliminary results.
ACKNOWLEDGEMENTS
This work has been partially supported by the
project GATOP - Genetic Algorithms for Team
Orienteering Problem (Ref PTDC/EME-GIN/
120761/2010), financed by national funds by FCT /
MCTES, and co-funded by the European Social
Development Fund (FEDER) through the
COMPETE - Programa Operacional Fatores de
Competitividade (POFC) Ref FCOMP-01-0124-
FEDER-020609.
This work has been partially supported by FCT –
Fundação para a Ciência e Tecnologia within the
Project Scope: PEst-OE/EEI/UI0319/2014
The authors would like to thank the NEOS
Server at the University of Wisconsin in Madison
for providing support to this study.
The authors would like to thank the anonymous
reviewers for their valuable comments and
suggestions to improve the paper.
REFERENCES
Archetti, C., Bianchessi, N., & Speranza, M. G. (2013).
Optimal solutions for routing problems with profits.
Discrete Applied Mathematics, 161(4), 547-557.
Archetti, C., Speranza, M. G., & Vigo, D. (2013). Vehicle
routing problems with profits. Tech. Report
WPDEM2013/3, University of Brescia.
ARSN (2011). http://portal.arsnorte.min-saude.pt/portal/
page/portal/ARSNorte.
Begur, S. V., Miller, D. M., & Weaver, J. R. (1997). An
integrated spatial DSS for scheduling and routing
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
268

home-health-care nurses. Interfaces, 27(4), 35-48.
Bellamy, G. R., Stone, K., Richardson, S. K., &
Goldsteen, R. L. (2003). Getting from here to there:
Evaluating West Virginia's rural nonemergency
medical transportation program. The Journal of Rural
Health, 19(S5), 397-406.
Berbeglia, G., Cordeau, J. F., & Laporte, G. (2010).
Dynamic pickup and delivery problems. European
Journal of Operational Research, 202(1), 8-15.
Butt, S. E., & Cavalier, T. M. (1994). A heuristic for the
multiple tour maximum collection problem.
Computers & Operations Research, 21(1), 101-111.
Chao, I., Golden, B. L., & Wasil, E. A. (1996). A fast and
effective heuristic for the orienteering problem.
European Journal of Operational Research, 88(3),
475-489.
Cordeau, J. F., & Laporte, G. (2007). The dial-a-ride
problem: models and algorithms. Annals of Operations
Research, 153(1), 29-46.
Czyzyk, J., Mesnier,M. P., Moré. J. J. (1998). The NEOS
server. IEEE J. Computational Sci. Engrg. 5, 68-75.
Díaz-Parra, O., Ruiz-Vanoye, J. A., Bernábe Loranca, B.,
Fuentes-Penna, A., & Barrera-Cámara, R. A. (2014).
A Survey of Transportation Problems. Journal of
Applied Mathematics, vol. 2014, Article ID 848129,
17 pages, 2014. doi:10.1155/2014/848129.
Dolan, E. D.( 2001). NEOS server 4.0 administrative
guide. Technical Memorandum ANL/MCS-TM-250,
Mathematics and Computer Science Division,
Argonne National Laboratory, Argonne, IL, 2001.
DRE (2011). Despacho n.º 16843/2011, Diário da
República, 2.ª série — N.º 239 — 15 de Dezembro de
2011, 48767-48768.
DRE (2012a). Portaria n.º 142-A/2012. Diário da
República, 1.ª série — N.º 94 — 15 de maio de 2012,
2532-(2)-2532-(3).
DRE (2012b). Portaria n.º 142-B/2012. Diário da
República, 1.ª série — N.º 94 — 15 de maio de 2012,
2532-(3)-2532-(6).
DRE (2012c). Declaração de Retificação n.º 27-A/2012.
Diário da República, 1.ª série — N.º 107 — 1 de junho
de 2012, 2928-(2).
DRE (2012d). Portaria nº178-B/2012. Diário da
República, 1.ª série — N.º 107 — 1 de junho de 2012,
2928-(2).
DRE (2012e). Despacho n.º 7702-A/2012. Diário da
República, 2.ª série — N.º 108 — 4 de junho de 2012,
20410-(2).
DRE (2012f). Despacho n.º 7702-C/2012. Diário da
República, 2.ª série — N.º 108 — 4 de junho de 2012,
20410-(3)-20410-(6).
DRE (2012g). Despacho nº 8705/2012. Diário da
República, 2.ª série — N.º 125 — 29 de junho de
2012, 22880- 22881.
DRE (2012h). Declaração de Retificação n.º 36/2012.
Diário da República, 1.ª série — N.º 135 — 13 de
julho de 2012, 3657- 3664.
Gribkovskaia, I., Laporte, G., & Shyshou, A. (2008). The
single vehicle routing problem with deliveries and
selective pickups. Computers & Operations Research,
35(9), 2908-2924.
Gropp, W., & Moré, J.J. (1997). Optimization
environments and the NEOS server. M. D. Buhmann,
A. Iserles, eds. Approximation Theory and
Optimization: Tributes to M. J. D. Powell. Cambridge
University Press, Cambridge, UK, (1997) 167-182.
Gutiérrez-Jarpa, G., Marianov, V., & Obreque, C. (2009).
A single vehicle routing problem with fixed delivery
and optional collections. IIE Transactions, 41(12),
1067-1079.
Hains, I. M., Marks, A., Georgiou, A., & Westbrook, J. I.
(2011). Non-emergency patient transport: what are the
quality and safety issues? A systematic review.
International Journal for Quality in Health Care,
23(1), 68-75.
Hu, Q., & Lim, A. (2014). An iterative three-component
heuristic for the team orienteering problem with time
windows. European Journal of Operational Research,
232(2), 276-286.
Labadie, N., Mansini, R., Melechovský, J., & Wolfler
Calvo, R. (2012). The team orienteering problem with
time windows: An lp-based granular variable
neighborhood search. European Journal of
Operational Research, 220(1), 15-27.
Madsen, O. B., Ravn, H. F., & Rygaard, J. M. (1995). A
heuristic algorithm for a dial-a-ride problem with time
windows, multiple capacities, and multiple objectives.
Annals of Operations Research, 60(1), 193-208.
Psaraftis, H. N. (1988). Dynamic vehicle routing
problems. Vehicle routing: Methods and studies, 16,
223-248.
Safaei, J. (2011). A ride to care–a non-emergency medical
transportation service in rural British Columbia. Rural
and Remote Health, 11(1637).
Stiver, H. G., Trosky, S. K., Cote, D. D., & Oruck, J. L.
(1982). Self-administration of intravenous antibiotics:
an efficient, cost-effective home care program.
Canadian Medical Association Journal, 127(3), 207.
Vaisblat, A., & Albert, D. (2013). Medical non-emergency
patient centered scheduling solution. New Magenta
Papers, 40.
Vansteenwegen, P., Souffriau, W., & Oudheusden, D. V.
(2011). The orienteering problem: A survey. European
Journal of Operational Research, 209(1), 1-10.
Wilken, P., Ratnapradipa, D., Presley, D., & Wodika, A.
B. (2014). An evaluation of the non-emergency
medical transportation system of rural southern
illinois. American Journal of Health Studies, 29(2).
NonEmergencyPatientsTransport-AMixedIntegerLinearProgramming
269
