
Face and Facial Expression Recognition
Fusion based Non Negative Matrix Factorization
Humayra Binte Ali
1
and David M. W. Powers
1,2
1
School of Computer Science, Engineering, and Mathematics, Flinders University, Adelaide, South Australia
2
Beijing Municipal Lab for Multimedia and Intelligent Software, Beijing University of Technology, Beijing, China
Keywords:
NMF-Non Negative Matrix Factorization, OEPA- Optimal Expression- specific Parts Accumulation, FR-Face
Recognition, FER- Facial Expression Recognition.
Abstract:
Face and facial expression recognition is a broad research domain in machine learning domain. Non-negative
matrix factorization (NMF) is a very recent technique for data decomposition and image analysis. Here we
propose face identification system as well as a facial expression recognition, which is a system based on NMF.
We get a significant result for face recognition. We test on CK+ and JAFFE dataset and we find the face
identification accuracy is nearly 99% and 96.5% respectively. But the facial expression recognition (FER) rate
is not as good as it required for the real life implementation. To increase the detection rate for facial expression
recognition, our propose fusion based NMF, named as OEPA-NMF, where OEPA means Optimal Expression-
specific Parts Accumulation. Our experimental result shows OEPA-NMF outperforms the prevalence NMF
for facial expression recognition. As face identification using NMF has a good accuracy rate, so we are not
interested to apply OEPA-NMF for face identification.
1 INTRODUCTION
The face has been termed as the most prominent per-
ceptual stimulus in real world for social and person-
to-person communication (Frith and Baron-Cohen,
1987). Each face possesses the uniqueness and ro-
bustness, which makes is completely distinguishable
from other faces. For this reason, from safety en-
hancement to person authority checking, face recog-
nition is a valuable application area. Face recogni-
tion covers both the domain of Face Identification
and Face Verification. Face Identification means to
find the identity of a given person out of a pool of
N persons (1 to N matching) and this Face Identi-
fication is widely used in video surveillance, infor-
mation retrieval, video games and some other hu-
man computer interaction areas. On the other hand,
Face Verification establishes the process of confirm-
ing or denying the identity claimed by a person (1 to 1
matching). To verify access control into computer or
mobile device or building gate, and digital multime-
dia data access control, Face Verification technique is
needed. Facial expression plays a great role in both
human to human and human to machine communica-
tion. (Charlesworth and Kreutzer, 1973) mentioned
infants as young as three months old are able to dis-
cern facial emotion. To express emotion, attitude and
feelings human communicate through speech, facial
expression and also body language. Facial expres-
sion has a wide variety of applications, like, pain level
measurement for medical purpose, terrorist identifi-
cation, lie detection etc. Stemming from Darwin’s
work, the earliest discrete theories of emotion hypoth-
esized the existence of a small number of basic emo-
tions, such as happiness, sadness, fear, anger, surprise
and disgust (Ekman, 1994). In this research work our
main concern is to increase the detection rate of these
basic emotions only. We apply here NMF for data fac-
torization and euclidian distance as classifier, to rec-
ognize basic facial expressions. We also compare the
system with principal component analysis based FER
system.
2 RESEARCH BACKGROUND
Subspace learning algorithms has been successfully
used in image analysis, data mining and video com-
pressing areas. Basically these methods are widely
used to handle large amount of data as it performs
dimension reduction as well as finds the direction
along with certain properties. The most prevalence
426
Binte Ali H. and M. W. Powers D..
Face and Facial Expression Recognition - Fusion based Non Negative Matrix Factorization.
DOI: 10.5220/0005216004260434
In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART-2015), pages 426-434
ISBN: 978-989-758-074-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

subspace learning techniques are Principal Compo-
nent Analysis (PCA), Independent Component Anal-
ysis (ICA), Linear Discriminant Analysis (LDA), Non
Negative Matrix Factorization (NMF) etc. Compared
with others, NMF is a recent technique in machine
learning areas. This research work is mainly based
on NMF and comparison with PCA following same
procedure. PCA based face recognition system has
been developed in (J. Buhmann and Malsburg, 1990),
where singular value decomposition (SVD), an ex-
tension of PCA, has been used. PCA by apply-
ing Bayesian method is used for face recognition
(Moghaddam and Pentland, 1997). These (M. Lades
and Konen, 1993) (C. Hesher and Erlebacher, 2003)
are some other successful applications of PCA. Many
of these mentioned works are performed based on the
early research of PCA (Turk and Pentland, 1991) with
some extensions.
NMF is becoming popular in face recognition re-
search areas. for sparse representation of data (Ci-
chocki, 2009). Now we are going to discuss some
research works based on NMF. An extension of basic
NMF has been implemented on ORL face database
(Ensari and Zurada, 2012). (Li and Oussalah, 2010)
claims 75% recognition rate for face recognition.
(L. Zhao and Xu, 2008) proposes polynomial ker-
nel NMF for both face and facial expression recog-
nition on JAFFE and CK dataset of facial expres-
sion. They identified PNMF is superior to KPCA
or KICA although NMF has very competitive re-
sult with PCA and ICA based on classifier diversity.
They also concluded that NMF algorithm retrieves
more powerful latent variables for pattern classifica-
tion, as evidenced by their experimental results (I. Bu-
ciu and Pitas, 2007). The work of (Yeasin and Bul-
lot, 2005) compares the performance of linear and
non-linear data projection techniques in classifying
facial expressions using Principal Component Analy-
sis (PCA), Non-negativeMatrix Factorization (NMF),
Local Linear Embedding (LLE) and concludes that
90.9%, 88.7% and 92.3% accuracy for PCA, NMF
and LLE respectively. Research work of (L. Zhao and
Xu, 2008) and (Zilu and Guoyi, 2009) have also done
the similar work for NMF based face and expression
analysis.
In this section we have discussed some research
approach of face and facial expression recognition
using NMF and PCA on 2D images. It is really
difficult to compare among several subspace learn-
ing algorithms as they have been tested on different
datasets. Also the normalization and distance mea-
sure varies method to method. One method which has
high recognition rate and tested on neutral front faced
images may not be logically better than the method
with low error rate tested on noisy images with vary-
ing head poses and vice versa.
3 PRINCIPAL COMPONENT
ANALYSIS
Research shows that Principal Component Analysis is
a well established method in subspace learning algo-
rithm areas. It has been implemented widely in ma-
chine learning, computer vision and data mining ar-
eas. Basically PCA is a linear transformation method,
which finds the directions that maximizes the vari-
ance of datasets. It projects the dataset in a differ-
ent subspace without the class labels. Mathematically
for an mXm matrix P, Data can be decomposed into
P = P∧ P
T
, here eigenvector is each column of P and
eigenvalue is the diagonal matrix ∧. This way of ma-
trix decomposition is called eigen decomposition. Be-
low are the steps of PCA algorithm. Now we want to
finally give PCA algorithm.
It is given
D = p
1
,..., p
n
. (1)
First compute
¯p =
1
n
∑
i
p
i
(2)
and
∑
=
1
n
n
∑
i=1
(p
i
− ¯p)(p
i
− ¯p)
T
. (3)
Then find the k eigenvectors of equation(3)with
largest eigenvalues:
U
1
,....,U
k
(4)
These are called principal components Project
Z
i
= ((p
i
− ¯p)
T
U
1
,....,(p
i
− ¯p)
T
U
k
) (5)
It is to be noted that only the top eigenvectors need to
be calculated, not all of them, which is a lot faster for
computation.
4 NON-NEGATIVE MATRIX
FACTORIZATION
In the previous section, many machine learning re-
search shows that Non-negative matrix factorization
(NMF) is a useful decomposition for multivariate data
like face and facial expression recognition. According
to research studies (Lee and Seung, 2009) it is clear
that NMF can be understood as part based analysis
as it decomposes the matrix only into additive parts.
This factorization technique of NMF is completely
FaceandFacialExpressionRecognition-FusionbasedNonNegativeMatrixFactorization
427

different of Principal Component Analysis (PCA) or
Vector Quantization (VQ) in terms of the nature of the
decomposed matrix. PCA and VQ works on holistic
features where as NMF decomposes a part based rep-
resentation of matrix (Lee and Seung, 2009). Here we
apply NMF and PCA on whole faces and on different
facial parts. PCA, ICA, VQ, NMF all these subspace
learning techniques reduces the dimension and make
a distributed represented in which each facial image
can be approximated using a linear combinations of
all or selected basis images.
The factorization problem can be written like this,
X ≈ W.H (6)
where X ∈ R
MxN,≧0
This is similar to the PCA or ICA initialization.
In the above equation, R defines the low-rank dimen-
sionality. Here [W] and [H] are quite unknown; [X]
is the known input source. Now we have to estimate
the two factors. We have to start with random [W]
and [H]. Columns of [W] will contain vertical infor-
mation about [X] and the horizontal information will
be extracted in the rows of [H]. NMF does additive
decompositions and parts make this decomposition.
We first have to define the cost functions to solve an
approximate representation of the factorization prob-
lem of X ≈ W.H. By using some measure of distance
between two non-negative matrices [P] and [Q], such
cost functions can be constructed. The square of the
Euclidian distance between the matrices [P] and [Q],
is one fruitful measure.
||P− Q||
2
=
∑
i, j
(P
ij
− Q
ij
)
2
(7)
The above equation is lower bounded by zero and ab-
solutely vanishes if and only if [P] = [Q]. To define
the cost function, another useful representation is,
D(P k Q) =
∑
i, j
(P
ij
log
P
ij
Q
ij
− p
ij
+ Q
ij
) (8)
In the aboveequation, when
∑
i, j
P
ij
=
∑
i, j
Q
ij
= 1,
the above Kullback-Leibler or relative entropy re-
duces. Here [P] and [Q] can be regarded a normal-
ized probability distribution. Now, following the cost
function of equation (2), we have to define it for the
input matrix [X] and the non-negative decomposed
matrix [W] and [H]. If we do that, the cost function
would be,
k V = WH k
2
(9)
The main goal is now to reduce the distance ||V −
WH||. To do that, first we have to initialize [W] and
[H] matrix. Then we apply the multiplicative up-
date rule, which is described in the paper of (Lee and
Seung, 2009). They claim and prove that the mul-
tiplicative update rules minimize the Euclidean dis-
tance ||P − Q|| and also the divergence, D(P||Q) is
decreasing when multiplicative update rule is applied.
In our programming here, we use the Euclidian dis-
tance as a cost function and apply the multiplicative
update rule to minimize the distance. The rules are
defined below,
H
pβ
← H
pβ
(W
T
V)
pβ
(W
T
WH)
pβ
(10)
W
αp
← W
αp
(VH
T
)
αp
(WHH
T
)
αp
(11)
According to the mathematical analysis, if we use
the equation (5) and (6) to decrease the Euclidian dis-
tance ||V −WH||, the distance ||V −WH|| converges.
Our experimental analysis also shows that and we get
a significant output on facial expression dataset.
5 DATASETS
For experimental purpose we implemented our algo-
rithm on both Cohn Kanade and JAFFE Facial Expes-
sion dataset. Nearly 2000 image sequences from over
200 subjects are in CK+ dataset. All the expression
dataset maintain a sequence from neutral to highest
expressive grace. We took two highest graced expres-
sive image of each subject. As we took 100 subjects,
so the total image becomes 1200. 100 subject x 6
different expression x 2 of each expression. So it be-
comes 100 x 6 x 2=1400. There is a significant varia-
tion of age group, sex and ethnicity.
In the JAFFE datasat, each of the ten subjects
posed for 3 or 4 examples of each of the six basic fa-
cial expressions (happiness, sadness, surprise, anger,
disgust, fear) as well as a neutral face expression. Al-
together JAFFE has 219 facial images, and we used
all of these in our experiments.In JAFFE set each sub-
ject took pictures of herself while looking through a
semi-reflective plastic sheet towards the camera. The
following figure (Fig. 1) shows a portion of the dataset
of our experiment. Fig. 2 is the prepared data to feed
in our fusion based prposed mathod which we want
to compare against the predominant NMF method.
These segmented dataset is prepared by using our al-
gorithm which is described in the corresponding sec-
tion and our work (Ali and Powers, 2014). In figure3,
The first, second, third and fourth rows show mouth,
left eye, and right eye and nose respectively.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
428

Figure 1: CK+ and JAFFE dataset.
Figure 2: Segmented Four Facial Parts.
6 EXPERIMENTS
6.1 Face and Facial Parts Detection
In CK dataset, the background is large with all the
face images. First we apply the Viola-Jones algo-
rithm (Paul and Jones, 2001) to find the faces. For
eyes, nose and mouth detection we applied cascaded
object detector with region set on already detected
frontal faces (Fig. 3). This cascade object detector
with proper region set can identify the eyes, nose and
mouth. Actually it uses Viola-Jones Algorithm as an
underlying system. This object detection algorithm
uses a cascade of classifiers to efficiently process im-
age regions for the presence of a target object. Each
stage in the cascade applies increasingly more com-
plex binary classifiers, which allows the algorithm to
rapidly reject regions that do not contain the target. If
the desired object is not found at any stage in the cas-
cade, the detector immediately rejects the region and
processing is terminated. This process has been de-
scribed in our previous work (Ali and Powers, 2014).
We perform face identification and facial parts de-
tection on 1200 images (6 expression X 100 subjects
X 2 imagees each images) in CK+ and 219 images
on JAFFE dataset. The CK dataset varies greatly in
image brightness.For image pre normalization proce-
dure, first we use Contrast Adjustment to enhance the
image from very light images. Then to improve the
contrast of the very dark images we apply Histogram
equalization.
Figure 3: Face and Facial Parts Detection replicated from
our previous work (Ali and Powers, 2014).
6.2 Training and Testing Data
For face recognition using NMF we separated the data
as 60% for train and 40% for test data. But while us-
ing PCA we use 70% of the data as train and 30% of
the total data as test images. This is because, PCA
gives a good result when the train dataset is large
enough than the test portion and this has been seen
by our programme. We have given a table in result
analysis section in which way the recognition result
is depended upon the training sample programmed by
PCA and NMF separately.
6.3 Face vs Facial Expression
Recognition
We achieved a good recognition result for face recog-
nition using straight PCA and NMF. But result shows
NMF has a greater recognition result than PCA. This
is because Non-negative matrix factorization (NMF)
learns a parts-based representation of faces and part
based representation is very suitable for occluded and
low intensity or high brightness images.
On the other hand, NMF and also PCA has a poor
recognition capability for facial expression compared
to face recognition capability. Like some other sub-
space learning techniques, PCA and NMF tends to
find similar faces rather than similar expression. To
improve the recognition rate we propose fusion based
NMF and PCA algorithms to fuse the parts of faces
to recognize the facial expressions and we term it
as Optimal Expression-specific Parts Accumulation
(OEPA) method. Actually this method has been de-
veloped in our previous work (Ali and Powers, 2013).
We apply here NMF based OEPA and compare this
proposed system with PCA based OEPA.
6.4 Proposed Algorithm
Sometimes a subset of all the four parts of the face
is optimal in terms of processing time and accuracy
FaceandFacialExpressionRecognition-FusionbasedNonNegativeMatrixFactorization
429

for identifying an expression. In second approach,
we adapt similar approach and named it as Optimal
Expression-specific Parts Accumulation (OEPA). In
case of identifying an expression, if more than one
subset of four parts give almost equal accuracy within
a threshold value, this algorithm picks the subset of
minimal number of parts in order to reduce the pro-
cessing time. It results in an increased efficiency of
the program.
After dividing faces into four facial parts each part
has been made of similar size. We make subspace
or reduced dimension space for whole face, left eyes,
right eyes, nose, mouth. Then we make a fusion of
all the different type of combinations of four facial
parts. These subspaces have been made for all the six
expressions. When a test image needs to classify, we
divide it into four facial parts. Then we project it on
all the decomposed spaces making different combina-
tions of fusions and take the space with minimum eu-
clidian distance. To compare test data with different
face parts and the combination of different parts and
whole faces also, the comparison time is more than
to compare with only whole face subspaces. But the
recognition rate is much much better than the whole
face based decomposition and comparison. Pragmat-
ically we can also find the regions of which are face
parts are more likely to express a particular expres-
sion. We formulate a table which shows the influence
of different facial parts for a emoting specific expres-
sion.
Also to validate our results, we tested each expres-
sion at a time and project it on the whole sets of fea-
ture spaces from the whole train dataset which con-
tains a mixture of all six expressions.
The following figure (Fig. 4) is the flow chart of
the whole procedure.
6.5 Euclidian Distance Classifier
Here we use euclidian distance to take the minimum
distance from the feature subspace. Euclidian dis-
tance is the shortest distance between two points on
a plane is a straight line and is known as Euclidean
distance as shown in the following equation and is a
non-parametric classifier. In Euclidean distance met-
ric difference of each feature of query and database
image is squared which effectively increases the di-
vergence between them.
d
Euc
= (A,B) =
s
m
∑
k−1
|A
k
− B
k
|
2
(12)
In many machine learning data matching areas,
euclidian distance classifier (EDC) has been proven a
successful classifier. For an example, EDC performs
Algorithm 1: Pseudocode for Optimal Expression-specific
Parts Accumulation (OEPA) approach.
procedure OEPA
2: Step 1 (Initialization):
Initialize random population
4: Step 2 (Evaluation):
Let I be the vector [IL, IR, IM,
IN] of an image’s subregions (Left
eye, Right eye, Mouth, Nose)
.
6:
for
i in I
do
8:
Evaluate fitness f(i) where f(i)
is chance-corrected accuracy (kappa)
Let E be the vector [Hap, Sad,
Disgust, Anger, Fear, Surprise]
representing the six basic emotions.
10:
for
e in E
do
12: for
k = 1 to 4
do
for
P in powerset(I)
do
14:
K(e,k)=argmaxP:|P|=k f(P)
is the best set of k regions for
e. L(e,k)= maxP:|P|=kf(P) is the
corresponding fitness value.
K(e)=argmaxk:1-4,P:|P|=k
f(P) is the best set of regions for e.
L(e) = maxk:1-4,P:|P|=k f(P) is the
corresponding fitness.
16:
K =
argmaxe:E,k:1-4,P:|P|=k f(P) is best
regions and emotion.
L = max e:E,k:1-4,P:|P|=k f(P) is
the corresponding fitness.
as well as or superior to the sample LDF(inear dis-
criminant function) , even for nonsphericalcovariance
configurations (Marco and Turner., 1987).
7 RESULT ANALYSIS
7.1 Subspace Visualization
NMF works in different approach than PCA. It can be
seen through the visual decomposition of both meth-
ods. Figure 5 shows a portion of the NMF decom-
posed faces. The next figure(Fig.6) shows the NMF
reduced subspace of several facial parts.
Some Eigenfaces of different expressions (single
and mixed expression dataset) and Eigen images of
separate face parts are given below in figure 7.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
430
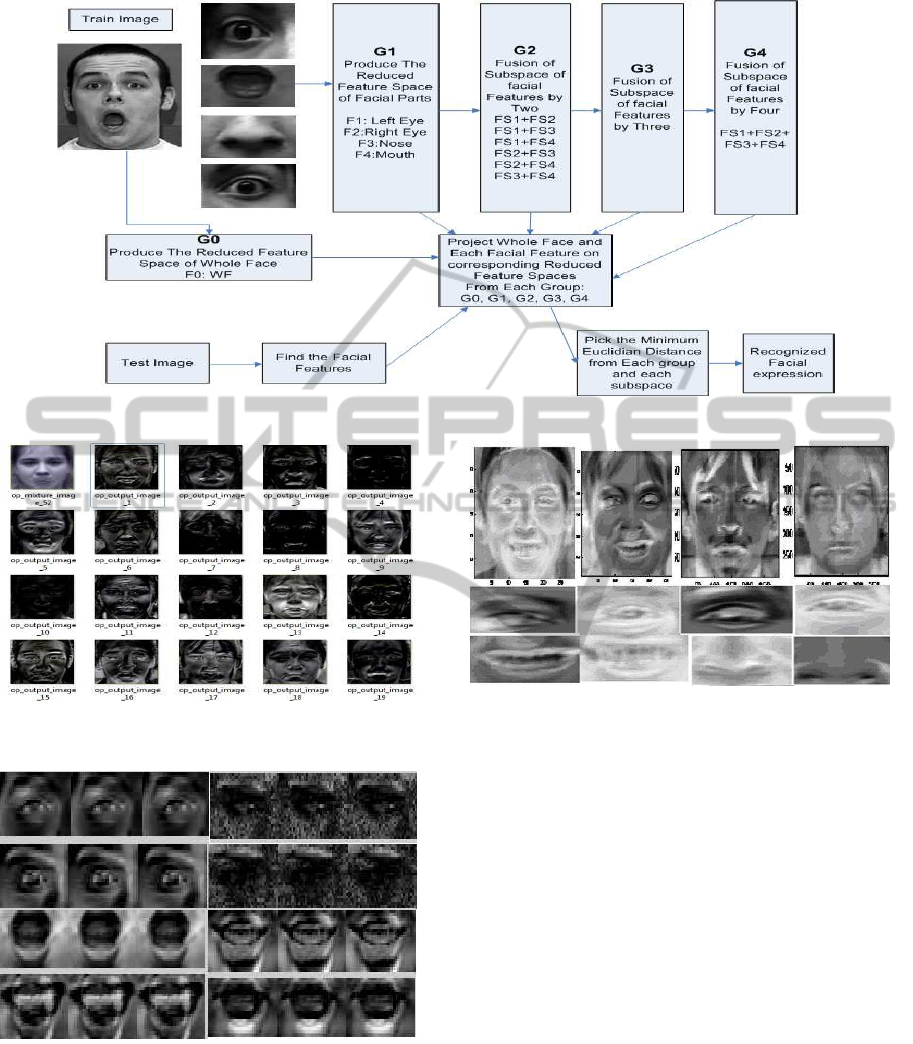
Figure 4: Proposed Method.
Figure 5: A portion of the NMF-decomposed faces from the
whole dataset (1200 images).
Figure 6: NMF decomposed facial parts.
7.2 Face Recognition
For face recognition, we apply we different variables
for segmenting the whole data into train and test
folder and do the projection. We use 10% of the as
train set and another 90% for testing purpose. Then
we increment the train data by 10% each time while
Figure 7: 1st row: first two faces are the 1st and 2nd eigen-
face of happy faces, 3rd and 4th are the 1st and 2nd eigen-
face of neutral-angry faces. 2nd row: first two left and right
eigen eyes from happy-neutral faces.3rd row: first,2nd two
are first eigen mouth of happy faces and 3rd,4th are first,2nd
eigen nose of neutral faces.
deducting the test data by 10%. So it becomes when
train dataset is 20%, test dataset is 80%, then 30%
train data and 70% for test data and the same thing is
happened sequentially.
This way it is found that to achieve a good recog-
nition result using NMF 60% of the data should be
trained and decomposed to make a reduced feature
space. On the other hand, when PCA has been used
nearly 70% of the data should be trained to make the
feature space. The recognition result does not only
depend upon the accuracy rate but also it depends
upon how much data the programme is using for train
and test data. To produce the graph(figure.8) we com-
bine all the two datasets of CK+ and JAFFE to get
a proper insight. It is shown in the graph that more
training sample is needed for PCA based face recog-
nition than NMF based face recognition to get a good
result.
FaceandFacialExpressionRecognition-FusionbasedNonNegativeMatrixFactorization
431
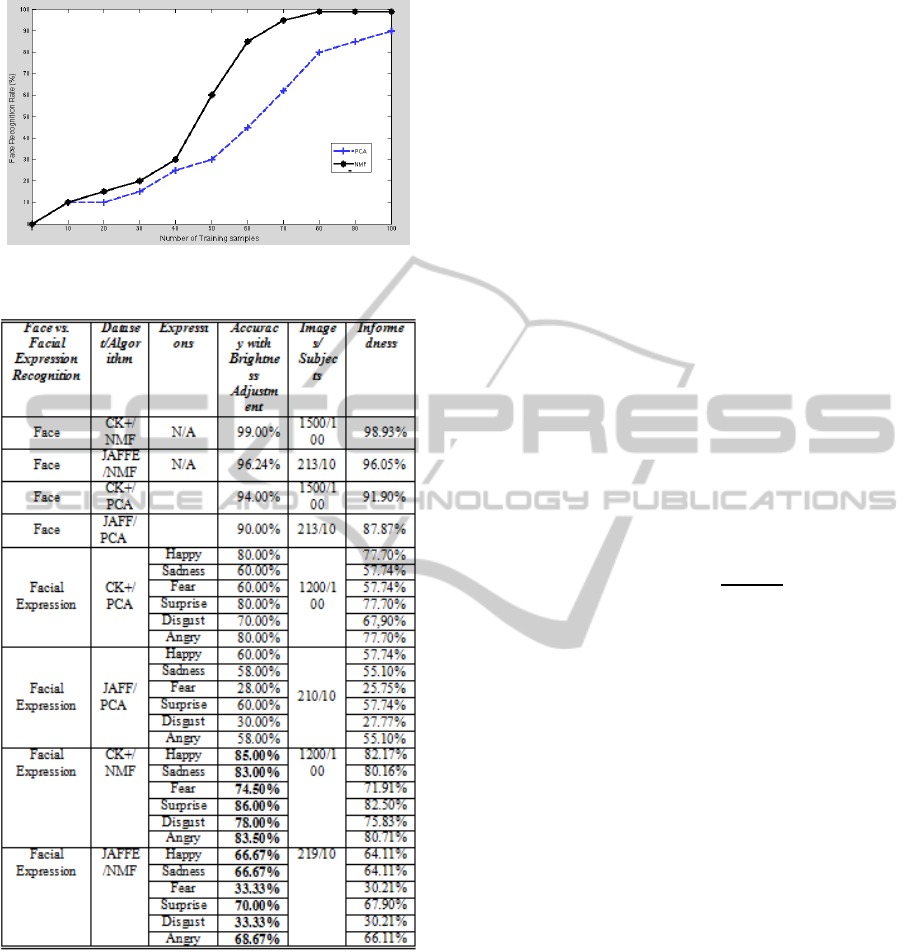
Figure 8: Face recognition rate vs. number of training sam-
ples.
Figure 9: Comparison of NMF and PCA for Face and Facial
Expression Recognition.
7.3 Performance Measurement:
Accuracy and Informedness
To evaluate the classifier’s performance, accuracy is
a usual measurement criterion. However, due to the
variability of number of classes and bias of the sys-
tems, accuracy does not show reliable the measure-
ment. (Powers, 2003) first introduced the concept
of informedness which is a concept of probabilistic
measurement based on decision, prediction or contin-
gency is informed, rather than due to chance. There-
fore we also adopt here informedness besides accu-
racy to enhance a better understanding of classifier’s
performance. Accuracy is calculated as the following
equation which indicates the proportion of right pre-
diction amount from the whole sample data set.
Accuracy =
m
∑
i=1
a
i
i/N. (13)
Where m is the number of expression (here m=6) and
N is the total number of images. To estimate the in-
formedness, bookmaker is an algorithm, which calcu-
lates from a contingency table encountering the idea
of betting with fair odds (Powers, 2011) and (Pow-
ers, 2012). It is shown that informedness subsumes
chance corrected accuracy estimates based on other
techniques that allow for chance, including Receiver
Operating Characters (ROC), Correlation and Kappa,
all of which are identical when bias is matched to
prevalence. Informedness calculates the probability
that the programme makes an informed decision ver-
sus guessing. It is calculated by the following equa-
tion.
Informedness =
winloss
N
(14)
Where winloss =
∑
i6= j
(a
ij
∗ bias[ j]/(prev[ j] − 1)) +
∑
i= j
(a
ij
∗ bias[ j]/(prev[ j])) and prev[i] = X
i
/N,
bias
i
= Y
i
/N. For clarity prev= prevalence, N is the
total samples in the dataset, X
i
and Y
i
are the derived
values which is the number of samples in original and
predictaed set correspondingly. Figure. 9 shows the
comparison of PCA and NMF based face and facial
expression recognition. It is identified that facial ex-
pression recognition is not as good as face recogni-
tion rate. So we propose OEPA based method and it
is shown that our system has a better performance.
7.4 Evaluation: OEPA based Facial
Expression Recognition
From Figure. 9 it is clear that PCA and NMF based fa-
cial expression recognition rate is not as good as face
recognition rate. So we propose OEPA based method
and it is shown that our system has a better perfor-
mance in Table1 and Table2.
This is because that some face parts make the test
image to be confused with two or three near similar
expressions, like sad and disgust face has some simi-
larity. So for near similar expressions it is tough to get
the good recognition rate with whole face or using the
fusion of some face parts while some other combina-
tion of facial parts have good distinguishable criteria
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
432

than others. Table1 and Table2 shows the recogni-
tion rate of facial expression using OEPA-PCA and
OEPA-NMF. This result is from the joint dataset of
CK+ and JAFFE. As we achieve good recognition
rate for face recognition using PCA and NMF, we are
not interested to apply OEPA based method for face
recognition.
8 CONCLUSIONS
In this work we propose a multi feature fusion based
algorithm to fuse different combination of facia fea-
ture subspace and to analyze how it improves the
facial expression recognition rate. We name this
method as Optimal Expression Specific Parts Accu-
mulation (OEPA). Here our main work is to imple-
ment OEPA based NMF algorithm and to compare
it with OEPA based PCA. As written before, we
only apply OEPA based approach for facial expres-
sion recognition, not for face recognition. As for
face recognition we achieve a reasonable result using
straight PCA and NMF. Oue result shows OEPA-PCA
and OEPA-NMF outperforms the predominant PCA
and NMF method.
ACKNOWLEDGEMENTS
This work was supported in part by the Chinese Nat-
ural Science Foundation under Grant No. 61070117,
the Beijing Natural Science Foundation under Grant
No. 4122004, and the Australian Research Council
under ARC Thinking Systems Grant No. TS0689874
as well as the Importation and Development of High-
Caliber Talents Project of Beijing Municipal Institu-
tions.
REFERENCES
Ali, H. B. and Powers, D. M. W. (2013). Facial expres-
sion recognition based on weighted all parts accu-
mulation and optimal expression specific parts accu-
mulation. In Digital Image Computing Techniques
and Applications (DICTA),International Conference
on. IEEE,Hobart, Tasmania,Vol.2,No. 1.pp.1-7.
Ali, H. B. and Powers, D. M. W. (2014). Fusion based fas-
tica method: Facial expression recognition. Journal
of Image and Graphics, 2(1):1–7.
C. Hesher, A. S. and Erlebacher, G. (2003). A novel tech-
nique for face recognition using range images. In Sev-
enth Intl Symp. on Signal Processing and Its Applica-
tions.
Charlesworth, W. R. and Kreutzer, M. A. (1973). Facial
expressions of infants and children. In In P. Ekman
(Ed.), Darwin and facial expression: A century of re-
search in review, pages 91–138. New York; Academic
Press.
Cichocki, Andrzej, e. a. (2009). Nonnegative matrix
and tensor factorizations: applications to exploratory
multi-way data analysis and blind source separation.
John Wiley and Sons.
Ekman, P. (1994). Strong evidence for universals in facial
expressions: A reply to russell’s mistaken critique. In
Psychological Bulletin., pages 115(2): 268–287.
Ensari, Tolga, J. C. and Zurada, J. M. (2012). Occluded
face recognition using correntropy-based nonnegative
matrix factorization. In Machine Learning and Appli-
cations (ICMLA),2012 11th International Conference
on IEEE.vol 1.
Frith, U. and Baron-Cohen, S. (1987). Perception in autistic
children. In Advances in Neural Information Process-
ing Systems, pages 85–102. Handbook of autism and
pervasive developmental disorders.New York: John
Wiley.
I. Buciu, N. N. and Pitas, I. (2007). Nonnegative matrix fac-
torization in polynomial feature space. IEEE Transac-
tions on Neural Network, 42:300–311.
J. Buhmann, M. J. L. and Malsburg, C. (1990). Size and
distortion invariant object recognition by hierarchical
graph matching. In Proceedings, International Joint
Conference on Neural Networks, pages 411–416.
L. Zhao, G. Z. and Xu, X. (2008). Facial expression recog-
nition based on pca and nmf. In Proceedings of the 7th
World Congress on Intelligent Control and Automa-
tion, Chongqing, China.
Lee, D. D. and Seung, H. S. (2009). Learning the parts of
objects by non-negative matrix factorization. In Let-
ters to Nature, pages 788–791.
Li, J. and Oussalah, M. (2010). Automatic face emotion
recognition system. In Cybernetic Intelligent Systems
(CIS), 2010 IEEE 9th International Conference.
M. Lades, J. Vorbruggen, J. B. J. L. C. M. R. W. and Konen,
W. (1993). Distortion invariant object recognition in
the dynamic link architecture. IEEE Transaction on
Computing, 42300-311.
Marco, Virgil R., D. M. Y. and Turner., D. W. (1987).
The euclidean distance classifier: an alternative to the
linear discriminant function. In Advances in Neu-
ral Information Processing Systems, pages 485–505.
Communications in Statistics-Simulation and Compu-
tation.
Moghaddam, B. and Pentland, A. (1997). Probabilistic vi-
sual learning for object representation. IEEE Trans-
action on Pattern Analysis and Machine Intelligence,
19:696–710.
Paul, V. and Jones, M. (2001). Rapid object detection using
a boosted cascade of simple features. In Computer
Vision and Pattern Recognition.
Powers, D. M. W. (2003). Recall and precision versus the
bookmaker. In Interna- tional Conference on Cogni-
tive Science (ICSC-2003), page 529534.
Powers, D. M. W. (2011). Evaluation: From precision, re-
call and f-measure to roc., informedness, markedness
FaceandFacialExpressionRecognition-FusionbasedNonNegativeMatrixFactorization
433
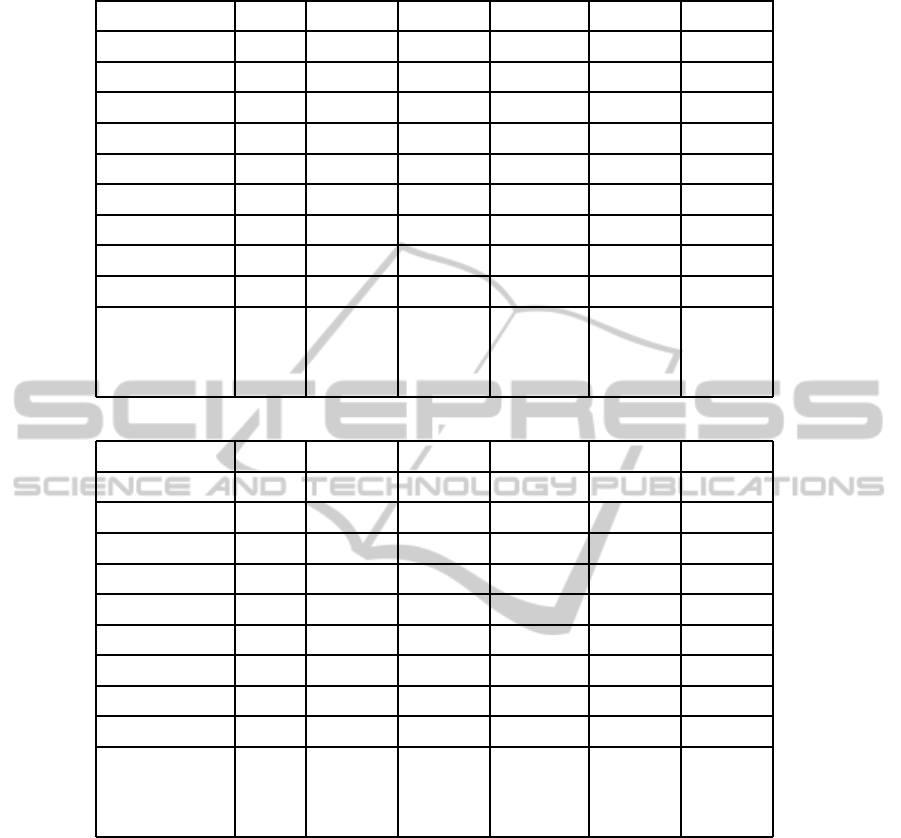
Table 1: Facial Eecognition based on OEPA-PCA(LE:Left Eye, RE:Right Eye, N:Nose, M:Mouth).
F-Parts Surp. Ang. Sad. Hap. Fear Disg.
LE 76% 58% 60% 68% 40% 48%
RE 76% 58% 60% 68% 40% 48%
LE+RE 76% 58% 60% 68% 40% 48%
N 12% 16% 50% 14% 30% 54%
M 88% 52% 52% 80% 70% 44%
LE+RE+N 60% 52% 50% 70% 54% 80%
LE+RE+M 80% 74% 72% 86% 78% 70%
N+M 64% 44% 44% 60% 40% 62%
LE+RE+N+M 76% 86% 82% 74% 74% 68%
OEPA-PCA 88% 86% 82% 86% 78% 80%
(M) (LE+RE (LE+RE (LE+RE) (LE+RE (LE+RE
+N+M) +N+M) +M) +M) +N)
Table 2: Facial Eecognition based on OEPA-NMF(LE:Left Eye, RE:Right Eye, N:Nose, M:Mouth).
F-Parts Surp. Ang. Sad. Hap. Fear Disg.
LE 84% 67% 68% 72% 44% 57%
RE 84% 67% 68% 72% 44% 57%
LE+RE 84% 67% 68% 72% 44% 57%
N 18% 20% 57% 18% 36% 59%
M 96% 52% 58% 88% 84% 54%
LE+RE+N 64% 58% 52% 78% 60% 89%
LE+RE+M 89% 82% 78% 92% 88% 80%
N+M 74% 44% 44% 60% 40% 72%
LE+RE+N+M 86% 90% 86% 85% 83% 80%
OEPA-NMF 96% 90% 86% 92% 88% 89%
(M) (LE+RE (LE+RE (LE+RE) (LE+RE (LE+RE
+N+M) +N+M) +M) +M) +N)
and correlation. Journal of Machine Learning Tech-
nologies, 2(1):3763.
Powers, D. M. W. (2012). The problem with kappa. In Con-
ference of the Euro- pean Chapter of the Association
for Computational Linguistics,. Avignon France.
Turk, M. A. and Pentland, A. P. (1991). Face recognition
using eigenfaces. Proceedings of International Con-
ference on Pattern Recognition, pages 586–591.
Yeasin, M. and Bullot, B. (2005). Comparison of linear
and non-linear data projectiontechniques in recogniz-
ing universal facial expressions. In proceedings of In-
ternational Joint Conference on Neural Networks.
Zilu, Y. and Guoyi, Z. (2009). Facial expression recognition
based on nmf and svm. In 2009 International Forum
on Information Technology and Applications.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
434
