
Automatic Image Annotation Using Convex Deep Learning Models
Niharjyoti Sarangi and C. Chandra Sekhar
Department of CSE, Indian Institute of Technology Madras, Chennai, India
Keywords:
Image Annotation, Tensor Deep Stacking Networks, Kernel Deep Convex Networks, Deep Convolutional
Network, Deep Learning.
Abstract:
Automatically assigning semantically relevant tags to an image is an important task in machine learning. Many
algorithms have been proposed to annotate images based on features such as color, texture, and shape. Success
of these algorithms is dependent on carefully handcrafted features. Deep learning models are widely used to
learn abstract, high level representations from raw data. Deep belief networks are the most commonly used
deep learning models formed by pre-training the individual Restricted Boltzmann Machines in a layer-wise
fashion and then stacking together and training them using error back-propagation. In the deep convolutional
networks, convolution operation is used to extract features from different sub-regions of the images to learn
better representations. To reduce the time taken for training, models that use convex optimization and kernel
trick have been proposed. In this paper we explore two such models, Tensor Deep Stacking Network and
Kernel Deep Convex Network, for the task of automatic image annotation. We use a deep convolutional
network to extract high level features from raw images, and then use them as inputs to the convex deep
learning models. Performance of the proposed approach is evaluated on benchmark image datasets.
1 INTRODUCTION
Developing techniques for efficient extraction of us-
able and meaningful information has become increas-
ingly important with the explosive growth of digital
technologies. Low level features like color, texture
and shape can be used to classify images into differ-
ent categories. However, in many cases it is not suit-
able to use a single class label because of the pres-
ence of more than one semantic concept in an image.
One way to handle this is by assigning multiple rele-
vant keywords to a given image, reflecting its seman-
tic content. This is often referred to as image annota-
tion.
Learning techniques such as Binary Relevance
(Boutell et al., 2004) and Classifier Chains (Read
et al., 2011), transform an annotation task into a
task of binary classification. Another approach to
tackle the problem of annotation is by adapting pop-
ular learning techniques to deal with multiple labels
directly (Tsoumakas and Katakis, 2007; Zhang and
Zhou, 2014). Multi Label k-Nearest Neighbors (ML-
kNN) (Zhang and Zhou, 2007), Multi Label Decision
Tree (ML-DT) (Vens et al., 2008) and Rank-SVM
(Elisseeff and Weston, 2001) are some of the com-
monly used methods in this category. Rank-SVM is
a ranking based approach coupled with a set size pre-
dictor which uses Support Vector Machines to min-
imize the ranking loss while having a large margin.
Among other models, semantic space auto-annotation
model (Hare et al., 2008) constructs a special form of
a vector space, called a semantic space, from the la-
bels associated with the images. Images are projected
into this space in order to be retrieved or annotated.
Latent semantic analysis (Hofmann, 1999) is used to
build this space. The success of these techniques is
largely dependent on the effectiveness of the features
used.
Learning representations of the data that makes it
easier to extract useful information is highly desirable
(Bengio et al., 2013) for developing a good classifica-
tion or annotation framework. Deep learning mod-
els are the commonly used techniques for learning
representation from raw data. These models aim at
learning feature hierarchies with features from higher
levels of the hierarchy formed by the composition of
lower level features, as illustrated in Figure 1.
Deep learning models such as Deep Belief Net-
works (DBN) (Hinton and Salakhutdinov, 2006) and
Deep Boltzmann Machines (DBM) (Salakhutdinov
and Hinton, 2009; Ranzato et al., 2010; Montavon
et al., 2012) have performed well in classification and
92
Sarangi N. and Chandra Sekhar C..
Automatic Image Annotation Using Convex Deep Learning Models.
DOI: 10.5220/0005216700920099
In Proceedings of the International Conference on Pattern Recognition Applications and Methods (ICPRAM-2015), pages 92-99
ISBN: 978-989-758-077-2
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

...
...
...
...
Input Layer
Hidden Layers
Output Layer (Optional)
These learn more abstract features.
This has raw sensory data or extracted features as input.
Figure 1: Scheme of learning representations in a multilay-
ered network. Raw pixel values or extracted features are
given as input. The input layer is followed by multiple hid-
den layers that learn increasingly abstract representation.
recognition tasks (Le Roux and Bengio, 2008). These
models are formed by pre-training individual layers
(Hinton et al., 2006a) and then stacking together and
training them using error back-propagation. Each
layer of a DBN consists of an energy-based model
known as Restricted Boltzmann Machine (RBM). An
RBM is trained using contrastive divergence to ob-
tain a good reconstruction of the input data (Hinton
et al., 2006b). Contrastive divergence and error back-
propagation are computationally complex methods.
In Deep Convolutional Networks (LeCun et al., 2010;
Lee et al., 2009; Krizhevsky et al., 2012), convolu-
tion operation is used to extract features from differ-
ent sub-regions of an image to learn a better repre-
sentation. Although Deep Convolutional Networks
are trained completely using error back-propagation,
they use sub-sampling layers to reduce the number
of inputs to each layer. To solve the issue of com-
plexity, a model known as Deep Stacking Network
(DSN) (Deng et al., 2012b) that consists of many
stacking modules was recently proposed. Each mod-
ule is a specialized neural network consisting of a
single non-linear hidden layer and linear input and
output layers. Since convex optimization is used to
speedup the learning in each module, this model is
also called as Deep Convex Network (DCN) (Deng
and Yu, 2011). Tensor Deep Stacking Networks (T-
DSN) (Hutchinson et al., 2013) , introduced as an ex-
tension of the DSN architecture, captures better rep-
resentations by using two sets of nonlinear nodes in
the hidden layer. The T-DSN model has been shown
to perform better than the DSN model for image clas-
sification and phone recognition tasks. Kernel Deep
Convex Network(K-DCN) (Deng et al., 2012a) on the
other hand uses kernel trick so that the number of hid-
den nodes in each module is unbounded.
In this paper, we propose a framework that uses
convex deep learning models (T-DSN and K-DCN)
for the task of image annotation. We also propose us-
ing the features extracted from a Deep Convolutional
Network as input to the convex models. The remain-
der of this paper is organized as follows: Section 2
gives a brief discussion on T-DSN and K-DCN. In
Section 3 we describe the details of our experiments
and compare the results with the existing methods.
2 CONVEX DEEP LEARNING
MODELS
2.1 Tensor Deep Stacking Networks
A tensor deep stacking network is a generalized form
of a deep stacking network. The input data is provided
to the nodes in the input layer of the first module. The
input to the higher modules is obtained by appending
output from the module just below it to the original
input data. Unlike DSN, each module of TDSN has
two sets of hidden layer nodes and thus, two sets of
connections between the input layer and the hidden
layer as shown in Figure 2. The output layer nodes
are bilinearly dependent on the hidden layer nodes.
Figure 2: Architecture of tensor deep stacking network.
Let the target vectors t be arranged to form the
columns of matrix T, the input data vectors v be ar-
ranged to form the columns of matrix V, and H
1
and
H
2
denote the set of matrices of the outputs of the
hidden units. There are two sets of lower weight pa-
rameters (W
1
and W
2
). They are associated with con-
nections from the input layer to the two hidden layers
containing L
1
and L
2
sigmoidal nodes respectively.
Since the hidden layers contain sigmoidal nodes,
the output of a hidden layer can be expressed as:
H
1
= logistic(W
T
1
V)
H
2
= logistic(W
T
2
V)
(1)
AutomaticImageAnnotationUsingConvexDeepLearningModels
93
Let h
1
be the vector of outputs from the first set of
hidden nodes and h
2
be the vector of outputs from the
second set of hidden nodes. Let h
1
i
be the i
th
entry in
h
1
and h
2
j
be the j
th
entry in h
2
.
If C is the number of nodes in the output layer,
weights of connections from hidden layers to the
output layer are represented as a tensor U ∈ R
L
1
×
R
L
2
× R
C
. The tensor U can be considered as a 3-
dimensional matrix.
Let y
k
denote the output of k
th
node in output
layer. The output vector can be obtained by comput-
ing (U ×
1
h
1
) ×
2
h
2
where ×
i
stands for multiplica-
tion along the i
th
dimension. In a simplified notation
y
k
=
L
1
∑
i=1
L
2
∑
j=1
U
ijk
h
1
i
h
2
j
(2)
Let
˜
h = h
1
⊗ h
2
where ⊗ is the Kronecker product. Let
˜
u
k
be the vec-
torized version of matrix U
k
in which all columns are
appended to form a single vector. The matrix U
k
is
obtained by setting the third dimension of tensor U
equal to k. Hence, length of
˜
u
k
is L
1
L
2
. Now, we can
rewrite equation (2) as,
y
k
=
˜
u
k
T
˜
h (3)
Arranging all
˜
u
k
’s for k = 1, 2, ...,C, into a matrix
˜
U
= [
˜
u
1
˜
u
2
...
˜
u
C
], the overall prediction becomes
y =
˜
U
T
˜
h (4)
where y is the estimate of target vector t.
Thus, bilinear mapping from two hidden layers
can be seen as a linear mapping from an implicit hid-
den representation
˜
h. Aggregating the implicit hidden
layer representations for each of the N instances into
the columns of an L
1
L
2
× N matrix
˜
H, we obtain
Y =
˜
U
T
˜
H (5)
where
˜
H contains h
k
in k
th
column.
The convex formulation for
˜
U in this case is,
min
˜
U
T
k
˜
U
T
H − Tk
2
(6)
where k.k
2
represents the squared norm operation.
Solving the optimization (6) we get:
˜
U
T
= T
˜
H
T
(
˜
H
˜
H
T
)
−1
(7)
We see that the output of each hidden node in first
layer appears L
2
number of times in
˜
h. So, we have
to add errors due to all those terms in order to get
the error caused by this particular node. Hence, the
equation for weight update needs to be modified to
account for this and the modified equations are:
∆W
1
= ηV[H
T
1
◦ (Γ− H
T
1
) ◦ Ψ
1
] (8)
∆W
2
= ηV[H
T
2
◦ (Γ− H
T
2
) ◦ Ψ
2
] (9)
Here ◦ is the element-wise multiplication of two ma-
trices, Γ is a matrix of all ones, η is the learning rate
and
Ψ
1
nk
=
L
2
∑
k=1
H
2
nk
˜
Θ
((i−1)L
2
+k),n
Ψ
2
nk
=
L
1
∑
k=1
H
1
nk
˜
Θ
((i−1)L
1
+k),n
(10)
˜
Θ = 2
˜
H
+
(
˜
HT
T
)(T
˜
H
+
) − 2T
T
(T
˜
H
+
) (11)
Here H
1
is the matrix of outputs of nodes in the first
hidden layer, H
2
is the matrix of outputs of nodes in
the second hidden layer. The dimensions of matrices
Ψ
1
and Ψ
2
are N × L
1
and N × L
2
respectively. Each
of these two matrices Ψ
1
and Ψ
2
acts as a bridge be-
tween high dimensional implicit representation
˜
h and
low dimensional representations u and v.
Since T-DSN uses convexoptimization techniques
to directly determine the upper-layer weights, the
training time is greatly reduced. However, computing
the lower-layer weights is still an iterative process.
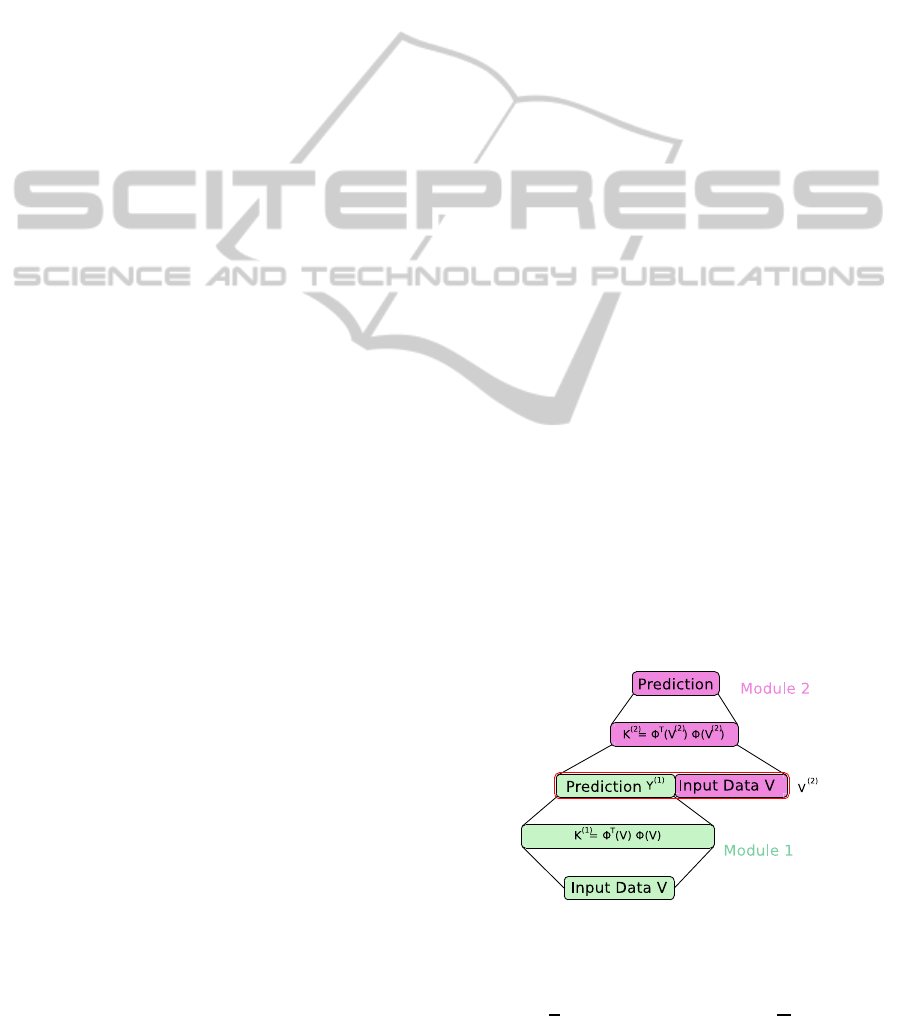
2.2 Kernel Deep Convex Networks
A kernel deep convex network (K-DCN), like a T-
DSN, is composed by stacking of shallow neural net-
work modules. This model completely eliminates the
non-convexlearning for the lower-layerweights using
the kernel trick. In case of K-DCN, a regularization
term C is included in the expression for computing the
upper-layer weights U. This modification helps bound
the values of elements of U and prevents the model
from over-fitting on the training data.
Figure 3: Architecture of kernel deep convex network with
two modules.
The formulation for U takes the form of,
min
U
[
1
2
∗ Tr{(Y − T)
T
(Y − T)} +
C
2
U
T
U]
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
94

where Y is the predicted output for the output nodes
and T is the target output. The closed form expres-
sion for U is obtained by solving this minimization as
follows :
U = (CI + HH
T
)
−1
HT
T
(12)
The output of the given module of KDCN is given
by,
y
k
= TH
T
(CI + HH
T
)
−1
h
i
(13)
The sigmoidal function of hidden units is replaced
with a generic nonlinear mapping function Φ(v) from
the raw input features v. The mapping Φ(v) will have
high-dimensionality (possibly infinite) which is deter-
mined implicitly by a chosen kernel function. The
unconstrained optimization problem can be reformu-
lated as follows :
min
U
[
1
2
∗ Tr{(Y − T)
T
(Y − T)} +
C
2
U
T
U]
subject to
T − U
T
G(V) = Y − T
where columns of G(V) are formed by applying the
transformation Φ(.) on each input v. Solving this
problem gives
U = G(V)(CI + K)
−1
T
T
(14)
where K = G
T
(V)G(V) is the kernel gram matrix of
V.
Finally, for each new input vector v in the test set,
the prediction of KDCN module is given by
y(v) = U
T
Φ(v) = T(CI + K)
−1
k
T
(v) (15)
Here k(v) is the kernel vector such that k
n
(v) =
k(v
n
, v) and v
n
is a vector from training set.
For the subsequent modules, the output of nodes
in the output layer is appended with the raw input.
For l
th
module (l > 2) equation (14) is valid with a
slight modification in the kernel function to account
for this extra input as follows :
K = G
T
(Z)G(Z) (16)
where Z = V|Y
(l−1)
|Y
(l−2)
|....|Y
1
, Y
m
is the predic-
tion of module m, and U|V represents the concatena-
tion of U and V.
Using the equations (15) and (16) we eliminate the
need of back-propagationand get a convexexpression
for training the model. The KDCN model combines
the power of deep learning and kernel learning in a
principled way. It is fast because there is no back-
propagation.
2.3 Framework for Image Annotation
If a concept is present in an image, the corresponding
bit in a binary target output vector t is turned on. Each
module of a T-DSN is trained to predict t. Once the
module is trained and the weights W
1
, W
2
, and U are
learned, equation (4) is used to compute the estimated
output. For the higher modules, the input data is con-
catenated with the output of the module below it (or
with the output of n modules below it) and used as an
augmented input. This process is repeated for all the
modules and the output obtained at the last module
is retained. Similarly, in case of a K-DCN, equation
(15) is used to find predictions for each module.
One of the following methods to obtain the anno-
tation labels from the outputs of a model is used.
1. A threshold value is decided empirically using a
held-out validation set. In the estimated output
vectors, if the posterior probability value for a par-
ticular concept exceeds the threshold, it is consid-
ered as an annotation label for the image.
2. Based on the average number of labels present in
the images, a value k is selected. An image is an-
notated with those concepts that correspond to the
top k values in the estimated output vector.
3 EXPERIMENTS AND RESULTS
In this section, we present the details of image anno-
tation datasets used and the experimental results for
T-DSN and K-DCN. We compare the performance of
these models with the state-of-the-art performance.
3.1 Experimental Setup
We used MATLAB on an Intel i7 8-core CPU with 16
GB of RAM for running the Rank-SVM. For T-DSN
and K-DCN, we used NVIDIA Tesla K20C GPU with
CUDA.
In order to reduce the number of multiplications in
the computation of
˜
Θ, equation (11) is re-written as:
˜
Θ = 2(
˜
H
+
˜
HT
T
− T
T
)(T
˜
H
+
)
= 2(
˜
H
+
˜
HT
T
− T
T
)
˜
U
+
(17)
In order to reduce the memory requirements for
the computation of
˜
Θ, equation (17) is parenthesized
as follows:
˜
Θ = 2(
˜
H
+
(
˜
HT
T
) − T
T
)
˜
U
+
(18)
In this order of multiplication, we avoid comput-
ing
˜
H
+
˜
H, which is a N × N matrix. In general, the
AutomaticImageAnnotationUsingConvexDeepLearningModels
95

value of N is large (20,000 - 50,000). Accommodat-
ing such a large matrix in the GPU memory is prob-
lematic. Many matrices are reused in the process of
training. Matrices are allocated memory only when
required and freed immediately after their use in or-
der to make the best use of memory available.
For K-DCN, we used three different types of ker-
nel functions, namely, Gaussian kernel, Polynomial
kernel and Histogram Intersection Kernel (HIK). The
kernel parameters and regularization parameter were
tuned to obtain a range of values for the first mod-
ule. For the later modules, the tuning is done with
respect to the range of parameters obtained for the
previous module, and a set of globally optimum pa-
rameters was obtained.
3.2 Feature Extraction
We used a deep convolutionalnetwork to obtain a use-
ful representation from an image. A deep convolu-
tional network consists of several layers. A convolu-
tional layer consists of a rectangular grid of neurons.
Each neuron takes inputs from a rectangular section
of the previous layer. The weights for this rectangular
section are constrained to be the same for each neuron
in the convolutional layer. Constraining the weights
makes it work like many different copies of the same
feature detector applied to different positions. This
constraint also helps in restricting the number of pa-
rameters. The output of a neuron in the convolutional
layer, l for a filter of size (m∗ n) is given by
s
l
ij
= f(
m
∑
x=0
n
∑
y=0
w
xy
s
(l−1)
(x+i)(y+ j)
) (19)
where f(x) = log(1 + e
x
). This nonlinearity was
approximated using a simpler function, f(x) =
max(0, x), which is known as the rectifier function.
The nodes that use the rectifier function are referred
to as Rectified Linear Units (ReLU). Use of ReLU re-
duced the time taken significantly.
The pooling layer takes outputs of small rectangu-
lar blocks in the convolutional layer and subsamples it
to produce a single output from that block. The pool-
ing layer can take the average, or maximum, or learn
a linear combination of outputs of the neurons in the
block. In all our experiments, we used max-pooling.
Pooling helps the network achieve small amount of
translational invariance at each level. Also, it reduces
the number of inputs to the next layer. Finally, after
two convolutional and max-pooling layers, we added
two fully connected layers. The activity of the nodes
in the last fully connected layer was used as input to
the T-DSN and K-DCN models.
Apart from this, we also used the SIFT features
(Lowe, 2004) as input to the deep learning models.
3.3 Datasets Used
We test our models with two real-world datasets that
contain color images with their annotations: Uni-
versity of Washington annotation benchmark dataset
(Washington, 2004) and the MIRFLICKR-25000 col-
lection (Huiskes and Lew, 2008).
The Washington dataset had 1109 color images
corresponding to 22 different categories with an av-
erage annotation length of 6. Out of all the concepts
available, we selected only 45 concepts that had more
than 25 images associated with each of them. The list
of these 45 concepts is given in Table 1.
Table 1: List of 45 concepts selected for our study on Uni-
versity of Washington annotation benchmark dataset.
trees bushes grass sidewalk ground
rock flowers camp sky trees
trunk people water dog woman
street cars pole house beach
ocean clouds mountain river building
lantern window bridge band man
stone Snow Boats sun Huskies
football Stadium stand field hiker
mosque frozen players temple smoke
Some of the images from this dataset with their
annotation labels are shown in Figure 4. Because of
the small number of images, we do not use convolu-
tional features for this dataset.
Figure 4: Illustration of images with their annotation labels
from the University of Washington annotation benchmark
dataset.
MIRFLICKR-25000 is a database of 25,000 color
images belonging to various categories. The aver-
age number of tags per image is 9. Some of the im-
ages from this dataset with their annotation labels are
shown in Figure 5. For our studies, we consider the
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
96

Figure 5: Illustration of images with their annotation labels
from the MIRFLICKR dataset.
30 most frequently occurring tags. These tags have at
least 150 images associated with each of them.
We randomly selected 30% of the images for test-
ing, and repeated our studies over 5 folds.
3.4 Results
A T-DSN consisting of 3 modules with 100 nodes in
each of the hidden layers was used on the University
of Washington dataset. In our experiments we ob-
served that having the same number of nodes in both
the sets of hidden nodes generally give a better per-
formance.
The precision, recall and F-measure for different
thresholds in the threshold based decision logic are
reported in Table 2.
We repeated the previous experiment with differ-
ent values of k in the top-k based decision logic, and
the precision, recall, and F-measure values are re-
ported in Table 3.
We repeated these experiments with K-DCN. Best
performance was observed for a Gaussian Kernel.
The results of these experiments are reported in Ta-
ble 4 and Table 5.
It is observed that the F-measure values for K-
DCN are slightly lower when compared with that for
T-DSN. One of the possible reasons for this could be
that the kernel parameters used might not be the best.
The state-of-the-art methods for image annotation,
namely, Rank-SVM and semantic space model give
F-measure values of 0.61 and 0.63 respectively. Fig-
ure 6 compares the actual annotation labels for some
randomly selected images in University of Washing-
ton dataset with the annotations generated by the T-
DSN model.
It is observed that the number of annotation labels
generated by the models were slightly higher than that
of the ground truth. In many cases, the extra labels are
somehow related to the image.
Table 2: Precision, recall, and F-measure for different
thresholds in the threshold based decision logic for anno-
tation of images in the University of Washington data with
T-DSN.
Threshold Precision Recall F-measure
0.20 0.50 0.87 0.64
0.25 0.58 0.81 0.67
0.30 0.63 0.75 0.68
0.35 0.68 0.70 0.68
0.40 0.72 0.64 0.67
0.45 0.73 0.58 0.64
0.50 0.75 0.47 0.58
Table 3: Precision, recall, and F-measure for different val-
ues of k in the top-k based decision logic for annotation of
images in the University of Washington data with T-DSN.
k Precision Recall F-measure
2 0.42 0.27 0.33
3 0.51 0.46 0.48
4 0.52 0.60 0.56
5 0.50 0.70 0.58
6 0.49 0.79 0.60
7 0.44 0.84 0.58
8 0.41 0.88 0.56
Table 4: Precision, recall, and F-measure for different
thresholds in the threshold based decision logic for anno-
tation of images in the University of Washington data with
K-DCN.
Threshold Precision Recall F-measure
0.20 0.39 0.90 0.54
0.25 0.50 0.84 0.63
0.30 0.52 0.81 0.63
0.35 0.59 0.76 0.66
0.40 0.64 0.68 0.66
0.45 0.73 0.59 0.65
0.50 0.77 0.49 0.59
Table 5: Precision, recall, and F-measure for different val-
ues of k in the top-k based decision logic for annotation of
images in the University of Washington data with K-DCN.
k Precision Recall F-measure
2 0.31 0.21 0.25
3 0.43 0.49 0.46
4 0.48 0.53 0.50
5 0.48 0.61 0.54
6 0.46 0.68 0.55
7 0.41 0.77 0.53
8 0.37 0.85 0.52
For the MIRFLICKR dataset, the study is carried
out using the SIFT features and convolutional fea-
AutomaticImageAnnotationUsingConvexDeepLearningModels
97

Figure 6: Illustration of images with actual annotation la-
bels and predicted annotation labels in the University of
Washington dataset with T-DSN.
Table 6: Performance comparison of models for image an-
notation task on MIRFLICKR dataset.
Model
Input
Features
F-Measure
Semantic Spae SIFT 0.26
Rank-SVM SIFT 0.25
TDSN SIFT 0.24
TDSN Convolutional 0.29
KDCN SIFT 0.26
KDCN Convolutional 0.34
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Recall
Precision
Precision−Recall curves on MIRFLICKR dataset
T−DSN (Convolutional)
K−DCN (Convolutional)
K−DCN (SIFT)
T−DSN (SIFT)
Semantic Space (SIFT)
Figure 7: Precision-recall curves for different models on
MIRFLICKR dataset.
tures. Fig. 7 shows the precision-recall curves for dif-
ferent models. The best F-measure values for differ-
ent models are presented in Table 6.
It is observed that K-DCN and T-DSN perform
better with convolutional features. It is also noted that
convex deep learning methods perform better than the
semantic space annotation method.
4 SUMMARY AND
CONCLUSIONS
In this paper, we used the convex deep learning mod-
els, such as T-DSN and K-DCN for image annotation
tasks. We also used features extracted from a deep
convolutional network for this task. Through the ex-
perimental studies, it is observed that the T-DSN and
K-DCN models with convolutional features as input
give an improved performance. Once the convolu-
tional network is trained on a large set of images, it
is easy to extract features. The convex networks take
less time to train, making them useful for image an-
notation tasks in practice.
For the K-DCN model, we have used only a sin-
gle kernel function for a module. We can extend this
by using multiple types of kernel functions. Finding a
set of globally optimal parameters for K-DCN is dif-
ficult. Similarly, for T-DSN we observed that having
different number of nodes in each hidden layer is not
beneficial. However, we did not find any criterion for
selecting the suitable number of hidden layer nodes.
A recipe for selecting the number of nodes in T-DSN
and globally optimum parameters for K-DCN will be
useful.
REFERENCES
Bengio, Y., Courville, A., and Vincent, P. (2013). Represen-
tation learning: A review and new perspectives. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 35(8):1798–1828.
Boutell, M. R., Luo, J., Shen, X., and Brown, C. M.
(2004). Learning multi-label scene classification. Pat-
tern Recognition, 37(9):1757–1771.
Deng, L., T¨ur, G., He, X., and Hakkani-T¨ur, D. Z. (2012a).
Use of kernel deep convex networks and end-to-end
learning for spoken language understanding. In IEEE
Workshop on Spoken Language Technologies, pages
210–215.
Deng, L. and Yu, D. (2011). Deep convex network: A scal-
able architecture for speech pattern classification. In
Interspeech.
Deng, L., Yu, D., and Platt, J. (2012b). Scalable stacking
and learning for building deep architectures. In Pro-
ceedings of the International Conference on Acous-
tics, Speech, and Signal Processing.
Elisseeff, A. and Weston, J. (2001). A kernel method for
multi-labelled classification. In Advances in Neural
Information Processing Systems 14, pages 681–687.
ICPRAM2015-InternationalConferenceonPatternRecognitionApplicationsandMethods
98

Hare, J., Samangooei, S., Lewis, P., and Nixon, M. (2008).
Semantic spaces revisited: investigating the perfor-
mance of auto-annotation and semantic retrieval us-
ing semantic spaces. In Proceedings of the Interna-
tional conference on Content-based image and video
retrieval, pages 359–368.
Hinton, G. E., Osindero, S., and Teh, Y.-W. (2006a). A
fast learning algorithm for deep belief nets. Neural
Computation, 18(7):1527–1554.
Hinton, G. E., Osindero, S., Welling, M., and Teh, Y. W.
(2006b). Unsupervised discovery of nonlinear struc-
ture using contrastive backpropagation. Cognitive Sci-
ence, 30(4):725–731.
Hinton, G. E. and Salakhutdinov, R. R. (2006). Reducing
the dimensionality of data with neural networks. Sci-
ence, 313(5786):504–507.
Hofmann, T. (1999). Probabilistic latent semantic analysis.
In Proceedings of the Uncertainty in Artificial Intelli-
gence, pages 289–296.
Huiskes, M. J. and Lew, M. S. (2008). The mir flickr re-
trieval evaluation. In Proceedings of the 2008 ACM
International Conference on Multimedia Information
Retrieval.
Hutchinson, B., Deng, L., and Yu, D. (2013). Tensor deep
stacking networks. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 35(8):1944–1957.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Proceedings of the Neural Information
Processing System, volume 22, pages 1106–1114.
Le Roux, N. and Bengio, Y. (2008). Representational power
of restricted Boltzmann machines and deep belief net-
works. Neural Computation, 20(6):1631–1649.
LeCun, Y., Kavukcuoglu, K., and Farabet, C. (2010). Con-
volutional networks and applications in vision. In Pro-
ceedings of International Symposium on Circuits and
Systems, pages 253–256.
Lee, H., Grosse, R., Ranganath, R., and Ng, A. Y. (2009).
Convolutional deep belief networks for scalable unsu-
pervised learning of hierarchical representations. In
Proceedings of the 26th Annual International Confer-
ence on Machine Learning, pages 609–616.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision, 60(2):91–110.
Montavon, G., Braun, M. L., and Mller, K.-R. (2012). Deep
Boltzmann machines as feed-forward hierarchies. In
Proceedings of the International Conference on Ar-
tificial Intelligence and Statistics, volume 22, pages
798–804.
Ranzato, M., Krizhevsky, A., and Hinton, G. E. (2010). Fac-
tored 3-way restricted Boltzmann machines for mod-
eling natural images. Journal of Machine Learning
Research - Proceedings Track, 9:621–628.
Read, J., Pfahringer, B., Holmes, G., and Frank, E. (2011).
Classifier chains for multi-label classification. Ma-
chine Learning, 85(3):333–359.
Salakhutdinov, R. and Hinton, G. (2009). Deep Boltzmann
machines. In Proceedings of the International Con-
ference on Artificial Intelligence and Statistics, vol-
ume 5, pages 448–455.
Tsoumakas, G. and Katakis, I. (2007). Multi-label classi-
fication: An overview. International Journal of Data
Warehousing and Mining, 3(3):1–13.
Vens, C., Struyf, J., Schietgat, L., Dˇzeroski, S., and Block-
eel, H. (2008). Decision trees for hierarchical multi-
label classification. Machine Learning, 73(2):185–
214.
Washington, U. (2004). Washington ground truth database.
http://www.cs.washington.edu/research/imagedatabase.
Zhang, M.-L. and Zhou, Z.-H. (2007). Ml-knn: A lazy
learning approach to multi-label learning. Pattern
Recognition, 40(7):2038 – 2048.
Zhang, M.-L. and Zhou, Z.-H. (2014). A review on multi-
label learning algorithms. IEEE Transactions on
Knowledge and Data Engineering, 26(8):1819–1837.
AutomaticImageAnnotationUsingConvexDeepLearningModels
99
