
Coupling of Self-activating Genes Induces Spontaneous Synchronized
Oscillations in Cells
Jesus Miro-Bueno
Research Institute of the IT4Innovations Centre of Excellence, Faculty of Philosophy and Science,
Silesian University in Opava, 74601 Opava, Czech Republic
Keywords:
Multicellular Clock, Synchronization, Genetic Clock, Positive Feedback, Synthetic Gene Oscillator.
Abstract:
Genetic oscillators are present in a wide range of organisms from bacteria to neurons and coordinate important
biological functions. Current models of genetic oscillators are based on auto-repressed genes. In these models
a gene produces a repressor protein that binds to the promoter of its own gene repressing the transcription.
Different versions of these models have been studied in living organisms and for engineering synthetic clocks.
Synchronization of genetic clocks based on this model has also been studied. However, genes with positive
feedbacks are also present in natural and synthetic genetic clocks. These self-activating genes provide robust-
ness and frequency tuning to genetic clocks. In this paper we show a novel role of self-activating genes. We
demonstrate that the coupling of self-activating genes by small molecules in a cell population produces syn-
chronized oscillations. Our model could be useful for engineering new robust multicellular clocks and better
understanding of natural genetic oscillators.
1 INTRODUCTION
Synchronization is an essential process for the proper
functioning of living organisms from bacteria to
mammals. Synchronization is important to coordi-
nate the gene expression of bacteria populations in
order to act in unison (Waters and Bassler, 2005; Ng
and Bassler, 2009). In mammals, cells produce re-
liable and synchronized oscillations in the gene ex-
pression which control important functions such as
metabolism, signalling and cell cycle (Mohawk et al.,
2012; Welsh et al., 2010). Moreover, cell populations
that oscillate synchronously have been implemented
in the laboratory in the last few years (Danino et al.,
2010; Prindle et al., 2014). In the above cases, the
presence of feedback loops is ubiquitous in genetic
networks. Feedback loops have been important in the
design and implementation of initial synthetic genetic
devices. For example, the genetic toggle switch is a
synthetic device constructed in Escherichia coli bac-
teria (Gardner et al., 2000). This genetic network has
two stable states, and it is possible to flip from one
to the other induced by external signals. The toggle
switch consists basically of two genes with two re-
pressible promoters. Each gene encodes a different
repressor protein, which is able to bind to the pro-
moter of the other gene and inhibits its expression.
Other example is the so-called repressilator, that is
the first synthetic genetic oscillator constructed. The
repressilator is also a synthetic device implemented
in Escherichia coli (Elowitz and Leibler, 2000). It
is a genetic network that can produce an oscillatory
behaviour. It consists of three genes with three re-
pressible promoters. The genes are connected to each
other forming a ring. As in the toggle switch, each
gene encodes a repressor protein that is able to bind to
the promoter of the next gene and inhibits its expres-
sion. The result of these three repressive interactions
is the creation of a negative feedback loop with de-
lay, which is known to produce sustained oscillations
(Nov
´
ak and Tyson, 2008). Several synthetic genetic
oscillators, based on different designs, have also been
implemented after the repressilator (Atkinson et al.,
2003; Fung et al., 2005; Stricker et al., 2008; Bala-
gadd
´
e et al., 2008; Tigges et al., 2009; Toettcher et al.,
2010; Kim and Winfree, 2011; Montagne et al., 2011;
Weitz et al., 2014).
Genes often express transcription factors that reg-
ulate their own transcription rates in genetic networks.
This behaviour of the genes produces feedback loops.
If a gene expresses a transcription factor that increases
its own transcription rate, a positive feedback loop is
created. In contrast, when a gene expresses a tran-
scription factor that decreases its own transcription
121
Miro-Bueno J..
Coupling of Self-activating Genes Induces Spontaneous Synchronized Oscillations in Cells.
DOI: 10.5220/0005216801210127
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2015), pages 121-127
ISBN: 978-989-758-070-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: The model. Population of cells in which each cell contains a self-activating gene. External small molecules (squares)
can diffuse across the membrane and couples the self-activating genes. The small molecules inhibit the proteins in the positive
feedback loop.
rate, a negative feedback loop is created. A gene
with positive feedback loop can produce bistability
(Keller, 1995; Smolen et al., 2000; Becskei et al.,
2001; Ferrell Jr., 2002; Mitrophanov and Groisman,
2008). This means that two steady states are possi-
ble in the system. In one state there is a high num-
ber of molecules, for example proteins, and in other
state there is a low number of molecules. Positive
feedbacks are also present in many natural genetic
clocks (Reppert and Weaver, 2002; Gallego and Vir-
shup, 2007; Purcell et al., 2010; Lenz and Søgaard-
Andersen, 2011; O’Brien et al., 2012). In genetic
oscillators, it seems that the negative feedback is
mainly involved in generating oscillations, whereas
the positive feedback allows tuning the oscillations
without changing the amplitudes (Tsai et al., 2008),
contributes to increase the robustness of these os-
cillations (Vilar et al., 2002; Tsai et al., 2008) and
could provide robust adaptation to environmental cy-
cles (Rand et al., 2004; Mondrag
´
on-Palomino et al.,
2011). Models of genetic clocks involving negative
and positive auto-regulated genes have been stud-
ied in the last few years (Barkai and Leibler, 2000;
Smolen et al., 2001; Hasty et al., 2001; Franc¸ois,
2005; Guantes and Poyatos, 2006; Rodrigo et al.,
2007; Hong et al., 2008; Conrad et al., 2008; Kr-
ishna et al., 2009; Nandi et al., 2009; Munteanu
et al., 2010). In these models the positive feed-
back loops increase the expression of repressor genes.
Moreover, positive auto-regulated genes with sim-
ple negative interactions can produce reliable oscilla-
tions (Mir
´
o-Bueno and Rodr
´
ıguez-Pat
´
on, 2011). Be-
yond increasing robustness, studies about the role
of self-activating genes in the direct production of
oscillations are needed to understand better cellular
clocks. Coupling of negative auto-regulated genes is
the usual way for producing synchronized oscillations
in the study and modelling of synthetic gene clocks
(McMillen et al., 2002; Garcia-Ojalvo et al., 2004).
Here, we present and study a new model to eluci-
date the role of self-activating genes in the produc-
tion of rhythms in cell populations. We show that the
coupling of self-activating genes by transmembrane
movement of small molecules, such as metabolites,
produces synchronized oscillations in a cell popula-
tion.
2 MODEL
The model is a population of cells in which each cell
contains a self-activating gene (Fig. 1). We consider
the simplest form of a self-activating gene without
protein cooperation or multimers (Vilar et al., 2002;
Mir
´
o-Bueno and Rodr
´
ıguez-Pat
´
on, 2011). This gene
expresses a protein that produces a positive feedback
loop. The protein binds to the promoter of its own
gene and increases the transcription rate. An exter-
nal small molecule is in charge of coupling the self-
activating genes. This small molecule enters into
the system at constant rate. This molecule can pass
through the membrane. We do not assume an specific
way, the only condition is that the molecule can pass
in both directions, from outside to inside of cells and
vice versa. Inside cells, the small molecule can inhibit
the protein that produces the positive feedback. Then,
the protein can not bind to its promoter when attached
to the small molecule. At the same time, the small
molecule can not go outside the cell because it is at-
tached to the protein. When the protein is degraded
the small molecule is released and can bind to other
protein or leave the cell crossing the membrane. The
model is described by 12N + 2 biochemical reactions,
where N is the number of cells. The chemical reac-
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
122

tions that describe the gene with positive feedback in
each cell i are as follows:
Activation: G
i
+ Ai
k
1
−→ G
a
i
Deactivation: G
a
i
k
−1
−−→ G
i
+ A
i
Slow transcription: G
i
k
2
−→ G
i
+ M
i
Fast transcription: G
a
i
k
3
−→ G
a
i
+ M
i
mRNA degradation: M
i
k
4
−→ φ
Translation: M
i
k
5
−→ M
i
+ A
i
A degradation: A
i
k
6
−→ φ
(1)
where G
i
denotes the gene without A
i
bound to its
promoter, M
i
denotes mRNA transcribed from G
i
, A
i
denotes the activator protein translated from M
i
, G
a
i
denotes the gene with A
i
bound to its promoter. The
description of the rates is as follows: k
1
is the binding
rate of A
i
to the promoter of G
i
, k
−1
is the unbinding
rate of A
i
from the promoter of G
i
, k
2
is the basal tran-
scription rate, k
3
is the activated transcription rate, k
4
is the degradation rate of M
i
, k
5
is the translation rate
and k
6
is the degradation rate of A
i
.
On the other hand, the chemical reactions that de-
scribe the dynamics of the small molecule are as fol-
lows:
Complex creation: S
i
+ A
i
k
7
−→ C
i
Complex decay: C
i
k
8
−→ S
i
S entry: S
k
9
−→ S
i
S
i
exit: S
i
k
10
−−→ S
S
i
degradation: S
i
k
11
−−→ φ
S creation: φ
k
12
−−→ S
S degradation: S
k
13
−−→ φ
(2)
where S
i
denotes the small molecules inside cell i, C
i
denotes S
i
bound to protein A
i
and S denotes the small
molecules in the extracellular medium. The descrip-
tion of the rates is as follows: k
7
is the binding rate
of S
i
to A
i
, k
8
is the decay rate of C
i
into S
i
, k
9
is the
entry rate of S into the cell, k
10
is the exit rate of S
i
from the cell i, k
11
is the degradation rate of S
i
, k
12
is the synthesis rate of S and and k
13
is the degrada-
tion rate of S. We perform stochastic simulations of
the model since it is more realistic than determinis-
tic simulations and takes into account the random na-
ture of chemical reactions (Gillespie, 1977). We have
chosen typical parameter values to produces circadian
rhythms (24-hour period) due to its relevance in bio-
logical systems (Vilar et al., 2002; Mir
´
o-Bueno and
Figure 2: Production of oscillations. The number of pro-
teins start oscillating in cells when the small molecule can
diffuse across the membrane. These oscillations are unsyn-
chronized.
CouplingofSelf-activatingGenesInducesSpontaneousSynchronizedOscillationsinCells
123
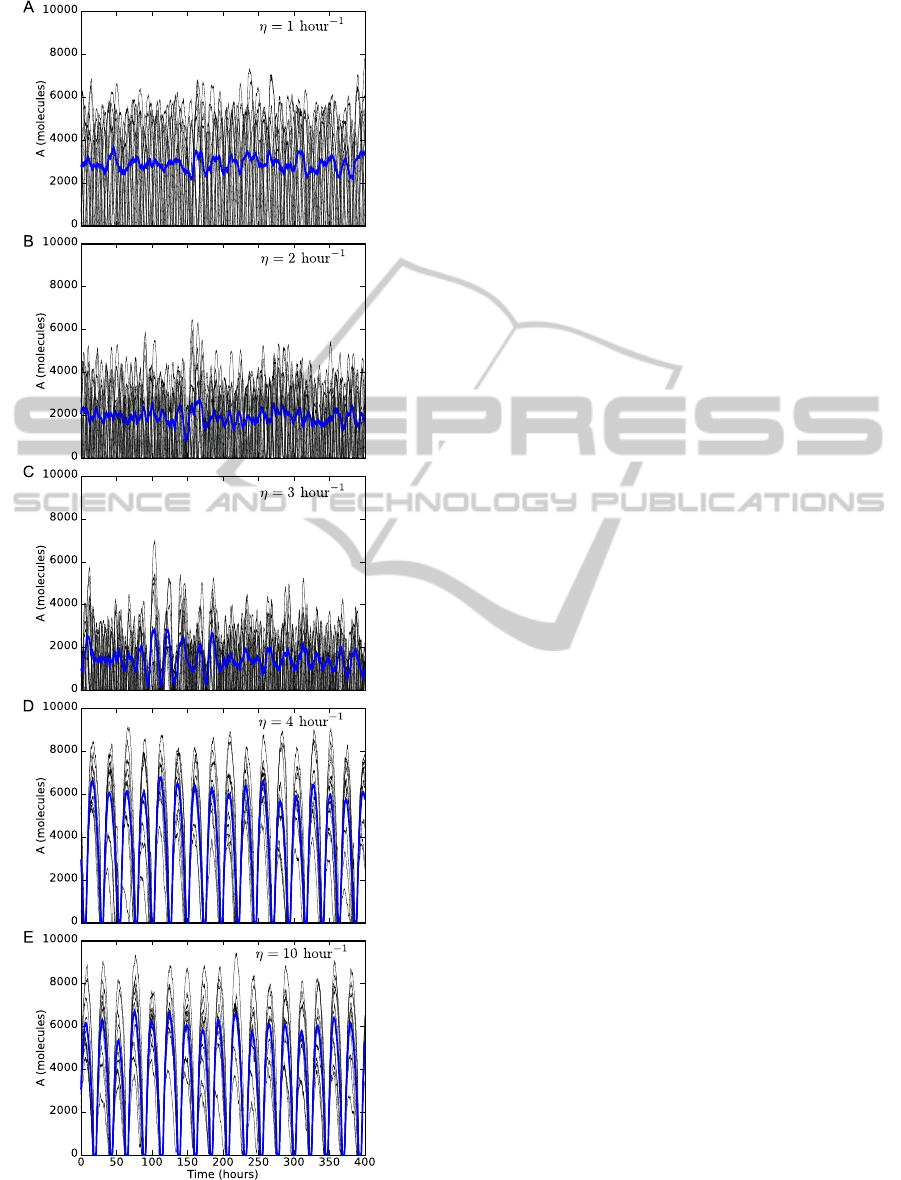
Figure 3: Synchronization of oscillations. Increasing the
diffusion rate across the membrane produces synchronized
oscillations. Blue lines represent the average.
Rodr
´
ıguez-Pat
´
on, 2011). The values of the rates are:
k
1
= 1 molecule
−1
hour
−1
, k
−1
= 50 hour
−1
, k
2
= 50
hour
−1
, k
3
= 500 hour
−1
, k
4
= 10 hour
−1
, k
5
= 50
hour
−1
, k
6
= 0.1 hour
−1
, k
7
= 0.5 molecule
−1
hour
−1
,
k
8
= 2.6 hour
−1
, k
9
= η, k
10
= η, k
11
= 1 hour
−1
,
k
12
= 50 molecule hour
−1
and k
13
= 1 hour
−1
. We
have chosen random initial conditions for each simu-
lation. Each type of molecule was randomly set to be
between 0 and 1,000 molecules. For the number of
genes we choose G
i
= 1 molecule. The first 100 hours
of transient behaviour were discarded. In this model,
the synchronization of the cell population depends on
the diffusion rate across the membrane (η). The small
molecules can pass through the cell membrane from
extracellular to intracellular space and vice versa. In
our model, this means that the rates k
9
and k
10
are
the same, i.e., η = k
9
= k
10
. We assume that diffu-
sion of the small molecule in the extracellular medium
reaches the equilibrium fast in comparison with typi-
cal biochemical reactions such as transcription, trans-
lation or degradation.
3 RESULTS AND DISCUSSION
The dynamics for ten coupled cells are shown in
Figs. 2 and 3. In Fig. 2 we show that the number
of proteins start oscillating in cells when the small
molecule can diffuse across the membrane. When η is
0 there is not coupling, and each cell in the population
expresses the protein until its maximum value 25,000
molecules, i.e., a fixed point is reached (Fig. 2A).
When η increases from 0 to 0.01 hour
−1
the number
of proteins oscillates in each cell (Fig. 2B). This oscil-
latory behaviour appears in each cell due to the neg-
ative interaction between the small molecule and the
positive feedback loop (Mir
´
o-Bueno and Rodr
´
ıguez-
Pat
´
on, 2011). The negative interaction is the inhi-
bition of proteins by small molecules. The oscilla-
tions involved two stages. In the first one, the small
molecules are accumulated in the cells, due to the
positive feedback is at its maximum strength. In the
second stage the small molecules are released or de-
graded in cells, due to the positive feedback is in its
minimum strength. The amplitude is about 15,000
molecules and the period is about 150-200 hours.
Each cell in the population produces oscillations but
these oscillations are not synchronized. If the rate η is
increased the amplitude and period of the oscillations
are decreased (Figs. 2C,D,E).
In Fig. 3 we show that increasing the diffusion
rate η produces synchronized oscillations. When
η = 1 hour
−1
the oscillations are not synchronized
(Fig. 3A). In this case, the diffusion rate across the
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
124
membrane is not fast enough to induce synchronized
oscillations in the cell population. When η is in-
creased the oscillations are still not synchronized and
the amplitude is decreased (Figs. 3B,C). This reduc-
tion in the amplitude of the oscillations is because
proteins are inhibited by small molecules. When η
= 4 hour
−1
the oscillations are synchronized with a
period of about 24 hours due to small molecules can
diffuse fast enough between the cells (Fig. 3D). The
amplitude in the synchronized oscillations is higher
than the oscillations showed in Fig. 3A. If the vale of
η is increased to 10 hour
−1
(Fig. 3E), the dynamics of
the oscillations is the same as in Fig. 3D.
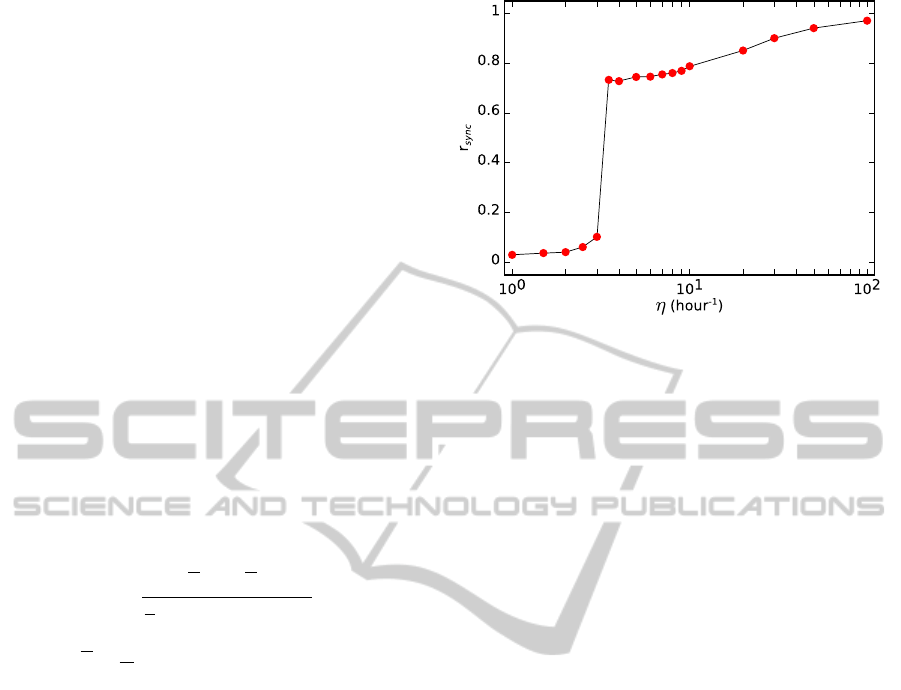
In Fig. 4 we show that the synchronization of the
oscillations in the cell population increases when the
value of η is raised. Specifically, we show that there
is a transition from unsynchronized to synchronized
oscillations as a function of the diffusion rate of the
small molecule. We use the so-called order parame-
ter (r
sync
) to measure the degree of synchrony over a
time interval (Garcia-Ojalvo et al., 2004). The r
sync
for the proteins A is the ratio of the variance of the
mean number of A in all the cells to the mean vari-
ance of each cell in a time interval:
r
sync
=
hA
2
i − hAi
2
1
N
∑
N
i=1
(hA
2
i
i − hA
i
i
2
)
,
A =
1
N
N
∑
i=1
A
i
,
(3)
where brackets denote time average. The value of
r
sync
is between 0 and 1, where 0 corresponds to un-
synchronized oscillations and 1 corresponds to per-
fect synchronized oscillations. The oscillations are
unsynchronized when η is lower than about 3 hour
−1
.
In this case, the value of r
sync
is lower than 0.1. How-
ever, when η is increased until about 3.5 hour
−1
the
oscillations spontaneously synchronized. In this case,
the value of r
sync
is about 0.7. And if the value of η
is higher than 3.5 hour
−1
the value of the order pa-
rameter r
sync
approximates to 1. The coupling of the
self-activating genes by a small molecule produces
the oscillations first and then the transition from un-
synchronized to synchronized oscillations. This type
of transition in a coupled population of oscillators was
predicted by Winfree (Winfree, 2002). For example,
this transition has been found in a cell population with
coupled genetic clocks (Garcia-Ojalvo et al., 2004).
The difference is that we do not have genetic clocks
in our model if the coupling agent is not present. In
our model the small molecules are the coupling agents
and also are directly involved in the production of os-
cillations. Another difference is that our model does
not involve genes with negative feedback loops. Our
Figure 4: Order parameter as a function of the diffusion rate
of the small molecule across the membrane. Computed time
for each point: 2,500 hours (1,000 hours for η= 20, 30, 50
and 100 hour
−1
).
study shows that there is an alternative possibility for
a cell population to produces synchronized oscilla-
tions. We speculate that both auto-repressed and self-
activating genes can participate in the production of
synchronized oscillations together or separately. It is
known that a positive feedback loop can provide ro-
bustness to molecular noise in a genetic clock driven
by a gene with negative feedback. We hypothesize
that the presence of self-activating genes could also
increase the robustness to failures in a cell population
that produces synchronized rhythms. A future work is
study how self-activating genes can produce synchro-
nized oscillations with simple conditions if the genes
with negative feedback failed. Another future work is
to study the behaviour of the cell population when the
synthesis rate of the small molecules is not a constant
value.
4 CONCLUSIONS
We have found that the coupling of self-activating
genes by small molecules in a cell population can
produce synchronized oscillations. This finding is a
new role of self-activating genes. In our model, the
small molecules are the coupling agents and are also
directly involved in the production of oscillations. We
have found a transition from unsynchronized to syn-
chronized oscillations as a function of the diffusion
rate of the small molecule. This behaviour could be
interesting for engineering new synthetic multicellu-
lar clocks and for better understanding the role of self-
activating genes in genetic clocks.
CouplingofSelf-activatingGenesInducesSpontaneousSynchronizedOscillationsinCells
125

ACKNOWLEDGEMENTS
This work was supported by the European Regional
Development Fund in the IT4Innovations Centre
of Excellence project (CZ.1.05/1.1.00/02.0070)
and EU project Development of Research Ca-
pacities of the Silesian University in Opava
(CZ.1.07/2.3.00/30.0007).
REFERENCES
Atkinson, M. R., Savageau, M. A., Myers, J. T., and Ninfa,
A. J. (2003). Development of genetic circuitry ex-
hibiting toggle switch or oscillatory behavior in Es-
cherichia Coli. Cell, 113(5):597–607.
Balagadd
´
e, F. K., Song, H., Ozaki, J., Collins, C. H., Barnet,
M., Arnold, F. H., Quake, S. R., and You, L. (2008).
A synthetic escherichia coli predator–prey ecosystem.
Molecular systems biology, 4(1).
Barkai, N. and Leibler, S. (2000). Circadian clocks limited
by noise. Nature, 403(6767):267–268.
Becskei, A., Seraphin, B., and Serrano, L. (2001). Positive
feedback in eukaryotic gene networks: cell differen-
tiation by graded to binary response conversion. The
EMBO Journal, 20(10):2528–2535.
Conrad, E., Mayo, A. E., Ninfa, A. J., and Forger, D. B.
(2008). Rate constants rather than biochemical mech-
anism determine behaviour of genetic clocks. Journal
of the Royal Society Interface, 5(supp1):S9–S15.
Danino, T., Mondragon-Palomino, O., Tsimring, L., and
Hasty, J. (2010). A synchronized quorum of genetic
clocks. Nature, 463(7279):326–330.
Elowitz, M. B. and Leibler, S. (2000). A synthetic oscil-
latory network of transcriptional regulators. Nature,
403(6767):335–338.
Ferrell Jr., J. E. (2002). Self-perpetuating states in sig-
nal transduction: positive feedback, double-negative
feedback and bistability. Current Opinion in Cell Bi-
ology, 14(2):140–148.
Franc¸ois, P. (2005). A model for the Neurospora circadian
clock. Biophysical Journal, 88:2369–2383.
Fung, E., Wong, W. W., Suen, J. K., Bulter, T., Lee, S.,
and Liao, J. C. (2005). A synthetic gene-metabolic
oscillator. Nature, 435(7038):118–122.
Gallego, M. and Virshup, D. M. (2007). Post-translational
modifications regulate the ticking of the circadian
clock. Nature Reviews Molecular Cell Biology,
8(2):139–148.
Garcia-Ojalvo, J., Elowitz, M. B., and Strogatz, S. H.
(2004). Modeling a synthetic multicellular clock: re-
pressilators coupled by quorum sensing. Proceedings
of the National Academy of Sciences, 101(30):10955–
10960.
Gardner, T. S., Cantor, C. R., and Collins, J. J. (2000).
Construction of a genetic toggle switch in Escherichia
coli. Nature, 403(6767):339–342.
Gillespie, D. T. (1977). Exact stochastic simulation of
coupled chemical reactions. The Journal of Physical
Chemistry, 81(25):2340–2361.
Guantes, R. and Poyatos, J. F. (2006). Dynamical principles
of two-component genetic oscillators. PLoS Compu-
tational Biology, 2(3):e30.
Hasty, J., Isaacs, F., Dolnik, M., McMillen, D., and Collins,
J. J. (2001). Designer gene networks: Towards funda-
mental cellular control. Chaos, 11(1):207–220.
Hong, C. I., Jolma, I. W., Loros, J. J., Dunlap, J. C., and
Ruoff, P. (2008). Simulating dark expressions and in-
teractions of frq and wc-1 in the Neurospora circadian
clock. Biophysical Journal, 94(4):1221–1232.
Keller, A. D. (1995). Model genetic circuits encoding au-
toregulatory transcription factors. Journal of Theoret-
ical Biology, 172(2):169–185.
Kim, J. and Winfree, E. (2011). Synthetic in vitro transcrip-
tional oscillators. Molecular Systems Biology, 7.
Krishna, S., Semsey, S., and Jensen, M. H. (2009). Frus-
trated bistability as a means to engineer oscillations in
biological systems. Physical Biology, 6(3):036009.
Lenz, P. and Søgaard-Andersen, L. (2011). Temporal and
spatial oscillations in bacteria. Nature Reviews Micro-
biology, 9(8):565–577.
McMillen, D., Kopell, N., Hasty, J., and Collins, J. (2002).
Synchronizing genetic relaxation oscillators by inter-
cell signaling. Proceedings of the National Academy
of Sciences, 99(2):679–684.
Mir
´
o-Bueno, J. M. and Rodr
´
ıguez-Pat
´
on, A. (2011). A sim-
ple negative interaction in the positive transcriptional
feedback of a single gene is sufficient to produce reli-
able oscillations. PLoS ONE, 6(11):e27414.
Mitrophanov, A. Y. and Groisman, E. A. (2008). Posi-
tive feedback in cellular control systems. BioEssays,
30(6):542–555.
Mohawk, J. A., Green, C. B., and Takahashi, J. S. (2012).
Central and peripheral circadian clocks in mammals.
Annual review of neuroscience, 35:445.
Mondrag
´
on-Palomino, O., Danino, T., Selimkhanov, J.,
Tsimring, L., and Hasty, J. (2011). Entrainment of
a population of synthetic genetic oscillators. Science,
333(6047):1315–1319.
Montagne, K., Plasson, R., Sakai, Y., Fujii, T., and Ron-
delez, Y. (2011). Programming an in vitro DNA oscil-
lator using a molecular networking strategy. Molecu-
lar Systems Biology, 7.
Munteanu, A., Constante, M., Isalan, M., and Sole, R.
(2010). Avoiding transcription factor competition at
promoter level increases the chances of obtaining os-
cillation. BMC Systems Biology, 4(1):66.
Nandi, A., Vaz, C., Bhattacharya, A., and Ramaswamy, R.
(2009). miRNA-regulated dynamics in circadian os-
cillator models. BMC Systems Biology, 3(1):45.
Ng, W.-L. and Bassler, B. L. (2009). Bacterial quorum-
sensing network architectures. Annual review of ge-
netics, 43:197–222.
Nov
´
ak, B. and Tyson, J. J. (2008). Design principles of bio-
chemical oscillators. Nature Reviews Molecular Cell
Biology, 9(12):981–991.
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
126

O’Brien, E. L., Van Itallie, E., and Bennett, M. R. (2012).
Modeling synthetic gene oscillators. Mathematical
Biosciences, 236(1):1–15.
Prindle, A., Selimkhanov, J., Li, H., Razinkov, I., Tsimring,
L. S., and Hasty, J. (2014). Rapid and tunable post-
translational coupling of genetic circuits. Nature.
Purcell, O., Savery, N. J., Grierson, C. S., and di Bernardo,
M. (2010). A comparative analysis of synthetic ge-
netic oscillators. Journal of the Royal Society Inter-
face, 7(52):1503–1524.
Rand, D. A., Shulgin, B. V., Salazar, D., and Millar, A. J.
(2004). Design principles underlying circadian clocks.
Journal of the Royal Society Interface, 1(1):119–130.
Reppert, S. M. and Weaver, D. R. (2002). Coordi-
nation of circadian timing in mammals. Nature,
418(6901):935–941.
Rodrigo, G., Carrera, J., and Jaramillo, A. (2007). Evolu-
tionary mechanisms of circadian clocks. Central Eu-
ropean Journal of Biology, 2(2):233–253.
Smolen, P., Baxter, D. A., and Byrne, J. H. (2000).
Mathematical modeling of gene networks. Neuron,
26(3):567–580.
Smolen, P., Baxter, D. A., and Byrne, J. H. (2001). Mod-
eling circadian oscillations with interlocking positive
and negative feedback loops. The Journal of Neuro-
science, 21(17):6644–6656.
Stricker, J., Cookson, S., Bennett, M. R., Mather, W. H.,
Tsimring, L. S., and Hasty, J. (2008). A fast, ro-
bust and tunable synthetic gene oscillator. Nature,
456(7221):516–519.
Tigges, M., Marquez-Lago, T. T., Stelling, J., and Fusseneg-
ger, M. (2009). A tunable synthetic mammalian oscil-
lator. Nature, 457(7227):309–312.
Toettcher, J. E., Mock, C., Batchelor, E., Loewer, A., and
Lahav, G. (2010). A synthetic-natural hybrid oscil-
lator in human cells. Proceedings of the National
Academy of Sciences of the United States of America,
107(39):17047–17052.
Tsai, T. Y., Choi, Y. S., Ma, W., Pomerening, J. R., Tang,
C., and Ferrell, J. E. (2008). Robust, tunable biologi-
cal oscillations from interlinked positive and negative
feedback loops. Science, 321(5885):126–129.
Vilar, J. M. G., Kueh, H. Y., Barkai, N., and Leibler, S.
(2002). Mechanisms of noise-resistance in genetic
oscillators. Proceedings of the National Academy of
Sciences of the United States of America, 99(9):5988–
5992.
Waters, C. M. and Bassler, B. L. (2005). Quorum sensing:
cell-to-cell communication in bacteria. Annual Review
of Cell and Developmental Biology, 21:319–346.
Weitz, M., Kim, J., Kapsner, K., Winfree, E., Franco, E.,
and Simmel, F. C. (2014). Diversity in the dynami-
cal behaviour of a compartmentalized programmable
biochemical oscillator. Nature chemistry.
Welsh, D. K., Takahashi, J. S., and Kay, S. A. (2010).
Suprachiasmatic nucleus: cell autonomy and network
properties. Annual review of physiology, 72:551.
Winfree, A. T. (2002). On emerging coherence. Science,
298(5602):2336–2337.
CouplingofSelf-activatingGenesInducesSpontaneousSynchronizedOscillationsinCells
127
