
A Comparative Study of Network-based Approaches for Routing in
Healthcare Wireless Body Area Networks
Pablo Adasme
1
, Rafael Andrade
2
, Janny Leung
3
and Abdel Lisser
4
1
Departamento de Ingenier´ıa El´ectrica, Universidad de Santiago de Chile, Avenida Ecuador 3519, Santiago, Chile
2
Departamento de Estat´ıstica e Matem´atica Aplicada, Universidade Federal do Cear´a,
Campus do Pici - Bloco 910, 60455-760, Fortaleza, Cear´a, Brazil
3
Department of Systems Engineering & Engineering Management, Chinese University of Hong Kong, Shatin, Hong Kong
4
Laboratoire de Recherche en Informatique, Universit´e Paris-Sud XI, Bˆatiment 650, 91405 Orsay Cedex, France
Keywords:
Healthcare Wireless Body Area Networks, Network Design Topology Approach, Mixed Integer Linear
Programming, Variable Neighborhood Search.
Abstract:
In this paper, we propose a minmax robust formulation for routing in healthcare wireless body area networks
(WBAN). The proposed model minimizes the highest power consumption of each bio-sensor node placed in
the body of a patient subject to flow rate and network topology constraints. We consider three topologies in
the problem: a spanning tree, a star, and a ring topology as well. In particular, we use an equivalent poly-
nomial formulation of the spanning tree polytope (Yannakakis, 1991) to avoid having an exponential number
of cycle elimination constraints in the model. For the ring topology approach, we use constraints from the
well known mixed integer linear programming (MILP) formulation of the traveling salesman problem (Pataki,
2003). Thus, we compute optimal solutions and lower bounds directly using the MILP and linear program-
ming (LP) relaxations. Finally, we propose a Kruskal-based (Cormen et al., 2001) variable neighborhood
search metaheuristic to improve the solutions obtained with the star topology approach. Our preliminary nu-
merical results indicate that the tree approach is more convenient as it allows saving significantly more power
while the ring approach is the most expensive one. They also indicate that the difference between the opti-
mal objective function values for the tree and star formulations is not very large and that VNS can improve
significantly the solutions obtained with the star configuration, although, at a higher computational cost.
1 INTRODUCTION
Wireless sensor networks (WSN) have been consid-
ered by the research community as one of the most
promising technologies within last decades. Mostly
due to the innumerable applications that can be re-
alized in order to enhance people’s quality of life.
Regarding healthcare systems, a major concern is
to deal with the problem of preventive monitoring
systems. Particularly, for elderly population whose
growth has significantly increased around the globe
in last decades (Kinsella and Phillips, 2005). This
technology would also provide high quality care ser-
vices for young children in situations where both par-
ents are absent or in cases where people living in
rural areas can not reach hospitals and medical cen-
ters easily. Wireless body area networks (WBANs)
are composed of tiny biological sensors (bio-sensors)
which are placed in the body or in the clothes of a
person in order to remotely monitor healthcare status
conditions such as fever, blood pressure, body tem-
perature, heart rate, and so on. In a WBAN, pre-
serving the energy of the nodes is of great impor-
tance as their energy resources are limited. Addi-
tionally, an extremely low transmit power per node
is required in order to minimize interference. A com-
mon approach to deal with these problems is by im-
proving the performance of routing protocols. The
authors in (Fang and Dutkiewicz, 2009) propose an
efficient medium access control (MAC) protocol re-
ferred to as BodyMAC. This protocol uses flexible
bandwidth allocation to improve node energy effi-
ciency. In (Kwak et al., 2009) the authors compare
and analyze different protocols from WBAN require-
ments whereas in (Huang et al., 2010) the authorspro-
pose a weighted random value protocol for multiuser
WBANs (WRAP). Finally, in (Elias and Mehaoua,
2012) the authors consider explicit mathematical pro-
125
Adasme P., Andrade R., Leung J. and Lisser A..
A Comparative Study of Network-based Approaches for Routing in Healthcare Wireless Body Area Networks.
DOI: 10.5220/0005218001250132
In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 125-132
ISBN: 978-989-758-075-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

gramming formulations in order to efficiently design
optimal routing protocols in WBANs. WBAN is an
emerging research field where new routing protocols
are mandatorily required to efficiently manage power
consumption in order to maximizing the lifetime of
the network. Additionally, finding the “best” net-
work topology configuration in a WBAN is a very
important issue as it significantly affects the proto-
col design as well as the overall performance of the
system. Finally, we mention that research on rout-
ing protocols for WBANs is still at its infancy. In
this paper, we present a minmax robust formulation
to optimally route sensed information by nodes in a
WBAN. The model minimizes the worst power con-
sumption of each bio-sensor subject to flow rate and
network design topology constraints. We consider
three topologies in the problem: a spanning tree one,
a star one and a ring topology as well. In partic-
ular, we use an equivalent polynomial formulation
of the spanning tree polytope due to (Yannakakis,
1991) in order to avoid an exponential number of cy-
cle elimination constraints in the model. For the ring
topology approach, we use constraints from the well
known mixed integer linear programming(MILP) for-
mulation of the traveling salesman problem (Pataki,
2003). All the proposed models are formulated as
MILP models and thus we compute optimal solutions
and lower bounds directly using the MILP and lin-
ear programming (LP) relaxations, respectively. Fi-
nally, we propose a Kruskal-based variable neighbor-
hood search (VNS for short) metaheuristic to improve
the optimal solutions found with the star network con-
figuration. We only consider a VNS procedure that
works with the tree topology approach as it is the one
that achieves significantly more power savings. The
paper is organized as follows. Section 2 presents the
minmax robust formulation with the generic topology
constraint. In section 3, we present three MILP for-
mulations for each different topology. Subsequently,
in section 4 we present the Kruskal-based variable
neighborhood search procedure. Then, in section 5
we present preliminary numerical results in order to
compare the three MILP formulations together with
their LP relaxations. Next, we compare the VNS pro-
cedure with the star and tree MILP models. Finally,
section 6 concludes the paper.
2 PROBLEM FORMULATION
We model a fixed WBAN by the means of a graph
G = (V = V
n
∪V
s
, E), where V
n
denotes a set of bio-
sensor nodes that sense and collect the data to be
transmitted while V
s
represents a sink node where all
the data is finally received. The set E represents the
set of edges in the graph G. For sake of simplicity, in
the remainder of the paper we assume that the graph
G is a complete graph. We consider the following
generic model we denote hereafter by P
0
as
min
{x,y}
max
{i∈V
n
}
∑
j∈V:(i, j)∈E
p
ij
y
ij
(1)
s.t.y
ij
≤ Lx
ij
, ∀i ∈ V
n
, j ∈ V : (i, j) ∈ E (2)
∑
j∈V:(i, j)∈E
y
ij
−
∑
j∈V:( j,i)∈E
y
ji
≥ r
i
,
∀i ∈ V
n
(3)
R
min
≤ r
i
≤ R
max
, ∀i ∈ V
n
(4)
Topology constraints on x
ij
variables (5)
x
ij
∈ {0, 1}, y
ij
≥ 0, ∀i, j ∈ V (6)
In P
0
, variable x
ij
= 1 if node i is connected to node
j and x
ij
= 0 otherwise. Variable y
ij
, i, j ∈ V repre-
sents the amount of flow to be transmitted in edge
(i, j) ∈ E. The input parameter p
ij
denotes the unitary
power required by node i to transmit a unit of flow
y
ij
. Hence, the objective function in (1) minimizes
the worst power consumption of each bio-sensor node
j ∈ V
n
overall edges (i, j) ∈ E. Constraint (2) implies
that y
ij
should be equal to 0 if nodes i and j are not
connected, i.e. when x
ij
= 0. Here, we assume that
each edge (i, j) ∈ E has a maximum link capacity de-
noted by L. Constraint (3) are flow constraints forcing
each node i ∈ V
n
to transmit the sensed and collected
data through the network. For this purpose, we intro-
duce data rate variables r
i
for each node i ∈ V
n
. In
constraint (4), we further impose the condition that
each variable r
i
must be bounded as 0 ≤ R
min
≤ r
i
≤
R
max
, i ∈ V
n
where R
min
and R
max
are minimum and
maximum data rate parameters. In general, constraint
(4) is justified by the fact that low power medium ac-
cess control (MAC) and routing protocols allow vary-
ing the amount of data to be transmitted by a partic-
ular node depending on the quality of the channels
(Reusens et al., 2009; Ullah et al., 2012). Finally, con-
straint (5) represents a generic topology constraint we
should impose with variables x
ij
as stated in section
3.
In general, there exists several WBAN configura-
tions such as star, tree, or mesh type networks (Ullah
et al., 2012). The most common topology approach
is a star one where the nodes are connected to the
sink node in star manner (Ullah et al., 2012). How-
ever, the star configuration follows a single hop strat-
egy which is not always the best choice. In (Reusens
et al., 2009), the authorsdiscuss about energy efficient
topology designs for WBANs. They consider a tree
network topology and discuss on the energy savings
when using single hop and multi hop strategies. They
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
126

conclude that both single hop or multi hop strategies
can achieve energy savings under different conditions
(Reusens et al., 2009). In this paper, we compare
three topology approaches for WBANs, a tree one, a
star one and a ring topology as well. For this purpose,
we assume that all bio-sensors can communicate with
each other, i.e. we assume that the WBAN can be rep-
resented by means of a complete graph. Notice that
the parameter L in P
0
might lead to infeasible solu-
tions when using a multi hop strategy in some cases.
This can happen since the flow constraints (3) accu-
mulate the amount of data to be transmitted from one
node to another. Whereas in the single hop strategy
this can rarely happen because the maximum capac-
ity of L is always larger than R
max
.
3 MILP FORMULATIONS
In this section, we present MILP formulations for the
spanning tree, star and ring network configurations.
For this purpose, we replace constraint (5) in model P
0
by different set of constraints depending on the topol-
ogy approach under consideration.
3.1 Spanning Tree Topology Approach
We propose the following spanning tree MILP formu-
lation and denote this model hereafter by P
1
as follows
min
{x,y,r,λ,t}
t (7)
s.t.
∑
j∈V:(i, j)∈E
p
ij
y
ij
≤ t, ∀i ∈ V
n
(8)
y
ij
≤ Lx
ij
, ∀i ∈ V
n
, j ∈ V : (i, j) ∈ E (9)
∑
j∈V:(i, j)∈E
y
ij
−
∑
j∈V:( j,i)∈E
y
ji
≥ r
i
,
∀i ∈ V
n
(10)
R
min
≤ r
i
≤ R
max
, ∀i ∈ V
n
(11)
λ
kij
+ λ
kji
≥ x
ij
, ∀k, i, j ∈ V (12)
∑
j∈V−{i}
λ
kij
≤ 1, ∀k, i ∈ V, (k 6= i) (13)
λ
kki
= 0, ∀k, i ∈ V, (k 6= i) (14)
∑
i, j∈V,i< j
x
ij
= |V| − 1 (15)
x
ij
∈ {0, 1}, y
ij
≥ 0, ∀i, j ∈ V (16)
λ
kij
∈ {0, 1}, ∀k, i, j ∈ V (17)
In particular, we replace the topology constraint (5)
in P
0
by the set of constraints (12)-(15) and (17) in
P
1
. This set of constraints characterizes the set of
all spanning trees in graph G (Yannakakis, 1991).
In P
1
, λ
kij
, ∀k, i, j ∈ V are binary decision variables
required to characterize the spanning tree polytope
(Yannakakis, 1991).
3.2 Star Topology Approach
Similarly, a star MILP formulation can be obtained
by replacing the topology constraint (5) by the set of
constraints (23)-(24) and (26). Thus, we state the fol-
lowing model we denote by P
2
as follows
min
{x,y,r,ϕ,t}
t (18)
s.t.
∑
j∈V:(i, j)∈E
p
ij
y
ij
≤ t, ∀i ∈ V
n
(19)
y
ij
≤ Lx
ij
,
∀i ∈ V
n
, j ∈ V : (i, j) ∈ E (20)
∑
j∈V:(i, j)∈E
y
ij
−
∑
j∈V:( j,i)∈E
y
ji
≥ r
i
,
∀i ∈ V
n
(21)
R
min
≤ r
i
≤ R
max
, ∀i ∈ V
n
(22)
x
ij
≤ ϕ
j
, ∀i, j ∈ V, (i 6= j) (23)
∑
j∈V
ϕ
j
= P (24)
x
ij
∈ {0, 1}, y
ij
≥ 0, ∀i, j ∈ V (25)
ϕ
j
∈ {0, 1}, ∀ j ∈ V (26)
In P
2
, ϕ
j
, ∀ j ∈ V are binary decision variables re-
quired to characterize the feasible set of the star con-
figuration. In particular, we require that the input pa-
rameter P = 1 in order to obtain a star network con-
figuration centred at the sink node with all the edges
flowing into it. Notice that the constraints (23)-(24)
can be merged into a single constraint as x
ij
≤ 1, ∀i ∈
V
n
, j ∈ V
s
. However, we write them as such in or-
der to further consider the more general case when
1 < P ≤ |V| where |V| denotes the cardinality of V.
This means we relax the star topology condition and
allow a fully connected scenario, although at the cost
of flooding the network.
3.3 Ring Topology Approach
Finally, we obtain a ring topology MILP formulation
by replacing the topology constraint (5) by the set of
constraints (32)-(36) and (38). In particular, we use
the set of constraints from the MILP formulation of
the traveling salesman problem (Pataki, 2003). Thus,
we formulate P
3
as follows
min
{x,y,r,u,t}
t (27)
s.t.
∑
j∈V:(i, j)∈E
p
ij
y
ij
≤ t, ∀i ∈ V
n
(28)
AComparativeStudyofNetwork-basedApproachesforRoutinginHealthcareWirelessBodyAreaNetworks
127

y
ij
≤ Lx
ij
,
∀i ∈ V
n
, j ∈ V : (i, j) ∈ E (29)
∑
j∈V:(i, j)∈E
y
ij
−
∑
j∈V:( j,i)∈E
y
ji
≥ r
i
,
∀i ∈ V
n
(30)
R
min
≤ r
i
≤ R
max
, ∀i ∈ V
n
(31)
∑
j∈V:(i, j)∈E
x
ij
= 1, ∀i ∈ V (32)
∑
j∈V:(i, j)∈E
x
ji
= 1, ∀i ∈ V (33)
u
1
= 1 (34)
2 ≤ u
i
≤ |V|, ∀i ∈ V, (i 6= 1) (35)
u
i
− u
j
+ 1 ≤ (|V| − 1)(1− x
ij
),
∀i, j ∈ V, (i 6= 1), ( j 6= 1) (36)
x
ij
∈ {0, 1}, y
ij
≥ 0, ∀i, j ∈ V (37)
u
j
∈ Z
+
, ∀ j ∈ V (38)
In P
3
, u
i
, ∀i ∈ V are integer decision variables required
to characterize the feasible set of the traveling sales-
man problem (Pataki, 2003). Hereafter, we denote by
LP
1
, LP
2
and LP
3
the LP relaxations of P
1
, P
2
and
P
3
, respectively. In the next section, we present a
Kruskal-based VNS algorithm that allows improving
the optimal solutions found with the star topology ap-
proach.
4 KRUSKAL-BASED VNS
ALGORITHM
Metaheuristics are simple algorithmic procedures
commonly used to find near optimal (or suboptimal)
solutions for combinatorial optimization problems.
From a practical point of view, they have proven to
be highly effective when solving many of these hard
problems (Glover and Kochenberger, 2003). Espe-
cially when the dimensions of the problem increase
rapidly which is often the case in real world applica-
tions and where no solver is available to solve these
problems to optimality. The most frequently utilized
metaheuristics approaches are: genetic algorithms,
tabu search, ant colony system, particle swarm op-
timization, variable neighborhood search, simulated
annealing, among others. For a detailed explanation
on how these metaheuristics procedures work, we re-
fer the reader to the book in (Glover and Kochen-
berger, 2003). Basically, any metaheuristic approach
would serve to compute feasible solutions for our tree
MILP formulation. However, we choose VNS mainly
due to its simplicity and low memory requirements.
In particular, we adopt a reduced VNS strategy which
drops the local search phase of the basic VNS algo-
rithm as it is the most time consuming step (Hansen
and Mladenovic, 2001). In order to compute feasible
solutions for P
1
using a VNS approach, we observe
that for any fixed assignment of variable x = ¯x in P
1
,
the problem reduces to solve the following linear pro-
gramming problem
min
{y,r,t}
t (39)
s.t.
∑
j∈V:(i, j)∈E
p
ij
y
ij
≤ t, ∀i ∈ V
n
(40)
y
ij
≤ L¯x
ij
, ∀i ∈ V
n
, j ∈ V : (i, j) ∈ E (41)
∑
j∈V:(i, j)∈E
y
ij
−
∑
j∈V:( j,i)∈E
y
ji
≥ r
i
,
∀i ∈ V
n
(42)
R
min
≤ r
i
≤ R
max
, ∀i ∈ V
n
(43)
y
ij
≥ 0, ∀i, j ∈ V (44)
Hereafter, we denote by P
r
the LP problem (39)-
(44). Notice that the number of feasible assignments
for x in P
1
grows rapidly with the size of the instances.
Also notice that not all of these trees are feasible for P
r
since the capacity of each edge (i, j) ∈ E is limited by
L. We propose a Kruskal VNS approach to compute
feasible solutions for P
1
by randomly generating these
trees. VNS is a recently proposed metaheuristic ap-
proach (Hansen and Mladenovic, 2001) that uses the
idea of neighborhood change during the descent to-
ward local optima and to avoid the valleys that contain
them. The VNS approach we propose is presented in
Figure 1.
It receives an instance of problem P
1
as input and
provides a feasible solution for it. We denote by
( ˜x, ˜y, ˜r,
˜
t) the final solution obtained with the algo-
rithm where
˜
t represents the objective function value
of P
r
. The algorithm is simple and works as fol-
lows. In Step 0, we initialize all the required vari-
ables. Then, in Step 1 we obtain an initial feasible
solution for the problem. For this purpose, we solve
P
2
and obtain the star network configuration x = ¯x.
Then, we construct a cost vector c(i, j) for each edge
(i, j) ∈ E in such a way that x = ¯x can also be obtained
with Kruskal algorithm (Cormen et al., 2001). Find-
ing vector c(i, j) is required since we start our VNS
from the optimal solution of P
2
. Next, we save the
optimal objective function value of P
2
and the con-
structed vector c(i, j) as the bests found so far. We
define the neighborhood structure Ng(c) as the set of
neighbor vectors c
′
at a distance “h” from c where the
distance “h” corresponds to the number of entries in
vector c that are randomly swapped. There are |E|!
number of vectors c
′
in Ng(c) including c. Here, we
denote by |E| the cardinality of E. During the execu-
tion of the while loop in Step 2, the algorithm per-
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
128

Input: A problem instance of P
1
Output: A feasible solution ( ˜x, ˜y, ˜r,
˜
t) for P
1
Step 0:
Time ← 0; H ← θ; min ← ∞
count ← 0; x
i, j
← 0, ∀i, j ∈ V
Step 1:
Solve P
2
; Let ( ¯x, ¯y, ¯r,
¯
t) be the optimal solution of P
2
.
Construct a cost vector c = c(i, j), ∀(i, j) ∈ E
such that ¯x can be obtained with Kruskal algorithm.
min ←
¯
t; cOpt(i, j) ← c(i, j), ∀(i, j) ∈ E
Step 2:
while (Time ≤ maxTime)
For h = 1 to H
choose randomly two different edges (i, j), (k, l) ∈ E
aux ← c(i, j); c(i, j) ← c(k, l); c(k, l) ← aux
end for
¯x ← Kruskal(G, c);
Solve the linear problem P
r
.
if(P
r
is feasible)
Let ( ¯y, ¯r,
¯
t) be the optimal solution of P
r
with
objective function value
¯
t
if(min >
¯
t)
min ←
¯
t; cOpt(i, j) ← c(i, j), ∀(i, j) ∈ E
H ← 1; count ← 0
else
c(i, j) ← cOpt(i, j), ∀(i, j) ∈ E
count ← count +1
if (count > η)
if (H ≤ θ)
H ← H + 1
else
H ← 1
end if
count ← 0
end if
end if
end if
end while
Figure 1: VNS Algorithm.
forms a variable neighborhood search by randomly
swapping H ≤ θ valuesin vector c where θ represents
a parameter for the maximum number of swapping
movements. For each generated vector c
′
in Ng(c),
we find a maximum spanning tree x = ¯x for G using
Kruskal algorithm. Then, for each found tree we solve
P
r
. If P
r
is feasible we obtain a new solution ( ¯y, ¯r,
¯
t)
with objective function value
¯
t that we compare with
the best found so far. If this new solution is better, we
save
¯
t and the new vector c(i, j), (i, j) ∈ E. In case P
r
is infeasible, the solution is discarded and not consid-
ered as a valid solution. Initially, H ← 1 while it is
increased in one unit when there is no improvement
after new “η” solutions have been evaluated. On the
other hand, if a new current solution is better than the
best found so far, then H ← 1, the new solution is
recorded and the process goes on. Note that if “η” so-
lutions have been evaluated without improvement and
if H = θ, then we also set H ← 1. This gives the pos-
sibility of searching in a loop manner from small to
large zones of the feasible space. The whole process
is repeated while the cpu time variable “Time” is less
than or equal to the maximum available “maxTime”.
5 NUMERICAL RESULTS
In this section, we present preliminary numerical re-
sults in order to compare the three MILP and LP for-
mulations. Then, we compare the proposed VNS al-
gorithm with the tree and star MILP formulations. Fi-
nally, we present numerical results for P
2
when in-
crementing the parameter P from 1 to |V|. The latter
resembles the case where a flooding data transmission
situation is possible.
In our numerical tests, we assume that we only
have one node acting as a sink node which receives
all sensed and collected data sent by the remaining
nodes in the network. The input data is randomly gen-
erated as follows. The entries in matrix P
ij
are drawn
from the interval (0, 2] (Elias and Mehaoua, 2012).
The maximum capacity for each edge (i, j) ∈ E is
set to L = 5Mbps and L = 10Mbps. The minimum
acceptable data rate generated by each node i ∈ V
n
is R
min
= 128 kbps whereas the maximum data rate
is set to R
max
= 512 kbps. The parameters θ and η
in the VNS algorithm were calibrated to the values
of θ =
|V|
2
and η = 50, respectively. A Matlab pro-
gram is implemented using CPLEX 12 to solve the
MILP and LP models. The numerical experiments
have been carried out on a Intel(R) 64bits core(TM)
with 3.4 Ghz and 8 GoBytes of RAM. In Table 1, col-
umn 1 shows the number of nodes considered for each
instance. Then, columns 2-5, 6-9, and 10-13 present
the optimal solutions, lower bounds, and cpu time in
seconds for the MILP and LP models respectively. Fi-
nally, in columns 14-16 we present gaps we compute
as
P
i
−LP
i
P
i
∗100 for P
i
, i= 1, 2, 3, respectively. With-
out loss of generality, we set the maximum available
cpu time for CPLEX to solve the MILP formulations
to 1 hour. From Table 1, we observe that the objec-
tive function values of the LP models are equal for all
the instances. On the opposite, the objective function
values of P
1
are lower than those obtained with P
2
and
P
3
for the instances 1-28 when using L = 5Mbps and
for the instances 1-22 when using L = 10Mbps, re-
spectively. For the instances 28-60, these values are
larger than P
2
and P
3
in most of the cases. This can
be explained by the fact that P
1
has more variables
and constraints than P
2
and P
3
. Consequently, it is
harder to find feasible solutions with CPLEX in one
hour of cpu time. This is also confirmed by the cpu
times required by CPLEX to solve LP
1
which is not
the case for LP
2
and LP
3
. In general, we observe that
the star topology approach is more restrictive than the
ring one. Similarly, the ring approach is more restric-
tive than the tree one. Indeed, the star topology ap-
proach represented by P
2
is not a combinatorial op-
timization problem when P = 1 as it has only one
AComparativeStudyofNetwork-basedApproachesforRoutinginHealthcareWirelessBodyAreaNetworks
129
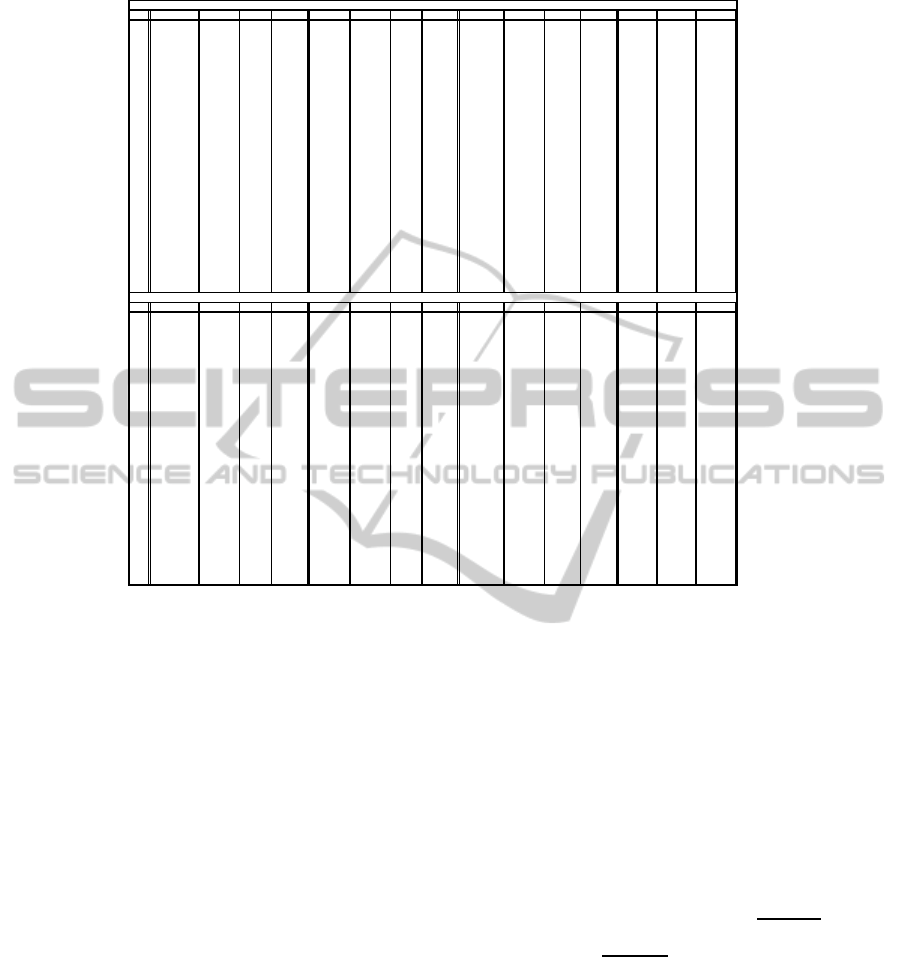
Table 1: Numerical results for the MILP and LP formulations.
Randomly generated instances using L = 5Mbps.
|V| P
1
LP
1
cpu P
1
cpu LP
1
P
2
LP
2
cpu P
2
cpu LP
2
P
3
LP
3
cpu P
3
cpu LP
3
Gap
1
(%) Gap
2
(%) Gap
3
(%)
4 172.9123 128.3024 0.10 0.08 230.4138 128.3024 0.08 0.08 259.3685 128.3024 0.09 0.08 25.80 44.32 50.53
6 116.5641 98.4527 0.13 0.08 216.1431 98.4527 0.09 0.12 318.5687 98.4527 0.12 0.08 15.54 54.45 69.10
8 130.0117 98.1275 0.63 0.09 233.8014 98.1275 0.08 0.08 227.0687 98.1275 0.13 0.08 24.52 58.03 56.79
10 110.5027 78.2920 13.93 0.11 251.9203 78.2920 0.08 0.08 364.8153 78.2920 0.65 0.08 29.15 68.92 78.54
12 130.4526 97.9122 40.04 0.16 245.1696 97.9122 0.09 0.08 604.7503 97.9122 2.03 0.09 24.94 60.06 83.81
14 92.1095 71.1643 105.58 0.28 211.3495 71.1643 0.09 0.08 360.7896 71.1643 64.14 0.09 22.74 66.33 80.28
16 82.5006 59.6906 199.44 0.36 241.4101 59.6906 0.09 0.09 371.4371 59.6906 48.42 0.09 27.65 75.27 83.93
18 140.0872 86.8162 3600 0.45 245.6945 86.8162 0.08 0.08 522.0311 86.8162 142.72 0.11 38.03 64.66 83.37
20 141.7066 95.2401 3600 1.04 255.1937 95.2401 0.09 0.08 628.2930 95.2401 3600 0.09 32.79 62.68 84.84
22 124.0203 49.9234 3600 2.28 232.0149 49.9234 0.09 0.09 596.5942 49.9234 3600 0.11 59.75 78.48 91.63
24 111.3924 66.8960 3600 2.57 252.9113 66.8960 0.09 0.09 737.1375 66.8960 3600 0.09 39.95 73.55 90.92
26 195.2991 65.0101 3600 4.35 252.6639 65.0101 0.10 0.09 1196.3041 65.0101 3600 0.11 66.71 74.27 94.57
28 239.6097 57.6606 3600 11.50 250.5124 57.6606 0.10 0.10 1593.2391 57.6606 3600 0.10 75.94 76.98 96.38
30 4173.3474 73.5776 3600 14.59 250.1774 73.5776 0.11 0.10 1549.9782 73.5776 3600 0.11 98.24 70.59 95.25
32 2524.4269 63.6507 3600 21.48 241.8655 63.6507 0.11 0.13 1156.7195 63.6507 3600 0.13 97.48 73.68 94.50
34 3263.2263 79.1640 3600 38.41 250.6571 79.1640 0.11 0.11 2515.5312 79.1640 3600 0.13 97.57 68.42 96.85
36 3449.0415 90.2439 3600 61.26 249.3930 90.2439 0.13 0.11 2386.0148 90.2439 3600 0.13 97.38 63.81 96.22
38 6435.0315 53.0661 3600 88.53 253.0734 53.0661 0.11 0.11 2305.0976 53.0661 3600 0.14 99.18 79.03 97.70
40 3767.6438 69.0079 3600 152.87 254.6958 69.0079 0.19 0.11 2920.8120 69.0079 3600 0.36 98.17 72.91 97.64
42 6478.9697 66.3856 3600 232.83 251.4469 66.3856 0.13 0.13 * * * * 98.98 73.60 *
44 404.3876 41.0750 3600 355.35 242.7594 41.0757 0.14 0.17 * * * * 89.84 83.08 *
46 - 70.0438 3600 505.22 253.9118 70.0677 0.14 0.13 * * * * - 72.40 *
48 - 52.1815 3600 3017.54 255.5081 52.1907 0.14 0.12 * * * * - 79.57 *
50 3772.5815 92.4267 3600 1439.90 254.7817 92.4267 0.16 0.13 * * * * 97.55 63.72 *
52 - 65.1555 3600 2845.34 254.1981 65.1555 0.16 0.14 * * * * - 74.37 *
54 5584.2879 - 3600 3600 254.6640 76.2489 0.16 0.16 * * * * - 70.06 *
56 - - 3600 3600 252.0183 67.3089 0.19 0.16 * * * * - 73.29 *
58 - - 3600 3600 249.9084 26.5575 0.16 0.19 * * * * - 89.37 *
60 - - 3600 3600 249.7696 57.4137 0.17 0.19 * * * * - 77.01 *
Randomly generated instances using L = 10Mbps.
|V| P
1
LP
1
cpu P
1
cpu LP
1
P
2
LP
2
cpu P
2
cpu LP
2
P
3
LP
3
cpu P
3
cpu LP
3
Gap
1
(%) Gap
2
(%) Gap
3
(%)
4 161.3486 161.3486 0.12 0.11 161.3486 161.3486 0.09 0.11 236.2260 161.3486 0.09 0.08 0.00 0.00 31.70
6 158.8516 113.4866 0.19 0.11 206.0860 113.4866 0.09 0.09 306.9530 113.4866 0.13 0.09 28.56 44.93 63.03
8 167.8537 118.2662 2.20 0.11 231.5832 118.2662 0.11 0.11 317.6564 118.2662 0.20 0.09 29.54 48.93 62.77
10 109.7763 79.6662 17.94 0.14 254.6038 79.6662 0.11 0.09 197.6088 79.6662 0.44 0.09 27.43 68.71 59.68
12 94.1630 71.2765 20.19 0.19 223.6883 71.2765 0.11 0.12 347.9636 71.2765 2.79 0.14 24.31 68.14 79.52
14 207.4696 152.5034 598.04 0.31 237.1391 152.5034 0.11 0.09 986.0484 152.5034 1.45 0.11 26.49 35.69 84.53
16 131.7450 86.6705 602.14 0.91 237.6965 86.6705 0.13 0.13 519.7352 86.6705 12.56 0.11 34.21 63.54 83.32
18 85.2014 54.9582 3600 0.98 233.4220 54.9582 0.11 0.14 523.4773 54.9582 589.97 0.12 35.50 76.46 89.50
20 157.2792 81.2429 3600 0.97 234.7924 81.2429 0.11 0.11 667.5973 81.2429 3600 0.12 48.34 65.40 87.83
22 110.0376 45.6260 3600 8.33 246.2602 45.6260 0.11 0.11 647.3801 45.6260 3600 0.11 58.54 81.47 92.95
24 843.3065 41.1025 3600 56.91 250.8984 41.1025 0.11 0.11 967.8684 41.1025 3600 0.13 95.13 83.62 95.75
26 209.3268 92.9892 3600 4.15 253.9718 92.9892 0.14 0.11 994.8130 92.9892 1156.95 0.13 55.58 63.39 90.65
28 2016.8067 42.6314 3600 12.10 255.3950 42.6314 0.13 0.09 1281.6073 42.6314 3600 0.14 97.89 83.31 96.67
30 5373.1321 58.1214 3600 16.65 251.0201 58.1214 0.17 0.11 1230.8660 58.1214 3600 0.14 98.92 76.85 95.28
32 3332.8286 30.1231 3600 25.69 254.4229 30.1231 0.11 0.13 1074.1794 30.1231 3600 0.13 99.10 88.16 97.20
34 3392.8137 93.6433 3600 39.80 253.7157 93.6433 0.13 0.14 2732.1523 93.6433 3600 0.14 97.24 63.09 96.57
36 5244.9209 29.3966 3600 60.01 255.9196 29.3966 0.13 0.14 3235.5210 29.3966 3600 0.14 99.44 88.51 99.09
38 5444.6537 57.5281 3600 78.61 241.8270 57.5281 0.13 0.13 2428.3402 57.5281 3600 0.14 98.94 76.21 97.63
40 4250.6198 38.5896 3600 144.18 249.9781 38.5896 0.14 0.19 3640.3934 38.5896 3600 0.16 99.09 84.56 98.94
42 6679.8978 41.1930 3600 216.37 255.4910 41.1930 0.14 0.14 3467.4348 41.1930 3600 0.33 99.38 83.88 98.81
44 3851.1773 46.0622 3600 298.01 252.7924 46.0622 0.16 0.13 4608.9222 46.0622 3600 0.16 98.80 81.78 99.00
46 8659.6065 76.6142 3600 469.25 255.1479 76.6142 0.16 0.13 3781.4271 76.6142 3600 0.16 99.12 69.97 97.97
48 10308.6667 52.3929 3600 796.32 254.1402 52.3929 0.16 0.16 4131.4633 52.3929 3600 0.17 99.49 79.38 98.73
50 6110.0211 39.9700 3600 1418.00 241.4975 39.9700 0.19 0.14 4126.8010 39.9700 3600 0.17 99.35 83.45 99.03
52 3277.5764 50.6042 3600 2301.87 254.2301 50.6042 0.19 0.16 4906.0580 50.6042 3600 0.17 98.46 80.10 98.97
54 7135.9017 - 3600 3600 253.9738 51.9915 0.36 0.17 6287.3268 51.9915 3600 0.37 - 79.53 99.17
56 13236.6801 - 3600 3600 253.6447 81.6661 0.19 0.17 6068.5311 81.6661 3600 0.23 - 67.80 98.65
58 8488.0286 - 3600 3600 248.2675 28.4356 0.20 0.19 6648.1337 28.4220 3600 0.22 - 88.55 99.57
60 11134.9972 - 3600 3600 255.3221 43.8373 0.20 0.19 6911.7691 43.8373 3600 0.39 - 82.83 99.37
-: No solution found.
*: Infeasible.
possible trivial solution for variable x which is the
star configuration. We also see that for instances with
more than 40 nodes, the ring models P
3
and LP
3
are
infeasible when using L = 5Mbps. This can be ex-
plained by the fact that the edge capacities in the net-
work are limited by parameter L. This is not the case
for the tree and star topology approaches which are
always feasible. As an example of this, we consider
again the star network configuration which is also a
tree. We also see that the gaps are smaller for the
tree topology approach for instances 1-28 and 1-22,
and larger for instances 30-60 and 24-60 when us-
ing L = 5Mbps and L = 10Mbps, respectively. But,
again this can be explained by CPLEX performance
which deteriorates when solving large size instances
of the problem. Finally, we see that the optimal solu-
tions found with the star topology approach are con-
siderably lower than those obtained with the ring ap-
proach which suggests that it is more convenient to
simply use the star configuration when a tree solu-
tion is not available in a reasonable cpu time. Since
the tree topology approach can provide better feasible
solutions for the WBAN problem, in Tables 2 and 3
we compare the proposed VNS algorithm presented
in Figure 1 with the optimal objective function values
of P
1
. In particular, in Table 2, we present numeri-
cal results for L = 5Mbps whereas in Table 3, we set
L = 10Mbps. Both tables present the same column
information. Column 1 shows the number of nodes
considered for each instance. In columns 2-3 and 4-
5 we present the objective function values and cpu
time in seconds for P
1
and P
2
, respectively. Here, we
also set the maximum available cpu time for CPLEX
to one hour and 300 seconds for the VNS approach.
Then, in columns 6-7 we present the best solution
found with VNS approach and its cpu time in seconds.
Finally, in columns 8-9 we show gaps for the initial
solution and best solution found with VNS. These
gaps are computed as Gap
Ini
TVNS
=
P
1
−IniSol
P
1
∗ 100
and Gap
TVNS
=
P
1
−TVNS
P
1
∗ 100 respectively. Here,
IniSol denotes the initial solution found with P
2
as ex-
plained in the VNS algorithm presented in Figure 1.
Note that this gap coincides with the gap between P
2
and P
1
.
From Tables 2 and 3, we mainly observe that VNS
approach improves the optimal objectivefunction val-
ues of P
2
for most of the instances. We also see that
the solutions found with the star topology approach
are not very far from the optimal solutions found with
P
1
. This is the case for instances with up to 16 nodes
where CPLEX can solve the problem to optimality in
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
130

Table 2: Comparing the VNS algorithm with the tree and
star topology approaches for L = 5Mbps.
|V| P
1
cpu P
1
P
2
cpu P
2
TVNS cpu TVNS Gap
Ini
TV NS
(%) Gap
TVNS
(%)
4 162.7889 0.15 181.7955 0.10 162.7889 0.28 11.68 0.00
6 130.7177 0.13 237.5767 0.09 130.7177 4.89 81.75 0.00
8 138.2804 0.46 253.2526 0.11 138.2804 27.48 83.14 0.00
10 204.3663 48.08 239.1874 0.11 204.3663 17.71 17.04 0.00
12 161.4248 162.49 232.9846 0.11 161.4248 74.87 44.33 0.00
14 109.1878 536.17 242.8569 0.13 173.1598 300 122.42 58.59
16 125.7083 625.16 251.7890 0.13 175.4427 300 100.30 39.56
18 104.7611 3600 246.8710 0.13 169.0028 300 135.65 61.32
20 136.3206 3600 220.1141 0.12 157.5897 300 61.47 15.60
22 132.9221 3600 241.1231 0.13 205.2670 300 81.40 54.43
24 238.3949 3600 255.3129 0.13 238.3949 2.11 7.10 0.00
26 243.4611 3600 252.3117 0.12 243.4611 1.78 3.64 0.00
28 182.2605 3600 234.3619 0.12 212.9248 300 28.59 16.82
30 243.6324 3600 247.7179 0.13 243.6324 3.25 1.68 0.00
32 4054.8263 3600 255.4642 0.14 226.9286 300 < 0 < 0
34 1736.2377 3600 245.4668 0.16 242.9136 300 < 0 < 0
36 6688.2599 3600 253.5267 0.16 249.3354 300 < 0 < 0
38 5507.4285 3600 251.5471 0.33 231.1319 300 < 0 < 0
40 4404.3266 3600 252.7837 0.16 248.3448 300 < 0 < 0
42 3997.2096 3600 254.4504 0.19 244.3861 300 < 0 < 0
44 409.0830 3600 247.5290 0.17 247.5290 300 < 0 < 0
46 - 3600 253.1534 0.17 250.1164 300 - -
48 - 3600 255.8555 0.17 255.8555 300 - -
50 4383.5935 3600 251.9520 0.19 249.4831 300 < 0 < 0
52 - 3600 254.4080 0.17 249.7041 300 - -
54 3970.1243 3600 254.5704 0.19 245.4474 300 < 0 < 0
56 - 3600 254.4691 0.20 254.4691 300 - -
58 - 3600 244.6565 0.23 244.6565 300 - -
60 - 3600 255.9535 0.34 249.3236 300 - -
-: No solution found.
< 0: Negative gap.
Table 3: Comparing the VNS algorithm with the tree and
star topology approaches for L = 10Mbps.
|V| P
1
cpu P
1
P
2
cpu P
2
TVNS cpu TVNS Gap
Ini
TVNS
(%) Gap
TV NS
(%)
4 224.9149 0.11 252.7684 0.11 224.9149 1.16 12.38 0.00
6 157.9910 0.13 249.5453 0.08 157.9910 6.47 57.95 0.00
8 122.0700 0.86 223.3105 0.11 140.3444 300 82.94 14.97
10 86.0596 4.26 245.3015 0.13 91.4057 300 185.04 6.21
12 154.3654 219.71 235.0383 0.13 156.7696 300 52.26 1.56
14 228.2618 569.32 253.9770 0.13 239.0206 300 11.27 4.71
16 96.0876 511.14 236.5652 0.13 156.4360 300 146.20 62.81
18 148.2626 3600 244.0291 0.31 174.1759 300 64.59 17.48
20 212.1160 3600 254.9278 0.11 212.1160 50.25 20.18 0.00
22 276.3054 3600 244.1628 0.17 218.1632 300 < 0 < 0
24 412.0215 3600 249.2979 0.14 245.7859 300 < 0 < 0
26 4005.5097 3600 249.7173 0.31 209.0481 300 < 0 < 0
28 340.8418 3600 236.4095 0.14 155.4772 300 < 0 < 0
30 3220.0005 3600 250.7632 0.34 223.3664 300 < 0 < 0
32 3501.5596 3600 252.3360 0.14 236.5049 300 < 0 < 0
34 2926.9978 3600 254.4703 0.14 251.3070 300 < 0 < 0
36 4534.1685 3600 251.3342 0.16 223.2100 300 < 0 < 0
38 6013.2241 3600 253.5718 0.19 248.8768 300 < 0 < 0
40 4641.5615 3600 244.5667 0.14 244.5667 300 < 0 < 0
42 5388.5247 3600 255.5524 0.16 237.7339 300 < 0 < 0
44 4038.1242 3600 245.8233 0.19 228.4913 300 < 0 < 0
46 8611.3871 3600 252.3020 0.36 245.9307 300 < 0 < 0
48 5434.4153 3600 243.5083 0.37 240.8507 300 < 0 < 0
50 4998.2235 3600 254.3199 0.19 254.3199 300 < 0 < 0
52 8623.4855 3600 253.8108 0.19 248.0597 300 < 0 < 0
54 6383.7045 3600 255.2982 0.36 252.4182 300 < 0 < 0
56 10061.0697 3600 255.8105 0.39 255.8105 300 < 0 < 0
58 8297.8535 3600 254.9113 0.39 254.9113 300 < 0 < 0
60 4660.1790 3600 254.1911 0.22 254.1911 300 < 0 < 0
-: No solution found.
< 0: Negative gap.
less than one hour. On the opposite, for instances with
more than 28 nodes in Table 2 and with more than 22
nodes in Table 3, the solutions obtained with P
1
in one
hour are significantly deteriorated since solving these
instances with CPLEX becomes rapidly prohibitive.
Next, we observe that the cpu time required to solve
P
2
is less than one second for all the instances in Ta-
bles 2 and 3, respectively. Finally, we see that the ma-
jor improvements for the VNS approach occur when
solving small and medium size instances with up to 40
nodes. The latter suggests that the star configuration
is not a bad choice when the instances dimensions in-
crease. We believe that VNS can not find significantly
better solutions for large size instances of the prob-
lem because there are more infeasible solutions in the
WBAN when the number of nodes increase. The in-
feasibility can be explained by the fact that having a
larger number of nodes in the network implies send-
ing a larger amount of data through the network, and
then the edge capacities are rapidly saturated. Ob-
viously, this can be fixed by incrementing the edge
capacities in the network.
5.1 A Flooding Network Scenario
We also consider the case where all nodes can be di-
rectly connected to more than one node acting as a
star node. For this purpose, we relax the condition
imposed for the parameter P = 1 in P
2
and allow it
to vary from P = 1 to P = |V|. Notice that when
P = |V|, it means that all nodes in the network are
fully connected. In this case, the optimal solutions of
P
2
are equal to those obtained with LP
2
.
From a practical point of view, this situation
would provide some insight about how many nodes
acting as stars are required to obtain a minimum cost
energy consumption in the network. In Figure 2, we
solve four instances of P
2
with different number of
nodes while varying P . The horizontal axes show
the parameter P while vertical axes show the optimal
objective function values of P
2
and LP
2
, respectively.
From this figure, we mainly observe that the optimal
solutions of P
2
decrease rapidly when incrementing P
which means that very low energy consumption levels
can be obtained at the cost of low flooding levels as
well.
6 CONCLUSIONS
In this paper, we proposed a minmax robust formula-
tion for routing in healthcare wireless body area net-
works (WBAN). The model minimizes the worst case
power consumption of each bio-sensor node placed
in the body of a patient subject to flow rate and net-
work topology constraints. So far we considered three
topologies in the problem: a spanning tree, a star,
and a ring topology as well. In particular, we used
an equivalent polynomial formulation of the spanning
tree polytope (Yannakakis, 1991) to avoid having an
exponential number of cycle elimination constraints
in the model. For the ring topology approach, we
used constraints from the well known mixed integer
linear programming(MILP) formulation of the travel-
ing salesman problem (Pataki, 2003). Thus, we com-
puted optimal solutions and lower bounds directly us-
ing the MILP and LP relaxations. Finally, we pro-
posed a Kruskal-based variable neighborhood search
metaheuristic to improve the solutions obtained with
the star topology approach. Our preliminary numeri-
cal results showed that the tree approach is the most
convenient while the ring approach is the most expen-
sive one. We also noticed that the difference between
AComparativeStudyofNetwork-basedApproachesforRoutinginHealthcareWirelessBodyAreaNetworks
131
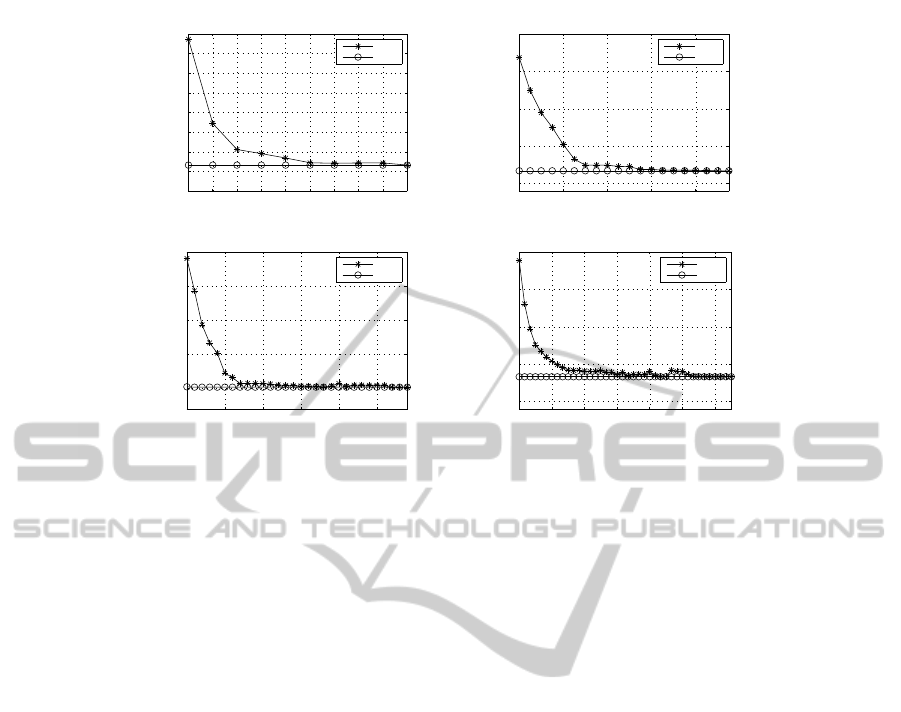
1 5 9 13 17 20
50
100
150
200
250
Optimal Solutions for V = 20
P
1 2 3 4 5 6 7 8 9 10
120
140
160
180
200
220
240
260
P
Optimal Solutions for V = 10
1 6 11 16 21 26 30
50
100
150
200
250
P
Optimal Solutions for V = 30
1 7 13 19 25 31 37 40
0
100
150
200
250
P
Optimal Solutions for V = 40
P
2
LP
2
P
2
LP
2
P
2
LP
2
P
2
LP
2
Figure 2: Optimal solutions for the star MILP when incrementing P .
the objective function values of the tree and star con-
figurations is not so large and that VNS improved the
solutions obtained with the star configuration in most
of the cases, although, at a higher computational cost.
Finally, we observed that only a few nodes acting as
star nodes are required to obtain low energy levels
rapidly at the cost of low flooding levels as well.
REFERENCES
Cormen, T., Leiserson, C., Rivest, R., and Stein, C. (2001).
Introduction to algorithms, second edition. MIT Press
and McGraw-Hill.
Elias, J. and Mehaoua, A. (2012). Energy-aware topology
design for wireless body area networks. In IEEE Inter-
national Conference on Communications, ICC 2012,
pages 3409–3410.
Fang, G. and Dutkiewicz, E. (2009). Bodymac: Energy
efficient tdma-based mac protocol for wireless body
area networks. In 9th International Symposium on
Communications and Information Technology, ISCIT
2009, pages 1455–1459.
Glover, F. and Kochenberger, G. A. (2003). Handbook
in metaheuristics. International Series in Operations
Research and Management Science, Kluver Academic
Publishers, Springer 2003, 57:556.
Hansen, P. and Mladenovic, N. (2001). Variable neighbor-
hood search: Principles and applications. European
Journal of Operational Research, 130:449–467.
Huang, C., Liu, M., and Cheng, S. (2010). Wrap: A
weighted random value protocol for multiuser wire-
les body area networks. In IEEE International Sym-
posium On Spread Spectrum Techniques and Applica-
tions, ISSSTA 2010.
Kinsella, K. and Phillips, D. (2005). Global aging. The
challenge of success, Population Bulletin, 60.
Kwak, K. S., Ameen, M. A., Kwak, D., and Lee, C. (2009).
A study on proposed ieee 802.15 wban mac protocols.
In 9th International Symposium on Communications
and Information Technology, ISCIT 2009, pages 834–
840.
Pataki, G. (2003). Teaching integer programming formu-
lations using the traveling salesman problem. SIAM
REVIEW, 45(1):116–123.
Reusens, E., Wout, J., Latre, B., Braem, B., Vermeeren, G.,
Tanghe, E., Martens, L., Moerman, I., and Blondia,
C. (2009). Characterization of on-body communica-
tion channel and energy efficient topology design for
wireless body area networks. IEEE Transactions on
Information Technology in Biomedicine, 13(6).
Ullah, S., Higgins, H., Braem, B., Latre, B., Blondia, C.,
Moerman, I., Saleem, S., Rahman, Z., and Kwak,
K. S. (2012). A comprehensive survey of wireless
body area networks on phy, mac, and network layers
solutions. Journal of Medical Systems, 36:1065–1094.
Yannakakis, M. (1991). Expressing combinatorial opti-
mization problems by linear programs. J. Comput.
Syst. Sci., 43(3):441–466.
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
132
