
A Decomposition Method for Frequency Assignment in Multibeam
Satellite Systems
Jean-Thomas Camino
1,2,3
, Christian Artigues
2,3
, Laurent Houssin
2,4
and Ste´phane Mourgues
4
1
Airbus Defence and Space, Space Systems, Telecommunication Systems Department,
31 Rue des Cosmonautes, 31402
Toulouse, France
2
CNRS, LAAS, 7 Avenue du Colonel Roche, F-31400 Toulouse, France
3
Univ de Toulouse, LAAS, F-31400 Toulouse, France
4
Univ de Toulouse, UPS, LAAS, F-31400 Toulouse, France
Keywords: Frequency Assignment, Multiprocessor Scheduling, Path Cover, Linear Programming, Constraint Program-
ming, Maximal Cliques Enumeration.
Abstract: To comply with the continually growing demand for multimedia content and higher throughputs, the telecom-
munication industry has to keep improving the use of the bandwidth resources, leading to the well-known
Frequency Assignment Problems (FAP). In this article, we present a new extension of these problems to the
case of satellite systems that use a multibeam coverage. With the models we propose, we make sure that for
each frequency plan produced there exists a corresponding satellite payload architecture that is cost-efficient
and decently complex. Two approaches are presented and compared : a global constraint program that handles
all the constraints simultaneously, and a decomposition method that involves both constraint programming
and integer linear programming. For the latter approach, we show that the two identified subproblems can re-
spectively be modeled as a multiprocessor scheduling problem and a path-covering problem, and this analogy
is used to prove that they both belong to the category of NP-hard problems. We also show that, for the most
common class of interference graphs in multibeam satellite systems, the maximal cliques can all be enumer-
ated in polynomial time and their number is relatively low, therefore it is perfectly acceptable to rely on them
in the scheduling model that we derived. Our experiments on realistic scenarios show that the decomposition
method proposed can indeed provide a solution of the problem when the global CP model does not.
1 INTRODUCTION
A common characteristic of any telecommunication
system is that it is bandwidth limited, and one of the
main challenges for the system engineers is to
optimally use this precious resource. Satellite
telecommunications systems are no exception to that
rule, and
this already difficult task is even more
complex when
the specific limitations and needs of
the satellite payload are taken into consideration.
Plenty of literature
can be found on the problem of
assigning frequencies under the name of “Frequency
Assignment Probems” (FAP). For instance, (Aardal
et al., 2007) is
a very thorough survey on the models
and the optimization methods that have been
developed over the
years to solve the frequency
assignment problems that
emerged in a lot of different
wireless communications
systems. The recent
litterature proposes more and
more sophisticated
methods to solve the FAP, such as parallel
hyperheuristics (Segura et al., 2011), differential
evolution (Salma et al., 2010), population-based
heuristics (Luna et al., 2011) (Yang et al.,
2014)
or considers more and more realistic variants of
the
FAP according to specific problem characteristics
(Koster and Tieves, 2012) (Muoz, 2012) (Wang and
Cai, 2014). This article aims at presenting new
models and approaches for this extension of the
frequency
assignment problem to multibeam satellite
systems,
and promising results on realistic scenarios.
A multibeam satellite system is characterized by
a plurality of relatively narrow beams used to provide
coverage to its service area as shown in Fig.1, each
beam being the representation of an antenna gain loss
threshold for the corresponding satellite radio source.
Still in Fig.1, the role of the satellite payload (2) is
to receive, downconvert, amplify, and retransmit the
signals of the uplink (1) in the different beams of the
23
Camino J., Artigues C., Houssin L. and Mourgues S..
A Decomposition Method for Frequency Assignment in Multibeam Satellite Systems .
DOI: 10.5220/0005218700230033
In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 23-33
ISBN: 978-989-758-075-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: The uplink (1), the satellite payload (2) and the
downlink (3) of the forward link of a multibeam satellite
system.
downlink (3) where the end-users are located. It is
assumed that the system bandwidth is divided into
identical frequency channels, the bandwidth of a
channel
being equal to that of one carrier signal.
For each
beam, it is either specified by the operator or
assessed
in advance how much bandwidth is needed
and there-
fore how many carriers must be transmitted
in it. Assuming that the carrier uplink frequencies are
known
or treated afterwards, system engineers have to
define
for each carrier of each beam:
-
The frequency channel used in the downlink
-
The polarization of the signal in the downlink
-
The high power amplifier in the payload that will
be amplifying the corresponding uplink carrier
These are the variables of the problem presented
in
this paper. Values must be assigned to them with
the
goal to minimize the levels of interferences in
each
beam, the number of high power amplifiers
needed
in the satellite payload, and the number of
hardware
needed for the downconversions. More
precisely, the
approach we have selected is to aim
at minimizing
the number of high power amplifiers
needed in the
satellite payload since they are heavy,
expensive, and
highly power-consuming, while we
will be using
constraints to limit the interferences and
the hardware
needed for the downconversions to what
is acceptable.
The rest of the article is structured as follows. In
section 2, the problem constraints are listed and
detailed. Then, section 3 focuses on the different
approaches we have devised to actually model the
problem. Finally, section 4 provides experimental
results
and concrete scenario examples, before some
concluding remarks in section 5.
2 THE PROBLEM CONSTRAINTS
2.1
Frequency
Related
Constraints
For the quality of transmission of a signal, the
interferences are a determining factor and any
frequency
assignment procedure should try to
minimize them.
Let us remind that a frequency and a
polarization must
be assigned to each carrier of each
beam in the downlink. Note that in this work, the
isolation of the signals
through the time-dimension is
not considered. In the
end, the frequency related
constraints that are taken
into account here are the
following :
-
Polarization Isolation:
A perfect radio antenna transmits and receives
waves in a particular polarization and is
insensitive to orthogonally polarized signals
(Bousquet
and Maral, 2009), meaning that the
same frequency channel can therefore be used
twice in the
same area without risking severe
interferences. In
actual facts, antennas cannot
transmit and receive
perfectly in one
polarization only, it is always a
combination of
two orthogonal polarizations, one
of them being
predominant. To take advantage of
that property
anyway, the choice here has been to
consider
that two carriers at the same frequency
using
orthogonal polarizations are allowed to be
transmitted in closer zones than two carriers
trans-
mitted at the same frequency and with
the same
polarization.
-
Spatial Isolation:
Thanks to antenna gain losses, two carriers can
use the same color (frequency or frequency-
polarization couple) as long as the two
corresponding beams are sufficiently distant
from each
other. This is often turned into a
constraint of
minimum distance between them,
leading the very
classic binary interference
constraints. The resulting representation is a
graph G
=
(B, E) where each vertex b
∈
B
corresponds to the zone covered
by a beam and
each edge e
∈
E is a link between two zones
where it is not allowed to use the same
color.
-
Limit on the Frequency Channel Reuse
Values:
Defining an upper-bound for these values
allows
to balance the number of times each
channel is
used, which reduces the hardware
needs for frequency conversions. Since two
uplink carriers can
only share a downconverter
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
24

in the satellite payload if they need the same
frequency downconversion, it is interesting to be
able to define the uplink
frequencies so as to
have as many of these situations as possible, and
this balance of the frequency reuse factors in the
downlink is advantageous on
that regard.
2.2 Amplification of the Signals
Constraints
A traveling-wave tube (TWT) is a type of high power
amplifier for radio frequency signals and a widely
used technology for satellite telecommunication
payloads (Bousquet and Maral, 2009). A TWT must
be
assigned to each carrier of each beam under the
following constraints:
-
Minimization of the Number of TWT:
A TWT is an expensive technology, one should
therefore aim at finding a distribution of the
carriers in the TWTs that minimizes their
number.
-
Frequency Ranges:
The TWTs can have a bandwidth narrower than
the overall system bandwidth. In that case, pay-
load engineers agree with the equipment
manufacturer on a limited number of frequency
ranges.
Therefore, the assignment of carriers to
the TWTs
must guarantee that the frequency
ranges are supported by the available equipment.
-
Carriers forbidden to use the same TWT:
Two carriers cannot be amplified by the same
TWT if their amplification requirements are too
different, because of the non-linearity of the
TWT.
These incompatibilities are known in
advance.
-
Single Use of the Frequency Channels:
A TWT cannot amplify two carriers using the
same frequency channel.
-
Limited Number of Carriers per TWT:
A TWT is characterized by its output power
level.
That power is shared by the carriers,
therefore the
number of carriers per TWT is
upper-bounded.
-
Contiguity of the Frequencies:
The payload complexity is assumed to be
significantly reduced when there are no
frequency gaps
between the carriers in the same
TWT.
3 MODELS
The first model we derived is a global constraint
program (section 3.1) that includes all the
aforementioned constraints. It has been able to
provide really interesting system solutions on some
scenarios, however, when the number of variables is
set to high realistic values, the global CP model fails
at providing solutions or proving unfeasibility in
reasonable time. That is why a decomposition
method has been developed, with a subdivision of
the problem
into a multiprocessor scheduling
(section 3.2) and a
path-covering (section 3.3)
problems. The two approaches, the single constraint
programming model
and the combination of the two
submodels, are then
compared experimentally in
section 4.
3.1 Global Constraint Programming
Model
The idea to derive a constraint programming model
has been motivated by an analysis of the constraints
on the problem variables (frequency, polarization,
TWT) that revealed that global constraints could be
used to model a large part of the problem. A global
constraint (Beldiceanu et al., 2005) is a set of con-
straints for which it is preferable to treat that set of
constraints as a whole than to treat all the constraints
of that conjunction of constraints individually. Using
global constraints is a way to have a better view on
the structure of the problem, which is then exploited
with powerful filtering algorithms. On that regard, a
very significant example is the all different constraint
(van Hoeve, 2001)
alldifferent(X )
that forces all the variables of the array X to be
different. In the model below, we also use the global
cardinality constraint
global_cardinality_constr(X ,Y ,m,M)
that allows to bound the number of times some items
appear in a list, X being that list, Y the set of sought
values, m the array of minimum number of
occurrences for each sought value, M the array of
maximum number of occurrences for each sought
value. Finally, the Gecode convexity global constraint
convex(X )
is used to force the integers of an integer set X to be
a convex sequence ({1, 2, 3} is one while {1, 2, 4} is
not). These global constraints are implemented in the
open source solver Gecode (Schulte et al., 2013) that
we chose to use.
ADecompositionMethodforFrequencyAssignmentinMultibeamSatelliteSystems
25

An instance of this particular frequency
assignment problem is defined by a set of N
B
beams,
each beam b
∈
B
=
{1, · · · , N
B
} being characterized by
the number n
b
of carriers transmitted in it, leading to
an overall number of carriers
For all
b
∈
B
and for all
c
∈
{
1
, · · · , n
b
}
,
ind
,
defines a 1D sorting of these carriers and for all
b
∈
B
,
C
b
=
{ind(
b, c
)
|
c
∈
{1
, · · · , n
b
}}
is the notation for the set of indices of the carriers of
the b
th
beam. Therefore, note that the C
b
sets
partition the set C
=
{1, · · · , N
C
}. The system
bandwidth is divided into N
F
sub-channels indexed
by F
=
{1, · · · , N
F
}. N
T
TWTs are available in the
payload, and N
P
orthogonal polarizations are
considered
(typically
N
P
=
2), the corresponding
index sets be
ing respectively denoted by T and P.
Each carrier
c
∈
C must be assigned a frequency
channel f
c
∈
F ,
a TWT t
c
∈
T and a polarization
p
c
∈ P. These are
the problem variables. Two graphs
G
=
(
B, E
) and
G′
=
(B, E′) with E′
⊂
E are defined:
an edge of E′ forbids the carriers in the two
corresponding beams to use the same frequency
channel whatever the polarization, whereas an edge
of E only forbids the multiple use of the same
frequency-polarization couple.
In the following
equations, note that card(X ) denotes
the cardinality of
the set X . Here follows the list of
the constraints
expressed with these variables:
-
For a given beam b such that n
b
> 1, the n
b
carriers must be contiguous in frequency, use the
same
TWT, and have the same polarization. For
such b
values, the constraints are:
∀
i
∈ {
2
,
· · ·
, n
b
}
,
t
ind(
b,
1)
=
t
ind(
b,i
)
(1
)
p
ind(
b,
1)
=
p
ind(
b,i
)
(2
)
f
ind(
b,i
1)
=
f
ind(
b,i
)
1
(3
)
-
As discussed in section 2.1, channel reuse
bounds
are a tunable parameter in input used to
limit hardware needs for the downconversions.
Let R
min
and R
max
be the arrays of size N
F
of
these bounds
(note that in practice the lower-
bound array is set
to 0, it is just there to fit the
definition of the global
constraint that use both
arrays), then the corresponding corresponding
is the following:
global_ cardinality_constr(f, F, R
min
, R
max
)
(4
)
-
The binary interference constraints associated
to E can be expressed as follows for all b, b′
∈
B
such that b < b′ and (b, b′)
∈
E :
alldifferent (f
c
+
N
F
(p
c
1)
|
c ∈ C
b
∪ C
b
ʼ)
(5
)
-
And for E′, for all b, b′
∈
B such that b < b′ and
(
b, b
′
)
∈
E
′
:
alldifferent
(
f
c
|
c
∈
C
b
∪
C
b’
)
(6
)
-
The same frequency cannot be used twice by the
carriers of a given TWT :
∀
t
∈
T,
∀
f
∈
F,
card(
T
t
∩
F
f
)
≤
1
(7
)
where T
t
⊂
C and F
t
⊂
C respectively are the set
of carriers using the TWT t and the set of carriers
using the frequency channel f , these set variables
being linked to the arrays t and f by side
channeling constraints that we do not provide
here for the
sake of conciseness.
-
The contiguity in the TWTs. Let us denote by F
t
the set of frequency channels used in the TWT
t,
these set variables being easily defined with
chan-
neling constraints involving the variable
arrays f
and t. Then, the global constraint convex
does exactly what is sought:
∀
t
∈
T,
convex(
F
t
)
(8
)
-
The maximum number of carriers in a given
TWT
that is upper bounded by a tunable
parameter n :
∀
t
∈
T,
card(
T
t
)
≤
n
(9
)
-
The incompatibilities between the carriers that
cannot use the same TWT. Let c, c’
∈
C be two
carriers forbidden to use the same TWT, then the
corresponding constraint is the following:
t
c
t
c
′
(10
)
-
The content of the TWTs must be of a given type.
Let F
1
⊂
F and F
2
⊂
F be two subparts of the
system bandwidth such that F
1
∪
F
2
=
F. These
two sets define two types of acceptable frequency
contents for the TWTs, which means that the
carriers
in a given TWT must either all be in F
1
or all be
in F
2
, which can be expressed as
follows:
∀
c, c
′
∈
C,
f
c
∈
F\F
2
∧
f
c’
∈
F\F
1
⇒
t
c
t
c
′
(11
)
The objective is the minimization of the number
of
available TWTs actually used. That number n
used
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
26

is
a variable that can be obtained from the array t
with
two successive global counting constraints, the
first
one generating an array of the number of times
each
TWT is used, the second counting the number of
non-
zero values in the latter:
min n
used
(12
)
3.2 Multiprocessor Scheduling Part
3.2.1 The Scheduling Model
An analogy with multiprocessor scheduling problems
is possible for the assignment of frequencies and
polarizations, that is for the subproblem that only
concerns the variable arrays f, p, and the constraints
(2), (3), (4), (5) and (6). That problem, denoted by
(S
1
), is an extension of the model proposed in
(Kiatmanaroj et al., 2013) where the frequency
assignment is addressed regardless of the
polarizations. Each beam b
∈
B is assimilated to a
single operation job whose processing time,
expressed in time units, is non-preemptive and equal
the number of carriers in that beam. Note that such
a model is only
valid because the frequencies of the
carriers in a same
beam are constrained by constraint
(8) to be contiguous, the contiguousness of
frequencies corresponding therefore to the non-
preemptiveness of the processing times. Each
maximal clique of G′ is assimilated to a machine with
non-overlapping constraints,
while each maximal
clique of G is associated to exactly two machines,
one for each polarization. For each beam/job b
∈
B ,
C′
b
denotes the set of machines that correspond to the
cliques of G′ that contain b, while C
b,1
and C
b,2
are
the sets of machines representing the cliques of G
containing b that are respectively
associated to the
polarizations 1 and 2. For constraint
(4), it is assumed
that the only restriction here is an upper-bound on
the reuse factor R
∈
N
+
of the channels (same bound
for each channel), which leads to
the definition of
M
=
{m
1
, · · · , m
R
} identical parallel machines. Each
job b
∈
B requires simultaneously multiple machines.
More precisely, it must be executed on:
-
all the machines of
C’
b
-
either all the machines of C
b,1
, or all the machines
of C
b,2
-
one machine of M
Note that relying on cliques is not necessary to make
this analogy with multiprocessor scheduling, another
option could be to define a machine for each binary
constraint, but relying on cliques allows to take into
account several constraints simultaneously, just like
global constraints in constraint programming. In the
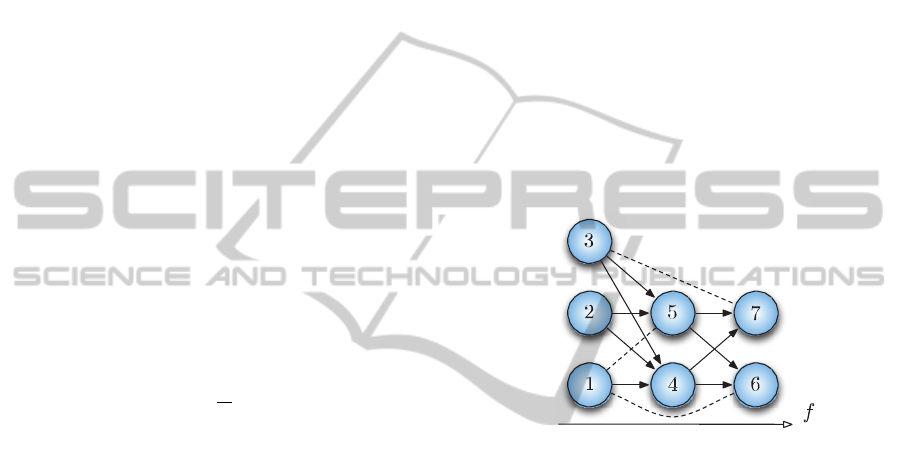
example of Fig.2, for the beam number 1 with the
notations
′
,
,
,
,
,
,,
,
,,
and
,
,,
,
,,
, we have:
-
′
,
and ′
,
associated to the cliques/machines
{1,2} and {1,3} of G’
-
,,
and
,,
associated to the machines of first
polarization for the cliques {1,2,3} and {1,3,4}
in G
-
,,
and
,,
associated to the machines of
second polarization for the cliques {1,2,3} and
{1,3,4} in G
-
the machine M used by the beam 1
In the example, the two carriers required in beam
1 use the second and third frequency channels and
the first kind of polarization. With a common
deadline for all the jobs being equal to the number of
frequency channels N
F
(equal to 4 in Fig.2), one can
see that solving this scheduling problem is equivalent
to solving the considered subpart of our frequency
assignment problem.
Figure 2: Example of execution of one job on the
machines.
Proposition: (S
1
) is equivalent to solving a
multiprocessor scheduling problem, it is
therefore
NP-hard.
Proof: The parallel machine problem is a par-
ticular case of (S
1
).
3.2.2 Maximal Cliques Enumeration in
Multibeam Satellites Interference
Graphs
As explained in the previous paragraph, one
promising direction to solve efficiently the
scheduling part of the frequency assignment problem
ADecompositionMethodforFrequencyAssignmentinMultibeamSatelliteSystems
27
considered is to use the cliques of the interference
graphs. It is thus of interest to study the theoretical
and practical complexity of enumerating the maximal
cliques. In multibeam systems, the analysis of their
exhaustive enumeration differs depending on the type
of graphs considered: regular layouts or random
interference graphs.
Cliques in Regular Layouts
A regular layout is an organization of the beams that
provides a continuous coverage of the zone with
overlapping beams that describe an hexagonal lattice,
as shown in Fig.1 for instance. It is a very common
choice for the system engineer since the contiguous
coverage it provides can be a crucial specification of
the customer, and also, it requires simpler antenna
designs than a non-uniform layout. For a beam b
∈
B,
let us denote by
c
b
the position of its center and by
Γ(b) the set of its adjacent beams. A common
industrial approach for a regular layout with beams of
radius r is have Γ(b)
= {
b
˜
∈
B
|
b
˜
≠ b and || c
b
˜
− c
b
||<d}
with d being equal to either 3r or 2
√
3
r leading to the
representations (a) and (c) of Fig.3. They are usually
called 3-colors pattern and 4-colors pattern because
with such edges in the interference graph, it is
possible to partition the set of vertices into
respectively 3 and 4 independent sets as shown in
figure (b) and (d) of Fig.3. An important property of
the regular interference graphs with the edges defined
this way is the following:
(a)
(b)
(c) (d)
Figure 3: (a) Adjacent beams, 3r threshold (b) Independent
sets, 3r threshold (c) Adjacent beams, 2
√
3
r threshold (d)
Independent sets, 2
√
3
r threshold.
Proposition: The maximal cliques of the
interference graphs corresponding to the regular
patterns
in regular layouts can all be enumerated in
polynomial time
Proof: The key idea is that for each exclusion
pattern, there exists a finite number m such that for
each vertex b
∈
B there exist m potential cliques that
might contain b, m being independent of the size N
B
of the graph. For instance, for a graph with the edges
of the 4-colors pattern, geometrical considerations
allow to understand that, for a given vertex :
-
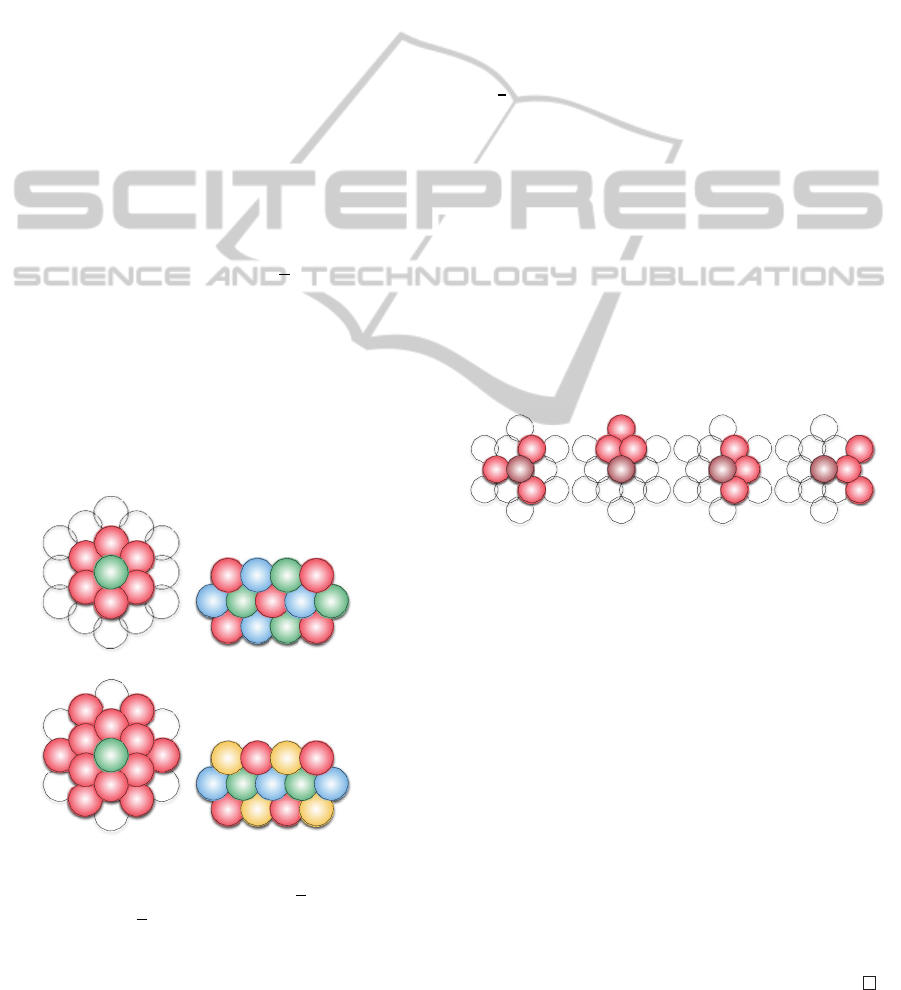
it cannot belong to a clique of size 5 and more,
-
the cliques of size 4 that might contain it are
those of Fig.4 plus those obtained by rotating of
around the center of the corresponding beam
leading to a total of 20 distinct potential cliques,
-
the only way it can belong to a maximal clique
of size 1, 2 or 3 is that the corresponding beam
is
surrounded by less beams than in the full
configuration of Fig.4, which can happen either
because
the beam in question is near the bound
of the layout or because there are “holes” in it.
Therefore, if such a clique exists, it is a
subgraph of what
would have been a clique of
size 4 if some beams
had not been missing.
These situations are also in
finite number and can
be precisely enumerated.
Figure 4: Cliques of size 4 with 4-colors pattern.
Note that in the example of the 4-colors pattern, the
number of cliques is therefore upper-bounded by
20N
B
. Each potential clique is characterized by a
specific set of adjacent beams and, for the cliques of
size less than 4, a set of non-existing beams whose
positions are perfectly known in terms of distance to
the beam tested and orientation with respect to a given
reference direction, say the horizontal direction. The
same type of rationale applies for the graphs defined
with the 3-colors pattern. Therefore, to enumerate all
the maximal cliques in the case of regular layouts, one
would only have to iterate on the vertices b
∈
B, that
is on the beams, and test each clique possibility to
see which ones actually exist for each b. That way,
the list of maximal cliques can gradually grow,
simple tests allowing to avoid redundancies. In the
end, the maximal cliques of the regular layouts are
indeed
enumerated with a polynomial complexity.
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
28
Cliques in Realistic Random Layouts
Even if the standard way to design a layout is to rely
on the uniform patterns, it can be interesting to break
that regularity in order to match the heterogeneity of
the requirements over the service area. One can there-
fore have to work with a layout that can have beams
of differents widths and positions for their centers that
do not describe any particular known geometrical
pattern. It was therefore necessary in that case
to
determine whether it was still an acceptable
approach to enumerate the cliques before actually
solving the frequency assignment problem. To do
so,
the slightly modified version of the Bron-
Kerbosch
(Bron and Kerbosch, 1973) algorithm
proposed by
Tomita et al. (Tomita et al., 2006) has
been implemented and used on sets of graphs that were
randomly
generated with constraints on the vertex
degrees. In
practice, in multibeam satellite systems
interference
graphs, these vertex degrees are rarely
less than 1 and
greater than 12, so this has been
specified as the main
constraint in the constraint
program used to generate
these graphs. We generated
10000 different graphs of size |B]
=
200 (maximum
size for a realistic scenario) and observed that the
mean number of cliques was 881 and the mean
execution time was 14 millisec-
onds. These cliques
numbers are far from the 3
|
|
upper bound of the
number of cliques in an undirected
graph, which is
very interesting in practice because
too high numbers
of cliques could have made it impossible or
unreasonable to rely on a model based on
them. But
most importantly, the computational times
are
relatively low, even instantaneous at the time scale
of
the designing phases of the satellite
telecommunication systems. In the end, this means
that this preliminary enumeration of the cliques is a
pre-processing
operation for the frequency
assignment problem that
is perfectly acceptable,
whatever the type of layout.
3.3 Path Covering Part
Let us assume that the frequencies and the
polarizations have been assigned somehow to the
carriers
of a given system, possibly with a scheduling
based
procedure as the one presented in section 3.2.
Then,
one can wonder what the problem of
assigning the
TWTs to these carriers becomes, that
problem being
denoted by (S
2
). The first important
remark is that
the constraint 11 on the type of TWTs
can now be
seen as additional incompatibilities in
constraint 10
since the frequencies of the carriers are
now known.
The second is that it is now possible to
represent the
problem as a path-covering problem of
a digraph in
which the vertices represent the N
C
carriers of the
system (see Fig. 5), a path
representing a TWT and its content. In this graph,
for all f
∈
F\{N
F
}, the only possible direct successors
of the carriers using the frequency f are those using
the frequency f
+
1,
the in-degrees of the carriers
using the frequency 1
being all equal to 0, just like
the out-degrees of the
carriers using the frequency
N
F
. As a consequence
of these few properties, such
graphs are acyclic. The
incompatibilities between
two carriers that cannot
be in the same TWT/path
are represented with
dotted-line connections. For a
given carrier, two
situations impact the number of
out-arcs : when this
carrier is not the last carrier of the
beam it belongs to,
and when there exist
incompatible carriers that use
the next frequency. In
the former case, only one arc
leaves the carrier
considered and its head is the next carrier in the
Figure 5: Carrier based graph for TWT assignment.
corresponding beam. In the latter case,
the carrier
cannot be connected to the carriers with
which an
incompatibility is shared. Otherwise, for a
carrier
that is not in any of these two situations, it is
connected to all the carriers using the next frequency.
One can then see that assigning TWTs to the carriers
comes down in that case to finding the minimum
number of disjoint paths that cover all the vertices,
the contiguity (constraint 8) and the fact that the same
frequency cannot be used twice in a TWT (constraint
7) being automatically verified with a graph built that
way. But there are also some additional constraints
to take into account such as the upper-bound for the
length of the paths (constraint 9), the constraint not
to use the same TWT for two incompatible carriers
(constraint 10), and finally the constraint that the
carriers of a block of carriers must use the same
TWT (constraint 1). In the end, an instance of the
problem considered is entirely defined by : an acyclic
digraph D whose vertices can be partitioned into a
certain number of ordered “levels” and whose arcs
are only between two vertices of a level and the next,
an upper bound l for the length of the paths, a set for
ADecompositionMethodforFrequencyAssignmentinMultibeamSatelliteSystems
29

each carrier of the carriers it must share a TWT with
(empty sets being allowed), and a set for each carrier
of the carriers incompatible with that carrier (empty
sets also allowed).
Proposition: (S
2
) is an NP-hard path-covering
problem
Proof: Without the additional constraints (1,9,10),
the problem of covering a digraph with a minimum
number of point-disjoint paths can be solved in
polynomial time as shown in (Boesch and Gimpel,
1977). But once they are taken into account, it can be
proven that the problem becomes NP-hard. Indeed,
let us consider an instance of the problem of finding
a minimum cardinality cover of the elements of a
partially ordered set (poset) with chains of restricted
length, whose NP-completeness has been proven in
(Shum and Trotter, 1996). It is common to represent
that poset with a digraph partitioned in ordered levels,
the edges connecting the comparable elements of
the set from one level to the next: this is precisely
a
Hasse diagram. Then, with the upper bound for
the
path lengths equal to the maximum length of a
chain
and with, for each carrier, empty sets for the
sets of
carriers that must use the same TWT and
the sets
of incompatible carriers, one can see that
solving
this poset cover instance is equivalent to
solving a
particular instance of the path-covering
problem
considered in this paper. Therefore, it is also
NP-
complete.
To solve it, the following integer linear
programming
model has been derived :
(13
)
s.t.
∀∈,
1
(14
)
∀∈,∀
∈,
1
(15
)
∀∈,
1
(16
)
∀∈,
(17
)
∀,
∈that are incompatible, ∀∈,
1
(18
)
∀,
∈ in the same block of carriers ∀∈,
0
(19
)
∀∈,∀∈
,
(20
)
where y
c f
∈
{0, 1} are input Boolean arguments that
indicate whether the carrier c
∈
C uses the frequency f
∈
F , x
ct
{0, 1} are the Boolean variables that indicate
if
the carrier
c
∈
C
uses the TWT
t
∈
T
, and finally
the
u
t
∈
{0, 1} are the Boolean variables that indicate
whether the TWT t is actually used. Constraint 14 is
the constraint to have only one TWT assigned to each
carrier, 15 forbids a given TWT to be used by two
different carriers using the same frequency channel,
16 is the constraint that forces the u
t
to be equal to 1
as
soon as the TWT t is used at least once, 17 is the
limit
on the number of carriers in the same TWT,
constraint
18 forbids two incompatible carriers to use
the same
TWT, 19 forces the carriers in the same block
of carriers to use the same TWT, 20 ensures the
contiguity of
the frequency channels in each TWT,
finally 13 is the
minimization of the number of TWT
actually used.
4 EXPERIMENTAL RESULTS
Experiments were needed to assess the performances
of the two following approaches:
-
Global Approach (GA):
The global constraint program of section 3.1
solved with a CP solver (Gecode)
-
Decomposition Method (DM) :
Sequential solving of (S
1
) of section 3.2 with
a
CP solver (Gecode) and then of (S
2
) of
section 3.3 with an ILP solver (Gurobi)
A first detailed example is presented in Fig.6 with a
fictitious scenario over France and Italy, with N
B
=
12
regularly organized beams. The characteristics of the
problem solved were the following :
-
Each beam
b
∈
{
1
, · · · ,
12
}
of Fig.6 has a required
number of carriers n
b
than is either equal to 1 or
to 2, the carriers being indexed as shown inside
the beams in Fig.6a
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
30

-
For the beams b with a number of carriers
n
b
>1,
we require contiguous carrier
frequencies, same
polarization and same TWT
-
The system bandwidth is divided into
N
F
=
6
channels
-
The acceptable frequency ranges for the
TWTs
are {1, 2, 3} and {4, 5, 6}
-
The TWT reuse upper-bound is set to 3, i.e.
the width of an admissible frequency range
-
The 4-color pattern is used to define binary
interference constraints for the reuse of the
same
frequency-polarization couple (Fig.3c)
-
The 3-color pattern is used to define binary
interference constraints for the reuse of the
same frequency, regardless of the polarization
(Fig.3a)
-
Carrier n◦5 is incompatible with carriers n◦9
and n◦10, carrier n◦13 is incompatible with
carriers n◦17 and n◦18, carrier n◦7 is
incompatible with n◦8, which means that they
cannot use the same TWT
-
Each frequency channel must be used at
most
third times
-
Objective function : number of TWTs used
(a)
(b)
Figure 6: (a) Multibeam coverage and polarizations (b)
Frequencies and TWTs.
This is one of the instances for which GA
solved
with Gecode is unacceptably long to find a
solution.
On the other hand, with DM, the scheduling
part and
the subsequent binary linear program are
both solved
extremely efficiently respectively by
Gecode and
Gurobi. On Fig.6a, the regular layout is
reprensented
with a ring color for each polarization,
and on Fig.6b,
the frequencies of the carriers found in
the scheduling
part can be read on the horizontal axis,
and each color
for the carriers represents one TWT.
Note that the
design of Fig.6 obtained for that
example is optimal
since the number of TWTs used
is exactly equal
to the number of carriers divided
by the maximum
number of carriers in a TWT.
When instances are randomly generated, note
that
there is no guarantee that they will be feasible.
Even
if this is true for both approaches, in the case of
DM,
this risk of infeasibility is even increased since
some
of the path-covering problem constraints are
currently not anticipated in the preceding scheduling
problem (the frequency ranges of the TWTs for
instance). In practice, infeasibility is significantly
harder to detect than actual solutions for feasible
instances, at least when Gecode is used, that is in GA
and in (S
1
) of DM. In the results of this section, the
statistic values presented only consider the instances
that turned out to be feasible.
For each instance tested with the DM approach,
the
corresponding (S
1
) scheduling problem is solved
with Gecode using the corresponding subset of
constraints in the global model of section 3.1. Then,
the solutions of (S
1
) are transformed into (S
2
)
path-
covering instances that are solved with Gurobi
thanks to the ILP model we derived in section 3.3.
With GA, let us remind that the problem is entirely
solved with Gecode. For the first phase of our series
of experiments, we generated FAP instances with
similar characteristics as the example detailed before,
with the following few changes :
-
Each beam b
∈
{1, · · · , 12} of Fig.6 has a now
required number of carriers n
b
than is either
equal to 0 or to 1
-
The TWT carrier incompatibilities are now
ran-
domly generated (about 10% of all the
possible
carrier couples)
-
The overall number of required carriers
N
C
=
∑
is gradually increased, from
4 to 12, 100 feasible instances being generated
at each stage
-
Each frequency channel cannot be used more
than
once when 4 ≤ N
C
≤ 6 and more than twice
when
7 ≤ N
C
≤ 12
ADecompositionMethodforFrequencyAssignmentinMultibeamSatelliteSystems
31

Figure 7: Comparison of GA and DM on 4-carriers to 12-
carriers instances with execution time statistics.
Figure 8: Comparison of GA and DM on 4-carriers to 12-
carriers instances with objective value statistics.
Fig. 8 and Fig. 7 allow to compare GA and DM
in
terms of objective values and execution times. As
expected, we can observe that in the the case of a
joint assignment of TWT, frequency and polarization
to the carriers (GA), the execution times are greater
than those of DM but the objective values are better
in average. In the particular case of the instances we
generated, GA always reaches the theoretical optimal
value which is equal to
ceiling
Overallnumberofcarriers
MaximumnumberofcarriersinaTWT
However, the decomposition method often manages
to reach that optimal number of TWTs too as shown
in Table 1. This is a crucial remark we wanted to
emphasize since it is what legitimates the use of DM
when GA is not usable in practice.
Table 1: Percentage of times the theoretical optimum is
reached with DM for each set of instances of varying num-
ber of carriers.
4 carriers 5 carriers 6 carriers
87% 72% 75%
7 carriers 8 carriers 9 carriers
83% 59% 53%
10 carriers 11 carriers 12 carriers
69% 76% 64%
In the next phase of our experiments, the overall
number of carriers in the system has been set to be
greater
than 12 and less than 19, the carrier
requirements in
each beam being either equal to 1 or
2, and the frequency channel reuse limit being now
set to 3. As a
result, some new constraints have to be
taken into account for the beams b such that n
b
> 1 :
contiguity of
frequencies, same polarization and same
TWT for the
carriers belonging to the same beam. In
practice, this
is the point where GA becomes unusable
both for feasible and infeasible instances, because of
extremely
long execution times even on these
instances that are
still relatively small compared to the
biggest realistic
situations. This explains why it has
been necessary to
develop DM. In Fig. 9, the
execution times of (S
1
)
(scheduling) and (S
2
) (path-
covering) are compared
on the whole range of
instances, from 4-carriers instances to 18-carriers
instances. Two main things can
be observed in that
figure. First, the difference between the instances
with at most 12 carriers and those
with at least 13
carriers is clear: the new constraints
linked to the
beams for which the carrier requirement
is strictly
higher than one slow the search. Also, we
see that
the computational times grow faster for the
scheduling problem than for the path-covering
problem. That remark is even more important when
we consider the fact that infeasible instances are also
re-
ally hard to detect for Gecode in the scheduling
part.
(S
1
) is therefore the subproblem that deserves
more
attention for future work, the goal being to
solve the
highest realistic instances. Our not yet
exploited analysis of the cliques in the interference
graphs could
certainly be an interesting direction.
Figure 9: (S
1
) (scheduling part) and (S
2
) (path-covering
part) execution times.
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
32

5 CONCLUSION
The models we proposed for this particular frequency
assignment problem applied to the design of multi-
beam satellite systems allowed to algorithmically
solve instances that could not be solved by satellite
telecommunications engineers. We showed that the
decomposition method we devised could produce so-
lutions and even optimal solutions in reasonable
computational times especially compared to the
perfor-
mances of the global constraint program for
that prob-
lem. We also showed that relying on the
cliques of
the interference graphs was an acceptable
direction
and most likely a way to improve our
current algorithms for the scheduling subproblem of
our decomposition method. Concerning the path-
covering problem, a series of experiments showed
that realistic instances where solved almost
instantaneously by the
solver Gurobi, which tells us
that we extracted an
interesting subproblem, and we
will definitely try to
take advantage of this in some
way in the next algorithms we will implement. To
solve the largest realistic instances, work still has to be
done to get faster results and improving the algorithms
for the scheduling
part might not be enough. Instead
of solving the two
identified subproblems
sequentially, we might aim at more integrated
approaches inspired by combinatorial
Benders’ cuts
for instance, or with filtering algorithms
solving
locally the path covering problem.
REFERENCES
Aardal, K. I., van Hoesel, S. P. M., Koster, A. M. C. A.,
Mannino, C., and Sassano, A. (2007). Models and so-
lution techniques for frequency assignment problems.
Annals of Operations Research, 153:79–129.
Beldiceanu, N., Carlsson, M., and Rampon, J.-X. (2005).
Global constraint catalog. SICS Research Report.
Boesch, F. T. and Gimpel, J. F. (1977). Covering the points
of a digraph with point-disjoint paths and its appli-
cation to code optimization. Journal of the ACM,
24:192–198.
Bousquet, M. and Maral, G. (2009). Satellite Communica-
tions Systems : Systems, Techniques and Technology.
5
th
edition.
Bron, C. and Kerbosch, J. (1973). Finding all cliques of
an undirected graph. Communications of the ACM,
16:575–577.
Kiatmanaroj, K., Artigues, C., and Houssin, L. (2013). On
scheduling models for the frequency interval assign-
ment problem with cumulative interferences.
Koster, A. and Tieves, M. (2012). Column generation for
frequency assignment in slow frequency hopping net-
works. EURASIP Journal on Wireless Communica-
tions and Networking, 2012(1):1–14.
Luna, F., Estbanez, C., Len, C., Chaves-Gonzlez, J., Nebro,
A., Aler, R., and Gmez-Pulido, J. (2011). Optimiza-
tion algorithms for large-scale real-world instances of
the frequency assignment problem. Soft Computing,
15(5):975–990.
Muoz, D. (2012). Algorithms for the generalized weighted
frequency assignment problem. Computers and Oper-
ations Research, 39(12):3256–3266.
Salma, A., Omran, I. A. M., and Mohammad, M. (2010).
Frequency assignment problem in satellite communi-
cations using differential evolution. Computers and
Operations Research, 37(12):2152–2163.
Schulte, C., Tack, G., and Lagerkvist, M. Z. (2013). Mod-
eling and programming with gecode. 522.
Segura, C., Miranda, G., and Len, C. (2011). Parallel hy-
perheuristics for the frequency assignment problem.
Memetic Computing, 3(1):33–49.
Shum, H. and Trotter, L. E. (1996). Cardinality-restricted
chains and antichains in partially ordered sets. Dis-
crete Applied Mathematics, pages 421–439.
Tomita, E., Tanaka, A., and Takahashi, H. (2006). The
worst-case time complexity for generating all maxi-
mal cliques and computational experiments. Theoret-
ical Computer Science, 363:28–42.
van Hoeve, W.-J. (2001). The alldifferent constraint: A sur-
vey. Cornell University Library.
Wang, J. and Cai, Y. (2014). Multiobjective evolutionary al-
gorithm for frequency assignment problem in satellite
communications. Soft Computing, pages 1–25.
Yang, C., Peng, S., Jiang, B., Wang, L., and Li, R.
(2014).
Hyper-heuristic genetic algorithm for solv-
ing
frequency assignment problem in td-scdma. In
Proceedings of the 2014 conference companion on
Genetic and evolutionary computation companion,
ACM:1231–1238.
ADecompositionMethodforFrequencyAssignmentinMultibeamSatelliteSystems
33
