Resource Allocation and Scheduling based on Emergent behaviours in

Multi-Agent Scenarios

Hanno Hildmann and Miquel Martin

NEC Laboratories Europe, Kurf¨ursten-Anlage 36, D-69115 Heidelberg, Germany

Keywords:

Resource Allocation, Scheduling, Emergence, Optimization, Stochastic Optimization, Routing, Logistics.

Abstract:

We present our observations regarding the emergent behaviour in a population of agents following a recently

presented nature inspired resource allocation / scheduling method. By having agents distribute tasks among

themselves based on their local view of the problem, we successfully balance the work across agents, while

remaining ﬂexible to adapt to dynamic scenarios where tasks are added, removed or modiﬁed. We explain the

approach and within it the mechanisms that give rise to the emergent behaviour; we discuss the model used

for the simulations, outline the algorithm and provide results illustrating the performance of the method.

1 INTRODUCTION

Resource allocation, as discussed in (Luss, 2012), of

which scheduling is a prominent type, is a wide ﬁeld

and applicable to a large number of commercial en-

deavors, e.g. (Pinedo, 2012). Many approaches to

this domain exist and it is not the goal of this paper to

compare between these, nor is it to champion one over

the other. The pervasive nature of the topic suggests

that different instances of the problem with a range of

attributes and challenges will make it unlikely for any

single approach to consistently outperform all others.

In this paper we would like to discuss one dis-

tributed resource allocation method (Hildmann and

Martin, 2014) and, speciﬁcally, the emergence of sim-

ple properties in a population of agents using this

method. Emergence is normally linked to the interac-

tion between members of a population, not to their in-

dividual actions (Holland, 1998); we discuss the inter-

action between agents, and investigate the effect this

has on the behaviour of the population as a whole.

The example problem we simulated to evaluate

the approach is a scheduling scenario. Application

of the method to civil security services like police or

ﬁre ﬁghters is currently considered, but for the run-

ning example in this paper we chose the utility sector

and the daily schedules of ﬁeld service personnel.

We think the views presented in this paper are

of interest to the optimization community and to re-

search in Artiﬁcial / Swarm Intelligence; furthermore

we see applications in the areas of Transportation and

Scheduling (Dussutour et al., 2004).

2 PROBLEM DESCRIPTION

We simulated the dispatching of service personnel,

tasked with executing a number of tasks within their

shift. The time required to handle a task is predicted

in advance. In day to day operations trafﬁc conditions

affect travel times between locations and, when arriv-

ing on site, a task might transpire to require less or

more time than originally predicted. The problem can

be stated as the sequential scheduling of service or

maintenance tasks for a group of ﬁeld engineers, with

the cost of the schedule being calculated in terms of

the time it takes to process the schedule:

Description: Let A be a set of agents a

, . . . , a

, each

with a ﬁnite amount of resources r

as well as a depot

, let T be a set of tasks t

, . . . , t

each with a cost

and assume that function f(L × L ) → c

l1l2

maps

tuples of locations (for the agents or depots) to a cost.

The problem is then to allocate the tasks to agents

such that (a) all tasks are allocated to exactly one

agent and (b) the minimal sum of the cost to connect

the depot to all tasks allocated to this agent (i.e. the

shortest path) plus the sum of the costs of the tasks

themselves does not exceed the agent’s capacity. 

The presented approachis designed to handle non-

static problems (Hildmann and Martin, 2014) and the

following 4 aspects are considered to be dynamic:

(1) A (agents may join the population or drop out),

(2) T (tasks may be added or removed),

(3) f() (tasks may change their location) and

(4) c

(tasks may change their cost).

140

Hildmann H. and Martin M..

Resource Allocation and Scheduling based on Emergent behaviours in Multi-Agent Scenarios.

DOI: 10.5220/0005219501400147

In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 140-147

ISBN: 978-989-758-075-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

3 MODEL

The model simpliﬁes the problem in the following

ways: the act of re-allocating a task from one agent to

another (stealing) is assumed to be instantaneous and

cost free. In each iteration, all agents are activated in

randomized order, and ﬁnally, agents have a starting

location (depot) and maintain individual schedules.

Parameters: The problem model has the following

parameters: numbers of both, agents and tasks, the ca-

pacity of each individual agent (which is the same for

all agents), the visibility range, the map size (we used

100 × 100 for all the simulations discussed in this pa-

per) and ﬁnally a ﬂag determining whether a single

depot is used or whether there are multiple depots.

Furthermore, formula 1, given below, includes the

tuning parameter α. Changes in α will affect the

speed with which the approach converges towards a

stable state, and on the other hand, the degree of

change in the problem that the algorithm can handle.

Formulae: The decision to re-allocate a task from

the active agent A to the passive agent B is stochastic.

If agent A is balanced this probability (P

bal

) is:

bal

= 1−

(rem.cap

)

(rem.cap

)

+ (rem.cap

)

(1)

with rem.cap

the remaining capacity of X. The prob-

ability for a maximizing agent A (P

max

) is the inverse:

max

= 1− P

bal

(2)

4 METHOD, APPROACH AND

ALGORITHM

There is plenty of evidence (e.g. (Bartholdi and

Eisenstein, 1996)) for the potential of nature-inspired

scheduling to be extremely efﬁcient; our work is in-

spired by the behavior of social insects (Camazine

et al., 2001). It is known (Bonabeau et al., 2000) that

colonies of social insects like bees, termites or ants

seem to operate in a semi-stable pattern until some

catalyzing event like e.g. the discovery of a new food

source or an attack on the colony takes place. This

then triggers a paradigm shift in the whole colony

which persists until the event is dealt with, after which

the system returns to the semi-stable state.

We present our work on 3 levels: the method, the

approach and the implemented algorithm. By method

we mean the generic description of how a population

of agents can cooperate to collectively cope with a

large number of tasks in dynamic environments. The

approach describes how this method can be applied in

computer science and to our example.

4.1 Method

Two opposing mechanisms govern the interaction be-

tween the agents: one to exchange tasks between

themselves with the aim to balance the length of their

respective schedules; and the other to re-schedule

tasks in order to largely reduce some agents’ loads.

Both mechanisms deﬁne interaction between ex-

actly two agents and in both cases the decision to

re-allocate a task is stochastic (using the formulae 1

and 2, respectively). The process is applied continu-

ously; converging towards balanced or highly unbal-

anced workloads. As the mechanisms are stochastic

they rely in a large number of interactions to achieve

their goals, but on the other hand facilitate the ability

to overcome deadlocks and local optima.

The ﬁrst mechanism enforces a semi-stable equi-

table state where agents exchange tasks to maintain a

level of fairness: individual tasks can be moved from

one schedule to another if this decreases the differ-

ence in the respective agents’ loads.

The second mechanism, which differs only

marginally from the ﬁrst, is used to achieve its ex-

act opposite: the re-allocation of tasks between two

agents is determined on the basis of whether the re-

allocation increases the difference in loads. This

mechanism is used when unallocated tasks appear /

are discovered in the vicinity of an agent. The im-

balance this creates reduces the load on some of the

agents, thus allowing them to take on some of these

unallocated tasks, even if this require a signiﬁcant

portion of the agent’s entire capacity.

The decision which of the two mechanisms to

use is based on the stance or behaviour paradigm of

an agent, which corresponds to whether the agent is

aware of any allocated tasks. To maintain the anal-

ogy to social insects, the presence of unallocated tasks

constitutes the catalyzing event that causes a (local)

behaviour shift of the population. Agents that are

unaware of unallocated tasks operate under the bal-

anced stance which follows the “rich gets poorer”

paradigm. Conversely, if an agent becomes aware of

unallocated tasks it switches to the maximizing stance

and adopts the “rich gets richer” paradigm.

Note that as, we deﬁned it, P

bal

= P

max

(cf. formu-

lae 1 and 2). This is in line with the idea that switch-

ing stances reverses the probabilities of the outcomes,

i.e. if A is likely to succeed at stealing a task for rich

gets richer then it should be equally likely to have it

stolen for rich gets poorer.

ResourceAllocationandSchedulingbasedonEmergentbehavioursinMulti-AgentScenarios

141

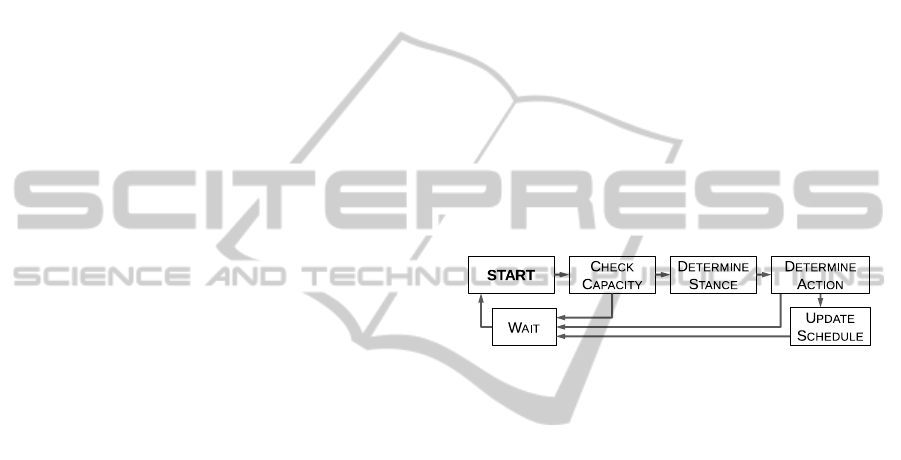
4.2 Approach

Iteration Design: We designed the approach with

a distributed implementation in mind. Agents are ex-

pected to execute their algorithms individually and re-

peatedly. The ﬂow diagram in Figure 1 shows the ﬁve

stages of each iteration for the agents. These are:

•

Check Capacity:

agents ensure that it has ca-

pacity left to take on tasks from another agent.

•

Determine Stance:

the agent chooses which of

the two mechanisms it should use (see above):

1. balanced (“rich gets poorer”)

2. maximizing (“rich gets richer”)

•

Determine action:

the agent will attempt to

schedule any unallocated tasks it is aware of. If

no unallocated tasks are available, then the stances

of the two agents determine the interaction. Since

there are two stances (

bal

and

max

) four possible

combinations can occur:

1. bal - bal

If both agents are balanced they will use the

balanced approach between themselves. For-

mulae like e.g. formula 1 are used for this.

2. max - max

If both agents are set to maximization they will

use the max approach between themselves us-

ing e.g. formula 2 to determine whether a task

is moved from the passive to the active agent.

3. bal - max

If a balanced agent interacts with a maximizing

agent, the balancing agent will always take the

task from the maximising agent. The motiva-

tion for this is that a balanced agent is merely

aiming to distribute the load between itself and

its surrounding colleagues, while a maximizing

agent is concerned with the allocation of cur-

rently unallocated tasks. By passing tasks from

maximizing agents to balanced agents we ef-

fectively shift load from the problematic part of

the problem space to the regions where we are

merely optimizing distribution.

4. max - bal

The last case is when the active agent is maxi-

mizing and the passive agent is load balancing;

in this case no task is re-allocated (with the mo-

tivation being the same as above).

•

Update Schedule:

both agent’s schedules need

to be updated if a task was exchanged.

•

Wait:

after a cycle an agent will wait for a certain

amount of time before becoming active again.

Variations and Design Choices: We discussed the

approach in the context of the example application

where the resources are service engineers (agents)

which are allocated to tasks (locations which the

agents have to visit). As mentioned, the pre-

sented method expects interaction between exactly

two agents, where one agent is taking the active part

(by, amongst other things, choosing the other agent),

and the other is the passive one.

This leaves two possible interpretations or varia-

tions on how to implement the approach: either the

active agent is choosing the passive agent from a list

of agents, or the active agent chooses a task from a

list of tasks (in which case it indirectly chooses an

agent, namely the one currently being assigned to

this task). We implemented the latter interpretation.

This is partly motivated by the desire to stick close

the phenomena that inspired the approach (agents will

see tasks in their vicinity and then potentially interact

with the agent that is assigned these tasks).

Figure 1: Basic ﬂow diagram of the approach (for either

variation, discussed above) as implemented for all agents.

Emergence: The basis of the approach is a continu-

ous optimization of the schedules assigned to the indi-

vidual members of a population of resources / agents.

Pairs of spatially co-located agents attempt to pass

tasks to one another with the aim to equalize their

respective loads, using an easily calculated probabil-

ity based on a “rich gets poorer” paradigm. On top

of this we have designed a mechanism that enables a

paradigm shift, namely the switching of the individual

agent’s stance to “rich gets richer”. This paradigm is

triggered by the discovery of unallocated tasks.

By design, the mechanisms use computationally

cheap formulae to increase the number of possible it-

erations. The result of continuously iterating is the

effect that the population of agents, as a whole, be-

haves in a fashion that assists the individual agents.

The agents’ decision whether to engage with an-

other agent and which formula to use, is determined

by their interaction, i.e. by their own stance and the

stance of the agent they are interacting with. Therein

lies the key to the emergence of the following be-

haviour: agents in a stable environment will work

towards sharing the workload with their surrounding

agents, while agents in areas of unallocated tasks will

slowly lose tasks to their neighbours in stable envi-

ronments, increasing their ability allocated new tasks.

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

142

This results in the diffusion of tasks from agents

in areas of unallocated tasks to agents in areas where

all tasks are covered. In other words, agents in un-

problematic areas will slowly increase their average

load as they take on tasks from areas where there are

unallocated tasks, thereby freeing up capacity of the

agents in these problematic areas. Once all (visible)

tasks have been allocated, the population returns to

averaging out the loads of its members, which reverse

the trend of tasks gravitating towards balanced agents.

4.3 Algorithm

Algorithm 1 implements the overall approach, Algo-

rithm 2 (where the math from §3 is used) is called by

it. All agents are continuously running this algorithm

at intervals, the frequency of which being determined

by the wait period in line 25.

Algorithm 1 works as follows:

• First, a capacity check is performed (lines 1-4).

• Given available capacity, the agent determines

its stance (line 7) on the basis of the existence of un-

scheduled tasks (line 6) in its vicinity (line 5).

• Independent of the agent’s stance, if there are no

reachable tasks (line 8, 9) no action is taken.

• If there are any reachable tasks which are not

currently scheduled (lines 10, 11), one of them is cho-

sen (line 12) and immediately scheduled (line 13).

• However, if all reachable tasks are scheduled

and at least some are scheduled to a max agent (lines

14, 15), then one of those tasks is chosen (line 16).

Depending on the stance of the agent, the task is ei-

ther (in case the agent is bal, line 17) scheduled di-

rectly (line 18) or (in case of a max agent, line 19)

re-allocated stochastically (line 20) using the proba-

bilities deﬁned in §3 and as calculated by Alg. 2.

• Finally, if all reachable tasks are scheduled but

none of them is scheduled to a max agent (line 21),

then the action is again determined by the stance of

the agent: max agents categorically do not schedule

tasks from a bal agent so no action is taken (line 22),

but amongst themselves bal agents will pick a task

(lines 23) and compete for it (line 24) using Alg. 2.

Regarding the choosing of a task (lines 12 or 16)

this was implemented as a random choice. There are

of course ways to make an informed choice to speed

up convergence but in the context of evaluating the

performance of the generic approach this is omitted.

Algorithm 1: Main algorithm.

while True do

// Check capacity

1 load ←− check current load()

2 if load ≥ my

capacity then

3 shed task()

4 return

// Determine stance

5 tasks ←− get tasks in vincinity()

6 urgent ←− get unscheduled(tasks)

7 stance ←− bal if urgent is empty else max

// Determine action / Re-schedule

8 reach ←− get reachable(tasks)

9 if reach is empty then return

10 unscheduled ←− get

unscheduled(reach)

11 if unscheduled is not empty then

12 task ←− pick task(unscheduled)

13 schedule(task)

14 max task ←− schedule to max ag(reach)

15 if max tasks is not empty then

16 task ←− pick task(max task)

17 if stance is bal then

18 schedule(task)

19 else

20 steal(stance, task)

// cf. Alg. 2

21 else

22 if stance is max then return

23 task ←− pick

task(reach)

24 steal(stance, task)

// cf. Alg. 2

25 wait

Algorithm 2:

steal(

stance, task

)

Stochastically

determines wether a task gets re-scheduled.

formula bal()

uses formula 1, returns ⊤, ⊥

formula max()

uses formula 2, returns ⊤, ⊥

Input: stance, task

1 other ←− get

current owner(task)

2 if stance is bal then

3 if formula bal(sel f, other) then

4 schedule(task)

5 return

6 else

7 if formula max(sel f, other) then

8 schedule(task)

9 return

ResourceAllocationandSchedulingbasedonEmergentbehavioursinMulti-AgentScenarios

143

5 RESULTS

5.1 Simulations

For the performance evaluation we ran simulations

using a ﬁxed seed for the random number generator

to ensure that the initial starting positions were

the same across simulations. We then investigated

increasingly large number of agents. The results are

presented below in the graphs shown in Figures 2 to 4.

4 separate scenarios were used for the evaluation:

1. Scenario 1: to evaluate the ability of the popula-

tion to assimilating new tasks we added 40 tasks

at the outer edge of the map at iteration 25.

2. Scenario 2: robustness and the ability to coped

with high loads was tested by continuously adding

100 randomly located tasks every 25 iterations.

3. Scenario 3: for illustration purposes (i.e. screen-

shots in Figure 7) an additional 50 tasks, located

up to 20 units outside the original map, are added

at iteration 100. This guarantees that they are not

in proximity of agents or original tasks.

4. Scenario 4: for Figure 6, an additional 50 tasks

are added at iteration 100, each 10 units outside

the original map and all in a straight line, making

them visible to only a small number of agents.

It should be noted that determining the shortest path

from the depot through all tasks in a schedule is ba-

sically the same as solving the Multi-agent Travel-

ling Salesman Problem (MTSP); known to be NP-

complete (Hassan and Al-Hamadi, 2008). We approx-

imated the shortest path using simulated annealing.

5.2 Performance

Our results are generated using simulations: Figures

2, 3 and 5 compare single simulation runs while Fig-

Figure 2: Scenario 1, 4000 tasks and an agent capacity of

500. The graph shows the impact of scheduling 40 new

tasks at iteration 25. For populations larger than 400 the

impact is minimal; all converge quickly.

ure 4 compares three separate runs of a simulation. To

ensure that these results are representative we also ran

parallel simulations with larger agent populations (up

to 1000), higher initial task load (up to 10,000) and for

up to 1000 iterations. A more detailed discussion of

these is outside the scope of this paper, the interested

reader is referred to (Hildmann and Martin, 2014) for

a more detailed discussion of the evaluation.

Note that we intentionally omit reporting the stan-

dard deviation because the randomly generated lo-

cations for tasks and agents (which do not change)

result in different lengths for the optimal schedules,

making the standard deviation meaningless unless re-

ported for much larger numbers of simulations.

Figure 2 illustrates how population size impacts

the convergence properties: besides the higher load

per agent for smaller populations, convergence to-

wards stable values is consistent across populations.

Figure 3 shows the average load of the max agents

for the same simulation as above. Note that a value

of zero indicates the absence of max agents, (i.e. all

tasks are allocated). Smaller populations take longer

to assimilate the initial task load into their schedules,

but the time it takes for the extra tasks seems to be

identical across population sizes.

The results in Figures 2 and 3 are for agent popu-

lations operating under comparatively low loads (i.e.

with a lot of excess capacity). We now brieﬂy address

the question of how the approach performs when the

agents are approaching their maximum capacity.

Figure 4 shows the results of 3 separate runs. The

initial condition was 250 agents and 100 tasks, each

agent with a capacity of 75 and a visibility of 40. Ev-

ery 25 steps another 100 tasks are added to answer

the question whether the increasingly small (compar-

atively) additions or the decreasing remaining capac-

ity has a signiﬁcant impact and to test the adaptivity

of the approach. From the graphs shown we can see

that even for high task loads the population quickly

reverts to the balancing stance and converge to an av-

Figure 3: As in Figure 2, showing the average loads of the

max agents (zero means there are no max agents). There is a

correlation between population size and iterations taken for

the initial task allocation; allocation of new tasks is uniform.

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

144

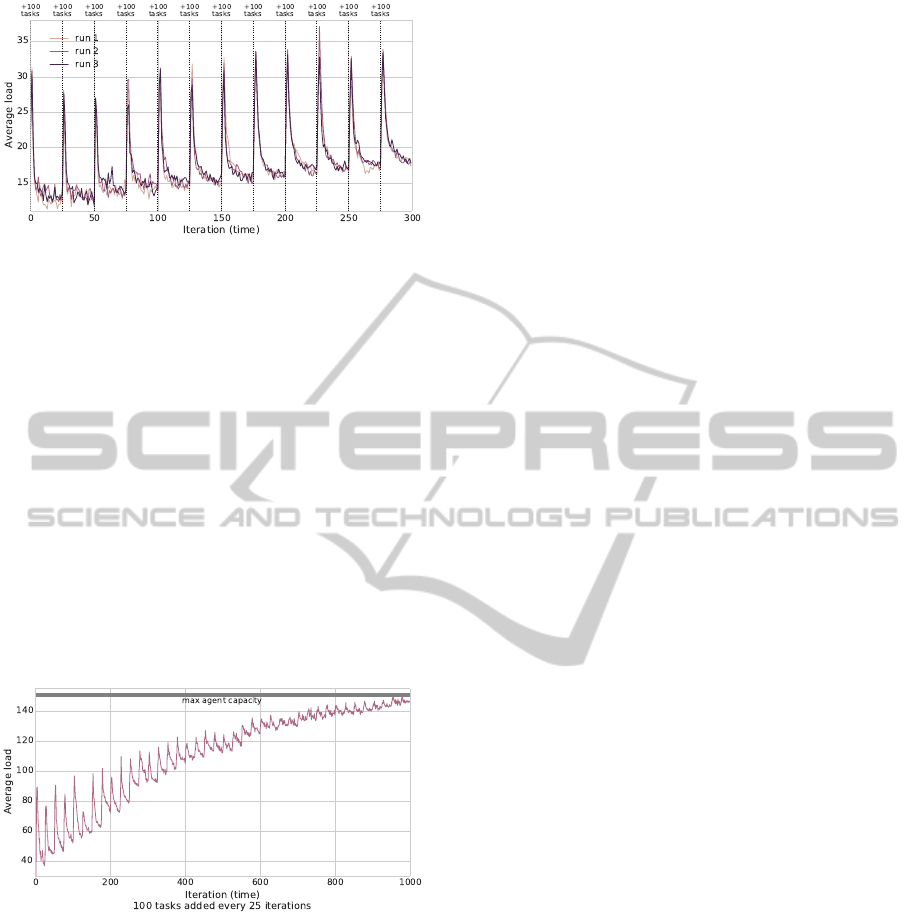
Figure 4: Scenario 2, 50 agents, capacity = 75. Every 25 it-

erations an additional 100 tasks are added, the graph shows

the average load of the agents from 3 separate runs. The

increase of the average is steadily increasing, as expected,

but the approach seems to continue to perform well.

erage which is consistently increasing in a linear way.

Figure 5 shows that even when approaching their

maximum capacity the performance of the population

does not deteriorate. It should be noted that in the

simulations the cost of a task is set to zero. If this

was not the case, there would be a linear increase in

the average load to match the aggregated cost of the

newly added tasks. The asymptotic curve seen above

results also from the fact that with increasing schedule

length the cost of adding a new task will (on average)

decrease (the more tasks you havethe higher the prob-

ability of two tasks being very close and thus having

a low distance cost associated with them).

Figure 5: Scenario 2 with 50 agents, capacity = 150, 100

tasks are added every 25 iterations: the graph shows the av-

erage load of the agents. Forlarge numbers of tasks (4000+)

the average load converges towards the agent’s capacity but

this does not affect the time to assimilate new tasks.

The above graphs support the claim that the

method does indeed scale and performs well. For a

detailed evaluation cf. (Hildmann and Martin, 2014).

5.3 Emergent Behaviour

For the screenshots used to show the emergent be-

haviour we used scenarios 3 and 4. 50 agents were

placed randomly on the map, together with 500 ini-

tial tasks (which were supplemented by 50 additional

tasks at the outer edge of the map in iteration 50 (sce-

nario 3) or 60 (scenario 4). The range of the agents

was 350 and their visibility was set to 60.

We show two screenshots in Figure 6 that show the

simulation at the iteration when the new tasks are in-

troduced (a) as well as 40 iterations later when almost

all the tasks have been assimilated into the agents’

schedules. In comparison it is visible that the agents

on the left and in the middle of the map have taken on

a larger number of tasks to their respective right, i.e.

freeing agents on their right.

The screenshots in Figure 7 show the impact of

large visibility on the behaviour of the population.

Scenario 3 was used here. In addition, in this sim-

ulation the visibility was set equal to reachability, that

is, any task within reach was visible. Given that the

agents have quite some capacity left when the new

tasks are introduced this resulted in many agents as-

similating the new tasks. As a result, the average load

increased substantially, because the tasks were allo-

cated on a ﬁrst come ﬁrst serve basis with no regard

for its distance to the agent. While this was later miti-

gated when the agents had returned to balancing their

loads, the convergence to substantially longer.

6 DISCUSSION

We have presented an approach that, while not pro-

ducing efﬁcient solutions with regard to the aggre-

gated workload, enable a population of agents to re-

act to changes in the environment and to dynamically

change according to changes in the problem space.

The graphs in the previous section show that the ap-

proach is scalable and that small as well as large prob-

lems can be handled.

Furthermore, the preliminary investigations (cf.

(Hildmann and Martin, 2014)) showed no dramatic

changes for growing problem space.

It was the stated aim of this paper to present the

mechanism that gives rise to the emergent behaviour

in the population. Through the two separate stances

the agents will, in effect, move tasks out of the realm

of the agents that can address the problem of unallo-

cated tasks. While the effect is rather hard to show on

still images, it is straight forward to see why this is

happening when one considers the 4 possible interac-

tions between agents: balanced agents will balance

the workload in the population of balanced agents.

Max agents will split into agents with very high load

and agents with very low load. The agents with a low

load will eventually assimilate the unallocated tasks,

while the agents with a high load are likely to lose

some of their load to balanced agents.

ResourceAllocationandSchedulingbasedonEmergentbehavioursinMulti-AgentScenarios

145

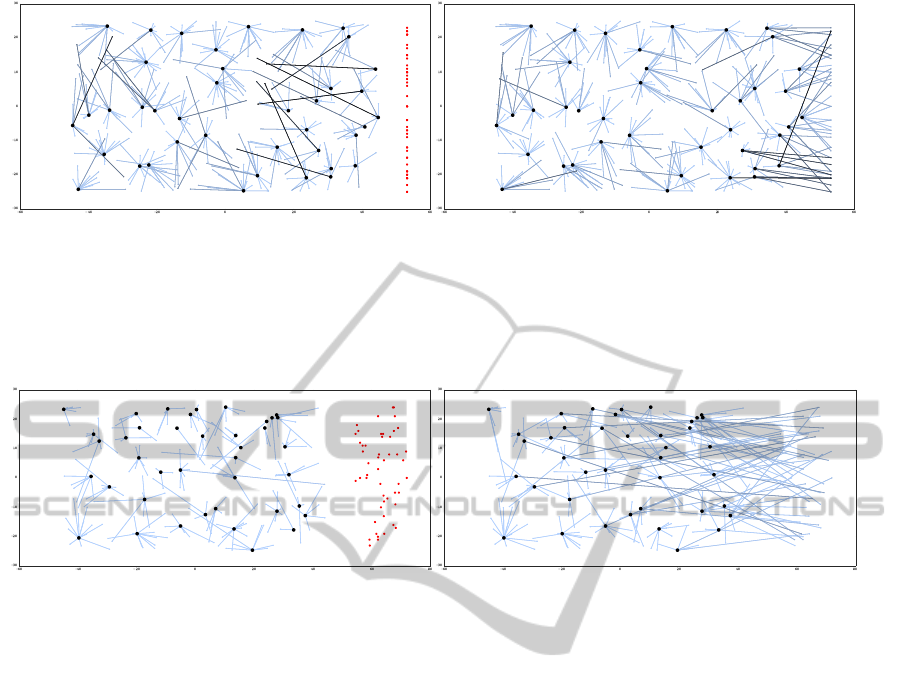
(a) (b)

Figure 6: The two screenshots, above, from a simulation running Scenario 4 with 400 initial tasks and 40 agents, each with a

maximum capacity of 220 and a visibility range of 65, illustrate the emerging behaviour of the population. In the map area,

each “star” is centered around a different agent’s depot, and the points connected to it radially represent the tasks the agent

currently has in its schedule. The darkness of the connection corresponds to its length. The red dots on the far right of the

map in (a) represent newly added and thus currently unscheduled tasks, all of which are scheduled in (b). When comparing

the right half of the maps in (a) and (b) we observe a shift in the orientation of the connections between tasks and agents.

Figure 7: The two pictures above illustrate the emergent behaviour in Scenario 3, using the same representation as Figure 6.

The settings are (in comparison to the above) half the initial tasks (200) for again 40 agents, which have a higher capacity

(320) and a much wider visibility (200). On a small map setting a high visibility range results in a large number of agents

assimilating the new tasks. This removes the collective behaviour where agents further from the tasks take on the load of

agents closer to the tasks. While this will allow for an quicker assimilation of all new tasks, it will take longer to distribute

the load fairly over the whole population. However, depending on the scenario, this might be a feasible parameter choice.

This should initially affect only balanced agents

that are close to max agents, but in time they will

share their load with other balanced agents, thereby

shedding some of their load to their colleagues as

well. As soon as the last unallocated task is assigned

to an agent all agents will become balanced and con-

tinuously strive to balance their loads.

We presented sufﬁcient materials to allow the

reader a comparative implementation. The math pro-

vided is intentionally kept simple so as to facilitate the

implementation on standard computer hardware.

Restrictions to the Approach

The proposed method relies on a number of agents

working in proximity, such that the schedule assigned

to a speciﬁc agent can be partly absorbed into another

agent’s schedule. This is expected to require a critical

mass in order to outperform other approaches.

Furthermore, there is an upper limit to the degree

of change over time which the method can be ex-

pected to handle well. If the changes are too rapid

or dramatic, recalculating the entire solution might be

the better approach. This is due to the iterative nature

of the approach, which quickly adapts to changes and

“follows” moving centers of gravity in the problem

space. If such centers appear and disappear seemingly

at random it becomes impossible to follow them, and

thus the method will lose the edge over other ap-

proaches. However, we do not expect such dramatic

changes in the envisioned application areas.

One ﬁnal issue should be raised here: we have

mentioned the Traveling Salesman Problem in the be-

ginning, and pointed out that it is known to be NP-

complete. We have then implemented our approach

and used a different way to calculate the cost of a

schedule. We haveinvestigated using the shortest path

from the depot through all tasks and back to the depot

as a cost function for a schedule, and will report on

these investigations separately; for now it sufﬁces to

say that the computational cost of calculating the least

cost to address all tasks in a schedule is far outweigh-

ing the cost to calculate everything else implemented

for our approach. While this indicates that our ap-

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

146

proach can be implemented efﬁciently it also means

that for a real world application, the algorithm will

need to use some insight into the problem space to

decrease the computational cost associate with it. We

do consider this to be a relevant restriction.

It should be noted that the chosen problem is only

one example, used in this paper to illustrate the ap-

proach. By no means do we restrict the application

domain to service personnel; for example: the transi-

tion cost (distance) between tasks can be interpreted

as the overhead associated with the switching be-

tween tasks. Likewise, we use the term schedule, but

do not restrict the application of the presented method

nor the algorithm to schedules; e.g. the assignment

of resources to elements of non-ordered sets of tasks

(Beckers et al., 1994) can be addressed as well.

REFERENCES

Bartholdi, J. J. and Eisenstein, D. D. (1996). A produc-

tion line that balances itself. Operations Research,

44(1):21–34.

Beckers, R., Holland, O., and Deneubourg, J.-L. (1994).

From local actions to global tasks: stigmergy and col-

lective robots. In Proceedings of the Workshop on

Artiﬁcial Life, pages 181–189, Cambridge, MA. MIT

Press.

Bonabeau, E., Dorigo, M., and Theraulaz, G. (2000). Inspi-

ration for optimization from social insect behaviour.

Nature, 406:39–42.

Camazine, S., Deneubourg, J.-L., Franks, N. R., Sneyd,

J., Theraulaz, G., and Bonabeau, E. (2001). Self-

Organization in Biological Systems. Princeton Univ

Press.

Dussutour, A., Fourcassie, V., Helbing, D., and

Deneubourg, J.-L. (2004). Optimal trafﬁc orga-

nization in ants under crowded conditions. Nature,

428:70–73.

Hassan, H. and Al-Hamadi, A. (2008). On compara-

tive evaluation of Thorndike’s psycho-learning exper-

imental work versus an optimal swarm intelligent sys-

tem. In Computational Intelligence for Modelling

Control Automation, 2008 International Conference

on, pages 1083 –1088.

Hildmann, H. and Martin, M. (2014). Adaptive scheduling

in dynamic environments. In 2014 Federated Confer-

ence on Computer Science and Information Systems

(FedCSIS), pages 1331–1336.

Holland, J. (1998). Emergence: From Chaos to Order. He-

lix books. Oxford University Press.

Luss, H. (2012). Equitable Resource Allocation: Models,

Algorithms and Applications. Information and Com-

munication Technology Series. Wiley.

Pinedo, M. (2012). Scheduling: Theory, Algorithms, and

Systems. SpringerLink : B¨ucher. Springer.

ResourceAllocationandSchedulingbasedonEmergentbehavioursinMulti-AgentScenarios

147