
Accelerating the Performance of Parallel Depth-First-Search
Branch-and-Bound Algorithm in Transportation Network Design
Problem
Amirali Zarrinmehr and Yousef Shafahi
Department of Civil and Environmental Engineering, Sharif University of Technology, Azadi Avenue, Tehran, Iran
Keywords: Transportation Network Design Problem, Parallel Branch-and-Bound Algorithm, Depth-First-Search,
Greedy Algorithm, Super-linear Speedup.
Abstract: Transportation Network Design Problem (TNDP) aims at selection of a subset of proposed urban projects in
budget constraint to minimize the network users’ total travel time. This is a well-known resource-intensive
problem in transportation planning literature. Application of parallel computing, as a result, can be useful to
address the exact solution of TNDP. This paper is going to investigate how the performance of a parallel
Branch-and-Bound (B&B) algorithm with Depth-First-Search (DFS) strategy can be accelerated. The paper
suggests assigning greedy solutions to idle processors at the start of the algorithm. A greedy solution,
considered in this paper, is a budget-wise feasible selection of projects to which no further project can be
added while holding the budget constraint. The paper evaluates the performance of parallel algorithms
through the theoretical speedup and efficiency which are based on the number of parallel B&B iterations. It
is observed, in four cases of TNDP in Sioux-Falls transportation network, that achieving high-quality
solutions by idle processors can notably improve the performance of parallel DFS B&B algorithm. In all
four cases, super-linear speedups are reported.
1 INTRODUCTION
Transportation Network Design Problem (TNDP) is
a well-know infrastructural problem in
transportation planning. As a combinatorial problem,
TNDP targets the selection of the optimal subset of a
set of proposed projects, i.e. construction of urban
highways, in budget constraint, so as to minimize
the users’ total travel time. This is an NP-Hard
problem which has been addressed by various
heuristic or meta-heuristic approaches (see for
example Vitins and Axhausen (2010), or Farahani et
al., (2013) as a more recent survey). The exact
solution of TNDP, however, is a resource-intensive
problem which becomes intractable soon as the
problem enlarges (Poorzahedy, 1980).
By advent of parallel computing facilities in
recent decades, much work has been directed to
address the exact solution of NP-Hard problems.
Parallel algorithms have been devised to tackle
many of moderate or rather large size combinatorial
problems (Roucairol, 1996). Parallel Branch-and-
Bound (B&B) algorithms with Depth-First-Search
(DFS) strategy have been among these algorithms
for which promissing results have been reported
(Anstreicher et al., 2002).
This paper is going to investigate accelerating
the performance of parallel B&B algorithm with
DFS strategy in TNDP. The B&B algorithm
proposed by LeBlanc (1975) and parallelized by
Zarrinmehr (2011) is taken into consideration. The
paper demonstrates how assigning greedy high-
quality solutions to the initial idle processors can
improve the parallel performance of the algorithm.
The rest of this paper is organized as follows:
Section 2 provides a formal discreption of TNDP.
Section 3 overviews in brief the related literature
and prerequisite concepts which will be refered in
subsequent sections. Section 4 presents the
methodology of this paper which will be about
feeding idle processors. In section 5, detailed results
of running the program on four cases of Sioux-Falls
transportation network are reported and discussed,
which will be followed by concluding remarks in
section 6.
359
Zarrinmehr A. and Shafahi Y..
Accelerating the Performance of Parallel Depth-First-Search Branch-and-Bound Algorithm in Transportation Network Design Problem.
DOI: 10.5220/0005220103590366
In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 359-366
ISBN: 978-989-758-075-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 FORMAL DESCRIPTION OF
TNDP
TNDP is often formulated as a bi-level optimization
problem. In this formulation, the optimal subset of
projects is selected at the Upper Level Problem
(ULP) and the users’ behaviour in route selection is
simulated at the Lower Level Problem (LLP), by
solving a Traffic Assignment Problem (TAP). To
formally describe the problem at the upper level,
assume that (Poorzahedy and Abulghasemi, 2005):
: set of proposed projects (links) to be added to
the current network,
: Binary decision variable corresponding to
project a, a ∈
, taking values 1 or 0 indicating
whether to construct a project or not,
y: binary vector of decision variables,
A(y): set of network links after decision y has been
made, A(y) = A U {a∈
∶
1,
: Amount of flow in link “a”, a∈,
x(y): vector of traffic flow on network links after
decision y has been made,
: Volume-delay function of link a, a∈,
assumed to be convex and differentiable for
≥0,
: Cost related to the construction of project a,
a∈
,
B: available budget for the construction of given
projects,
Now the TNDP at the upper level can be written
as (1)-(4).
ULP: Min
=
∑
∈
(1)
s.t:
= 0 or 1 ∀ ∈
(2)
∑
∈
≤ B
(3)
x(y): the user equilibrium flow, from
solution of LLP(y), corresponding to
decision vector y
(4)
In the above formulation, the objective function (1)
is the sum of users’ total travel time over all links of
the network. Decision variables are defined in
equation (2) as binary values. Equation (3) means
that the selection of projects must meet the budget
constraint. Constraint (4) expresses that the amounts
of traffic flows on the network links must follow the
pattern of User Equilibrium (UE) which is obtained
through a TAP. This problem, as shown in (5)-(8), is
formulated at the LLP and the following definitions
are further required for its description:
P: set of origin-destinations (ODs), P⊆ ,
: The travel demand from r to s,
,
∈,
: Non-empty set of different paths form r to s
after decision y has been made,
,
∈,
: Amount of flow in path k from r to s, ∈
,
: Binary variable taking values 1 or 0 indicating
whether link “a” belongs to path k or not, a∈,
∈
,
LLP(y): Min
∑
∈
d (5)
s.t.:
∑
∈
=
∀, ∈
(6)
≥ 0
∀ ∈
,∀,∈
(7)
∈
,∈
∀ ∈
(8)
In the LLP formulation, the objective function (5) is
the sum of the integrals of the link volume-delay
functions, which is a mathematical construct without
any clear interpretation (Sheffi, 1985). Equation (6)
shows the flow conservation constraint, while the
path flows are ensured to be non-negative in
equation (7). The relationship between link flows
and path flows is also considered as equation (8). It
expresses that the amount of flow at each link is the
summation of those path flows going through the
link (Sheffi, 1985).
Solving LLPs makes the model consider how
users select their route in the network, which is often
known as the UE situation. The UE in a
transportation network is a situation in which for any
origin-destination, all paths used by travellers have
an equal travel time which is less than or equal to the
travel time of unused paths (Sheffi, 1985). The TAP
formulation in (5)-(8) will be referred as a UE-TAP
through this paper. There is still another kind of
TAP which results in the System Optimal (SO) paths
and flows in the network, and therefore, will be
referred as SO-TAP. In the following is the
formulation of a SO-TAP which is the same as UE-
TAP unless in its objective function (Sheffi, 1985):
Min =
∑
∈
(9)
s.t. : (6), (7), (8)
The objective function (9) in SO-TAP has an
intuitive meaning, which is minimization of the
users’ total travel time at the entire network. The
resulting flow patterns, however, does not represent
the actual behaviour of users, though it can be useful
theoretically in transportation network problems.
It is easy to see that both formulations of UE-
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
360

TAP and SO-TAP are convex optimization problems
and can be solved using the iterative convex
combination algorithms (Sheffi, 1985).
3 RELATED LITERATURE
This section brief-reviews the related literature in
three subsections. First, speedup and efficiency, as
two basic measures in parallel computing are
introduced as well as Amdahl’s law. Parallel B&B
algorithms with DFS strategy are introduced next.
Finally the application of the B&B algorithm in
TNDP and its parallelization are addressed.
3.1 Two Basic Measures in Parallel
Computing
Two important parallelization measures used
extensively in the literature are known as speedup
and efficiency. Speedup is a measure indicating how
many times the parallel algorithm performs faster
due to the parallelization. Efficiency is also a
normalized version of speedup, which is the speedup
value divided by the number of processors (Barney,
2010).
A fundamental theorem in parallel computing is
known as Amdahl's law. According to Amdahl’s
law, the speedup can never exceed the number of
processors. This, in terms of efficiency measure,
means that the efficiency will always be less than 1.
A linear speedup is achieved when the speedup
almost equals to the number of processors (Barney,
2010).
3.2 Parallel DFS B&B Algorithms
The B&B algorithms are general heuristic search
procedures which can be applied in the exact
solution of combinatorial problems (Li and Wah,
1990). In these algorithms, the search space of the
problem is iteratively decomposed in the form of a
rooted search tree, in which the root is the main
problem and the descendents are partially solved
problems. The B&B algorithm selects iteratively
among the nodes of the search tree, expands the
selected node, and updates the search tree
information, until when there will be no node to be
selected in the search tree (Gendron and Crainic,
1994).
Various search strategies of B&B algorithms
arise at the stage of defining the selection priority
over nodes of the search tree. DFS is a very famous
strategy that selects the deepest node in the search
tree in each iteration. Parallelization of this strategy
has been an important research topic in 1980's and
1990's (Lai and Sahni, 1984; Li and Wah, 1986, Li
and Wah, 1990). This was mainly because of some
reports on super-linear speedup (i.e. a speedup
which is greater than the number of processors)
which seemed to be in contradiction with Amdahl's
law, introduced previously in 3.1. The super-linear
speedup in parallel DFS B&B algorithms was not,
however, a contradiction because in reported cases
the processors had been observed to access high
quality solutions in early iterations, which in turn
brought about a reduction in the search tree and
problem size (Pruul et al., 1988).
3.3 B&B Algorithms in TNDP
Due to the NP-Hard complexity of TNDP, extensive
research has investigated non-exact solutions for the
problem (see Farahani et al., (2013) for example).
Not much work has addressed the exact solution of
TNDP. The only exact solution, to our knowledge, is
the early study of LeBlanc (1975) which proposed a
B&B algorithm to tackle the problem.
LeBlanc organized a binary rooted tree in
correspondence with binary decision variables of the
problem. In partial solutions, LeBlanc proposed
solving a SO-TAP in which all undecided projects
were assumed to be added to the underlying
network. He proved that the users’ total travel time,
taken from such an assignment, would work as a
lower-bound for complete solutions located at the
last level of the search tree which are to be
evaluated, in turn, with a UE-TAP. LeBlanc’s
algorithm was a working method to tackle small size
TNDPs, but became inefficient soon as the problem
enlarged (Poorzahedy, 1980).
In a recent study, Zarrinmehr (2011) discussed
that the B&B algorithm proposed by LeBlanc (1975)
well-adapts to a master-slave parallelization
paradigm. In master-slave paradigm, one processor,
namely the master, holds the main information of the
problem. At the beginning of B&B iterations, the
master processor assigns the nodes of the search tree
to other processors, namely the slaves. Each slave
processor receives one node from the master for
which it solves a traffic assignment problem and
sends back to the master processor the
corresponding result. Receiving the results back
from the slaves, the master updates the information
and starts a new iteration if needed. This process
will be addressed throughout this paper as a parallel
iteration.
The results reported by Zarrinmehr (2011)
AcceleratingthePerformanceofParallelDepth-First-SearchBranch-and-BoundAlgorithminTransportationNetwork
DesignProblem
361

supported that, in low levels of parallelism, an
almost linear speedup can be assured. It was also
observed that, due to little idling overhead and
negligible communication between master and slave
processors, the performance of the parallel algorithm
can be roughly estimated by the theoretical speedup,
, and theoretical efficiency,
, which
account for the number of iterations in the parallel
B&B algorithm rather than the running-times (Li
and Wah, 1990).
Given that p is the number of parallel processors
and I(1) and I(p) stand for the number of B&B
iterations while using a single processor and p
processors, respectively, the theoretical speedup and
efficiency are defined as follows:
= I(1)/ I(p)
(10)
=
/p
(11)
4 METHODOLOGY
To address the solution of TNDP, this paper uses the
parallel DFS B&B algorithm developed in
Zarrinmehr (2011) as a base algorithm. The only
difference is about feeding initial idle processors at
the beginning of parallel B&B iterations.
The idling of processors in parallel B&B
algorithms usually takes place when the algorithm is
just started and there are not yet enough nodes
available in the search tree to be distributed among
processors (See Henrich (1993) for example).
Exploiting these idle processors to evaluate high-
quality solutions in parallel DFS B&B algorithms
can be helpful in achieving better solutions while
starting the search and it does not impose an extra
computational burden on the performance of parallel
program.
In many combinatorial problems (e.g. scheduling
problems, integer-programming problems, etc)
finding feasible solutions with good quality is an
NP-Hard problem, itself, which is not easier than the
main problem. In TNDP, however, simple greedy
algorithms can be devised to generate such
solutions. The next sub-section introduces one of
these algorithms.
4.1 Greedy Solutions for TNDP
Although addition of more projects to a
transportation network would not necessarily result
in reducing the users’ total travel time (known as
Brass’ paradox in transportation literature) it can
provide a greedy solution for the problem. In other
words, a transportation network with more projects,
in a greedy approach, is likely to provide less
congestion and travel time. As a result, a high-
quality solution for TNDP may be a feasible
selection of projects to which no further project can
be added in budget constraint. Zarrinmehr and
Shafahi (2014) named such a solution a dominant
solution in one dimensional binary integer
programming problems and proposed an algorithm
for Enumeration of Dominant Solutions (EDS).
Given that there are n projects in TNDP to be
selected, the EDS algorithm holds an n-length binary
string as a candidate solution. The algorithm does
not ignore any of dominant solutions and enumerates
each of them in O(3n) as a rough estimate. The
interested reader can follow Zarrinmehr and Shafahi
(2014) to find the details about the EDS algorithm
and its functionality.
4.2 Feeding Initial Idle Processors
As mentioned in the beginning of this section,
dominant solutions can serve as high-quality
solutions to feed initial idle processors in the parallel
DFS B&B solution of TNDP. Furthermore, the
greedy solutions provided by this algorithm can be
generated in no more that O(3n) which is
computationally negligible compared with other
computations e.g. the iterative traffic assignment
procedure. As a result, one way to feed initial idle
processors in the parallel B&B solution of TNDP
can be application of the EDS algorithm.
In the methodology used in this paper, whenever
some idle slave processors receive nothing from
master to work on, the master uses the EDS
algorithm to assign dominant solutions to those
processors. Assignment of dominant solutions to idle
processors is done in the same order as they are
computed by the EDS algorithm, as long as there are
some idle processors to be assigned. These solutions
are evaluated by idle slave processors and sent back
to the master. The master, then, may update the best
solution in starting iterations of the parallel DFS
B&B algorithm which, in turn, can be helpful in
directing the search and discarding useless nodes of
the search tree.
5 NUMERICAL RESULTS
To explore the effect of feeding initial idle
processors in the parallel DFS B&B algorithm in
TNDP, this section considers a problem with 12
given projects in the Sioux-Falls transportation
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
362
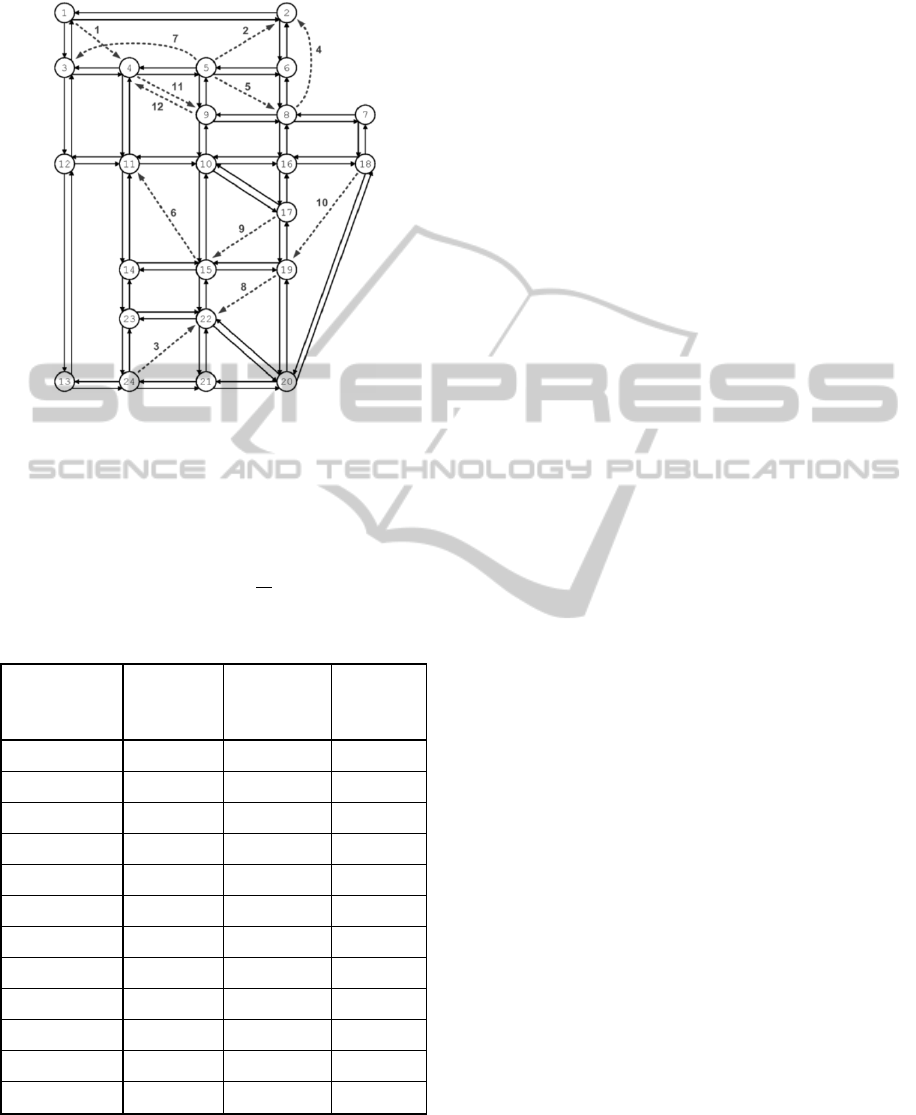
network (Bar-Gera, 2011) as shown in Figure. 1.
Figure 1: The Configuration of Sioux-Falls network and
projects.
Given that the volume-delay functions of the
network edges (i.e. highways) follow the pattern of
equation (12), details about the projects definition
are given in Table 1.
(
) =
(1+0.15
)
(12)
Table 1: Projects definition.
Project
Free Flow
Travel
Practical
capacity
Project
Cost
Number
Time
(
Minutes)
(
Vehicles per
Hour
)
(
Units of
Budget
)
1
(1 to4)
8.0 5000 20
2
(5 to 2)
6.0 5000 22
3
(24 to 22)
5.0 5000 27
4
(8 to 2)
7.0 5000 27
5
(5 to 8)
4.0 5000 27
6
(15 to 11)
6.5 5000 28
7
(5 to 3)
10.0 5000 31
8
(19 to 22)
5.0 5000 32
9
(17 to 15)
4.5 5000 34
10
(18 to 19)
6.0 5000 40
11
(4 to 9)
3.0 5000 40
12
(9 to 4)
3.0 5000 42
In equation (12),
is the travel time in link ‘a’
(minutes),
is the free flow travel time in link
‘a’ (minutes),
is the amount of traffic flow on link
‘a’ (vehicles per hour), and
is the practical
capacity of link ‘a’ (vehicles per hour).
The parallel programs of DFS B&B algorithm
were run before and after feeding the initial idle
processors. Each program was only run once,
because the performance of the parallel algorithm is
not subjected to a stochastic behaviour (Zarrinmehr,
2011). Four budget levels of 60, 100, 140, and 200
(in units of budget) have been considered. The
performance measures are theoretical speedup and
efficiency which are rough estimates for real
speedup and efficiency, according to Zarrinmehr
(2011). Results are reported for processor numbers
of 1, 2, 4, ..., 20. Table 2 presents the detailed
results.
There are some symbols in Table 2 that need to
be introduced beforehand:
#p: Number of processors,
#iter: Number of parallel iterations in parallel
B&B algorithm (as introduced earlier in subsection
3.3),
: Theoretical speedup,
: Theoretical efficiency,
Err: The gap, in percentage, between the objective
function of the best found solution by idle
processors and the global optimum.
Tables 2(a-d)-1 use the measure Err to show the
quality of greedy solutions found by the EDS
algorithm in the beginning of the parallel B&B
algorithm. When this measure is close to zero, a
better solution is initially available to direct the
search of the DFS strategy.
For example, in Table 2(a)-1, when 6 processors
are considered to parallelize the DFS B&B
algorithm, the solution [000000011000] is achieved
with the objective function (i.e. users’ total travel
time) of 6710836 (vehicle-minutes) which is a rather
high-quality solution due to Err = 100*(6710836-
6667832)/6667832 = 0.6
%. This initial solution
contributes to discard useless nodes in the search
tree of DFS B&B algorithm and leads to a notable
reduction in the number of parallel iterations of the
algorithm. This is shown in Table 2(a)-2 for #p=6
where the number of parallel iterations is reduced
from 40 to 32.
Addressing the speedup and efficiency through
the number of parallel iteration (as in 3.3), it is
interesting also to see that the reduction in the
number of parallel iterations due to feeding idle
processors may bring about a super-linear speedup.
Again, in Table 2(a)-2 when 6 processors are
assumed to be available, after feeding the idle
processors it can be observed that
AcceleratingthePerformanceofParallelDepth-First-SearchBranch-and-BoundAlgorithminTransportationNetwork
DesignProblem
363

6
=216/32=6.75 > 6 and
6
=6.75/6=1.13 >
1.00.
Table 2: Detailed Results of Parallel DFS B&B Algorithm
Before and After Feeding Idle Processors.
(a)-1: Solutions Found by Idle Processors When B=60
Best Solution Found Corresponding Objective
Gap
# p by Idle Processors Function (vehicle-minutes) (%)
1 - - -
2 [000000000011] 7443194 11.6
4 [000000001010] 7127291 6.9
6 [000000011000] 6710836 0.6
8-20 [000000110000] 6667832 0.0
The Global Optimum of the Problem
[000011000000] 6667832
(a)-2: Performance Measures When B=60
Before Feeding Processors After Feeding Processors
# p # iter
# iter
1 216 1.00 1.00 216 1.00 1.00
2 109 1.98 0.99 109 1.98 0.99
4 57 3.79 0.95 57 3.79 0.95
6 40 5.40 0.90 32
6.75 1.13
8 31 6.97 0.87 25
8.64 1.08
10 26 8.31 0.83 21
10.29 1.03
12 24 9.00 0.75 18
12.00 1.00
14 22 9.82 0.70 18 12.00 0.86
16 19 11.37 0.71 16 13.50 0.84
18 18 12.00 0.67 16 13.50 0.75
20 17 12.71 0.64 15 14.40 0.72
(b)-1: Solutions Found by Idle Processors When B=100
Best Solution Found Corresponding Objective
Gap
# p by Idle Processors Function (vehicle-minutes) (%)
1 - - -
2 [000000001111] 6951620 8.7
4 [000000011100] 6586257 3.0
6-20 [000000111000] 6395632 0.0
The Global Optimum of the Problem
[000000111000] 6395632
Table 2: Detailed Results of Parallel DFS B&B Algorithm
Before and After Feeding Idle Processors. (cont.)
(b)-2: Performance Measures When B=100
Before Feeding Processors After Feeding Processors
# p # iter
# iter
1 468 1.00 1.00 468 1.00 1.00
2 236 1.98 0.99 236 1.98 0.99
4 120 3.90 0.98 115
4.07 1.02
6 83 5.64 0.94 59
7.93 1.32
8 64 7.31 0.91 46
10.17 1.27
10 53 8.83 0.88 37
12.65 1.26
12 47 9.96 0.83 32
14.63 1.22
14 41 11.41 0.82 30
15.60 1.11
16 37 12.65 0.79 25
18.72 1.17
18 34 13.76 0.76 24
19.50 1.08
20 33 14.18 0.71 22 21.27 1.06
(c)-1: Solutions Found by Idle Processors When B=140
Best Solution Found Corresponding Objective
Gap
# p by Idle Processors Function (vehicle-minutes) (%)
1 - - -
2 [000000011111] 6575316 5.5
4 [000000111101] 6271596 0.6
6-20 [000000111110] 6259644 0.4
The Global Optimum of the Problem
[001000111000] 6233324
(c)-2: Performance Measures When B=140
Before Feeding Processors After Feeding Processors
# p # iter
# iter
1 717 1.00 1.00 717 1.00 1.00
2 362 1.98 0.99 362 1.98 0.99
4 183 3.92 0.98 166
4.32 1.08
6 124 5.78 0.96 111
6.46 1.08
8 95 7.55 0.94 84
8.54 1.07
10 76 9.43 0.94 68
10.54 1.05
12 65 11.03 0.92 58
12.36 1.03
14 59 12.15 0.87 51
14.06 1.00
16 53 13.53 0.85 45 15.93 1.00
18 47 15.26 0.85 42 17.07 0.95
20 45 15.93 0.80 39 18.38 0.92
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
364

Table 2: Detailed Results of Parallel DFS B&B Algorithm
Before and After Feeding Idle Processors. (cont.)
(d)-1: Solutions Found by Idle Processors When B=200
Best Solution Found Corresponding Objective
Gap
# p by Idle Processors Function (vehicle-minutes) (%)
1 - - -
2 [000001111111] 6254867 3.6
4 [000010111111] 6183311 2.4
6 [000100111111] 6159487 2.1
8 [000100111111] 6159487 2.1
10 [000110111110] 6120960 1.4
12 [001000111111] 6108631 1.2
14 [001000111111] 6108631 1.2
16-20 [001010111100] 6035512 0.0
The Global Optimum of the Problem
[001010111100] 6035512
(d)-2: Performance Measures When B=200
Before Feeding Processors After Feeding Processors
# p # iter
# iter
1 869 1.00 1.00 869 1.00 1.00
2 437 1.99 0.99 437 1.99 0.99
4 221 3.93 0.98 220 3.95 0.99
6 149 5.83 0.97 148 5.87 0.98
8 114 7.62 0.95 114 7.62 0.95
10 94 9.24 0.92 93 9.34 0.93
12 80 10.86 0.91 79 11.00 0.92
14 70 12.41 0.89 69 12.59 0.90
16 63 13.79 0.86 47
18.49 1.16
18 56 15.52 0.86 43
20.21 1.12
20 52 16.71 0.84 39
22.28 1.11
Similar results can be observed in Table 2(a)-2
for #p = 8, 10, and 12, as well as in Tables 2(b), (c),
and (d) where super-linear speedups, and
efficiencies greater than one have been bolded.
Figure 2 presents graphs for efficiencies before and
after feeding idle processing cores.
The results in Table 2 suggest that, when
assigning greedy TNDP solutions to idle processors,
the improvement in the performance of the parallel
DFS B&B algorithm is quite dependent on the
quality of the best solution found by initial idle
processors. This can be better found out in Figures
2(b) and 2(d). In Figure 2(b) the early access of
processors to the optimal solution of the problem
(i.e. Err =0.0) caused a notable increase in the
efficiency (e.g.
6
=1.32) of the parallel
algorithm. On the other side, in Figure 2(d) the
performance almost remains unchanged up to use of
14 processors, due to low-quality solutions accessed
by idle processors.
(a) TNDP When B = 60
(b) TNDP When B = 100
(c) TNDP When B = 140
(d) TNDP When B = 200
Figure 2: Theoretical Efficiencies of Parallel Algorithms
Before and After Feeding Idle Processors.
AcceleratingthePerformanceofParallelDepth-First-SearchBranch-and-BoundAlgorithminTransportationNetwork
DesignProblem
365

6 CONCLUDING REMARKS
This paper addressed accelerating the exact solution
of TNDP via a parallel DFS B&B algorithm with a
master-slave parallelization paradigm. Theoretical
measures of speedup and efficiency, based on the
number of parallel iterations, were considered to
evaluate performances. It was discussed that there
were some initial idle processors at the start of the
parallel iterations, as there were not sufficient nodes
to be worked on. The paper suggested assigning
greedy solutions in TNDP (namely dominant
solutions), to these idle processors and applied a
simple enumeration algorithm to provide such
solutions. It was shown, in four case studies of
TNDP with 12 projects, in Sioux-Falls transportation
network, that feeding the idle processors can be
helpful in reducing the number of parallel iterations
and accelerating the performance of the algorithm.
Super-linear speedups, and efficiency values greater
than one, were observed in all examples.
Numerical results in this paper suggested that
improving the performance of the algorithm was
quite dependent on the quality of the best found
solution by idle processors. Therefore, it is
interesting to investigate how application of more
promising solutions, rather than those computed first
by the EDS algorithm, can affect improving the
performance of the algorithm. Also, this paper
addressed the performance measures through
theoretical speedups and efficiencies of parallel
B&B algorithm which have been based on the
number of parallel iterations rather than running-
times. Reporting on the real speedups and
efficiencies based on the running-times and running
the programs on large transportation networks with
more than 12 projects and with higher number of
processors can all be helpful to extend the results of
this paper.
ACKNOWLEDGEMENTS
The authors appreciate the insightful comments
made by five anonymous referees which helped to
improve this paper.
REFERENCES
Anstreicher, K., Brixius, N., Goux, J.-P., and Linderoth, J.,
2002. Solving large quadratic assignment problems on
computational grids. Mathematical Programming,
91(3), 563-588.
Bar-Gera, H., 2011. Transportation network test problems.
http://www.bgu.ac.il/~bargera/tntp.
Barney, B., 2010. Introduction to parallel computing.
Lawrence Livermore Natl. Libr.
Farahani, R. Z., Miandoabchi, E., Szeto, W. Y., and
Rashidi, H., 2013. A Review of Urban Transportation
Network Design Problems, European Journal of
Operational Research, 229(2), 281-302.
Gendron, B., Crainic, T. G., 1994. Parallel Branch-and-
Branch Algorithms: Survey and synthesis. Operations
Research, 42(6), 1042-1066.
Henrich, D., 1993. Initialization of Parallel Branch-and-
Bound Algorithms. Proceedings of the Second
International Workshop on Parallel Processing and
Artificial Intelligence, Chamberry, France.
Lai, T. H., Sahni, S., 1984. Anomalies in parallel branch-
and-bound algorithms. Communications of the ACM,
27(6), 594-602.
LeBlanc, L. J., 1975. An algorithm for the discrete
network design problem. Transportation Science.,
9(3), 183-199.
Li, G. J., Wah, B. W., 1986. Coping with anomalies in
parallel branch-and-bound algorithms. IEEE
Transactions on Computers, 100(6), 568-573.
Li, G. J., Wah, B. W., 1990. Computational efficiency of
parallel combinatorial or-tree searches. IEEE
Transactions on Software Engineering, 16(1), 13-31.
Poorzahedy, H., 1980. Efficient algorithms for solving the
network design problem. Ph.D. Diss., Department of
Civil Engineering, Northwest University, Evanston,
Ill.
Poorzahedy, H., Abulghasemi, F., 2005. Application of ant
system to network design problem. Transportation,
32(3), 251-273.
Pruul, E., Nemhauser, G., Rushmeier, R., 1988. Branch-
and-bound and parallel computation: A historical note.
Operations Research Letters, 7(2), 65-69.
Roucairol, C., 1996. Parallel processing for difficult
combinatorial optimization problems. European
Journal of Operations Research, 92(3), 573-590.
Sheffi, Y., 1985. Urban transportation networks:
equilibrium analysis with mathematical programming
methods. Prentice Hall.
Vitins, B. J., Axhausen, K. W., 2010. Patterns and
Grammars for Transport Network Generation.
Proceedings of 14th Swiss Transport Research
Conference.
Zarrinmehr, A., 2011. Discrete network design using
parallel branch-and-bound algorithms. M.Sc. Thesis,
Department of Civil and Environmental Engineering,
Sharif University of Technology.
Zarrinmehr, A., Shafahi, Y., 2014. Enumeration of
Dominant Solutions: An Application in Transport
Network Design. M.Sc.
International Journal of
Transportation Engineering, 1(4), 335-348.
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
366
