
Descriptive Modelling of Clinical Conditions with Data-driven
Rule Mining in Physiological Data
Hadi Banaee, Mobyen Uddin Ahmed and Amy Loutfi
Center for Applied Autonomous Sensor Systems,
¨
Orebro University,
¨
Orebro , Sweden
Keywords:
Rule Mining, Pattern Abstraction, Health Parameters, Physiological Time Series, Clinical Condition.
Abstract:
This paper presents an approach to automatically mine rules in time series data representing physiological
parameters in clinical conditions. The approach is fully data driven, where prototypical patterns are mined for
each physiological time series data. The generated rules based on the prototypical patterns are then described
in a textual representation which captures trends in each physiological parameter and their relation to the other
physiological data. In this paper, a method for measuring similarity of rule sets is introduced in order to
validate the uniqueness of rule sets. This method is evaluated on physiological records from clinical classes
in the MIMIC online database such as angina, sepsis, respiratory failure, etc.. The results show that the rule
mining technique is able to acquire a distinctive model for each clinical condition, and represent the generated
rules in a human understandable textual representation.
1 INTRODUCTION
Wearable sensors are widely used in clinical settings
in order to collect a range of vital signs, which are
definitely necessary to be monitored and interpreted
during hospital care. Nowadays, the rate of accumu-
lating physiological sensor data is much faster than
the rate of analysing and modelling them (Chen et al.,
2006). These health parameters can be analysed in
different clinical conditions for early diagnosis or be-
havioural interpretation. For instance, monitoring the
continuous records of heart rate, respiration rate, glu-
cose level, etc. during or after clinical surgery is an
essential task in clinical settings. Often the measure-
ments of physiological attributes are sequential data,
i.e. time series. Consequently, the rapid growth of
health records in medical informatics improves to af-
fect the healthcare, increases the need to apply a com-
prehensive data mining in order to model the acquired
knowledge (Sow et al., 2013). Most automatic deci-
sion support systems in clinical applications apply di-
verse data mining techniques on sensor data in order
to acquire patient-specific information (Banaee et al.,
2013a). The study in (Cao et al., 2008) proposes a
predictive modelling approach based on the extracted
trends and features from heart rate and blood pres-
sure time series data. In (Rutledge et al., 1990), a
Bayesian network is proposed to model the inten-
sive care unit (ICU) data to derive a descriptive model
of physiological states of the patients. In (Buchman
et al., 2002), and (Riordan Jr et al., 2009) the us-
ability of analysing heart rate measurements to pre-
dict and diagnose of various clinical applications in
ICU is proposed. Also, few works have been applied
data mining tasks in clinical settings related to the vi-
tal signs, specifically in operating room monitoring
systems. For instance, (Agarwal et al., 2007) presents
a context-aware framework in order to analyse physi-
ological data collected in surgical procedure to detect
the significant changes and events. In (Garrard et al.,
1993) and (Lake et al., 2002), the authors present a
correlation of heart rate variability and sepsis.
In general, data mining approaches used in health
informatics are context-based so that the applied
methods leverage predefined domain knowledge. Us-
ing a knowledge-driven approach leads to have a su-
pervised model of information, which is restricted
with expert domain knowledge (Yoo et al., 2012).
An overview of the works that use data-driven meth-
ods in order to unsupervisely discover hidden and po-
tentially useful information through the physiological
sensor data and to build the corresponding model is
provided in (Banaee et al., 2013a). Automatic rule
generation as a data-driven approach in data min-
ing is an appropriate choice to extract the behaviour
of physiological data. Recently, temporal associa-
tion rule mining methods have been applied on clini-
cal data stream to identify complex relationships. In
103
Banaee H., Ahmed M. and Loutfi A..
Descriptive Modelling of Clinical Conditions with Data-driven Rule Mining in Physiological Data.
DOI: 10.5220/0005220901030113
In Proceedings of the International Conference on Health Informatics (HEALTHINF-2015), pages 103-113
ISBN: 978-989-758-068-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

(Combi and Sabaini, 2013), the authors present tem-
poral rule extraction for physiological data and ad-
dress the problem of visually analysing this kind of
data. (He et al., 2012) propose a novel multivariate
association rule mining based on change detection for
complex data set including numerical data streams.
The authors in (Muflikhah et al., 2013) introduce an
approach to generate the rules automatically from the
linguistic data of coronary heart disease using sub-
tractive clustering and fuzzy inference in order to de-
termine the diagnosis of disease. In this work, the pro-
cess of rule mining from the physiological time series
of clinical conditions is an unsupervised approach,
which leads to define a data-driven model to describe
the behaviour of vital signs in each clinical condition.
This approach helps the end user of the system to ap-
ply the models on unknown measurements, or to ex-
tract more descriptive features for clinical situations.
The main focus of this paper is to address 1) in-
dividualisation, and 2) representation of the extracted
rules from physiological sensor data of clinical con-
ditions. In this study, temporal rule mining has
been employed to generate meaningful and interest-
ing rules among physiological data streams in clinical
settings, in order to individually build a descriptive
model for clinical conditions. More precisely, first,
he temporal patterns of the given health parameters
are abstracted. Further, with clustering the extracted
patterns, the cluster centres are represented as proto-
typical patterns, which represent the significant pat-
terns of happenings through the data. Using associ-
ation rule mining, the relationships between the pro-
totypical patterns in multivariate data are discovered
as a set of rules. The proposed approach is applied
to health records in different classes of clinical con-
ditions such as angina, sepsis, respiratory failure, and
brain injury (Moody and Mark, 1996). The result is
an individual model of rule set for each of the classes.
To evaluate the uniqueness of the provided models for
clinical classes, a novel similarity function between a
pair of rule sets is proposed. This method calculates
the appearance ratio of rules from a rule set in another
rule set. Meanwhile, the description of the generated
rules is represented as a textual output by employing
natural language generation (NLG) approach to char-
acterise the main behaviours of trends (Banaee et al.,
2013b), but here, the patterns within the rules.
The paper is structured as follows: Section 2 de-
scribes the general methodology to achieve a descrip-
tive model of rules in sequential data. In Section 3,
first, data acquisition is described and then the gen-
eral methodology is characterised for physiological
data of clinical conditions. Also, a novel similarity
method to compare the rule sets is introduced in this
section. The results of rule sets for clinical conditions
are presented in Section 4, followingby the evaluation
results to assess the uniqueness of rule sets per clinical
conditions, along the textual outputs for a selection of
the provided rules. Finally, Section 5 concludes with
a discussion for the direction of future work.
2 RULE MINING IN
SEQUENTIAL DATA
This section describes the methodology used for rule
mining in sequential data in order to discover proto-
typical patterns and then qualitative rules. This pro-
cess applies data mining techniques to generate a de-
scriptive model of rules in one or several sequential
data in general (i.e. time series) for an individual case.
In this approach, an input time series are firstly discre-
tised into a set of subsequences of time series. Then,
a set of prototypical patterns is abstracted by clus-
tering the extracted subsequences. Afterwards, these
prototypical patterns are considered as the attributes
and items to discover the expressive rules among the
data. Finally, the rules which are linguistically infor-
mative are represented as a descriptive model. Figure
1 shows the general steps of the proposed methodol-
ogy in this paper.
!""#$%&'()"$!*"+,%
-./#&0#%#$!"+,%
-./#&-#1$#)#%"!"+,%
')),*+!"+,%&$./#)
2+)*$#"+)!"+,%
3/.)"#$+%4
5!".$!/&/!%4.!4#&
4#%#$!"+,%&65708
!"#$#"%&'()&*+,
!"#$%&'$&#()
*+,-$."./$0&")#$1()
-('$(-
!"#$#"%&'(-."+',
2(3#45&-(6)7!"()
8(#
Figure 1: Schematic overview of proposed methodology.
2.1 Prototypical Pattern Abstraction
The main objectiveof the prototypicalpattern abstrac-
tion is to provide a set of representative patterns from
HEALTHINF2015-InternationalConferenceonHealthInformatics
104

raw sequential data, which are temporally occurred in
time series. Here, two phases have been proposed for
this task: 1) discretisation and 2) clustering.
Discretisation. Since dealing with large time se-
ries with high granularities is typically challenge-
able (Kotsiantis and Kanellopoulos, 2006), discreti-
sation is a solution which transforms a time se-
ries t=(t
1
,...,t
n
), as a representative term of se-
quential data, into a discrete sequence of segments
S(t) : s
1
s
2
...s
m
, where usually m ≪ n. Different ap-
proaches can be applied for time series discretisation
(Fu, 2011). This work uses a sliding window method
in a sense that the time series t is discretised to a set
of segments S(t) by sliding a window of size w with a
given overlap on two consecutivewindows. Each seg-
ment s
i
= (t
i
1
,...,t
i
w−1
) is a subsequence of the time
series t, (1≤i≤m). The provided segments are poten-
tially the candidate to describe the unique attributes
of the input data.
Clustering. To exploit a reasonable number of rep-
resentative patterns from numerous segments, clus-
tering techniques are used for categorising the sub-
sequences. Before applying clustering methods on
the set of segments, each segment is normalised
to zero means (µ=0). This normalisation leads to
have a unified set of segments in order to only con-
sider the behaviour of segments by ignoring the ef-
fect of their amplitudes. Afterwards, k-means al-
gorithm as a widespread approach is used for pat-
tern clustering (Warren Liao, 2005). The algorithm
categorises all the segments s
i
∈ S(t) into k clus-
ters C
t
={c
1
,...,c
k
}. Now, the centre of each clus-
ter (o
j
) is considered as the prototypical pattern
for the segments which are labelled with c
j
, where
1≤ j≤k. Suppose O
t
={o
1
,...,o
k
} is the set of pro-
totypical patterns of time series t. Each centre (pat-
tern) o
j
=(t
′
i
1
,...,t
′
i
i+w−1
) is a sequence of time values,
which is not necessarily a subsequence of time series
t. So, in the sequence of segments S(t), By replac-
ing each segment s
i
with its label in clustering (proto-
typical pattern), the corresponding sequence of proto-
typical patterns P(t) for time series t is generated as:
P(t) : p
1
... p
m
, where p
i
∈ O
t
and 1 ≤ i ≤ m. The ad-
vantage of using clustering algorithm is that the pro-
totypical patterns are purely provided in a data-driven
way without involving any domain knowledge to cus-
tomise the typical patterns.
2.2 Automatic Rule Generation
Association rule discovery is a proper approach to
generate a meaningful set of rules from the abstracted
patterns of time series data (Schluter and Conrad,
2011). Here, first the standard association rule min-
ing method is described, and then the method of rule
generation in temporal data is presented. Suppose in
a system that I = {i
1
,...,i
d
} is a set of items that can
be occurred (e.g. all the products in a store). Let
D = {d
1
,...,d
N
} be a transactional database with N
transactions (e.g. all shopping lists in a week). The
support of an itemset A ∈ I is the frequency of the
occurrence of A in the transactions D. The standard
association rule discovery provides a set of rules in
form of A⇒B, where A and B are disjoint itemsets.
Generally, a rule like A⇒B in a system means if the
items of A appear in a transaction d
i
, then the items of
B also will plausibly appear in that transaction. Typ-
ical measures to show the strength of a rule are sup-
port (sup) and confidence (conf). Support of a rule
shows how often the rule appears in a given transac-
tional database. Further, the confidence of rule A⇒B
determines how frequent itemset B occurs in trans-
actions which contain itemset A. Let P
D
(A) be the
probability of the occurrence of A in D. Then, sup-
port and confidence are formally defined as (Schluter
and Conrad, 2011):
sup(A⇒B) = p
D
(A∪ B) (1)
conf(A⇒B) = p
D
(A|B) = sup(A⇒B)/p
D
(A) (2)
The rules with sufficient support and confidence
are typically called strong rules. Association rules
with low supports may be occurred accidentally
which would be not interesting as significant rules.
Similarly, a rule with low confidence cannot be effec-
tive on modelling the behaviour of the system. Thus,
the thresholds minsup and minconf given by the user
of the system can avoid involving the ineffective rules
in the final result. Several versions of association rule
mining algorithms have been introduced to deal with
non-transactional data which consist sequential items
(i.e time series) in order to give temporal rules (Kot-
siantis and Kanellopoulos, 2006). These algorithms
adapt the form of the terms in association rules based
on the time stamped data to involve temporal con-
straints in a rule like A
T
=⇒ B, which intends “If A hap-
pens, B will happen within time T” (Das et al., 1998).
In this study, each abstracted pattern from a time
series would be an item, which can occur before or
after another pattern (item). To define the collection
of transactions in the sequences of patterns (from sin-
gle or multi time series data), this work uses a mean-
ingful span around every pattern to make its corre-
sponding transaction. Thus, for a sequence of proto-
typical patterns P(t) : p
1
... p
m
, m transactions would
be generated, where each transaction, d
i
(1 ≤ i ≤ m)
contains the pattern p
i
together with a number of pat-
terns appropriately close to it. As an instance, if the
DescriptiveModellingofClinicalConditionswithData-drivenRuleMininginPhysiologicalData
105

approach wants to discover the rules from two time
series t
1
and t
2
(with the abstracted sequences of pat-
terns P(t
1
) : p
1
... p
m
and P(t
2
) : q
1
...q
m
and finds
the effect of t
1
on the behaviour of t
2
, the transaction
d
i
could be defined with the pattern p
i
in t
1
and in-
cluding the patterns q
(
i+ 1), .. ., q(i+ T − 1) within
time T in t
2
, which are occurred after p
i
. The next
step would be to apply the described association rule
mining algorithm on the provided set of transactions
d
1
,...,d
m
, using the abstracted patterns as the set of
items. The output of rule generation step is a set of
rules R = {r
1
,r
2
,...}, where each rule r
i
: A⇒B repre-
sents the effect of patterns in A ⊂ P(t
1
) on the patterns
in B ⊂ P(t
2
).
2.3 Rule Representation
A descriptive way of representing the rules is to pro-
vide a textual representation for the end user of the
system. Simple representation of a typical rule, r :
A⇒B in natural language text is to put the definition
of itemsets A and B in a textual format like: “If (when,
while) A occurs (happens, or any verb in context),
then (after that, simultaneously, just after that, within
time T) B will occur”. For instance, in the market
basket example (Silverstein et al., 1998), a rule could
be explained like: “If customers buying bread and
cheese, are likely to buy milk”. The purpose of this
study is to describe the itemsets (patterns) in a sense
that the provided rules from time series patterns be
linguistically meaningful. Particularly, if a rule like
r : A⇒B discovered from the method, it is important
to have a significant description for A and B, other-
wise the representation of “if A happens, then B hap-
pens” would be pointless. So, an output text like “Af-
ter a gradual decrease in pattern A, then pattern B has
a big rise and then a sharp drop” is more understand-
able, in order to interpret the behaviour of patterns in
discovered rules. A text generation method proposed
in (Banaee et al., 2013b) provides a framework to de-
tect partial trends in sequential data and then repre-
sent those trends in a textual form. By employing this
method, the patterns in a rule can be described based
on their partial trends. The benefit of using natural
language generation to represent the trends is that all
the rules from a set of time series data could be sum-
marised in a textual output, which helps the end user
to get a global perspective of the repetitive patterns
and their correlations in the input data.
3 MATERIALS AND METHODS
It is significant to analyse the prototypical patterns in
physiological time series data, due to formulate the
behaviour of sequential data, specially for different
clinical settings. This section presents the way of
characterising the proposed methodology in Section
2 to the health parameters under clinical conditions.
Moreover, the new similarity method to compare the
appearance of rules in other rule sets is introduced.
3.1 Data Acquisition
Database Outline. Throughout this paper, MIMIC
(Multi parameter Intelligent Monitoring for Intensive
Care) database
1
is considered which contains peri-
odic numeric measurements of physiological vari-
ables, such as heart rate, blood pressure, respira-
tion rate, and oxygen saturation, obtained from bed-
side ICU monitors (Moody and Mark, 1996). This
database includes multiple recordings of 90 subjects
with various lengths of measurements (from 1 hour to
77 hours), also different ages and genders. The sub-
jects are manually labelled in the database into dif-
ferent clinical classes related to their medical prob-
lems. In this work, the numeric records of the sub-
jects from nine major clinical conditions with suffi-
cient amount of data have been selected to be analysed
and modelled. The considered clinical conditions in-
clude Angina, Bleed (loss of blood from the circula-
tory system), Brain injury, Post-op CABG (coronary
artery bypass grafting surgery), CHF (chronic heart
failure), MI (myocardial infarction, i.e. heart attack),
Respiratory failure, Sepsis, and Post-op Valve (heart
valve surgery). The information of the subjects and
the physiological records for nine clinical conditions
in MIMIC database is shown in Table 1.
In order to analyse the coherence of vital signs and
also study the unique behaviour of physiological vari-
ables in clinical conditions, three physiological mea-
surements have been chosen to be processed: heart
rate (HR), blood pressure (BP) and respiration rate
(RR). Each measurement is a time series, sampled at
intervals of 1.024 seconds.
Data Cleansing and Preprocessing. Dealing with
the raw data in MIMIC database is faced with several
issues. Numeric physiological variables are available
for most of the records for 90 subjects, but not all
of them. In the first step, the records with all three
variables are selected for analysis. Next, the mea-
surements with a very short recorded times were dis-
carded, because finding significant rules in a short pe-
riod of data is not reasonable. Further, since the data
is gathered in a clinical environment with wearable
sensors, there are a lot of artefacts and noise among
1
physionet.org/physiobank/database/mimicdb/numerics
HEALTHINF2015-InternationalConferenceonHealthInformatics
106
Table 1: The information of clinical classes and their
records in MIMIC database.
Clinical
Condi-
tions
No.
of
records
Average
length
(hours)
No. of
Male/
Female
(%)
Age:
[min,max]
average
Angina 4 41.1 75/25
[67,68]
67
Bleed
4 44.7 75/25
[45,70]
57
Brain
injury
3 21.5 33/67
[68,75]
70
Post-op
CABG
3 40.3 33/67
[49,80]
66
CHF 17 33.2 35/65
[54,92]
75
MI 8 42.6 50/50
[63,80]
68
Resp.
failure
17 32.4 70/30
[38,90]
67
Sepsis 5 31.3 60/40
[27,88]
64
Post-op
Valve
5 40.7 20/80
[49,67]
58
the time series records. To avoid processing incorrect
information, 1) the data with unreliable values (e.g.
zero value for heart rate) are ignored; 2) a smoothing
function is applied on data to flatten the noisy data. It
is worth mentioning that these preprocessing steps are
applied on each segment of time series after discreti-
sation.
3.2 Rules in Physiological Data of
Clinical Conditions
To applying association rule discovery approach on
each clinical condition records, all the measurements
of subjects with the same condition are considered to-
gether. In this way, a prolonged amount of data is in-
volved in the process of modelling that makes a more
robust model of rules for each clinical condition. The
average length of available measurements for condi-
tions is about 100 hours, including all three mentioned
variables (HR, BP, and RR). Suppose there are three
time series t
hr
, t
bp
, and t
rr
, with the length of n. The
rule mining algorithm is applied to the physiological
time series in following phases:
Prototypical Pattern Abstraction. In order to pro-
vide the sequence of Prototypical patterns for each
time series, the algorithm starts with discretisation
method, described in Section 2. Since this approach
aims to provide a set of descriptive rules based on
the patterns, a meaningful range of values for the
size of the sliding window (w), from 1 minute to 10
minutes, has been tested. This range of data would
show seemingly the physiological changes and vari-
ations through the data, which is interpretable for
clinicians or the expert user. The length of over-
lap of two consecutive windows is initialised by
half of window’s size, to avoid concerning particu-
lar breaks between the segments. After discretisation
of time series, a sequence of segments will be ob-
tained for each signal, S(hr), S(bp), and S(rr), where
|S(var)|=2×(n/|w|)−1, and var ∈ {hr,bp, rr}.
The next step is to extract the prototypical patterns
of each time series using clustering methods. Here, k-
means method (Das et al., 1998) is applied to each set
of segments, in order to categorise the segments into
a set of clusters (k). Different values for the num-
bers of clusters (3 ≤ k ≤ 15) have been examined to
get the optimal clustering result with considering the
final patterns. Before applying clustering, each seg-
ment s
i
∈ S(var) is prepared as follows: If the num-
ber of artefacts in the segment’s values is more than
a defined threshold, the segment s
i
is removed from
S(var), otherwise, the artefacts will be replaced by
the values given by an interpolation method (i.e. cu-
bic interpolation). Then, each segment s
i
(with the av-
erage value µ
s
i
) is simply normalised to get zero mean
by subtracting the µ
s
i
from all values of s
i
. This nor-
malisation will invalidate the amplitude of segment
values. It is important while clustering of the seg-
ments, because the segments with the same shape and
treatment would be categorised in the same cluster,
rather than the segments with a similar range of am-
plitudes. The k-means algorithm classifies the pro-
cessed segments of S(var) into k clusters, with the set
of centres O
var
. Then, as described in Section 2.1, the
corresponding sequence of the Prototypical patterns
P(var) is provided as: P(var) : p
1
... p
|S(var)|
, where
p
i
∈ O
var
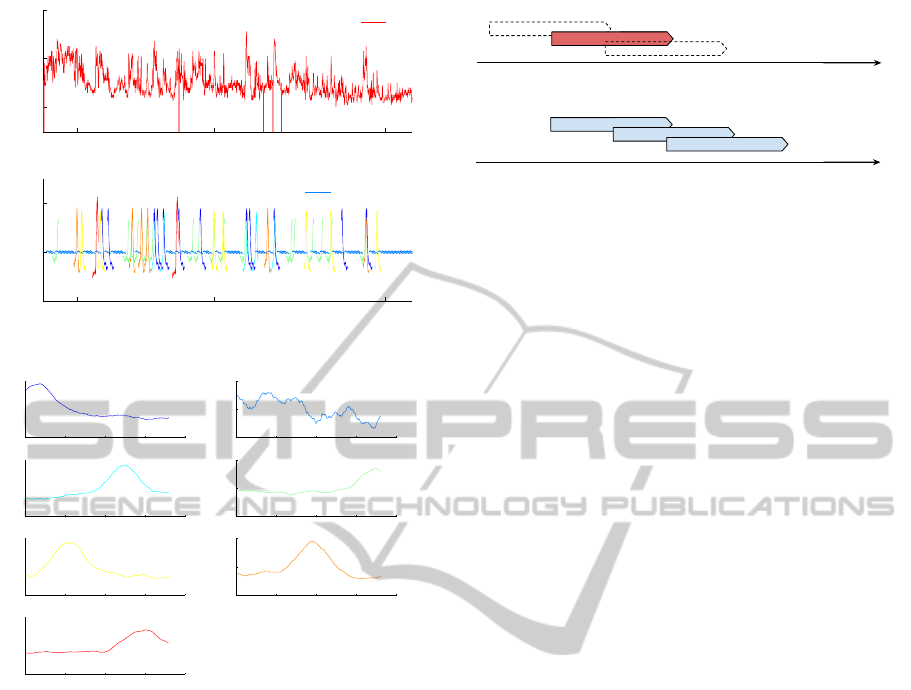
and 1 ≤ i ≤ |S(var)|. Figure 2 shows an
example of heart rate measurement in about 3 hours,
which depicts the extracted sequence of prototypical
patterns (Figure 2(a)), along the centres of the cluster-
ing method (Figure 2(b)), with window size 3 minutes
(|w|=240) and k=7 clusters.
Automatic Rule Generation. So far, there are se-
quences of patterns P
hr
, P
bp
, and P
rr
, obtained from
the prototypical pattern abstraction approach. Now to
find the coherence relation between the occurred pat-
terns among the multi variables, association rule dis-
covery can be applied. In this work, the focus is on the
association rules between two pairs of physiological
time series, heart rate with blood pressure and heart
DescriptiveModellingofClinicalConditionswithData-drivenRuleMininginPhysiologicalData
107
1000 5000 10000
60
80
100
beats/min
sec
HR
1000 5000 10000
−10
0
10
beats/min
sec
Ptterns on HR
(a)
50 100 150 200
−10
0
10
50 100 150 200
−0.5
0
0.5
50 100 150 200
−10
0
10
50 100 150 200
−10
0
10
50 100 150 200
−10
0
10
50 100 150 200
−10
0
10
50 100 150 200
−20
0
20
(b)
Figure 2: An example of physiological time series data,
with abstracted prototypical patterns. (a) raw data of HR
(about 3 hours) with corresponding sequence of patterns,
(b) Centres of clusters (O
hr
) as the prototypical patterns,
with |w|=180, and k=7.
rate with respiration rate. Here, the algorithm is de-
scribed for the first pair and it would be similarly ap-
plied on the second one. Without losing the general-
ity of the algorithms, let’s suppose that this method is
looking for the effect of HR patterns on the behaviour
of patterns in second signal (BP or RR). While con-
sidering the relation of HR and BP patterns, the al-
phabet set of items (I={i
1
,...,i
k×2
}) includes all the
prototypicalpatterns (centres of k clusters) in both HR
and BP, with k×2 members, I = O
hr
∪ O
bp
. As dis-
cussed in section 2.2, the first requirement for asso-
ciation rule discovery is to define the set of transac-
tions. For each pattern p
i
∈ P(hr), the corresponding
transaction d
i
is defined as: d
i
= {p
i
, q
i
, q
i+1
, q
i+2
}
(where q
j
∈ P(bp)), which means when the pattern p
i
occurs in heart rate data, at the same time or just af-
ter that the patterns q
i
, q
i+1
, and q
i+2
appear in blood
pressure data. Figure 3 shows the relational positions
!"#
!$%
!"
#!"
#!"$%
#!"$&
Figure 3: Relational positions of patterns in two sequences
of HR and BP.
of these patterns in their corresponding sequences.
The priori algorithm, introduced in (Agrawal
et al., 1993) is an efficient algorithm for association
rule discovery from a set of transactions D, which ini-
tialises all possible itemsets from the items I and then
determines the support and confidence of each poten-
tial rule like A⇒B in the transactions (where A and
B are two itemsets). This algorithm works based on
the symbolic order of items, so it could destroy the
temporal relations in sequential data. However, in the
proposed approach the temporal relations of the pat-
terns are hidden in the introduced definition of trans-
actions. So, applying the priori algorithm with accu-
rate values for minsup and minconf leads to have a
set of rules (R) as a result, consisting the main repet-
itive behaviours of physiological data in clinical con-
ditions.
3.3 Rule Set Similarity
The main idea to measure the uniqueness of rule sets
is to show that the number of rules from one rule
set which appear in another rule set is very low. It
means that the rules of one clinical class are not re-
peated frequently in other classes. So, they could
potentially represent the individual behaviour of their
clinical condition. For this reason, a novel similarity
function between a pair of rule sets is proposed here,
in order to compare the appearance of rules in another
rule set.
Appearance Ratio. In order to show that how much
the rule sets are different, a similarity measure needs
to compare each pair of rule sets. The overlapping
ratio of rule sets is a basic measure to investigate
the common properties of rule sets (Dudek, 2010).
Suppose there are two rule sets R
1
:{r
1
,...,r
m
} and
R
2
:{r
1
,...,r
n
} including m and n rules, respectively.
The overlapping ratio as a similarity function between
a pair of rule sets is typically defined as:
Overlap(R
1
,R
2
) = |R
1
∩ R
2
| / |R
1
∪ R
2
| (3)
In standard rule association approach with a fix
database of items, counting the intersection of the
HEALTHINF2015-InternationalConferenceonHealthInformatics
108

rules in R
1
and R
2
is uncomplicated, since it is easy
to check the equivalence of rules. Two rules r
i
: A⇒B
and r
j
: C⇒D are equivalent if their corresponding
itemsets are equal: A=C and B=D. But the main is-
sue in the rule sets produced in our approach is that
the items of different rule sets have completely dis-
tinct alphabets of items. In other word, for differ-
ent clinical conditions, there are different sets of pro-
totypical patterns (items), and consequently different
itemsets will be appeared in the final rules. Suppose
that the set of items (patterns) for the rule set R
1
is
I
1
= {i
1
,...,i
l
}, and for the rule set R
2
the set of items
is I
2
= {i
′
1
,...,i
′
l
}, where the items in two sets are
most likely distinct. Therefore, to find the equivalent
rule to r
i
: A⇒B ∈ R
1
in rule set R
2
(if exists), the ap-
proach searches for the closest rule r
′
i
: A
′
⇒B
′
∈ R
2
which is sufficiently similar to r
i
. If r
′
i
exists, then one
overlap is founded between R
1
and R
2
. Algorithm 1
shows how to find the most similar rule r
′
∈ R to an
input rule r. For this aim, the algorithm first finds
the best match patterns A
′
and B
′
from I to the pat-
terns A and B, respectively, and then makes the rule
r
′
: A
′
⇒B
′
. Further, it checks if the rule r
′
exists in
the rule set R. If it exists, that means two rules r and
r
′
are so similar together, and almost derive that the
rule r appears in R as well.
Algorithm 1: RuleMatch(r,R,I)
Finds the best match to the rule r in rule set R.
Data: r:A⇒B, R:{r
1
,...,r
n
} with the set of
items I={i
1
,...,i
l
}.
Result: r
′
:A
′
⇒B
′
, where r
′
∈R and A
′
,B
′
⊂I.
foreach r
i
∈ R do
A
′
← best match patterns to A from I;
B
′
← best match patterns to B from I;
r
′
← A
′
⇒B
′
;
if r
′
∈ R then
return r
′
;
end
end
return
/
0; //rule not found
The method for checking the appearance of a rule
in another rule set leads to define a non-symmetric
similarity measure, called the appearance ratio of
R
1
in R
2
, Appearance
R1
(R2), which represents how
much the rules in R
1
are appeared in R
2
, with consid-
ering their strength in R
2
. It means that while finding
the closest rules of R
2
to the rules in R
1
, the supports
and confidences of matched rules are also involved
in the value of Appearance ratio. The Algorithm 2
presents the details of the computing Appearance ra-
tio measure. If the appearance ratio of a rule set in
another one is high, it means these two rule sets are
meaningfully related to each other. If the ratio is low,
it means there are few connections between the rule
sets, in a sense that these two rule sets are distinct.
Algorithm 2: Appearance(R
1
, R
2
)
Calculates the appearance ratio of of R
1
in R
2
.
Data: Rule set R
1
and rule set R
2
with the set
of items I
2
={i
′
1
,...,i
′
l
}.
Result: Appearance ratio of R
1
in R
2
.
weight ← 0;
weight
R
2
← 0;
foreach r
i
∈ R
1
do
r
′
← RuleMatch(r
i
,R
2
,I
2
);
if r
′
6=
/
0 then
weight ← weight + sup(r
′
)×conf(r
′
);
end
end
foreach r
j
∈ R
2
do
weight
R
2
← weight
R
2
+ sup(r
j
)×conf(r
j
);
end
return weight/weight
R
2
;
4 RESULT AND EVALUATION
This section presents an experimental result of the
rule sets in clinical conditions from MIMIC database
records, with evaluating the uniqueness of generated
rules for each clinical class. This result followed by a
sample output of natural language generation to rep-
resent a textual description of the provided rules.
4.1 Rule Sets for Clinical Conditions
As discussed in Section 3.1 the raw data to test the
proposed approach is fetched from MIMIC numeric
database. The records of three health parameters heart
rate (HR), blood pressure (BP) and respiration rate
(RR) are considered from nine clinical conditions.
According to the phases shown in Figure 1, the pro-
posed algorithm is applied on two pairs of time series:
HR&BP and HR&RR. The important point through
applying the algorithm was the parameter selection.
To select the optimal values of parameters during pat-
tern abstraction and rule generation phases, a voting
approach is used with considering the strength of the
generated rules. Particularly, four measures are ap-
plied to compare the efficiency of association rules.
First, several experiments with various values for pa-
rameters, window size (w: between 1 to 10 minutes),
and number of clusters (k: between 3 and 15 clusters)
have been conducted. Then the provided rules for
each combination of parameters are examined with
the measures: support, confidence, Interest, and J-
measure (Tan et al., 2004). These measures show
DescriptiveModellingofClinicalConditionswithData-drivenRuleMininginPhysiologicalData
109
the quality of a rule in different aspects. By vot-
ing between the top rules with highest values in four
measures, the best values for the parameters are se-
lected as: w=3 minutes and k=7. After rule gen-
eration phase, in order to filter the produced rules,
the minimum support and minimum confidence of the
rules are set to the values 10% and 40%, respectively.
The output model is a collection of rule sets for clin-
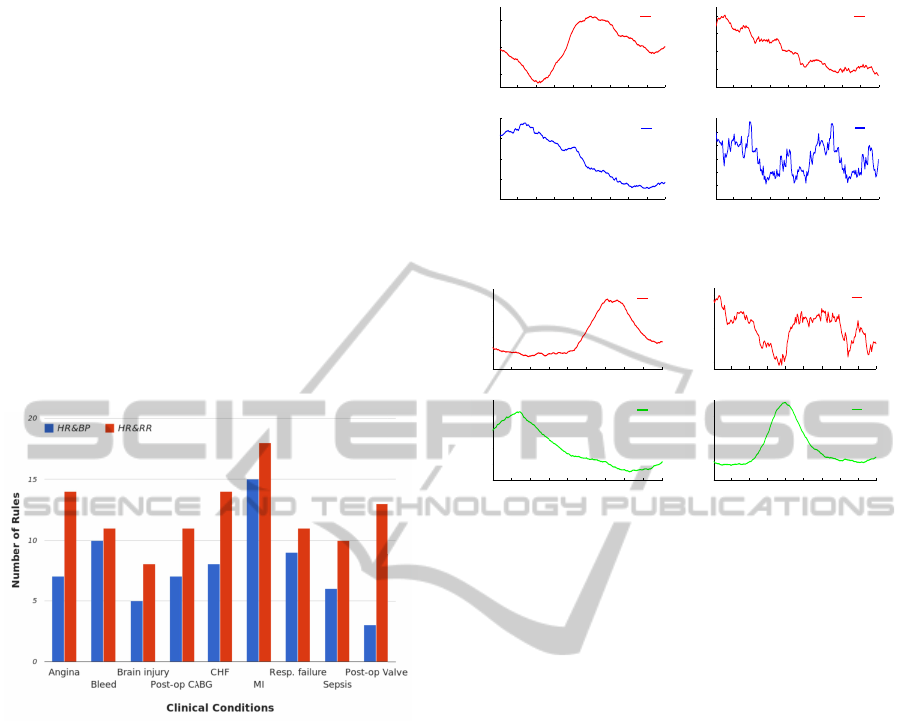
ical conditions. Figure 4 shows the number of pro-
vided rules in relation to the multivariate time series
(HR&BP and HR&RR) in each clinical class. The
output sets of rules specify a data-driven collection
of features which are independently able to describe
their corresponding clinical conditions. A random se-
lection of rules from different rule sets is visually rep-
resented in Figure 5, in order to illustrate the variation
of prototypical patterns among the rules.
Figure 4: The number of rules in each clinical class in rela-
tion to the multivariate time series HR&BP and HR&RR.
4.2 Evaluation of Individual Modelling
This section presents the evaluation of the uniqueness
of rule sets for clinical conditions, in a sense that a
set of rules which are extracted for one clinical class
is differentiable from other sets of rules in the model.
For this reason, the new evaluation method based on
the proposed similarity function in Section 3.3 is ap-
plied to measure the appearance ratio of rules in other
rule sets.
Appearance Ratio of Rule Sets in Clinical Con-
ditions. Based on the rule sets achieved from the
proposed method for clinical conditions, the evalu-
ation approach is applied to each pair of rule sets.
For nine clinical categories, the appearance ratios
for rule sets are calculated. The matrix in Ta-
ble 2 shows the obtained values of appearance ra-
tio for rule sets in HR&RR time series. Since,
the appearance ratio is a non-symmetric similarity
20 40 60 80 100 120 140 160 180
−2
0
2
beats/min
HR
20 40 60 80 100 120 140 160 180
−1
−0.5
0
0.5
1
mmHg
BP
(a) MI, HR&BP, sup=60%,
conf=71%
20 40 60 80 100 120 140 160 180
−4
−2
0
2
4
beats/min
HR
20 40 60 80 100 120 140 160 180
−0.1
−0.05
0
0.05
0.1
mmHg
BP
(b) CABG, HR&BP, sup=50%,
conf=98%
20 40 60 80 100 120 140 160 180
−4
−2
0
2
4
6
beats/min
HR
20 40 60 80 100 120 140 160 180
−4
−2
0
2
4
6
breaths/min
RR
(c) Angina, HR&RR, sup=10%,
conf=52%
20 40 60 80 100 120 140 160 180
−0.05
0
0.05
beats/min
HR
20 40 60 80 100 120 140 160 180
−4
−2
0
2
4
6
breaths/min
RR
(d) Resp. failure, HR&RR,
sup=60%, conf=90%
Figure 5: A selection of rules from the provided rule sets of
clinical conditions for the multivariate time series HR&BP
and HR&RR with the values of support and confidence.
function, the values in Table 2 are not symmetric.
For instance the Appearance
R
Angina
(R
Valve
) is 27%,
whereas Appearance
R
Valve
(R
Angina
) is 9%. The main
reason for this difference in the ratios is that appear-
ance ratio is a weighted function which is calculated
based on the values of supports and confidences of
rules in the second rule set. Therefore, a subset of
rules with strong supports and confidences can appear
in another rule set, but with weak supports and confi-
dences. However, the results in the matrix show that
the ratios of appearing the rules are mostly low.
Figure 6 depicts the boxplot of each row in Table
2, which is graphically presenting that most of the val-
ues are close to the zero ratio. More precisely, close
to 90% of all appearance ratios are lower than 30%,
besides, 70% of them are lower than 15%. So, this
evaluation guarantees the methods generates distinc-
tive rule sets, which the rules in one category of clin-
ical condition can sufficiently provide an individual
behaviour descriptions in vital signs for clinical care.
4.3 Sample Text of Descriptive Rules
Most significant task in representation of rules in nat-
ural language is to characterise the numeric informa-
tion among the rule’s elements. Based on the strength
of a rule, different terms and phrases can be used
HEALTHINF2015-InternationalConferenceonHealthInformatics
110
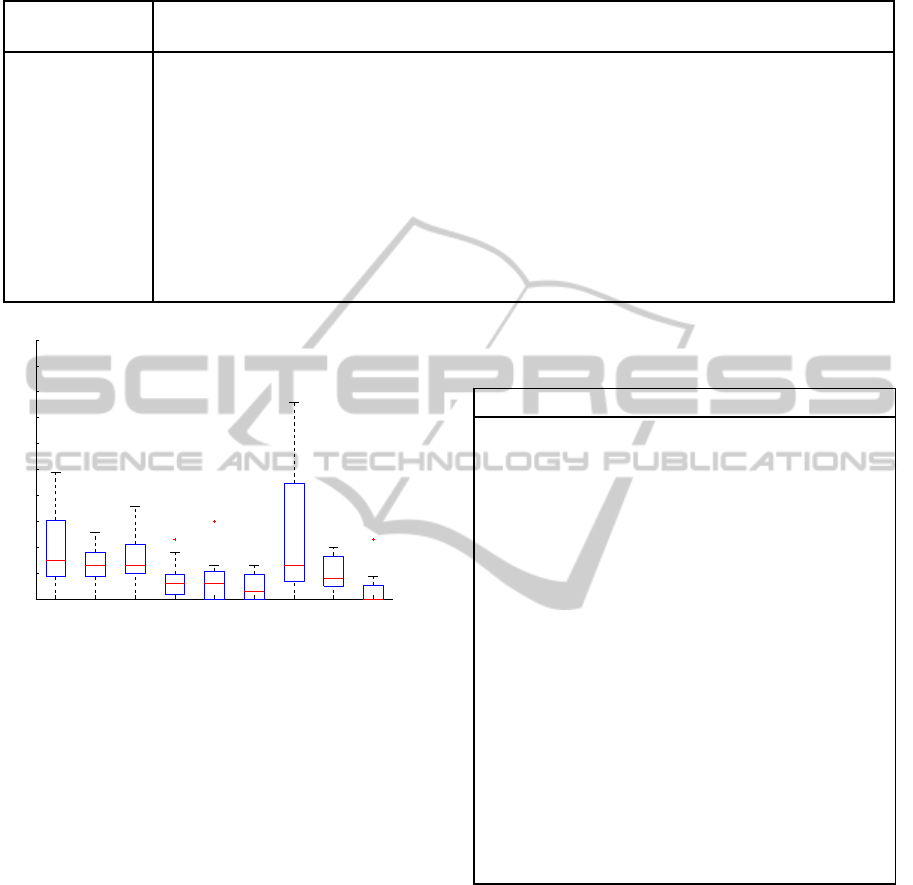
Table 2: The matrix of appearance ratios for each pair of rule sets provided from the clinical conditions in multivariate time
series HR&RR .
Clinical
Conditions
Angina Bleed
Brain
injury
Post-op
CABG
CHF MI
Resp.
failure
Sepsis
Post-op
Valve
Angina - 41% 23% 49% 14% 9% 15% 9%
27%
Bleed
13% - 18% 18% 9% 12% 26% 8%
16%
Brain injury
10% 25% - 36% 10% 13% 13% 14%
20%
Post-op CABG
2% 18% 7% - 6% 6% 2% 4%
23%
CHF
1% 10% 6% 30% - 13% 0% 0%
8%
MI 0% 11% 13% 9% 8% - 1% 3%
0%
Resp. failure 10% 44% 26% 47% 8% 13% - 4%
76%
Sepsis 8% 16% 20% 19% 2% 6% 7% -
8%
Post-op Valve 9% 4% 0% 23% 0% 0% 2% 0%
-
Angina Bleed Brain injury CABG CHF MI Resp. failure Sepsis Valve
0
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
Clinical Conditions
Appearance Ratio
Figure 6: Boxplot of the appearance ratios for each clinical
condition (each row) in Table 2.
in the corresponding sentence. For instance the sen-
tence of a rule with a high confidence value will be
started with the terms like: “most of the time” or “con-
stantly”. Similarly, the partial trends in the patterns of
the rule are represented based on their features and
components, as described in (Banaee et al., 2013b).
In this paper, since the rules are generated to show the
sequential happenings during the whole data, the gen-
eral conditional (if-then) sentence is implemented to
characterise the rule. It is worth to note that in order
to make the final text more natural, different templates
of conditional sentences have been applied (e.g. using
“when” or “after”, instead of “if”). Table 3 shows a
selection textual outputs for the acquired rules in Fig-
ure 5. Each sentence describes a discovered rule 1) to
specify the features of its corresponding clinical con-
dition in text format, and 2) to be understandable for
the end user of the system.
Table 3: A sample textual representation of the acquired
rules in Figure 5.
Rule Output text
Rule 1,
Fig 5 (a)
In MI condition, most of the time,
when heart rate first suddenly in-
creases (5 beats) and then steadily
decreases (2 beats), blood pressure
steadily reduces (2 units).
Rule 2,
Fig 5 (b)
In post-op CABG condition, com-
monly, if heart rate steadily decreases
(8 beats), then blood pressure fluctu-
ates in a very small range.
Rule 3,
Fig 5 (c)
In Angina condition, sometimes,
when heart rate first sharply rises (7
beats) and then steadily falls (6 beats),
respiration rate steadily decreases (9
breaths).
Rule 4,
Fig 5 (d)
In Respiratory failure condition, most
of the time, after heart rate fluctuates
in a very small range, respiration rate
first steadily rises (8 breaths) and then
steadily falls (7 breaths).
5 CONCLUSION AND FUTURE
WORK
Automatic rule generation from physiological sensor
data is still challenging while considering individual-
isation of clinical conditions. This paper presents an
approach of automatic rule mining and representation
from physiological sensor data considering the indi-
vidualisation of clinical conditions. Here, the main
role of rule generation as a data-driven method is to
model the behaviour of prototypical patterns in phys-
DescriptiveModellingofClinicalConditionswithData-drivenRuleMininginPhysiologicalData
111

iological data streams to produce a qualitative set of
rules in clinical settings. This paper addresses 1) rule
mining for modelling sensor data in clinical condi-
tions, 2) individualised modelling of rule sets, and
3) representation of the models in a descriptive tex-
tual output. The proposed approach considers 9 clin-
ical conditions such as angina, sepsis, and respiratory
failure, along three physiological measurements (i.e.
heart rate, blood pressure, and respiration rate). To
evaluate the uniqueness of the provided rule sets, a
novel rule set similarity, appearance ratio, is intro-
duced, which measure the occurrence of rules in other
rule sets. The results on clinical conditions show that
around 90% of all appearance ratios are lower than
30%, besides, 70% of them are lower than 15%. In
this study, a textual representation of the extracted
rules is also considered by applying natural language
generation techniques. However, the semantic mod-
elling based on the rule sets and characterising the
semantic model to improve the quality of text is lim-
ited in this paper. In future, the aim is to apply the
proposed approach in temporal abstraction for more
complex pattern extraction. Moreover, the text output
of descriptive models needs experimental evaluations
in application settings.
REFERENCES
Agarwal, S., Joshi, A., Finin, T., Yesha, Y., and Ganous, T.
(2007). A pervasive computing system for the operat-
ing room of the future. Mobile Networks and Appli-
cations, 12(2-3):215–228.
Agrawal, R., Imieli´nski, T., and Swami, A. (1993). Min-
ing association rules between sets of items in large
databases. In ACM SIGMOD Record, volume 22,
pages 207–216. ACM.
Banaee, H., Ahmed, M. U., and Loutfi, A. (2013a). Data
mining for wearable sensors in health monitoring sys-
tems: a review of recent trends and challenges. Sen-
sors, 13(12):17472–17500.
Banaee, H., Ahmed, M. U., and Loutfi, A. (2013b). A
framework for automatic text generation of trends in
physiological time series data. In Systems, Man, and
Cybernetics (SMC), 2013 IEEE International Confer-
ence on, pages 3876–3881. IEEE.
Buchman, T. G., Stein, P. K., and Goldstein, B. (2002).
Heart rate variability in critical illness and critical
care. Current opinion in critical care, 8(4):311–315.
Cao, H., Eshelman, L., Chbat, N., Nielsen, L., Gross, B.,
and Saeed, M. (2008). Predicting icu hemodynamic
instability using continuous multiparameter trends. In
Engineering in Medicine and Biology Society, 2008.
EMBS 2008. 30th Annual International Conference of
the IEEE, pages 3803–3806. IEEE.
Chen, H., Fuller, S. S., Friedman, C., and Hersh, W.
(2006). Medical informatics: knowledge management
and data mining in biomedicine, volume 8. Springer.
Combi, C. and Sabaini, A. (2013). Extraction, analysis,
and visualization of temporal association rules from
interval-based clinical data. In Artificial Intelligence
in Medicine, pages 238–247. Springer.
Das, G., Lin, K.-I., Mannila, H., Renganathan, G., and
Smyth, P. (1998). Rule discovery from time series.
In KDD, volume 98, pages 16–22.
Dudek, D. (2010). Measures for comparing association rule
sets. In Artificial Intelligence and Soft Computing,
pages 315–322. Springer.
Fu, T.-c. (2011). A review on time series data min-
ing. Engineering Applications of Artificial Intelli-
gence, 24(1):164–181.
Garrard, C. S., Kontoyannis, D. A., and Piepoli, M. (1993).
Spectral analysis of heart rate variability in the sepsis
syndrome. Clinical Autonomic Research, 3(1):5–13.
He, J., Zhang, Y., Huang, G., Xin, Y., Liu, X., Zhang, H. L.,
Chiang, S., and Zhang, H. (2012). An association rule
analysis framework for complex physiological and ge-
netic data. In Health Information Science, pages 131–
142. Springer.
Kotsiantis, S. and Kanellopoulos, D. (2006). Association
rules mining: A recent overview. GESTS Interna-
tional Transactions on Computer Science and Engi-
neering, 32(1):71–82.
Lake, D. E., Richman, J. S., Griffin, M. P., and Moorman,
J. R. (2002). Sample entropy analysis of neonatal
heart rate variability. American Journal of Physiology-
Regulatory, Integrative and Comparative Physiology,
283(3):R789–R797.
Moody, G. B. and Mark, R. G. (1996). A database to sup-
port development and evaluation of intelligent inten-
sive care monitoring. In Computers in Cardiology,
1996, pages 657–660. IEEE.
Muflikhah, L., Wahyuningsih, Y., et al. (2013). Fuzzy rule
generation for diagnosis of coronary heart disease risk
using substractive clustering method. Journal of Soft-
ware Engineering and Applications, 6:372.
Riordan Jr, W. P., Norris, P. R., Jenkins, J. M., and Mor-
ris Jr, J. A. (2009). Early loss of heart rate complexity
predicts mortality regardless of mechanism, anatomic
location, or severity of injury in 2178 trauma patients.
Journal of Surgical Research, 156(2):283–289.
Rutledge, G. W., Andersen, S. K., Polaschek, J. X., and
Fagan, L. M. (1990). A belief network model for
interpretation of icu data. In Proceedings of the An-
nual Symposium on Computer Application in Medical
Care, page 785. American Medical Informatics Asso-
ciation.
Schluter, T. and Conrad, S. (2011). About the analysis
of time series with temporal association rule min-
ing. In Computational Intelligence and Data Mining
(CIDM), 2011 IEEE Symposium on, pages 325–332.
IEEE.
Silverstein, C., Brin, S., and Motwani, R. (1998). Beyond
market baskets: Generalizing association rules to de-
pendence rules. Data mining and knowledge discov-
ery, 2(1):39–68.
HEALTHINF2015-InternationalConferenceonHealthInformatics
112

Sow, D., Turaga, D. S., and Schmidt, M. (2013). Mining of
sensor data in healthcare: A survey. In Managing and
Mining Sensor Data, pages 459–504. Springer.
Tan, P.-N., Kumar, V., and Srivastava, J. (2004). Selecting
the right objective measure for association analysis.
Information Systems, 29(4):293–313.
Warren Liao, T. (2005). Clustering of time series dataa sur-
vey. Pattern recognition, 38(11):1857–1874.
Yoo, I., Alafaireet, P., Marinov, M., Pena-Hernandez, K.,
Gopidi, R., Chang, J.-F., and Hua, L. (2012). Data
mining in healthcare and biomedicine: a survey of the
literature. Journal of medical systems, 36(4):2431–
2448.
DescriptiveModellingofClinicalConditionswithData-drivenRuleMininginPhysiologicalData
113
