
Enumeration of Pareto Optima for a Bicriteria Evacuation Scheduling
Problem
Kaouthar Deghdak, Vincent T’kindt and Jean-Louis Bouquard
Universit
´
e Franc¸ois–Rabelais Tours, Laboratoire d’Informatique (EA 6300)
Equipe Ordonnancement et Conduite (ERL CNRS 6305), 64 Avenue Jean Portalis, 37200 Tours, France
Keywords:
Scheduling Evacuation, Branch and Bound, Greedy Heuristic, Matheuristic.
Abstract:
In this paper, we consider a large-scale evacuation problem after an important disaster. We model the evac-
uation of a region from a set of collection points to a set of capacitated shelters with the help of buses, thus
leading to scheduling the evacuation operations by buses (Bus Evacuation Problem, BEP). The goal is twofold;
first, minimizing the total evacuation time needed to bring the resident out of the endangered region, and sec-
ondly, minimizing the total exposure to danger. The resulting problem is a bicriteria problem. We propose a
time-indexed formulation, as well as several approaches for finding both upper and lower bounds for BEP used
within a branch and bound algorithm. In computational experiments, we analyse and evaluate the efficiency
of the proposed solution algorithms.
1 INTRODUCTION
After a natural disaster the evacuation of people from
endangered region becomes necessary. Evacuating
of urban area is a highly difficult and complicated
task that requires the efficient utilization of the trans-
portation network to facilitate the movement of evac-
uees to safety. The major issue is congestion, which
can cause an extremely dangerous situation and life
threatening. Therefore, the choice of routes on which
people are evacuated is a crucial aspect, which leads
to the success or not, of an evacuation plan. Sev-
eral papers tackle the routing evacuation problem; to
model these problems, network flow approaches or
traffic assignment approaches are used. Early models
focus on building evacuation, as for example (Chal-
met et al., 1982), (Choi et al., 1988) and (Mamada
et al., 2005). We refer the reader to the survey of
(Hamacher and Tjandra, 2001) that discusses evacua-
tion models and methods for building evacuation.
For urban area evacuation, Yamada (Yamada,
1996) models city evacuation as a minimum cost flow
problem to assign the pedestrian evacuees to shel-
ters, knowing that the routes are calculated by solving
shortest path problems. (Lu et al., 2005) use a static
network with time dependent capacity on node as well
as time dependent arc capacity to define an evacua-
tion plan i.e., define routes and timetables to minimize
the total evacuation time. To solve this problem an
heuristic is presented, later on improved after by Kim
et al. (Kim et al., 2007) in terms of running time. Lim
et al. (Lim et al., 2009) propose an evacuation plan
for an urban area in case of an hurricane evacuation.
They use a maximum dynamic flow approach to find
the maximum number of evacuees transported outside
the damaged area within a given time period. A vari-
ety of dynamic network flow problems are considered
for region evacuation in Bretschneider (Bretschnei-
der, 2012). The decision variables in these models are
the evacuees’ flow, the number of lanes in each arc of
the network and the traffic routing. This study focuses
on the routing within intersection nodes and assures
that no crossing conflict occurs. All these models are
solved heuristically.
Dynamic traffic assignment modelling has been
extensively applied to regional vehicle evacuation
problems. The dynamic traffic assignment problems
allow to model time varying flow, different traffic sta-
tus and phenomena, like congestion. (Sattayhatewa
and Ran, 2000) are the first who suggest the use of
the system optimum traffic assignment model in the
evacuation context to minimize either the total evac-
uation time or the travel time between each origin-
destination pair. However, the model has been only
tested in a three-link network. Han et al. (Han et al.,
2006) analyse a different problem which is modelled
as a simple system optimum traffic assignment prob-
lem like the one proposed by Sheffi et al. (Sheffi et al.,
1982). This model allows multiple sources (collection
points) but only a single destination (shelter) and the
162
Deghdak K., T’kindt V. and Bouquard J..
Enumeration of Pareto Optima for a Bicriteria Evacuation Scheduling Problem.
DOI: 10.5220/0005221201620171
In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 162-171
ISBN: 978-989-758-075-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

objective is to minimize the total travel cost for all
evacuees in the network. The cell transmission model
(CTM), introduced by Daganzo (Daganzo, 1994), has
recently obtained significant attention of evacuation
modellers. The basic idea of the CTM is to divide the
network into homogenous cells that can be traversed
by a vehicle in one time period in free flow traffic. The
first one who uses this model is Ziliaskopoulos (Zil-
iaskopoulos, 2000). He proposes a linear model for a
system optimum dynamic traffic assignment problem
with a single sink. Liu et al. (Liu et al., 2006) model a
large scale evacuation problem using the model pro-
posed by (Ziliaskopoulos, 2000). They propose two
evacuation models: in the first model, the goal is to
maximize the number of evacuees reaching the desti-
nation within a given time horizon. The second one
aims at minimizing the total evacuation time. Other
similar studies that use cell transmission models in-
clude the work of Petta and Ziliaskopoulos (Peeta and
Ziliaskopoulos, 2001), and Chiu et al (Chiu et al.,
2007). Interesting studies look at more realistic sit-
uations that capture the uncertain factors of the risk
of a disaster. Yazici and Ozbay (Yazici and Ozbay,
2007) consider uncertain roads capacities while Ng
and Waller (Ng and Waller, 2010) take into consider-
ation the uncertain number of evacuees. These robust
evacuation models are also based on cell transmission
models.
Recently, Bish (Bish, 2011) has introduced and
studied a new model for bus-based evacuation plan-
ning. The choice of buses as a transportation mode
is motivated by the fact that car-based evacuation is
logistically complex, expensive, produces unaccept-
able levels of congestion, and is more dangerous than
bus-based evacuation. To solve the bus evacuation
problem, Bish proposes a mixed integer program and
two heuristics. Goerigk et al. (Goerigk et al., 2013b)
consider a problem closely related to the one dis-
cussed in (Bish, 2011), for which they propose sev-
eral Branch-and-Bound algorithms. Robust bus evac-
uation models have been considered in (Goerigk and
Gruen, 2014) and (Goerigk et al., 2013a).
A recent study is the one conducted by Bretschnei-
der (Bretschneider, 2012) in which she introduces the
multiple commodity evacuation problem using buses
and vehicles. The author proposes a mixed integer
program, where the number of lanes in each arc is
represented by integer variables. The lanes are par-
titioned into public and emergency lanes but only
within intersection. The objective function of the pro-
posed model is to minimize a weighted linear com-
bination of the flows of the commodities arriving at
their corresponding destinations and the total num-
ber of emergency lanes used. This problem is solved
heuristically and the proposed heuristic is only able to
solve small instances in a reasonable amount of time.
The problem adressed in this paper is related to
the one discussed in the paper of Bish (Bish, 2011).
We consider the evacuation of people due to a na-
turel disaster such as an earthquakes, where evacuees
have to change their centre of lives from several days
to several months with the eventual goal of returning
to their respective homes. In particular, we assume
that the locations of shelter (i.e., locations to which
people are evacuated, outside the damaged area), the
locations of collection points (i.e., where people are
gathered waiting to be evacuated) and the capacitated
transportation network are known. The goal is to de-
fine a macroscopic plan of evacuation, implying peo-
ple are considered homogeneously, i.e., the evacuees
are assumed to share the same behaviour and must
be transported from the collection points to the shel-
ters. During the evacuation it is efficient to use roads
that pass through safe area and not through the en-
dangered zone. The evacuees aim is to reach a shelter
without being injured as fast as possible. The evac-
uation is performed by a set of homogeneous buses.
In contrast of the works of Bish (Bish, 2011) and Go-
erigk et al. (Goerigk et al., 2013b), which minimize
the maximum travel time over all buses. We deal with
a bicriteria problem, where the total evacuation time
and the risk exposure of the evacuees are minimized.
The remainder of the paper is organized as fol-
lows. In Section 2, we describe the Bus Evacuation
Problem in details. In Section 3, we provide a mixed-
integer programming formulation. In Section 4, we
present Branch and Bound method, and provide lower
bounds, an upper bound and we discuss branching
rule. Computational results are presented in Section
5. Finally, Section 6 concludes the paper.
2 PROBLEM STATEMENT
Consider a network (N , A), where N and A denote
the set of nodes and edges, respectively. N is com-
posed of two subsets of nodes: P = {1,...,P} and
S = {1,...,S}. P is a set of collection points where
evacuees are initially located, and S is a set of shel-
ters. An edge (k, j) ∈ A exists, iff evacuees can be
transported from collection point k to shelter j. A set
B = {1,. . . ,B} of identical buses is used to evacuate
people. The number of evacuees at every collection
point k is known, and given in terms of integer mul-
tiples of bus loads, denoted by d
k
. Furthermore, we
denote by M = {1,. . .,M} the set of evacuation op-
erations, where M =
∑
k∈P
d
k
. Each operation is also
defined by a collection point at which the correspond-
EnumerationofParetoOptimaforaBicriteriaEvacuationSchedulingProblem
163

ing people to evacuate are located. Any shelter j ∈ S
has a capacity cap
j
expressed as a number of buses
that can bring evacuees. We denote by p
i, j,t
and r
i, j,t
the traveling time and risk value, respectively, of an
evacuation operation M
i
starting at time t from col-
lection point P
k
toward shelter S
j
. The risk values
correspond to the likelihood of buildings collapse or
the risk of congestion network. Travel times and risk
values are time-dependent. This means that they can
be increased or decreased, over time, depending on
the state of the network. This is a consequence of the
evolution of the transportation network through time
due to events such as earthquake aftershocks, road re-
pairs, roads congestion, etc. We consider that such s
events happen at known times t
l
and we define:
p
i, j,t
= p
0
+
a
0
i, j
if t ∈]0,t
1
]
a
1
i, j
if t ∈]t
1
,t
2
]
.
.
.
a
s−1
i, j
if t ∈]t
s−1
,t
s
]
r
i, j,t
=
b
0
i, j
if t ∈]0,t
1
]
b
1
i, j
if t ∈]t
1
,t
2
]
.
.
.
b
s−1
i, j
if t ∈]t
s−1
,t
s
]
where a
x
i, j
and b
x
i, j
are the travel times and the risk
values, respectively, if a bus starts evacuation opera-
tion M
i
from collection point P
k
toward shelter S
j
in
the x
th
time interval, i.e., it’s starting time t ∈]t
x−1
,t
x
].
The number of finite intervals [t
l−1
,t
l
] is determined
by a preliminary forecasting of the evolution of the
transportation network. The constant p
0
is the av-
erage travel time between the shelters and the cen-
ter of the damaged area. This constant is an estima-
tion of the returning time of empty buses. This ap-
proach to defining the p
i, j,t
’s enables us to approxi-
mate and therefore make simpler the bus routing prob-
lem. Throughout the paper, we refer to the scheduling
of evacuation operations as the transportation of evac-
uees from collection points to shelters using buses.
The problem we consider is to find a schedule
such that all evacuees are transported from the collec-
tion points P to the shelters S, minimizing the max-
imum evacuation time denoted by T
evac
and the sum
of the risk values denoted by R. It is important to
notice that criteria T
evac
and R are potentially con-
flicting since the fastest evacuation routes may not be
the safest ones, or because those routes which are the
fastest and the safest have a limited capacities (thus
requiring to use non fastest and safest routes).
In the field of multicriteria optimization, many
methods to compute Pareto front are known (T’kindt
and Billaut, 2006). In this work we use the ε-
constraint approach as follows: the total risk R is min-
imized under the constraint that the maximum evacu-
ation time T
evac
is lower or equal to given value ε. By
solving this problem for different values of ε, the set
of all pareto optima can be computed. In the first step,
ε is equal to the upper bound of the objective func-
tion T
evac
. The solution which is obtained (T
evac
,R)
is added to the set of solutions. We set ε = T
evac
− 1
and iterate. If no solution is obtained, then there is no
feasible solution and the procedure stops.
From practical point of view, solving one ε-
constraint problem, as defined above, makes sense:
the ε value represents a threshold which guarantee
that the evacuation is performed in no more than ε
time units. Then the aim becomes at minimizing the
total risk within that time limit. In this paper we are
interested in enumerating the set of Pareto optima for
criteria T
evac
and R by iteratively solving ε-constraint
problems as defined above. Additionally, while the
evacuation time is a very descriptive value, the total
risk is a more abstract value, and fixing a desired qual-
ity is hardly possible in practice. Thus, this implies
that the other possible ε-constraint problem (minimiz-
ing T
evac
under the constraint R ≤ ε) loses interest.
3 MATHEMATICAL
PROGRAMMING
To model the Bus Evacuation Problem we have
proposed a time-indexed mathematical formulation.
This choice is motivated by the paper of (Bergh-
man et al., 2010), in which various mathematical
formulations for a parallel-machine scheduling prob-
lem are compared. This problem represents a dock
assignment problem which is related to BEP. They
showed that their time-indexed formulation performs
significantly better than other formulations (which
were assignment-based and flow-based). The draw-
back of this formulation is the presence of a pseudo-
polynomial number of variables. Let us turn to the
model for our evacuation problem in which T
exp
evac
is
the desired quality of the criterion T
evac
, T is the time
horizon, and T = {1,...,T } is the set of time points.
The variables are as follows:
∀i ∈ M ,∀ j ∈ S, ∀t ∈ T ;
x
i, j,t
=
1 if a bus starts evacuation operation
i towards j at [t,t + 1[,
0 otherwise.
R : the total risk exposure.
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
164

The proposed (IP) formulation for the ε-constraint
problem, is as follows :
minR (1)
Subject to:
R ≤
∑
t∈T
∑
i∈M
∑
j∈S
x
i, j,t
∗ r
i, j,t
(2)
T
exp
evac
≥ (t + p
i, j,t
)x
i, j,t
∀i ∈ M ,∀ j ∈ S, ∀t ∈ T (3)
∑
t∈T
∑
i∈M
x
i, j,t
≤ cap
j
∀ j ∈ S (4)
∑
i∈M
∑
j∈S
∑
t
0
∈[0,t]
p
i, j,t
0
+t
0
>t
x
i, j,t
0
≤ B ∀t ∈ T (5)
∑
t∈T
∑
j∈S
x
i, j,t
= 1 ∀i ∈ M (6)
x
i, j,t
∈ {0,1} (7)
The objective (1) is to minimize the total exposure
to danger, this objective is calculated using constraint
(2). Constraints (3) define the value of the criterion
T
evac
and ensure the desired quality T
exp
evac
on the ob-
jective T
evac
. Constraints (4) are the shelter capacity
constraints; we cannot exceed the capacities of shel-
ters. Constraints (5) are the bus capacity constraints;
we cannot exceed the number of buses we have. Con-
straints (6) ensure that each operation is processed
once and only once. Constraints (7) are the logical
binary restrictions on the x
i, j,t
variables.
Notice that the bicreteria bus evacuation problem
is N P -hard, as it contains the single criterion bus
evacuation problem as a subproblem (see (Goerigk
and Gruen, 2014)).
4 BRANCH AND BOUND
ALGORITHM
In this section, we focus on the design of an exact
method, a branch and bound algorithm, for solving
the ε-constraint problem. We present hereafter the
different components of this algorithm.
4.1 Branching
The branching rule creates one node for each bus, col-
lection point and shelter with positive residual capac-
ity. In order to construct an optimal solution (in term
of the risk) for the partial sequence in each node, we
have proposed a dynamic programming approach be-
cause we have time dependent data: risk values and
traveling times. This dynamic programming approach
involves the functions F(Seq,t) which represent the
minimal sum of the risk values to process the subse-
quence of operations Seq, while starting the first evac-
uation operation after time t. These functions can be
computed by means of the following recursive equa-
tions:
F(Seq,t) = 0 , if Seq =
/
0, ∀t (8)
F(Seq,t) = min
t
0
∈T
i
and t
0
≥t
i=Seq[1]
F(Seq/{i},t
0
+ p
i, j,t
0
) + r
i, j,t
0
(9)
where Seq[ j] is the operation in the position j in
the sequence Seq, and T
i
is the set of time points,
when the travelling times and the risk values of the
operation i will be change. Notice that the con-
straint (3), which also holds for the subsequence Seq,
can be easily answered by setting to +∞ any value
F(Seq/{i},t
0
+ p
i, j,t
0
) + r
i, j,t
0
as soon as t
0
+ p
i, j,t
0
>
T
evac
.
The optimal value of the total risk for the sequence
Seq of a given bus is then F(Seq, 0). This can be com-
puted in O(k
|Seq|
) time with k = max
i∈seq(|T
i
|)
.
4.2 Lower Bounds
In the following, we present three lower bounds on
the sum of the risk values for an instance of BEP. The
first one is based on the linear relaxation of the BEP
model, the second one is based on a knapsack formu-
lation and the last one is a greedy heuristic. Note that
these three lower bounds can be computed in polyno-
mial time.
LB1. The first and most intuitive lower bound con-
sists in solving the continuous relaxation of the (IP)
model proposed previously. At each node of the
search tree, all the variables already scheduled, i.e.,
the variables of the partial solution are fixed to 0 or
1. Then the relaxed model is solved with the fixed
variables.
LB2. Since knapsack problems are maximisation
problems, we can use an upper bound proposed in the
literature to calculate lower bounds for an instance of
BEP. We can model a simplified version of BEP as a
multiple knapsack problem with the relaxation of the
bus constraints (5) as follows:
EnumerationofParetoOptimaforaBicriteriaEvacuationSchedulingProblem
165

max
∑
l∈M ∗T
∑
j∈S
x
0
l, j
∗ r
0
l, j
(10)
∑
l∈M ∗T
x
0
l, j
≤ cap
j
∀ j ∈ S (11)
x
0
l,t
∈ {0,1} (12)
where all data are positive and integer. Each vari-
able x
0
l, j
,l ∈ M ∗T , j ∈ S, is associated with a variable
x
i, j,t
of the (IP) formulation. Similarly, each value
r
0
l, j
is associated with a risk value r
i, j,t
and is defined
by r
0
l, j
= C − r
i, j,t
, with C a fixed constant such that
C r
u,v,w
, u ∈ M , v ∈ S, w ∈ T . We use the up-
per bound proposed by (Pisinger, 1995), the following
steps are used to calculate the lower bound of BEP:
• At each node and for each bus, we calculate T
opt
evac
of the subsequence of already scheduled opera-
tions. This can be done in polynomial time by
iteratively determining the starting time of the op-
erations in the order they appear in the sequence
of a given bus. The T
opt
evac
is calculated to obtain
the minimum starting time of the unscheduled op-
erations.
• Update the residual capacity cap
j
of shelter j tak-
ing account of the scheduled operations.
• All variables x
0
l, j
related to unscheduled opera-
tions are sorted by non-increasing order of r
0
l, j
.
The first one is then selected and fixed to 1, and
all other variables x
0
u,v
related to the same opera-
tion than the selected variable are removed from
that sorting an fixed to 0. Besides, the residual
capacities are updated.
From the obtained values of the x
0
l, j
’s, we can de-
duce the values of the x
i, j,t
. Then LB2 is calculated
as the sum of the risk for that variables plus the total
risk of the scheduled operation in this node using the
recursive equations (8) and (9).
LB3 This bound is calculated in a similar, but even
simpler, way than LB2, however, here, for the un-
scheduled operations for an incumbent node, we com-
pute r
0
i
= min
j∈S ,t∈T
r
i, j,t
. Then the lower bound on the
risk generated by the unscheduled operations is given
by
∑
r
0
i
.
4.3 Upper Bounds
UB. To construct a feasible solution of BEP, we pro-
pose a local search method called matheuristic. The
general idea of matheuristics is to exploit the strength
of both metaheuristic algorithms and exact methods
as well, leading to a hybrid approach (Della Croce
et al., 2014).
As any local search method, we need to construct
a feasible solution, which will be improved after-
ward using the matheuristic. For this, we develop
two greedy approaches. These approaches are used
to enumerate the Pareto front. Figure 1 presents the
general algorithm of the proposed greedy heuristic,
which takes upon entry a sequencing rule R and the
desired value of the total evacuation time T
exp
evac
. Let
oprlist be the set of the evacuation operations that
will be assigned on buses, sortlist(i,j) be the set of
sorted operations according to the rule R at a given
time t, feassortlist(i, j) be the set of operation from
sortlist(i, j) for which LB
T
evac
< T
exp
evac
, T
b
evac
be the to-
tal evacuation time of a bus b, and R
b
the sum of the
risk values accumulated when the bus is used. The
greedy heuristic’s solution is stored in schedulelist.
Each operation added in schedulelist will be deleted
from oprlist, sortlist(i,j) and feassortlist(i, j).
The function event, presented in the pseudo code
of the greedy algorithm (Figure 1), checks if there
is an event requiring to recalculate the priority list
sortlist. Each rule R has a specific event func-
tion. Notice that an external archive, referred to as
nondominated, is maintained through different calls
of the greedy heuristic. This archive contains the
set of Pareto optima computed so far. Also the
greedy heuristics are ran for different values of T
exp
evac
.
Each time, for a given T
exp
evac
value, a greedy heuris-
tic finds a feasible solution schedulelist, the function
UpdateArchive() is called to update the current set of
Pareto optima. If schedulelist is not dominated by a
solution from nondominated, then it is added to that
set. If a solution from nondominated is dominated by
schedulelist then it is removed from the archive.
In the following, we have tested two greedy
heuristic versions.
1. Version 1: this version uses rule R
1
. The evacua-
tion operations are sorted according to increasing
order of the risk value r
i, j,t
.
2. Version 2: this version uses rule R
2
. In this rule,
evacuation operations opr
i
are sorted by increas-
ing order of their values
r
i, j,t
r
1
N
∑
S
j=1
∑
T
t=1
(r
i, j,t
−¯r
i, j,t
)
2
,
where the denominator is the standard deviation
of the risk value associated to operation i. Using
this rule, we would like to ensure that if an opera-
tion opr
i
has a small risk value at t and after this
time the risk value for this operation will be huge,
then it is preferable to schedule opr
i
at time t.
In these two versions, the function event returns
true if there are modifications in the values of
evacuation operations’ risk.
Let there be an initial heuristic solution given as
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
166
Generic Algorithm (R )
Input: /* A sorting rule R , T
exp
evac
*/
schedulelist ←
/
0, sortlist ←
/
0
oprlist ← {opr
1
,opr
2
,....,opr
M
}
t ← 0, k ← B, f easible ← f alse
Arrange operations of oprlist in the sortlist(i,j) using
the rule R
Repeat
Arrange operations in feassortlist(i,j) from sortlist;
if |feassortlist| < k and |sortlist| > 0 then
f easible ←false;
else
f easible ←true;
Add the k first operations in schedulelist(i,j,t)
from feassortlist ;
Delete the k operations added in schedulelist from
oprlist, sortlist and feassortlist ;
if t=0 then k ← 0;
Let b ∈ B be a bus with the minimum T
b
evac
;
t ← T
b
evac
;
k ← k +1;
if event() then
sortlist ←
/
0 ;
Arrange operations from oprlist in sortlist(i,j)
using the rule R ;
end if
end if
Until |oprlist| = 0 and t > T and f easible =true
UpdateArchive(schedulelist).
Figure 1: Greedy-Heuristic algorithm.
one pareto optima solution obtained by the greedy
heuristics. We use the time-indexed formulation
introduced in Section 3 to construct a matheuris-
tic for BEP. The matheuristic tries to improve that
solution by exploring its neighborhood as follows.
Let be a feasible schedule (heuristic solution) ¯x =<
¯x
i jt
,i ∈ M , j ∈ S,t ∈ T >, where ¯x
i, j,t
= 1, if oper-
ation i is goes to shelter j at time t. We define a
neighberhood N ( ¯x,r, h) by choosing a date r in the
schedule and a size parameter h. Let
˜
S(r,h) be the
index set of the operations starting in the time inter-
val [r, r + h[. We call such a subset of operations an
”operation-window” and is denoted by w.
The best solution in the neighbourhood N (¯x, r,h)
is computed by minimizing the sum risk R
w
, subject
to (3)-(7) and by adding the following constraint:
x
i, j,t
= ¯x
i, j,t
∀i /∈
˜
S(r,h),∀ j ∈ S,t ∈ [0, r[ (13)
We call this reduced minimization problem the
window reoptimization problem, and it is solved to
optimality by a mathematical solver such as CPLEX.
The additional constraints (13) forces the changes to
occur within the operation-window. If we have an im-
provement in R
w
, then, in the new solution ˜x, all of the
operations that started after the time r +h in the initial
solution ¯x will be left time shifted keeping their pre-
vious positions and respecting the bus-constraint (5).
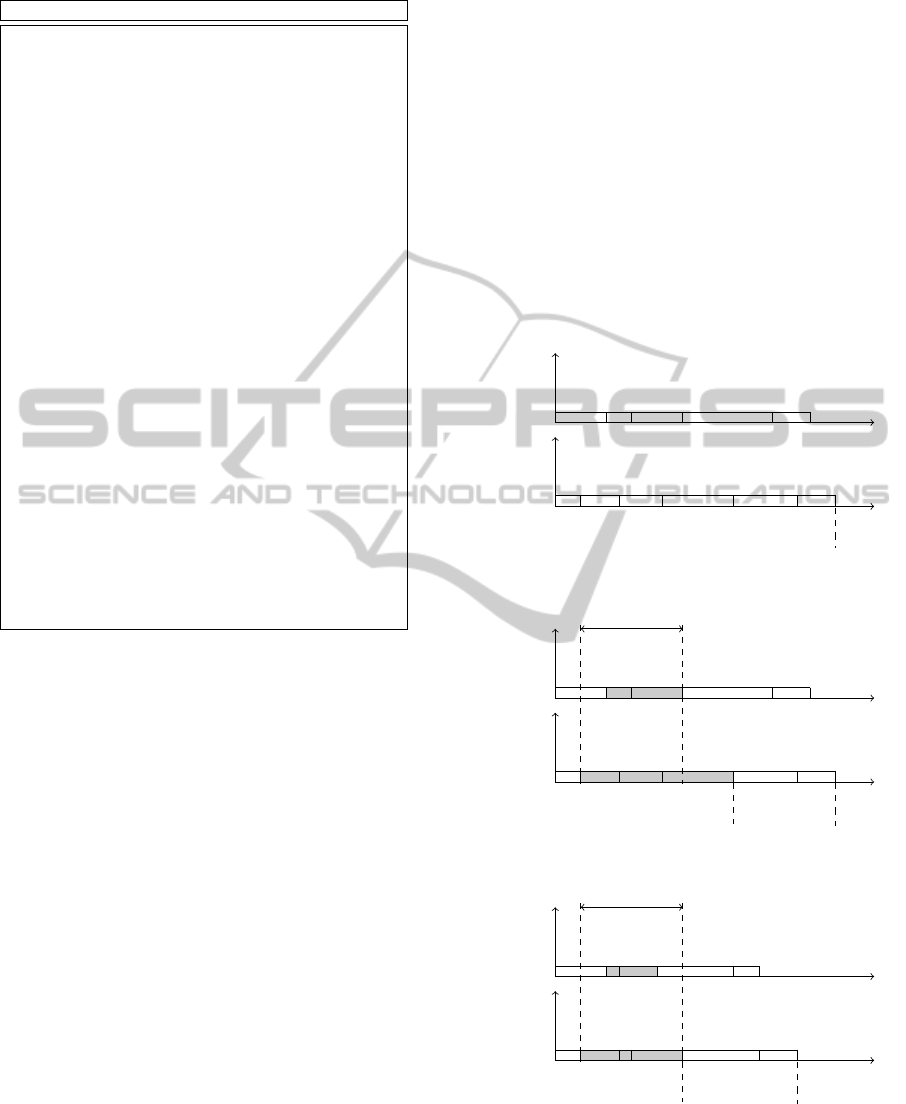
The idea is sketched in figure 2.
If no improved solution is found, first we test
using the function UpdateArchive(), if this solu-
tion is nondominated by another solution in the
nondominated set. If so, this solution will be added to
nondominated set. Second, a new operation-window
(i.e., new value of r) is selected to be optimized,
and so on until all possible windows have been se-
lected. The search is stopped if no window reop-
timization problem has an optimal solution solution
that improves the current solution or if a predefined
time limit is exceeded.
Bus2
Bus1
t
t
T
evac
= 17
R = 50
0
0
3
3
8
4
9
10
13
2
1
2
6
7
9
5
11
7 11
16
15
5
4
(a) the current solution ¯x
Bus2
Bus1
t
t
T
evac
= 17
R = 50
0
0
3
3
8
4
9
10
2
13
1
2
6
7
9
5
11
7 11
16
T
evac
= 11
R
w
= 30
r + h
5
4
(b) the operation-window
Bus2
Bus1
t
t
T
evac
= 15
R = 43
0
0
3
3
9
6
6
10
2
11
1
2
7
4
8
5
11
5
13
13
15
T
evac
= 9
R
w
= 20
r + h
4
4
(c) the neighbor ˜x
Figure 2: Example of operations window reoptimized.
Example 1. Consider the example of Figure 2. We
have two shelters, eleven operations and two buses
EnumerationofParetoOptimaforaBicriteriaEvacuationSchedulingProblem
167

available (bus 1 and bus 2). The current solution
is depicted in Figure 2(a): operations 3, 8, 4, 10,
and 2 are processed by Bus 1 and operations 1, 6
,7, 9, 5, and 11 are processed in Bus 2. The start-
ing time of the operation-window is r = 2 and the
size of this window is h = 7 (Figure 2(b)). The to-
tal evacuation time of this solution is T
evac
= 17, the
total risk is R = 50, the maximum evacuation time
of the operation-window is T
w
evac
= 11 and the total
risk of the operation-window is R = 30. The solution
obtaining ˜x from the neighbourhood, after the win-
dow reoptimization problem has been solved, is given
in Figure 2(c). The figure shows that both the total
risk, the maximum evacuation time of the operation-
window, the maximum evacuation time and the total
risk of the whole schedule have been reduced. Op-
erations 5, 10, 2, and 11 have been left time shifted
keeping their previous positions. The total risk values
and the maximum evacuation time of the new solution
are T
evac
= 15 and R = 43, respectively.
The algorithm of the matheuristic is given in Figure
3.
The Matheuristic Algorithm
Input:
¯x =<heuristic solution calculated by greedy algoritthm>.
vect =<vector of starting times of all operations in ¯x >.
nondominated =<set of the pareto optima solutions >.
Repeat
Set improved ← f alse;
Set i ← 0;
Repeat
r ← vect[i] ;
˜x ← Neighborhood( ¯x, r, h)
if ( R( ¯x) > R( ˜x) and T
evac
( ¯x) ≥ T
evac
( ˜x)) then
¯x ← ˜x
improved ← true
For r ← r + h to T
evac
− r + h do
¯y ← Neighborhood( ¯x, r,h)
if (R( ¯x) > R( ¯y) and T
evac
( ¯x) ≥ T
evac
( ¯y)) then
¯x ← ¯y
else UpdateArchive( ¯y)
end if
end For
recompute vect from ¯x
else i ← i + 1
UpdateArchive( ˜x)
end if
Until i ≥ |vect| or improved or time limit expired
Until not improved or time limit expired
Return the nondominated set nondominated.
The Neighborhood Procedure
Calculate
˜
S(r,h);
Reschedule operations in tha time window [r,r + h[ by
minimizing R
w
( ¯x) subject to (2)-(7), and (13);
Let ˜y be the solution obtained;
Return solution ˜y.
Figure 3: The matheuristic algorithm.
5 EXPERIMENT RESULT
In this section, we focus on the experimental evalua-
tions of the (IP) solution, the heuristic algorithms, and
on the branch and bound algorithm. We first describe
how the experimentation has been configured.
Environment. All experiments were run on a com-
puter with a 4-core Intel processor, running at 2.60
GHz with 20MB cache, 8 GB RAM and Windows 7.
We wrote our code in C++ , and used the commercial
IP solver CPLEX v.12.6. CPLEX was pinned to one
core for the solution of the time-indexed formulation
in order to be consistent with the branch and bound
algorithm.
Dataset. This work is partly a research project,
called DSS-Evac-Logistic, and was partially granted
by the French research agency ANR. In this project,
we consider the real-world instance of Nice (France),
as a case study. Therefore, the datasets are randomly
generated in such a way that we always have feasible
and realistic instances for the city of Nice. The num-
ber of shelter S takes values {2, 4, 6, 8, 10} and the
capacity cap
j
of each shelter draws at random from
{20, 21, 22,..., 40}. The number of collection points
P takes values {10, 20, 30, 40} and the number of
evacuees d
i
waiting on the collection point i is gener-
ated randomly from the following:
1
4
0.9
∑
j
cap
j
P
;
7
4
0.9
∑
j
cap
j
P
This generation ensures that the total evacuees’
number M is fewer than the total shelters’ capacity.
We assume that the time period of evacuation is [D,
D+1[, where D is the day of disaster. In the following,
we set time discretization as one-quarter hour, which
implies that T is equal to 192 quarters.
We assume that we have five events happening
after time 0 and changing the value of the opera-
tions’ traveling times and risks. To do so, we gen-
erated two degradation dates: T
D
1
,T
D
2
∈[0, 192[, com-
mon to all evacuation operations, and three improve-
ment dates: T
A
1
∈ U[0,T
D
1
],T
A
2
∈ U]T
D
1
,T
D
2
], T
A
3
∈
U]T
D
2
,192[, specific to each evacuation operation.
Operations’ travelling times are drawn randomly from
{2,3,4, ..., 8} and operations’ risk values are gener-
ated randomly from [0, 10], where the value 0 means
that roads are completely safe, whilst the value 10
means that roads are very dangerous. Finally, the
number of buses B =
∑
d
l
∗
¯
P
180
, where ¯p is the average
traveling time, which ensures that we have enough
buses to accomplish the evacuation in 180 quarters of
an hour.
We generate 20 instances for each couple (P ,S).
For each instance, we run the following algorithms:
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
168

• Exact Solution Algorithms: we have tested the
solution of the (IP) model by CPLEX solver. In
the remainder of the paper, this solution algorithm
will be denoted by IP. We also refer to B&B as
the solutions of the Branch and Bound algorithm
using the LB1, LB2 and LB3, simultaneously as
follows: In the top of the three it is clear that LB1
outperform LB1 and LB2, for this reason in the
first level of the search tree we calculate in each
node only the LB1. For the remainder of level
tree, in each node we compute first the LB3, if we
cannot prune this node we calculate then the LB2,
this may be lead to cut this node.
Notice that we impose a time limit of 2000 sec-
onds and a memory limit of 1 GB per instance
and algorithm.
• Heuristic Algorithm:
– For each pareto optima obtained by the greedy
heuristic, we have tested the matheuristic with a
time limit of 600 seconds. Previous preliminary
experimentations have shown that the best re-
sults are obtained with the window size h = 30.
In what follows, we will call reference set RS, the
set of pareto optima obtained by CPLEX, approxima-
tion MAS and HAS sets obtained by matheuristcs and
greedy heuristic algorithms, respectively. In order
to compare the solution obtained by the matheuris-
tic against the solutions delivered by CPLEX, we use
the quality measures proposed in (Jaszkiewicz, 2004).
As defined in (Jaszkiewicz, 2004) we use the follow-
ing metrics:
The first metric is to evaluate the quality with
which the set AS of points approximates the nondom-
inated set MRS
Q
1
(MAS) =
|MAS ∩RS|
|RS|
The second metric is a ratio of points in the approxi-
mation set that are nondominated points
Q
2
(MAS) =
|MAS ∩RS|
|MAS|
The third metric tends to measure the distance be-
tween the nondominated set of a reference set and the
solutions of the approximation set. In other words, the
measure is the average distance from each reference
set to its closest neighbour in AS.
Q
3
(MAS) =
1
|RS|
∑
r∈RS
min
z∈MAS
{d(z,r)}
Q
3
(HAS) =
1
|RS|
∑
r∈RS
min
z∈HAS
{d(z,r)}
where d(..,..) denotes Euclidean distance in the ob-
jectives space.
The last metric aim to see the dispersion of the
nondominated set points.
Q
4
(MAS) =
∑
z
i
,z
i+1
∈MAS
{d(z
i
,z
i+1
)}
|MAS| − 1
−
∑
r
i
,r
i+1
∈RS
{d(r
i
,r
i+1
)}
|RS| − 1
Q
4
(HAS) =
∑
z
i
,z
i+1
∈HAS
{d(z
i
,z
i+1
)}
|HAS| − 1
−
∑
r
i
,r
i+1
∈RS
{d(r
i
,r
i+1
)}
|RS| − 1
Table 1 presents the average values of metrics
Q
3
and Q
4
. The reference sets are obtained by
CPLEX and the approximation sets are obtained by
the matheuristic or greedy heuristics. Column #oprs
presents the number of evacuation operations, column
#shel reports the number of shelters, column #bus
presents the number of buses, and column #inst tot
presents the number of instances for each problem
size. Notice that the instances are randomly generated
based on a number of collection points and a number
of shelters. However, the size of the instances solved
by CPLEX, B&B and Matheuristic depends on the to-
tal number of evacuation operations, i.e.,
∑
i
d
i
. Con-
sequently, after having generating instances we gath-
ered them in classes of ”equivalent size instances” but
in term of number of evacuation operations, number
of shelters and number of buses.
First, notice that the average values of Q
3
(MAS)
are very small then the average values of Q
3
(HAS)
especially when the number of shelter equal to two,
which means that matheuristic improve the quality of
the solutions obtained by the greedy heuristic. On the
other hand, according to the metric Q
4
, we observe
that for all instances, matheuristic helps to spread the
points in the objectives space. Moreover, matheuris-
tic allows to approach the approximate set obtained
by the greedy heuristic to the reference set delivred
by the IP. Notice that the average values of the met-
rics Q
1
and Q
2
is always equal to 0.
Table 1: Evaluation of the matheuristic.
#oprs #shel #bus #inst
Q3(moy) Q4(moy)
HAS MAS HAS MAS
[20,35[ 2 [1,2] 32 71,33 37.91 -32,82 -6,29
[35,40[ 2 2 17 73,02 38.04 -26,18 -3,17
[40,60[ 2 [2,3] 31 83,73 43.39 -36,98 -5,80
[40,60[ 4 [2,3] 6 90,63 20,43 -92,92 -90,85
[60,70[ 4 3 13 93,43 50,25 -100,56 -93,96
[70,80[ 4 [3,4] 18 114,9 62,35 -88,43 -57,67
[80,90[ 4 4 27 132,3 100,57 -120,6 -100,6
[90,110[ 4 [4,5] 18 171,5 155,32 -147,9 -120,50
Table 2 presents the running times and the num-
ber of explored nodes of the IP and B&B. Columns
IP (time(s)) report the average and the maximum run-
ning times of CPLEX when enumerating the non-
dominated set. Similarly, B&B columns report the
EnumerationofParetoOptimaforaBicriteriaEvacuationSchedulingProblem
169

Table 2: Comparison of running times and number of explored nodes.
#oprs #shel #bus #inst tot
# solved opt IP (time(s)) B&B(time(s)) #nodes (IP) #nodes(B&B)
IP B&B avg max avg max avg max avg max
[20,35[ 2 [1,2] 32 7 2 2000 2000 2000 2000 9781 84290 27370 139800
[35,40[ 2 2 17 3 0 2000 2000 2000 2000 7930 12390 17600 84760
[40,60[ 2 [2,3] 31 2 0 2000 2000 2000 2000 12260 209600 2070 115500
[40,60[ 4 [2,3] 6 0 0 545 560 2000 2000 0 0 45,17 70
[60,70[ 4 3 13 0 0 522,3 2000 2000 2000 0 0 27,77 32
[70,80[ 4 [3,4] 17 0 0 590,5 2000 2000 2000 0 0 19,65 22
[80,90[ 4 4 26 0 0 599,5 2000 2000 2000 0 0 16,58 18
[90,110[ 4 [4,5] 18 0 0 636 2000 2000 2000 0 0 12,86 14
CPU times for B&B enumeration approach. Col-
umn #solved opt presents the number of instances
that have been solved to optimality by IP and B&B.
Additionally, the number of explored nodes is also
reported. As the results in Table 2 illustrate, when
the number of shelter equals 2, both IP and B&B
spend the time limit to enumerate the nondominated
set. Furthermore, for some instances, IP is very effec-
tive; it is able to enumerate the exact nondominated
set for 12 instances, while the B&B to enumerate the
exact nondominated set for two instances. In addi-
tion, the IP explores fewer nodes than the B&B algo-
rithm. Unfortunately, when the number of operations
is larger than 40, in some cases, IP fails to produce
feasible solutions due to the imposed memory limit,
hence, the number of explored nodes is always equal
to 0 and the CPU times is less than 2000 seconds. We
can also observe that the number of explored nodes by
the B&B are significantly decreased, it is interpreted
by the fact that the continuous relaxation of the (IP)
using to calculate LB1 is very slow.
From Table 2, we can conclude that the IP outper-
formed the B&B in some instance when the number
of shelter equal to 2. But the IP fails to give feasible
solution due to memory limit for more larger instance.
We can also conclude that the B&B will be compet-
itive if we use two new lower bound more effective
than the three lower bounds proposed in this paper.
6 CONCLUSION
In this work, we have studied the Bicriteria problem
of scheduling evacuation operations which we have
called the bus evacuation problem (BEP). To enumer-
ate the exact nondominated sets, we have provided
a time-indexed formulation (IP) for this problem and
B&B algorithm. Computational experiment shows
that for most instances, neither the IP nor the B& B
can enumerate the exact nondominated sets. Next, we
have provided two heuristics, the first one is a set of
greedy heuristics. The second one is a local search
called matheuristic based on the mathematical formu-
lation provided, which improves the greedy heuristic
solutions.
Future investigation needs to be done in order to
implement in a real-life situation the proposed heuris-
tic algorithms. They will be used in an off-crisis con-
text as a tool for designing an evacuation plan. A key
issue is now to capture the preferences of the end user
in order to select, from the approximated set of Pareto
optima, the solution to implement.
ACKNOWLEDGEMENTS
This research has been supported by ANR-11-SECU-
002-01, project DSS EVAC LOGISTIQUE (CSOSG
2011).
REFERENCES
Berghman, L., Leus, R., and Spieksma, F. (2010). Optimal
solutions for a dock assignment problem with trailer
transportation. FBE Research Report KBI 1010,
pages 1–28.
Bish, D. R. (2011). Planning for a bus-based evacuation.
OR Spectrum, 33(3):629–654.
Bretschneider, S. (2012). Mathematical Models for Evacu-
ation Planning in Urban Areas. Springer- Heidelberg
New York Dordrecht London.
Chalmet, L., Francis, R., and Saunders, P. (1982). Net-
work models for building evacuation. Fire Technol-
ogy, 18(1):90–113.
Chiu, Y.-C., Zheng, H., Villalobos, J., and Gautam, B.
(2007). Modeling no-notice mass evacuation using a
dynamic traffic flow optimization model. IIE Trans-
actions, 39(1):83–94.
Choi, W., Hamacher, H., and Tufekci, S. (1988). Model-
ing of building evacuation problems by network flows
with side constraints. European Journal of Opera-
tional Research, 35(1):98 – 110.
Daganzo, C. F. (1994). The cell transmission model: a
dynamic representation of highway traffic consistent
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
170

with the hydrodynamic theory. Transportation Re-
search Part B, 28(4):269.
Della Croce, F., Grosso, A., and Salassa, F. (2014). A
matheuristic approach for the two-machine total com-
pletion time flow shop problem. Annals of Operations
Research, 213(1):67–78.
Goerigk, M., Deghdak, K., and T’Kindt, V. (2013a). A
two-stage robustness approach to evacuation planning
with buses. Technical report, Technische Universit
¨
at
Kaiserslautern.
Goerigk, M. and Gruen, B. (2014). A robust bus evacuation
model with delayed scenario information. OR Spec-
trum, pages 1–26.
Goerigk, M., Gruen, B., and Hessler, P. (2013b). Branch
and bound algorithms for the bus evacuation problem.
Computers & Operations Research, 40(12):3010–
3020.
Hamacher, H. W. and Tjandra, S. A. (2001). Mathematical
modeling of evacuation problems: A state of the art. In
In Pedestrian and Evacuation Dynamics (Schreckin-
berg, M. and Sharma, S. D. eds), volume 1964, pages
227–266. Springer.
Han, L. D., F.Yuan, Chin, S.-M., and Hwang, H. (2006).
Proposed framework for simultaneous optimization
of evacuation traffic destination and route assign-
ment. Transportation Research Record: Journal of
the Transportation Research Board, 1964(1):50 – 58.
Jaszkiewicz, A. (2004). Evaluation of multiple objec-
tive metaheuristics. In Metaheuristics for Multiobjec-
tive Optimisation, volume 535, pages 65–89. Springer
Berlin Heidelberg.
Kim, S., B.George, and Shekhar, S. (2007). Gis ’07: Pro-
ceedings of the 15th annual acm international sympo-
sium on advances in geographic information systems.
New York, NY, USA. ACM.
Lim, G., S.Zangeneh, Baharnemati, M., and Assavapokee,
T. (2009). A simple binary search algorithm for short
notice evacuation scheduling and routing.
Liu, Y., Lai, X., and Chang, G. (2006). Two-level inte-
grated optimization system for planning of emergency
evacuation. Journal of Transportation Engineering,
132(10):800–807.
Lu, Q., George, B., and Shekhar, S. (2005). Capacity con-
strained routing algorithms for evacuation planning:
A summary of results. In Bauzer Medeiros, C., Egen-
hofer, M., and Bertino, E., editors, Advances in Spa-
tial and Temporal Databases, volume 3633 of Lecture
Notes in Computer Science, pages 291–307. Springer
Berlin Heidelberg.
Mamada, S., Uno, T., Makino, K., and Fujishige, S. (2005).
A tree partitioning problem arising from an evacuation
problem in tree dynamic networks. J Oper Res Soc
Jpn, 48(3):196–206.
Ng, M. and Waller, S. T. (2010). Reliable evacuation plan-
ning via demand inflation and supply deflation. Trans-
portation Research Part E: Logistics and Transporta-
tion Review, 46(6):1086 – 1094.
Peeta, S. and Ziliaskopoulos, A. K. (2001). Foundations
of dynamic traffic assignment: the past, the present
and the future. Networks and Spatial Economics, 1(3-
4):233.
Pisinger, D. (1995). Algorithms for knapsack problems.
Sattayhatewa, P. and Ran, B. (2000). Developing A Dy-
namic Traffic Management Model For Nuclear Power
Plant Evacuation. Transportation Research Board,
79th Annual Meeting.
Sheffi, Y., Mahmassani, H. S., and Powell, W. (1982). A
transportation network evacuation model. Transporta-
tion Research Part A, 16(1):209–218.
T’kindt, V. and Billaut, J.-C. (2006). Multicriteria schedul-
ing: theory, models and algorithms. Springer-Verlag
Berlin Heidelberg, 2nd edition.
Yamada, T. (1996). A network flow approach to a city emer-
gency evacuation planning. International Journal of
Systems Science, 27(10):931–936.
Yazici, M. and Ozbay, K. (2007). Impact of probabilistic
road capacity constraints on the spatial distribution of
hurricane evacuation shelter capacities. Transport Res
Rec: J Transport Res Board, 2022(1):55–62.
Ziliaskopoulos, A. K. (2000). A linear programming model
for the single destination system optimum dynamic
traffic assignment problem. Transportation Science,
34(1):37–49.
EnumerationofParetoOptimaforaBicriteriaEvacuationSchedulingProblem
171
