Multiagent Planning by Plan Set Intersection and Plan Verification
Jan Jakub
˚
uv, Jan To
ˇ
zi
ˇ
cka and Anton
´
ın Komenda
Agent Technology Center, Department of Computer Science, Czech Technical University, Prague, Czech Republic
Keywords:
Multiagent Planning, Action Landmarks, Plan Verification, Process Calculi, Type Systems, Delete Relaxation.
Abstract:
Multiagent planning is a coordination technique used for deliberative acting of a team of agents. One of vital
planning techniques uses declarative description of agents’ plans based on Finite State Machines and their
later coordination by intersection of such machines with successive verification of the resulting joint plans.
In this work, we firstly propose to use projections of agents’ actions directly for multiagent planning based
on iterative building of a coordinated multiagent plan. Secondly, we describe integration of the static analysis
provided by process calculi type systems for approximate verification of exchanged local plans. Finally, we
compare our approach with current state-of-the-art planner on an extensive benchmark set.
1 INTRODUCTION
Intelligent agents requested to act together in a team
require to some extent an ability to plan their actions
in advance. If the agents prepare complete plans to-
wards their goals, the problem they have to solve is a
form of multiagent planning.
Similarly to classical planning, our multiagent
planning approach assumes STRIPS (Fikes and Nils-
son, 1971) actions, which are deterministic and de-
scribed by precondition and effects on the environ-
ment they are executed in. Thereby, the action state
progression follows the STRIPS principles as well.
Although the action model is STRIPS, the com-
plete multiagent planning model is subsequent to a
recent extension of STRIPS by Brafman & Domshlak
called MA-STRIPS (Brafman and Domshlak, 2008).
In MA-STRIPS, the agents are cooperative with com-
mon goals and the resulting multiagent plan pre-
scribes their coordinated acting from the initial state
of the environment towards the goals. The agents are
heterogeneous with different capabilities described by
their STRIPS actions. Straightforwardly, their actions
define parts of the environment they can affect and
this gives rise to their local planning problems. Con-
veniently, this (partial) “separation of concerns” helps
to increase efficiency of the planning process and pro-
vides intrinsic separation of public information the
agents have to share and internal facts, which can be
kept private.
The multiagent planning approach proposed in
this work extends recent works by To
ˇ
zi
ˇ
cka, et al.
on representation of multiagent plans in form of Fi-
nite State Machines and their merging (To
ˇ
zi
ˇ
cka et al.,
2014b) and plan generation using diverse planning
with homotopy class constraints with testing of us-
ability of partial plans among the agents by compila-
tion into planning landmarks (To
ˇ
zi
ˇ
cka et al., 2014a).
In this work, we initially propose to use a pro-
jections of actions (Nissim and Brafman, 2012) di-
rectly for multiagent planning, which was in the lit-
erature used so far only in relaxation heuristic es-
timations (
ˇ
Stolba and Komenda, 2014). The main
improvement is based on integration of theory and
analysis provided by process calculi and their type
systems. Concretely, we use generic process calculi
type system scheme POLYV (Makholm and Wells,
2005; Jakub
˚
uv and Wells, 2010) for approximate ver-
ification of foreign plans received from other agents,
which prospectively increases efficiency of search
for coordinated multiagent plans. Finally, we com-
pare our approach with current state-of-the-art plan-
ner FMAP (Torre
˜
no et al., 2014) on an extensive
benchmark set.
2 MULTIAGENT PLANNING
We consider a number of cooperative and coordinated
agents featuring distinct sets of capabilities (actions)
which concurrently plan and execute their local plans
in order to achieve a joint goal. The environment
wherein the agents act is classical with deterministic
actions. The following formal preliminaries restate
173
Jakub˚uv J., Toži
ˇ
cka J. and Komenda A..
Multiagent Planning by Plan Set Intersection and Plan Verification.
DOI: 10.5220/0005222101730182
In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART-2015), pages 173-182
ISBN: 978-989-758-074-1
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

the MA-STRIPS problem (Brafman and Domshlak,
2008) required for the following sections.
2.1 Planning Problem
An MA-STRIPS planning problem Π is defined as a
quadruple Π = hP, {A
i
}
n
i=1
, I, Gi, where P is a set of
facts, A
i
is the set of actions of i-th agent, I ⊆ P is
an initial state, and G ⊆ P is a set of conditions on
the goal states. Given Π, we use A to denote all the
actions from Π, that is, A =
S
n
i=1
A
i
.
An action an agent can perform is a triple of sub-
sets of P which in turn denote the set of preconditions,
the set of add effects, and the set of delete effects.
Selector functions pre(a), add(a), and del(a) are de-
fined so that a = hpre(a), add(a), del(a)i. Moreover
let eff(a) = add(a) ∪ del(a).
An agent is identified with its capabilities, that is,
an agent α = A
i
= {a
1
, . . . , a
m
} is characterized by a
finite repertoire of actions it can perform in the envi-
ronment. We use metavariables α and β to range over
agents from Π. A planning state s is a finite set of
facts and we say that fact p holds in s iff p ∈ s. When
pre(a) ⊆ s then state progression function γ is defined
classically as γ(s, a) = (s \ del(a)) ∪ add(a).
2.2 Public and Internal Classification
In multiagent planning each fact is classified either
as public or as internal out of computational or pri-
vacy concerns. MA-STRIPS specifies this classifica-
tion as follows. A fact is public when it is mentioned
by actions of at least two different agents. A fact is
internal for α when it is not public but mentioned by
some action of α. A fact is relevant for α when it
is either public or internal for α. Relevant facts con-
tain all the facts which agent α needs to understand,
because other facts are internal for other agents and
thus not directly concerns α. Given Π, the set pub of
public facts, and sets int(α) and rel(α) of facts inter-
nal and relevant for α are formally defined as follows.
Let facts(a) = pre(a) ∪ add(a) ∪ del(a) and similarly
facts(α) =
S
a∈α
facts(a).
pub =
S
α6=β
(facts(α) ∩ facts(β))
int(α) = facts(α) \ pub
rel(α) = pub ∪ int(α)
It is possible to extend the set of public facts to
contain additionally some facts that would be inter-
nal by the above definition. It is common in litera-
ture (Nissim and Brafman, 2012) to require that all the
goals are public. Then pub is defined as the minimal
superset of the intersection from the definition that
satisfies G ⊆ pub. In the rest of this paper we suppose
G ⊆ pub and also another simplification common in
literature (Brafman and Domshlak, 2008) which says
that A
i
are pairwise disjoint
1
.
MA-STRIPS further extends this classification of
facts to actions as follows. An action is public when
it has a public effect (that is, eff(a) ∩ pub 6=
/
0) , oth-
erwise it is internal. Strictly speaking, MA-STRIPS
defines an action as public whenever it mentions a
public fact even in a precondition (that is, when
facts(a) ∩ pub 6=
/
0). However, as our approach does
not rely on synchronization on public preconditions,
we can consider actions with only public precondi-
tions as internal. For our approach it is enough to
know that internal actions do not modify public state.
2.3 Local Planning Problems
In MA-STRIPS model, agent actions are supposed to
manipulate a shared global state when executed. In
our approach to multiagent planning, a local planning
problem is constructed for every agent α. Each local
planning problem for α is a classical STRIPS problem
where agent α has its own internal copy of the global
state and where each agent is equipped with informa-
tion about public actions of other agents. These local
planning problems allow us to divide an MA-STRIPS
problem to several STRIPS problems which can be
solved separately by a classical planner. This paper
describes a way to find a solution of an MA-STRIPS
problem but it does not address the question of execu-
tion of a plan in some real-world environment.
The projection F  α of an arbitrary set F ⊆ P of
facts to agent α is the restriction of F to the facts rel-
evant for α, that is, F  α = F ∩ rel(α). Projection
removes from F facts not relevant for α and thus it
represents F as understood by agent α. The projec-
tion a  α of action a to agent α removes from a facts
not relevant for α, again representing a as seen by α.
a α = hpre(a) α, add(a)  α, del(a) αi
Note that a  α = a when a ∈ α. Hence projection to
α alters only actions of other agents.
In the multiagent planning approach presented
in this paper, every agent α is from the beginning
equipped with projections of other agents public ac-
tions. These projections, which we call external ac-
tions, describe how agent α sees effects of public ac-
tions of other agents. Given Π, the set ext(α) of ex-
1
These two conditions rules out private goals and joint
actions. Any MA-STRIPS problem which does not satisfy
the two conditions can be translated to an equivalent prob-
lem which satisfies them. However, a solution that would
take advantage of private goals and joint actions is left for
future research.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
174

ternal actions of agent α is defined as follows.
ext(α) = {a α : a is a public action of β 6= α}
Recall that A denotes the set of all the actions from
Π. The set A  α contains actions of α plus external
actions it is defined as follows.
A α = α ∪ ext(α)
Now it is easy to define a local planning problem
Π α of agent α also called projection of Π to α.
Π α = hP  α, A  α, I  α, Gi
2.4 Plans and Extensibility
We would like to solve agent local problems sepa-
rately and compose local solutions to a global solu-
tion of Π. However, not all local solutions can be
easily composed to a solution of Π. Concepts of pub-
lic plans and extensibility helps us to recognize local
solutions which are conductive to this aim.
A plan π is a sequence of actions ha
1
, . . . , a
k
i. A
plan π defines an order in which the actions are exe-
cuted by their unique owner agents. It is supposed that
independent actions can be executed in parallel. A so-
lution of Π is a plan π whose execution transforms the
initial state I to subset of G. A local solution is a so-
lution of a local planning problem. Let sols(Π) and
sols(Π α) denote the set of all solutions of a given
problem.
A public plan σ is a plan that contains only pub-
lic actions. A public plan can be seen as a solution
outline that captures execution order of public ac-
tions while ignoring agents internal actions. In order
to avoid confusions between public and external ver-
sions of the same action, we suppose that actions are
annotated with unique ids which are preserved under
projection. From now on we consider public plans to
be sequences of public action ids.
Let operator ·

construct a public plan from plan
π, that is, let π

be the sequence of all public action
ids from π preserving their order. A public plan σ is
called extensible iff it be can extended to a solution of
Π by insertion of internal actions of any agent, that is,
iff there is π ∈ sols(Π) such that π

= σ. A public plan
is called α-extensible iff it can be extended to a local
solution of Π α by insertion of internal actions of α,
that is, iff there is agent α’s plan π
α
∈ sols(Π  α) such
that π

α
= σ.
The following proposition states the correctness
of the used approach to multiagent planning. Its di-
rect consequence is that to find a solution of Π it is
enough to find a local solution π
α
∈ sols(Π  α) which
is β-extensible for every other agent β. A constructive
proof can be found in (To
ˇ
zi
ˇ
cka et al., 2014a).
Proposition 1. Let public plan σ of Π be given. Pub-
lic plan σ is extensible if and only if σ is α-extensible
for every agent α.
3 PLANNING STATE MACHINES
This section briefly restates the previous work
by (To
ˇ
zi
ˇ
cka et al., 2014b) our work is based on,
while its extensions, which are the main contribu-
tions of this paper, are described in following sec-
tions. We use nondeterministic finite state machines
(NFS) (Hopcroft et al., 2006) as a compact represen-
tation of a set of solutions of a STRIPS problem. We
call an NFS that represents a set of solutions a plan-
ning state machine (PSM).
A planning state machine (PSM) of a STRIPS
problem Π = hP, A, I, Gi is a NFS Γ = hA, S, I, δ, Fi
where the alphabet A is the set of actions of Π, states
from S are subsets of P, the state transition function
δ resembles the classical STRIPS state progression
function γ, and F ⊆ S contains all the states that sat-
isfies goal G. To avoid confusions, we suppose that
alphabet A contains unique action ids rather than full
actions. The only requirement
2
on the state transition
function δ is that δ(s, a) = γ(s, a). It is possible to con-
struct a complete PSM that contains all possible states
and transitions. A complete PSM of Π represents ex-
actly all the solutions of Π. As the computation of
a complete PSM can be inefficient, we also consider
partial PSMs which represents only a subset of all so-
lutions.
For every PSM Γ we can construct its public pro-
jection PSM Γ

that represents public projections of
the solutions. When Γ represents the set of solu-
tions S we want Γ

to represent exactly the set {π

:
π ∈ S}. Once we have a PSM for every agent’s lo-
cal planning problem Π α, we can compute public
projections of these PSMs and intersect them using a
well-known intersection algorithm for NFS (Hopcroft
et al., 2006). Any public solution σ in a non-empty
intersection constitutes a public solution of the orig-
inal MA-STRIPS problem Π. That is because σ is
α-extensible for every α (as it comes from the inter-
section) and thus extensible by Proposition 1.
Figure 1 provides an example PSM Γ
1
demon-
strating PSM public projection algorithm. First, PSM
Γ
2
is obtained from the input Γ
1
by renaming internal
actions to ε-transitions and eliminating them by the
2
Although a PSM as defined here suggests a determinis-
tic finite state machine, a non-deterministic transitions can
be introduced by public projection defined later. Thus we
prefer to work with non-deterministic machines from the
beginning.
MultiagentPlanningbyPlanSetIntersectionandPlanVerification
175

(Γ
1
) (Γ
2
) (Γ
3
)
Figure 1: Example of computing PSM public projec-
tion (To
ˇ
zi
ˇ
cka et al., 2014b). We suppose a context where
pn are public and in internal actions, and where a, b, c are
public and x, y internal facts.
intersection algorithm (Hopcroft et al., 2006). Sec-
ond, the public projection Γ
3
of Γ
1
is obtained from
Γ
2
by projecting states (removing internal facts) and
by unification of states with equal public projection.
Hence Γ

1
= Γ
3
. When two states with equal pub-
lic projection differ in outgoing edges then they can
not be unified and an integer mark is introduced to
distinguish them. Note that if the two states {a}-0
and {a}-1 were unified in Γ
3
, then the resulting PSM
would also represent a public plan hp1, p4, p5i which
does not correspond to any plan from Γ
1
.
Algorithm 1 provides an overview of a distributed
algorithm (To
ˇ
zi
ˇ
cka et al., 2014b) to find a solution
of an MA-STRIPS problem. We suppose that every
agent α executes PsmPlanDistributed in a separate
process, possibly on a separate machine. We suppose
that agent processes can communicate with each other
by sending structured messages. Every agent α starts
with an empty PSM Γ
α
which contains only the ini-
tial state of Π α. In every loop iteration, every agent
generates a new plan of its local problem Π α and
it adds this plan to Γ
α
. Then public projection Γ

α
is
computed and exchanged with other agents. The eas-
iest way to implement PSM projections exchange is
when every agent sends its projection to every other
agent. The projections can also be exchanged in a
round-robin manner. The loop in the algorithm con-
tinues until the intersection
T
β
(Γ

β
) is not empty. The
operation written in bold italics is an optional exten-
sion described in Section 5.
By a new plan in the first step we mean a plan that
was not generated in any of the previous iterations.
To achieve this we have modified an existing planner
FastDownward
3
so that it is able to generate a plan
which differs from plans provided as an input. This
extension is inspired by diverse planning with homo-
topy class constraints (Bhattacharya et al., 2010). Ho-
motopy classes of plans are naturally defined by their
3
http://www.fast-downward.org/
Algorithm 1: Distributed algorithm to find a solution
of MA-STRIPS problem Π.
Function PsmPlanDistributed(Π α) is
Γ
α
← empty PSM (initial state of Π  α);
loop
generate a new plan π
α
of Π α;
analyse plan π
α
(Sec. 5);
extend Γ
α
with π
α
;
compute public projection Γ

α
of Γ
α
;
exchange PSM public projections;
if intersection
T
β
(Γ
pub
β
) 6=
/
0 then
return the intersection;
end
create landmarks from plans;
end
end
public projections, that is, two plans belong to same
homotopy class iff they have equal public projection.
In the last step of the loop, other agents plans are
incorporated into the local planning problem Π  α
using the principle of prioritizing actions and soft-
landmarks. Prioritizing actions are implemented us-
ing action costs so that internal actions are preferred
to public actions, and α’s public actions are preferred
to other agent actions. When agent α finds a new local
solution it sends its public projection to all the other
agents. Other agents then extend their local problem
Π β to contain duplicated landmark actions from the
received plan. These landmark actions have signifi-
cantly decreased cost and they are interlinked using
additional facts to ensure they are used in the order
suggested by the public plan. See (To
ˇ
zi
ˇ
cka et al.,
2014a) for details.
4 PLANNING CALCULUS
In this section we show how classical planning can
be expressed as a process calculus. Furthermore we
show how to use existing process calculi type systems
for static analysis of classical planning problems and
how to use this static analysis for approximation of
planning problem solvability. In the next section, this
static analysis will be incorporated into the multiagent
planning algorithm from the previous section (Algo-
rithm 1).
4.1 Planning as Process Calculus
A typical process calculus is defined by a set of pro-
cesses together with a binary rewriting relation (→)
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
176

on these processes. Processes describe possible sys-
tem states while the rewriting relation describes possi-
ble transitions between states. Hence Q
0
→ Q
1
means
that the system can be transformed (in one step) from
the state described by Q
0
to state Q
1
.
Process calculi are usually used to model concur-
rent environments where several units (processes) en-
gage in activity at the same time. Processes usually
take form of programs and thus system states are iden-
tified with programs currently running in the system,
while rewriting relation captures program evaluation.
Processes are usually constructed from atomic
processes using standard operators. In this paper, we
will use only the parallel composition operator (“|”).
Process “Q
0
| Q
1
” describes a system where processes
Q
0
and Q
1
are running in parallel. We will also use
standard null or inactive process denoted “0”. Par-
allel composition is considered commutative and as-
sociative with 0 being an identity element (that is,
Q | 0 = Q).
Given a STRIPS problem Π with set of facts P, we
use facts p ∈ P as atomic processes. Hence our pro-
cesses correspond to planning states while the rewrit-
ing relation emulates action application by adjusting
state (process) appropriately. The set of our processes
is generated by the following grammar.
Q ::= 0 | p | (Q
0
| Q
1
)
That is, null process 0 is a process, every fact p is a
process, and other processes can be constructed using
parallel composition. Function dse encodes a state as
a process.
d{p
1
, p
2
, . . . , p
n
}e = p
1
| p
2
| ··· | p
n
| 0
Furthermore, to simplify the presentation we consider
processes to be equal modulo fact duplications (that
is, “(p | p) = p” and so on).
The rewriting relation → is the minimal relation
which satisfies the following rules.
a ∈ A
dpre(a)e → dγ(pre(a), a)e
Q
0
→ Q
1
Q
0
| Q
2
→ Q
1
| Q
2
Recall that the state progression function γ for action
a applied to the state pre(a) is defined as follows.
γ(pre(a), a) = (pre(a)\ del(a)) ∪ add(a)
Hence the first rule says that, for every action a,
the process dpre(a)e can be rewritten to the process
dpre(a)e with delete effects removed and add effects
added. The second rule is a context rule which al-
lows us to apply rewriting in the presence of addi-
tional facts. The following formally states that the
rewriting relation → correctly captures planning ac-
tion execution.
Proposition 2. Let Π = hP, A, I, Gi be a classical
STRIPS problem such that del(a) ⊆ pre(a) for every
action a ∈ A. For any two planning states s
0
and s
1
the following holds.
ds
0
e → ds
1
e iff ∃a ∈ A : γ(s
0
, a) = s
1
The requirement that every action deletes only
facts mentioned in its preconditions (del(a) ⊆ pre(a))
is necessary because the right-hand side of a rewriting
rule can refer only to processes mentioned on the left-
hand side. This requirement simplifies formal presen-
tation while it does not restrict usability because prob-
lems not fulfilling the requirement can be translated
4
to equivalent problems which do so. Moreover, it is
usually satisfied in practice.
4.2 Planning Calculus Type System
In this section we show how to use existing pro-
cess calculi type systems for static analysis of plan-
ning problems. Type systems for processes calculi
are used to prove various properties of processes.
A type system is usually handcrafted for a specific
calculus and thus we can not use an arbitrary type
system for our planning process calculus. However,
there is a generic process calculi type system scheme
POLYV (Makholm and Wells, 2005) which works for
many calculi including ours. Furthermore, POLYV
has already been successfully used for static analysis
(Jakub
˚
uv and Wells, 2010).
A detailed description of POLYV is beyond the
scope of this paper and thus we provide only a nec-
essary background. POLYV provides a syntax to de-
scribe rewriting rule axioms. Here we just state that
rewriting rules from the previous section can be eas-
ily described in this syntax. Once rewriting rules are
given, POLYV automatically derives syntax of types
together with a type system for the given calculus.
Furthermore, an effective type inference algorithm is
provided to compute a principal (most general) type
of an arbitrary process.
For our purposes, it is enough to state that a
POLYV type τ for our planning process calculus can
be understood as a set of facts. POLYV defines a typ-
ing relation, written ` Q : τ, which states that Q has
type τ. The most important property of the typing re-
lation is subject reduction which ensures that types
are preserved under rewriting, that is, when ` Q
0
: τ
and Q
0
→ Q
1
then ` Q
1
: τ. Another property that in-
terests us is that whenever ` Q : τ then τ contains all
4
Briefly, for a delete effect p 6∈ pre(a), we can introduce
a new fact p
−
complementary to p and then provide two
rewriting rule axioms for a; the first applies in states where
p holds while the second in states where p
−
holds.
MultiagentPlanningbyPlanSetIntersectionandPlanVerification
177

the facts mentioned in Q. In particular, ` dse : τ im-
plies s ⊆ τ for any state s.
The previous paragraph suggests the following
procedure. Given a STRIPS problem Π = hP, A, I, Gi,
we can use POLYV to compute the principal type τ
of the initial state process dIe. Hence ` dIe : τ. Be-
cause types are preserved under rewriting, we know
that whenever dIe rewrites using an arbitrary many
applications of → to some process Q, then also ` Q : τ.
In other words, whatever state s is reachable from I,
we know that s ⊆ τ. Hence when G 6⊆ τ then Π is
not solvable. The opposite implication, which would
also allow us to recognize solvable problems, does
not generally hold because POLYV type τ only over-
approximates all reachable states.
In this way we can use POLYV types to recognize
some unsolvable problems. We instantiate POLYV
by translating actions to rewriting rules, and we use
POLYV to compute the principal type τ of dIe. When
G 6⊆ τ then the problem is clearly unsolvable. Other-
wise we can not conclude anything. This is the price
we pay for effectiveness as POLYV types can be com-
puted in polynomial time while planning is PSPACE-
complete.
Our experiments have shown that POLYV type
analysis is essentially equivalent to computing a plan-
ning graph with the delete effect relaxation. The
POLYV type contains exactly the same facts as the
last layer of a relaxed planning graph. A possible
extensions of POLYV analysis that would give more
precise results than relaxed planning graphs are left
for future research. One of the advantages of using
POLYV over relaxed planning graphs is in that we can
rely on its already proved formal properties (subject
reduction, principal typings) and that there is no need
to implement equivalent methods because an effective
type inference algorithm is already implemented.
5 PSM WITH PLAN ANALYSIS
This section describes improvements from the ba-
sic version of Algorithm 1 denoted in bold italics in
the algorithm. We introduce two different methods
(PSM+ and PSMV) to incorporate the static analysis
from the previous section into our PSM-based plan-
ner (Algorithm 1). The static analysis is used to an-
alyze plans at the second line of the loop in the al-
gorithm. Section 5.1 describes an encoding of an α-
extensibility check into a planning problem, which is
a technique shared by both the methods. It basically
restates our previous work (To
ˇ
zi
ˇ
cka et al., 2014a) re-
quired for the understanding of the next sections. Sec-
tions 5.2 and 5.3 describe in turn the methods PSM+
and PSMV.
5.1 Plan Extensibility as Planning
First we describe how the static analysis from the
previous section can be used to approximate α-
extensibility of public plan σ. This is done by running
the static analysis on a classical planning problem Π
σ
constructed as follows. Problem Π
σ
is similar to Π α
but it contains only a subset of its actions. Concretely,
Π
σ
contains all the internal actions of α but only those
public or external actions which are mentioned in σ.
Furthermore, actions from σ are interlinked using ad-
ditional facts to ensure they are executed in the order
suggested by σ. Formally, let a
i
be the action from
A α which corresponds to the i-th action in σ. Let
mark
0
, . . . , mark
n
be additional facts (n is the length
of σ). Then Π
σ
contains the following action b
i
.
b
i
= h pre(a
i
) ∪ {mark
i−1
},
add(a
i
) ∪ {mark
i
},
del(a
i
) ∪ {mark
i−1
} i
Finally mark
0
is added to the initial state of Π
σ
and
mark
n
is added to the goal state. When action b
i
is used, the mark is increased which enables action
b
i+1
. In the end we want all b
i
’s to be used, pos-
sibly interleaved with some α-internal actions which
are just added to Π
σ
without any additional changes.
It can be proved that Π
σ
is solvable iff σ is α-
extensible (To
ˇ
zi
ˇ
cka et al., 2014a).
5.2 Simplified Plan Analysis (PSM+)
The previous section suggests the following plan ver-
ification procedure. When agent α generates a new
plan π
α
, it sends its public projection π

α
to all the
other agents. Once other agent β receives π

α
, it
uses the static analysis to check whether π

α
is β-
extensible. That is, agent β constructs Π
σ
(for σ = π

α
)
and executes the POLYV analysis yielding the type τ.
When G 6⊆ τ then agent β informs α that π

α
is not
β-extensible. Otherwise agent β returns an unknown
status back to agent α.
Once the initiator agent α receives back results
from all the other agents it simply checks whether π

α
was rejected by, that is, found not β-extensible for, at
least one agent. When the plan is rejected by at least
one agent, then agent α simply drops the plan and
directly continues with the next loop iteration by gen-
erating another plan. Optionally, agent α can incor-
porate plans generated by other agents as landmarks
(last operation in the loop) provided these plans were
not rejected.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
178

5.3 Partial Plan Reuse (PSMV)
Experiments with PSM+ showed that plan analysis
had increased the number of solved problems when
compared to the basic variant PSM without any plan
analysis. However, there were some problems solved
by PSM which were no longer solved by PSM+. A
more detailed analysis revealed that in some cases a
useful landmark was created from the beginning of a
plan that was rejected in PSM+. This is because it
can happen that a rejected plan is correct up to some
point. The method introduced in this section tries to
find a usable plan prefix and use it as a landmark.
The procedure starts as in the previous section,
that is, agent α generates a new plan π
α
and sends
its public projection π

α
to all the other agents. Once
Π
σ
is constructed by other agent β, the POLYV anal-
ysis of Π
σ
is executed yielding the type τ. When the
last mark mark
n
is not in τ, not only we know that
σ is surely not β-extensible, but the maximum mark
present in τ gives us other insight into σ. Hence type
τ is examined and the maximum i such that mark
i
∈ τ
is found. From that we can conclude that it is not pos-
sible for β to follow the public plan σ to a state where
the (i + 1)-th action of σ can be executed. Hence this
maximum i is returned as a result of β’s analysis of σ
back to agent α.
Finally, agent α collects analysis results from all
the other agents and computes their minimum j. Plan
σ is then stripped so that only the first j actions re-
main in it. This stripped plan is then sent to the other
agents to be used as a landmark and to guide future
plan search.
6 EXPERIMENTAL RESULTS
We have performed a set of experiments to evaluate
an impact of plan verification on a PSM-based plan-
ner and also to compare our planners with another
state-of-the-art multiagent planner
5
. We have decided
to compare our approach with FMAP (Torre
˜
no et al.,
2014) which uses well defined problems taken from
International Planning Competition (IPC) problems.
FMAP classifies facts as public or internal using a
manual selection of public predicate names. In prac-
tice, FMAP public facts are a superset of MA-STRIPS
public facts and thus FMAP classification is compat-
ible with our algorithms. In our experiments we use
exactly the same input files as the authors of FMAP
5
All the tests were performed on a single PC, CPU In-
tel i7 3.40GHz with 8 cores, and memory limited to 8GB
RAM.
Table 1: Number of problems solved by the compared plan-
ners.
Domain FMAP
PSM PSM+ PSMV
Blocksworld (34) 19 27 26 26
Driverlog (20) 15 10 9 14
Elevators (30) 30 1 3 4
Logistics (20) 10 0 0 0
Openstacks (30) 23 30 30 30
Rovers (20) 19 7 14 14
Satellite (20) 16 6 13 9
Woodworking (30) 22 27 27 27
Zenotravel (20) 18 17 17 17
Total (224) 172 125 139 141
used during its evaluation
6
, and we also use the same
time limit of 30 minutes for each problem. The binary
and source codes of our PSM-based planner are avail-
able on demand. Please contact us by email in order
to obtain them.
Table 1 shows an overall coverage of solved prob-
lems. We can see that the FMAP has better results
in most of the domains and also in the overall cov-
erage. Nevertheless PSM+ performed better in two
tightly-coupled domains as it was able to solve all the
Openstacks problems and two additional Woodwork-
ing problems over FMAP. We can see that PSMV out-
performs PSM+ in Driverlog and Elevators domains
but it loses in Satellite domain. Moreover, there were
eight other differences in individual problems, where
half of them in each domain were in favor of each
method and thus these differences are not reflected in
the table. The results show that a possible enhance-
ment of POLYV verification could bring even higher
coverage. This will be part of our future research.
Also note that PSMV is strictly better in coverage
7
than the basic variant PSM.
For a more detailed analysis of PSM variants we
have chosen three domains with the highest coverage.
Table 2 shows an average number of iterations and run
times needed to find a solution for problems which
were solved by all the three variants. Sequential times
show how long it would take if all the agents share a
single CPU, while the parallel time correspond to a
6
We would like to thank the authors of FMAP for a kind
support with their planner.
7
However, there were still two individual problems
which were solved by PSM but not by PSMV. As this hap-
pens relatively rarely, it is left for future research to find
out whether this is because of the approximation in POLYV
analysis or whether it can happen that in some cases a useful
landmark is constructed from a rejected plan part.
MultiagentPlanningbyPlanSetIntersectionandPlanVerification
179

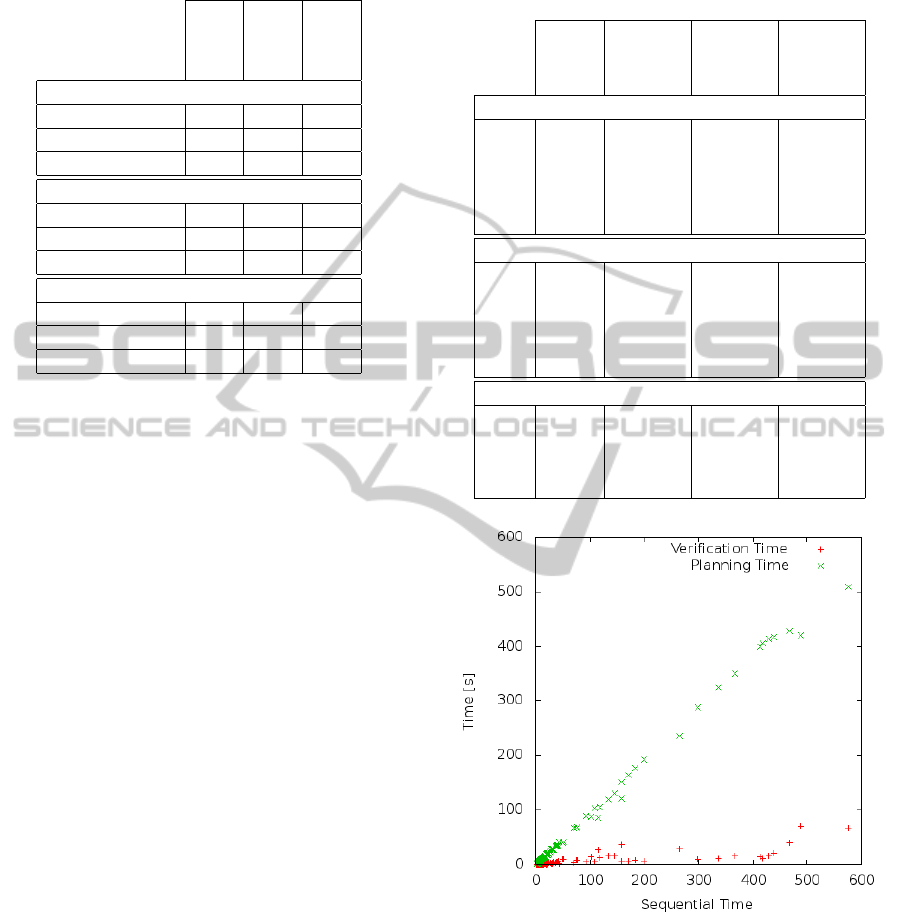
Table 2: Performance cost of PSM extended with plan ver-
ification. The table shows average values for all the solved
problems. Run times are in seconds.
PSM PSM+ PSMV
Driverlog
Iterations 3.4 2 2.3
Sequential time 23.5 9.6 12.1
Parallel time 9.7 4.5 5.6
Openstacks
Iterations 1 1 1
Sequential time 2.6 7.1 7.1
Parallel time 1.3 4.4 4.4
Woodworking
Iterations 1.4 1.3 1.3
Sequential time 79.1 84.1 84.0
Parallel time 20.3 21.7 21.6
situation where each agent is equipped with its own
CPU. The results show that in Driverlog domain the
number of iterations decreased which also caused a
decrease in run times. PSM+ achieved the best re-
sults for this domain. All problems of Openstacks do-
main have been solved during the first iteration even
by the simplest version PSM. Therefore run times
needed by the other versions are higher because of the
time needed for the verification. Only a tiny decrease
of iteration count in Woodworking domain could not
outweigh the price for verification and thus the ver-
sions with plan verification are a bit slower than PSM.
A slight increase of run time in PSMV over PSM+
is caused by additional landmarks which come from
plans which were completely rejected by PSM+.
Table 3 compares run times needed to solve se-
lected tasks solvable by all the planners. We can see
that PSM-variants are able to find solution faster than
FMAP in the case of complex problems.
Graph in Figure 2 compares times needed for
planning and plan verification in PSMV. It shows that
the time needed for verification in PSMV is much
smaller than the time needed for agent internal plan-
ning. The graph is constructed as follows. The x-
axis in the graph shows total time needed to solve a
problem, that is, planning together with verification.
For each problem, planning and verification times are
depicted as two values in the same column whose
x-coordinate correspond to the total sequential time.
Thus the sum of the two values in each column is al-
ways equal to the x-coordinate of the column.
Graphs in Figure 3 show, for each domain, an av-
erage number of iterations and an average amount of
communication among all the agents measured in ac-
Table 3: Comparison of run times on selected problems
solved by all the planners. Times are in seconds, PSM times
correspond to parallel times, and PSM variants have number
of iterations in parenthesis.
FMAP
PSM PSM+ PSMV
Driverlog
p-01 0.6 2.2 (2) 2.3 (2) 2.3 (2)
p-05 1.8 34.1 (9) 4.0 (2) 6.5 (3)
p-08 11.9 11.6 (3) 5.4 (2) 6.2 (2)
p-10 2.1 3.0 (2) 4.2 (2) 4.6 (2)
p-13 16.2 14.3 (3) 8.7 (2) 14.8 (3)
Openstacks
p-01 1.4 1.2 (1) 1.3 (1) 1.3 (1)
p-06 9.7 1.1 (1) 1.7 (1) 1.7 (1)
p-11 51.0 1.2 (1) 2.3 (1) 2.3 (1)
p-16 171.0 1.2 (1) 4.3 (1) 4.5 (1)
p-21 497.0 1.4 (1) 6.7 (1) 6.5 (1)
Woodworking
p-01 2.7 4.7 (2) 5.6 (2) 5.6 (2)
p-06 200.3 30.1 (2) 33.7 (2) 33.8 (2)
p-11 1.9 1.8 (1) 2.3 (1) 2.3 (1)
p-21 0.4 1.3 (1) 1.5 (1) 1.5 (1)
Figure 2: Verification and planning times in PSMV.
tions. The average values are computed only for the
problems solved by all PSM, PSM+ and PSMV vari-
ants. The communication is measured as the number
of actions communicated between each pair of agents.
These actions are communicated during the verifica-
tion and during the exchange of created public PSMs.
During communication, each action is represented by
its unique id and thus the number of actions commu-
nicated directly corresponds to the number of bytes.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
180

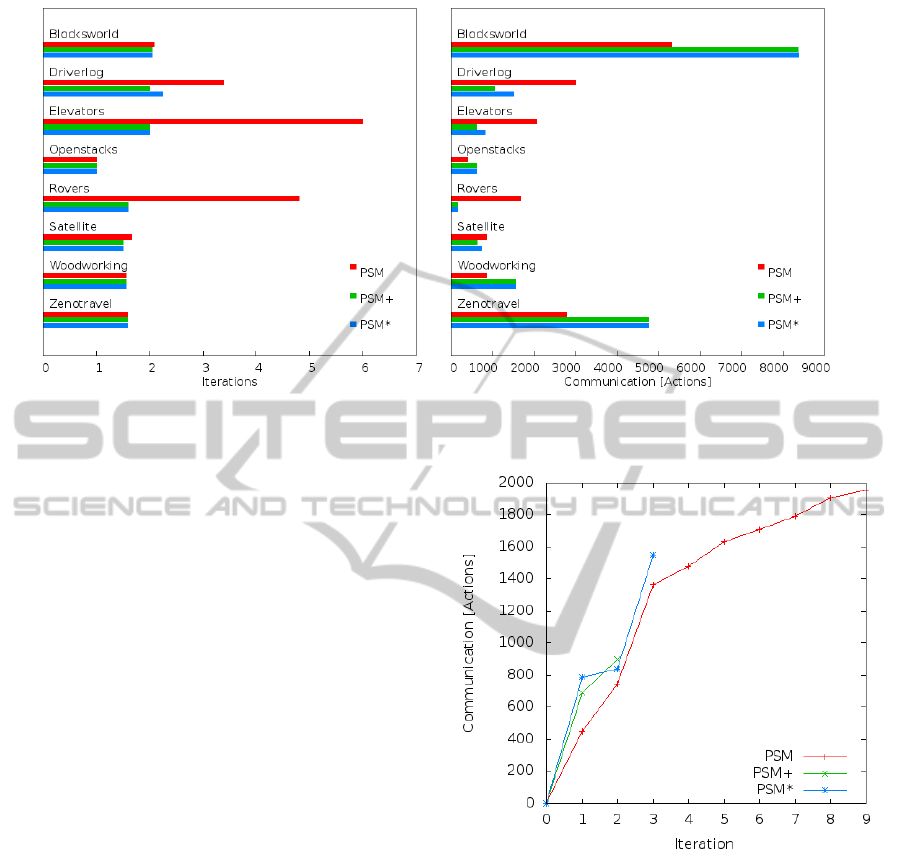
Figure 3: An average number of iterations (left) and an average amount of communication (right) for each domain in PSM,
PSM+, and PSMV variants.
We can see that in some domains (e.g.
Blocksworld) the communication grows substantially
in PSMV and PSM+, while in other domains the
communication is decreased. The reason for that is
that in the first case all the plans are accepted and
thus the verification process brings no advantage.
In the domains where the verification helped, the
overall communication in PSM+ and PSMV variants
is smaller than in PSM. The domains where the
verification was useful can be identified either from
the overall results (Table 1) or from the average
number of iterations (Figure 3, left) because the
average number of iterations is decreased by success
of the verification process (see domains Driverlog,
Elevators, Rovers). In the domains where all the
solved problems were solved in first few iterations
even by the simplest PSM variant (Blocksworld,
Openstacks, Woodworking, Zenotravel), the verifi-
cation can not really help to decrease the number
of iterations (as it is already small) and thus the
verification only creates communication overhead.
An exception is the Satellite domain where individual
iteration numbers have a higher variance (which is
not apparent from the average values in the graph).
Graph in Figure 4 shows amount of communica-
tion among the agents in a single selected problem
(Driverlog05). This problem was chosen because it
was solved by all the approaches but not in a trivial
manner (in the first or second iteration). Each curve
ends in the column that corresponds to the last iter-
ation. We can see that the verification creates com-
munication overhead in individual iterations but the
total communication is smaller with verification be-
cause the number of iterations is decreased.
Figure 4: Amount of communication during solving of
Driverlog05.
7 CONCLUSIONS
We have shown how integration of a static analysis
based on process calculi type systems in validation
phase of a planner based on merging of Planning State
Machines strictly improves coverage of solved plan-
ning problem instances. Although the approach loses
against a state-of-the-art multiagent planner, the re-
sults are promising. Moreover usage of the static
analysis can improve other multiagent planning ap-
proaches using cooperation by coordination of partial
agents’ plans.
Furthermore, we have also extended our approach
MultiagentPlanningbyPlanSetIntersectionandPlanVerification
181

with a new heuristic with notable improvements. This
new heuristic will be part of our future research. In
future research, we want also to focus on more pre-
cise static analysis by POLYV and therefore hypothet-
ically less approximate test of the extensibility of par-
tial plans.
ACKNOWLEDGEMENTS
This research was supported by the Czech Science
Foundation (grant no. 13-22125S).
REFERENCES
Bhattacharya, S., Kumar, V., and Likhachev, M. (2010).
Search-based path planning with homotopy class con-
straints. In Felner, A. and Sturtevant, N. R., editors,
SOCS. AAAI Press.
Brafman, R. and Domshlak, C. (2008). From One to Many:
Planning for Loosely Coupled Multi-Agent Systems.
In Proceedings of ICAPS’08, volume 8, pages 28–35.
Fikes, R. and Nilsson, N. (1971). STRIPS: A new approach
to the application of theorem proving to problem solv-
ing. In Proc. of the 2nd International Joint Conference
on Artificial Intelligence, pages 608–620.
Hopcroft, J. E., Motwani, R., and Ullman, J. D. (2006). In-
troduction to Automata Theory, Languages, and Com-
putation (3rd Edition). Addison-Wesley Longman
Publishing Co., Inc., Boston, MA, USA.
Jakub
˚
uv, J. and Wells, J. B. (2010). Expressiveness of
generic process shape types. In TGC’10, volume 6084
of LNCS, pages 103–119. Springer.
Makholm, H. and Wells, J. B. (2005). Instant polymorphic
type systems for mobile process calculi: Just add re-
duction rules and close. In ESOP’05, volume 3444 of
LNCS, pages 389–407. Springer.
Nissim, R. and Brafman, R. I. (2012). Multi-agent A*
for parallel and distributed systems. In Proc. of AA-
MAS’12, AAMAS ’12, pages 1265–1266, Richland,
SC.
ˇ
Stolba, M. and Komenda, A. (2014). Relaxation heuristics
for multiagent planning. In Proceedings of ICAPS’14.
Torre
˜
no, A., Onaindia, E., and Sapena, s. (2014). Fmap:
Distributed cooperative multi-agent planning. Applied
Intelligence, 41(2):606–626.
To
ˇ
zi
ˇ
cka, J., Jakub
˚
uv, J., Durkota, K., Komenda, A., and
P
ˇ
echou
ˇ
cek, M. (2014a). Multiagent Planning Sup-
ported by Plan Diversity Metrics and Landmark Ac-
tions. In Proceedings ICAART’14.
To
ˇ
zi
ˇ
cka, J., Jakub
˚
uv, J., and Komenda, A. (2014b). Gen-
erating Multi-Agent Plans by Distributed Intersection
of Finite State Machines. In Proceedings ECAI’14,
pages 1111–1112.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
182