
A Greedy Heuristic for Workforce Scheduling and Routing With
Time-dependent Activities Constraints
J. Arturo Castillo-Salazar, Dario Landa-Silva and Rong Qu
Automated Scheduling, Optimisation and Planning (ASAP) Research Group, School of Computer Science,
University of Nottingham, Jubilee Campus, Wollaton Road, Nottingham, NG8 1BB, U.K.
Keywords:
Employee Scheduling, Workforce Optimization, Personnel Routing, Greedy Heuristic, Benchmark Data,
Connected Activities Constraints.
Abstract:
We present a greedy heuristic (GHI) designed to tackle five time-dependent activities constraints (synchroni-
sation, overlap, minimum difference, maximum difference and minimum-maximum difference) on workforce
scheduling and routing problems. These types of constraints are important because they allow the modelling
of situations in which activities relate to each other time-wise, e.g. synchronising two technicians to complete
a job. These constraints often make the scheduling and routing of employees more difficult. GHI is tested on
set of benchmark instances from different workforce scheduling and routing problems (WSRPs). We compare
the results obtained by GHI against the results from a mathematical programming solver. The comparison
seeks to determine which solution method achieves more best solutions across all instances. Two parameters
of GHI are discussed, the sorting of employees and the sorting of visits. We conclude that using the solver is
adequate for instances with less than 100 visits but for larger instances GHI obtains better results in less time.
1 INTRODUCTION
The workforce scheduling and routing problem
(WSRP) refers to the assignation of a diverse skilled
workforce to a series of visits at different locations.
Each visit requires an activity completion before trav-
elling to the next visit. Activities require different
skills and might need more than one employee. Other
constraints which relate activities to each other, i.e.
connected activities constraints, are also present in
WSRP (Castillo-Salazar et al., 2014). Particularly,
in this paper we focus on those connected activi-
ties constraints that are time-dependent (synchronisa-
tion, overlap, minimum difference, maximum differ-
ence and minimum-maximum difference). These type
of connected activities constraints are also known in
the literature as temporal dependencies (Rasmussen
et al., 2012) or interdependant services (Mankowska
et al., 2014). For applications and solution meth-
ods of WSRP in sectors such as home health-care
(Akjiratikarl et al., 2007; Kergosien et al., 2009),
security provision (Misir et al., 2011; Chuin Lau
and Gunawan, 2012), retail and maintenance services
(Cordeau et al., 2010; G
¨
unther and Nissen, 2012), etc.
we refer the reader to the survey by Castillo-Salazar et
al. (2012) . In such sectors, daily employee schedul-
ing and routing is necessary to complete a diverse set
of activities across several client locations. In what
follows, we use connected activities constraints and
time-dependent constraints indistinctly. These con-
straints allow to model situations in which two activ-
ities need to start at the same time, e.g. two techni-
cians to calibrate a fiber optic segment. Also, when
one activity needs to start after the completion of an-
other one, e.g. a care worker to help ironing only after
completing the washing. The related activities do not
have to be performed by the same employee.
The model by Rasmussen et al. (2012) supports
connected activities constraints as long as the activ-
ities involved do not have time window restrictions.
They argue that introducing time windows to activ-
ities involved in time-dependent constraints reduces
flexibility. Their study focused on instances in home
health care. A more recent approach was developed
by Mankowska et al. (2014) using variable neigh-
bourhood search to tackle artificially generated in-
stances with up to 300 activities, time windows and
4 out of the 5 time-dependent constraints consid-
ered here (except Overlap). Castillo-Salazar et al.
(2014b) performed a computational study on several
benchmark instances which contain time windows for
all activities and all 5 types of time-dependent con-
367
Arturo Castillo-Salazar J., Landa-Silva D. and Qu R..
A Greedy Heuristic for Workforce Scheduling and Routing With Time-dependent Activities Constraints.
DOI: 10.5220/0005223203670375
In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 367-375
ISBN: 978-989-758-075-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

straints. They used an adapted version of the mixed
integer linear model by Rasmussen et al. (2012) .
The model was solved by a state of the art solver in
order to provide benchmark results. Nevertheless, no
other solution method was explored. The benchmark
presents a series of daily real-based problems. The
authors clarify the need to obtain good enough solu-
tions within a reasonable time. For real-world based
instances, daily problems need to be solved during the
night before the planning day if not faster. Solving
WSRP as close as possible to the start of the plan-
ning horizon helps to include all updated availabil-
ity of employees. Nevertheless, often changes are
required due to unexpected absences or urgent prior-
ity services. In their experiments, Castillo-Salazar et
al. (2014b) used two hours as maximum computa-
tional time. It has been reported that medium to large
WSRP instances cannot be solved using a mathemat-
ical solver within 10 hours (Mankowska et al., 2014)
and for some small instances solvers could require
67 hours to prove optimality (Castillo-Salazar et al.,
2014). Our objective when developing the greedy
heuristic is to obtain at least the same quality of re-
sults as the solver (measured by the gap to the re-
ported lower bound) in the benchmark data set but
faster, as this would help to incorporate unexpected
changes near the start of the planning horizon.
A greedy heuristic is a procedure based on con-
secutive decisions that at every step, if possible, leads
to a better result. Greedy heuristics rely in some in-
formation about the domain of the problem and of-
ten obtain good feasible results in short time. Al-
though, there are greedy heuristics that have tackled
workforce scheduling and routing problems (Xu and
Chiu, 2001; Mankowska et al., 2014), to the best of
our knowledge none can support time windows on
activities that are also related to other activities by
any of the 5 types of time-dependent constraints. The
main contribution of this work is tackling activities
that have any of the 5 time-dependent constraints.
There are four more sections in this paper. Section
2 explains the MILP model of the WSRP. Section 3
presents the proposed greedy heuristic. Section 4 de-
scribes the experiments settings. Section 5 presents
our results. Finally, section 6 concludes the paper.
2 MIP MODEL FOR WSRP
The MILP model used as a reference to compare
the greedy heuristic can be found in (Castillo-Salazar
et al., 2014). Here we provide an overview of it.
C represents the set of visit locations. 0
k
and n
k
re-
fer to the starting and ending locations for employee
k. K is the set of employees. N
k
= C ∪ {0
k
, n
k
} is
the set of available locations for employee k. Activ-
ity i starting time window is given by two values α
i
(earliest start time) and β
i
(latest start time). Binary
variable ρ
k
i
is set to 1 if employee k can perform ac-
tivity i based on skill requirement, and 0 if not. Activ-
ities can be left unassigned when there is not enough
employees to perform all of them. Binary variable y
i
is set to 1 if activity i is left unassigned and 0 other-
wise. The duration of activity i plus the travel time
from activity location i to activity location j for em-
ployee k is given by s
k
i j
. The starting time of activity
i by employee k is t
k
i
. Employee k starts his working
time at α
n
k
and must finish by β
n
k
. Time-dependent
constraints are indicated by a set of pairs of activities
P. For every pair of activities i and j, a constant value
p
i j
is given depending on the type of time-dependent
constraint (Rasmussen et al., 2012, pg. 601). Finally,
binary variables x
k
i j
are set to 1 if employee k moves
to activity location j after performing activity i.
Minimise:
ω
1
∑
k∈K
∑
i∈N
k
∑
j∈N
k
C
k
i j
x
k
i j
+ω
2
∑
k∈K
∑
i∈C
∑
j∈N
k
δ
k
i
x
k
i j
+ω
3
∑
i∈C
γ
i
y
i
(1)
Subject to:
∑
k∈K
∑
j∈N
k
x
k
i j
+ y
i
= 1 ∀ i ∈ C, (2)
∑
j∈N
k
x
k
i j
≤ ρ
k
i
∀ k ∈ K, ∀ i ∈ C, (3)
∑
j∈N
k
x
k
0
k
, j
= 1 ∀ k ∈ K, (4)
∑
i∈N
k
x
k
i,n
k
= 1 ∀ k ∈ K, (5)
∑
i∈N
k
x
k
ih
−
∑
j∈N
k
x
k
h j
= 0 ∀ k ∈ K, ∀ h ∈ C, (6)
α
i
∑
j∈N
k
x
k
i j
≤ t
k
i
∀k ∈ K, ∀i ∈ C ∪ {0
k
}, (7)
t
k
i
≤ β
i
∑
j∈N
k
x
k
i j
∀k ∈ K, ∀i ∈ C ∪ {0
k
}, (8)
α
n
k
≤ t
k
n
k
≤ β
n
k
∀ k ∈ K, (9)
t
k
i
+ s
k
i j
x
k
i j
≤ t
k
j
+ β
i
(1 − x
k
i j
)∀k ∈ K, ∀i, j ∈ N
k
, (10)
α
i
y
i
+
∑
k∈K
t
k
i
+ p
i j
≤
∑
k∈K
t
k
j
+ β
j
y
j
∀(i, j) ∈ P, (11)
x
k
i j
∈ {0, 1} ∀ k ∈ K, ∀i, j ∈ N
k
, (12)
t
k
i
∈ R
+
∀k ∈ K, ∀i ∈ N
k
, (13)
y
i
∈ {0, 1} ∀ i ∈ C. (14)
The objective function (1) includes the cost of em-
ployee k performing activity i and moving to loca-
tion of activity j when finished (C
k
i j
). It also consid-
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
368

ers employees preferences with regards to activities.
Employee k preference to perform activity i is given
by the term (δ
k
i
). Finally, the priority of the activ-
ities is also consider in the objective function since
some locations might not be visited and therefore its
activity left unassigned. Activity i priority is given by
γ
i
. Every component of the objective function has a
weight associated. The weights (ω
1
,ω
2
,ω
3
) are set as
in (Rasmussen et al., 2012).
Constraints are as follows: visits are either per-
formed or left unassigned (2). Activities can only be
assigned to employees able to perform them (3). All
employees must start from the initial location (4) and
return to their own final location (5). Constraint (6)
ensures that once employee k visits activity location
h, he leaves it, i.e. it maintains flow conservation.
Time windows of visits must be satisfied (7, 8). Vis-
its should be performed during the employees starting
and ending times (9). Constraint (10) ensures travel-
ling times are respected by the start of activities. Con-
nected activities constraints (11) exist among related
activities. Decision variables x
k
i j
are set to 1 when em-
ployee k travels from location i to j and 0 otherwise
(12). Scheduling variables are positive integers (13).
Finally, if an activity i is not performed the binary de-
cision variables y
i
is set to 1 and 0 otherwise (14).
3 GREEDY HEURISTIC (GHI)
The data structure that holds the solution at any time
is presented in Figure 1. The main list is defined by
the number of employees plus one additional node for
unassigned visits. Within each node there is a list of
visits which the employee has been assigned to. The
list of visits is maintained in ascending order accord-
ing to time. Rectangles represent activity duration,
traveling time, and idle time. The last rectangle of
each list of activities represents the traveling time to
the ending location of the employees. Activities in the
bottom node (Unassigned) have no particular order.
The proposed constructive heuristic GHI works as
follows (Algorithm 1). It starts by creating a copy
visitList with all visits, creating the solution struc-
ture described above and sorting visitList according
to listCriterion (section 3.1.1). In each iteration of
the assignation cycle (lines 5 to 13), GHI sorts the
solution structure sol according to solCiterion (sec-
tion 3.1.2) and processes the next visit v from Vis-
itList. For processing, visit v is passed to the PRO-
CESS function which returns the list of related vis-
its lrv (step 8). Then, each visit v2 (if any) related
to v through a connected activity constraint, is pro-
cessed by the PROCESSDEP function which consid-
Figure 1: Solution structure for WSRP.
ers the constraint and maintains feasibility (lines 9 to
13). Processing v and its dependent visits v2 means
that they are removed from the visitList and a new it-
eration starts. This assignation cycle continues until
no visits are left in visitList.
Algorithm 1: GHI: SOLVE.
1: procedure SOLVE
2: visitList ← copy of visits(V)
3: sol ← CREATESOLUTIONSTRUCTURE
4: SORT(visitList, listCriterion)
5: while visitList is not empty do
6: SORT(sol, solCriterion)
7: v ← visitList.remove(0)
8: lrv ← PROCESS(v)
9: if lrv.size > 0 then
10: while lrv is not empty do
11: v2 ← lrv.get(0)
12: lrv ← PROCESSDEP(v,v2,lrv)
13: visitList.remove(v2)
We tackle activities with time-dependent con-
straints by creating different functions for the inde-
pendent and the dependent activities within such con-
straints. We seek to assign the independent activity
first as this provides the starting time upon which the
dependent activities adhere to. Functions PROCESS
for independent activities (Algorithm 2) and PRO-
CESSDEP for dependent activities (Algorithm 3) are
almost identical, except that PROCESSDEP performs
one extra validation to ensure the time-dependent con-
straint is enforced (call to function CONSIDERRC).
PROCESS searches sol for idle times where v can be
inserted. The possibilities for insertion are sorted
(lines 2 to 6). Then, it tries to assign the same number
of idle times from different employees as the num-
ber of employees required for to perform v. If there
are not enough candidates as required employees then
visit v is unassigned (lines 7 to 13 ). Once v has been
assigned the related visits are searched and returned
AGreedyHeuristicforWorkforceSchedulingandRoutingWithTime-dependentActivitiesConstraints
369

as result (steps 14 & 15). PROCESSDEP works simi-
larly but also considers any time-dependent constraint
involving v2 (step 3). PROCESSDEP requires that v
is assigned to use its start time to enforce the time-
dependent constraint in all its related visits v2.
Algorithm 2: GHI: PROCESS.
1: procedure PROCESS(v)
2: can ← ALLOCPOSSIBLEANY(v,sol)
3: SORT(can)
4: if can is not empty then
5: ca ← can.remove(0)
6: INCLUDE(c,sol)
7: i ← v.required
8: for i > 1 do
9: if can is not empty then
10: ca ← can.remove(0)
11: INCLUDE(ca,sol)
12: else
13: UNALLOCATE(v,sol)
14: lrv ← GETRELATED(v)
15: return lrv
Algorithm 3: GHI: PROCESSDEP.
1: procedure PROCESSDEP(v, v2, lrv)
2: can ← ALLOCPOSSIBLEANY(v2,sol)
3: CONSIDERRC(v,v2,can)
4: if can is not empty then
5: SORT(can)
6: ca ← can.remove(0)
7: INCLUDE(ca,sol)
8: i ← v.required
9: for i > 1 do
10: if can is not empty then
11: ca ← can.remove(0)
12: INCLUDE(ca,sol)
13: else
14: UNALLOCATE(v,sol)
Within PROCESS and PROCESSDEP, the ALLOC-
POSSIBLEANY function looks for idle times in an
employee daily schedule. The INCLUDE function as-
signs the candidate structure with possible allocations
to the solution structure. The UNALLOCATE function
unassigns a visit from its current employee schedule
and leaves it in the unassigned node. GETRELATED
identifies other activities that are time-dependent to v
via a connected activity constraint.
ALLOCPOSSIBLEANY (Algorithm 4) is the func-
tion that searches the solution structure to find idle
time so that new activities can be assigned. It returns
a collection of candidate allocations. It iterates the
Algorithm 4: GHI: ALLOCPOSSIBLEANY.
1: function ALLOCPOSSIBLEANY(v,sol)
2: for n ← sol.nodes do
3: emp ← n.emp
4: if ¬ PERFORM(emp,v) then
5: next
6: if n.sch is empty then
7: w ← LASTAVWINDOW(n.sch)
8: ca ← ENOUGH(w,v.win,emp)
9: if ca is not nil then
10: can.add(ca)
11: else
12: for w ← 1, n.sch do
13: ca ← ENOUGH(w,v.win,emp)
14: if ca is not nil then
15: can.add(ca)
16: w ← LASTAVWINDOW(n.sch)
17: ca ← ENOUGH(w,v,emp)
18: if ca is not nil then
19: can.add(ca)
whole structure looking for idle times where the visit
(v) can be inserted, it considers the travel time to get
to the visit and the difference in travel time from the
visit to the following destination (ENOUGH). It avoids
exploring nodes representing employees that cannot
perform the activity of the visit (PERFORM). LAS-
TAVWINDOW returns the last idle block in an em-
ployee schedule. The last idle block is defined as the
time between the last activity completion and the em-
ployee’s shift ending. This is a special case because
it needs to consider the travel time to the ending loca-
tion of the employee.
A candidate allocation structure represents several
possible employee-activity assignations. It is defined
by a starting time, a flexible component, idle time and
a worker reference. The starting time provides the
first possible start time in which an activity can start,
the flexible component provides a time length which
that start time can be delayed and still fit in the idle
block. Idle time represents the time left before the
starting time. Figure 2 shows how a candidate alloca-
tion structure is formed. The line indicates the activ-
ity’s time window, the series of dark blocks represent
the number of possibilities that the activity could fit
in the idle space number 2.
Some of our previous heuristics do not tackle con-
nected activities constraint first. Therefore, it was
possible that no feasible solution was found if such
constraints were not satisfied. We allow unassigned
activities as sometimes there is not enough employ-
ees to cover all visits. One valid, but extreme re-
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
370
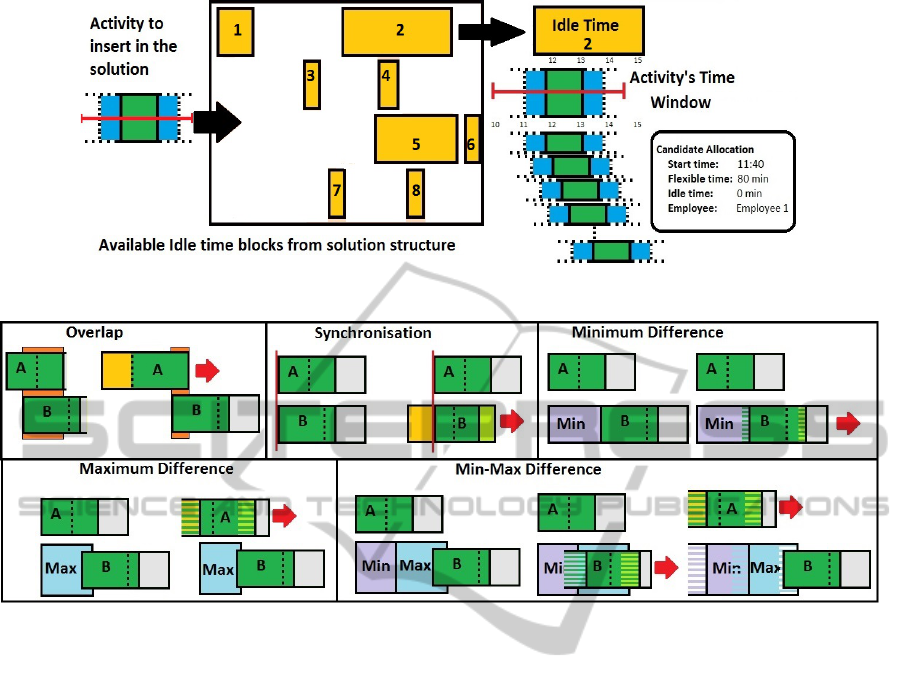
Figure 2: Represents how the AllocPossibleAny function considers idle time blocks and creates candidate allocations.
Figure 3: Examples of how the heuristics consider each of the connected activities constraints.
pair mechanism is to leave all activities with time-
dependent constraints unassigned, because if a visit
is left unassigned then any constraints that it relates
to are disabled by the logic of the model. But, we
now aim to process those constraint early in the cre-
ation of the solution and keep them satisfied because
leaving visits unassigned comes at a high cost. There-
fore, GHI includes a preventive step which verifies if
the current visit is associated with another visit (via a
connected activities constraint) and if so, it tries to al-
locate the related visit in a suitable manner after con-
sidering the starting time of the first visit to comply
with the constraint. Such procedure is described in
Figure 3 dealing with each of the 5 connected activ-
ities constraints (overlapping, synchronisation, mini-
mum, maximum and min-max time difference). Fig-
ure 3 shows an example for each type where activ-
ities A and B are related by each of the connected
activities constraint types. In the figure, the dark rect-
angle is the activity duration, the lighter rectangle is
the flexible time (the activity can move forward and
still comply with other time constraints), the dotted
line inside the dark rectangle is the latest start time
for the activity. Every example in the figure considers
two cases, first (left one) both activities A and B com-
ply with the time-dependent constraint, second (right
one) delays the start of A or B so we can comply to a
constraint that otherwise would not be enforced. For
example, in the maximum difference sub-figure, the
right case shows B starting within the maximum time
allowed after the A starting. The left shows that A
starting as originally makes B starting after the max-
imum allowed period. By delaying A (arrow shifting
A to the right), activity B now enters into the max-
imum allowed zone, hence satisfying the constraint.
Notice, that B could not be started earlier because it
was already at its earliest starting time.
3.1 Parameters of the Greedy Heuristic
GHI has two parameters that need to be set, ones is
listCriterion, the sorting of the list of activities dur-
ing initialisation and the other one is solCriterion, the
solution structure sorting after each iteration.
3.1.1 Parameter listCriterion Values
Duration sorts visits in descending order based on the
duration of the activity (v.dur).
Maximum Finish Time sorts visits in ascending or-
der based on the maximum time the visit can finish
given its time window. The sorting parameter is v.let.
AGreedyHeuristicforWorkforceSchedulingandRoutingWithTime-dependentActivitiesConstraints
371

Maximum Start Time sorts visits in ascending order
based on the maximum time the visit can start given
its time window. The sorting parameter is v.lst.
Minimum Finish Time sorts visits in ascending or-
der based on the minimum time the visit can finish
given its time window. The sorting parameter is v.eet.
Minimum Start Time sorts visits in ascending order
based on the minimum time the visit can start given
its time window. The sorting parameter is v.est.
Number of Employees sorts visits in descending or-
der based on the number of employees required. The
parameter for sorting is v.req.
Density sorts visits in descending order based on
the density factor. The density factor is obtained by
adding the number of employees required plus the
number of connected activities constraints that the
visit is involved in. This aims to process activities that
are more constrained first and leave the simpler ones
at the end. The number of employees in the team is
modelled using synchronisation constraints.
3.1.2 Parameter solCriterion values
Remaining Time sorts the solution list in descending
order based on the time available left for every em-
ployee. The time available is calculated from the last
visit until the end of the employees shift minus the
time needed for the trip to the ending location. In all
the instances, shift starting and finishing times coin-
cide with the beginning and end of the time horizon.
It aims to reduce the number of employees, since it
avoids using a new employee unless the available time
of the previous ones are full or no other allocation is
possible. If the sorting is in ascending manner, visits
will be balanced across all possible employees with
the right skills.
Solution Size orders the solution structure main list
in ascending order based on the number of visits that
employees have. When two nodes have the same
number of visits, the tie-break criterion is the longest
remaining time explained above.
4 EXPERIMENTS
The aim of the experiments is to evaluate the quality
of the solutions obtained by GHI when compared to
the solver. The comparison seeks to determine which
solution method achieves more best solutions across
all instances.
In this study we used the benchmark data set from
Castillo-Salazar et al. (2014b). The data set is an
adaptation of different WSRP from the literature. We
used 4 groups of instances Sec, Sol, Mov and HHC.
Sec is based on security guards patrolling different
buildings (Misir et al., 2011). Sol is based on adap-
tations to the Solomon data set. Three different ver-
sion of each instance are used 25, 50 and 100 vis-
its (Solomon, 1987). Mov originates from a multi-
objective VRPTW study which controlled variability
of time window sizes (Castro-Gutierrez et al., 2011).
HHC is a home health care data set. It includes a good
level of skills, preferences on employees and patients
(Rasmussen et al., 2012). The total number of in-
stances used is 374. The original benchmark has 375
instances, the instance that is not being used belong
to a single-instance group of technicians on field for
which the benchmark does not provides results.
All instances are solved first using a mathematical
solver. A time limit of 2 hours is set for the solver
and we keep the solution found after this. The solver
achieves optimal solutions for 33 instances. There are
37 instances in which no solution was found by the
solver within the time limit. All instances are solved
also by GHI (coded in Java). As part of our experi-
ments we want to find which combination of values
for listCriterion (7 possible values) and solCriterion
(2 possible values) obtains the best results. Therefore,
GHI is executed for all 374 instances for the 14 com-
binations of parameters. We use all combinations to
identify the best values for the two parameters.
5 RESULTS
Out of the 374 instances, the solver obtained better
results for 187. GHI also obtained 187 best feasible
solutions. For none of the instances solver and heuris-
tic produced the same result.
In Figure 4 the results are segmented for each of
the 4 data sets. GHI has better results than the solver
in Sec, HHC and Mov. In group Sol the solver out-
performs the heuristic. In order to investigate this fur-
ther we analyse the three subgroups within the Sol
group. The subgroups are those with 25, 50 and 100
visits. Figure 5 shows the subgroups segmented re-
sults. The solver is better in subgroups with 25 and
50 visits. But for instances of 100 visits GHI out-
performs the solver. GHI obtained the same number
of best feasible result as the solver. However, overall
GHI is significantly faster spending less than 1 second
in each instance.
5.1 Evaluating the Quality of Results
This section presents a measure by which results from
GHI and the solver can be evaluated. We divided the
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
372

Sec-GHI Sol-GHI HHC-GHI Mov-GHI
0
50
100
61
121
0
5
119
47
11
10
# best feasible solutions
Solver GHI
Figure 4: Results GHI when compared to the solver. The
graphs show the number of best feasible solutions obtained
by each method. The results are segmented according to the
data set group the belong (Sec, Sol, HHC and MOV).
Sol25-GHI Sol50-GHI Sol100-GHI
0
20
40
60
55 55
11
1 1
45
# best feasible solutions
Solver GHI
Figure 5: Solomon 25, 50 and 100 visits Sol sub-groups re-
sults of GHI (in red) when compared to the solver (in blue).
instances in 4 groups depending on the results ob-
tained. The first group are instances for which the
solver obtained optimal solutions, the gap from the
GHI to the optimal is reported. The second group
are instances for which the solver obtained better fea-
sible solutions but not optimal, the gap between the
GHI and the best feasible solution by the solver is
reported. The third group are instances where GHI
is better than the solver, the gap between the solver
and GHI is reported. Finally, the fourth group are
instances where no solutions were obtained by the
solver within the time limit, no gap is provided for
this group. The gap calculation for groups 1 and
2 is (GHI − Solver)/ABS(Solver) and for group 3
is (Solver − GHI)/ABS(GHI). The principle is the
same, because it is a minimisation problem, in every
group we subtract the best result(minimum) from the
worst one(maximum) and normalise according to the
best one(minimum). Absolute value of the denomina-
tor is necessary to avoid providing negative gaps.
Table 1: Group result type: 1 optimal, 2 solver best, 3 GHI
best and, 4 only GHI available. Number of instances #,
mean number of employees µ
emp
, mean number of visits
µ
visits
, mean time horizon duration µ
tHor
, mean visit dura-
tion µ
v.dur
and mean time window size µ
v.win
.
G # µ
emp
µ
visits
µ
tHor
µ
v.dur
µ
v.win
1 33 12.8 43.1 1817.3 60.3 291.7
2 154 10.3 47.0 1088.1 149.8 382.9
3 150 26.3 117.2 1311.6 284.7 422.9
4 37 66.0 171.6 1147.8 333.9 402.8
Table 1 shows some characteristics of each group.
GHI found better results in groups 3 and 4, which
have on average more employees, more visits, longer
visits and longer time window sizes. The solver per-
forms better in groups 1 and 2, but could only find
optimal solutions for group 1. There is not signifi-
cant difference in the average number of visits (43.1
vs 47.0) and employees (12.8 vs 10.3) between group
1 and 2. But, group 2 seems more difficult for the
solver. We argue that not only the number of employ-
ees and visits define how difficult a WSRP might be.
Other factors like duration of visits, time to perform
them (time horizon) and flexibility of time windows
could also affect the degree of difficulty as shown
by group 2 when compare to group 1. Group 2 has
longer visits to perform in less time (time horizon)
with greater flexibility of the time windows.
Figure 6 plots the gap result of groups 1, 2 and 3.
The overall observation for group 1 (GHI vs. optimal
solution), is that no gap was less then 10% and for 1/2
of the instances the gap was 77% or less. For group 2
(feasible but not optimal solutions by the solver better
than GHI), the minimum gap achieved was 1% and
for 1/2 of the instances the gap is less than 63% (for
the other 1/2 the gap was higher). Finally, for group 3
(feasible but not optimal solutions by the solver worse
than GHI), the minimum gap achieved was less than
1% but only 1/4 of the instances had a gap less than
68% (for the other 3/4 the gap was higher). THs
means that GHI is a better runner-up against the solver
than the opposite. For the solver to do better in group
3, the computational time needs to be increased sub-
stantially. This is investigated in the next section.
5.1.1 Increasing Computational Time
Here, the computational time given to the solver for
some instances in Group 3 is doubled to 4 hours. We
consider those instances in which the gap to GHI was
100% or less. In total 62 instances match this require-
ment (the other 150 − 62 = 88 instances had much
bigger gaps). Only 2 instances out of these 62 ob-
AGreedyHeuristicforWorkforceSchedulingandRoutingWithTime-dependentActivitiesConstraints
373

0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
320
340
10
−2
10
−1
10
0
10
1
10
2
10
3
Instance
Gap
Group 1
Group 2
Group 3
Figure 6: Gap plot for instances in Group 1-blue, Group 2-red and Group 3-black. Notice the logarithmic scale in the y-axis.
tain better results than GHI with a gap of less than 2%
within the 4 hours. Therefore, even doubling the com-
putational time does not really make the solver a bet-
ter runner-up on the instances of group 3. The same
behaviour has been reported in the literature (Castillo-
Salazar et al., 2014) for this benchmark data set, after
two hours the solver improvements are minimal and
at a high cost (in computational time).
6 CONCLUSION
This paper presents a deterministic greedy heuristic
(GHI) to tackle the workforce scheduling and rout-
ing problem (WSRP). We perform computational ex-
periments using a data set consisting of 374 instances
from four different WSRP scenarios. The proposed
heuristic needs only two parameters. One to decide
the order in which activities are processed. The other
one to decide the order in which employees are con-
sidered for the assignation. This tailored heuristic
is able to tackle time-dependent activities constraints
which arise when activities are related to each other.
We run experiments to compare the results obtained
by GHI against the results produced by a commercial
mathematical programming solver. Our experiments
also seek to identify the best settings for the two pa-
rameters mentioned above.
The deterministic greedy heuristic GHI generates
better results for one half of Castillo-Salazar et al.
(2014b) benchmark instances. Apart from the reduc-
tion in the objective function value, GHI runs at a
marginal time (less than 1 second) compared to the
two hours given to the solver. For the instances in
which the solver produces better results, GHI follows
closely. But for the instances in which GHI produces
better results, the solver stays far behind even after
doubling the computation time. In relation to GHI’s
parameter setting, we found no difference between the
two values for solutionCriterion, but for listCriterion,
time-based sorting is better. This is because the range
of values provided by the time-based sorting mecha-
nism facilitates a better distribution of the visits. It
is left for future investigation whether combining two
sorting mechanisms in listCriterion, e.g. density with
minimum start time could produce better results. The
hypothesis is that density could help allocate complex
visits first, such as those requiring multiple employees
or involved in time-dependent activities constraints,
whilst the time-based sorting could impose a better
order to those activities that are less complex.
Given our results we conclude that for instances
with less than 100 visits, a mathematical solver is
likely to provide an optimal solution or a good fea-
sible solution. As soon as the number of visits raises,
the quality of the solution obtained by the solver de-
creases, and in some cases no solution is found within
two hours. We also demonstrated than increasing the
time limit of the solver to 4 hours in those instances
in which the solver is runner-up to GHI, does not
help the solver to perform better than GHI. Therefore,
for obtaining good-quality feasible solutions for in-
stances with more than 100 visits in fast computation
time, we suggest the use of GHI. Future work will
consider using GHI for providing an initial solution
to a meta-heuristic method such as Tabu Search.
ACKNOWLEDGEMENTS
We thank the financial support of CONACYT and the
LANCS Initiative.
ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems
374

REFERENCES
Akjiratikarl, C., Yenradee, P., and Drake, P. R. (2007).
Pso-based algorithm for home care worker schedul-
ing in the uk. Computers & Industrial Engineering,
53(4):559–583, doi:10.1016/j.cie.2007.06.002.
Castillo-Salazar, J. A., Landa-Silva, D., and Qu, R. (2012).
A survey on workforce scheduling and routing prob-
lems. In Proceedings of the 9th International Con-
ference on the Practice and Theory of Automated
Timetabling (PATAT 2012), pages 283–302, Son, Nor-
way.
Castillo-Salazar, J. A., Landa-Silva, D., and Qu, R. (2014).
Workforce scheduling and routing problems: litera-
ture survey and computational study. Annals of Oper-
ations Research, doi:10.1007/s10479-014-1687-2.
Castro-Gutierrez, J., Landa-Silva, D., and Moreno-Perez,
J. (2011). Nature of real-world multi-objective ve-
hicle routing with evolutionary algorithms. In Sys-
tems, Man, and Cybernetics (SMC), 2011 IEEE In-
ternational Conference on, pages 257 –264.
Chuin Lau, H. and Gunawan, A. (2012). The patrol schedul-
ing problem. In Proceedings of the 9th International
Conference on the Practice and Theory of Automated
Timetabling (PATAT 2012), pages 175–192, Son, Nor-
way.
Cordeau, J.-F., Laporte, G., Pasin, F., and Ropke, S. (2010).
Scheduling technicians and tasks in a telecommuni-
cations company. Journal of Scheduling, 13(4):393–
409, doi:10.1007/s10951-010-0188-7.
G
¨
unther, M. and Nissen, V. (2012). Application of parti-
cle swarm optimization to the british telecom work-
force scheduling problem. In Proceedings of the 9th
International Conference on the Practice and Theory
of Automated Timetabling (PATAT 2012), pages 242–
256, Son, Norway.
Kergosien, Y., Lente, C., and Billaut, J.-C. (2009). Home
health care problem, an extended multiple travelling
salesman problem. In Blazewicz, J., Drozdowski, M.,
Kendall, G., and McCollum, B., editors, Proceedings
of the 4th Multidisciplinary International Scheduling
Conference: Theory and Applications (MISTA 2009),
pages 85–92.
Mankowska, D. S., Meisel, F., and Bierwirth, C. (2014).
The home health care routing and scheduling prob-
lem with interdependant services. Health Care Man-
agement Science, 17:15–30, doi:10.1007/s10729-013-
9243-1.
Misir, M., Smet, P., Verbeeck, K., and Vanden Bergue, G.
(2011). Security personnel routing and rostering: a
hyper-heuristic approach. In Proceedings of the 3rd
International Conference on Applied Operational Re-
search, ICAOR11, Istanbul, Turkey, 2011, pages 193–
206.
Rasmussen, M. S., Justesen, T., Dohn, A., and Larsen, J.
(2012). The home care crew scheduling problem:
Preference-based visit clustering and temporal depen-
dencies. European Journal of Operational Research,
219(3):598–610, doi:10.1016/j.ejor.2011.10.048.
Solomon, M. M. (1987). Algorithms for the vehicle
routing and scheduling problems with time windows
constraints. Operations Research, 35(2):254–265,
doi:10.1287/opre.35.2.254.
Xu, J. and Chiu, S. Y. (2001). Effective heuristic procedures
for a field technician scheduling problem. Journal of
Scheduling, 7:495–509.
AGreedyHeuristicforWorkforceSchedulingandRoutingWithTime-dependentActivitiesConstraints
375
