
Wave Equation Model of Soft Tissue for a Virtual Reality
Laparoscopy Training System
A Validation Study
Sneha Patel and Jackrit Suthakorn
Center for Biomedical and Robotics Technology (BART LAB), Department of Biomedical Engineering, Mahidol University,
Salaya, Nakhon Pathom, Thailand
Keywords: Soft Tissue Modeling, Surgical Training, Wave Equation, Finite Element Analysis (FEA).
Abstract: Laparoscopic procedures have various benefits for the patients but come with environmental limitations for
the surgeons. Therefore to prevent serious complications, surgeons require intensive and repetitive training
to acquire essential techniques, skills or tasks. There are various training systems used in surgical programs;
a recent technology that shows promise is virtual reality (VR) training. An important aspect of these training
systems is the realism of the soft tissue model and the user interface, which allow effective transference of
skills from the training system to the operating room. This paper discusses a novel method to model soft
tissue in virtual reality training systems and the validation of this model. Wave equation, a mathematical
model, is used to model the soft tissue and laparoscopic tools’ interaction. This model is validated using
finite element analysis, which is used to compare the mechanical properties of the resulting material and
human skin. The model discussed in this paper will be applied to a novel surgical training system, which
trains the user in laparoscopic suturing techniques.
1 INTRODUCTION
Laparoscopic surgeries, today, are the procedure of
choice due to the benefits of this technique for the
patients. These benefits include: shorter recovery
period, reduced blood loss, and less scarring; all of
which are a result of the smaller incisions utilized in
the procedure (Basdogan et al., 2001). Despite the
benefits for patients, this procedure comes with a
number of limitations for the surgeon, some of
which include (Bashankaev et al., 2011, Roberts et
al., 2006, Derossis et al., 1998):
2-dimensional view of operating area
Limited hand-eye coordination
Increased tremor due to long, inflexible tools
Restricted movement
1.1 Need for Laparoscopic Surgery
Training
Due to the limitations of the operating environment,
surgeons require intensive training to prevent serious
complications, e.g. bleeding, infection, visceral
injury or death. These complications are most
commonly observed in procedures performed by
inexperienced surgeons (See et al., 1993, Wherry et
al., 1998).
1.2 Present Surgical Training Systems
Figure 1: Physical interface, of BART LAB’s VR training
system, which attaches laparoscopic tools to two Phantom
Omnis; haptic devices used for user interaction.
The conventional surgical training device is live
or cadaveric human, but due to the cost and ethical
issues associated with these systems, surgical
programs are moving towards inanimate training
systems. These systems can utilize either synthetic
65
Patel S. and Suthakorn J..
Wave Equation Model of Soft Tissue for a Virtual Reality Laparoscopy Training System - A Validation Study.
DOI: 10.5220/0005224800650074
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2015), pages 65-74
ISBN: 978-989-758-070-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

models or virtual reality (VR) models, which allow
repetitive training and quantitative assessment
(Munz et al., 2004). VR training systems show
promise in this field and are being extensively
researched because it allows user-specific, repetitive,
and intensive training with continuous, objective
user assessment metric (Roberts et al., 2006, Munz
et al., 2004). This is one of the many reasons for
research into the development of a VR training
system at our lab. The physical interface is displayed
in figure 1 (Itsarachaiyot, 2012).
2 LITERATURE REVIEW
Presently, various VR training systems are used in
medical schools to provide students or young
surgeons with the required laparoscopic skills. These
systems also utilize various modeling techniques to
mimic the mechanical and material properties of soft
tissue, in real time.
2.1 VR Training Systems
There are various VR training systems that are either
commercially available or within the research
process. These systems range in price from
US$5,000 to US$200,000 (Sutherland et al., 2006).
They also vary in the skills that they teach, since
some focus on basic skills while others provide
training in entire laparoscopic procedures (Ali et al.,
2002). Some commercial VR training systems are:
SIMENDO simulator, LAP Mentor, and LapSim
Virtual Reality Simulator.
At our research lab, a previous researcher has
developed a VR training system, with a focus on the
forces applied and experienced, during a
laparoscopic procedure (Itsarachaiyot, 2012). The
forces are based on studies on porcine tissue
(Itsarachaiyot et al., 2011). However, the realism of
the virtual environment can still be improved; this
environment is shown in figure 2.
Figure 2: This figure shows the virtual environment of the
training device, designed at our lab (Itsarachaiyot, 2012).
2.2 Representation of Soft Tissue in
Present VR Training Systems
There are three, most commonly used, modeling
techniques that are utilized to represent soft tissue in
VR training systems: mass-spring model, finite
element model, and mesh-free model.
Mass-spring model is the simplest form of
modeling, which makes it an ideal model for real
time manipulations. This method is based on the
Kelvin-Voigt model which utilizes spring and
dashpots to represent the viscoelastic properties of
the soft tissue (Basdogan et al., 2004). This is the
most commonly used technique to model biological
materials in VR (Brown et al., 2002). A simple
mass-spring model is utilized in our current training
system (Itsarachaiyot, 2012).
On the other hand, the finite element model is a
very accurate model of the interactions between a
soft tissue and the laparoscopic tools. This accuracy
comes at the price of computation which makes this
a very slow model and therefore undesirable for a
real time VR surgical training system (Brown et al.,
2002). This model is a mesh, which is the initial
condition of the surface, where vector fields are
utilized to calculate deformation as a result of
manipulations and interactions. (Brown et al., 2002,
Basdogan et al., 2004).
Mesh-free model is designed to meet the needs
of a surgical training system. The utility of this
model comes from its ability to reconnect the tissue
after being cut. This uses the principles of finite
element modeling but is simplified to reduce the
computation time. The material is manipulated using
the displacement of clusters of nodes around the area
of change (Basdogan et al., 2004).
2.3 Problems with Present Soft Tissue
Models
VR training systems complement surgical training
by preparing surgeons before they perform the
procedure on a patient; however present systems
have a few disadvantages. A major problem with
present inorganic training systems is their lack of
realistic simulations of internal organs and
laparoscopic tools’ interaction (Munz et al., 2004).
Present soft tissue models are either over
simplified, e.g. mass-spring model and mesh-free
models, or are computationally expensive, e.g. finite
element model. Therefore, there is a need for the
development of a model that can mimic the
mechanical, material, and visual properties of the
soft tissue for real time manipulations. This paper
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
66
discusses the use of wave equation to model the
behavior of soft tissue in a VR training system to
produce more effective transference from the
training system to the operating room.
3 APPROACH
The flow chart in figure 3 outlines the method
employed in this study; from developing the model
to validating it. Each of the steps is covered in
further detail in the following subsections. The
computer that is used to study the wave equation and
heterogeneous material model, has the following
specifications: Intel Core 2 Duo 2.66 GHz processor,
NVIDIA GeForce 9400 GT graphics card, 4 GB
RAM, and 160 GB hard disk.
Figure 3: Overview of the approach of this study.
3.1 Wave Equation as a Modeling Tool
in Engineering
Wave equations are partial differential equations that
are used to study vibrations in elastic and flexible,
threads and membranes. In this study, two-
dimensional wave equation is used to model soft
tissue as it defines vibrations in thin membranes.
2
2
2
2
2
2
2
;
2
(1)
Equation (1) shows the two dimensional wave
equation, where u(x,y,t) is the displacement
function, T is the initial force on the membrane, and
ρ is the density of the membrane. This equation is
developed using Newton’s 2
nd
Law.
,,
cos
∗
sin
sin
sin
;
1,2,3…
,1,2,3…
(2)
4
,
sin
sin
(3)
where
&
(4)
Kreyszig et al. determined the solution for the
two dimensional equations using boundary and
initial conditions; equations 2-4 (Kreyszig et al.,
2011).This solution is developed using the idea of a
drum membrane and the vibrations it experiences
upon contact with the drumstick (Kreyszig et al.,
2011). In these solutions m and n are integers,
is the Euler formula used to determine the shape of
the membrane,
∗
is the relation associated with
the initial velocity (which is 0 in this scenario), a and
b are the boundary conditions of the membrane, and
are the eigenvalues of the membrane model.
Structural engineers use wave equations to
observe the effects of vibrations on beams, rods,
cables and plates. In these studies, the objects are
considered homogeneous and isotropic, with
continuous properties of mass and spring. This
model is used by engineers to determine the strength
of various components of a building (Beards, 1996).
For example, to observe the effects of vibrations,
from earthquakes, to a building’s integrity (Sánchez-
Sesma et al., 2002). A model that is also related to
soft tissue is the use of 2D wave equation to model
vibrations of a drum membrane (Kreyszig et al.,
2011).
Based on the authors’ research, there is presently
no study that utilizes wave equation to model the
behavior of soft tissue in a surgical setting. A
biomedical application of wave equation is the
modeling of blood flow using partial differential
equations, which define the fluid’s dynamics
(Bessems et al., 2007).
3.2 Mechanical & Material Properties
of the Dermis
Table 1 covers essential properties of the dermis
because of its role in the mechanical behavior of the
skin. Other layers of the skin, studied by the authors
are the epidermis and subcutaneous fat (Silver et al.,
2002). These properties are essential for the
development of a 2D wave equation solution for
dermis.
WaveEquationModel
•Applyassumptionstodermis
•Modelusingliteraturevaluesfordermis
ModelAnimation
•Inputthedevelopedmodeltotestthe
visualization
HeterogeneousMaterial
•Developwaveequationmodelforeach
layerofskinandassembleintoone
Validation
•Finiteelementanalysistotestthe
propertiesofthedevelopedmaterial
WaveEquationModelofSoftTissueforaVirtualRealityLaparoscopyTrainingSystem-AValidationStudy
67

Table 1: Essential Properties of Dermis to Develop
the 2D Wave Equation.
Properties of
Dermis
Values
Area of Dermis
60603600
Thickness of
Dermis
1 (Silver et al., 2002)
Volume of
Dermis
606013600
Weight of
Dermis
1.810
(MacLaughlin and
Holick, 1985)
∴1.810
3600
6.4810
Density of
Dermis
6.4810
3600
1.810
18
Prestress (along
the fibers)
0.024 MPa (Hendriks, 2001)
Prestress
(across the
fibers)
0.0093 MPa (Hendriks, 2001)
Prestress
a
0.024
0.0093
2.5710
Tension
2.5710
6010
1.5410
a. Prestress identifies the natural force that affects skin, as a result of the
connective tissues and bones, and their interaction with the skin.
3.3 Developing a Mathematical Model
for a Layer of the Skin (Dermis)
3.3.1 Applying the Assumptions of 2D Wave
Equation to the Dermis
1. Mass of the dermis per unit area is constant.
2. The dermis is flexible therefore experiences
bending without resistance.
3. The dermis is stretched and fixed throughout
its boundary; as it is held in place by bones and
connective tissues. This stretching results in a
uniform tension per unit length T, which is
constant during motion.
4. The deformation of the membrane is small
compared to the size of the dermis, which is
plausible since the area of deformation is
smaller than the dermis that covers the entire
body.
5. The membrane is thin, this is the reason why
only a layer of skin, the dermis, is modeled
using this equation. Multiple two dimensional
wave equations are used to model all of the
layers of the skin to show how they would
interact to create a specific manipulation.
3.3.2 Wave Equation Solution Modeling the
Mechanics of Human Dermis
Based on the 2D wave equation solution shown in
subsection 3.1, the material properties of the dermis
and the assumptions of the model, the equation
below (equation (6)) is developed to model the
dermis. On the other hand, equation 5 is the Euler
formula.
,
4
6060
5
1
.
.
sin
0.06
sin
0.06
1
6.1110
(5)
,,
6.1110
cos
0.686
sin
.
sin
.
(6)
3.4 Animation of the Dermis Model
The author created an animated model of the dermis
in a symbolic math toolbox. This animation is used
to test the 2D wave equation and the visualization
that the model produces. The simple interaction of a
laparoscopic tool pushing down on the soft tissue,
causing deformation of the soft tissue and then the
return of the tissue to its original form, is
demonstrated in this animation.
3.5 Creating a Heterogeneous Model to
Replicate the Soft Tissue
In this paper, the author describes the development
of a two-dimensional wave equation for a single
layer of the soft tissue. However, the researcher has
developed this model for two other layers of the skin
(as can be seen in the appendix); therefore allowing
the representation of the mechanical and material
properties of the different layers of the skin. The
models for each of the layers are put together to
create a heterogeneous material like biological skin.
This model will represent the soft tissue in the VR
training system.
To create a heterogeneous material, the author
created a 6060__
model for each of the three layers of the skin, which
are epidermis, dermis, and subcutaneous fat. An
assembly of all these sections is created in a finite
element analysis software; in which important
material and mechanical properties of the soft tissue
are applied. The material properties that are used to
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
68

define each of the layers are: density, damping
factor, Young’s Modulus, Poisson’s ratio, and
tensile yield strength. These values are based on the
data from the following studies: (Zahouani et al.,
2009, Silver et al., 2002, Geerligs et al., 2011,
Geerligs et al., 2008, Gibney et al., 2010).
3.6 Validation of the Skin Model
As this is a novel soft tissue model, a validation
study is performed to corroborate the mathematical
model with the behavior of the biological tissue.
This study looks at the mechanical properties of the
designed wave equation models with respect to the
skin. Previous studies have used qualitative
methods, e.g. surveys or questionnaires to assess
their tissue models (Fried et al., 2004, Gavazzi et al.,
2011). On the other hand, this study aims to use a
quantitative method for a more objective analysis.
Because of this, the authors are using FEA models to
get data from an accurate model and compare this to
the wave equation model developed in the
subsections above.
For this study, a heterogeneous material is
recreated in a FEA program to ensure correct
material properties’ assignment to each of the layers
that are modeled. The material properties of the soft
tissue are introduced for each layer, to accurately
mimic the properties of the soft tissue.
Using the FEA model, a static study is
performed on the resulting heterogeneous material.
In this system, the boundaries of all the layers are
treated as fixed supports to complement the
assumption applied to the solution of the wave
equation. A total force of 5N is applied at
increments of 0.05N over a time period of 100
seconds. Like the deformation in the wave equation
model, this model focuses on the simple action of
pushing down on the soft tissue with a laparoscopic
tool. To get solutions for a comparison, the data
from the developed wave equation models are
manipulated to find the maximum deformation at
each layer at every time increment.
Using this data, a statistical analysis is
performed to compare the two models. First, a
normal distribution study is performed to compare
the behavior of the two models. Subsequently, a t-
test is performed to compare the two models at each
of the layers of the skin. The researchers use the
maximum deformation values to compare the two
models, because the aim of the wave equation model
is a novel method to improve the visualization of the
soft tissue model in a VR training system.
4 RESULTS
4.1 Animation of the Dermis
The animation that is developed using the wave
equation shows the behavior of the modeled soft
tissue when pushed on and its return back to the
original shape. Figure 4 is a set of screenshots from
the developed animation and shows the transitions of
the soft tissue during the described tool
manipulation.
(a) At 0 seconds
(b) At 1.5 seconds
(c) At 4.8 seconds
Figure 4: The animation, which is created to check the
visualization of the 2D wave equation for the dermis.
Figures (a-c) show the steps the model takes to defor
m
downward whereas figure 2 (d) shows the soft tissue as i
t
returns back to its original shape. The units of the x,y,z are
meters therefore the values are very small as the
deformation would be very minute at this unit.
WaveEquationModelofSoftTissueforaVirtualRealityLaparoscopyTrainingSystem-AValidationStudy
69

(d) At 8.5 seconds
Figure 4: The animation, which is created to check the
visualization of the 2D wave equation for the dermis.
Figures (a-c) show the steps the model takes to deform
downward whereas figure 2 (d) shows the soft tissue as it
returns back to its original shape. The units of the x,y,z are
meters therefore the values are very small as the
deformation would be very minute at this unit.(cont.)
4.2 Heterogeneous Material: Skin
Figure 5 looks at the heterogeneous material that is
developed for the finite element analysis. This image
shows the exploded view of the developed material
to demonstrate the three skin layers that are makeup
the soft tissue model. As mentioned earlier, the
layers that this model focuses on are the epidermis,
dermis, and subcutaneous fat. As can be seen from
figure 5, the layers can be distinguished by their
thicknesses; this information is based on literature
values from: (Hendriks, 2001, Silver et al., 2002,
Gibney et al., 2010).
Figure 5: This figure shows the isometric and exploded
view of the soft tissue. Here, the hatched layer is the
epidermis, the dotted layer is the dermis and the layer with
the zigzag pattern is the subcutaneous fat.
4.3 Mechanical Properties of the
Heterogeneous Model
This section, demonstrates the results that are
statistically analyzed to compare the two models.
Figure 6 aims to demonstrate the maximum
deformations from the two models, during the soft
tissue manipulations. On the other hand, figure 7,
shows results from the finite element analysis. These
results are like those seen in the wave equation
animation.
Figure 6: This graph shows the maximum deformations
observed in the wave equation and finite element models
of the dermis.
(a) (b)
(c)
Figure 7: Here, is a representation of the deformation of
three layers in the FEA model [(a) epidermis, (b) dermis
and (c) subcutaneous fat] of the heterogeneous material.
4.4 Statistical Analysis
4.4.1 Normal Distribution
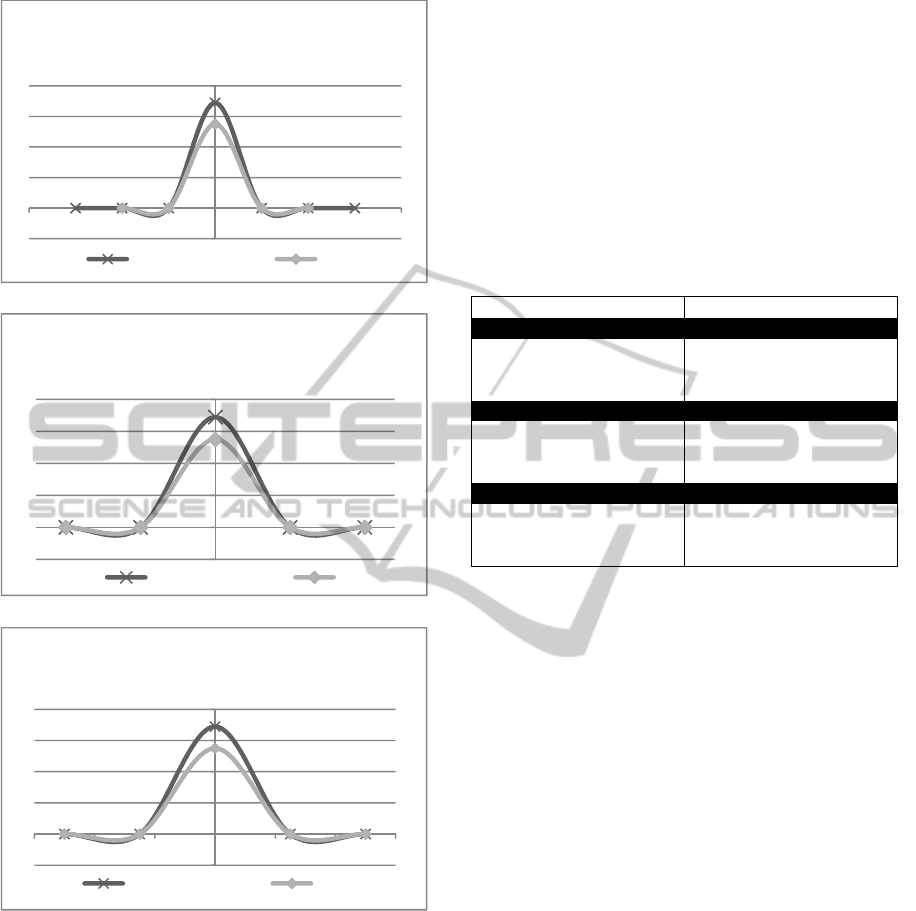
The normal distribution studies, graphed in figure 8
(a-c), show high variability between the wave
equation models and the heterogeneous FEA
material. The values that are plotted in figure 8 are
based on the maximum deformations at different
time periods in the FEA software. On the other hand,
for the wave equation model, the models for the
different layers are calculated and maximum
deformation values at each time interval are found,
from the raw data. The calculations in this statistical
analysis are performed using various functions in
Microsoft Excel.
0,00E+00
2,00E-02
4,00E-02
6,00E-02
8,00E-02
0 20406080100120
Maximum
Deformations (m)
Time (s)
Finite Element Analysis Wave Equation
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
70
(a)
(b)
(c)
Figure 8: Figures (a-c) are graphs that demonstrate normal
distribution tests for the different layers (epidermis,
dermis, subcutaneous fat; respectively) to show the
relationships between the two models discussed in the
methods section. Here the line with (x) marker represents
the results from the wave equation whereas the line with
(♦) marker represents the results from the mechanical
study of the finite element model.
4.4.2 T-Test
The t-test results that are displayed in table 2 are
based on the results found using the Data Analysis
Toolpak in Microsoft Excel. The t-test is designed
for two samples assuming equal variances where
0.05; alpha is the significance level that we are
employing in the analysis. The null hypothesis in
this analysis is that the means are equal, which we
would expect since the models are of the same
tissue. On the other hand, the alternative hypothesis
is that the means are not equal. All the values
displayed in the table are rounded to the nearest
thousandth.
Table 2: This table shows the t-values found for the
comparison between the wave equation model and finite
element model for each layer of the skin.
T-test Results
Epidermis
P (Two Tail) 0.364
t Stat -0.912
t Critical Value 1.975
Dermis
P (Two Tail) 0.395
t Stat 0.911
t Critical Value 1.975
Fat
P (Two Tail) 0.363
t Stat 0.853
t Critical Value 1.975
5 DISCUSSION
5.1 Data Analysis
Despite the fact that the plot of the maximum
deformations for the two models are different
(Figure 6), due to the rate at which the two models
move, the two datasets show similarities as expected
from models of the same material. Along with that
the wave equation has a smoother transittion when
there is a change in the direction of the force
applied.
The results from the statistical analysis can
provide a comparison between the wave equation
and heterogeneous material models.
When we analyze the normal distribution of the
data, from the two models for each of the layers of
the soft tissue, it can be concluded that the two data
sets have high variability. High variability in the
normal distribution study suggests high correlation
between the two models, which would be expected
since they model the same biological material.
The t-test is performed with the null hypothesis
that the two data sets have equal variances. There
are two ways the results from table 2 can be used to
determine whether the null hypothesis is rejected or
not. The first is if 0.05 whereas the
‐2
0
2
4
6
8
‐1 ‐0,5 0 0,5 1
WaveEquationvs.FEAResults
(Epidermis)
WaveEquation FEA
‐2
0
2
4
6
8
‐0,6 ‐0,4 ‐0,2 0 0,2 0,4 0,6
WaveEquationvs.FEAResults
(Dermis)
WaveEquation FEA
‐2
0
2
4
6
8
‐0,6 ‐0,4 ‐0,2 0 0,2 0,4 0,6
WaveEquationvs.FEAResults
(SubcutaneousFat)
WaveEquation FEA
WaveEquationModelofSoftTissueforaVirtualRealityLaparoscopyTrainingSystem-AValidationStudy
71

second is if . These two
relationships are seen in the three t-tests that are
performed for each of the layers of the skin. These
results therefore suggest that the null hypothesis can
not be rejected and the means are the same. These
results display similarities and correlations as would
be expected from models of the same soft tissue.
As discussed earlier in the literature review, FEA
is computationally expensive for real time
simulation and therefore, despite its accuracy, it is
not the choice of model for surgical simulation.
During this study the user is able to observe the
difference between the wave equation model and the
FEA model, and their computational cost. The wave
equation results are acquired in 6 seconds whereas
solving the FEA model takes approximately 4
minutes.
The computational cost and the statistical
analysis support the use of wave equation as a model
of soft tissue in a surgical simulation.
5.2 Protocol Analysis
The heterogeneous material in this paper is an
oversimplified version of the actual soft tissue. This
is because it does not take into consideration the
connective tissues, blood vessels, hair follicle and
other components that makeup the skin structure. It
is important to look into the effects of these
components on the mechanics and therefore the
model of skin. Also, the thickness of the layers in
the novel model is consistent throughout the layer,
which wouldn’t be the case for the biological
material. This inaccuracy can be resolved by adding
materials of various sizes to the assembly of the
heterogeneous material, in future models.
Although, this study models skin using wave
equation, the ultimate goal of this study is to
transform this mathematical model, so that it can
easily be modified or altered to complement the
mechanical behavior of different soft tissues based
on the needs of the trainee, surgeon, or procedure.
5.3 Future Application of Model
This model of skin will be implemented into a VR
training system for the development of laparoscopic
surgery skills. Figure 9 shows the overall system that
will be developed using the soft tissue model
discussed in this paper.
Located in a developing nation, our lab
appreciates the need for skilled doctors in
laparoscopic procedures. This knowledge is less
attainable in the rural parts of the country and this
lack of information makes it extremely challenging
for doctors in these parts of the country to provide
the same level of healthcare as seen in the capital
city.
(a) (b)
Figure 9: This diagram shows the conceptual design of the
overall system that the authors aim to design. As can be
seen, there are two components: a) the graphical user
interface that consists of the soft tissue model from this
paper, laparoscopic tools, and directions for proper
technique and b) the haptic interface that will allow
realistic interaction with the user interface.
This system aims to produce a more realistic
interaction between the user and the user interface
therefore allowing a more accurate transference of
skills from the training system to the operating
room. This VR training system will teach the user
proper laparoscopic suturing techniques; a difficult
task. It will also provide the user with an objective
assessment of their performance on the device
therefore monitoring the user’s skills and techniques
over the training period. A successful system will
provide people around the country with quality
healthcare.
6 CONCLUSIONS
Laparoscopic surgeries are trending due to the
benefits for the patient, despite the constraints the
surgeons experience in a minimally invasive
environment. This paper discusses a novel
mathematical model to improve the realism and
visualization of the soft tissue in a VR training
system. The proposed method utilizes wave equation
to model soft tissue and laparoscopic tools’
interaction. The soft tissue model shows promise,
based on the comparison with the FEA model, which
is one of the most accurate methods of modeling in
VR. In future studies, this model will be
implemented into a novel training system and the
effectiveness of the system as a training device will
be assessed based on the ability of the device to
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
72

allow repetitive training with continuous
performance feedback.
ACKNOWLEDGMENT
The authors would like to thank Thailand’s National
Research Universities Grant through Mahidol
University for their financial support. The first
author would like to take this opportunity to thank
Aditya Birla Group’s Pratibha Scholarship, and the
Department of Biomedical Engineering’s
Biomedical Engineering Scholarship (BMES) for
providing financial aid for her graduate education.
The first author would also like to thank her
colleagues at BART LAB for their continuous
support and assistance, throughout her time at the
laboratory.
REFERENCES
Ali, M. R., Mowery, Y., Kaplan, B. & Demaria, E. J.
2002. Training The Novice In Laparoscopy. More
Challenge Is Better. Surg Endosc, 16, 1732-6.
Basdogan, C., De, S., Kim, J., Muniyandi, M., Kim, H. &
Srinivasan, M. A. 2004. Haptics In Minimally
Invasive Surgical Simulation And Training. Ieee
Comput Graph Appl, 24, 56-64.
Basdogan, C., Ho, C.-H. & Srinivasan, M. A. 2001.
Virtual Environments For Medical Training: Graphical
And Haptic Simulation Of Laparoscopic Common
Bile Duct Exploration. Mechatronics, Ieee/Asme
Transactions On 6, 269-285.
Bashankaev, B., Baido, S. & Wexner, S. D. 2011. Review
Of Available Methods Of Simulation Training To
Facilitate Surgical Education. Surg Endosc, 25, 28-35.
Beards, C. 1996. The Vibration Of Continuous Structures.
Structural Vibration: Analysis And Damping.
Burlington, Ma: Butterworth-Heinemann.
Bessems, D., Rutten, M. & Van De Vosse, F. 2007. A
Wave Propagation Model Of Blood Flow In Large
Vessels Using An Approximate Velocity Profile
Function. Journal Of Fluid Mechanics, 580, 145-168.
Brown, J., Sorkin, S., Latombe, J. C., Montgomery, K. &
Stephanides, M. 2002. Algorithmic Tools For Real-
Time Microsurgery Simulation. Med Image Anal, 6,
289-300.
Derossis, A. M., Fried, G. M., Abrahamowicz, M.,
Sigman, H. H., Barkun, J. S. & Meakins, J. L. 1998.
Development Of A Model For Training And
Evaluation Of Laparoscopic Skills. Am J Surg, 175,
482-7.
Fried, G. M., Feldman, L. S., Vassiliou, M. C., Fraser, S.
A., Stanbridge, D., Ghitulescu, G. & Andrew, C. G.
2004. Proving The Value Of Simulation In
Laparoscopic Surgery. Ann Surg, 240, 518-25;
Discussion 525-8.
Gavazzi, A., Bahsoun, A. N., Van Haute, W., Ahmed, K.,
Elhage, O., Jaye, P., Khan, M. S. & Dasgupta, P.
2011. Face, Content And Construct Validity Of A
Virtual Reality Simulator For Robotic Surgery (Sep
Robot). Ann R Coll Surg Engl, 93, 152-6.
Geerligs, M., Peters, G. W., Ackermans, P. A., Oomens,
C. W. & Baaijens, F. P. 2008. Linear Viscoelastic
Behavior Of Subcutaneous Adipose Tissue.
Biorheology, 45, 677-88.
Geerligs, M., Van Breemen, L., Peters, G., Ackermans, P.,
Baaijens, F. & Oomens, C. 2011. In Vitro Indentation
To Determine The Mechanical Properties Of
Epidermis. J Biomech, 44, 1176-81.
Gibney, M. A., Arce, C. H., Byron, K. J. & Hirsch, L. J.
2010. Skin And Subcutaneous Adipose Layer
Thickness In Adults With Diabetes At Sites Used For
Insulin Injections: Implications For Needle Length
Recommendations. Curr Med Res Opin, 26, 1519-30.
Hendriks, F. M. 2001. Mechanical Behaviour Of Human
Skin In Vivo: A Literature Review. Koninklijke
Philips Electronics N.V., Nat. Lab. Unclassified
Report 1-46.
Itsarachaiyot, Y. 2012. Haptic Interaction Of
Laparoscopic Surgery In Virtual Environment. Master
Of Engineering, Mahidol University.
Itsarachaiyot, Y., Pochanakorn, R., Nillahoot, N. &
Suthakorn, J. Force Acquisition On Surgical
Instruments For Virtual Reality Surgical Training
System. 2011 International Conference On Computer
Control And Automation (Iccca 2011), May 1-May 3
2011 Jeju Island, South Korea. Ieee, 173-176.
Kreyszig, E., Kreyszig, H. & Norminton, E. J. 2011.
Partial Differential Equations (Pdes). In: Corliss, S.
(Ed.) Advanced Engineering Mathematics. 10 Ed.
United States Of America: John Wiley & Sons Inc.
Maclaughlin, J. & Holick, M. F. 1985. Aging Decreases
The Capacity Of Human Skin To Produce Vitamin
D3. J Clin Invest, 76, 1536-8.
Munz, Y., Kumar, B. D., Moorthy, K., Bann, S. & Darzi,
A. 2004. Laparoscopic Virtual Reality And Box
Trainers: Is One Superior To The Other? Surg Endosc,
18, 485-94.
Roberts, K. E., Bell, R. L. & Duffy, A. J. 2006. Evolution
Of Surgical Skills Training. World J Gastroenterol,
12, 3219-24.
Sánchez-Sesma, F. J., Palencia, V. J. & Luzón, F. 2002.
Estimation Of Local Site Effects During Earthquakes:
An Overview. Iset Journal Of Earthquake
Technology, 39, 167-193.
See, W. A., Cooper, C. S. & Fisher, R. J. 1993. Predictors
Of Laparoscopic Complications After Formal Training
In Laparoscopic Surgery. Jama, 270, 2689-2692.
Silver, F. H., Seehra, G. P., Freeman, J. W. & Devore, D.
2002. Viscoelastic Properties Of Young And Old
Human Dermis: A Proposed Molecular Mechanism
For Elastic Energy Storage In Collagen And Elastin.
Journal Of Applied Polymer Science, 86, 1978-1985.
WaveEquationModelofSoftTissueforaVirtualRealityLaparoscopyTrainingSystem-AValidationStudy
73

Sutherland, L. M., Middleton, P. F., Anthony, A.,
Hamdorf, J., Cregan, P., Scott, D. & Maddern, G. J.
2006. Surgical Simulation: A Systematic Review. Ann
Surg, 243, 291-300.
Weigand, D. A., Haygood, C. & Gaylor, J. R. 1974. Cell
Layer And Density Of Negro And Caucasian Stratum
Corneum. J Investig Dermatol, 62, 563-568.
Wherry, D. C., Rob, C. G., Marohn, M. R. & Rich, N. M.
1998. An External Audit Of Laparoscopic
Cholecystectomy Performed In Medical Treatment
Facilities Of The Department Of Defense. Ann Surg,
220, 626–634.
Zahouani, H., Pailler-Mattei, C., Sohm, B., Vargiolu, R.,
Cenizo, V. & Debret, R. 2009. Characterization Of
The Mechanical Properties Of A Dermal Equivalent
Compared With Human Skin In Vivo By Indentation
And Static Friction Tests. Skin Res Technol, 15, 68-76.
APPENDIX
2D Wave Equation Solution to Model
Other Layers of the Skin
As discussed in this paper, the skin is considered a
heterogeneous material, in this study; therefore this
section of the appendix shows the models for the
two other layers.
,,
6.11
10
cos
0.0032
(7)
sin
0
.
06
sin
0
.
06
The equation above (equation 7) models the
properties of the epidermis, using data from studies
on the human skin (Hendriks, 2001, Weigand et al.,
1974).
The second equation (equation 8), here,
represents the 2D model of the subcutaneous fat.
The equation is determined using the following
studies: (Hendriks, 2001, MacLaughlin and Holick,
1985, Gibney et al., 2010).
,,
6.1110
(8)
cos
5.3110
sin
0.06
sin
0.06
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
74
