
Fast Item-based Collaborative Filtering
David Ben-Shimon, Lior Rokach, Bracha Shapira and Guy Shani
Department of Information System Engineering, Ben-Gurion University of the Negev, Beer Sheva, Israel
Keywords: Item-based, Locality Sensitive Hashing, Collaborative-filtering, Top-N Recommendations.
Abstract: Item-based Collaborative Filtering (CF) models offer good recommendations with low latency. Still,
constructing such models is often slow, requiring the comparison of all item pairs, and then caching for each
item the list of most similar items. In this paper we suggest methods for reducing the number of item pairs
comparisons, through simple clustering, where similar items tend to be in the same cluster. We propose two
methods, one that uses Locality Sensitive Hashing (LSH), and another that uses the item consumption
cardinality. We evaluate the two methods demonstrating the cardinality based method reduce the
computation time dramatically without damage the accuracy.
1 INTRODUCTION
There are two dominant approaches to the
computation of CF recommendations; the memory -
based approach and the model-based approach
(Breese et al., 1998). A memory-based approach
computes recommendations directly over the raw
data – typically a user-item ratings matrix. Memory-
based methods require no pre-computation and
execute all computations online. Model-based
approaches construct statistical models – some
summarization of the raw data – that allows rapid
responses to recommendation queries online, and are
more commonly used in productive environments.
The item-item or item-based CF method is a
popular model-based approach (Sarwar et al., 2001).
This approach computes and caches for each item a
set of similar items, ordered by decreasing
similarity. When a user selects a specific item for
browsing or purchasing, the system can display a list
of N recommendations such as “similar items to the
item you just choose are…”, and so forth. Item-
based models have shown good performance and
low latency (Sarwar et al., 2001; Linden and Smith
2003).
Constructing such item-based models typically
requires that we compute the similarity between
each item to every other item, using O(I
2
)
computations, where I is the item set. When the
similarity function is symmetric, i.e. when
similarity(i,j)=similarity(j,i) the number of actual
computations is reduced to
2/)1( II
. Linden and
Smith (2003) further show that the complexity could
be effectively reduced to O(A·I) where A is the
average number of users that have selected each
item in the item set I. This is because many item
pairs were never consumed together, resulting in a
zero CF similarity score, thus, computing
similarities for such pairs can be avoided.
Nevertheless, those nearest neighbours’ algorithms
require computation that increases with both the
number of items and the number of users. With
current situation in many web sites, where the
number of users and items reach millions, these
neighbourhood algorithms suffer from scalability
issues.
In this paper we present two fast clustering
methods for offline computation of item-based CF
models for providing top-N recommendations. The
first method uses Locality Sensitive Hashing (LSH),
and the second using the cardinality of the item
consumption set. The methods clusters the item
space so similar items tend to be in the same cluster.
The suggested clustering methods are very simple
and cheap, but yet very efficient, decreasing the
computational complexity of the model building
phase to
/2 where C is a constant
representing the number of clusters and I is the items
set. We experiment with public and private data sets
showing significant reduction in computation time
using the suggested methods, with very minor
accuracy reduction.
The main contribution of this paper is hence to
suggest a very rapid approach for computing the
457
Ben Shimon D., Rokach L., Shapira B. and Shani G..
Fast Item-Based Collaborative Filtering.
DOI: 10.5220/0005227104570463
In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART-2015), pages 457-463
ISBN: 978-989-758-074-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

item-based CF model, which is a very common
scenario for practitioners. Additionally, we argue in
this paper that using a clustering algorithm as a pre-
process for neighbourhood models in RS
(Recommender Systems) must satisfies two
conditions - 1) that the clustering algorithm have to
be very cheap in term of computations and 2) that
there has to be some resemblance between the
clustering metric and the similarity metric used for
the neighbours computation in order to achieve
reduction in the neighbours computation; reduction
with minor damage to the accuracy if any.
The rest of the paper is as follows: section 2
provides a background and related work, section 3
presents the suggested methods, section 4 describes
the experiments and the results, and section 5
concludes with a discussion.
2 BACKGROUND AND RELATED
WORK
2.1 Top-N Recommendations for
Implicit Datasets
One of the most explored problems in
recommendation system research is the task of
predicting ratings for items. The RS is provided with
a user u and an item i, and predicts the rating that
user u will assign to the item i. Another common
recommendation task in e-commerce applications is
to display a list of items that the system considers to
be relevant for the user; often called top-N
recommendations. For example, Amazon presents to
the users a list of products under the title
“Recommendations for you in books”. In this case
the input data does not contain explicit ratings of
users to items, but rather events, such as purchases
or selections of items, often considered to be implicit
indications of the user preferences. Hence this task is
often known as top-N recommendations for implicit
datasets (Cremonesi et al., 2010).
Top-N recommendations given implicit data is a
very common scenario in productive environments
for varies reasons. First, rating data is not always
available. Many users do not provide explicit ratings
for items. Also, in many cases people do not
necessarily choose the top-rated items. For example,
people often choose to watch 3-star rated movies
rather than 5-star movies (Shani and Gunawardana
2011). Secondly, the calculation of the prediction
that every user will give to any item in a prediction-
based system, just for providing the top-N out of it,
may be an exhaustive one as web-sites nowadays
may have millions of users and items. Moreover, in
case the task is to present interesting items to the
user, the results of a prediction-based approach
might be inferior to an approach that directly
maximizes the likelihood that an item will be
chosen. Thus, we choose to focus on top-N
recommenders for implicit datasets.
A popular approach to top-N recommendations
uses a neighbourhood-based item-item model. That
is, for each item we identify a list of nearest
neighbours, assuming that these neighbours would
make good suggestions for a user that has chosen the
item. A neighbourhood is defined based on some
similarity metric between items. These similarities
are cached in a model, which is used online to
provide recommendations for a given item, by
looking at the cached nearest neighbours list for that
item. In a CF approach for implicit data sets, two
items may be considered to be similar, if users tend
to consume them together. A simple and popular
example of a similarity function for implicit datasets
is the Jaccard metric (Jaccard 1901) as presented in
equation (1).
,
|
∩
|
|
∪
(1)
here Ui and Uj are the sets of users that consumed
items i, and j respectively.
2.2 Clustering Approaches for
Improving Neighbourhood CF
There have been a numerous studies in the literature
that indicates the benefits of applying clustering in
the pre-processing step for the neighbourhood-based
CF computation (Bridge and Kelleher 2002; Chee
2000; Sarwar et al., 2002; Lin et al., 2014). The
majority of these works are using k-means or some
variation of k-means for clustering the item space or
the user space, and by that decreasing the dimension
of the problem so that similarities will be then
computed only among objects within the same
cluster. Although such a method is indeed
decreasing the computations of the pairs, it is well
known that k-means by itself is very expensive
algorithm yielding complexity from the order of
)log(
1
nNO
dk
where d is the number of
dimensions, k is the number of clusters and n is the
number of entities. Thus, even in one dimension and
two clusters this is a very exhaustive computation
which makes it not applicable in large scale systems.
In fact, most clustering and partitioning algorithms
suggested in the literature for this task require a
distance metric or similarity metric to guide the
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
458

learning process of the clusters. Since our goal is to
decrease the computation of the item-pairs, which is
also offline in systems aimed to deliver top-N
recommendations, we cannot consider as pre-
processing step applying clustering algorithms that
are from the order of
2
()OI
.
O’Connor and Herlocker (1999) apply sets of
experiments to evaluate the efficiency of several
partition techniques as a pre-processing step to the
item-based CF computation. They end up with
suggesting the k-Metis (Karypis and Kumar 1998) as
a partitioning algorithm because of its shorter
execution time, the ability to create distributed
clusters and of course due to the final accuracy the
model achieved. Metis represents the item space as a
graph and partition it into k predefined partitions
using multi-level graph partitioning methods.
Although the complexity of this problem is NP
complete, representing implicit feedback dataset as
such a graph is already involved a lot of
computations. The representation will include the
items as vertexes and the edges will represent the CF
relation among the items, i.e. the value on each edge
may be a number which indicating how many users
consume these two items together. This
representation will consume tremendous amount of
computation as potentially Metis will need to know
whether two items consumed together or not. In the
best case, just for building the graph, it will have to
compute the upper part of equation (1) for every two
items is the system which of course not feasible.
Moreover, the majority of those studies consider
the pre-processing clustering step as an offline step
and the actual item-based CF as an online step; the
pre-processing step aimed to reduce the computation
of the item-based CF. As such, they are not
concerned about the cost of the clustering algorithm.
This stands in contradiction to our case, where the
entire computation, clustering and neighbours
computation are done offline and we wish to
minimize it entirely.
We hence argue that for the specific scenario we
handling, top-N recommendations given implicit
dataset, our following suggested methods are far
simpler and require much less (logarithmic with the
number of items or/and users) computation in the
clusters computation.
3 FAST ITEM-BASED MODEL
BUILDING
This section presents two methods for clustering the
items as a pre-process step to the CF model
computation. We use a straightforward item-based
recommendation algorithm which computes the
item-to-item Jaccard similarities, showing how
linear clustering techniques can reduce the amount
of computation.
Our approaches divide the item space into hard
clusters, such that similar items tend to belong to the
same cluster. We then compute the item pairs
similarity only for items within each cluster,
ignoring inter-cluster similarities. As stated before,
clustering requires additional computational
overhead and it is crucial that the clusters will be
computed very rapidly. For efficient access to items
and users, we use a data-structure that allows us to
rapidly access all the users who have used an item,
and all the items that a given user has used.
3.1 Locality Sensitive Hashing
The first pre-processing clustering method for
rapidly compute the item-based CF model relies on
Locality sensitive hashing (LSH) (Gionis et al.,
1999). Given a set of high-dimensional item
descriptors, LSH uses Min-Hashing to map each
item to a reduced space using one or more hashing
functions. This reduced space is called the signature
matrix, where each item is represented by a
signature - a low dimensional vector of features. A
good hashing function maintains item-item
similarities, such that similar items will have similar
signatures with high probability.
To generate the signature matrix, we follow
Google news personalization (Das et al., 2007)
where the hash value for an item in a given
dimension in the signature of an item, is the first
user id that consumed this item in a random
permutation of the user ids list. We generate P
permutations of the user ids and apply this hash
function on each of the permutations, generating an
item signatures matrix of size
PxI
. Hence P is the
dimension of the signatures matrix.
We now leverage the generated signature matrix
to create a clustering of the items, using the
following recursive procedure; we split the item set
into two disjoint subsets, such that the items in each
subset are expected to be more similar to one
another, than to items in the other subset. We first
compute the median of each dimension (row in
PxI
) in the signature matrix independently. Then, for
each item (column in
PxI
) in the signature matrix,
we compute the portion of its dimensions entries
whose value is higher than the median of that
dimension. If this portion is lower than 0.5, the item
FastItem-BasedCollaborativeFiltering
459

is placed in the left child subset, otherwise it is
placed in the right child subset. We then continue
with the left and right subsets recursively, until the
intended number of clusters has been reached.
This splitting approach creates a balanced binary
tree, where every two disjoint subsets created
through the splitting process are always the full set
of their related parent. Figure 1 illustrates the tree
construction and the number of items in each node
and leaf.
The construction of the tree is the actual pre-
process clustering step to the item-item Jaccard
similarities computation. The time complexity of
this phase is
)log( IPIO
where P is the number of
dimensions in the signatures matrix, and I is the
number of items. In practice, it is very fast in
comparison with the item pairs computations
required for the item-item similarities because the
number of dimensions P is no more than dozens.
Figure 1: The amount of items I, is divided evenly on each
level according to the medians. Each level in the tree
comprises all the items.
After the tree construction, we compute the item-
item Jaccard similarities only among the items
which are in the same leaf. Following the example in
figure 1, where the number of clusters is 4, this will
result in
)8/(
2
IO
item-item computations
compared with the
)2/(
2
IO
required for computing
all item pairs similarities. Assuming the hashing
function maintains the similarity among the items as
in the original data, and that the median splits the
items into two homogenous groups during the
construction of the tree, we expect that items with
high similarity will be located in the same
cluster/leaf.
3.2 The Cardinality of the Item Profile
The second method relies on the hypothesis that the
likelihood of obtaining a higher similarity score
between two items increases, as the difference
between the cardinality of the set of users who
consumed those items decreases.
That is, given two items i and j, J(i,j) is more
likely to be high when the difference between their
cardinality, ||Ui|-|Uj||, is low.
Following this assumption, we sort and list the
items by decreasing cardinality, and then divide the
list into a set of sub-lists (clusters) such that each
cluster comprising items with the same or similar
cardinality. As our data structure allows us to
compute this cardinality rapidly, these clusters are
extremely fast to generate. As with the LSH method,
we then compute the similarities only among items
that are within the same cluster and cache the scores
as an item-based model.
Following is a pseudo code of the Cardinality
similarity approach.
NC = number of desired clusters
L = items sorted by popularity
clusterSize = L.size()/NC;
Clusters clusters;
For i=0 to NC ; i++
clusters.add(L.subList(i*clusterSi
ze,(i+1)*clusterSize))
For each Cluster c in clusters
For i = 0 to |c|-1
For j = i+1 to |c|
compute J(ci,cj)
3.3 Initialization Complexity
Let I be the number of items, A be the average
number of users who have chosen each item, and P
be the reduced dimension in the LSH reduction. The
complexity for the Tree LSH clustering requires
)( AIPO
for computing the signatures matrix.
Then, constructing the tree requires
)log( IPIO
operations, for finding the medians in each level in
the tree, and there are at most
)(logIO
levels.
Hence, assuming that A and P are much smaller than
I, the computation time is dominated by
)log( IIO
.
The complexity of the clustering cardinality
method is
)log( IIO
for sorting the items by the
number of users who consumed them. In the results
below the clustering time is included. For both
methods it required no more than a few dozens of
milliseconds and is therefore negligible.
4 EMPIRICAL EVALUATION
We now compare the performance of the two
clustering methods. In both methods we compute the
similarities only for pairs of items which were
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
460
located in the same cluster. When there is only a
single cluster, our approach is equivalent to the
efficient Amazon approach (Linden et al., 2003).
We conduct experiments on three datasets, a
games web shop
1
buying events, and on Movie-
Lens
2
100000 ratings and Movie-Lens 1,000,000
ratings. The datasets described in table 1. For
Movie-Lens, we attempt to recommend movies that
the user may rate, given other movies she has rated.
To model that, we ignore the actual ratings, and use
a dataset where users either rate, or did not rate a
movie. The games dataset contains real data from an
online shop selling software games collected during
the year of 2010. In the games dataset we compute a
list of recommended items given other items that the
user has bought.
Table 1: The benchmark datasets used in the experiments.
Name #events # items # users Sparsity
Games 320,641 3304 72,347 0.9986
Movie-Lens 100,000 1682 943 0.9369
Movie-Lens 1,000,000 3706 6040 0.9553
Each users’ consumption set is divided into a
train and test set. For each user u we randomly pick
a random number k between 0 and the number of
items that u has rated or bought. We then pick k
random items from u’s consumption set and use
them as the training set; the remaining items are
used for testing. We execute both methods on all the
three datasets, each run with different predefine
number of clusters. We build the model over the
training set and measure the time it took to build the
model. We then measure the precision over the test
set. Due to the nature of the predictions we provide,
we found precision@N (Herlocker et al., 2004) to be
the most appropriate metric for evaluating the
models’ performance.
Below, we provide results for N=5, i.e., we ask
the algorithm to supply us with 5 recommendations.
We also experimented with N=10, but we found no
sensitivity to N. We measure the performance of the
methods with 128, 64, 32, 16, 8, 4, 2, and 1 cluster.
On the Movie-Lens 1 million ratings dataset we also
measured with 256, 512 and 1024 clusters.
Both methods were executed 5 times with
different train-test splits on each predefined number
of clusters, and the results in the figures below are
averaged over the 5 repetitions. The standard
deviation was below 10
-5
and is hence omitted from
the graphs. Both algorithms use the same random
train-test split.
1
Due to privacy issues we cannot publish the data
2
http://www.grouplens.org/node/73
4.1 Results
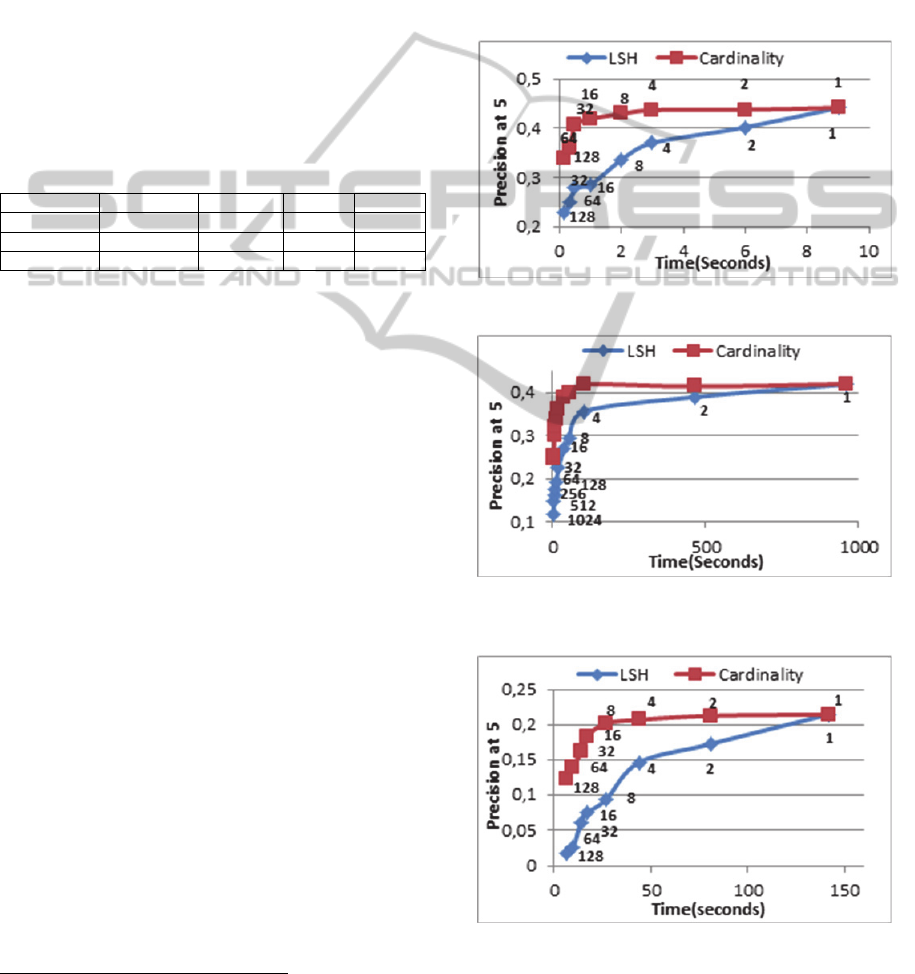
Figures 2, 3 and 4 present precision as a function of
computation time. Each point in a curve represents
the precision of a model with a different predefined
number of clusters. As the number of clusters drops,
more items fall into each cluster, requiring more
computation time. Both methods require the same
amount of time for a given number of clusters, and
split the item set evenly into clusters of identical
sizes.
Figure 2: Performance for the Movie-lens 100k dataset.
Figure 3: Performance for the Movie-lens 1 million
dataset.
Figure 4: Performance for the games dataset.
The clustering time for both methods is
negligible, hence, the overall time is dominated by
FastItem-BasedCollaborativeFiltering
461

the pairwise similarity computations for the larger
clusters. The data points in the curves are average
over 5 repetitions and labelled with the number of
predefined clusters.
5 CONCLUSIONS AND
DISCUSSION
This paper suggests two methods for speeding up the
building of an item-based CF model for top-N
recommendations over implicit datasets. By splitting
items into clusters, and computing pairwise
similarities only for items within the same cluster,
we reduced the computation time dramatically. The
first approach based on LSH and the second on the
cardinality of the item consumption set. Our
experiments show that the cardinality approach
outperformed the LSH, resulting in no decrease in
precision while reducing the computation time up to
10% for the larger dataset.
The cardinality method somehow claims that
similar items also have similar popularity. Although
it might be true and make sense, it is true in our case
only because the similarity function we choose was
Jaccard coefficient which utilized exactly this
aspect. Means that item with low cardinality will
have very small similarity score to item with high
cardinality, if any, because the intersection between
them, the upper part of equation (1), will be close to
zero.
We hence suggest that in order to obtain an
efficient clustering method as pre-process step for
item-base model computation, there has to be some
resemblance between the clustering metric and the
proximity metric used for the items similarity.
Otherwise results may look a bit arbitrary, unless the
clustering method is completely generic as like the
above suggested LSH. For instance applying
content-based clustering such that movies items will
be grouped together according to their Genre may be
a good idea as a clustering method, if the proximity
metric which is used for the item-item similarity
considers the Genres of a movie as part of the
similarity computation. A successful clustering
method will not only be cheap, but also will
encapsulate a hint from the proximity metric which
is later used to calculate the similarity scores. We
therefore suggest that LSH clustering method, which
is not related at all to the similarity metric, is more
recommended if one cannot define a clustering
method which is somehow correlated with the
similarity metric.
An additional benefit of our methods is that the
item-pairs computation of each cluster can be done
in parallel, to further reduce the actual time required
for computing the item-based model.
REFERENCES
J. S. Breese. D. Heckerman, C. Kadie (1998). Empirical
analysis
of predictive algorithms for collaborative
filtering. UAI-98, 43–52.
D. Bridge, J. Kelleher (2002). Experiments in sparsity
reduction: Using clustering in collaborative
recommenders. In Artificial Intelligence and Cognitive
Science (pp. 144-149). Springer Berlin Heidelberg.
S. H. S Chee.(2000) RecTree: A Linear Collaborative
Filtering Algorithm. M.Sc Thesis. Simon Fraser
University.
P. Cremonesi , Y. Koren, R. Turrin (2010). Performance
of recommender algorithms on top-n recommendation
tasks. In Proc. 4th ACM Conference on Recommender
Systems, 39-46.
A. S. Das, M. Datar, A. Garg, S. Rajaram (2007). Google
news personalization: scalable online collaborative
filtering. In Proceedings of the 16th international
conference on World Wide Web (pp. 271-280). ACM.
P. Gionis, P. Indyk, R. Motwani (1999). Similarity search
in high dimensions via hashing. Proceedings of VLDB,
pp. 518–529.
J. L. Herlocker, J. A. Konstan, L. G Terveen, J. T. Riedl
(2004). Evaluating Collaborative Filtering
Recommender Systems. ACM Trans. Information
Systems, vol. 22, no. 1, pp. 5-53, 2004.
P. Jaccard (1901). Étude comparative de la distribution
florale dans une portion des Alpes et des Jura. Bulletin
de la Société Vaudoise des Sciences Naturelles 37:
547–579.
G. Karypis, V. Kumar (1998). A software package for
partitioning unstructured graphs, partitioning meshes,
and computing fill-reducing orderings of sparse
matrices. University of Minnesota, Department of
Computer Science and Engineering, Army HPC
Research Center, Minneapolis, MN.
C. Lin, G. R., Xue, H. J. Zeng, B. Zhang, and Wang, J.
(2014). U.S. Patent No. 8,738,467. Washington, DC:
U.S. Patent and Trademark Office.
G. Linden, B. Smith, J. York (2003). Amazon.com
recommendations: Item-to-item collaborative filtering.
IEEE Internet Computing, 7, 76-80.
B. Sarwar, G. Karypis, J. Konstan, J. Riedl. (2001). Item-
based collaborative filtering recommendation
algorithms. WWW10.
B. M. Sarwar, G. Karypis, J. Konstan, J. Riedl.(2002)
Recommender systems for large-scale e-commerce:
Scalable neighborhood formation using clustering.
In Proceedings of the fifth international conference on
computer and information technology (Vol. 1).
M. O’Connor, J. Herlocker (1999). Clustering items for
collaborative filtering. In Proceedings of the ACM
SIGIR workshop on recommender systems (Vol. 128).
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
462

UC Berkeley.
G. Shani, A. Gunawardana (2011). Evaluating
Recommendation Systems. Recommender Systems
Handbook: 257-297.
FastItem-BasedCollaborativeFiltering
463
