
Low-rank and Sparse Matrix Decomposition with a-priori Knowledge
for Dynamic 3D MRI Reconstruction
Dornoosh Zonoobi, Shahrooz Faghih Roohi and Ashraf A. Kassim
1
Department of Electrical & Computer Engineering, National University of Singapore, Singapore, Singapore
Keywords:
Low-rank and Sparse Matrix Decomposition, a-priori knowledge, Dynamic 3D MRI, Image Reconstruction,
Compressive Sensing.
Abstract:
It has been recently shown that incorporating priori knowledge significantly improves the performance of basic
compressive sensing based approaches. We have managed to successfully exploit this idea for recovering a
matrix as a summation of a Low-rank and a Sparse component from compressive measurements. When applied
to the problem of construction of 4D Cardiac MR image sequences in real-time from highly under-sampled
k−space data, our proposed method achieves superior reconstruction quality compared to the other state-of-
the-art methods.
1 INTRODUCTION
A fundamental problem in dynamic MRI, such as
real-time cardiac MRI (rtCMR), is the limitation of
spatial and temporal resolution which is due to the
slow data acquisition process of this modality. This
problem is even more profound when dealing with 4D
MR volumes. Compressive Sensing (CS) has been
shown to be able to overcome these challenges and
recover MRI images from much smaller k-space mea-
surements than conventional reconstruction methods.
To achieve this, earlier CS-based methods assumed
that the MRI images have a sparse representation
in some known transform domain (Zonoobi et al.,
2014; Hu et al., 2012; Lustig et al., 2008; Zonoobi
et al., 2011) and the idea was easily extended to
the reconstruction of dynamic MRI images data by
jointly reconstructing the entire sequence by treating
it as higher dimensional data (Gamper et al., 2008;
Venkatesh et al., 2010). In other works, the high
spatiotemporal correlation was utilized to recover dy-
namic images by solving a low rank matrix comple-
tion problem in which each temporal frame is a col-
umn of the recovered matrix (Zhao et al., 2010), (Hal-
dar and Liang, 2011).
Some studies have reported much improved re-
sults that were obtained by combining rank deficiency
and transform domain sparsity. These include propos-
als to recover the image as a solution which is both
sparse and low rank (Majumdar and Ward, 2012b),
(Gao et al., 2012); and other proposals that decom-
pose the data in two low-rank (L) and sparse (S) com-
ponents (Majumdar and Ward, 2012a), (Gao et al.,
2012; Goud et al., 2010), where L models the cor-
related information between frames and S represents
the rapid change of data over time.
More recently, it has been shown that incorpo-
ration of the priori knowledge into the reconstruc-
tion of sparse signals can significantly improve their
performance (Zonoobi and Kassim, 2013; Vaswani
and Lu, 2010a; Zonoobi and Kassim, 2014b). This
idea have been used in the Modified-CS (Vaswani and
Lu, 2010b) to recursively reconstruct a time sequence
of MRI images in real-time from highly under sam-
pled measurements by using a-priori knowledge ob-
tained from the previous reconstructed image. The
Modified-CS uses the support of the previous time in-
stance as a partially known part of the current support
and finds a signal which satisfies the observations and
is sparsest outside the support of the previous time in-
stant. The a-priori based methods, only model the sig-
nal of interest as one sparse component. However, it
is observed that the L and S decomposition can model
dynamic MRI data significantly better than a low-rank
or a sparse model alone, or than a model in which both
constraints are enforced simultaneously (Otazo et al.,
2013; Zonoobiand Kassim, 2012; Ensafi et al., 2014).
To the best of our knowledge, no previous work has
been done to incorporate the priori information into
image recovery while the image is modelled as a sum-
mation of a low rank and a sparse component.
In this paper we first propose a re-formulation of
the L and S decomposition to take into account some
82
Zonoobi D., Faghigh roohi S. and Kassim A..
Low-rank and Sparse Matrix Decomposition with a-priori Knowledge for Dynamic 3D MRI Reconstruction.
DOI: 10.5220/0005228800820088
In Proceedings of the International Conference on Bioimaging (BIOIMAGING-2015), pages 82-88
ISBN: 978-989-758-072-7
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
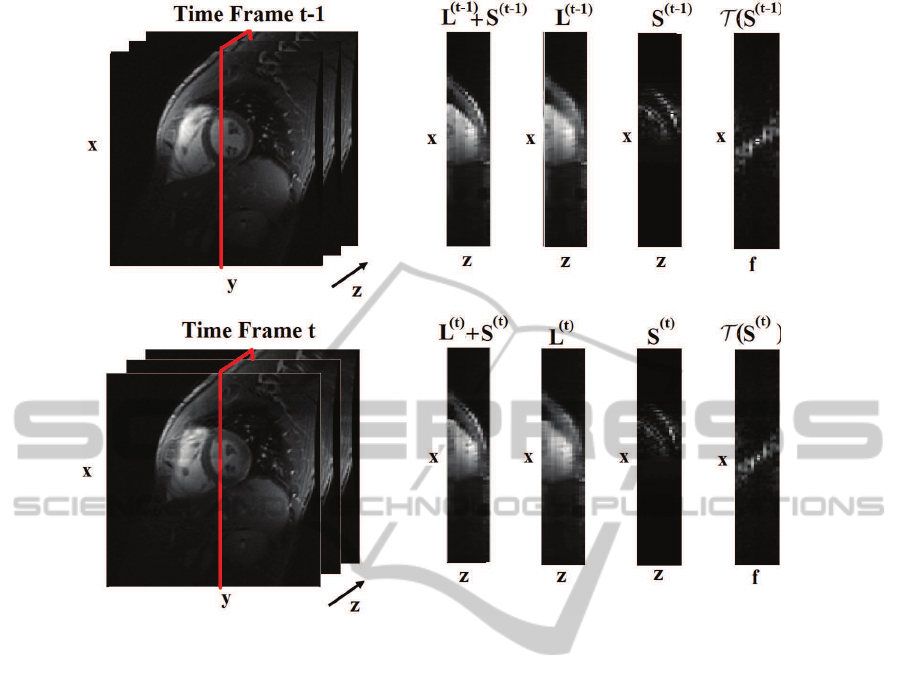
Figure 1: Illustration of L+S decomposition of fully-sampled 3D cardiac cine at time t and t + 1.
priori knowledge and then use a soft-thresholding
based algorithm to efficiently solve it. The algorithm
is then employed to reconstruct a time sequence of
3D cardiac MRI volumes from highly undersampled
measurements.
The rest of this paper is organized as follows: this
section ends with a description of the notations used.
Section 2 presents the problem of reconstruction of
3D dynamic MRI volumes and the current state-of-
the-art CS-based approaches that address this prob-
lem. In section 3, we provide details of our pro-
posed algorithm which we call Priori L+S. Finally,
we present and analyze our experimental results in
section 4 before providing the concluding remarks in
section 5.
Notations: Throughout the paper, matrices are
denoted by boldface letters (e.g. X,S) while scalars
are shown by small regular letters (e.g. n, m, k,r) and
linear maps and operators are denoted by bold calli-
graphic uppercase letters (T , A,Σ) and A
−1
denotes
the adjoint of the operator. Superscript (t) added to a
matrix refers to that of time t. For a matrix, the no-
tation M|
S
forms a sub-matrix that contains elements
with indices in S .
2 PROBLEM FORMULATION
The low rank and sparse matrix decomposition (L+S)
is particularly suitable to the problem of dynamic
imaging, where the low rank component models
the temporally correlated background and the sparse
component represents the dynamic information that
lies on top of the background (Gao et al., 2012;
Lingala et al., 2011). To apply the low-rank and
sparse matrix decomposition to 3D dynamic MRI,
lets assume that the 3D volume of interest is of size
[n
x
× n
y
× n
z
],(n
x
,n
y
> n
z
) which is changing with
time. At each time instance t the 3D volume is con-
verted to a matrix X
(t)
∈ R
(n
x
n
y
)×n
z
, where each col-
umn is consist of a frame. This matrix could be then
decomposed into a low rank matrix L
(t)
and a matrix
S
(t)
, which we assume to have a sparse representation
in some known basis T (such as Wavelets (Kassim
et al., 2008)), as X
(t)
= L
(t)
+ S
(t)
.
Figure 1 shows a cross section of the low rank
and sparse components of cardiac data sets for two
adjacent time instances (t and t + 1). It can be seen
that L
(t)
represents the background component and
S
(t)
corresponds to the changes from a frame to an-
other, e.g., organ motions or contrast -enhancement,
Low-rankandSparseMatrixDecompositionwitha-prioriKnowledgeforDynamic3DMRIReconstruction
83

etc (Majumdar and Ward, 2012b; Zonoobi and Kas-
sim, 2014a; Feng et al., 2012).
With this the problem can be posed as follows: let
A be the acquisition/sampling operator that performs
a frame-by-frame k-space under-sampling of the t
th
volume (A : R
(n
x
n
y
)×n
z
→ R
m×n
z
, where m ≪ n
x
n
y
).
Using this operator, the under-sampled acquisition of
X
(t)
can be expressed as:
d
(t)
= A(X
(t)
) + η
where Y
(t)
is the observation matrix of size m × nz,
and is assumed to be incoherent with respect to the
sparsity basis. Also η is the measurement noise with
finite energy (i.e. kηk
2
≤ ε
1
), which can be modelled
as a complex Gaussian noise. The problem, at each
time instance t, is then to recover the original X
(t)
,
from the corresponding compressive samples Y
(t)
as-
suming that the signal of interest is can be decom-
posed into low rank and sparse components. The
problem of recovering each volume from the com-
pressive measurements can be then formulated as:
(L
(t)
,S
(t)
) =argmin{kΣ(L
(t)
)k
0
+ kT (S
(t)
)k
0
} (1)
subject to kY
(t)
− A(L
(t)
+ S
(t)
)k
2
≤ ε
1
,
where T is a sparsifying transform for S, and Σ is
an operator that maps any matrix to the vector of its
singular values (i.e. kΣ(L
(t)
)k
0
= rank(L
(t)
)).
Solving the above minimization problem is known
to be computationally unwieldy in view of its combi-
natorial nature. As a consequence, we are compelled
to resort to an alternative convex approximation as
follows:
(L
(t)
,S
(t)
) =argmin{kΣ(L
(t)
)k
1
+ kT (S
(t)
)k
1
} (2)
subject to kY
(t)
− A(L
(t)
+ S
(t)
)k
ℓ
2
≤ ε
1
,
where kΣ(L
(t)
)k
1
is the nuclear norm of L
(t)
. This
convex problem can be solved efficiently using an
iterative algorithm, thereafter referred to as L+S
method (Otazo et al., 2013), which is closely related
to (Beck and Teboulle, 2009) and (Cai et al., 2010) for
sparse (T (S)) and low-rank matrix recovery (L), re-
spectively. The L+S method starts from a signal proxy
and then at each iteration proceeds through three steps
to update its estimates of the low rank matrix and the
sparse component using a soft-thresholding operator.
This operator is defined as:
S{x, λ} =
x
|x|
max(|x| − λ,0)
in which x could be a complex number and the thresh-
old λ is real valued. This is extended to matrices by
applying it to each element of that matrix.
It is known from the literature that recovery of
sparse vectors and low-rank matrices can be accom-
plished when the measurement operator A satisfies
the appropriate RIP or RRIP conditions (Candes et al.,
2009). The above formulation, however, does not take
into account any priori information that may be avail-
able about the low rank/sparse components.
3 LOW-RANK AND SPARSE
MATRIX DECOMPOSITION
WITH a-priori INFORMATION
To reconstruct images from even fewer number of
samples than L+S method (Otazo et al., 2013), we
aim to use the L and S components of the previously
reconstructed volume to guide the reconstruction of
the current time volume. The idea is based on the ob-
servation that the L and S components of each MRI
volume is very closely related to those of the adjacent
time instances. This is not surprising as it is known
that dynamic images are highly redundant in space
and time (Jung et al., 2009). To illustrate this, figure
1 shows a cross-section of the low rank and sparse
components of a fully-sampled cardiac data set for
two adjacent time instances. From the figure it can
be seen that L
(t−1)
and L
(t)
are quite similar, in fact
kΣ(L
(t)
) − Σ(L
(t−1)
)k
2
= 0.04. This means that vec-
tor of singular values of L
(t−1)
and L
(t)
are very close
in Euclidean space. Similarly, support of T (S
(t)
) is
much the same as the one of T (S
(t−1)
). In this case,
for instance, the support change turns out to be less
than 5% of the support size. Therefore, support of
T (S
(t−1)
) can be viewed as an a-priori knowledge of
the partial support of T (S
(t)
). Based on the above
observations, to recover X
(t)
, we modify the formula-
tion of the problem to incorporate the information of
T (S
(t−1)
) and L
(t−1)
as follows:
(L
(t)
,S
(t)
) =argmin{kΣ(L
(t)
)k
1
+ kT (S
k
)|
¯
T
(t−1)
k
1
}
subject to kY
(t)
− A(L
k
+ S
k
)k
2
≤ ε
1
,
kΣ(L
k
) − Σ(L
k−1
)k
2
≤ ε
2
(3)
where T
(t−1)
denotes the support of T (S
(t−1)
) and
¯
T
(t−1)
is the complement of T
(t−1)
. Basically we are
searching for an image which satisfies the observa-
tions, its S component is sparsest outside T
(t−1)
and
at the same time it has Σ(L
(t)
) closest to Σ(L
(t−1)
).
The above formulation is convex and therefore it
has a unique solution, however using convex-based
optimization methods may not be practical for large-
scale problems due to their considerable computa-
tional complexity and memory requirements (Needell
BIOIMAGING2015-InternationalConferenceonBioimaging
84
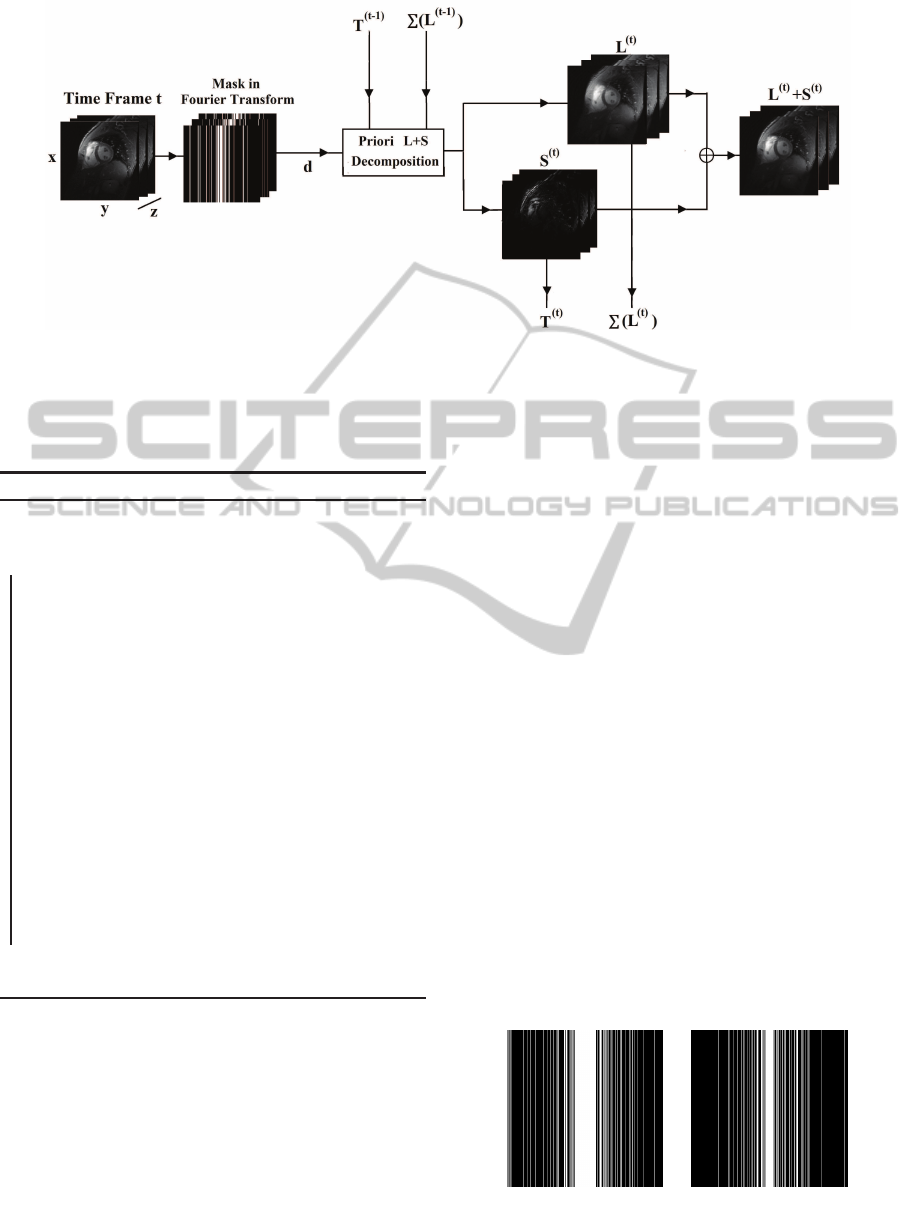
Figure 2: Overview of the priori L+S scheme.
and Tropp, 2009). Therefore we solve (1) using an
iterative algorithm inline with L+S method (Otazo
et al., 2013).
Algorithm 1: PrioriL+S decomposition.
Input: Y
(t)
,A, S
(t−1)
,L
(t−1)
,λ
T
,λ
S
(0) Initialization: X
0
= A
−1
(Y
(t)
),S
0
= 0;
while not converged do
(1) Singular-value soft-thresholding of L:
L
it−1
= X
it−1
− S
it−1
;
L
it
= Σ
−1
(S{ Σ(L
it−1
),λ
L
});
(2) Imposing the priori knowledge on L:
D
it
= (Σ(L
it
) − Σ(L
(t−1)
));
L
it
= Σ
−1
(Σ(L
it
) − λ
p
D
it
)
(3) Imposing Sparsity and the priori knowledge
on S:
T
(t−1)
= supp(T (S
(t−1)
));
S
it
= T
−1
(S{T (S
it−1
)|
¯
T
(t−1)
,λ
S
};
(4) Update estimation to minimize error:
E
it
= Y
(t)
− A(L
it
+ S
it
);
X
it
= L
it
+ S
it
− A
−1
(E
it
);
end
Output: L
(t)
← L
it
,S
(t)
← S
it
Our proposed algorithm, which is summarized
below, mainly differs with (Otazo et al., 2013) in
two steps where we impose the available priori-
knowledge into estimation of S and L components.
Initialization: similar to the original L+S algorithm,
we start with an initial estimation of X
(t)
and we set
the sparse component to be all zeros.
Singular-value Soft-thresholding: to impose the
low-rank property on L
(t)
, in this step at the i− th it-
eration the vector of singular values of (X
it−1
− S
it−1
)
is soft thresholded.
Imposing the Priori Knowledge on L: this step
is designed to imposed the available priori knowledge
of the low rank component L
(t)
which is extracted
from L
(t−1)
. To this end at each iteration it, it min-
imizes the Euclidean distance between the singular
values of L
(it)
and the previously reconstructed com-
ponent, L
(t−1)
, by moving into its gradient decent di-
rection.
Imposing Sparsity and the Priori Knowledge
on S: In this step the goal is only force T (S
it
) to be
sparse in locations not belonging to the spikes of the
previous time instance (T
(t−1)
). To this end, the al-
gorithm only shrinks those elements not belonging to
T
(t−1)
.
Update Estimation to Minimize Error: the new
X is finally obtained by enforcing measurement con-
sistency, where the aliasing artifacts corresponding to
the residual in k-space are subtracted from L
it
+ S
it
.
The algorithm iterates until the relative change in the
solution is less than 10
−3
.
Figure 2 shows the priori L+ S scheme for recon-
structing the entire time sequence. At each time t,
Algorithm 1 is used to recover X
(t)
except for t = 1,
where the simple L + S algorithm is used as no priori
knowledge is available for the reconstruction of the
first volume.
Figure 3: Cartesian sampling mask for (left) t=1 and (right)
subsequent frames.
Low-rankandSparseMatrixDecompositionwitha-prioriKnowledgeforDynamic3DMRIReconstruction
85
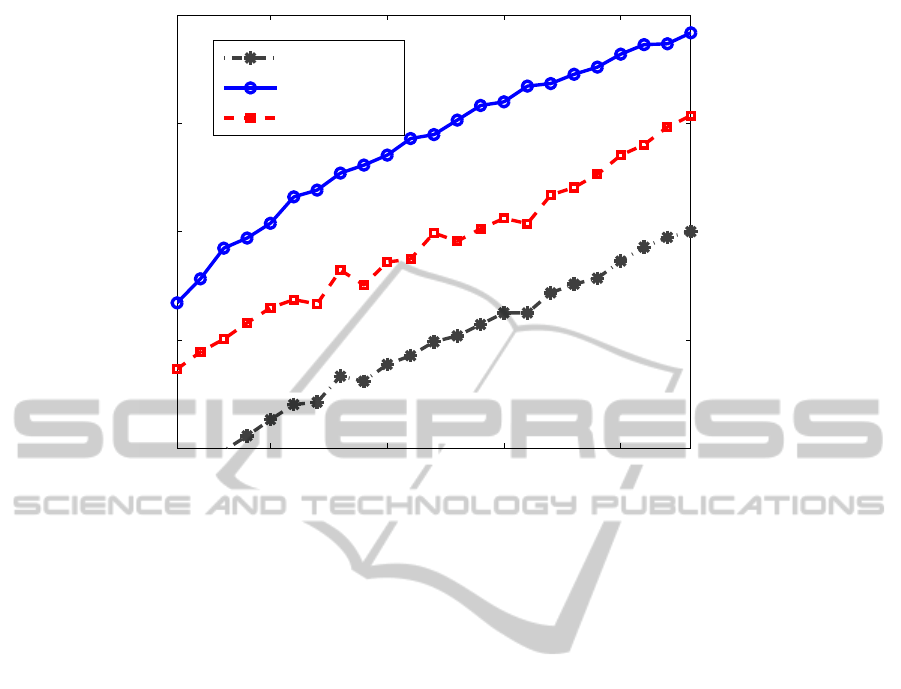
0.1 0.15 0.2 0.25
20
25
30
35
40
Sampling rate
PSNR
L+S
Priori−L+S
Mod−CS
Figure 4: PSNR of the reconstructed images vs. sampling rate.
4 EXPERIMENTAL RESULTS
To evaluate the performance of the proposed Priori
L + S method, we applied it to the reconstruction of
dynamic 3D Cardiac volumes of size 256 × 256 ×
14 × 20. The results are then compared with that
of L+S method (Otazo et al., 2013), and also with
Modified-CS method (Vaswani and Lu, 2010b) (Mod-
CS in figures 3 &4). In all the experiments, we used
a variable density Cartesian sampling mask which in
practice is less time consuming than random sam-
pling. However, to take the energy distribution of MR
images in k-space into account, we used a variable-
density sampling with denser sampling near the cen-
ter. Figure 3 shows the sampling masks used in these
experiments with two different. It should be noted
that for the very first time-frame, since no priori in-
formation is available %50 of the k-space samples are
taken and the sampling rate reported in figure 3 is for
the successive frames. Moreover, the sparse domain
is assumed to be the Wavelet domain and the recon-
struction quality is measured using the Peak signal-
to-noise ratio (PSNR).
Figure 4 compares the average PSNR of the re-
constructed volumes vs. percentage of the samples
taken in the k-space. It can be seen that our method
consistently out-performs the others in terms of the
improved PSNR. To compare the visual quality of the
reconstructed images, figure 5 shows a slice of the re-
constructed volume using different methods together
with the difference images (reconstruction error) am-
plified by a factor of 4. It is evident that the recon-
structed image using the Priori-L+S method is percep-
tually better with less loss of details and significantly
reduced reconstruction error.
5 CONCLUSIONS
In this paper, we presented a method which utilizes
a-priori knowledge for high resolution and fast recon-
struction of dynamic 3D MRI image sequences from
undersampled k-space data. First, the problem of re-
covering a MRI images as a sum of low-rank and
sparse components ( L + S) has been reformulated,
to incorporate the priori knowledge extracted from
previous reconstructions. Then we proposed an iter-
ative soft thresholding-based algorithm to efficiently
solve this minimization problem. To evaluate its per-
formance, we used it to reconstruct a time sequence
of 3D cardiac MRI volumes from highly undersam-
pled k-space data. Our experiments show that our pro-
posed method is superior to the other state-of-the-art
CS-based methods, in terms of both visual quality and
improved PSNR. Further investigation is still needed
to study the effect of the sparsifying transforms and
sampling patterns on the performance of the proposed
Priori-L+S.
BIOIMAGING2015-InternationalConferenceonBioimaging
86

(a) L+S (b) Mod-CS (c) Priori-L+S
Figure 5: Comparison of the reconstructed images (1/7 of samples taken), together with the difference images that are ampli-
fied by a factor of 4.
ACKNOWLEDGEMENTS
This work is supported by a grant (TDSI/11-014/1A)
from the Temasek Defence Systems Institute (TDSI),
Singapore.
REFERENCES
Beck, A. and Teboulle, M. (2009). A fast iterative
shrinkage-thresholding algorithm for linear inverse
problems. SIAM Journal on Imaging Sciences,
2(1):183–202.
Cai, J.-F., Cand`es, E. J., and Shen, Z. (2010). A singular
value thresholding algorithm for matrix completion.
SIAM Journal on Optimization, 20(4):1956–1982.
Candes, E., Li, X., Ma, Y., and Wright., J. (2009). Robust
principal component analysis? Journals of the ACM,
58(3):1–37.
Ensafi, S., Lu, S., Kassim, A. A., and Tan, C. L. (2014). 3d
reconstruction of neurons in electron microscopy im-
ages. In Engineering in Medicine and Biology Society
(EMBC), 2014 36th Annual International Conference
of the IEEE, pages 6732–6735.
Feng, L., Srichai, M. B., Lim, R. P., Harrison, A., King, W.,
Adluru, G., Dibella, E. V., Sodickson, D. K., Otazo,
R., and Kim, D. (2012). Highly accelerated real-time
cardiac cine MRI using k–t SPARSE-SENSE. Mag-
netic Resonance in Medicine.
Gamper, U., Boesiger, P., and Kozerkey, S. (2008). Com-
pressed sensing in dynamic MRI. Magnetic Reso-
nance in Medicine, 59(2):365–373.
Gao, H., Rapacchi, S., Wang, D., Moriarty, J., Meehan, C.,
Sayre, J., Laub, G., Finn, P., and Hu, P. (2012). Com-
pressed sensing using prior rank, intensity and sparsity
model (prism): applications in cardiac cine MRI. In
Proceedings of the 20th Annual Meeting of ISMRM,
Melbourne, Australia.
Goud, S., Hu, Y., and Jacob, M. (2010). Real-time car-
diac MRI using low-rank and sparsity penalties. In
Biomedical Imaging: From Nano to Macro, 2010
IEEE International Symposium on, pages 988–991.
IEEE.
Haldar, J. P. and Liang, Z.-P. (2011). Low-rank approxima-
tions for dynamic imaging. In Biomedical Imaging:
From Nano to Macro, 2011 IEEE International Sym-
posium on, pages 1052–1055.
Hu, Y., Lingala, S. G., and Jacob, M. (2012). A
fast majorize–minimize algorithm for the recovery
of sparse and low-rank matrices. Image Processing,
IEEE Transactions on, 21(2):742–753.
Jung, H., Sung, K., Nayak, K. S., Kim, E. Y., and Ye, J. C.
(2009). k-t FOCUSS: A general compressed sensing
framework for high resolution dynamic MRI. Mag-
netic Resonance in Medicine, 61(1):103–116.
Kassim, A. A., Yan, N., and Zonoobi, D. (2008). Wavelet
packet transform basis selection method for set par-
titioning in hierarchical trees. Journal of Electronic
Imaging, 17(3):033007.
Low-rankandSparseMatrixDecompositionwitha-prioriKnowledgeforDynamic3DMRIReconstruction
87

Lingala, S. G., Hu, Y., DiBella, E., and Jacob, M. (2011).
Accelerated dynamic MRI exploiting sparsity and
low-rank structure: kt slr. Medical Imaging, IEEE
Transactions on, 30(5):1042–1054.
Lustig, M., Donoho, D. L., Santos, J. M., and Pauly, J. M.
(2008). Compressed sensing MRI: A look at how CS
can improve on current imaging techniques. IEEE Sig-
nal Processing Magazine, 25(2):72–82.
Majumdar, A. and Ward, R. K. (2012a). Causal dynamic
MRI reconstruction via nuclear norm minimization.
Magnetic Resonance Imaging, 30:1483–1494.
Majumdar, A. and Ward, R. K. (2012b). Exploiting rank
deficiency and transform domain sparsity for MR im-
age reconstruction. Magnetic resonance imaging,
30(1):9–18.
Needell, D. and Tropp, J. (2009). Cosamp: Iterative sig-
nal recovery from incomplete and inaccurate sam-
ples. Applied and Computational Harmonic Analysis,
26(3):301 – 321.
Otazo, R., Sodickson, D. K., and Cand`es, E. J. (2013).
Low-rank+ sparse (l+ s) reconstruction for acceler-
ated dynamic MRI with seperation of background and
dynamic components. In SPIE Optical Engineer-
ing+ Applications, pages 88581Z–88581Z. Interna-
tional Society for Optics and Photonics.
Vaswani, N. and Lu, W. (2010a). Modified-CS: Modify-
ing compressive sensing for problems with partially
known support. IEEE Transactions on Signal Process-
ing, 58(9):4595 –4607.
Vaswani, N. and Lu, W. (2010b). Modified-cs: Modify-
ing compressive sensing for problems with partially
known support. IEEE Transactions on Signal Process-
ing, 58(9):4595 –4607.
Venkatesh, Y. V., Kassim, A. A., and Zonoobi, D. (2010).
Medical image reconstruction from sparse samples us-
ing simultaneous perturbation stochastic optimization.
In Proc. of the ICIP Conference, Hong Kong, pages
3369–3372.
Zhao, B., Haldar, J. P., Brinegar, C., and Liang, Z.-P. (2010).
Low rank matrix recovery for real-time cardiac MRI.
In Biomedical Imaging: From Nano to Macro, 2010
IEEE International Symposium on, pages 996–999.
Zonoobi, D., Kassim, A., and Venkatesh, Y. (2011). Gini in-
dex as sparsity measure for signal reconstruction from
compressive samples. IEEE Journal of Selected Top-
ics in Signal Processing, 5(5):927 –932.
Zonoobi, D. and Kassim, A. A. (2012). Weighted-CS for
reconstruction of highly under-sampled dynamic MRI
sequences. In Signal & Information Processing As-
sociation Annual Summit and Conference (APSIPA
ASC), 2012 Asia-Pacific, pages 1–5.
Zonoobi, D. and Kassim, A. A. (2013). On the reconstruc-
tion of sequences of sparse signals - The Weighted-
CS. Journal of Visual Communication and Image Rep-
resentation, 24(2):196 – 202.
Zonoobi, D. and Kassim, A. A. (2014a). A computationally
efficient method for reconstructing sequences of MR
images from undersampled k-space data. Medical im-
age analysis, 18(6):857–865.
Zonoobi, D. and Kassim, A. A. (2014b). On ecg reconstruc-
tion using weighted-compressive sensing. Healthcare
Technology Letters, 1(2):68–73.
Zonoobi, D., Roohi, S. F., and Kassim, A. A. (2014).
Dependent nonparametric Bayesian group dictionary
learning for online reconstruction of dynamic MR im-
ages. arXiv preprint arXiv:1408.5667.
BIOIMAGING2015-InternationalConferenceonBioimaging
88
