SysML Modeling for Embedded Systems Design Optimization

A Case Study

Patrick Leserf

, Pierre de Saqui-Sannes

, Jérôme Hugues

and Khaled Chaaban

CERIE, ESTACA, F-53000 Laval, France

ISAE-SUPAERO, University of Toulouse, F31055 Toulouse, France

Keywords: Architecture Optimization, SysML, Embedded Systems, Model Variability.

Abstract: Model-Based Systems Engineering (MBSE) with the SysML language allows the designer to include

requirement capture and design representation in a single model. This paper proposes a methodology to

obtain the best design alternative, from a SysML design, by using multi-objective optimization techniques.

A SysML model is extended with stereotypes, objective functions, variability and constraints. Then an

integer representation of the problem can be generated and solved as a constraint satisfaction problem

(CSP). The paper illustrates our methodology using an Embedded Cognitive Safety System (ECSS) design.

From a component repository and redundancy alternatives, the best design alternatives are generated, to

minimize the total cost and maximize the estimated system reliability.

1 INTRODUCTION

Embedded system design has become an important

development activity, due to the industrial demands

for new functions integration and design. These

systems are mainly composed of software. However

hardware components such as sensors, CPU and

embedded networks have to be considered too.

The designer must implement an architecture that

fulfills the functionalities according to the

requirements, but numerous indicators such as cost,

weight and reliability have to be optimized too.

These indicators typically compete with one another:

Improving one of them often leads to degrading

another one.

In this context, this paper considers that the

designer has a twofold objective: to obtain the set of

optimal architecture designs and to obtain it using a

Model-Based System Engineering approach that

seamlessly unifies system modeling in SysML and

architecture optimization. Such an optimization may

be automated using architecture models and

transformations. Then the designer can select the

appropriate design alternative, according to his or

her preferences. These activities shall be integrated

into Model-Based System Engineering (MBSE)

where the recommendation for engineers is to

capture their knowledge about all aspects of the

problem in one model.

The expected benefits of MBSE include the

capacity to simulate and formally verify models in

order to detect design errors as soon as possible in

the life cycle of systems. A great number of papers

present tools (e.g. TOPCASED (http://www.

topcased.org/), TTool (Ttool, 2011)) that enable

SysML model simulation and verification. By

contrast, little work has been published on SysML

modelling as a front-end to come up and compare

different design alternatives. Current approaches

such as (Van Huong and Binh, 2012) and

(Spyropoulos and Baras, 2013) address design

optimization from SysML models but differ from

our approach by focusing on component parameters

tuning, like CPU frequency or memory size. In our

work we propose to take into account the hardware

component selection, the component redundancy

level and the component connection, in order to

optimize the system cost and reliability.

The paper is organized as follows. Section 2

introduces the methodology we propose for model-

based system design optimization in the context of

embedded systems. Section 3 and Section 4

respectively address SysML modeling and

architecture optimization. Section 5 surveys related

work. Section 6 concludes the paper and outlines

future work.

449

Leserf P., de Saqui-Sannes P., Hugues J. and Chaaban K..

SysML Modeling for Embedded Systems Design Optimization - A Case Study.

DOI: 10.5220/0005229204490457

In Proceedings of the 3rd International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2015), pages 449-457

ISBN: 978-989-758-083-3

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 METHODOLOGY

2.1 Design flow with MBSE

We consider architecture design in the context of

systems engineering activities with MBSE, as

described in (Friedenthal, et al., 2011). The output of

systems engineering activities is a coherent model of

the system (figure 1). The model can be separated

between a Platform Independent Model (PIM) and a

Platform Specific Model (PSM). PIM and PSM

concepts come from the Model Driven Architecture

standard of the Object Management Group

(http://www.omg.org/mda/). Figure 1 uses the

system model to specify both hardware and software

components requirements. The system model as

defined in SysML (figure 2) is a set of diagrams.

Among these elements, the requirement diagram

(req) describes the requirements and the activity

diagram (act) represents the system behavior. The

Block Definition Diagram (BDD) and Internal Block

Diagram (IBD) describe the system’s structure.

Finally the parametric diagram captures

relationships among properties. An important

activity of system engineering is to find the best

design alternatives, for the whole system. However

the exploration space is very large, especially, with

current approach like (Apvrille, 2008) that does

exploration on PSM. In this paper, we focus on

system model optimization issue (dashed elements

in figures 1 and 2) because it comes first in the

design activity and it will substantially restrict the

design space exploration (DSE).

Figure 1: design flow with MBSE.

With this approach, the DSE can be done in a

stepwise manner, exploring the system model first,

and then the software, hardware and allocation

alternatives with current DSE approaches.

Figure 2: system models with SysML.

The system structure is also a key point for metric

evaluation (i.e. cost, weight and reliability). In this

context, the objective for the designer using MBSE

and SysML is to obtain the best trade-off system

structure, in order to optimize objective functions

such as cost and reliability. This multi-objective

optimization problem can be described in

mathematical term as follows:

Above, f is the objective function vector and S the

set of constraints. Our approach is to suggest the

best configurations to the designer, that is, to find

the Pareto-optimal solutions. Pareto-optimal

solutions have the lowest (or equivalently low)

values for all objective functions. The set of

solutions is presented to the decision-maker by the

Figure 3: Methodology overview.

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

450

designer for the selection of optimal solutions.

The methodology we propose is presented in the

next sub-section. The requirement and structure

model are adapted for the optimization, including

objective function definition, variability and

constraints. We assume that the system design is

done using the SysML language. Also, a component

repository is available including parameters for

objective functions.

All the SysML diagrams of this paper are built

up with the Papyrus tool from CEA

(http://www.eclipse.org/papyrus/).

2.2 Our Proposal

Figure 3 presents the methodology we propose for

optimizing system architecture, showing the

activities and the produced artifacts. The first stage

is the SysML modeling for optimization, described

in section 3. In a preliminary step, the requirements

are captured using requirement diagrams.

Architecture requirements are taken into account.

This allows to express constraints and to add

traceability between requirements and architecture

elements.

Then the SysML model is completed for

optimization, adding objective function definitions

in parametric diagram and adding model variability.

The model variability expresses the different design

alternatives that the designer wants to explore. The

model variability is represented by several degrees

of freedom from the model, represented by

variability variables inserted in comments. We

distinguish between the instance variability variable

(IVV), meaning that we may have several instances

of the same component in the model, and component

variability variable (CVV), meaning that a

component instance may be replaced.

The second stage, described in section 4, is the

optimization model generation and solving. To do

this, the variability variables of the SysML model

are transformed into a new set of 0-1 variables in the

Figure 4: ECSS system.

optimization model. By re-using the constraints from

the SysML model, the problem can be resolved as a

Constraint Satisfaction Problem (CSP), using a

standard solver. Then the designer can select among

the trade-off solutions the ones that best fit to his or

her needs.

3 SysML MODELING FOR

OPTIMIZATION

This section presents the Embedded Cognitive

Safety System (ECSS, Figure 4) that serves as

running case study throughout the paper and

discusses each step of ECSS modeling in SysML.

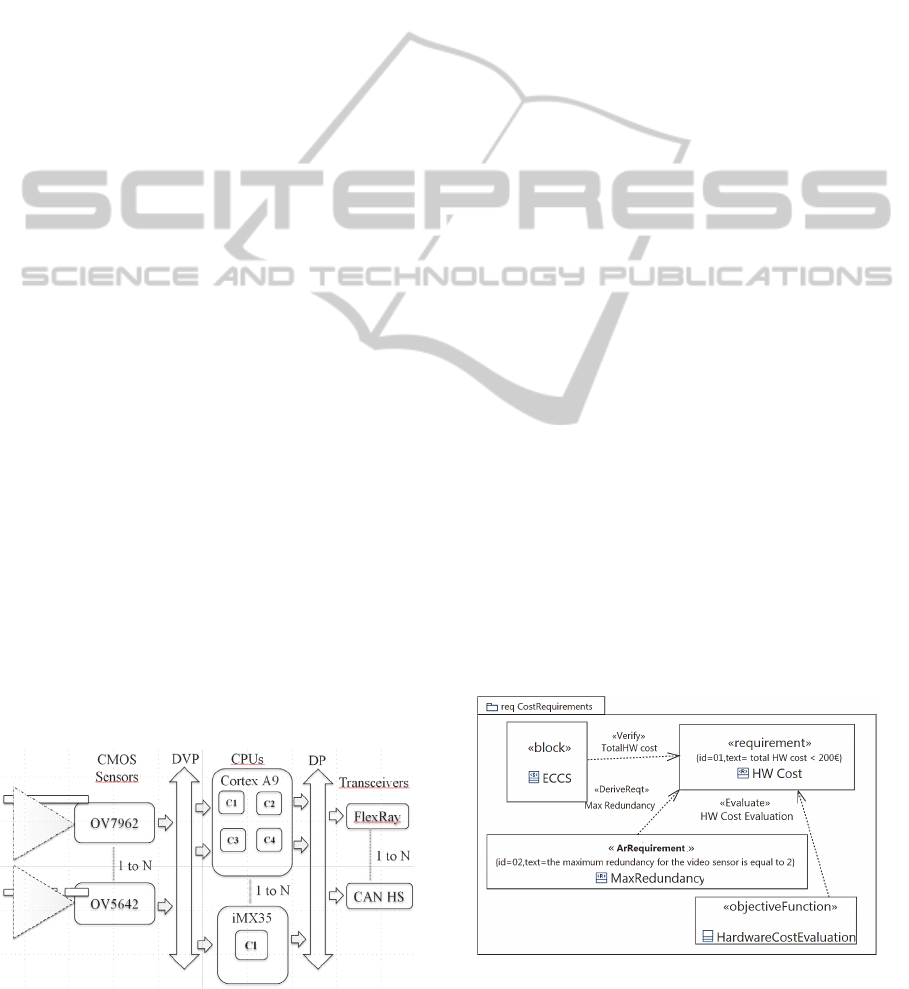
3.1 Case Study

The ECSS system can be integrated in an on-board

vehicle digital system or in aeronautics systems such

as drones. Typical features for ECSS are line

detection, obstacle detection and distance

measurement with stereoscopic view.

The embedded hardware platform is composed

of CMOS image sensors, processing elements and

vehicle interface networks. These three components

types may be redundant, for safety purposes or

stereoscopic processing. CMOS image sensors

support auto focus engine and image stabilization.

Image sensors are connected to processing elements

through Digital Video Port (DVP), a type of parallel

bus interface. Processing elements are CPU

supporting image processing like Cortex A9 or

iMX35. Vehicle interface is an embedded serial bus

like CAN High Speed or FlexRay. The vehicle

interface is integrated into the ECSS system with a

transceiver component, connected to the processing

element with a digital port (DP) which is a parallel

bus interface.

Figure 5: requirements for optimization.

SysMLModelingforEmbeddedSystemsDesignOptimization-ACaseStudy

451

3.2 Requirements Capture

SysML provides modeling constructs to capture and

represent textual requirements, and to link the

requirements to other modeling elements. The

requirement diagram depicts requirements, but a

requirement can also appear on other diagrams to

show its relationship to other modeling elements. A

standard requirement includes a unique identifier

and a text requirement. “Satisfy” and “Verify”

relationships relate requirements and other model

elements such as blocks and test cases.

In our context of architecture optimization,

specific requirements for the architecture, so-called

the “architecture requirements,” are derived from

standard requirements. To clearly identify

architectural requirements, a stereotype

“ArRequirement” extends the standard SysML

requirement. On the other hand, a standard

requirement is evaluated by an objective function.

The objective function is a stereotype extending the

standard SysML constraint block. This objective

function is related to a requirement with a stereotype

“evaluate” extending the basic UML-2 dependency

relationship. A dependency is a design-time

relationship between definitions. In Figure 5, the

“MaxRedundancy” architecture requirement limits

the sensor component redundancy to two for a cost

reason, and the system cost requirement is evaluated.

3.3 MDO Context and Objective

Functions Definition

To integrate the multi-domain optimization (MDO)

into the system model design, we propose to define a

MDO context, a type of analysis context. The MDO

context is represented by a BDD diagram and a

parametric diagram, both including constraint

blocks. The parametric diagram captures the internal

structure of a constraint block, in term of parameters

and connectors between parameters. The BDD is

used to define constraint blocks and their

relationship. This BDD diagram contains a top-level

constraint block, named “ECSS MDO Context” in

Figure 6. This constraint block has a reference to the

block representing the system under analysis and

including the variability for alternative

representation. The MDO context diagram contains

also the objective functions and the optimization

model representation. The Pareto front, a result of

the MDO context, is used to present alternatives to

the designer. The MDO context can be passed to an

external optimization solver, and the result can be

provided back as Pareto front values of the MDO

context.

The objective function block extends the

standard SysML Constraint Block and contains an

optimization goal parameter (i.e. maximize or

minimize). A constraint provides a description of the

analytical function supporting the objective function.

Other parameters specify interactions point between

the objective function and the system under analysis,

and between the objective functions and the

optimization model. Figure 6 shows the MDO

context definition for our case study, in a BDD. The

MDO context is called ECSS MDO Context, to

perform a multi-objective optimization of the ECSS

system. The ECSS MDO Context constraint block

Figure 6: BDD diagram for ECSS MDO context Definition.

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

452

has two value vectors, /BestCost[1..*] and /BestRel

[1..*], representing the Pareto front. The

ParetoFront constraint block produces these value

vectors from the two objectives functions. It is

intended in the analysis that the equations are solved

by external optimization solver for these two

vectors, so they are shown as derived. The result

values obtained with an external CSP solver are

presented later in sub-section 4.2 and 4.3.

As indicated by its associations, ECSS MDO

context contains two constraint properties, both

typed by objective function, HWCostEvaluation and

SystemReliability. A precision to the modeling of the

objective function is added, with a constraint. The

two constraints describe the equation underlying the

total cost and the reliability calculation. In this case,

the Python language can be used as constraint

language, because it is used by the CSP solver

(Niemeyer, 2014) in our case. For the

SystemReliability function, the system reliability R is

calculated with parameters coming from the system

under analysis (the components reliability) and from

the Zero One Model.

The ECSS MDO context also contains one

reference property typed by ECSS, the system under

analysis including variability. Finally, ECSS MDO

contains a constraints property Zero One Model,

representing the optimization model described in

section 4. The Zero One Model has a parameter and

a set of constraints deduced from the ECSS system

(see section 4, equation 2) and from the model itself.

These constraints can be expressed using the Object

Constraint Language (OCL).

Figure 7 shows a parametric diagram. Its frame

represents the ECSS MDO context constraint block.

This diagram is similar to an internal block diagram

but uses binding connectors exclusively. Binding

connectors link constraints parameters.

Figure 7: Parametric diagram for MDO context definition.

3.4 System Composition and

Redundancy Modeling

The architecture modeling represents the set of

hardware resources available for the execution of the

application, representing the hardware system. At

the first level, the hardware system is made up of

several components and described by a block

definition diagram (see Figure 8). A SysML block

definition diagram defines features of blocks and

their relationship such as associations. In our

optimization problem, the composition is known, but

the redundancy level of each component is not. The

redundancy level is the first degree of freedom for

the optimization problem. At this step, we specify

instance variability variables (IVV) in comments.

Each IVV is related to a composition association,

between the top-level component and the low-level

component.

As depicted in Figure 8, the ECSS system

contains between one and two sensors, processing

elements and networks. We have three IVVs,

respectively related to the sensor, CPU and

Transceiver composition. Each composition satisfies

with the maximum redundancy requirement, derived

from the global cost requirement.

Figure 8: BDD for HW composition.

The hardware components selection is the second

degree of freedom for the optimization process. For

this second degree of freedom, Component

Variability Variable (CVV) is inserted in the model

as a comment. CVV indicates that the component

instance can be replaced by another hardware

component specification. Hardware component

specification is provided by the designer, and

belongs to a component repository. The repository

includes a set of tables. Each table is associated to

one component of the block definition diagram. In

our example, we define three tables and three CVV,

respectively associated with the sensor, the

processing element and the network block. Each

SysMLModelingforEmbeddedSystemsDesignOptimization-ACaseStudy

453

table contains the list of available components, with

their cost and reliability (See Table 2). These tables

are provided by the user, in addition to the SysML

model.

3.5 Component Interface Modeling

Component interface modeling is useful for the

optimization problem, because new constraints arise

during this stage. These constraints will be added to

the computational model for the problem solving.

The Internal Block Diagram in SysML captures the

internal structure of a block in terms of properties

and connectors between properties. If we consider

the IBD depicted by Figure 9, we have one or two

sensors with one output DVP port connected to one

or two processing elements for video data

transmission. At this step we do not specify a

connection matrix between components. The goal is

to retain the valid configurations with a constraint

used by the optimization process. In our case and for

the digital video port (DVP), the sum of input ports

for processing elements shall be greater than the sum

of output port for video sensors. This constraint may

be expressed in OCL and attached to the VideoData

connection.

Figure 9: Interface modeling using IBD.

Figure 10: Activity diagram.

3.6 Application Modeling

An application represents the functionality that the

modeled system will accomplish during its

execution time. The activity diagram in Figure 10

represents workflows of stepwise activities. With the

allocation concept, it is possible to allocate

individual actions to hardware components

represented by blocks.

An activity diagram combined with allocation to

blocks is used to generate a reliability block

diagram, in order to estimate the application

reliability.

4 OPTIMIZATION MODEL

Previous section has shown how the SysML model

could be prepared for optimization. But a

mathematical representation is required to perform

the optimization with suitable algorithms. In this

section we propose a representation and show how

to obtain it from the SysML model. This

representation is based on zero-one variables, and

can be solved as a constraint satisfaction problem.

4.1 Problem Statement

Optimization models have been developed to select

software or hardware components and redundancy

levels. The system (see Figure 11) consists of

independent subsystem S

. S

is associated to a given

block with instance variability (the VideoSensors

aggregation in Figure 11). Subsystem S

is composed

of components selected in a repository of

components C

. C

represents the component number

j in the repository C

. Each selected component has a

position k in the final subsystem S

, after the problem

resolution. Figure 11 shows there exists two possible

positions for a selected component in the final

subsystem.

Figure 11: from BDD to problem formulation.

We define the following sets and parameters:

 S

the set of components with position k. C

the

set of component available in the component

repository

 c

the cost of component C

and θ

interconnection cost for any component

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

454

 r

the reliability of component C

 e

and s

the input and output port numbers of

component C

. For sensors ( the first block)

we have no input port and one output port, so

we have : e

=0 and s

The range of k is given by the SysML aggregation

multiplicity in BDD (Figure 11), the range of i by

the system composition in the BDD and the range of

j by the component table size. A zero-one

programming formulation of this problem is as

follow, by defining decision variables:

∀∈,



∈



,∈













1









 

0; 

(1)

Regarding as constraints applied to the system, the

first set of constraints comes from the decision

variable definition. At any position of the final

subsystem S

we can have only one component in

position k :

∀,







1 (2)

Other constraints can be expressed such as exclusion

between components.

Table 1: Association between SysML model elements and

optimization model.

Sets and

parameters

SysML model element

S and S

S is the system, modeled by the top-

level block in the BDD. The ECSS

block in Figure 10 represents the

system.

One sub-system S

per sub-block in the

BDD with instance variability variable

(IVV).

and s

One C

per block associated to

component variability variable (CVV),

from BDD diagram. In Figure 10, C

the set of video sensor components,

with cost and reliability in video sensor

table (Table 2).

and s

are deduced from the IBD

diagram

When a CPU component is not compatible with a

particular transceiver, it can be expressed as a

constraint, such as a sum lower than one. In the

same way, a sum comparison is used to express a

component dependency. Connection information is

given by the IBD diagram (see Figure 12).

Figure 12: from IBD to connection constraints.

First, the place of each Si in the component flow is

given. Then connection constraints are provided. At

each interface we have constraints between total

input port number and total output port number. In

our example of Figure 12, for VideoData

connection, sensors and CPUs satisfy the following

connection constraint:

















,,



(3)

For DigitalData connection, each transceiver input

is connected to CPU, and each CPU has at least one

connected output:

















,,

(4)

















,,

(5)

The objective functions are included in the

parametric diagram. In our example, the goal is to

minimize the cost and maximize reliability. The total

system cost including interconnection cost, is given

by:

min  



















,,

(6)

The system reliability to be maximized, using serial-

parallel interconnection model, can be calculated by:

max   11









,





(7)

+Connectionconstraints

SysMLModelingforEmbeddedSystemsDesignOptimization-ACaseStudy

455

4.2 Problem Solving

The previous problem can be seen as a constraint

satisfaction problem (CSP). A CSP requires a set of

values, selected from a given domain, to be assigned

to each variable. Researchers in artificial intelligence

usually adopt CSP when they try to solve such

problems. CSP problems are combinatorial by

nature. These problems are NP-complete and an

efficient algorithm (i.e with polynomial time for all

inputs) does not exist, but some heuristics produce

good approximate solutions. A feasible solution for

the problem consists in an assignment of values

from its domain to every variable, in such a way that

each constraint is satisfiable. In this case, we may

want to find just one solution, all solutions or an

optimal solution. In our case an optimal solution is

given by the objective functions defined in the

SysML model. The selected approach in this paper

consists in finding all solutions and then to evaluate

the different solutions with objective functions, to

determine the best ones. Algorithms for solving CSP

usually search systematically through the possible

assignments of values to find a solution. SC

Brailsford et al. (Brailsford et al., 1999) shows that a

simple algorithm is the backtracking algorithm, and

others are forward checking and MAC algorithm. In

these algorithms, a search tree is used, as it would be

done in a branch and bound algorithm. In the

backtracking algorithm, the current variable is

assigned and then checked against the partial

solution.

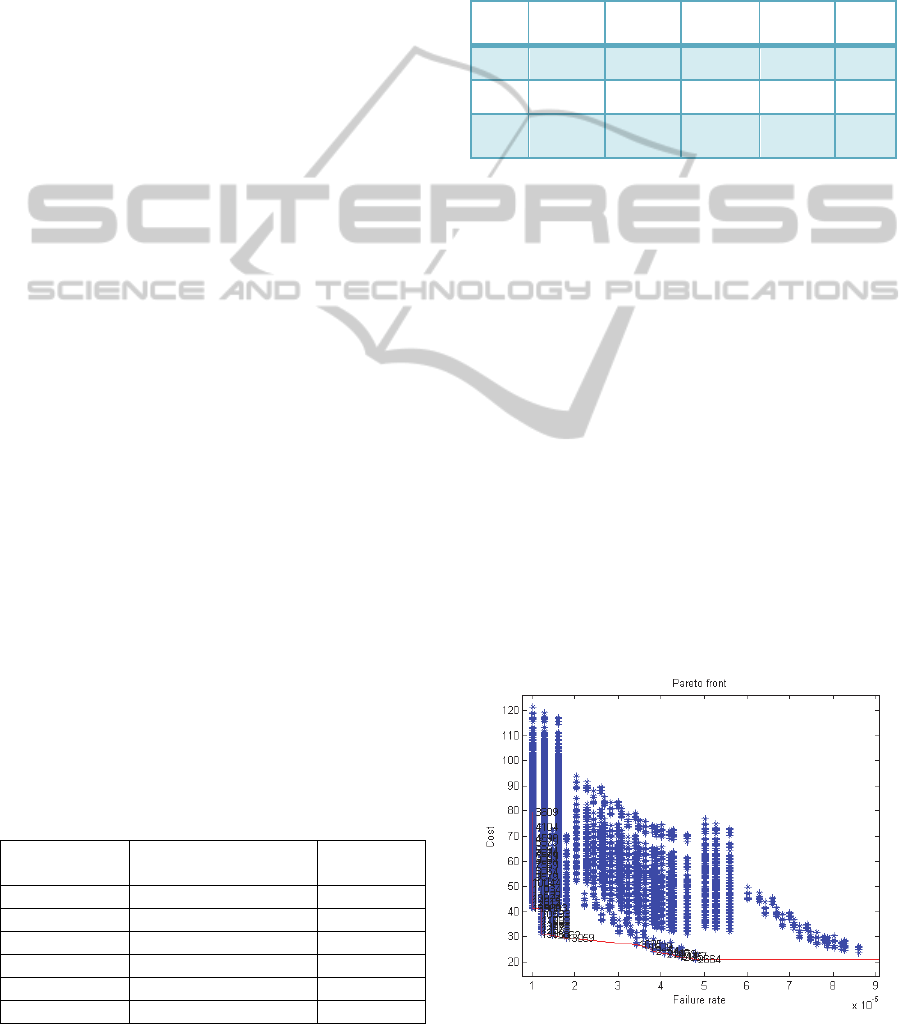
4.3 Results from the Case Study

We consider the case study with the following

parameters:

 A maximum redundancy of two for sensors,

processing elements and transceiver

 Four connection constraints between sensors,

processing elements and network transceivers

 A repository of 18 components with

specifications in Table 2.

Table 2: Component repository extract.

Component Reliability min-max Cost min-

max

Sens. 1 to 3 0.99997-0.99998 16.9-21.5

Sens. 4 to 6 0.999976-.999985 20.2-25.7

CPU 1 to 3 0.99996-0.99998 12.6-28.4

CPU 4 to 6 0.99997-0.999985 21.2-34.5

Trans. 1 to 3 0.9934-0.9969 12.8-13.1

Trans. to 6 0.9971-0.9995 13.8-15.4

We obtain a 36 variables problem to be solved. With

a CSP solver using backtracking algorithm

implemented in Python, and a posteriori objective

function evaluation, we obtain the Pareto front

illustrated in Figure 13, with 13,500 solutions in 36

minutes of computation time. That figure displays

the Failure rate (1-R

) instead of reliability R

Table 3: Three best trade-off configurations.

Sol. Sens. CPU Trans. Cost (€) FR

-5

1 S1+S1 CPU1 T4+T1 30.3 1.48

2 S1+S3 CPU1 T1+T1 35 1.22

3 S1+S3 CPU1+

CPU1

T1+T1 41.2 1.02

For a maximum cost of 50€ and a failure rate <

0.00002, table 3 presents the three best trade-off

configurations selected by the user.

5 RELATED WORK

In recent literature, there are approaches on the

integration of SysML with external analysis tools

and solvers. One of them (Schamai et al., 2009) is

Paramagic for integration of SysML and Modelica,

Matlab and Mathematica. However these approaches

lack support of multi-criteria optimization that help

designers to perform design space exploration and

trade-off analysis. The approach proposed by P. Van

Huong (Van Huong and Binh, 2012) and

Spyropoulos (Spyropoulos and Baras, 2013) allows

the user to perform multiple analyses in the same

environment. These approaches are adapted to the

component parameters optimization like CPU

frequency or memory size, not to the architecture

Figure 13: Pareto Front with CSP Solver.

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

456

composition and redundancy problem we want to

address.

In (Meyer et al., 1998) an optimization technique

is proposed for a micro-wave module design, with

combination of alternatives for part modules, but

without redundancy constraint. In the Design Space

Exploration (DSE) approach (Apvrille, 2008), the

problem to solve is related to the hardware/software

partitioning and the mapping of application onto

hardware elements. Our approach comes earlier in

the design flow and is complementary, providing a

limitation of the design space exploration.

The redundancy allocation problem (RAP, (Coit

and Smith, 1995), (Limbourg and Kochs, 2008))

deals with component selection, for cost and

reliability optimization at system level. In these

approaches (DSE, RAP), the problem is formalized

as an optimization problem, and not with the MBSE

approach. Similarly, the RAP formulation does not

take into account heterogeneous component

selection and the connection topology is fixed as a

serial-parallel model.

6 CONCLUSIONS AND FUTURE

WORK

The paper presents a methodology for multi-

objective optimization of system architecture.

Starting from a SysML model, we add information

concerning objective functions, variability and

architecture constraints. The redundancy level and

the component alternatives are tagged with variables

that describe variability. Then the SysML model can

be further exploited to generate a mathematical

representation, based on: integer variables, linear

constraints and objective functions. The problem can

be solved using a CSP solver. Finally, the ECSS

case study shows there exists three best

configurations, minimizing cost and maximizing

reliability, from a repository of 18 components.

Ongoing work includes the design of an

algorithm to generate the optimization model

instance from the system model. This representation

will be compatible with CSP solvers. In addition to

instance and component variability, the value

variability, relative to component parameters, will be

integrated too.

REFERENCES

TOPCASED, The Open source Toolkit for critical

systems; in http://www.topcased.org/

TTool, The TURTLE Toolkit, 2011. in

http://labsoc.comelec.telecom-paristech.fr/ttool.

Van Huong, P., & Binh, Nov 2012. Embedded System

Architecture Design and Optimization at the Model

Level., IJCCE, Vol.1, No 4,

Spyropoulos, D., & Baras,. 2013.Extending Design

Capabilities of SysML with Trade-off Analysis:

Electrical Microgrid Case Study. Procedia Computer

Science, 16, 108-117.

Friedenthal, S., Moore, A., & Steiner, R. 2011. A practical

guide to SysML: the systems modeling language.

Elsevier.

MDA, the Model Driven Architecture; in

http://www.omg.org/mda/

Papyrus tool from CEA, in

http://www.eclipse.org/papyrus/

Meyer, J., Ball, M., Baras, J., Chowdhury, A., Lin, E.,

Nau, D., ... & Trichur, V., 1998. Process Planning in

Microwave Module Production. Artificial Intelligence

and Manufacturing: State of the Art and State of

Practice.

Apvrille, L. ,2008. TTool for DIPLODOCUS: an

environment for design space exploration. In

Proceedings of the 8th international conference on

New technologies in distributed systems (p. 28). ACM.

Coit, D. W., & Smith, A. E., 1995. Optimization

approaches to the redundancy allocation problem for

series-parallel systems. In Fourth Industrial

Engineering Research Conference Proceedings (pp.

342-349).

Limbourg, P., & Kochs, H. D., 2008. Multi-objective

optimization of generalized reliability design problems

using feature models—A concept for early design

stages. Reliability Engineering & System Safety, 93(6),

815-828.

Brailsford, S. C., Potts, C. N., & Smith, 1999. Constraint

satisfaction problems: Algorithms and applications.

European Journal of Operational Research, 119(3),

557-581.

Niemeyer G, retrieved in 2014, API Documentation

python-constraint, http://labix.org/doc/constraint/

Schamai, W., Fritzson, P., Paredis, C., & Pop, A., 2009.

Towards unified system modeling and simulation with

ModelicaML: modeling of executable behavior using

graphical notations. In Proceedings 7th Modelica

Conference, Como, Italy.

SysMLModelingforEmbeddedSystemsDesignOptimization-ACaseStudy

457