
Mathematical Model of a Human Leg
The Switched Linear System Approach
Artur Babiarz, Adam Czornik, Michał Niezabitowski and Radosław Zawiski
Institute of Automatic Control, Silesian University of Technology, 16 Akademicka St., 44-100 Gliwice, Poland
Keywords:
Human Leg, Switched Linear System, State-dependent Switching.
Abstract:
This article presents a novel approach to modelling of the human leg with the use of linear switched systems.
Second order differential equations forming a two-segments leg model moving in a vertical plane are shown.
State space linear equations describing given model are derived. A linear switched system for such model
is presented, where the switching function is modelled as state-dependent. Based on this approach a linear
system is presented, which is composed of four subsystems between which switching occurs depending on two
state variables. These variables represent angular displacements. As a consequence, a state space division is
shown together with a linear system describing human leg in this setting. Finally, a set of simulations presents
differences between standard linear modelling approach and a switched linear system approach.
1 INTRODUCTION
Hybrid systems have become very popular during the
last decade (Sun, 2006), (Sun and Ge, 2011). There
are numerous adaptations of these systems into prac-
tical solutions. They own their popularity to possi-
bilities of applying them to both, continuous and dis-
crete dynamical systems. Switched systems are sub-
group of hybrid systems, where the switching signal
may depend on the logic-based switching function.
Switched systems can be categorized into two groups:
autonomous and controlled (Liberzon, 2003). In ad-
dition, each of these types of systems can be classified
into state-dependent and time-dependent. In this pa-
per, we consider a switched linear systems:
˙x = A
σ(·)
x+ B
σ(·)
u,
y = C
σ(·)
x+ D
σ(·)
u
(1)
defined for all t ≥ 0 where x ∈ R
n
is a state, u ∈ R
m
is control, y ∈ R
q
is output, σ(·) : P → {1, 2, . . ., N}
is a switching rule and A
i
, B
i
,C
i
, D
i
, i = 1, 2, . . . , N are
constant matrices.
The authors are not aware of any traces in the
literature of modelling of human leg in the above
framework. In the paper (Bai et al., 2001), authors
present dynamics of a human arm, as a second or-
der continuous object with delay. Such mathemat-
ical model is convenient from the point of view of
generating a trajectory and executed computer simu-
lation. The approach presented in (Zhao et al., 2008)
is based on classical mechanics, which approximates
the limb as a combination of rigid links. Using the
Euler-Lagrange formalism a matrix second order dif-
ferential equation can be obtained. Matrices in this
equation describe moments of inertia, Coriolis forces
and gravity forces. Depending on the individual case
(Zhao et al., 2008) it is possible to take into account
various additional forces from external factors. In
the same article, the authors also take into account
a ground reaction force during the movement of the
foot.
Recently, researchers devote an increasing atten-
tion to mechanical systems such as exoskeletons.
Their main purpose is to aid and strengthen move-
ment attributes of a human body (Pons et al., 2007),
(Kong and Tomizuka, 2009) and to support motion
of people with reduced mobility (Sekine et al., 2013).
The authors of (Csercsik, 2005) describe the attempt
to create a control system of the lower limb exoskele-
ton with a PID controller. They also perform a stabil-
ity analysis by means of Nyquist criterion. The paper
contains a full description of the experiments for one
degree of freedom only. Obviously, such approach at
the design of control systems is appropriate (Zawiski
and Błachuta, 2012), (Błachuta et al., 2014), but it
does not fully reflect the dynamics of the movement
having seven degrees of freedom, and in a further per-
spective is a significant limitation. Another group of
articles tackles the research focusing on impedance
control (Burdet et al., 2006), (Chang et al., 2013). In
90
Babiarz A., Czornik A., Niezabitowski M. and Zawiski R..
Mathematical Model of a Human Leg - The Switched Linear System Approach.
DOI: 10.5220/0005230300900097
In Proceedings of the 5th International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2015), pages 90-97
ISBN: 978-989-758-084-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

the paper (Chang et al., 2013), authors present an ap-
plication of the theoretical results of impedance con-
trol for trajectory generation and control of robot mo-
tion imitating the movement of a human arm with two
degrees of freedom.
By scrutinizing the literature describing a human leg
the problem of geometric description of the human
limbs should be distinguished, along with the prob-
lem of stability during movement, the optimal con-
trol problem and the control problem with limitations
on the value of the driving torque as a control sig-
nal (Ueyama and Miyashita, 2014). The information
from (Burdet et al., 2006), (Chen, 2011), (Lee et al.,
2010), (Neumann et al., 2013) became the inspiration
to develop the idea of application of hybrid systems.
1.1 Background and Significance
The applications of hybrid systems are based on the
results in (Pavlovic et al., 2001), (Lee et al., 2010),
(Neumann et al., 2013). According to the informa-
tion in (Lee et al., 2010) and (Neumann et al., 2013),
shape of upper and lower limbs is changing strongly
during the execution of any movement. In addition,
the construction of a single muscle and the occurrence
of muscle synergism is precisely described. As a re-
sult, we can assume that the matrix of inertia and the
distance from the center of gravity of each link, are
changing. However, changes of these parameters de-
pend on the configuration of the leg.
Furthermore, research results published in (Babi-
arz et al., 2013) justify the application of hybrid sys-
tems for modeling objects with complex biomechan-
ical structure. On the other hand, results presented in
the work by (Burdet et al., 2006) and (Chen, 2011)
indicate that the human arm is unstable in the consid-
ered range of motion. In addition, the state space of
the object can be naturally divided and one can get a
family of subsystems. Those subsystems form a basis
for the modeling of the human leg by means of the
switched systems. In this setting a switching function
depends on the state vector. Consequently, we con-
clude that utilising of switching between the subsys-
tems designated by given states of the limb’s motion
is a novelapproach modeling and analysis of dynamic
properties of human limbs.
The structure of this paper is as follows. We be-
gin by presenting mathematical model of vertical hu-
man two-link leg. Next section describes proposed
switched linear systems. In this section, we show the
partition of the state space and switching functions.
Section 3 presents a comparison of human leg linear
and switched model. Moreover, the obtained results
are shown for two simulation experiments. Finally,
we conclude our proposition of mathematical model.
2 A HUMAN LEG MODEL
2.1 A State-space Model
In general terms the motion of a rigid body can be de-
scribed by second-order differential nonlinear equa-
tion resulting from Euler-Lagrange formalism
M(q) ¨q+C(q, ˙q) ˙q+ G(q) = u, (2)
where: M(q) is an inertia matrix, C(q, ˙q) is a Cori-
olis and centrifugal forces matrix, G(q) is a gravity
forces vector, u are forces and moments acting on the
system, q is an angular displacement.
The human leg model is presented in Figure 1.
The equation describing dynamics of a two-link leg
Figure 1: The model of two–link human leg.
in nonlinear state equation form (2) is
M(q) =
c
1
c
2
cos(q
1
− q
2
)
c
2
cos(q
1
− q
2
) c
3
,
C(q, ˙q) =
0 c
2
sin(q
1
− q
2
) ˙q
2
−c
2
sin(q
1
− q
2
) ˙q
1
0
,
G(q) =
−sinq
1
−c
5
sinq
2
,
c
1
= m
1
l
2
c1
+ m
2
l
2
1
+ I
1
, c
2
= m
2
l
1
l
c2
, c
3
= m
2
l
2
c2
+ I
2
,
c
4
= (m
1
l
c1
+ m
2
l
1
)g, c
5
= m
2
l
c2
g.
where m is a mass, l is a link’s length, l
c
is a distance
from the joint to the center of mass, I is a moment of
inertia, g is a gravity acceleration.
Physical parameters of a modelled leg are pre-
sented in Table 1. Namely, the dynamics of model in
MathematicalModelofaHumanLeg-TheSwitchedLinearSystemApproach
91

Table 1: The parameters of human leg.
m[kg] l[m] l
c
[m] I [kgm
2
]
Link 1 5.7 0.32 0.14 0.061
Link 2 2.65 0.40 0.17 0.038
terms of the state vector
q
T
, ˙q
T
T
can be expressed
as (Babiarz et al., 2013), (Babiarz et al., 2014b)
d
dt
q
˙q
=
˙q
M(q)
−1
[u−C(q, ˙q) ˙q− G(q)]
. (3)
Now, a new set of variables can be assigned to each
of the state variables. In accordance with (3), the new
set of state variables and their equivalences can be ex-
pressed as
x
1
= q
1
, x
2
= q
2
, (4)
x
3
= ˙x
1
= ˙q
1
, x
4
= ˙x
2
= ˙q
2
.
We can write the general state and output equations in
the following way
˙x = Ax+ Bu, (5)
y = Cx+ Du, (6)
where
˙x =
˙q
1
˙q
2
¨q
1
¨q
2
, x =
q
1
q
2
˙q
1
˙q
2
,
y =
¨q
1
¨q
2
, u =
u
1
u
2
.
(7)
2.2 An Approach Switched Linear
System
According to section 1 and subsection 1.1, we can
design switched linear system based on (3) and (7).
Analysing the activity of the human leg, we can as-
sume that the switching times depend on state vector
and the switched linear system is controlled (Liber-
zon, 2003). According to these assumptions the math-
ematical model can be described by equations (Babi-
arz et al., 2014a)
˙x(t) = A
σ(x)
x(t) + B
σ(x)
u(t), (8)
y(t) = C
σ(x)
x(t) + D
σ(x)
u(t). (9)
We consider the switched linear systems with state-
dependent switching. For the switched system de-
scribed above we propose a state-dependent switch-
ing function
˙x =
A
1
x+ B
1
u if x
1
= 0, x
2
≥ 0
A
2
x+ B
2
u if x
1
> 0, x
2
> 0
A
3
x+ B
3
u if x
1
< 0 or x
1
> 0, x
2
= 0
A
4
x+ B
4
u if x
1
< 0, x
2
> 0
(10)
y=
C
1
x+ D
1
u if x
1
= 0, x
2
≥ 0
C
2
x+ D
2
u if x
1
> 0, x
2
> 0
C
3
x+ D
3
u if x
1
< 0 or x
1
> 0, x
2
= 0
C
4
x+ D
4
u if x
1
< 0, x
2
> 0
(11)
Under the above assumption about the division of
state space, the model’s description can be made using
four linear subsystems forming a linear switched sys-
tem (equations (10) and (11)). Switching between any
dynamics depends only on angular displacement be-
cause only this parameter influences leg’s shape and
configuration during motion. The direct consequence
is that for each switching the angular velocity may be
arbitrary.
Figure 2: The first case.
Figure 3: The second case.
Figure 4: The third case.
Figure 5: The fourth case.
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
92
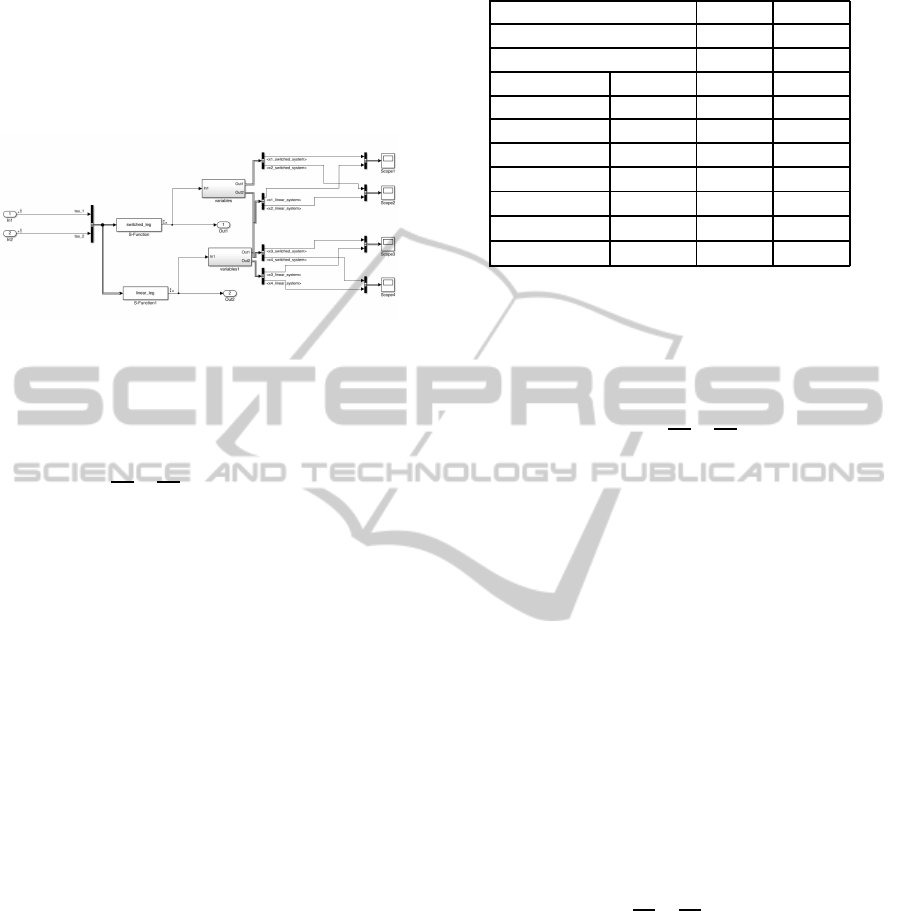
3 SIMULATION STUDY
This paragraph presents human leg model’s simula-
tion conditions for linear as well as for switched sys-
tem. All simulations were performed with the use of
Matlab Simulink package. A block diagram is given
in Figure 6.
Figure 6: The Simulink model.
3.1 A Linear Model
For the purpose of obtaining a linear model equation
2 was linearized about equilibrium point (x
0
;u
0
) =
([0rad, 0rad, 0
rad
s
, 0
rad
s
];[0Nm, 0Nm]). Parameters
taken for linearization are given in Table 1. The mo-
ment of inertia was calculated for truncated cone ap-
proximating the shape of a human leg.
A
L
=
0 0 1 0
0 0 0 1
−61.44 21.14 0 0
77.27 −65.14 0 0
, (12)
B
L
=
0 0
0 0
3.806 −4.8
−4.8 14.75
, (13)
C
L
=
−61.44 21.14 0 0
77.27 −65.14 0 0
, (14)
D
L
=
3.806 −4.8
−4.8 14.75
. (15)
3.2 A Switched Linear System
For a linear switched system equation (2) was lin-
earized about arbitrary selected working points which
are contained within particular regions Ω
i
, i =
1, 2, 3, 4 of a state space. Parameters used for calcu-
lation of matrices A
i
, B
i
,C
i
, D
i
, i = 1, 2, 3, 4 in state
equation (8) and output equation (9) are gathered in
Table 2. Values of parameter l
c
and moments of in-
ertia for each Ω
i
region are in the same table. The
moment of inertia was calculated also for a truncated
cone, the radii of which were changing depending on
the values of state vector elements x
1
and x
2
.
Table 2: The parameters of switched model.
Link 1 Link 2
m[kg] 5.7 2.65
l[m] 0.32 0.40
The case I l
c
[m] 0.14 0.17
The case II l
c
[m] 0.14 0.17
The case III l
c
[m] 0.14 0.17
The case IV l
c
[m] 0.14 0.17
The case I I[kgm
2
] 0.061 0.038
The case II I[kgm
2
] 0.061 0.038
The case III I [kgm
2
] 0.061 0.038
The case IV I [kgm
2
] 0.061 0.038
A First Example
3.2.1 Case I (Figure 2)
Matrices A
1
, B
1
,C
1
, D
1
calculated for (x
0
;u
0
) =
([0.349rad, −0.349rad, 0
rad
s
, 0
rad
s
];[0Nm, 0Nm])
working point belonging to Ω
1
region are presented
below:
A
1
=
0 0 1 0
0 0 0 1
−31 −1.8 0 0
14.52 −19.3 0 0
, (16)
B
1
=
0 0
0 0
3.05 −3.02
−3.02 13.9
, (17)
C
1
=
−31 −1.8 0 0
14.52 −19.3 0 0
, (18)
D
1
=
3.05 −3.02
−3.02 13.9
. (19)
3.2.2 Case II (Figure 3)
From the Ω
2
region a working point (x
0
;u
0
) =
([0rad, −0.523rad, 0
rad
s
, 0
rad
s
];[0Nm, 0Nm]) was
selected, for which matrices A
2
, B
2
,C
2
, D
2
were
obtained:
A
2
=
0 0 1 0
0 0 0 1
43 4.65 0 0
44.1 −35.5 0 0
, (20)
B
2
=
0 0
0 0
3.04 −3.4
−3.4 14.7
, (21)
C
2
=
43 4.65 0 0
44.1 −35.5 0 0
, (22)
MathematicalModelofaHumanLeg-TheSwitchedLinearSystemApproach
93

D
2
=
3.04 −3.4
−3.4 14.7
. (23)
3.2.3 Case III (Figure 4)
Working point (x
0
;u
0
) = ([−0.523rad, 0rad, 0
rad
s
,
0
rad
s
];[0Nm, 0Nm]) belonging to Ω
3
region was
used for linearization resulting with matrices
A
3
, B
3
,C
3
, D
3
:
A
3
=
0 0 1 0
0 0 0 1
−32.06 2.54 0 0
20.11 −26, 8 0 0
, (24)
B
3
=
0 0
0 0
3.33 −3.8
−3.8 15.5
, (25)
C
3
=
−32.06 2.54 0 0
20.11 −26, 8 0 0
, (26)
D
3
=
3.33 −3.8
−3.8 15.5
. (27)
3.2.4 Case IV (Figure 5)
Matrices A
4
, B
4
,C
4
, D
4
present in the state and
output equations of subsystem four of switched
system are obtained by linearization about (x
0
;u
0
) =
([−0.523rad, −0.523rad, 0
rad
s
, 0
rad
s
];[0Nm, 0Nm])
working point:
A
4
=
0 0 1 0
0 0 0 1
−45 12.3 0 0
58.2 −50.1 0 0
, (28)
B
4
=
0 0
0 0
3.02 −3.9
−3.9 16
, (29)
C
4
=
−45 12.3 0 0
58.2 −50.1 0 0
, (30)
D
4
=
3.02 −3.9
−3.9 16
. (31)
3.2.5 The Results
Figures 7-10 present time history of four elements
of state vector. Each figure shows comparison be-
tween consecutive elements of state vector of a
simple linear system and a switched system. Ini-
tial condition used for every simulation was x(t =
0) = [0.349rad, −0.349rad, 0
rad
s
, 0
rad
s
] and simula-
tion time was equal to 20 seconds.
Figure 7: Result of the first example - x
1
signal.
Figure 8: Result of the first example - x
2
signal.
Figure 9: Result of the first example - x
3
signal.
Figure 10: Result of the first example - x
4
signal.
3.3 Second Example
In the second simulation example the same sim-
ulation time of 20 seconds is set but initial
conditions are changed. The nonlinear sys-
tems described by (2) was in this case linearize
about arbitrary selected working point (x
0
, u
0
) =
([0.349rad, −0.349rad, 0
rad
s
, 0
rad
s
];[0Nm, 0Nm]).
The resulting matrices A
L
, B
L
,C
L
i D
L
are of the form
A
L
=
0 0 1 0
0 0 0 1
−31 −1.8 0 0
14.5 −19.3 0 0
, (32)
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
94

B
L
=
0 0
0 0
3.05 −3.021
−3.021 13.9
, (33)
C
L
=
−31 −1.8 0 0
14.5 −19.3 0 0
, (34)
D
L
=
3.05 −3.021
−3.021 13.9
. (35)
Matrices in the state and output equation of the
switched system remained unchanged.
Another simulation was run, this time
with the initial condition x(t = 0) =
[0rad, −0.349rad, 0
rad
s
, 0
rad
s
] for both, linear
”standard” and switched system. Figures 11-14
depict, as previously, comparison of every member
of the state vector. Based on presented simulation
results for both examples we state that the modelling
with the use of switched systems gives better outcome
than standard approach with linear systems. As a re-
sult the modelled object exhibits smaller oscillations,
Figure 11: Result of the second example - x
1
signal.
Figure 12: Result of the second example - x
2
signal.
Figure 13: Result of the second example - x
3
signal.
Figure 14: Result of the second example - x
4
signal.
what translates directly into the synthesis of control
algorithms.
Although the presented model of a human leg
is largely simplified, on the current state of work
it is sufficient for the analysis of dynamical prop-
erties which will be of interest to us in further re-
search (Czornik and
´
Swierniak, 2004), (Czornik and
´
Swierniak, 2005).
4 CONCLUSIONS
In future research authors aim at using linear switched
system to modelling of the human leg with seven de-
grees of freedom. Moreover, as shown in (Babiarz
et al., 2013) the subsystems of given object may be
unstable or on the stability boundary and may be un-
observable. For this reason we plan conduct the anal-
ysis of properties such as stability (Shorten, 2007) or
controllability and observability (Czornik and Niez-
abitowski, 2013), (Klamka and Niezabitowski, 2013),
(Klamka et al., 2013). In the next step we will in-
corporate systems with fractional order, as in (Hos-
seinNia et al., 2013), (Kaczorek, 2013), (Tejado et al.,
2013b), (Klamka et al., 2014) into this framework.
ACKNOWLEDGEMENTS
The work of the first author was partially supported
by Polish Ministry of Science and Higher Edu-
cation, no. BK-265/RAu1/2014/t.2 (A.B.). The
research presented here were done by the authors
as parts of the projects funded by the National
Science Centre granted according to decisions DEC-
2012/05/B/ST7/00065 (A.C.), DEC-2012/07/N/ST7/
03236 (M.N.) and DEC-2012/07/B/ST7/01404
(R.Z.), respectively. The calculations were performed
with the use of IT infrastructure of GeCONiI Upper
Silesian Centre for Computational Science and Engi-
neering (NCBiR grant no POIG.02.03.01-24-099/13).
REFERENCES
Babiarz, A., Czornik, A., et al. (2014a). The mathemat-
ical model of the human arm as a switched linear
system. In Methods and Models in Automation and
Robotics (MMAR), 2014 19th International Confer-
ence on, pages 508–513.
Babiarz, A. et al. (2013). The dynamics of the human arm
with an observer for the capture of body motion pa-
rameters. Bulletin of the Polish Academy of Sciences:
Technical Sciences, 61(4):955–971.
MathematicalModelofaHumanLeg-TheSwitchedLinearSystemApproach
95

Babiarz, A., Klamka, J., et al. (2014b). An approach to
observability analysis and estimation of human arm
model. In 11th IEEE International Conference on
Control and Automation, pages 947 –952. IEEE.
Bai, O., Nakamura, M., and Shibasaki, H. (2001). Com-
pensation of hand movement for patients by assistant
force: relationship between human hand movement
and robot arm motion. Neural Systems and Rehabili-
tation Engineering, IEEE Transactions on, 9(3):302–
307.
Błachuta, M., Czyba, R., Janusz, W., and Szafra´nski, G.
(2014). Data Fusion Algorithm for the Altitude and
Vertical Speed Estimation of the VTOL Platform.
Journal of Intelligent and Robotic Systems, 74(1-
2):413–420.
Burdet, E., Tee, K. P., Mareels, I., Milner, T. E., Chew, C.-
M., Franklin, D. W., Osu, R., and Kawato, M. (2006).
Stability and motor adaptation in human arm move-
ments. Biological cybernetics, 94(1):20–32.
Chang, P. H., Park, K., Kang, S. H., Krebs, H. I., and Hogan,
N. (2013). Stochastic estimation of human arm
impedance using robots with nonlinear frictions: An
experimental validation. Mechatronics, IEEE/ASME
Transactions on, 18(2):775–786.
Chen, K. (2011). Modeling of equilibrium point trajectory
control in human arm movements. PhD thesis, New
Jersey Institute of Technology.
Csercsik, D. (2005). Analysis and control of a simple non-
linear limb model. PhD thesis, University of Technol-
ogy.
Czornik, A. and Niezabitowski, M. (2013). Controllability
and stability of switched systems. In Methods and
Models in Automation and Robotics (MMAR), 2013
18th International Conference on, pages 16–21.
Czornik, A. and
´
Swierniak, A. (2004). On direct controlla-
bility of discrete time jump linear system. Journal of
the Franklin Institute, 341(6):491–503.
Czornik, A. and
´
Swierniak, A. (2005). Controllability
of discrete time jump linear systems. Dynamics of
Continuous Discrete and Impulsive Systems-Series B-
Applications & Algorithms, 12(2):165 – 189.
HosseinNia, S. H., Tejado, I., and Vinagre, B. M. (2013).
Stability of fractional order switching systems. Com-
puters & Mathematics with Applications, 66(5):585–
596.
Kaczorek, T. (2013). Stability of positive fractional
switched continuous-time linear systems. Bulletin of
the Polish Academy of Sciences. Technical Sciences,
Vol. 61(2):349–352.
Klamka, J., Czornik, A., and Niezabitowski, M. (2013).
Stability and controllability of switched systems. Bul-
letin of the Polish Academy of Sciences. Technical Sci-
ences, 61:547–555.
Klamka, J., Czornik, A., Niezabitowski, M., and Babi-
arz, A. (2014). Controllability and minimum en-
ergy control of linear fractional discrete-time infinite-
dimensional systems. In 11th IEEE International
Conference on Control and Automation, pages 1210–
1214. IEEE.
Klamka, J. and Niezabitowski, M. (2013). Controllability of
switched linear dynamical systems. In Methods and
Models in Automation and Robotics (MMAR), 2013
18th International Conference on, pages 464–467.
Klamka, J. and Niezabitowski, M. (2014). Controllabil-
ity of switched infinite-dimensional linear dynamical
systems. In Methods and Models in Automation and
Robotics (MMAR), 2014 19th International Confer-
ence on, pages 171–175.
Kong, K. and Tomizuka, M. (2009). Control of ex-
oskeletons inspired by fictitious gain in human
model. Mechatronics, IEEE/ASME Transactions on,
14(6):689–698.
Lee, D., Glueck, M., et al. (2010). A survey of modeling
and simulation of skeletal muscle. ACM Transactions
on Graphics, 28(4):162.
Liberzon, D. (2003). Switching in systems and control.
Springer.
Neumann, T., Varanasi, K., Hasler, N., Wacker, M., Mag-
nor, M., and Theobalt, C. (2013). Capture and statisti-
cal modeling of arm-muscle deformations. In Com-
puter Graphics Forum, volume 32, pages 285–294.
Wiley Online Library.
Pavlovic, V., Rehg, J. M., and MacCormick, J. (2001).
Learning switching linear models of human motion.
In Leen, T., Dietterich, T., and Tresp, V., editors, Ad-
vances in Neural Information Processing Systems 13,
pages 981–987. MIT Press.
Pons, J., Moreno, J., Brunetti, F., and Rocon, E. (2007).
Lower-Limb Wearable Exoskeleton In Rehabilitation
Robotics. Monografie - Komitet Automatyki i Robo-
tyki P. I-Tech Education and Publishing.
Sekine, M., Sugimori, K., Gonzalez, J., and Yu, W. (2013).
Optimization-Based Design of a Small Pneumatic-
Actuator-Driven Parallel Mechanism for a Shoulder
Prosthetic Arm with Statics and Spatial Accessibil-
ity. Evaluation. International Journal of Advanced
Robotic Systems, 286(10).
Shorten, R. (2007). On Quadratic Stability of State-
dependent Planar Switching Systems. Forschungs-
berichte der Fakult¨at IV - Elektrotechnik und Infor-
matik // Technische Universit¨at Berlin. Techn. Univ.,
Fak. IV, Elektrotechnik und Informatik.
Sun, Z. (2006). Switched linear systems: Control and De-
sign. Springer.
Sun, Z. and Ge, S. S. (2011). Stability theory of switched
dynamical systems. Springer.
Tejado, I., Val´erio, D., Pires, P., and J., M. (2013a). Optimal
Feedback Control for Predicting Dynamic Stiffness
During Arm Movement. Mechatronics, 23(7):805–
812.
Tejado, I., Valrio, D., Pires, P., and Martins, J. (2013b).
Fractional order human arm dynamics with variabil-
ity analyses. Mechatronics, 23(7):805–812.
Ueyama, Y. and Miyashita, E. (2014). Optimal Feedback
Control for Predicting Dynamic Stiffness During Arm
Movement. Industrial Electronics, IEEE Transactions
on, 61(2):1044–1052.
Zawiski, R. and Błachuta, M. (2012). Model development
and optimal control of quadrotor aerial robot. In Meth-
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
96

ods and Models in Automation and Robotics (MMAR),
2012 17th International Conference on, pages 475–
480.
Zhao, Y., Xu, C., Luo, Y., and Wang, Y. (2008). Design,
modeling and simulation of the human lower extrem-
ity exoskeleton. In Control and Decision Conference,
2008. CCDC 2008. Chinese, pages 3335–3339. IEEE.
MathematicalModelofaHumanLeg-TheSwitchedLinearSystemApproach
97
