A MapReduce-based Approach for Finding Inexact Patterns in Large

Graphs

∗

Péter Fehér, Márk Asztalos, Tamás Mészáros and László Lengyel

Department of Automation and Applied Informatics, Budapest University of Technology and Economics, Budapest, Hungary

Keywords:

Graph Isomorphism, MapReduce, Pattern Matching.

Abstract:

Finding patterns in graphs is a fundamental problem in graph theory, and also a practical challenge during

the analysis of big data sets. Inexact patterns may correspond to a set of possible exact graphs. Their use

is important in many ﬁelds where pattern matching is applied (e.g. mining in social networks or criminal

investigations). Based on previous work, this paper introduces a pattern speciﬁcation language with special

language features to express inexact patterns. We also show a MapReduce approach-based algorithm that is

able to ﬁnd matches. Our methods make it possible to deﬁne inexact patterns and to ﬁnd the exact matches in

large graphs efﬁciently.

1 INTRODUCTION

Finding patterns efﬁciently in large graphs is a core

challenge in the analysis of big data sets. Pattern

matching is based on subgraph isomorphism that

deals with the problem of deciding if there is an injec-

tive morphism from one graph to another. It is already

proven that ﬁnding such a morphism is NP-complete

in general (Plump, 1998). To perform the pattern

matching efﬁciently, especially in the processing of

big data sets, distributed algorithms such as MapRe-

duce gain focus. To ﬁnd a match, we need a pat-

tern speciﬁcation language and a matcher algorithm

that performs the actual searching. The language may

contain special features that make it possible to deﬁne

not just a single graph but inexact patterns as well. An

inexact pattern covers a set of possible exact graphs

by using constraints. Being able to detect inexact pat-

terns might be critical in some cases, for example,

when the analyzer needs to match a general pattern

without knowing all of the details, the host graph is

not completely known, or some aspect of the searched

pattern is incorrect (Coffman et al., 2004). Moreover,

inexact patterns lead to more concise speciﬁcations

that is an important aspect in graph rewriting-based

model transformations (Ehrig et al., 2006).

As an example, consider the graph depicted in

∗

This work was partially supported by the European

Union and the European Social Fund through project Fu-

turICT.hu (grant no.: TAMOP-4.2.2.C-11/1/KONV-2012-

0013) organized by VIKING Zrt. Balatonfüred.

Figure 1. This graph illustrates the retail banks be-

longing to the central bank. The graph also represents

the different type of loans the retail banks offered

to their customers. Moreover, the dotted lines be-

tween the customers indicate personal relationships.

Although this example contains only a several dozens

of elements, it is easy to see, that a real life example

from this ﬁeld might consist of millions of elements,

therefore its analysis with MapReduce can be not only

reasonable but inevitable.

Assume that the central bank wants to know the

households, where at least two members of the family

have mortgages. Since it does not matter to the central

bank whether the relatives have their mortgages at the

same bank or not, there are two different patterns. In

the ﬁrst case (depicted in Figure 2(a)), the customers

have their mortgages at different banks, therefore the

pattern should match two bank elements. However,

the family members might get their mortgages from

the same bank, and in this case there should be only

one bank element matched (depicted in Figure 2(b)).

The answer is formulated from the union of the two

cases.

By the usage of traditional pattern matching lan-

guages and solutions, the central bank needs to match

two different patterns. However, with the help of in-

exact patterns, a simple pattern can be formulated to

answer the question of the central bank. The inex-

act pattern to solve this problem is presented in Fig-

ure 3 (the purpose of the labels is to identify the el-

ements later). The optional blocks (depicted as dot-

205

Fehér P., Asztalos M., Mészáros T. and Lengyel L..

A MapReduce-based Approach for Finding Inexact Patterns in Large Graphs.

DOI: 10.5220/0005231102050212

In Proceedings of the 3rd International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2015), pages 205-212

ISBN: 978-989-758-083-3

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

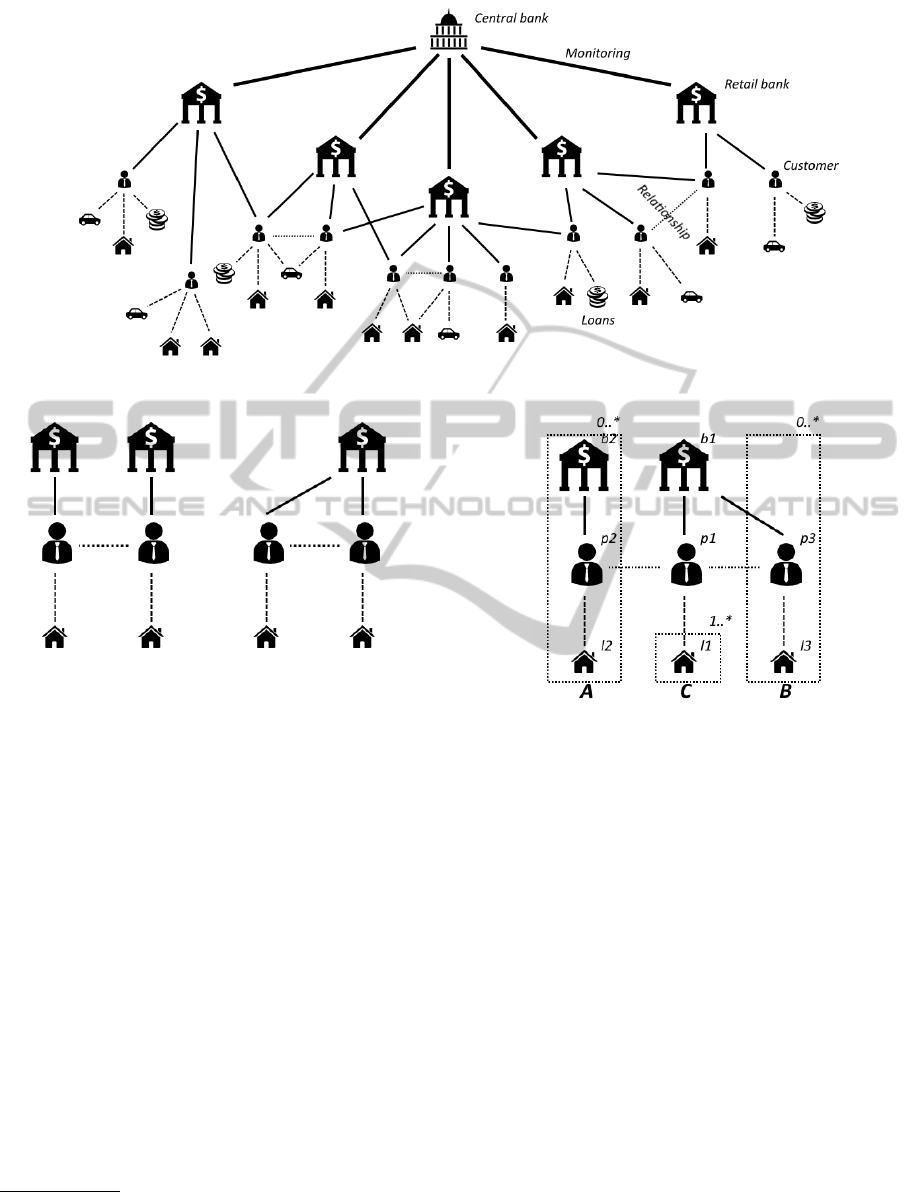
Figure 1: Graph representing the Bank-Customer relationships

(a) (b)

Figure 2: The traditional patterns.

ted rectangles) are internal parts of the language our

metamodel-based matcher relies on. The language

makes it possible to not only use optional blocks, but

to deﬁne logical relations between them. In our exam-

ple, the match is only complete if either one or both

optional blocks from the block A and block B can be

matched beside the block C.

In previous work, we presented a MapReduce-

based algorithm (MRSI

) that performs the matching

of exact graph patterns, and we have analyzed its per-

formance. In this paper, we introduce the adapta-

tion of the method to handle inexact matches. The

main contributions are twofold: (i) We introduce an

improved pattern speciﬁcation language that can de-

scribe inexact matches. (ii) We present the improved

version of the MapReduce-based matcher algorithm

(MRMM) that is able to handle the new language. In

the design phase, our goal was to provide advanced

language features that make it possible to specify in-

The icons used in Figure 1-3 were made by

Freepik from www.ﬂaticon.com and is licensed by http://

creativecommons.org/licenses/by/3.0/.

Figure 3: A simple pattern with optional blocks.

exact pattern and still allow to provide efﬁcient dis-

tributed algorithms for the matching.

The remainder of the paper is organized as fol-

lows. Section 2 presents the new language designed

for deﬁning patterns. The basics of the MapReduce

framework are discussed in Section 3. Next, Section 4

describes the pattern matching algorithm. Section 5

provides an overview of related work. Finally, Sec-

tion 6 closes with concluding remarks.

2 THE PATTERN

SPECIFICATION LANGUAGE

In this section, we introduce our concept to describe

inexact graph patterns. Pattern speciﬁcation lan-

guages are developed with two important goals kept

in mind: (i) the language should be expressive enough

to be able to specify possible matches in a concise

way. (ii) Moreover, it is important to have efﬁcient

algorithms that can search for the matches.

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

206

Figure 4: Language features of pattern matchers.

The most trivial speciﬁcation language would

simply allow us to specify exact patterns, i.e. each

element that will be present in the match. In other

words, we provide a pattern where we specify the

types of the nodes and edges along with optional ad-

ditional constraints, and the actual matches will be

isomorph occurrences of this pattern. In many cases,

we may need more advanced language features (such

as multiplicities, negative application conditions etc.)

that lead to inexact patterns. Multiplicities (or car-

dinalities) added to the nodes and to the ends of the

edges mean that the given element of the pattern may

occur several times in the actual match. With this fea-

ture, the patterns of the speciﬁcation language can

be turned into small metamodels whose all possi-

ble instances that are present in the model are valid

matches. Two sample patterns (with and without mul-

tiplicities) along with possible matches are depicted

in the ﬁrst and second columns of Figure 4. Col-

ors denote the types of the elements. Negative ap-

plication conditions (NACs) consists of additional el-

ements that will not be matched, on the contrary, they

must not be able to be found.

The language features detailed above obviously

increase the expressiveness of the language, but also

make the match ﬁnder algorithms more complex and

harder to be implemented. In the following, we intro-

duce our pattern speciﬁcation language. Our goal is to

ﬁnd a good balance between these two goals. There-

fore, this language contains several language features,

but has a few limitations compared to the previously

mentioned fully metamodel-based approach.

In theory, patterns of our language consists of

nodes and edges. We deﬁne their types and additional

constraints on their attributes in the usual way. We

can deﬁne groups in a pattern. A group is a set of con-

nected nodes. Each node can be a member of at most

one group, so the groups are disjoint. Moreover, it is

required that if two nodes are members of two differ-

ent groups, they cannot have edges between them in

the pattern. We can assign multiplicity constraints to

the groups. When searching for the possible matches

of the pattern, each group can be present multiple

times according to their multiplicity constraints. The

nodes that are not members of any groups represent

single nodes in the matches just as in exact patterns.

When an edge of the pattern connects a group mem-

ber and a traditional node, this means that the instance

of the exact node will be connected to every instances

of the group. The third column of Figure 4 shows a

sample pattern where there is one group and its mul-

tiplicity is 2..8. This means that at least 2, but at most

8 instances of the group must be present in a possi-

ble match. The ﬁgure also presents an instance of the

pattern. It can be seen that the node in the top left cor-

ner of the pattern is connected to all instances of the

group.

Because of the space limits of this paper, we do

not go into deeper details about other features of the

language, but we mention that application conditions

(negative and positive) and logical statements on op-

tional blocks can be speciﬁed as well.

We have implemented a textual language. Accord-

ing to the previous concepts, we can deﬁne nodes,

edges, and blocks with multiplicities. Nodes and

edges may have labels. Additionally, logical state-

ments using block identiﬁers can be speciﬁed. The

code belonging to the inexact pattern presented in Fig-

ure 3 is as follows:

rule MultipleMortgages {

node p1 [Person] node l1 [Loan] node b1 [Bank]

node p2 [Person] node l2 [Loan] node b2 [Bank]

node p3 [Person] node l3 [Loan]

edge from p1 to l1 [Mortgage]

edge from b1 to p1 [Customer]

edge from p1 to p2 [Relationship]

edge from p2 to l2 [Mortgage]

edge from b2 to p2 [Customer]

edge from p1 to p3 [Relationship]

edge from b1 to p3 [Customer]

edge from p3 to l3 [Mortgage]

block A (b2, p2, l2)?

block B (b1, p3, l3)?

block C (l1)1..*

with A or B

}

We believe that our concept is efﬁcient enough to

be applied in real-world scenarios. Moreover, in the

next sections, we will show an efﬁcient distributed al-

gorithm that is able to ﬁnd the actual matches spec-

iﬁed by the patterns of the language. This demon-

strates the practical applicability of our approach.

Moreover, our experiences gained from practical so-

lutions show that the presented language is expres-

sive enough to be used in model transformations as

well, which is an important application ﬁeld of pat-

tern speciﬁcation languages.

AMapReduce-basedApproachforFindingInexactPatternsinLargeGraphs

207

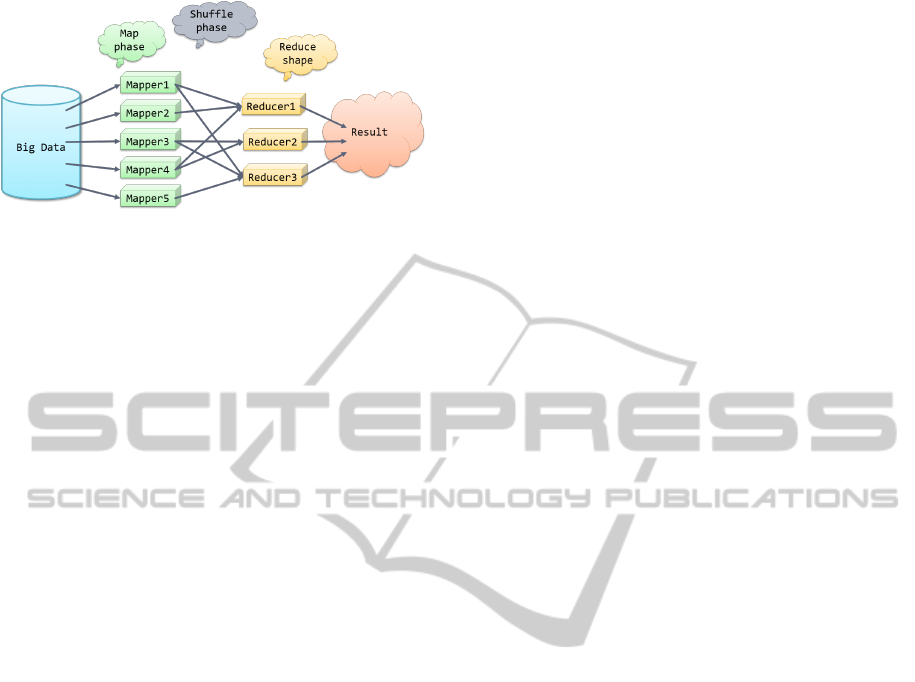
Figure 5: The structure of a MapReduce algorithm.

3 THE MAPREDUCE

TECHNIQUE

The MapReduce framework is a parallel computing

paradigm (Dean and Ghemawat, 2008). The frame-

work was originally developed at Google, and to-

day has become the de facto approach for process-

ing large-scale data. One of its open source imple-

mentations is the Apache Hadoop (Apache Hadoop,

2011). The MapReduce framework was designed for

utilizing distributed computing resources and for han-

dling large data sets. Data is always assumed to be

distributed, and the data balancing is managed by the

Hadoop Distributed File System (HDFS).

One of the biggest differences between the

MapReduce and other parallel computing frameworks

is that MapReduce implements both parallel and se-

quential computation: the framework calls the map

and reduce functions sequentially, but in each phase

the functions are executed in parallel.

The structure of a MapReduce algorithm is illus-

trated in Figure 5. Basically, the MapReduce algo-

rithm consists of three phases. First, the map function

is executed. The framework assigns the same mapper

task µ to several processes, but these processes take

different inputs as the lone argument of µ. The map-

per function is stateless, because it does not have any

information on the previously processed data, nor can

it communicate with other mapper tasks. In this man-

ner, it only requires the input value to compute its out-

put value. This way the mapper function can be run

against the values in parallel, which provides great ef-

ﬁciency. Generally, the mapper µ takes a single string

input and produces any number of <key, value> pairs

as output.

The second phase is referred to as shufﬂe or as

group. At this stage, the framework seamlessly sorts

the outputs of the mappers by their keys. As a result,

the values are grouped by their key values.

The shufﬂe step makes it possible to assign every

value with the same key to the same reducer in the

ﬁnal phase. A reducer ρ takes a single key and all

the values associated with it as input. After process-

ing, the reducer produces arbitrary number of <key,

value> pairs, as output. Like the mapper tasks, the

reducers are stateless as well. An important attribute

of the MapReduce framework is that all mapper tasks

must ﬁnish before the reducer tasks can begin. This

aspect of the framework supports the sequential pro-

cessing. However, by assigning different keys to dif-

ferent processes, the reducer task also supports paral-

lelization.

The map, shufﬂe, and reduce phases constitute a

MapReduce job. The MapReduce algorithm can be

implemented as a series of MapReduce jobs. In this

case, the output of the λ

job (i.e. the <key, value>

pairs produced by the ρ

reduces) is the input of the

job (i.e. the string input of the µ

mapper)(Fehér

et al., 2013).

Based on (Karloff et al., 2010), the formal deﬁni-

tion of the MapReduce programming paradigm is the

following.

Deﬁnition 1. A mapper is a function that takes a bi-

nary string (which might be a <key, value> pair) as

input. As output, the mapper produces a ﬁnite set of

<key, value> pairs.

Deﬁnition 2. A reducer is a function whose input is

a binary string, a key (k), and a sequence of values

, v

, . . . ) that are also binary strings. As output, the

reducer produces a ﬁnite multiset of pairs of binary

strings <k, v

k,1

>, <k, v

k,2

>, <k, v

k,3

>, . . . . The key in

the output pair is identical to the key in the input.

As it was mentioned before, the main strength of

the MapReduce approach is the ease of paralleliza-

tion. Since one mapper task processes one element

from the input set at a time, the framework can have

multiple instances from the same map function as-

signed to different computing nodes in parallel. Sim-

ilarly, one reducer task operates on one key value and

on the values associated with it. Therefore, if the

number of different keys is denoted with n, then at

most n different reducer instances can be executed si-

multaneously.

4 THE PATTERN MATCHING

ALGORITHM

The MapReduce MetaMatcher algorithm (MRMM) is

a novel approach to detect arbitrary patterns in graphs

with millions of edges and vertices. The algorithm is

constructed to extend the MapReduce Subgraph Iso-

morphism - version S algorithm (MRSI

), therefore

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

208

the pattern matching utilizes the advantageous prop-

erties of the MapReduce framework. In this manner,

the algorithms make it possible to move the pattern

matching into the cloud, which offers the following

beneﬁts: (i) The graph can be stored in the cloud

(typically in a BLOB), (ii) the size of the cluster can

be dynamically changed depending on the graph and

the pattern to match. There are a number of differ-

ent cloud vendors offering these possibilities, for ex-

ample (Amazon Web Services, 2013) and (Windows

Azure, 2013).

This section brieﬂy presents the basics of the

MRSI

algorithm, then introduces the MRMM algo-

rithm, which enables the inexact pattern matching.

4.1 The MRSI

Algorithm

The MRSI

is a MapReduce algorithm to detect sub-

graph isomorphism. At each iteration, the algorithm

adds a new pair of vertices to each partial mapping.

All partial mappings are subgraphs isomorphic to the

target graph. In case the partial mapping contains the

same number of vertices as the target graph, then the

two sets are isomorphic to each other. In this man-

ner, the algorithm terminates after at most n iterations,

where n denotes the number of vertices contained by

the target graph. In case a partial mapping cannot be

extended with a new pair of vertices in a way to re-

main subgraph isomorphic to the target graph, the al-

gorithm does not emit any information related to this

partial mapping, therefore, it does not participate in

the next iteration. The algorithm terminates either af-

ter the n

iteration, or when there are no partial map-

pings that can be extended with a new pair of vertices.

In order to minimize the required I/O operations,

the algorithm uses a special data structure, which con-

tains only the necessary information about a source

graph node. Since the processing of a textual ﬁle in

a MapReduce framework is performed line-by-line,

each line represents a source graph vertex. The neces-

sary information about a given node is the following:

• The identiﬁer of the node,

• In case of labeled graph, the labels of the vertex

(if there is any),

• The sources of the incoming edges and their labels

(if there is any),

• The targets of the outgoing edges and their labels

(if there is any).

Since the node may have multiple vertex labels

and incoming/outgoing edges with multiple edge la-

bels, the information must be carefully separated.

The data structure in Extended Backus–Naur Form

(EBNF) is depicted in the following listing, where the

rule of thumb is the following:

1. The identiﬁer of the node is the most important in-

formation, therefore it is the ﬁrst, and is followed

by a tabulator that is typically used as the sepa-

rator between the key and the value emitted by

either the mapper or the reducer.

2. The remaining sets, i.e. the labels, incoming

edges and outgoing edges are separated by a semi-

colon character.

3. Each item in an array (e.g. the different labels of

the node) are separated by a comma character.

4. The end points of the edges are separated from

their labels by a dash character.

5. Each item in a subarray (e.g. the different labels

of the edges) are separated by a colon character.

row = ID, "\t", { NodeLabels }, ";",

{ IncomingEdges }, ";",

{ OutgoingEdges }, ";", HelperBit;

ID = alphabetic character | digit,

{ alphabetic character | digit };

NodeLabels = Label, { ",", NodeLabels };

IncomingEdges = ID, { "-", EdgeLabels },

{ ",", IncomingEdges };

OutgoingEdges = ID, { "-", EdgeLabels },

{ ",", OutgoingEdges };

EdgeLabels = Label, { ":", EdgeLabels };

HelperBit = "0" | "1";

The MRSI

algorithm consists of a chain of two

MapReduce jobs. The ﬁrst job is responsible for

adding a new node pair to the partial mappings. Each

mapper function in this job takes a partial mapping

and a candidate node from the source graph. The

function then calculates the next target graph node

to match and determines whether this node can be

mapped to the candidate node regarding to the par-

tial mapping. In case of a successful match, the func-

tion extends the partial mapping with this node pair.

In order to be able to produce all possible candidate

nodes for this new partial mapping, the mapper func-

tion emits a new <key, value> pair for each source

graph node contained by the mapping, where the key

is the source graph node and the value is the new par-

tial mapping. The function then moves on to the next

partial mapping related to this candidate node. The re-

ducer functions group the emitted <key, value> pairs

by their keys. In this manner, after the ﬁrst job, the

partial mappings are extended with another node pair,

and each emitted line consists of all information of a

source node, and all partial mappings the given source

node is part of.

The second job is responsible for generating the

candidate pairs for each partial mappings. This

means, that the job transforms the data in such a way

that the partial mappings appear in the line of ev-

ery candidate source graph node. Therefore, each

mapper function obtains a source graph node and the

AMapReduce-basedApproachforFindingInexactPatternsinLargeGraphs

209

mappings the node is part of. Then, for each partial

mapping, the function iterates through the neighbors

of the source graph node, and if the neighbor is not

contained by the given partial mapping, the function

emits it as the key of a <key, value> pair. The related

value is the partial mapping. The reducer functions

group the emitted lines by their key values and drop

the recurrences.

4.2 The MRMM Algorithm

Recall that, the MRMM algorithm is based on the

MRSI

algorithm. This section presents the main dif-

ferences between the two algorithms.

The MRMM algorithm is capable of detecting pat-

terns with optional parts. These parts are organized

into blocks. The blocks have the following three prop-

erties:

• The identiﬁer of the block, which must be unique.

• The identiﬁers of the nodes contained by the

block. None of the nodes can be contained by

more than one block.

• The multiplicity of the block.

Since the algorithm supports optional blocks, that

is, the ﬁnal match is valid with and without the nodes

contained by the block as well, the identiﬁer of the al-

ready examined blocks must be maintained through-

out the MapReduce iterations. This is particularly im-

portant in those cases, when a block cannot be part of

a valid partial mapping, because otherwise the algo-

rithm would repeatedly check the nodes of this block,

causing an inﬁnite loop.

The obligation of maintaining the block identiﬁers

means that the data structure must be extended. The

information about the examined blocks is related to

the partial mapping, therefore, each partial mapping

has an additional value in the outputs, which con-

tains the identiﬁer of the last unsuccessfully matched

block. This information is enough, because of the fol-

lowing:

• The identiﬁer unambiguously determines the

block.

• The identiﬁers of the successfully matched blocks

can be deduced from the partial mapping.

• The algorithm orders the nodes of the target

graph, therefore, if there are more than one unsuc-

cessfully matched blocks, the last one determines

the previous ones as well.

Since the MRSI

algorithm detects isomorphic

subgraph patterns, the number of nodes contained

by the ﬁnal match equals to the number of nodes

contained by the target graph. However, in case of

the pattern matching this is not true anymore, be-

cause of the multiplicity of the blocks, the number

of nodes contained by the valid matches might dif-

fer from the number of nodes contained by the target

graph. Therefore, the MRMM uses an indicator that

signals when at• least one partial mapping is extended

with a new node pair. In this case, another iteration

of MapReduce jobs is justiﬁed. Otherwise, the algo-

rithm terminates.

The main difference between the two algorithms

is the selection of the next candidate node. As it was

mentioned, the algorithm maintains a sorted list based

on the nodes of the target graph. The MRSI

algo-

rithm simply chooses the ﬁrst from this list that is

not already contained by the partial mapping. How-

ever, in case of optional blocks this cannot be a solu-

tion. Therefore, a new node selection algorithm was

needed, which is shown in Algorithm 1.

Algorithm 1: The algorithm of selecting the next candidate

node for a partial mapping.

Require: the given partial mapping as actualMatch and the identiﬁer of the

last unsuccessfully matched block as lastBlockId

Ensure: the identiﬁer of the next candidate node

1: if actualMatch.isEmpty then

2: return GETFIRSTNODE()

3: Nodes[] SortedNodes ← GETSORTEDNODES()

4: Nodes[] possibleNodes ← SortedNodes

5: if not lastBlockId.isEmpty then

6: Nodes[] blockNodes ← GETUNUSEDBLOCKNODES()

7: possibleNodes.Remove(blockNodes)

8: Node lastNode ← GETNODEBYID(actualMatch.Last.TargetNode)

9: string lastNodeBlockId ← lastNode.BlockId

10: if not lastNodeBlockId.isEmpty ∧ lastNodeBlockId 6= lastBlockId

then

11: Nodes[] blockNodes ← GETNODESFORBLOCK(lastNodeBlockId)

12: if blockNodes.count > 0 ∧ lastNode 6=

SortedNodes.LastInBlock(blockNodes) then

13: return SortedNodes.GetNextFromBlock(lastNode).Id

14: if blockNodes.count > 0 ∧ lastNode 6=

SortedNodes.LastInBlock(blockNodes)

∧ ISBLOCKSTILLANOPTION(lastNodeBlockId, actualMatch)

then

15: return SortedNodes.GetFirstInBlock(lastNodeBlockId).Id

16: for all m|m ∈ actualMatch∧GETNODEBYID(m.TartgetNode)∈

possibleNodes do

17: possibleNodes.Remove(m)

18: Node nextNode ← possibleNodes.First()

19: return nextNode.Id

The algorithm consists of four parts. First, if the

partial mapping is empty, then the identiﬁer of the ﬁrst

node in the sorted list is returned. This node cannot

be part of any optional block, because then the algo-

rithm could not ﬁnd the mappings without this op-

tional node.

The second part (lines 4–8) ﬁlters the possible

nodes. The GETUNUSEDBLOCKNODES() method

returns all nodes that are contained by any block that

appears before the last unsuccessfully matched block

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

210

in the sorted list. These nodes cannot be part of

the candidate nodes because they are either already

matched or determined as an unsuccessful match.

Therefore, these nodes are removed from the possi-

ble nodes.

The third part (lines 10–17) is responsible for

returning the next candidate node when the lastly

matched node was part of a block. In case there are

still nodes contained by this block left in the sorted

list, the algorithm returns with the identiﬁer of the ﬁrst

one of these. In case the lastly matched node was the

last one contained by the block, but the multiplicity of

the block indicates another matching, the algorithm

returns the ﬁrst node of the sorted list contained by

the block.

Finally, the fourth part (lines 19–22) returns the

identiﬁer of the next possible node. This way the al-

gorithm handles all possibilities regarding to the de-

ﬁned language.

The ﬁrst mapper function of the MRMM, which is

responsible for adding new pairs to the partial map-

pings, now might take an optional node as the candi-

date. In this case the candidate node either extends

an optional block currently contained by the partial

mapping or not. If it is an extension then the algo-

rithm runs as usual. However, if it is not an extension,

that is, this is a new block, then the algorithm emits

the original partial mapping as well, and sets its last

unsuccessfully matched block to the identiﬁer of this

block. This way the partial mapping with and without

the optional block constitutes two different branches.

The second mapper function, which is responsible

for moving the partial mappings to the row of can-

didate source graph nodes, must also check, whether

the partial mapping contains all non-optional nodes

from the target graph. If so, and there is no candidate

source node related to this mapping, then the mapping

should be marked as a complete match.

With the help of these modiﬁcations, the MRMM

algorithm is able to detect different patterns with op-

tional parts. The algorithm also possesses the advan-

tageous properties of the MRSI

algorithm.

5 RELATED WORK

In related work (Berry et al., 2007), Berry et al. devel-

oped a parallel implementation for supporting mas-

sive multithreading. The implementation is based

on the large shared memory of the machines in the

cluster. The algorithms are designed for ﬁnding con-

nected components and st-connectivity. Experimental

results were measured on a synthetic power law graph

with 234 million edges. Berry also developed heuris-

tics for inexact subgraph isomorphism (Berry, 2010).

Our approach is capable of handling large problems

as well with no need for large shared memory.

In (Plantenga, 2012), Plantenga presents a new al-

gorithm, which ﬁnds inexact subgraph isomorphisms.

The main contribution of his work is a scalable

MapReduce algorithm for ﬁnding all type-isomorphic

matching subgraphs and also introduces the concept

of walk-level constraints. The suggested algorithm

adds new edges to the already matched ones at each

iteration. Experimental results are also provided on

graphs with size of billions of vertices and edges. The

MRMM algorithm is also suitable for inexact pattern

matching, moreover, it is capable of detecting even

more complex patterns.

In (Tong et al., 2007), Tong et al. suggest an algo-

rithm that returns a speciﬁed number of “best effort”

matches. The complexity of the Graph X-ray algo-

rithms is linear to the number of nodes in the source

graph. In contrast, the MRMM algorithm returns all

exact matches and can handle not only vertex labels

but edge labels as well.

In (Liu et al., 2009), Liu et al. present a MapRe-

duce algorithm for “pattern ﬁnding”. Similarly to

MRMM, their algorithm increases the size of partial

mappings. However, the algorithm was used on a

graph with 2000 edges with a cluster of 48 nodes.

Since they assume the full adjacency matrix is avail-

able at each cluster node, the algorithm may have dif-

ﬁculty with larger graphs. The MRMM algorithm do

not use the whole adjacency matrix at each mapper,

this way it is more scalable.

In (Kim et al., 2013), Kim et al. developed a

method to efﬁciently process multiple graph queries

based on MapReduce. The method uses a ﬁlter-and-

verify scheme to reduce the number of subgraph iso-

morphism test. In contrast to the MRMM algorithm,

their work focuses on multiple graph queries instead

of pattern matching.

The purpose of the solution presented in (Mezei

et al., 2009) is to compute one of the possible matches

for a pattern. The algorithm is executed in a com-

puting grid consisting of several worker and a mas-

ter node coordinating their operation. The individual

worker nodes are performing the same matching algo-

rithm on the same graph, but the matching is started

from different points of the host graph. The selec-

tion of the starting point is coordinated by the master

node. Once either of the nodes ﬁnds a match, it noti-

ﬁes the master node that lets the other worker nodes

stop the algorithm. In contrast, our algorithm is ca-

pable of computing all the possible matches. Another

important drawback of this approach is that it needs

the complete host graph to be stored on each worker

AMapReduce-basedApproachforFindingInexactPatternsinLargeGraphs

211

nodes, while our approach is more scalable since the

workers always see only a small portion of the com-

plete graph.

The pattern matching approach presented in (Dörr,

1995) can be used for matching multiple patterns hav-

ing isomorphic sub-patterns at the same time. The al-

gorithm runs on single-core environments, but by dis-

covering the identical parts of the different patterns

and performing their matching at once, it can achieve

noticeable performance gain, since only the different

parts of the patterns must be matched separately af-

terwards.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we have introduced a new pattern spec-

iﬁcation language. The presented concept makes it

possible to deﬁne inexact patterns in a concise way.

We have also presented the algorithm MRMM, a

MapReduce-based method for detecting inexact pat-

terns in large graphs. The algorithm ﬁnds all sub-

graphs corresponding to the deﬁned pattern in the host

graph.

The MapReduce framework is designed to sup-

port processing large data sets. Therefore, it can be

suitable for graph related algorithms if the graphs are

represented as textual ﬁles. In this paper, we have also

described the applied data structure.

Because of the lack of space, in this paper, we fo-

cused on the description of the new language concept

and the new matcher algorithm. We plan to present

the detailed evaluation of the performance and the ex-

periences collected during the application of the ap-

proach in a separate publication.

Other future work contains the analysis of the pre-

sented algorithms. Since the MapReduce framework

is not optimized for I/O operations, the sizes of the

produced outputs are critical. In order to evaluate the

efﬁciency of the algorithms, we also intend to perform

different measurements.

REFERENCES

Amazon Web Services (2013). http://aws.amazon.com.

Apache Hadoop (2011). Apache Hadoop Project. http://

hadoop.apache.org/.

Berry, J. W. (2010). Practical heuristics for inexact sub-

graph isomorphism.

Berry, J. W., Hendrickson, B., Kahan, S., and Konecny, P.

(2007). Software and algorithms for graph queries on

multithreaded architectures. In International Parallel

and Distributed Processing Symposium, pages 1–14.

IEEE.

Coffman, T., Greenblatt, S., and Marcus, S. (2004). Graph-

based technologies for intelligence analysis. Commu-

nications ACM, 47(3):45–47.

Dean, J. and Ghemawat, S. (2008). Mapreduce: simpliﬁed

data processing on large clusters. Communications of

the ACM, 51(1):107–113.

Dörr, H. (1995). Efﬁcient Graph Rewriting and Its Imple-

mentation. Springer-Verlag New York, Inc., Secaucus,

NJ, USA.

Ehrig, H., Ehrig, K., Prange, U., and Taentzer, G. (2006).

Fundamentals of Algebraic Graph Transformation

(Monographs in Theoretical Computer Science. An

EATCS Series). Springer-Verlag New York, Inc., Se-

caucus, NJ, USA.

Fehér, P., Vajk, T., Charaf, H., and Lengyel, L. (2013).

Mapreduce algorithm for ﬁnding st-connectivity. In

4th IEEE International Conference on Cognitive Info-

cocommunications - CogInfoCom 2013.

Karloff, H., Suri, S., and Vassilvitskii, S. (2010). A model

of computation for mapreduce. In Proceedings of the

Twenty-First Annual ACM-SIAM Symposium on Dis-

crete Algorithms, pages 938–948. Society for Indus-

trial and Applied Mathematics.

Kim, S.-H., Lee, K.-H., Choi, H., and Lee, Y.-J. (2013).

Parallel processing of multiple graph queries using

mapreduce. In DBKDA 2013, The Fifth International

Conference on Advances in Databases, Knowledge,

and Data Applications, pages 33–38.

Liu, Y., Jiang, X., Chen, H., Ma, J., and Zhang, X. (2009).

Mapreduce-based pattern ﬁnding algorithm applied

in motif detection for prescription compatibility net-

work. In Advanced Parallel Processing Technologies,

pages 341–355. Springer.

Mezei, G., Levendovszky, T., Meszaros, T., and Madari, I.

(2009). Towards truly parallel model transformations:

A distributed pattern matching approach. In EURO-

CON 2009, EUROCON ’09. IEEE, pages 403–410.

Plantenga, T. (2012). Inexact subgraph isomorphism in

mapreduce. Journal of Parallel and Distributed Com-

puting.

Plump, D. (1998). Termination of graph rewriting is unde-

cidable. Fundamenta Informaticae, 33(2):201–209.

Tong, H., Faloutsos, C., Gallagher, B., and Eliassi-Rad,

T. (2007). Fast best-effort pattern matching in large

attributed graphs. In Proceedings of the 13th ACM

SIGKDD international conference on Knowledge dis-

covery and data mining, pages 737–746. ACM.

Windows Azure (2013). http://www.windowsazure.com/

en-us/.

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

212