
Performance-optimized Indexes for Inequality Searches on
Encrypted Data in Practice
Jan Lehnhardt
1,2
, Tobias Rho
1,2
, Adrian Spalka
1,2
and Armin B. Cremers
2
1
Department of Security and System Architecture, CGM AG, Koblenz, Germany
2
Department of Computer Science III, University of Bonn, Bonn, Germany
Keywords: Databases, Indexes, Cryptography, Cloud-based Information Systems.
Abstract: For information systems in which the server must operate on encrypted data (which may be necessary
because the service provider cannot be trusted) solutions need to be found that enable fast searches on
that data. In this paper we present an approach for encrypted database indexes that enable fast inequality,
i.e., range searches, such that also prefix searches on lexicographically ordered but encrypted data are
possible. Unlike common techniques that address this issue as well, like hardware-based solutions or order-
preserving encryption schemes, our indexes do not require specialized, expensive hardware and use only
well-accredited software components; they also do not reveal any information about the encrypted data
besides their order. Moreover, when implementing the indexing approach in a commercial software product,
multiple application-centric optimization opportunities of the index’s performance did emerge, which are
also presented in this paper. They include basic performance-increasing measures, pipelined index scans and
updates and caching strategies. We further present performance test results proving that our indexing
approach shows good performance on substantial amounts of data.
1 INTRODUCTION
Along with the risen popularity of cloud-based
informations systems (IS), the need increases as well
for such systems that store highly sensitive data,
like, e.g., medical data. For instance, software
companies developing a cloud-based ambulatory
information system for medical data have to comply
with strict legal obligations considering data
confidentiality, meaning all data on the server need
to be encrypted, and the decryption keys need to
reside outside of the scope of all entities (especially
server entities) without a need-to-know for that data.
On the other hand, requirements regarding flexibility
and performance still have to be fulfilled.
In order to enable good performance for
inequality searches (i.e., range searches) on
encrypted data values that constitute a linear order,
this paper focuses on design, usage and especially
optimization of encrypted indexes for such searches.
Similar to order-preserving encryption (OPE)
schemes, our indexes disclose the values’ order, so
the server can use that information for fast data
access. The order is stored in the index in a binary
tree representation as well as simultaneously in a
linear list representation. During searches, the binary
tree is used for fast determination of the boundary
values of a range search interval, and the linear list
for fast collection and sorting of all values lying
between the boundary values.
The work that has to be done for such a search is
split between client and server under the paradigm
of letting the server do as much work as possible.
However, unlike most OPE schemes (see (Popa et
al., 2013)), our indexes do not reveal further
plaintext bits of the indexed data. Furthermore, by a
slight modification the index can be used to perform
prefix searches on lexicographically ordered data.
The index is designed in such a way that it can
easily be implemented using only standard SQL
DDL components of the underlying DBMS; i.e., no
DBMS or even hardware components have to be
changed in order to use the index.
A further advantage of the index is that its
functionality and security do not rely on a specific
encryption scheme like, e.g., OPE or homomorphic
encryption (HOM). Instead, the index can be
implemented using an arbitrary, well-accredited
encryption scheme; at the time we use the Advanced
Encryption Standard (AES) encryption scheme in
221
Lehnhardt J., Rho T., Spalka A. and Cremers A..
Performance-optimized Indexes for Inequality Searches on Encrypted Data in Practice.
DOI: 10.5220/0005231702210229
In Proceedings of the 1st International Conference on Information Systems Security and Privacy (ICISSP-2015), pages 221-229
ISBN: 978-989-758-081-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Galois-Counter Mode (GCM) and 256 bits key
length. Nevertheless, the encryption scheme can
easily be replaced by another scheme if necessary.
We also present, from an application-centric
point of view, several extensions of the basic index
concept that significantly enhance its performance
and applicability in a real-life software product.
These extensions include performance-enhancing
measures by standard “on-board” DBMS means,
pipielined index scans and updates and caching
strategies on both client and sever for faster data
retrieval during read as well as write operations.
The remainder of the paper is organized as
follows. After giving an overview of previous and
related work in section 2 we introduce the index in
section 3, covering its basic idea, implementation
details and cryptographic considerations. In section
4, a set of basic performance-enhancing measures is
introduced before caching strategies are presented in
section 5. In section 6 performance test results are
presented and discussed. The paper is concluded
with summary and future considerations in section 6.
2 RELATED WORK
Many publications exist that target fast access to
encrypted data. E.g., in an early stage, (Hacigümüs
et. al., 2002) defined a paradigm of letting the server
do as much data processing as possible though
dealing only with encrypted data, and hence
presented a “coarse index” approach by labeling all
encrypted data on the attribute level with their
respective value domain partition.
More recent contributions have been made in the
HOM, e.g., in (Gentry, 2009), and the OPE sector,
e.g in (Agrawal et al., 2004), (Boldyreva et al.,
2009) and (Liu and Wang, 2013). However, both
classes of encryption schemes still lack
performance; moreover, (Popa et al., 2013) shows
that a whole list of OPE schemes leak a substantial
amount of plaintext bits.
Another approach to the topic is the use of
specialized hardware. Two examples of publications
using that approach are (Ramamurthy et. al., 2013)
and (Bajaj and Sion, 2011). Their basic idea is a
server component that uses a common CPU to
process all non-sensitive data, while all sensitive
data is transferred to a trusted hardware component
in which data enter and leave only in encrypted
form. The authors claim that their solution may be
less performant than plaintext systems, but orders of
magnitude faster than software-only solutions, i.e.,
OPE and HOM schemes. Nevertheless, such systems
relying on specialized hardware are probably
expensive and difficult to administer, apart from the
fact that decryption keys reside on the server, albeit
in a secure hardware module.
The focus of (Popa et. al., 2012) lies on the
design of IS with an encrypted database backend.
The authors present their system “CryptDB”, which
makes use of random, deterministic, homomorphic
and order-preserving encryption schemes in a “SQL-
aware” way, so that native SQL queries can be
executed on the encrypted data. The system also
allows for dynamically adjusting the encryption
layer on the DBMS server via a concept of “onions
of encryption”. The generic approach of CryptDB
that enables to process (almost) all kinds of SQL
queries is impressive. However, in this publication
performance-enhancing measures like caching and
pipelined index updates are neither considered nor
discussed; so our work provides a contribution to the
topic that is orthogonal to CryptDB’s approach.
The same holds for (Tu et al., 2013): The authors
present MONOMI, a system optimized for
processing analytical queries over sensitive,
encrypted data. It encompasses a designer and a
planner component responsible for an optimized
physical layout of the data at design time,
respectively for the specification of optimized query
execution plans at runtime. MONOMI’s expressive
power is demonstrated on the TPC-H benchmark,
where it shows impressive performance. MONOMI
focuses on analytical queries, which means it is
optimized for DRL operations, i.e., SELECT
statements. But again, in this publication the
performance enhancements we do present in this
paper are not considered. Furthermore, when
considering range searches, MONOMI also relies on
order-preserving encryption schemes, which we
chose to avoid.
Like mentioned before, the authors of (Popa et
al., 2013) show that current OPE schemes leak
information besides the items’ order; they propose
an alternative “order-preserving encoding scheme”
claimed to reveal no information apart from the
linear order of the encrypted elements. They follow
a similar approach to ours by encrypting the index
items with an arbitrary encryption scheme and
providing the items’ order by organzing them in a
binary tree. Yet we believe our indexes to have a
performance advantage, for it needs fewer
maintenance operations during normal DML
operations, and especially because of our
performance-enhancing measures presented in
sections 4 and 5.
ICISSP2015-1stInternationalConferenceonInformationSystemsSecurityandPrivacy
222
3 THE INDEX
In this section the basic idea of our index will be
briefly described, after it has been introduced and
described with greater detail in a previous
publication of ours, (Lehnhardt et al., 2014).
3.1 Basic Idea
The basic idea of our index evolves around a data
structure holding the encrypted contents of all index
items. It is persisted in and processed by a common
DBMS, although we consider a complete in-memory
solution as a next step. Each index item’s content
has been encrypted on the client such that the server
is not able to view the content’s plaintext.
Furthermore, the linear order constituted by the
index items is expressed in the index data structure
by two representations: first, a binary tree
representation and second, a representation as a
linear list (when referring to the index’s binary tree
representation, we will sometimes refer to the index
items als nodes; both terms are used synonymously).
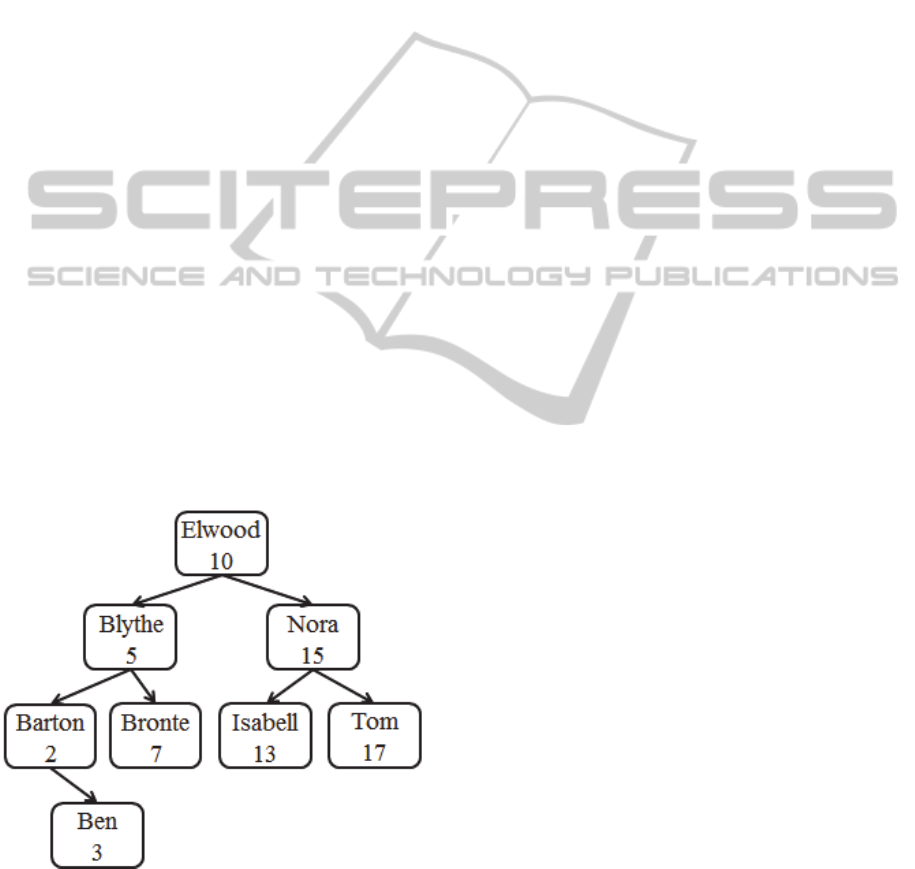
Figure 1 shows an example of the index
structure; note that the index item contents are only
shown in plaintext for better understanding. Note
further that the values of the linear list representation
of the item’s linear order are not related to the
respective item values. They are rather arbitrary
numbers chosen in such a way that they constitute
the same linear order as the index item values.
Figure 1: Index structure containing item contents, binary
tree organization and linear list numbers.
As the index items have a common structure,
they are well suited for being stored in a common
database relation, in which node ids, encrypted
contents, parent and child node references of the
binary tree representation and linear list numbers are
stored in separate attributes.
3.2 Write Access
When a new item is added to an index of binary tree
height containing up to 2
1 items, the index’s
binary tree is traversed, starting at its root, until the
right position for the insert is found, or it turns out
that the value of the new item is already in the index.
In this case the insert operation is skipped, because
the index contains only unique items.
Since the decision for a node during tree
traversal whether to proceed to its left or right child
must be made on the node’s plaintext content, that
content needs to be sent to the client, where it can be
decrypted. The decision of the next item to be
fetched from the index is sent back to the server.
Hence, every node of the traversal path to the new
node’s insert position must be transferred to the
client, meaning roundtrips between client and
server, because new items are inserted at the binary
tree’s leaf level.
3.3 Read Access
The main application of the index are range
searches, i.e., all values lying in an interval
,
(the interval can also be open or semi-open).
Another index application are prefix searches on
lexicographic data, e.g., all persons’ last names
starting with “sch”. Since lexicographically ordered
data also establish a linear order, this type of search
can easily transformed in a range search on that data:
The search for items matching the regular expression
Σ
∗
can be transformed in an equivalent range
search for items lying to the interval
, , .
When processing a range search with ,
being the search interval, the index’s binary tree is
first traversed looking for the appropriate index item
value being the closest match for the lower
interval boundary : min∈|.
The closest match for the upper interval boundary
is accordingly: max
∈|
.
Both values are found by tree traversal, similar
as described in 3.2; however, here the client keeps
track during traversal of the closest candidate so far
for a lower or upper boundary value match.
Having found and , a simple selection query
is submitted to the DBMS, requesting all index items
whose linear list number lies in the interval
,
,i.e., between the linear list numbers of ’s
Performance-optimizedIndexesforInequalitySearchesonEncryptedDatainPractice
223

and ’s index item. The DBMS can use the linear
list numbers also to sort the query’s result set.
3.4 Further Aspects
3.4.1 Division of Labor
We would like to point out that the presented
indexing approach implements a division of labor
between client and server under the paradigm of
letting the server do as much work as possible and
making the client do only those steps that are not
permitted for the server, i.e., accessing decrypted
index values.
3.4.2 Security
As mentioned before, in (Popa et al., 2013) it is
shown that most OPE schemes leak a substantial
amount of plaintext information. An “order-
preserving encoding scheme” is proposed that, like
we do, uses an arbitrary, non-order-preserving
encryption scheme like, e.g., AES, and expresses the
items’ linear order through additional structures. The
authors further show that this scheme does not leak
any plaintext information about the encrypted values
besides their order. Since the approach of the “order-
preserving encoding scheme” is very similar to our
range index data structure, the proof of (Popa et al.,
2013) is also transferable, meaning that our index
does not leak any plaintext information either,
besides the values’ order.
A further advantage of our index is not having to
rely on the security of a particular encryption
scheme. We have the liberty of choosing a fast, well-
accredited and widely accepted symmetric
encryption scheme like AES-256 in GCM mode.
And even if that scheme should be broken one day,
it can easily be replaced by a new, still secure
successor.
4 OPTIMIZATIONS
In this section a set of performance-enhancing
measures is presented that can be added to the
index’s basic idea given in section 3. Some of them
are quite obvious, but should nevertheless be
mentioned before the more sophisticated measures
like pipelining and caching strategies (in section 5)
are presented.
Regular Database Indexes. In order to perform fast
operations on the database relation holding our
index, a regular database index should be defined on
the index item id in order to find items fast; since
only punctual searches are performed on id, the
index should preferably be a hash index. Another
index should be defined on the linear list number
attribute, since it is part of the data access path
during read accesses (see 3.3). Because value ranges
are requested here, a B+-tree index is preferable.
Redundancy. In order to accelerate binary tree
operations, several information that is contained
implicitly in the index’s binary tree representation
should be made explicit:
The reference to a node’s parent node refParent
for fast server-sided subtree retrieval, preferably
with a (hash) database index defined on it. At the
same time, the database relation should contain
refLeft / refRight child reference attributes which
enable fast subtree traversal on the client.
The height attribute of an index item holds the
height of the subtree the item constitutes in the
index’s binary tree representation, such that the
value for height of item “Barton” in Figure 1
equals 2 and the height of “Elwood” equals 4.
This helps accelerating tree balancing.
isLeftChild tells whether the current index item is
the left child of its parent node. This is helpful
during determination of the change paths (see
5.3).
Subtree Retrieval. To reduce the number of server
roundtrips, whole portions of the tree can be
transferred to the client instead of single nodes, i.e.,
binary subtrees of a defined height limit
containing up to 2
1 nodes. This way only
/
roundtrips are necessary. The subtree is then
traversed in the client, until its leaf level is reached
and the next subtree is requested or the entire tree’s
leaf level is reached and traversal terminates. Note
that only the nodes of a subtree’s traversal path
need to be decrypted instead of all up to 2
1
nodes in the subtree.
AVL Tree. We chose an AVL tree for the index’s
binary tree representation, for it is easy to implement
and administer while still showing good
performance. Furthermore, the subtree height can
easily be varied in order to adapt roundtrip numbers
and data volumes being transferred from server to
client flexibly because of differing environmental
circumstances like network latency and bandwidth.
Deterministic Encryption. When choosing a
deterministic encryption function such that the
following equivalence holds:
⇔
,
ICISSP2015-1stInternationalConferenceonInformationSystemsSecurityandPrivacy
224

then the step of adding a new item to the index can
be improved the following way: If the population of
the indexed data values is expected to contain many
recurring values, i.e., that often a new index value
is to be inserted that is already in the index, then the
client can encrypt to
and let the server
check whether ′ is already in the encrypted index
value attribute of the index’s database relation. This
is obviously much faster than the tree traversal
described in 3.1. A database index defined on the
encrypted index value attribute is then
recommended.
Pipelining during Read Access. When processing
an interval search, every interval border requires a
separate tree traversal (see 3.3), so when a query
contains interval conditions, up to 2 tree
traversals are necessary, each requiring
/
server roundtrips, which would turn out to be
expensive when all 2 ∙
/
subtree retrievals
were executed consecutively.
Instead, all 2 traversals can be processed in
parallel by the client, while the database server
performs all subtree retrievals in a single worker
thread; hence, this procedure is rather a pipelined
subtree retrieval instead of a parallel one.
Nevertheless, because the database server is by
far not the bottleneck in our system architecture, it
can easily serve all the requests with little additional
latency for the entire query response time. Hence, a
query containing many range conditions does not
take substantially longer than a query with only a
single one.
Pipelining during Write Access. Pipelining is also
applicable for write accesses. Consider 1 items
are to be added to the index by the same client and
have to be added as new nodes to the binary tree
representation. Then the step of determining each
node’s designated parent node described in 3.2 can
be executed in parallel, for it consists solely of read-
only tree accesses.
When all parent nodes are determined, insertion of
the new index node with possibly necessary
subsequent tree re-balancing (see also 5.3) can be
performed. This has to be done by the database in a
pipelined instead of parallel mode in order to avoid
tree inconsistencies.
If all new nodes have different designated parent
nodes this is easy; a simple sequence of nodes is sent
to the server, which are all added to the tree one
after another. However, when the determined insert
position for 1 of the new nodes is the same
child position of the same parent node (see Figure
2), a slight modification has to be made to the basic
usage of AVL trees: A new node designated as the
left child of a determined parent node is then
either inserted exactly like that, if that place is
currently not taken by another node,
or inserted as the right child of the greatest item
in the designated parent’s left subtree.
All other AVL usage steps can remain the same,
including tree rebalancing. If the client now inserts
all conflicting new nodes in an ordered fashion,
starting with the smallest value proceeding to the
greatest, the AVL tree’s consistency will not be
affected by the set of insertions.
Figure 2: New nodes competing for the same insert
position.
Note that for the symmetric case, i.e., new nodes
competing for being the right child of the same
parent node, the above steps are simply turned to
their opposites: all new nodes are sorted from
greatest to smallest, and a new node is either
inserted as the right child of its parent node, or, if
that place is taken, as the left child of the smallest
value in the parent node’s right subtree.
5 CACHING
Caching plays a big part in our set of performance-
enhancing measures, which is why we devote an
entire section to this topic. We distinguish between
caching for read and for write access as well as
between client and server caching.
Performance-optimizedIndexesforInequalitySearchesonEncryptedDatainPractice
225

5.1 Server Caching
A first naïve caching approach is to store temporary
range search results on the server. For instance,
consider one client having submitted a range search
for all values of index lying in , , which
initiates according to 3.3 two tree traversals with the
result of a pair of closest match candidates and
for and . This is followed by a selection of all
index items whose linear list number lies between
the linear list numbers of and :
∈
,
∈
,
The resulting tuple set could be stored on the
server, in case another client issues the exact same
query for index values lying in , . However,
since storing the result sets for many search intervals
,
might occupy too much space, a more
compact caching method is preferable.
We therefore chose to cache for
,
instead of
a triple for each interval border value:
,,
and
, ,
, with
and being the encrypted border value,
which is used as an identifier,
andbeingthebordertypealso
usedaspartofanidentifier
and
beingthelinearlistvalueofthe
closest match in the current tree extension for the
given interval border, and .
When a client submits a range search request for
, , it first encrypts and and sends
, and
, to the server,
where the cache is scanned for possible hits. If one
cache hit occurs or both, the according triple’s linear
list number is fetched for the final selection of the
range search operation. If not, tree traversal starts as
described in 3.3.
A cached triple can be outdated when the index
is changed, e.g., when an index item value is
inserted whose value is a closer match for the
triple’s encrypted interval border. In that case the
triple needs to be erased from the cache. At the
moment we simply erase the server cache every time
the index changes, but as of now we develop a more
sophisticated cache-erasing algorithm soon.
5.2 Client Caching
In order to avoid as many redundant subtree
retrievals as possible, subtrees that have been
retrieved during previous searches can be stored on
the client for later use. The “root subtree” for
instance, i.e., the highest subtree below the entire
tree’s root node, is always needed, because every
traversal starts there. Other cached subtrees can be
useful as well if the client searches for nodes or
intends to insert nodes within close distance of
previous tree accesses. Note that the same kind of
subtrees is retrieved for both read and write
accesses.
So, after its retrieval, the subtree below the node
with id is stored on the client as a cache entry. It
contains the subtree’s 2
1 nodes and uses its
root node’s id as an identifier. It is also useful to
flag a cache entry as being the root subtree
,
such that a cache entry
is of the following
structure:
= (i, {(id
i,1
, left
i,1
, right
i,1
, cData
i,1
), … ,
(id
i,k
, left
i,k
, right
i,k
, cData
i,k
)}, isRoot)
So when a subtree with root node id is needed
during tree traversal, the client first checks its cache
whether it contains an entry
; if it does not, a
server call getSubtree(i) is submitted.
5.3 Erasing Client Caches
Erasing the cache is obviously necessary when the
index has been modified such that the cached
subtrees are no longer consistent with their
counterparts in the index’s current extension in the
database, i.e., when a new item is inserted into or
deleted from the index. Without restriction to
generality we consider only index insertions in the
following of this subsection; nevertheless, the
presented concepts apply as well to indexes that
allow deletions.
Following a naïve approach, cache erasure can
be done upon every index modification; whenever
an item is inserted into the index, all currently
connected clients are notified to erase all their cache
entries. However, although it produces correct
results, this is not a favorable approach, for it causes
many unnecessary erasures, as will be shown in the
following.
When a new item is inserted into the index, the
binary tree representation of the index items’ linear
order, which is implemented using an AVL tree,
may need to be rebalanced. The server does this by
re-traversing the new node’s traversal path back to
the tree root, checking the balance of each node
along the path.
In case of an imbalance, depending on its type,
an appropriate rebalancing operation (“rotation”) is
performed on the node (that node is referred to as
the “rotation point” in the following) . It changes the
positions, child-parent relations and subtree heights
ICISSP2015-1stInternationalConferenceonInformationSystemsSecurityandPrivacy
226

of several nodes around the rotation point. At most
one such rotation can occur during rebalancing, so if
a rotation has occurred, the entire AVL tree is
rebalanced, and the re-traversal is aborted. The
balance of all nodes lying outside of the traversal
path is not affected by the entire insert and
rebalancing operation.
Combining the rotation on the re-traversal path
with cached subtrees is best illustrated by an
example. Figure 3 shows a set of cache entries
identified by their respective root node id, and a
traversal path of a new node
inserted at the leaf
level of
. Since the traversal path crosses only
,
and
, the other three cache entries
,
and
are not affected by the insertion.
Moreover, supposing
’s insertion has caused a
rotation in
, this affects merely
itself,
while the other cache entries hosting the traversal
path,
and
, remain unchanged.
Figure 3: Traversal path after index item insertion, with a
rotation in
.
Hence, in theory only that cache entry in which
the rebalancing operation happens needs to be erased
(
in our example), and all others can remain.
Yet, from a practical perspective it is advisable to
erase more cache entries for the following reason:
A rotation that occurs in a subtree may not
change balances and heights of the nodes in the
subtree’s child subtrees, but it does change the tree
levels of some of those nodes. Because subtrees are
retrieved with a defined height, this would render a
subtree’s cached child subtrees useless, and in
special cases even erroneous.
In our example, supposing a subtree height
5, the root nodes
and
of
and
are both located at tree level 11 before the
rotation. After the rotation these tree levels may
have changed to 10 and 12 or vice versa. Yet during
all tree traversals, only subtrees with root nodes at
tree level 1, 6, 11, 16 etc are requested, and
and
would remain in the client cache as dead
entries.
Hence, in our practical implementation we chose
to erase the cache entry with the subtree containing
the rotation point and all cache entries with that
subtree’s transitive child subtrees as well, i.e., in our
example, cache entries
,
and
. All
other subtrees, and especially all subtrees along the
traversal path above the subtree containing the
rotation point can remain in the cache.
6 PERFORMANCE TESTS
We benchmarked insert operations and interval
searches on a publicly available database of 19,000
first and last names. The order of first and last names
were randomized to avoid insert patterns with
uncommon rebalance and re-caching operations.
The test environment consists of an Intel E5-
2640 server with 16 GB RAM, which hosts a
Wildfly 8.1 and a Postgresql 9.3 server.
A Macbook Pro i7-4850HQ running Chrome 37
32-bit accesses the server via a 30 Mbit cable
connection with a roundtrip time (RTT) of
approximately 25 ms. The best performance was
achieved with a maximum subtree depth of four,
which may vary depending on index size, RTT and
bandwidth.
6.1 Bulk Insert
We benchmarked a bulk insert of 19,000 patient
records with our index defined on both the first and
last name attribute (First 19k US/Spanish names
from https://github.com/enorvelle/Name Databases).
Caching and pipelining optimizations were
applied independently. See Table 1 for the results.
Table 1: Average bulk patient tuple insert time in
milliseconds.
Single Pipelined (8)
Not Cached
~290 ~38
Cached
~230 ~35
For single tuple inserts the performance mainly
depends on the number of client-server roundtrips.
The graph in Figure 4 illustrates that caching keeps
the average roundtrips for an insert low.
Still there are at least 3 roundtrips, which make
insertion of single tuples expensive. Here pipelining
improves the performance for bulk insert operations.
The performance improves nearly linear up to eight
pipelined patient inserts. The best performance is
Performance-optimizedIndexesforInequalitySearchesonEncryptedDatainPractice
227

achieved with a combination of caching and
pipelining.
Figure 4: Average number of client-server round trips per
pipelined insert. The x-axis is inserts in thousands, the
blue line represents uncached, the red line cached inserts.
Caching further results in much lower server
load and transfers. Table 2 illustrates the
improvement achieved by caching.
Table 2: Number of server calls and server-to-client
transfer in MB for 19.000 patients.
Not Cached Cached
Server Calls
161.095 89.077
Transfer (MB)
45 15
6.2 Queries
Caching and pipelining have a similar effect on
range queries. A prefix search on the first name
attribute results in two pipelined index traversals, the
lookups of two interval borders. The query times on
the 19,000 unique first / last names patients, ordered
and with a limit of 20 are summarized in the Single
Range column of Table 3.
Table 3: Average query times of a single and four
pipelined range searches in milliseconds.
Single Range Four Ranges
Not Cached
221 233
Root Cached
179 191
Two Cached
138 149
Full Cached
43 49
Complex queries benefit further from pipelining.
Consider a query for the two prefixes “No” and “So”
on both first and last names:
prefix(“No”, firstName) && prefix(“So”, lastName)
||
prefix(“So”, firstName) && prefix(“No”, lastName)
The query matches e.g. “Sophia Nordes” and
“Nouzha Soldeo”.
The query contains four independent range searches.
Pipelining keeps the overhead for the additional
searches low, see column Four Ranges in Table 3.
Again the results were ordered by first and last name
and are queried with a limit of at most 20 tuples per
result set.
7 SUMMARY
We presented an index structure enabling fast range
searches on encrypted data that is used and
maintained collaboratively on client and server. We
further introduced multiple performance-enhancing
measures for that index, including basic measures
like redundancy and regular indexes on database
relations as well as pipelined processing of read and
write accesses, and caching strategies. We further
showed the performance-enhanced index approach’s
good performance on a substantial set of data.
Future development includes further perfor-
mance optimizations, like a refinement for client
cache erasure in order to intelligently enforce a size
limit for client caches, a more sophisticated erasing
strategy for server caches, and an optimization of the
serialization method of subtrees being transferred to
the client using Google’s protocol buffer technology.
Some of our target devices, mobile and web
clients, are often unreliable and connected via high
latency links. For this reason classic transactions are
not a good choice for all concurrency scenarios,
since often used resources, like the presented index
structures, are locked for a long time. Therefore we
developed an optimistic transaction management
model aligned with our 3-tier architecture, which
will be a topic of a later publication.
Our long-term goal is to provide “Secure SQL”,
an extension of the SQL language: It comprises the
encrypted index operations described in this paper
along with other index operations on encrypted data,
while client operations would be encapsulated in
extensions of database access libraries like JDBC. In
Secure SQL, the creation of an index for range
searches on an attribute attr in a relation rel
would simply be achieved by the adapted SQL
statement:
CREATE RANGE INDEX ON rel(attr);
REFERENCES
Agrawal, R., Kiernan, J., Srikant, R. , Xu, Y., 2004. Order
preserving encryption for numeric data. In
ICISSP2015-1stInternationalConferenceonInformationSystemsSecurityandPrivacy
228

Proceedings of the 2004 ACM SIGMOD International
Conference on Management of Data. ACM.
Agrawal, D., El Abbadi, A., Emekci, F., Metwally, A.,
2009. Database management as a service: Challenges
and opportunities. In International Conference on
Data Engineering. IEEE.
Ang, G. W., Woelfel, J. H., Woloszyn, T. P., 2012.
System and method of sort-order preserving
tokenization. US Patent Application 13/450,809.
Arasu, A., Blanas, S., Eguro, K., Kaushik, R., Kossmann,
D., Ramamurthy, R., Venkatesan, R., 2013.
Orthogonal Security with Cipherbase. In Conference
on Innovative Data Systems Research,
www.cidrdb.org.
Bajaj, S., Sion, R., 2011. TrustedDB: A Trusted
Hardware-Based Database with Privacy and Data
Confidentiality. In SIGMOD – International
Conference on Management of Data. ACM.
Boldyreva, A., Chenette, N., Lee, Y., O’Neill, A., 2009.
Order-preserving symmetric encryption. In Inter-
national Conference on the Theory and Applications
of Cryptographic Techniques. Springer LNCS.
Boldyreva, A., Chenette, N., O’Neill, A., 2011. Order-
preserving encryption revisited: Improved security
analysis and alternative solutions. In Annual
Cryptology Conference. Springer LNCS.
Gentry, C., 2009. Fully Homomorphic Encryption Using
ideal Lattices. In STOC ’09 - ACM symposium on
Theory of computing, ACM.
Hacigümüs, H., Iyer, B., Li, C., Mehrotra, S., 2002.
Executing SQL over Encrypted Data in the Database-
Service-Provider Model. In SIGMOD – International
Conference on Management of Data. ACM.
Kadhem, H., Amagasa, T., Kitagawa, H., 2010. MV-
OPES: Multivalued-order preserving encryption
scheme: A novel scheme for encrypting integer value
to many different values. In IEICE Transactions on
Information and Systems, E93.D.
Kadhem, H., Amagasa, T., Kitagawa, H., 2010. A secure
and efficient order preserving encryption scheme for
relational databases. In International Conference on
Knowledge Management and Information Sharing,
Springer CCIS.
Lee, S., Park, T.-J., Lee, D., Nam, T., Kim, S., 2009.
Chaotic order preserving encryption for efficient and
secure queries on databases. In IEICE Transactions
on Information and Systems, E92.D.
Lehnhardt, J. Rho, T., Spalka, A. Cremers, A. B., 2014.
Ordered Range Searches on Encrypted Data. In:
Technical Report IAI-TR-2014-03, Computer Science
Department III, University of Bonn, ISSN 0944-8535.
Liu, D. Wang, S., 2012. Programmable order-preserving
secure index for encrypted database query. In
International Conference on Cloud Computing, IEEE.
Liu, D., Wang, S., 2013. Nonlinear order preserving index
for encrypted database query in service cloud
environments. In: Concurrency and Computation:
Practice and Experience, John Wiley & Sons, Ltd.
Özsoyoglu, G., Singer, D. A., Chung, S. S., 2003. Anti-
tamper databases: Querying encrypted databases. In
IFIP WG 11.3 Working Conference. on Database and
Applications Security. Springer LNCS.
Popa, R. A., Redfield, C. M. S., Zeldovich,
N., Balakrishnan, H., 2012. CryptDB: Processing
queries on an encrypted database. In Communications
of the ACM, 55(9).
Popa, R. A., Li, F. H., Zeldovich, N., 2013. An Ideal-
Security Protocol for Order-Preserving Encoding. In
Symposium on Security and Privacy, IEEE:
Tu, S., Kaashoek, M. F., Madden, S., Zeldovich, N., 2013.
Processing Analytical Queries over Encrypted Data. In
Proceedings of the VLDB Endowment, Vol. 6 Issue 5,
ACM.
Xiao, L., Yen, I.-L., Huynh, D. T., 2012. Extending order
preserving encryption for multi-user systems.
Cryptology ePrint Archive, Report 2012/192.
Xiao, L., Yen, I.-L., Huynh, D. T., 2012. A note for the
ideal order-preserving encryption object and
generalized order-preserving encryption. Cryptology
ePrint Archive, Report 2012/350, 2012.
Yum, D., Kim, D., Kim, J., Lee, P., Hong, S., 2011.
Order-preserving encryption for non-uniformly
distributed plaintexts. In: International Workshop on
Information Security Applications, Springer LNCS.
Performance-optimizedIndexesforInequalitySearchesonEncryptedDatainPractice
229
