
A Novel Heuristic Algorithm for Mapping AUTOSAR Runnables to
Tasks
Fouad Khenfri
1,2
, Khaled Chaaban
1
and Maryline Chetto
2
1
S2ET, ESTACA, Rue Georges Charpak, 53061 Laval, France
2
IRCCyN, University of Nantes, 1 Rue de la Noe, 44321 Nantes, France
Keywords:
Optimization, Real-time scheduling, AUTOSAR.
Abstract:
This paper describes a novel algorithm that permits to automate the process to map runnables to tasks in
any AUTOSAR architecture. This enables to boost system performance by reducing the number of tasks
to be implemented and while preserving system schedulability. Our algorithm uses some properties related
to the activation offset for mapping runnables with distinct periods to the same task. We consider periodic,
independent and fixed-priority tasks running on a single processor. The results of an experimental study are
reported. First, they show that our algorithm reduces significantly the number of tasks with distinct periods
while preserving system schedulability. And second, the system schedulability bound is increased by 34%
compared to the typical periodic solution and the average response time of tasks is reduced by 30% related to
ohers solutions.
1 INTRODUCTION
AUTOSAR (AUTomotive Open System ARchitec-
ture) development partnership has been created by
automotive manufacturers, suppliers and tool devel-
opers in order to establish an open industry standard
for automotive E/E (Electrical/Electronic) architec-
tures (Partnership, 2011). AUTOSAR provides a set
of concepts and defines a methodology for the auto-
motive software development process. Some key fea-
tures of this standard are modularity and configura-
bility of automotive architectures. AUTOSAR per-
mits functional reuse of software modules from differ-
ent suppliers and guarantees interoperability of these
modules through standardized interfaces.
In AUTOSAR, runnables represent the internal
behavior of each SoftWare Component (SWC) and
are the smallest pieces of code to be scheduled. Each
SWC contains at least one runnable. All runnables
are triggered in response to an event such as a tim-
ing event (for periodic runnables), data receiving, or
operation invoking of runnables. If no event is spec-
ified for the runnable, it will never be activated. Fur-
thermore, runnables can be executed only if they are
mapped to tasks. The process of mapping runnable to
task is illustrated in Figure 1.
Developing an automotive application which is
compliant to the AUTOSAR standard needs the ini-
Assigning
runnables to tasks
Sequencing
runnables
Application Description
(SW architecture)
Task 1
ISR 1
Task1
r
1
(1,10,0) r
2
(1,15,0) r
3
(1,15,0) r
4
(1,30,5)
T
Task y
ISR z
SWC1
SWC2
Figure 1: Runnable mapping process in AUTOSAR.
tialization of many parameters. They are mainly re-
lated to SWCs, allocation of SWCs to the hardware
architecture, and finally configuration of each Elec-
tronic Control Unit (ECU). In the ECU configuration
phase, mapping runnables to OS (Operating System)
tasks is crucial since it may impact system perfor-
mance and its real-time behavior significantly. Sev-
eral design decisions have to be considered including:
• How many tasks are needed to implement the en-
tire set of runnables?
• How to specify priorities of tasks?
• How to define the execution order and activation
offset of runnables which are mapped to the same
task?
There are mainly three ways to address this prob-
lem as shown in Figure 2.
239
Khenfri F., Chaaban K. and Chetto M..
A Novel Heuristic Algorithm for Mapping AUTOSAR Runnables to Tasks.
DOI: 10.5220/0005234202390246
In Proceedings of the 5th International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2015), pages
239-246
ISBN: 978-989-758-084-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
N
5
sásrár N
6
sáswár N
7
sátrár N
8
sáurár
First solution: Periodic Solution (PS)
Second solution: Multiple Periodic Solution (MPS)
Third solution: Arbitrary Periodic Solution (APS)
6
5
6
6
6
7
6
8
6
5
6
6
6
5
N
Ü
S?APá LANEK@á KBBOAP ã
Figure 2: Solutions to map runnables to different tasks.
The first and simplest solution is to map runnables
with same period to one task. In this Periodic Solution
(PS), the worst-case execution time (WCET) of the
task is the sum of WCET of all runnables mapped to
it. Hence, the number of tasks is equal to the number
of the different periods assuming that a task WCET is
less or equal than its period. However, tasks priorities
are assigned according to the rate monotonic priority
assignment (RMPA) or the deadline monotonic prior-
ity assignment (DMPA) in order to guarantee system
schedulability.
Another solution consists in mapping runnables
with multiple periods to the same task. In this Multi-
ple Periodic Solution (MPS), the period of the task is
the shortest period among different runnables mapped
to it. Its maximum WCET is the sum of the WCET
of all these runnables. The number of tasks in this so-
lution is less than the first one when considering the
same assumptions.
However, in order to obtain a minimal number of
tasks, the best solution is to map the runnables with
different periods to the same task using their activa-
tion offset. In this Arbitrary Periodic solution (APS),
the period of a task is the greatest common divisor
(GCD) of all runnables periods mapped to it. Task
WCET in this case must be less than the task period.
The advantages of this solution are multiple, namely
the minimization of time overhead due to task context
switch and the minimization of stack memory usage
by minimizing the number of tasks.
For MPS and APS, system schedulability may be
guaranteed using RMPA or DMPA by assuming that
the task deadline is less than its period. Otherwise,
if the deadline is arbitrary (i.e. the deadline may
be higher than the period), the Audsley’s algorithm
(Audsley, 1991) may be used to assign tasks priori-
ties. Nevertheless, the issue here is how to determine
the set of runnables that can be mapped to the same
task in order to guarantee system schedulability.
Currently and in industrial practices, system de-
signers use the first two solutions (PS and MPS) and
their best knowledge of the system in order to con-
figure empirically ECU software. Nevertheless, this
may reveal to be an error-prone and time-consuming
process. Thus, an optimization approach appears to
be necessary to realize this configuration phase.
The aim of the work presented in this paper is
to propose an efficient algorithm, based on APS, for
mapping runnables to tasks while preserving system
schedulability. This algorithm allows determining
simultaneously, the number of OS tasks needed to
schedule the set of runnables, the priorities of tasks,
and the sequencing of the different runnables inside
tasks.
The paper is organized as follows: section 2
presents relevant related works. Section 3 describes
the system model. Section 4 details our proposed so-
lution to solve the mapping problem. Section 5 re-
ports and discusses experimental results before we
conclude the paper in section 6.
2 RELATED WORKS
In the context of AUTOSAR, there are many works
that address the problem of mapping runnables to
tasks (Rongshen et al., )(Haibo and Di Natale, )(Zeng
et al., 2012)(Monot et al., 2012)(Navet et al., 2010).
In (Rongshen et al., ), the authors discuss several rules
for mapping runnables to tasks based on intra-ECU
communication (communication between runnables
located on the same ECU), but there is no specified
optimization method. Further, this work does not con-
sider system schedulability. In (Haibo and Di Na-
tale, ), a MILP (Mixed Integer Linear Programming)
method is applied to solve an optimization problem.
This method chooses between protection mechanisms
to ensure data consistency. It considers that runnables
are already mapped to tasks and task priority assign-
ment is given.
In (Zeng et al., 2012), a simulated annealing
method is applied to find the optimal mapping and
tasks priorities assignment using MPS so as to op-
timize stack memory usage. After each transition
of the optimization loop, execution order and pre-
emption threshold of runnables are computed using
a heuristic method. Authors of (Monot et al., 2012;
Navet et al., 2010) developed two heuristics for multi-
core architectures. The first one distributes runnables
to different cores in order to uniformize core loads.
The second one maps runnables from the same core
to one sequencer task using the activation offset of
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
240

runnables. This heuristic assumes that the WCET of
runnales is much smaller than their periods since it
considers only one sequencer task per core. In (Ming
and Zonghua, ), a genetic algorithm is used to se-
lect protection mechanisms in order to guarantee data
consistency of each ECU with the objective of mini-
mizing the memory size. The authors use PS to map
runnables to tasks. In (Wozniak et al., 2013), the au-
thors propose a method using genetic algorithm for
the synthesis of AUTOSAR architecture (to solve the
SWCs to ECUs mapping problem, runnables to tasks
mapping problem and data elements to bus frame
mapping problem). In their work, MPS is used to map
runnables to tasks.
To the best of our knowledge, there is no work
uses the APS for mapping runnables to many tasks.
By the following, we detail the system model con-
sidered in this study and the proposed optimization
approach.
3 SYSTEM MODEL
This section describes the system model for both
runnables and tasks. AUTOSAR OS is based on the
industry standard OSEK OS. It is responsible for ex-
ecuting real-time tasks and ISRs (Interrupt Service
Routines). It provides a fixed-priority scheduling
policy. Each task is assigned a static priority and
higher priorities are given to ISRs. During execu-
tion time, the scheduler decides which ready task is
to be executed next, based on its priority. However,
AUTOSAR does not specify the priority assignment
scheme. Rate Monotonic or Deadline Monotonic
schemes can be used within its context. The configu-
ration of AUTOSAR OS is done statically. All the ob-
jects of the OS and their parameters have to be defined
before the deployment of the software. Moreover,
let’s recall that two types of tasks/runnables exist in
AUTOSAR: time-triggered and event-triggered. In
this work we assume that all tasks/runnables are time-
triggered and periodic. Dealing with non-periodic
tasks/runnables may be more difficult because of the
non-deterministic release times. Hence, we start by
developing a solution for periodic tasks/runnables
which can be later extended to cover non-periodic
ones.
3.1 Runnables
Any runnable, say r
i
, is the basic element to be exe-
cuted in the context of any task, say τ
j
, with priority
P
τ
j
. r
i
is characterized by four timing parameters O
i
,
C
i
, T
i
, D
i
and position parameter k
i
:
• O
i
, activation offset, i.e. triggering instant of the
execution request.
• C
i
, worst-case execution time (WCET), with 0 ≤
C
i
≤ D
i
≤ T
i
.
• T
i
, period.
• D
i
, relative deadline, i.e. the maximum acceptable
delay for its processing.
• k
i
, execution order in task τ
j
.
The two parameters O
i
and k
i
can be tuned to sat-
isfy system schedulability.
3.2 Tasks
Let us denote by ∆ = {r
1
,r
2
,...,r
n
}, the set of
runnables mapped to the same task τ
j
. An execution
order i (where 1 is the first execution order and n is
the last) is assigned to each runnable r
i
.
In order to map runnables with distinct periods to
the same task, we need to determine the activation off-
set of each runnable. This task is called dispatcher
(or sequencer) task which stores the runnables offsets
in a scheduling table and releases them at the right
points in time (Monot et al., 2012). The period of the
dispatcher task (micro-cycle) T
tic
j
is defined by the
greatest common divisor (GCD) of all runnables peri-
ods mapped to it. Moreover, the dispatcher task exe-
cutes these runnables in a cyclic manner (major-cycle)
T
cycle
j
, which is the least common multiple (LCM) of
all runnables mapped to it (see Fig. 1). The WCET of
dispatcher tasks C
τ
j
= {C
0
,C
1
,...,C
s
,...,C
N−1
}, is a
vector, where N = T
cycle
j
/T
tic
j
is the number of slots.
The WCET C
s
of the s
th
slot is given by:
C
s
=
n
∑
i=1
x
i
(s) ∗C
i
(1)
where the function x
i
(s) indicates the presence or
not of the i
th
runnable in the s
th
slot. This function is
given by:
x
i
(s) =
1 i f a
i
(s) = s
0 i f a
i
(s) ̸= s
(2)
with,
a
i
(s) =
s
γ
i
+ δ
i
(3)
where a
i
(s) is the release time position of the i
th
runnable in the s
th
slot (see example 1). γ
i
= T
i
/T
tic
j
and δ
i
= O
i
/T
tic
j
represent respectively the repetition
factor and the first position of the i
th
runnable in the
slots .
ANovelHeuristicAlgorithmforMappingAUTOSARRunnablestoTasks
241

Proposition 1. The relative deadline D
τ
j
of dis-
patcher task τ
j
guarantees the timing requirements of
all runnables mapped to it if, and only if, the worst
case response time of τ
j
is less than or equal to D
τ
j
given by:
D
τ
j
= min
s=0...N−1
{D
s
} (4)
with,
max
s=0...N−1
{C
s
} ≤ D
τ
j
≤ T
cycle
j
(5)
D
s
=
min
k∈R(s)
D
k
+
∑
n
i=k+1
x
i
(s).C
i
i f R(s) ̸=
/
0
∞ i f R(s) =
/
0
(6)
NOTE: R(s) denotes the set of runnables posi-
tioned in the slot s.
Proof. Let us consider that a set of runnables
∆ = {r
1
,r
2
,...,r
k
,...,r
n
} is mapped to the same task
τ
j
. Each runnable r
k
is assigned an execution order k
(where 1 is the first execution order and n is the last)
and a deadline D
k
. When all runnables are mapped in
the first slot (i.e., ∀k, x
k
(s) = 1 with s=0), the deadline
of dispatcher task (4) is rewritten as follows:
D
τ
j
= min
k=1...n−1
D
k
+
n
∑
i=k+1
C
i
,D
n
(7)
To verify timing constraints for all runnables, we
need to find the deadline of dispatcher task which re-
spects the following inequalities:
D
τ
j
≤ D
n
D
τ
j
−C
n
≤ D
n−1
.
.
.
D
τ
j
− (C
n
+ ... +C
k+1
) ≤ D
k
.
.
.
D
τ
j
− (C
n
+ ... +C
2
) ≤ D
1
(8)
It can be observed that equation (7) satisfies the in-
equality above. When all runnables are positioned in
different slots, the relative deadline of dispatcher task
is the minimum of deadlines among all slots. These
deadlines are computed by equation (7) applied for
each slot given by (6).
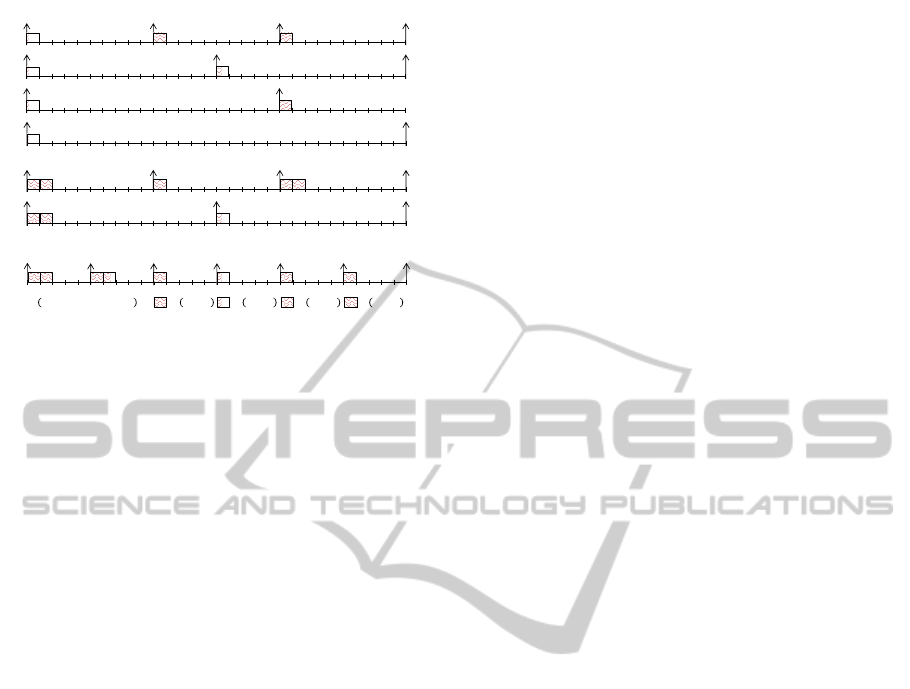
Example 1: Figure 3 illustrates a dispatcher task
for a set of four periodic runnables r
i
(O
i
,C
i
,T
i
,D
i
,k
i
):
r
1
(0,1,10, 8,1), r
2
(5,1,15, 10,2), r
3
(0,1,15, 12,3)
and r
4
(25,1,30, 20,4). The period of the dispatcher
task is GCD(10,15,15,30)=5ms, and its major cycle is
LCM(10,15,15,30)=30ms. Thus, the number of slots
is 6.
Figure 3: Illustration of activation offset for runnables with
position in task.
Table 1 displays values for an example to com-
pute the WCET C
s
of equation (1) and the deadline
of equation (6) of the s
th
slot. From equation (4), the
deadline of dispatcher task D
τ
j
is 8 ms.
Table 1: Computation of WCET and deadline of s
th
slot.
s
th
slot a
i
(s) x
i
(s) C
s
D
s
r
1
r
2
r
3
r
4
r
1
r
2
r
3
r
4
0 0 1 0 5 1 0 1 0 2 9
1 0 1 0 5 0 1 0 0 1 10
2 2 1 0 5 1 0 0 0 1 8
3 2 4 3 5 0 0 1 0 1 12
4 4 4 3 5 1 1 0 0 2 9
5 4 4 3 5 0 0 0 1 1 20
Note: If T
cycle
j
= T
tic
j
, there is one slot where
all runnables are mapped to the same task τ
j
. Thus,
runnables are activated at the same instant and have
the same period. In this case, the dispatcher task
model comes close to the task model of Liu and Lay-
land τ
j
(C
τ
j
,T
τ
j
,D
τ
j
) (Liu and Layland, 1973). Fur-
ther, the task WCET equals to the sum of the WCET
of all runnables mapped to it, its period T
τ
j
equals
to the period of its runnables, and its deadline D
τ
j
is
given by (7).
Let us note that the Liu and Layland’s task model
τ
j
(C
τ
j
,T
τ
j
,D
τ
j
) is a particular case of the dispatcher
task model τ
j
(C
τ
j
,T
tic
j
,T
cycle
j
,D
τ
j
).
In the following section, we introduce a new
heuristic that relies on the APS solution, inspired
by Audsley’s priority assignment approach (Audsley,
1991). A Least Loaded (LL) algorithm (Monot et al.,
2012) is adapted to find the activation offset of every
periodic runnable that respects its execution order.
4 APS-BASED HEURISTIC
ALGORITHM
In this section, a heuristic is developed to solve the
next optimization problem:
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
242

Find: Runnables assigned to tasks,
Activation offset for runnables,
Execution order of runnables,
Tasks priorities.
Minimize: Number of tasks
Subject to: Schedulability of the task set
Our heuristic is inspired by Audsley’s priority as-
signment in order to establish a minimal set of tasks
τ = {τ
1
,...,τ
m
}. Furthermore, each task τ
j
is assigned
a priority j (where 1 is the lowest priority and m is
the highest). The cardinal number m represents the
number of tasks. The task τ
j
is built from a set of
runnables Π
j
which is a subset of the entire input set
of runnables ∆ to be mapped. The activation offset
and execution order parameters are specified to assign
each runnable set Π
j
to task τ
j
. Thus, for each prior-
ity level j (starting with the lowest priority) there are
the two following steps:
1. The first step tries to find an optimal set of
runnables Π
j
to assign it to the same task τ
j
. A
scheduling feasibility test is applied to find Π
j
of
∆ as detailed in the next subsection (4.1).
2. The second step permits to specify activation off-
set and execution order of runnable set Π
j
, in or-
der to ovoid overload situation in the slots (i.e., the
max of WCET of dispatcher task is greater than its
period T
tic
j
or its deadline D
τ
j
). Otherwise, a re-
ject set Λ
j
will contain the first runnables leading
to overload situations.
At priority level j+1, a task τ
j+1
assigned to this
priority level is created of Π
j+1
, which is a subset of
(∆\Π
j
) ∪ Λ
j
. Hence, the set of tasks Γ = {τ
1
,...,τ
m
}
is set up until obtaining an empty set of ∆, where
Π
1
∩ Π
2
,...,∩Π
m
is empty and Π
1
∪ Π
2
,...,∪Π
m
is
equal to ∆ (see Algorithm 1).
Algorithm 1: Heuristic for mapping runnables to
tasks.
Data: runnable set ∆
1 Γ ←
/
0 ;
2 Failed ← False ;
3 j ← 1 ;
/* index of lower priority */
4 while ((∆ ̸=
/
0)&&(Failed = False)) do
5 Π
j
← Algorithm2(∆) ;
6 if Pi
j
̸=
/
0 then
7 (Λ
j
,τ
j
) ← Algorithm3(Π
j
, j) ;
8 Γ ← τ
j
;
9 ∆ ← (∆\Π
j
) ∪ Λ
j
;
10 j ← j + 1 ;
11 end
12 Failed ← True ;
/* The system is unschedulable */
13 end
14 return Γ
4.1 Assignment of Runnables to Tasks
We detail here the first step of Algorithm 1 whose ob-
jective is to find, for each priority level j, an optimal
set of runnables Π
j
⊆ ∆ to be assigned to the same
dispatcher task τ
j
. The following proposition explains
how the set of runnables Π
j
is selected.
Proposition 2. Let us assume a set of runnables
Π
j
= {r
1
,r
2
,...,r
p
} of cardinality p. If each runnable
r
i
∈ Π
j
is schedulable by assigning r
i
to a lower pri-
ority level, where the rest of runnables (∆ − r
i
) are
assigned a higher priorities level, then all runnables
of Π
j
could be allocated to the same task.
By Proposition 2, Algorithm 2 finds the set of
runnables Π
j
⊆ ∆ which can be allocated to the same
task. Algorithm 2 is based on the feasibility test (9)
used by the Audsley’s algorithm:
∋ t
0
≤ t ≤ D
i
:
C
i
t
+
I
i
(t)
t
≤ 1 (9)
where,
I
i
(t) =
∑
j∈∆−r
i
t
T
j
C
j
(10)
Algorithm 2: Assignment of runnables to tasks.
Data: runnable sets ∆
1 Π
j
←
/
0 ;
2 t
0
←
∑
i∈∆
C
i
;
3 for r
i
in ∆ do
4 t ← t
0
;
5 continue ← True ;
6 while continue do
7 if
C
i
t
+
I
i
(t)
t
≤ 1
then
8 if (t ≤ D
i
) then
9 Π
j
← r
i
;
/*
r
i
is schedulable */
10 end
11 continue ← False;
12 end
13 t= I
i
(t) + C
i
;
14 if (t > D
i
) then
15 continue ← False ;
/*
r
i
is unschedulable */
16 end
17 end
18 end
19 return Π
j
4.2 Sequencing of Runnables
The second step of Algorithm 1 is described by Algo-
rithm 3 which builds the dispatcher task τ
j
using the
activation offsets between the runnables of Π
j
given
by Algorithm 2. For each runnable r
i
∈ Π
j
, we have
γ
i
= T
i
/T
tic
j
possibilities to define the first position
δ
i
of runnable r
i
, where 0 ≤ δ
i
≤ γ
i
− 1. Thus, the
ANovelHeuristicAlgorithmforMappingAUTOSARRunnablestoTasks
243
offset of the runnable r
i
is θ
i
= δ
i
∗ T
tic
j
, since the
max WCET of slots is lower than T
tic
j
. Our algo-
rithm adapts the Least Loaded (LL) heuristic devel-
oped by Monot et al in (Monot et al., 2012) so as to
integrate deadlines of runnables. These ones enable
us to find the deadline of the task through equation
(4) with max
s=0...N−1
{C
s
} ≤ D
τ
j
≤ T
cycle
j
and the ex-
ecution order of runnables sorted in increasing order
of laxity. Laxity L
i
= D
i
− C
i
represents the maxi-
mum time during which a task can be delayed while
still completing before deadline.
Algorithm 3: Sequencing runnables inside task.
Data: Input : runnable set Π
j
& j
1 ∧
j
←
/
0 ;
2 T
tic
j
← GCD(Π
j
) ;
3 l ← 1 ;
/* index of the first runnable */
4 Sort Π
j
by increased laxity order ;
5 for i ← 1...
|
Π
j
|
do
6 Look for δ
i
that represents the least loaded slot in the γ
i
first
slot ;
7 Allocate r
i
in every γ
i
slot, starting from this slot δ
i
;
8 Calculate the vector of WCET C
τ
j
by the equation (1) ;
9 if max(C
τ
j
) > T
tic
j
or max(C
τ
j
) > D
τ
j
then
10 Reject the first runnable ∧ ← r
l
;
11 l ← l + 1 ;
12 Update allocation for r
l
to r
i
in the slots using lines 7 & 8
;
13 end
14 end
15 Calculate the deadline D
τ
j
by the equation (4) ;
16 return ∧
j
& τ
j
(C
τ
j
,T
tic
j
,D
τ
j
)
5 EXPERIMENTATION
This section presents and discusses several experi-
mental results. Our study has been conducted in order
to evaluate the proposed approach and validate its ef-
ficiency. To correctly assess the different methods un-
der different execution scenarios, a set of runnables is
randomly generated according to a realistic distribu-
tion of WCETs and periods for covering typical auto-
motive applications.
5.1 Set Up
A system is characterized by the following parame-
ters: number of runnables n, processor utilization fac-
tor U, configuration number, and deadline intervals.
In order to randomly generate the n runnables, we use
the UUnifast algorithm developed in (Bini and But-
tazzo, 2005). This algorithm distributes the total uti-
lization factor U to smaller utilization factor u
i
for n
runnables. For each runnable r
i
, we specify its WCET
C
i
by the following equation:
C
i
= T
i
× u
i
(11)
where T
i
is the period of the i
th
runnable randomly
chosen from a set of non-harmonic periods 1, 2, 3, 5,
8, 10, 15, 20, 25, 40, 50, 100, 150, 200, 250, 300, 500,
900, 1000 ms.
Deadline D
i
of the i
th
runnable is determined from
the following equation:
D
i
= (T
i
−C
i
) × rand(a,b) +C
i
(12)
Where rand(a,b) generates values from the uni-
form distribution on the interval [a, b] with 0 ≤ a ≤ b.
In the case of a=b=1, the deadline is equal to period.
5.2 Results and Discussion
This subsection reports experimental results obtained
by applying our approach using APS and compares it
to both PS and MPS solutions.
Overall, 304 systems have been generated using
the above method and corresponding to 16 cardinal-
ities of period sets and 19 deadline intervals. Each
generated system is composed of 100 runnables that
are generated randomly with a processor utilization
factor fixed to 69%.
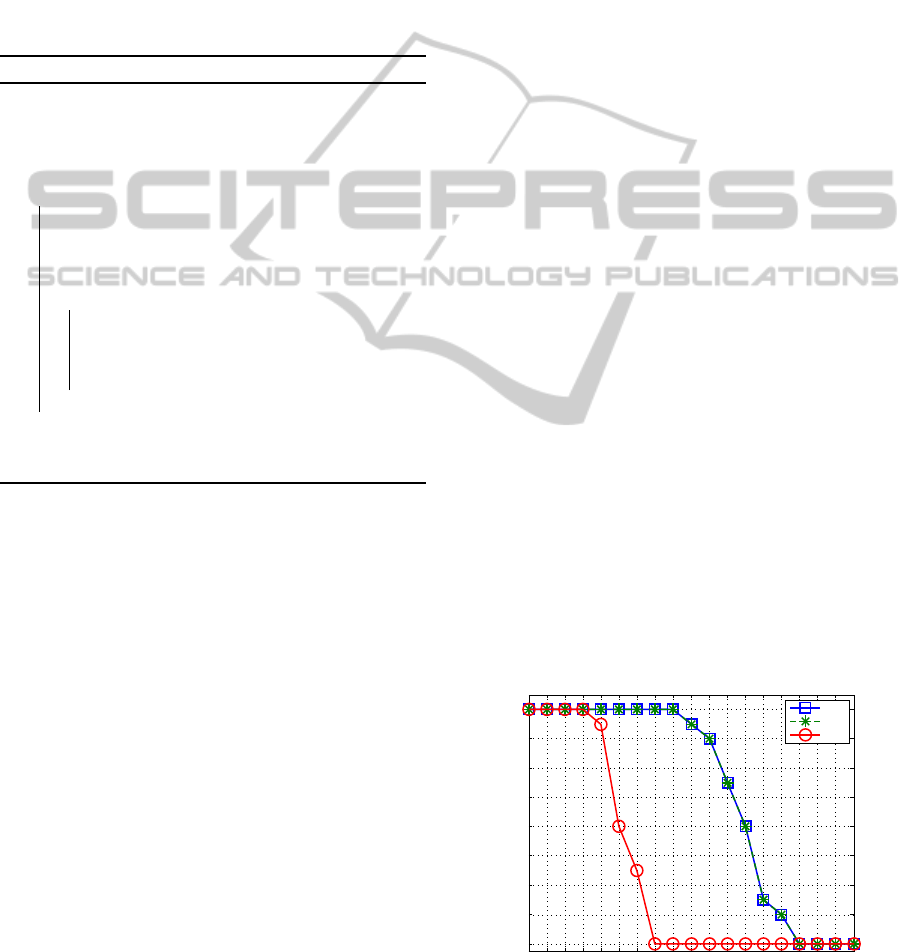
Figure 4 shows the evolution of number of schedu-
lable systems according to the range of runnable
deadlines. Using MPS and APS, we obtained 197
schedulable systems for an overall of 304 analyzed
systems. i.e., we have 64.80% of schedulable sys-
tems for both MPS and APS approaches. However,
using PS approach, we obtained 30.26% of schedula-
ble systems. Thus, our approach increases by 34.54%
the system schedulability compared to PS approach.
Moreover, APS outperforms both MPS and PS ap-
proaches regarding the number of tasks and the avear-
age response time as discussed thereafter.
[1,1] [0.8,1] [0.6,1] [0.4,1] [0.2,1] [0.1,0.9][0.1,0.7][0.1,0.5][0.1,0.3][0.1,0.1]
0
2
4
6
8
10
12
14
16
deadline [a,b]
Number of schedulable system
APS
MPS
PS
Figure 4: Number of schedulable systems with PS, MPS
and APS.
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
244
From Figure 4, we could identify three different
zones based on the strictness of the deadline con-
straint: zone A corresponds to a system with slack
constraints of deadline’ interval [1,1] until [0.4,1],
where B corresponds to a system with tight con-
straints of deadline’ interval [0.5,1] until [0.1,0.5],
and zone C corresponds to systems with firm con-
straints of deadline’ interval [0.1,0.4] until [0.1,0.1].
In the following, we discuss the performance results
obtained by our APS approach for the three zones and
we compare it to PS and MPS. To do that, we define
for each period cardinality, two performance metrics:
• The maximum number of tasks among all dead-
lines intervals for a given zone,
• The benefit percentage of the average response
time (ART) among deadlines intervals for a given
zone.
Zone A: in this zone, we note that APS approach
reduces by 1 to 16 the total tasks number compared to
PS and by 1 to 3 compared to MPS (see Figure 5(a)).
On the other side, Figure 5(b) shows the relative im-
provement (in benefit %) of APS approach regarding
the average response time (ART). This improvement
increases with period cardinality.
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2
4
6
8
10
12
14
16
18
20
Cardinality of period sets
Maximum number of tasks
(a) Maximum number of task among all deadlines’ interval
APS
MPS
PS
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
25
30
35
40
45
50
55
60
65
70
75
Cardinality of period sets
Benefit in [%]
(b) Benefit percentage of avreage response time (ART)
Benefit APS/MPS
Benefit APS/PS
Figure 5: Performance results for zone A.
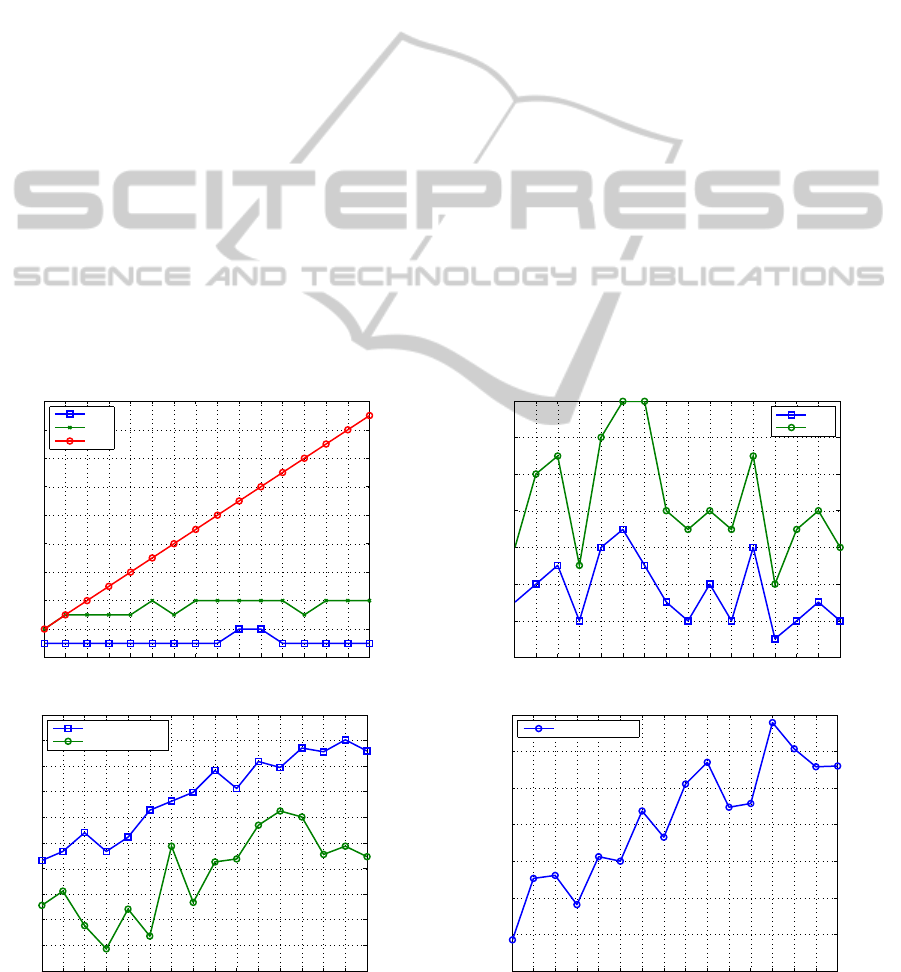
Zone B: in this part, the PS approach is unschedu-
lable and thus it is excluded from comparisons. Fig-
ure 6(a) shows the evaluation of the number of tasks.
We note that APS approach reduces by 3 to 9 the tasks
number compared to MPS. Moreover, APS approach
outperforms MPS approach regarding the improve-
ment (in benefit %) of average response time (see Fig-
ure 6(b)).
Zone C: in this part, there is no system that can be
schedulable by any approach due to the tight deadline
constraints.
6 CONCLUSION
In the AUTOSAR software design methodology,
mapping runnables of software components to OS
tasks represents a central design decision. This may
impact system performance, real-time schedulability
and execution determinism of the application. Several
approaches have been proposed to solve this design
issue, ranging from the simplest solution that map to-
gether runnables with same periods (PS) or multiple
periods (MPS) to the same task, up to a more ad-
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2
4
6
8
10
12
14
16
Cardinality of period sets
Maximum number of tasks
(a) Maximum number of task among all deadlines’ interval
APS
MPS
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
35
40
45
50
55
60
65
70
Cardinality of period sets
Benefit in [%]
(b) Benefit percentage of avreage response time (ART)
Benefit APS/MPS
Figure 6: Performance results for zone B.
ANovelHeuristicAlgorithmforMappingAUTOSARRunnablestoTasks
245

vanced solution based on task sequencer with arbi-
trary periods (APS). However, to our knowledge no
efficient solution has been proposed to optimize both
the number of tasks and system schedulability.
In this paper, a novel method has been proposed
for mapping runnables to tasks based upon the APS
approach. This method uses the activation offset
property of runnables in order to minimize the re-
sulting number of tasks. Experimental results show
that the number of tasks is reduced significantly. Fur-
thermore, our method increases by 34% the system
schedulability bound in comparison to PS approach.
It can be outlined that the PS approach exhibits a
better performance in terms of system response time
compared to the MPS approach but this is in the
detriment of the tasks number. Simulations demon-
strate that our APS approach outperforms both PS and
MPS ones regarding both the number of tasks and
the system response time. We aim also to investi-
gate the experiments setup by extending it to cover
more complex system configuration. In particular,
we would like to measure the performance of our ap-
proach when varying both utilization factor and tasks
deadline. Further, a work in progress has been started
to test our approach on a real board (NEC V850) with
AUTOSAR 3.2. The preliminary obtained results are
satisfactory but have to be also investigated to cover
more system configuration.
Precedence and shared resources constraints will
be also considered in the ongoing work. Finally, we
plan to apply this heuristic to multi-cores architec-
tures in a short future.
REFERENCES
Audsley, N. (1991). Optimal Priority Assignment and Fea-
sibility of Static Priority Tasks with Arbitrary Start
Times. Technical report. University of York, Depart-
ment of Computer Science.
Bini, E. and Buttazzo, G. C. (2005). Measuring the per-
formance of schedulability tests. Real-Time Systems,
30(1-2):129–154.
Haibo, Z. and Di Natale, M. Efficient implementation of
autosar components with minimal memory usage. In
Industrial Embedded Systems (SIES), 2012 7th IEEE
International Symposium on, pages 130–137.
Liu, C. L. and Layland, J. W. (1973). Scheduling algo-
rithms for multiprogramming in a hard-real-time en-
vironment. Journal of the ACM (JACM), 20(1):46–61.
Ming, Z. and Zonghua, G. Optimization issues in mapping
autosar components to distributed multithreaded im-
plementations. In Rapid System Prototyping (RSP),
2011 22nd IEEE International Symposium on, pages
23–29.
Monot, A., Navet, N., Bavoux, B., and Simonot-Lion, F.
(2012). Multisource software on multicore automo-
tive ecus: Combining runnable sequencing with task
scheduling. Industrial Electronics, IEEE Transactions
on, 59(10):3934–3942.
Navet, N., Monot, A., Bavoux, B., and Simonot-Lion, F.
(2010). Multi-source and multicore automotive ecus
- os protection mechanisms and scheduling. In In-
dustrial Electronics (ISIE), 2010 IEEE International
Symposium on, pages 3734–3741.
Partnership, A. (2011). Technical overview.
http://www.autosar.org/, V2.2.2 R3.2 Rev 1.
Rongshen, L., Hong, L., Wei, P., Yi, Z., and Minde, Z. An
approach to optimize intra-ecu communication based
on mapping of autosar runnable entities. In Embedded
Software and Systems, 2009. ICESS ’09. International
Conference on, pages 138–143.
Wozniak, E., Mehiaoui, A., Mraidha, C., Piergiovanni,
S. T., and Gerard, S. (2013). An optimization ap-
proach for the synthesis of AUTOSAR architectures.
In Proceedings of 2013 IEEE 18th Conference on
Emerging Technologies & Factory Automation, ETFA
2013, Cagliari, Italy, September 10-13, 2013, pages
1–10.
Zeng, H., Di Natale, M., and Zhu, Q. (2012). Optimiz-
ing stack memory requirements for real-time embed-
ded applications. In Emerging Technologies & Fac-
tory Automation (ETFA), 2012 IEEE 17th Conference
on, pages 1–8. IEEE.
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
246
