
GP-based Methodology for HW/SW Co-synthesis of Multiprocessor
Embedded Systems with Increasing Number of Individuals Obtained
by Mutation
Adam Górski
1
and Maciej Ogorzałek
2
1
Department of Information Technologies, Jagiellonian University in Cracow, Reymonta 4, Cracow, Poland
2
Department of Information Technologies, Jagiellonian University in Cracow, Cracow, Poland
Keywords: Embedded Systems, Genetic Programming, Genetic Algorithm, Architecture, Hardware/Software
Co-Design, Multiprocessor System.
Abstract: In this work, a genetic programming methodology for co-synthesis of multiprocessor systems is presented.
Genotype is a tree which nodes include system construction procedures. Thus the design methodology is
evolving. Next generations are obtained using genetic operators: mutation, reproduction and crossover.
Unlike other algorithms in presented methodology number of individuals obtained by mutation operator is
not const. Therefore number of individuals in each population is increasing. The size of final generation is
found by the algorithm.
1 INTRODUCTION
Nowadays embedded systems (Acasandrei and
Barriga 2012) can be find almost everywhere:
mobile phones, digital cameras, modern cars, etc.
Embedded systems are also used to help
coordination of different teams in crisis management
(Mahdjoub and Rousseaux 2014). First embedded
systems were not too much complicated. Therefore
it was not necessary to find special methodologies
for designing them. While complexity of embedded
systems was increasing (Kopetz 2008) more
effective design methodologies were needed (Martin
2006, Henzinger, Sifakis 2006). Co-synthesis is a
process which automatically generates an
architecture of embedded system using specification
contained in a task graph. The goal of the process is
to optimize parameters such cost, time or power
consumption. Most of existing solutions (eg. Jiang,
Eles and Peng 2012) assume distributed target
architecture. The architecture consists of many
processing elements (PEs). PEs can be divided into
two groups: programmable processors (PPs) and
hardware cores (HCs). PPs can execute more than
one task thus theirs cost is low but they are not very
fast. HCs can execute only one task thus the time of
task execution is reduced, but cost of the resource is
relatively high.
Co-synthesis process consists of three phases:
1. resource allocation – selection of number and
types of PEs and communication channels; 2. task
assignment – choice of PE for each task and
transmission between resources; 3. task scheduling –
determining when each task should begin its
execution.
Existing methodologies can be divided on two
basic groups. The most popular are iterative
improvement algorithms (Deniziak 2004, Yen and
Wolf 1995, Górski and Ogorzałek 2014a) which
start from sub-optimal solution and refine systems
by making local changes (moving task between PEs,
allocating or removing PEs from system). Usually,
as the initial solution, the fastest architecture is
selected. Unfortunately the results obtained by most
of these methodologies are still sub-optimal.
The second group includes constructive
algorithms (eg. Dave, Lakshminarayana and Jha
1997). In those methodologies system is built by
choosing PE for each task separately. Therefore
those algorithms are tend to stop in local minima of
optimizing parameters.
Probabilistic solutions, especially genetic
algorithms (Chehida and Auguin 2002; Purnaprajna,
Reformat and Pedrycz 2007) can escape from local
minima. This group of algorithms contains for
example simulated annealing (Eles, Peng,
Kuchciński and Doboli 1997). Especially good
275
Górski A. and Ogorzalek M..
GP-based Methodology for HW/SW Co-synthesis of Multiprocessor Embedded Systems with Increasing Number of Individuals Obtained by Mutation.
DOI: 10.5220/0005238702750280
In Proceedings of the 5th International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2015), pages
275-280
ISBN: 978-989-758-084-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

results were obtained using developmental genetic
programming (Deniziak and Górski 2008). In this
algorithm genetic programming evolves design
methodology to obtain the best system.
Adaptive algorithms are also more and more
popular in computer system design process
(Shankaran, Roy, Schmidt, Koutsoukos, Chen,
and Lu, 2008, Górski and Ogorzałek 2014b).
Genetic programming (Koza, Bennett III, Lohn,
Dunlap, Keane and Andre, 1997) extends genetic
algorithms (Holland, 1992). In genetic programming
there is a strong the difference between phenotype
and genotype. The genotype is a tree which consists
of computer programs. The phenotype is the final
solution. Genetic programming is wildly used
amount other things in: machine learning (Krawiec
2002), design problems like synthesis computational
circuits (Koza, Bennett III, Lohn, Dunlap, Keane
and Andre, 1997) and in medicine for example
in prediction survival in cancer (Giacobini, Provero,
Vanneschi and Mauri 2014).
In every genetic methodology number of
individuals obtained in every population is constant.
Therefore large number of individuals have to be
generated to make the algorithm effective. In the
environment the situation is completely different.
The number of individuals in most of species
increases.
In this article a new approach based on
developmental genetic programming (Koza 2010) is
presented. Unlike other methodologies in presented
algorithm the number of individuals obtained by
mutation operator in each generation is increasing.
In section 3 the methodology is described. Sections
4 and 5 present experimental results (obtained using
set of benchmarks with 10, 20 and 30 nodes) and
conclusions.
2 PRELIMINARIES
Like in many works (eg. Engelhardt, Dallou,
Elhossini and Juurlink 2014) we assume, that the
behaviour of embedded system is described by an
acyclic, directed graph called the task graph
G = {V, E}. Each node v
i
V represents task, and
edge e
i
E presents dependence between tasks.
Label d
ij
describes the amount of data that has to be
transferred between two connected tasks (v
i
and v
j
).
Transmission t
ij
is defined as follows:
CL
ij
ij
b
d
t
(1)
where: b
CL
is a bandwidth which characterises
communication link (CL).
As an example we use task graph proposed by
Górski and Ogorzalek (Górski and Ogorzałek 2014).
It is presented on fig. 1. The graph includes 7 tasks.
T2
T0
T1
T3 T4
114 114
20
20
20
T5
20
T6
20
Figure 1: Example of task graph.
An example of a resource database for the system
described by the graph above is presented in table 1.
It contains two communication links (CL1 and CL2)
and four PEs: two programmable processors (PP1
and PP2), two Hardware cores (HC1 and HC2).
Every task is defined by area occupied by this task
(s) and a time of execution (t). Areas occupied by
the tasks mean the size of memory needed to execute
these tasks. Communication links are defined by
a bandwidth (b) and an area (s) occupied by the link
connected to PE. Table 1 also includes the area (S)
occupied by each PE. The area of the tasks
implemented in HC includes the area occupied by
the core.
Table 1: Resource database.
Task
PP1
S=200
PP2
S=300
HC1 HC2
t s t s t s t s
T0 150 4 120 6 50 180 30 250
T1 40 3 35 2 14 100 10 140
T2 - - 320 17 250 200 150 650
T3 235 10 220 15 140 160 90 200
T4 165 8 150 10 65 100 40 140
T5 70 4 40 5 25 100 - -
T6 23 2 20 1 5 40 2 80
CL1,
b=6
s=2 s=2 s=10
CL2,
b=15
- s=2 s=15
Task T2 is not compatible with PP1, and task T5
cannot be implemented in HC2. Communication link
CL2 is not compatible with PP1.
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
276

The final architecture of designing system
contains p communication links and m
programmable processors and hardware cores,
(selected from table 1.) which execute n processes.
Overall area (S
o
) of the system is described by the
following formula:
p
k
P
l
PCCL
n
j
j
m
i
PEo
k
iki
ssSS
11
,
11
(2)
The goal of co-design is to find an architecture
with the lowest S
o
value. The value must satisfy time
constrains.
3 INITIAL POPULATION
In genetic programming it is strong difference
between genotype and phenotype. According to
genetic programming rules in this methodology
genotype is a system construction tree, which
evolves. The phenotype is the final solution. At the
beginning embryo is created. The embryo is an
randomly implementation of the first task. The
number of possible embryos is the number of
possible PEs in the database. Every next node in the
genotype describes system constructing decision. To
ensure that system executes all tasks the structure of
genotype has to be based on the task graph. Each
node in the tree must correspond to equal system
constructing function. The options for constructing
system are presented in table 2. To check the
efficiency of proposed methodology we decided to
use the same system constructing function as were
proposed by Deniziak and Górski in DGP08
algorithm (Deniziak and Górski 2008). However
there are differences in evolution process. Therefore
we are certain that quality of obtained solutions is
a result of using presented methodology. The last
column includes probability of selection of system-
construction options. The initial population contains
of randomly generated genotypes. П
0
is the size of
initial population:
0
= *n*p
(3)
where: n – number of tasks in task graph,
p – number of possible embryos, α – control
parameter which determines the number of
individuals in populations; it is set manually.
The system is constructed by executing functions
in order corresponding to the level of the node in the
genotype tree. Then solutions are sorted by the
lowest cost.
Table 2: Options for constructing system.
Step Option Probability
PE
a. Used PE 0.6
b. The smallest area 0.1
c. The fastest 0.1
d. Min (s*t) 0.1
e. The least used 0.1
Used PE
a1. The smallest area 0.2
a2. The fastest 0.2
a3. The lowest
utilization
0.2
a4. Idle for the longest
time
0.2
a5. The same as a
predecessor
0.2
CL
a. Used CL 0.5
b. The highest b 0.2
c. The last used 0.2
d. The smallest area 0.1
Used CL
a1. The smallest area 0.3
a2. The fastest 0.3
a3. The lowest
utilization
0.2
a4. Idle for the longest
time
0.2
Task
scheduling
list scheduling 1
4 EVOLUTION
To obtain new population we used standard genetic
operators: crossover, mutation and reproduction. The
number of individuals obtained by using genetic
operators is given:
Φ = β*П – individuals obtained by
reproduction;
Ψ = γ*П – individuals obtained by crossover;
Ω = δ*П – individuals obtained by mutation;
Parameters β, γ, δ are used to control the evolution
process. They are set manually.
Unlike other methodologies number of
individuals in each population is not const. Thus:
1
(4)
Reproduction randomly copies the Φ genotypes
from the current population. Individuals are chosen
randomly but with different probability P.
The probability depends on the position q in rank
list. It is described as follow:
c
c
q
P
(5)
П
c
in formula above is a size of current
GP-basedMethodologyforHW/SWCo-synthesisofMultiprocessorEmbeddedSystemswithIncreasingNumberof
IndividualsObtainedbyMutation
277
population. It can be defined as follows:
1
()*
cc
(6)
Crossover chooses randomly the Ψ solutions.
The crossing point is selected randomly. It is the
same for both genotypes. Afterwards the sub-trees
are substituted.
Mutation is responsible for providing fresh genes
to the environment. Thus we decide to increase
number of individuals obtained using mutation
operator. The operator randomly selects one
individual and one node, than changes option in this
node to a different one from the option list.
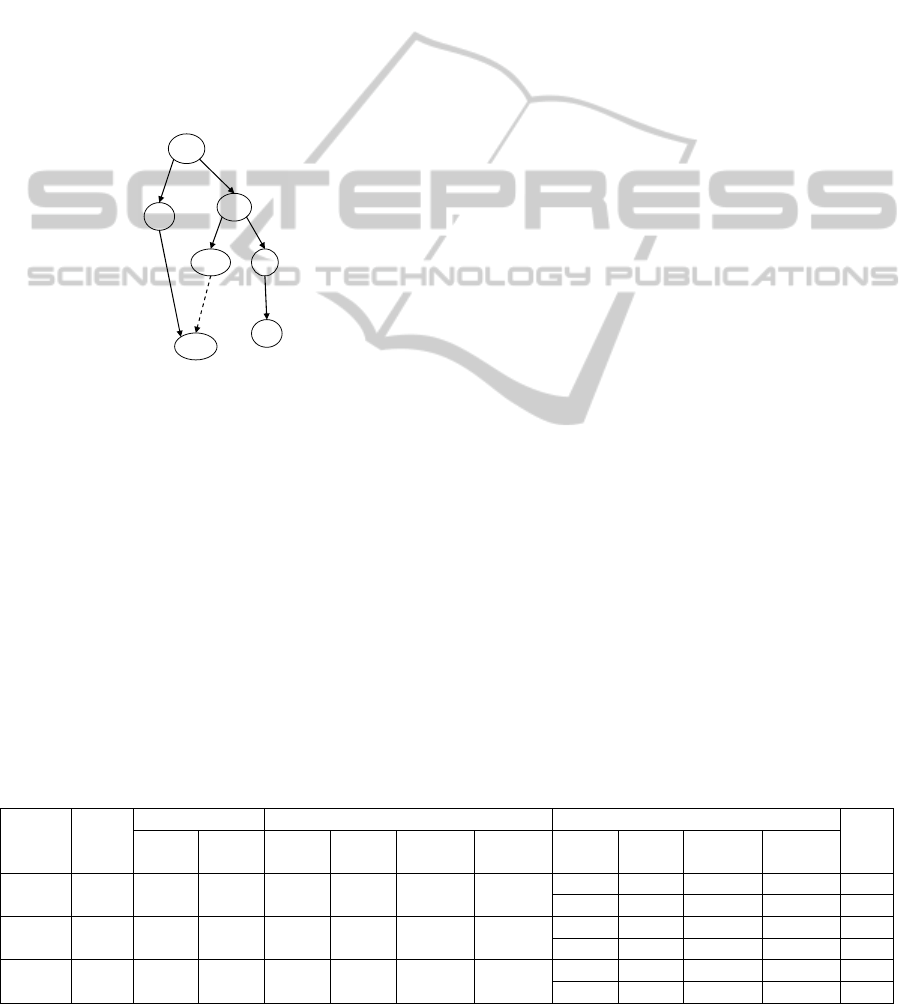
Figure 2 shows an example of genotype for the
task graph of figure 1.
a4/b
PP0
b/a2
a1/a1 a3/c
a5/a4
c/d
Figure 2: Example of genotype.
After generating new population new rank list is
created. The process is stopped when cheapest
solution which satisfies time constrains wasn’t found
in next ε steps (last ε generations). Parameter ε is set
manually.
5 EXPERIMENTAL RESULTS
Because of very large computational complexity of
the co-design problem, the best way to check
effectiveness of proposed methodology is to
compare the performance with other existing
methods. All experiments were carried out on
benchmarks with 10, 20 and 30 nodes. We compared
presented methodology with algorithm DGP08
(Deniziak and Górski, 2008) and algorithm Ewa
(Deniziak, 2004). DGP08 is genetic programming
algorithm for co-synthesis. It was compared with
algorithm Yen-Wolf (Yen and Wolf 1995) for co-
synthesis. Algorithm Ewa was proved to be more
effective than MOGAC (Dick and Jha, 1998).
MOGAC is a genetic algorithm for co-synthesis.
Therefore we believe that this comparison is the best
to check effectiveness of the proposed methodology.
Because of probabilistic nature of the
methodologies, for each graph 30 tries were made.
In table 3 the comparison results are presented.
In the table the best and average values of cost and
execution time for the algorithms are presented. For
both genetic methodologies parameters α=100,
β=0,2, γ=0,7 and ε=5. For algorithm DGP08 δ=0,1.
The time constrains were set as follow: 350 for
graph with 10 nodes, 500 for graph with 20 nodes,
800 for graph with 30 nodes. In table 4 values of
δ parameter for algorithm GP 2015 are given. We
decided to check efficiency of proposed algorithm
with δ values 0,2 and 0,3. In all of the experiments
parameter α=100.
For graph with 10 nodes the best result obtained
for all of the genetic methodologies has cost 1590
and time 326. However average cost is lower for the
methodology presented in this paper. For DGP08
average cost is 1602. In our algorithm average costs
are: 1594 when parameter δ=0,2 and the lowest 1593
when δ=0,3. The same situation can be observed for
the rest of graphs. Best average results were
obtained when parameter δ=0,3. For graph 20
average cost was: 2652 when δ=0,2 and 2649 when
δ=0,3, while for DGP08 it was 2669. For both
genetic methodologies the best obtained cost was
2649. For bigger graph (with 30 nodes) the results
indicates on high efficiency of proposed solution.
The average cost for DGP08 was 3130, while for
presented approach was 3107 (when δ=0,2) and
3074 (when δ=0,3). What is worth to underline the
Table 3: Experimental results.
Graph T
max
Ewa DGP08
GP 2015
δ
time cost time cost
average
time
average
cost
time cost averag
e time
averag
e cost
10 350 204 2975 326 1590 296 1602
326 1590 308 1594 0,2
326 1590 316 1593 0,3
20 500 457 3020 396 2649 396 2649
396 2649 396 2652 0,2
396 2649 396 2649 0,3
30 800 789 5330 792 3081 793 3130
792 3081 792 3107 0,2
792 3056 792 3074 0,3
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
278

average cost obtained by presented algorithm for
graph with 30 nodes when δ=0,3 (3074) is lower
than the best obtained result using DGP08 (3081).
For presented methodology, when δ=0,2, the best
obtained solution is the same as for DGP08 (3081).
Results obtained by algorithm Ewa was: time 204,
and cost 2975 for graph 10, for graph with 20 nodes
the execution time was 457 while cost was 3020.
Also for bigger graph (with 30 nodes) the results
were much worse that obtained by DGP08 and
GP2015 – obtained time was 789 and cost was 5330.
6 CONCLUSIONS
In this paper we present a new methodology based
on genetic programming for hardware/software co-
synthesis. Unlike other genetic programming
approaches the number of individuals in populations
is not const. Moreover the number of individuals
increases in each population. This is achieved by
increasing number of individuals obtained using
mutation operator.
First obtained results indicates that the results
obtained by proposed methodology are better than
obtained using other algorithms. In every genetic
approach number of individuals in each population
has to be large. Presented methodology allows to
generate less individuals in initial population and
obtain good solutions during evolution process. The
size of final population will be found by the
algorithm.
Some test like t-test, Mann-Whittey test or
Wilcoxon test (Ruxton, 2006) can be made to
compare DGP08 and GP 2015, but we were afraid
that they may underestimate the true significance of
obtained results.
The future work will concentrate on examining
the influence of another genetic operators on quality
of the results and different representation of
genotype tree. We will also test different genetic
operators and chromosomes.
ACKNOWLEDGEMENTS
This work is supported by the Foundation for Polish
Science, under grant “Mistrz 2012” No. 9/2012:
“New computational approaches for solving next
generation microelectronic design problems”.
REFERENCES
Acasandrei, L., Barriga, A., 2012. FPGA implementation
of an embedded face detection system based on
LEON3. In Proceedings of the International
Conference on Image Pro-cessing, Computer Vision,
and Pattern Recognition.
Mahdjoub, J., Rousseaux, F., 2014. Planning and
Optimization of Resources Deployment: Application
to Crisis Management. In Proceedings of the 11th
IEEE International Conference on Embedded
Software and Systems.
Kopetz, H., 2008. The complexity challenge in embedded
system design. In Proceedings of the 11th IEEE
International Symposium on object Oriented Real-
Time Distributed Computing.
Martin, G., 2006. Overview of the MPSoC Design
Challenge. In Proceedings of the 43rd annual Design
Automation Conference.
Henzinger, T.A., Sifakis, J., 2006. The Embedded Systems
Design Challenge. In Lecture Notes in Computer
Science, vol. 4085, pp 1-15.
Jiang, K., Eles, P., Peng, Z., 2012. Co-design techniques
for distributed real-time embedded systems with
communication security constrains. Design
Automation and Test in Europe (DATE 2012).
Deniziak, S., 2004. Cost-efficient synthesis of
multiprocessor heterogeneous systems. In Control and
Cybernetics, vol. 33, No. 2.
Yen, T., Wolf, W., 1995. Sensivity-Driven Co-Synthesis
of Distributed Embedded Systems. In Proceedings of
the International Symposium on System Synthesis.
Górski, A., Ogorzałek, M., 2014a. Iterative Improvement
methodology for hardware/software co-synthesis of
embedded systems based on genetic programming. In
Proceedings of the 11th IEEE International
Conference on Embedded Software and Systems
(Work in Progress session).
Dave, B., Lakshminarayana, G., Jha, N., 1997. COSYN:
Hardware/software Co-synthesis of Embedded
Systems. In Proceedings of the 34th annual Design
Automation Conference (DAC’97).
Chehida, K., B., Auguin, M., 2002. HW/SW Partitioning
Approach for Reconfigurable System Design. In
Proceedings of the International Conference on
Compilers, Architectures and Synthesis for Embedded
Systems, CASES 2002.
Purnaprajna, M., Reformat, M., Pedrycz, W., 2007.
Genetic algorithms for hardware-software partitioning
and optimal resource allocation. In Journal of Systems
Architecture, 53(7).
Eles, P., Peng, Z., Kuchciński, K., Doboli, A., 1997.
System Level Hardware/Software Partitioning Based
on Simulated Annealing and Tabu Search. In Design
Automation for Embedded Systems, vol. 2, No 1.
Deniziak, S., Górski, A., 2008. Hardware/Software Co-
Synthesis of Distributed Embedded Systems Using
Genetic programming. In Proceedings of the 8th
International Conference Evolvable Systems: From
GP-basedMethodologyforHW/SWCo-synthesisofMultiprocessorEmbeddedSystemswithIncreasingNumberof
IndividualsObtainedbyMutation
279

Biology to Hardware, ICES 2008. Lecture Notes in
Computer Science, Vol. 5216. Springer-Verlag.
Shankaran, N., Roy, N., Schmidt, D. C.,
Koutsoukos, X. D. C., Chen, Y., Lu, C., 2008. Design
and performance evaluation of an adaptive resource
management framework for distributed real-time and
embedded systems. EURASIP Journal on Embedded
Systems.
Górski, A., Ogorzałek, M., 2014b. Adaptive GP-based
algorithm for hardware-software co-design of
distributed embedded systems. In Proceedings of the
4th International Conference on Pervasive and
Embedded Computing and Communication Systems.
Koza, J., R., Bennett III, F., H., Lohn, j., Dunlap, F.,
Keane, M., A., Andre, D., 1997. Automated synthesis
of computational circuits using genetic programming.
In Proceedings of the IEEE Conference on
Evolutionary Computation. IEEE.
Holland., J., H., 1992. An Introductory Analysis with
Applications to Biology, Control, and Artificial
Intelligence. IN MIT Press, Cambridge, MA.
Krawiec, G., 2002. Genetic programming-based
construction of features for machine learning and
knowledge discovery tasks. In Genetic Programming
and Evolvable Machines, vol. 3, No. 4., pp. 329–343.
Giacobini, M., Provero, P., Vanneschi L., Mauri, G. 2014.
Towards the Use of Genetic Programming for the
Prediction of Survival in Cancer. In Evolution,
Complexity and Artificial Life, pp177-192.
John R. Koza. 2010. Human-competitive results produced
by genetic programming. In Genetic programming and
evolvable machines, vol. 11, issue 3-4. Springer-
Verlag.
Engelhardt, N., Dallou, T., Elhossini, A., Juurlink, B 2014.
An Integrated Hardware-Software Approach to Task
Graph Management. In Proceedings of the 16th IEEE
International Conference on High Performance and
Communications.
Dick, R., P., Jha, N., K., 1998. MOGAC: a multiobjective
Genetic algorithm for the Co-Synthesis of
Hardware-Software Embedded Systems. In IEEE
Trans. on Computer Aided Design of Integrated
Circiuts and systems, vol. 17, No. 10.
Ruxton., G., D., 2006. The unequal variance t-test is an
underused alternative to Student’s t-test and the
Mann–Whitney U test. In Behavioral Ecology, 17(4).
doi:http:// dx.doi.org/10.1093/beheco/ark016.
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
280
