
A Formalisation of Analysis-based Model Migration
Ingrid Chieh Yu and Henning Berg
Department of Informatics, University of Oslo, Oslo, Norway
Keywords:
Metamodelling, Co-evolution, Adaptation, Composition, Variability.
Abstract:
Supporting adaptation of metamodels is essential for realising Model-Driven Engineering. However, adapting
and changing metamodels impact other artefacts of the metamodelling ecosystem. In particular, conformant
models will no longer be valid instances of their changed metamodel. This gives rise to co-evolution issues
where metamodels and models are no longer synchronised. This is critical as systems become inconsistent. A
typical approach for re-establishing conformance is to manually craft transformations which update existing
models for the new metamodel variant. In this paper we present an analysis-based approach that addresses this
concern. The approach enables an arbitrary number of metamodels to evolve based on an adaptation strategy.
During analysis we accumulate information required to automatically transform existing models to ensure
conformance. We formalise the approach and prove model conformance.
1 INTRODUCTION
From a broad view, software engineering is the pro-
cess of understanding a system and representing it as
a set of models that can be understood by comput-
ers. The models allow reasoning about the system and
perform various analyses and evaluation of system-
specific data; whether the system already exists or is
to be built. Modelling is the process of creating ab-
stractions of a system. A system may itself be a model
(Favre, 2004)(Seidewitz, 2003), something that has
given us the notion of metamodelling. Metamodelling
is the process of formalising models by indentifying
their structure and semantics. The result of such a
process is one or more metamodels.
Metamodelling is a key process in several Model-
Driven Engineering (MDE) (Kent, 2002) disciplines
including language design, product line engineer-
ing, variability management and domain modelling.
The promised benefits of using model-oriented ap-
proaches are increased efficiency, quality and consis-
tency in software. Using models also supports code
generation, multi-view modelling and improved veri-
fication of system properties. There are clear incen-
tives in the industry for applying MDE approaches,
as shorter time to market for software products and
mechanisms that support variability are needed.
A metamodel is defined according to the rules and
constraints of a metamodelling architecture or meta-
modelling framework. The prominent metamodelling
architecture in the industry is the Object Manage-
ment Group (OMG) standardised MetaObject Facility
(MOF) (ObjectManagementGroup, 2014), and a vari-
ant based on Essential MOF (EMOF) implemented
in the Eclipse Modeling Framework (EMF) named
Ecore (TheEclipseFoundation, 2014). Both MOF and
Ecore have concepts for creating standalone meta-
models of arbitrary domains. However, the architec-
tures do not have built-in mechanisms that address co-
evolution of models as metamodels change. One such
change or adaptation is composition of metamodels.
Composition may be used to increase a metamodel’s
expressiveness or to weave in variability (Didonet
Del Fabro et al., 2006)(Fleurey et al., 2008)(Kolovos
et al., 2006a)(Morin et al., 2008)(Morin et al., 2009).
A model is said to conform to its metamodel when
all elements in the model are legal instances of struc-
tural elements found in the metamodel. Changing the
metamodel typically causes the conformance relation
to be broken. Consequently, the models are no longer
valid according to the changed metamodel. This is
unfortunate as it creates system inconsistencies.
There are three main categories of approaches
available that address how models, transformations
and tools may adapt to changes of evolving meta-
models (Rose et al., 2009). These are manual speci-
fication, operator-based co-evolution and metamodel
matching, where the latter category may be further di-
vided into change recording and differencing. In this
paper we present a novel approach of model migra-
86
Yu I. and Berg H..
A Formalisation of Analysis-based Model Migration.
DOI: 10.5220/0005240900860098
In Proceedings of the 3rd International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2015), pages 86-98
ISBN: 978-989-758-083-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

tion by using analysis as a core process. Specifically,
our approach is a hybrid between operator-based co-
evolution and metamodel matching, where informa-
tion required to re-establish model conformance is
generated automatically during the analysis step. All
model migration approaches we have come across are
limited to what we refer to as serial evolution, i.e.
model migration is only addressed for evolution of
one metamodel at a time, where the metamodel is
evolved from an initial version to a revised version in-
dependently of other metamodels. However, this is an
ideal case. In practice, metamodels may evolve in par-
allel due to dependencies that exist or are introduced
between the metamodels. We refer to this as paral-
lel evolution. Examples of dependencies that may
be introduced are when metamodels are composed,
e.g. by merging or interfacing classes. In the general
case, there may be an arbitrary number of metamod-
els for which dependencies are introduced. Hence,
evolving one metamodel should be reflected on the
other metamodels as well. Furthermore, the evolu-
tion of the metamodels should be propagated to all
existing models of all the metamodels. That is, ex-
isting models conforming to the metamodels must all
be updated to conform to the new metamodel versions
or resulting composite metamodel. This is not trivial
due to the dependencies introduced, and is the rea-
son why analysis is required. The proposed analysis
framework is able to process an arbitrary number of
metamodels simultaneously, and accumulates infor-
mation about changes performed on the metamodels.
The information is later used as input to model-to-
model transformations that update existing models.
Changing or adapting metamodels do not only
impact the models. Changing a metamodel also
severely impacts other artefacts in the metamod-
elling ecosystem that are defined relative to the meta-
model. Such artefacts include editors, concrete syn-
taxes, transformations and interpreters. Changing or
altering a metamodel results in co-evolution issues
with these artefacts, as the metamodel and artefacts
do not evolve in a synchronised manner. Our ap-
proach is also applicable for co-evolution of artefacts.
Specifically, the information generated indicates what
changes that must be performed in the artefacts for
these to be valid with respect to evolved metamodels.
In this paper we limit our scope to describing how the
conformance between models and metamodels may
be re-established as the metamodels are changed or
adapted. We exemplify the approach by studying how
two metamodels are composed (we view metamodel
composition as an adaptation).
We formalise an analysis framework based on a
set of basic adaptation operations. The adaptation
operations are fine grained and can be traced back to
the catalogue of operators presented in (Herrmanns-
doerfer et al., 2011). The analysis framework system-
atically generates information which is needed for re-
establishing conformance between the adapted meta-
models and existing models. We focus on model
structure and leave semantics for future work. We do
not consider matching of metamodels using heuris-
tics (Del Fabro and Valduriez, 2007), as this is outside
of our scope. However, we give our thoughts on this
topic with respect to our approch in Sec. 6 where we
briefly describe how to incorporate the use of ontolo-
gies in the analysis.
The contribution of this paper is two-fold. First,
we discuss a new approach for model migration and
how conformance between models and metamodels
can be re-established as metamodels are adapted or
composed. The approach is applicable to other arte-
facts in the metamodelling ecosystem, e.g. it supports
metamodel-tool co-evolution. Second, we present a
thorough formalisation of the analysis that is used in
our approach. The formalisation not only describes
our approach in details, but it gives a formalisation
of how model conformance may be re-established
as metamodels evolve, i.e. metamodel-model co-
evolution. There is not much work available that for-
malises metamodel-model co-evolution. As far as we
know, the only formalisations on this topic is in the
form of typed graphs and category theory (Taentzer
et al., 2012)(Mantz et al., 2010).
Paper overview. Sec. 2 gives a motivating ex-
ample, Sec. 3 introduces adaptation operations for
metamodel evolution, Sec. 4 addresses model confor-
mance, Sec. 5 discusses related work, and Sec. 6 con-
cludes the paper.
2 MOTIVATING EXAMPLE
We will motivate and explain our approach using
a simplified example in the domain of ecommerce.
The example will be developed throughout the pa-
per. Ecommerce is an industry concerned with sale
and purchase of products and services using Inter-
net technologies. Ecommerce is a multi-facetted con-
cept comprising e.g. financing and payment, pricing
and marketing analysis, logistics, product modelling,
business modelling and business strategies. All of
these concerns are modelled in some way - either in-
formal or in a more formal manner using e.g. a set
of UML models. An increasingly popular approach
is to create a set of domain-specific languages (DSLs)
for each of the major concerns. This approach allows
stakeholders to model their solution directly at the
AFormalisationofAnalysis-basedModelMigration
87
level of ecommerce domain concepts. That is, each
domain-specific language contains a set of constructs
for modelling of one explicit concern. An ecommerce
solution is then the sum of all the models that describe
it.
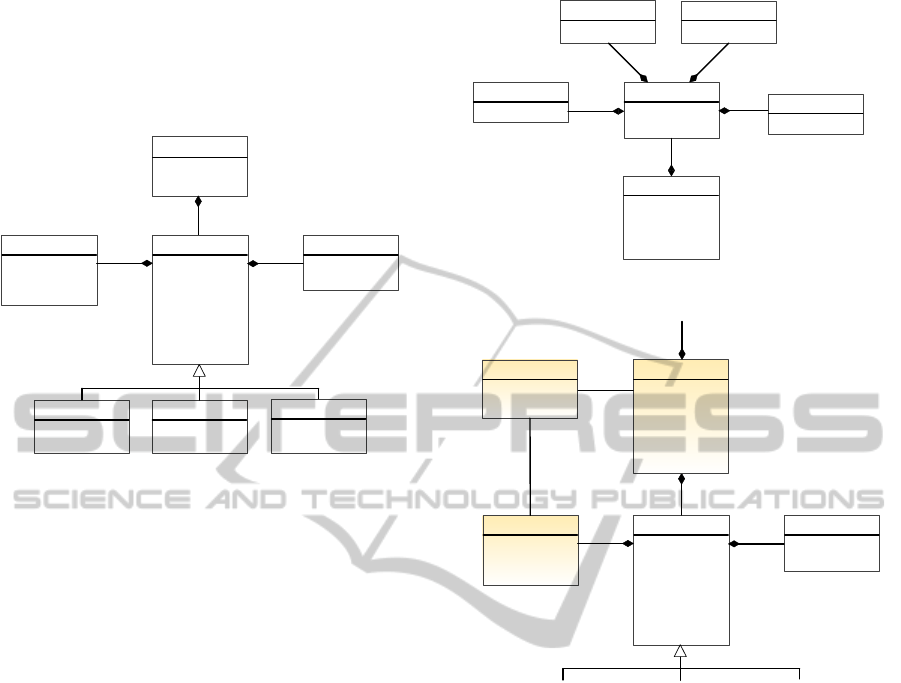
Product
- id
- year
- title
- genre
- ageLimit
- country
- language
Merchandise
- id : String
- format() : String
- value : Real
- firm : String
- country : String
RightsOwnership
- width
- height
Dimension
1..1
1..*
1..*
products
dimension
rightsOwnership
Book Film
Audio
- duration
- format
Figure 1: Metamodel for modelling of products/merchan-
dise.
To keep our example manageable, we will only fo-
cus on two aspects of an ecommerce solution: prod-
uct modelling and business context modelling. Prod-
uct modelling, as we use the term here, is the pro-
cess of describing a product intended for sale - in-
cluding all its metadata. Business context modelling
deals with concerns such as ownership, regions where
a given product or group of products should be avail-
able, price and such.
We assume that the conceptual domain of our ex-
ample is sale of media products like books, films and
audio. That is, our target software solution is that of
an online retailer like Amazon. A product, see Fig-
ure 1, has attributes like year of publication or release,
title, genre, etc. A product has a dimension and a set
of copypright owners (note that most attribute types
and attribute multiplicites are excluded for clarity rea-
sons). A product model describes either one specific
product or a product group. The product model does
not describe any aspects related to sale of this product.
The trading perspective is covered by the business
context model, see Figure 2, which describes the busi-
ness dimension of a product or product group. That is,
the business model puts a product in a business con-
text. This includes describing the price of the product,
availability, fees and eventual discounts. A product
may have several business contexts. As an example,
a product may have different prices and discounts de-
pending on the region of sale.
The two metamodels, supporting modelling of
concerns in two different domains, may be combined
Availability
- region
- country
Discount
- value
Price
- value : Real
- value
Shipping
- id : String
- region : String
- country : String
- format() : String
BusinessContext
CustomsTaxFee
- percent
1..*
0..1
1..1
1..1
0..*
shipping
discount price
availability
customsTaxFees
Figure 2: Metamodel for modelling of business contexts.
Product
- id
- year
- title
- genre
- ageLimit
- country
- language
- value : String
- firm : String
- country : String
RightsOwnership
- width
- height
Dimension
1..1
1..*
1..*
products
dimension
rightsOwnership
- id : String
- #id : String
- region : String
- country : String
- format() : String
- #format() : String
MBC
1..*
availability
- percent : Real
ProfitShare
1..*
profitShares
1..*
stakeHolders
...
... ... ...
Figure 3: The metamodel resulting from composing the
metamodels for product and business context modelling.
to form a new metamodel for ecommerce, see Fig-
ure 3. The new metamodel has a class named MBC
that is a combination of the Merchandise and Business-
Context classes. The metamodel is also extended with
a new ProfitShare concept. In the subsequent sections,
we will demonstrate how the new metamodel is sys-
tematically derived.
3 METAMODEL ADAPTATIONS
We base our analysis framework and example on
an excerpt of the MOF structural concepts (Object-
ManagementGroup, 2014)(Steel and Jzquel, 2007).
The excerpt represents the most essential concepts of
MOF:
MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
88

a
Metamodel ::= package P {ClassDecl}
ClassDecl ::= class C extends C
0
{PropDecl OpDecl}
PropDecl ::= t P (Multi)? (containment)? (# P
0
)?
Multi ::= [lower .. upper]
OpDecl ::= t O(t
i
P
i
)
t ∈ Type ::= Primitive | C | sethCi | Void
Primitive ::= Boolean | Integer | Real | String
A metamodel consists of a package with one or
more classes. (In general a metamodel may have sev-
eral packages, which can be easily accommodated by
our approach.) A class may have an arbitrary number
of properties and operations. Properties do either have
primitive types or class types. Hence, they either act
as attributes or references. containment takes the val-
ues true or false, whereas lower and upper are natural
numbers. In this paper, we use the term well-typed
metamodel as a model satisfying the requirements
in (ObjectManagementGroup, 2014). Specifically we
have the following typing restrictions on property and
operation definitions in MOF metamodels that inher-
ently affect the proposed adaptation rules:
• A property name can only occur once in a class
hierarchy
• Operations may be overloaded in the same class,
but only occur once with the same signature
• Overloaded operations in a class hierarchy that
have the same parameter types require the same
return type
We formalise metamodel adaptations in terms
of basic adaptation operations. We consider con-
structive operations that are not neccessarily model-
preserving (Herrmannsdoerfer et al., 2011). The oper-
ations can be combined to form more complex adap-
tation strategies. We do not aim at theoretical com-
pleteness but rather focus on common practical adap-
tations. The framework is structured in such a way
that it can easily be extended by adding more opera-
tions.
Metamodels can be adapted using the following
basic adaptation operations, where N and N
0
are class
names, C a class term, P a property definition, O an
operation definition, and R a tuple hN, Pi:
• merge(N, N
0
) creates a new class by merging two
classes named N and N
0
• addClass(C) adds a new class definition
• addSuperClass(N, N
0
) extends the class named N
with a new superclass N
0
• addInterfaceClass(C, R ) adds a class C that
serves to bridge classes according to the relations
specified in R
• override(N, N
0
) overrides the class named N with
the definition of N
0
• addProp(N, P) extends class N with a new prop-
erty P
• addOp(N, O) extends a class N with a new opera-
tion O
• addBiProp(N, P, N
0
, P
0
) extends class N with a
property P and N
0
with a property P
0
, where P and
P
0
combined describe a bi-directional relation
Note that the merge, addSuperClass and override
operations differ from other operations in the sense
that existing models may have objects that relate to
the structure of the operands (i.e. the classes). That is,
addClass, addInterfaceClass, addProp, addOp and
addBiProp deal with adding new metaelements for
which no existing objects relate to. Still, it may be re-
quired to generate default objects of added structure.
We will return to this later.
A sequence of adaptation operations, ϕ
1
· ϕ
2
·
··· · ϕ
n
, defines an adaptation strategy Φ for a par-
ticular metamodel adaptation. An adaptation strat-
egy can be seen as a description that differentiates
one metamodel variant from another. The adapta-
tion strategy and sequence of operations are given
by the user, e.g. as provided using a graphical tool
(i.e. not specified textually). Figure 4 gives a concep-
tual overview of the analysis framework and how two
metamodels are composed by using the merge oper-
ation. Specifically, the classes represented by filled
boxes are merged according to a merge strategy spec-
ified by the user. Notice the references to the classes
marked with x. The multiplicities have a lower bound
equal to 1, which indicates that objects of the classes
need to be created to have conformant models. We
will later see how this is addressed by the framework.
3.1 The Analysis Environment
The analysis environment for metamodel adaptations
consists of a tuple hE, σ, δi:
Definition 1. The environment mapping E maps class
names Nc to class definitions: E : Nc → Class, where
Class is a set of classes hNc, Inh, Prop, Opi. Nc is the
name of the class. Inh is a list of class names defining
class inheritance (direct superclasses). Prop is a set
of properties hType, Np, Multi, Cont, Oppi where Type
is a type, Np a property name, Multi the property’s
multiplicity comprising a lower and upper bound,
Cont describing whether the property is of contain-
ment type, and Opp the name of an optional op-
posite relation. Op is a set of class operations
hType, No, Parami where Type is the operation’s re-
turn type, No is the operation’s name and Param is a
list of input parameter declarations.
AFormalisationofAnalysis-basedModelMigration
89

Framework : Analysis
φ
adaptation strategy
σ
δ
name
mappings
object creation
specifications
MM
1
MM
2
MM
1-2
Environment
Environment’
1
1 1
x
x
x
x
x
x
1
1
1
Figure 4: Illustration of the analysis and the merge operation.
Dot notation is used to access the elements
of tuples such as properties and operations; e.g.
(C, I, P, O).Prop = P, where we use overlines to denote
sets or list structures. Prop(N) denotes a subset of
properties in Prop with name N and Prop.Np gives all
property names in Prop. Similar notation is used for
Op . The empty list is denoted ε.
Definition 2. The environment mapping σ consists of
a family of mappings hσ
c
, σ
p
, σ
o
i:
σ
c
: Nc → Nc
σ
p
: Np
Nc
→ Np
σ
o
: No
Nc
→ No
where Nc , N p and No are class, property and oper-
ation names, respectively. For σ
p
and σ
o
, Nc (above
the arrow) specifies the containing class of the prop-
erty and operation.
The family of mappings contains substitutions ac-
cumulated during the analysis of classes, properties
and operations, respectively. Substitutions are in-
troduced in the adaptation analysis to resolve con-
flicts associated with overlapping metamodel defini-
tions and will be used to ensure conformance for the
underlying models. A mapping family σ is built from
the empty mapping family
/
0.
Default objects have to be created of a property’s
type if the lower bound of its multiplicity is unequal to
zero. This is required to preserve conformance. It is
irrelevant if the property has a class type or primitive
type. A property implicitly has a multiplicity of 0..1
if no multiplicity is stated. δ contains tuples of the
form hNc, Np, Nati which maintain information of what
objects that have to be created in the existing models
as a consequence of new properties. Nc is the name
of the class whose objects will contain or refer objects
of Np’s type
1
. The number of objects that need to be
created is described by the natural number Nat, e.g. a
property with multiplicity 3..4 requires the creation of
three default objects to preserve conformance.
The adaptation analysis of a syntactic construct D
is formalised by a deductive system for judgements
1
The exact realisation of object containment is depen-
dent on the underlying implementation.
hE, σ, δi ` D hE
0
, σ
0
, δ
0
i, where hE, σ, δi is the analysis
environment before and hE
0
, σ
0
, δ
0
i is the environment
after the analysis of D, where E
0
represents a pack-
age containing the derived metamodel. For updating
the analysis environment, we use the associative op-
erator + on mappings with the identity element
/
0. Let
E + E
0
denote E overriden by E
0
. Mappings are now
formally defined.
Definition 3. Let n be a name, d a declaration, i ∈ I
a mapping index, and [n
c
7→
i
d] the binding of n to d
indexed by i. A mapping family σ is built from the
empty mapping family
/
0 and indexed bindings by the
constructor +. The extraction of an indexed mapping
σ
i
from σ and application for the mapping E , are de-
fined as follows
/
0
i
= ε
(σ + [n
c
7→
i
0
d])
i
= if i = i
0
then σ
i
+ [n
c
7→
i
d]
else σ
i
ε(n) = ⊥
(E + [n 7→ d])(n
0
) = if n = n
0
then d
else E(n
0
)
Assume given two well-typed metamodels, M M
1
and M M
2
. Since the metamodels are from two dif-
ferent domains, we assume unique class names (oth-
erwise, this can easily be resolved by package anno-
tations on class names). The environment E will ini-
tially contain well-typed class definitions from M M
1
and M M
2
and through a series of adaptation opera-
tions, we adapt or compose M M
1
and M M
2
, causing
modifications to E and σ, and additions to δ. The final
environment that is returned after the analysis is the
adapted metamodel(s) and the mappings constructed
during the analysis for resolving name conflicts (i.e.
substitutions generated by the framework) in addition
to a specification of objects that need to be created
due to property multiplicities with a non-zero lower
bound.
MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
90

(ADD CLASS)
E(C) = ⊥ E
0
= E +[C 7→ hε,
/
0,
/
0i]
E
0
, σ, δ ` addProp(C, P) · addOp(C, O)hE
0
, σ, δ
0
i
E, σ, δ ` addClass(hC, ε, P, Oi)hE
0
, σ, δi
(CLASS MERGE)
E(C) = hC, B, P, Oi E(C
0
) = hC
0
, B
0
, P
0
, O
0
i C 6= C
0
fresh(D) σ
0
= σ + [C 7→
c
D] + [C
0
7→
c
D]
σ
p
= anProp(E, C, C
0
) σ
o
= anOp(E, σ
0
, C, C
0
) σ
00
= σ
0
+ σ
p
+ σ
o
E
0
= [(E \{C, C
0
})]
σ
00
+ [D 7→ hD, B;B
0
, [P; P
0
]
σ
00
, [O; O
0
]
σ
00
i]
δ
0
= createInst(C, [P
0
]
σ
00
; f latten(E
0
, B
0
)) δ
00
= createInst(C
0
, [P]
σ
00
; f latten(E
0
, B))
E, σ, δ ` merge(C, C
0
)hE
0
, σ
00
, δ + δ
0
+ δ
00
i
(ADD SUPERCLASS)
E(C
0
) 6= ⊥ C 6= C
0
E(C) = hC, B, P, Oi E(C
0
) = hC
0
, B
0
, P
0
, O
0
i
σ
p
= anProp(E, C, C
0
) σ
o
= anOpInh(E, ε, C, C
0
)
σ
0
= σ
p
+ σ
o
δ
0
= createInst(C, P
0
; f latten(E
σ
0
, B
0
))
E, σ, δ ` addSuperClass(C, C
0
)h[E]
σ
0
+C 7→ hC, C
0
;B, [P]
σ
p
, [O]
σ
o
i, σ + σ
0
, δ + δ
0
i
(ADD INTERFACE CLASS)
isPrimitive(P) E, σ, δ ` addClass(hC, ε, P, Oi)hE
0
, σ, δi opposite(R )
∀(C
0
, P
00
) ∈ R · E
0
(C
0
) = hC
0
, B, P
0
, O
0
i ∧ P
00
.N p ∩ P
0
.N p =
/
0 ∧ createInst(C
0
, P
00
) = δ
00
uniqueProp(E
0
, P
00
, B) E
00
=
S
[C
0
7→ hC
0
, B, P
0
;P
00
, O
0
i] δ
000
=
S
δ
00
E, σ, δ ` addInterfaceClass(hC, ε, P, Oi, R )hE
0
+ E
00
, σ, δ + δ
000
i
(CLASS OVERRIDE)
E(C) = hC, B, P, Oi E(C
0
) = hC
0
, B
0
, P
0
, O
0
i ∀P ∈ P · P ∈ P
0
∀O ∈ O · O ∈ O
0
σ
0
= [C 7→
c
C
0
] σ
p
= anProp(E, C
0
, B) σ
o
= anOpInh(E , σ
0
, C
0
, B)
σ
00
= σ
0
+ σ
p
+ σ
o
E
0
= [(E \C)]
σ
00
+ [C
0
7→ hC
0
, B; B
0
, [P
0
]
σ
00
, [O
0
]
σ
00
i]
createInst(C, [P
0
\ P]
σ
00
; f latten(E
0
, B
0
)) = δ
0
createInst(C
0
, flatten(E
0
, B)) = δ
00
E, σ, δ ` override(C, C
0
)hE
0
, σ + σ
00
, δ + δ
0
+ δ
00
i
Figure 5: Definitions of the adaptation operations (rules) for class merging and additions. C and C
0
are class names.
(ADD PROPERTY)
isPrimitive(t) ∨ E (t) 6= ⊥ E(C) = hC, B, P, Oi uniqueProp(E, P,C)
P.Opp = ε E
0
= E +[C 7→ hC, B, P; P, Oi] createInst(C, P) = δ
0
E, σ, δ ` addProp(C, P)hE
0
, σ, δ + δ
0
i
(ADD BI-DIRECTIONAL PROPERTY)
P.Type = C
0
E(C) = hC, B, P, Oi uniqueProp(E, P, C)
P
0
.Type = C E(C
0
) = hC
0
, B
0
, P
0
, O
0
i uniqueProp(E, P
0
, C
0
)
P.Opp = P
0
.N p P
0
.Opp = P.N p E
0
= E +[C 7→ hC, B, P; P, Oi] + [C
0
7→ hC
0
, B
0
, P
0
;P
0
, O
0
i]
createInst(C, P) = δ
0
createInst(C
0
, P
0
) = δ
00
E, σ, δ ` addBiProp(C, P, C
0
, P
0
i)hE
0
, σ, δ + δ
0
+ δ
00
i
(ADD OPERATION)
∀t
0
∈ {t;O.Param} · isPrimitive(t
0
) ∨ E (t
0
) 6= ⊥ E(C) = hC, B, P, Oi
uniqueOp(E, O, C) E
0
= E +[C 7→ hC, B, P, O; Oi]
E, σ, δ ` addOp(C, O)hE
0
, σ, δi
Figure 6: Adaptation operations for adding new properties and operations. P and O are property and operation definitions and
C is used for class names.
3.2 The Adaptation Rules
Metamodels are adapted given an adaptation strategy
Φ, E of intitial metamodel definitions, an empty map-
ping σ, and an empty set of object creation specifica-
tions δ. Thus if E,
/
0,
/
0 ` Φ hE
0
, σ
0
, δ
0
i, then we derive
the resulting environment hE
0
, σ
0
, δ
0
i. The adaptation
rules are given in Figures 5 and 6. The involved oper-
ations are applied in a sequential manner as illustrated
in Rule (SEQ):
AFormalisationofAnalysis-basedModelMigration
91

anProp(E, C;C, B) = an(E, C, E(C).Prop, B) + anProp(E, C;E (C).Inh, B)
an(E, C, P; P, B) = an(E, C, P, B) + an(E , C, P, B)
an(E, C, P, ε) = ε
an(E, C, (t, P, m, c, P
i
), B; B) = if E(B).Prop(P) 6=
/
0 then [P
C
7→
p
P
0
] ∧ fresh(P
0
)
else an(E, C, (t, P, m, c, P
i
), B; E(B).Inh)
anOp(E, σ, C, C
0
) = anMerge(E, σ, C
0
, C, E (C).Op, C
0
) + anOpInh(E , σ, E(C).Inh, C
0
)
anOpInh(E, σ, C;C, B) = anCl(E, σ, C, E (C).Op, B) + anOpInh(E , σ, C; E (C).Inh, B)
anCl(E, σ, C, O; O, B) = anCl(E, σ, C, O, B) + anCl(E, σ, C, O, B)
anCl(E, σ, C, O, ε) = ε
anCl(E, σ, C, (t, O, (t
i
P
i
)), B; B) = if [type(E(B).Op(O).Param)]
σ
= [t
i
]
σ
then
if [E(B).Op(O).Type]
σ
= [t]
σ
then ε
else [O
c
7→
o
O
0
] ∧ fresh(O
0
)
else anCl(E, σ, C, (t, O, (t
i
P
i
)), B; E(B).Inh)
anMerge(E, σ, C
0
, C, O; O, B) = anMerge(E, σ, C
0
, C, O, B) + anMerge(E, σ, C
0
, C, O, B)
anMerge(E, σ, C
0
, C, O, ε) = ε
anMerge(E, σ, C
0
, C, (t, O, (t
i
P
i
)), B; B) = if [type(E(B).Op(O).Param)]
σ
= [t
i
]
σ
then
if B = C
0
then [O
c
7→
o
O
0
] ∧ fresh(O
0
)
else if [E(B).Op(O).Type]
σ
= [t]
σ
then ε
else [O
c
7→
o
O
0
] ∧ fresh(O
0
)
else anMerge(E, σ, C
0
, C, (t, O, (t
i
P
i
)), B; E(B).Inh)
Figure 7: Definition of the auxiliary functions anOp and anProp.
(SEQ)
E, σ, δ ` [ϕ
1
]
σ
hE
1
, σ
1
, δ
1
i
E
1
, σ
1
, δ
1
` [ϕ
2
]
σ
1
hE
2
, σ
2
, δ
2
i
E, σ, δ ` ϕ
1
· ϕ
2
hE
2
, σ
2
, δ
2
i
The analysis environment propagates throughout the
analysis, i.e. ϕ
2
is analysed in the context result-
ing from the analysis of ϕ
1
. Note that the substi-
tution, denoted [ϕ]
σ
, rewrites ϕ into normal form in
Rule (SEQ). σ is accumulated through sequential anal-
ysis of the adaptation operations, thus the substitu-
tion is deterministic; the rule substitutes input class,
property and operation names by mappings in σ be-
fore retrieving or updating class information and thus
ensures that class definitions from the latest environ-
ment are used in each basic rule application. By tran-
sitivity a sequence of class mergings is possible, e.g.
[X]
[X7→
c
Y ]+[Y 7→
c
Z]+[Z7→
c
V ]
maps the class named X to V .
Rules for metamodel composition and class addition
are given in Figure 5. In Rule (ADD CLASS) the anal-
ysis environment is extended with a new class def-
inition that is previously not defined. Rule (CLASS
MERGE) merges two classes C and C
0
into a class given
a fresh name D, represented by fresh(D). The new
class will replace C and C
0
in the analysis environ-
ment, hence the rule redirects references by creating
mappings from the old classes to D. We assume that
metamodels are well-typed prior to adaptation. How-
ever, it is likely that overlapping definitions occur
when classes are merged, which introduce type errors.
Consequently, the rule will consider and resolve over-
lapping definitions that exist between the classes, i.e.
C and C
0
, and their superclasses. The auxiliary func-
tions anProp and anOp (given in Figure 7) traverse
the inheritance tree and resolve conflicts so that all
property names are unique within the resulting class
hierarchy, and that equally named operations with the
same input types have the same return type. Map-
pings containing information of resolved conflicts are
returned from the application of the rule (σ
00
). Finally,
the class definition for D is constructed by specifying
the superclasses of both C and C
0
, and adding sets of
conflict-free properties and operations, i.e. [P; P
0
]
σ
00
and [O; O
0
]
σ
00
, respectively. The class D is added to E
0
whereas C and C
0
are removed. As other classes in E
may still have old references to C and C
0
, these classes
must also be updated. Consequently, we apply the
substitution mapping σ
00
on E when creating the new
environment (e.g. hN, I, (C
0
, P, m, c, P
i
);P, Oi
[C
0
7→
c
D]
→
hN, I, (D, P, m, c, P
i
);P, Oi). Moreover, σ
00
also contains
information of resolved conflicts in superclasses, thus
these superclasses must also be updated to ensure
well-typedness of the modified class hierarchy. cre-
ateInst is a function that builds specifications of de-
fault objects that need to be created to preserve con-
formance. We have to ensure that existing models
with objects of C or C
0
will have required objects as
imposed by properties with a lower bound unequal to
zero as reachable through D. That is, properties of
D, B and B
0
. createInst does only specify the small-
est number of required default objects needed to en-
sure conformance. flatten returns a set of all proper-
ties found in the set of classes given as argument and
their respective superclasses. The environment after
the application of (CLASS MERGE) is hE
0
, σ
00
, δ + δ
0
+ δ
00
i.
Note that we can not merge attributes with the same
names because these attributes may not represent the
same concept from an ontological perspective, i.e. the
attributes may describe different domain entities.
Rule (ADD SUPERCLASS) extends class C with a new
superclass C
0
and overrides the old class definition.
Similar to Rule (CLASS MERGE), the class hierarchy is
traversed and conflicting definitions are resolved. The
MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
92

resulting environment contains an updated version of
C that replaces the previous version of the class. In
particular, C additionally inherits from C
0
.
Rule (ADD INTERFACE CLASS) creates a new class (by
Rule (CLASS UNION)) and constructs references between
this and existing classes in the environment. oppo-
site verifies that bi-directional relationships are cor-
rectly specified in R . As there are no name conflicts,
the mapping σ remains unchanged after the analysis.
Rule (CLASS OVERRIDE) allows a class C
0
to override a
class C if C
0
subsumes C. Finally, rules for extending
classes with new operations and properties are given
in Figure 6.
As mentioned, since operations addClass, addIn-
terfaceClass, addProp, addOp and addBiProp add
new metaelements, there are no existing models that
refer to these elements. Consequently σ, which is
later used to update existing models, remains un-
changed for these operations. Rule (ADD PROPERTY) adds
a new primitive- or class-typed property to an existing
class. In contrast to Rule (ADD BI-DIRECTIONAL PROPERTY),
this rule addresses properties without an opposite re-
lation. Rule (ADD BI-DIRECTIONAL PROPERTY) adds a bi-
directional relationship between two classes and ver-
ifies that its constituent uni-directional relationships
are correct. Rule (ADD OPERATION) adds a new opera-
tion to a class. For the rules in Figure 6, uniqueProp
ensures that the new property is not previously de-
fined within super- or subclasses in the class hierarchy
and uniqueOp verifies correct overloading of the new
operation. See the requirements for well-typedness
stated in Section 3. Notice that we do not resolve con-
flicts when new structure is added to the environment.
As before, createInst creates a set of specifications for
objects that need to be created to ensure conformance.
3.3 Example Revisited
We revisit the example introduced in Sec. 2 and show
how the analysis framework addresses composition of
the metamodels, resulting in the metamodel in Fig-
ure 3. We show the intermediate analysis steps and
use the following abbreviations for class names: M
for Merchandise, ROS for RightsOwnership, BC for Busi-
nessContext and PS for ProfitShare. In the example we
will consider the adaptation strategy given in Figure 8.
The adaptation strategy comprises two operations: a
merge operation and an addInterfaceClass operation.
Φ = merge(M, BC) ·
addInter f aceClass(hPS, ε, h(Real, percent, (1, 1))i, εi,
(M, h(PS, pro f itShares, (1, ∗))i),
(PS, h(ROS, stakeholders, (1, ∗))i))
Figure 8: The adaptation strategy used in the example.
E = hhM, ε, h(String, id)i, h(String, f ormat)ii,
hBC, ε, h(String, id), (String, region), (String, country, (1, 1))i,
h(String, f ormat)ii,
hROS, ε, h(Real, value), (String, f irm), (String, country), εii, ...i
σ = δ =
/
0
Figure 9: The initial environment.
Figure 9 gives the initial environment which con-
sists of all classes from the two metamodels, e.g. the
M, BC and ROS classes. As can be read from the fig-
ure, M has no superclass, an attribute id of type String
and an operation format with type String as well. The
BC class has no superclass, three attributes and one
operation. Notice the lower bound in the multiplicity
for the country attribute, which is 1. This means that
an object of the BC class needs to have a value for this
attribute. The other two attributes in the class have a
0..1 multiplicity by default. Finally, the ROS class has
no superclass and three attributes.
The first operation in the adaptation strategy spec-
ifies that the M and BC classes should be merged.
Merging the two classes yields a new class with the
name MBC
2
. Merging of classes requires collecting in-
formation about the constituent classes of the merging
operation. In this case, two mappings are created and
stored, see Figure 10.
E, σ, δ ` merge(M, BC)hE
0
, σ
0
, δ
0
i
E
0
= hhMBC, ε, h(String, #id), (String, id), (String, region),
(String, country, (1, 1))i, h(String, # f ormat), (String, f ormat)ii,
hROS, ε, h(Real, value), (String, f irm), (String, country)i, εi, ...i
σ
0
= [M 7→
c
MBC] + [BC 7→
c
MBC] + [id
M
7→
p
#id] +
[ f ormat
M
7→
o
# f ormat]
δ
0
= hhM, country, 1ii
Figure 10: The result of analysing the merge operation.
The first mapping binds the name M with MBC and
the other mapping binds the name BC with MBC. Fur-
thermore, equally named properties in the two classes
need to be addressed, otherwise, this will result in a
name conflict. The classes M and BC both have a prop-
erty named id. Hence, the id property in the M class is
given the new name #id by the anProp function (#id
represents the new name for the id property). This re-
naming is also reflected by creating a new name map-
ping. The two classes also have an equally named
operation. This name conflict is handled in a simi-
lar manner as for the id property. We use the notation
id
M
7→
p
#id for specifying that the name of the property
id is mapped to the name #id in the M class.
Notice how an object creation specification is con-
structed since BC has an attribute country whose lower
bound is 1. Hence, existing product models need to
2
The name chosen is decided by the implementation.
AFormalisationofAnalysis-basedModelMigration
93

be updated with a value for this attribute in objects
of MBC (previously M). Finally, a new environment
is constructed and superfluous classes, that is M and
BC, are removed. Note that the new environment still
contains the remaining unaffected classes of the two
metamodels.
The next step is analysis of the addInterfaceClass
operation, refer Figure 8 for details on how the addIn-
terfaceClass operation is specified. First, a new class
named PS is added to the environment. The purpose
of this class is to bridge the MBC and RightsOwnership
classes, see Figure 3. Second, a selection of classes
in the environment is revised. Specifically, the classes
relating to the PS class, and potentially the PS class
itself, are updated with class references. Notice how
the accumulated mapping of [M 7→
c
MBC] has been ap-
plied (by SEQ) before the analysis by the (ADD INTERFACE
CLASS) rule. Thus, even though the addInterfaceClass
operation refers to M, the name mapping ensures that
the MBC class is used in the analysis. Also, pay note of
how the createInst function is applied to specify gen-
eration of default objects of the PS and ROS classes,
which is required since these classes are related to
by the references profitShares and stakeholders, respec-
tively. Both of these references have a non-zero lower
bound in their multiplicity.
E
0
, σ
0
, δ
0
` addInter f aceClass(hPS, ε, h(Real, percent)i, εi,
((MBC, h(PS, pro f itShares, (1, ∗))i),
(PS, h(ROS, stakeholders, (1, ∗))i))hE
00
, σ
00
, δ
00
i
createInst(MBC, h(PS, pro f itShares, (1, ∗))i) =
hMBC, pro f itShares, 1i
createInst(PS, h(ROS, stakeholders, (1, ∗))i) =
hPS, stakeholders, 1i
E
00
= hhMBC, ε, h(String, id), (String, #id), (String, region),
(String, country, (1, 1)), (PS, pro f itShares, (1, ∗))i,
h(String, # f ormat), (String, f ormat)ii,
hROS, ε, h(Real, value), (String, f irm), (String, country),
(PS, stakeholders, (1, ∗))i, εii, hPS, ε, h(Real, percent)i, εi, ...i
σ
00
= [M 7→
c
MBC] + [BC 7→
c
MBC] + [id
M
7→
p
#id] +
[ f ormat
M
7→
o
# f ormat]
δ
00
= hhM, country, 1i, hMBC, pro f itShares, 1i, hPS, stakeholders, 1ii
Figure 11: The final environment, mappings and object cre-
ation specifications.
The final environment, hE
00
, σ
00
, δ
00
i, can be seen
in Figure 11. The enviroment E
00
corresponds to the
metamodel in Figure 3 and contains updated versions
of the classes MBC and ROS, the new PS class, and all
remaining unaltered classes of the constituent meta-
models. δ has been updated to indicate that a default
object has to be created by both PS (profitShares is
typed with PS) and ROS (stakeholders is typed with
ROS) for all existing models that contain objects of
MBC (M and BC). Notice that it does not exist any mod-
els with objects of PS (since this is a new class), how-
ever, since MBC has a property typed with PS whose
lower bound is 1, this requires creation of an object of
PS in all existing models previously conforming to ei-
ther of the two metamodels. This in turn requires cre-
ation of default objects of ROS since PS has a property
typed with ROS whose lower bound is 1 as well.
4 CONFORMANCE
We use the definition of conformance as given in
(Henderson-Sellers, 2012). A model M conforms to
a metamodel M M if all objects in the model are clas-
sified by one concept in the metamodel. A concept
is described by a class. Γ denotes a classification ab-
straction. The extension of a concept, ε(C), is defined
by a set of predicates that characterise the same el-
ements. The set of these predicates is known as the
intension of the concept - ι(C).
Definition 4. A model M conforms to a metamodel
M M , denoted conformsTo(M , M M ), iff. M M is
well-typed and:
∀
i
o
i
∈ M , ∃
j
C
j
∈ M M such that o
i
Γ C
j
, where
o
i
Γ C
j
⇔ o
i
∈ ε(C
j
) , and
ε(C) = {x|P(x)} where P = ι(C)
Based on the definition of conformance we have
the following property:
Lemma 1. Let M M
1
and M M
2
be well-
typed metamodels, M a model, and E con-
tains all classes in M M
1
and M M
2
. If
conformsTo(M , M M
1
), then conformsTo(M , E).
Similarly, if conformsTo(M , M M
2
), then
conformsTo(M , E).
As the considered adaptation operations do not re-
move classes, operations or properties, or change their
type declarations, well-typedness is preserved for the
resulting metamodel.
We show that with an adaptation strategy Φ for
metamodel adaptation and the accumulated effects σ
and δ, the associated models can be updated so that
they conform to the altered metamodel. Figure 12
illustrates this for the merge operation. The figure
contains a model of each of the metamodels given in
Figure 4. The circles illustrate model objects. No-
tice how default objects are created to satisfy confor-
mance according to non-zero lower bound multiplici-
ties in the metamodels. Thus, two default objects are
required to be added to the M
a
model for this model
to conform to the MM
1−2
metamodel. Similarily, a de-
fault object has to be added to the M
b
model for this
to conform to MM
1−2
.
The semantics of model evolution is described
by the transform function, see Figure 13. Let
MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
94
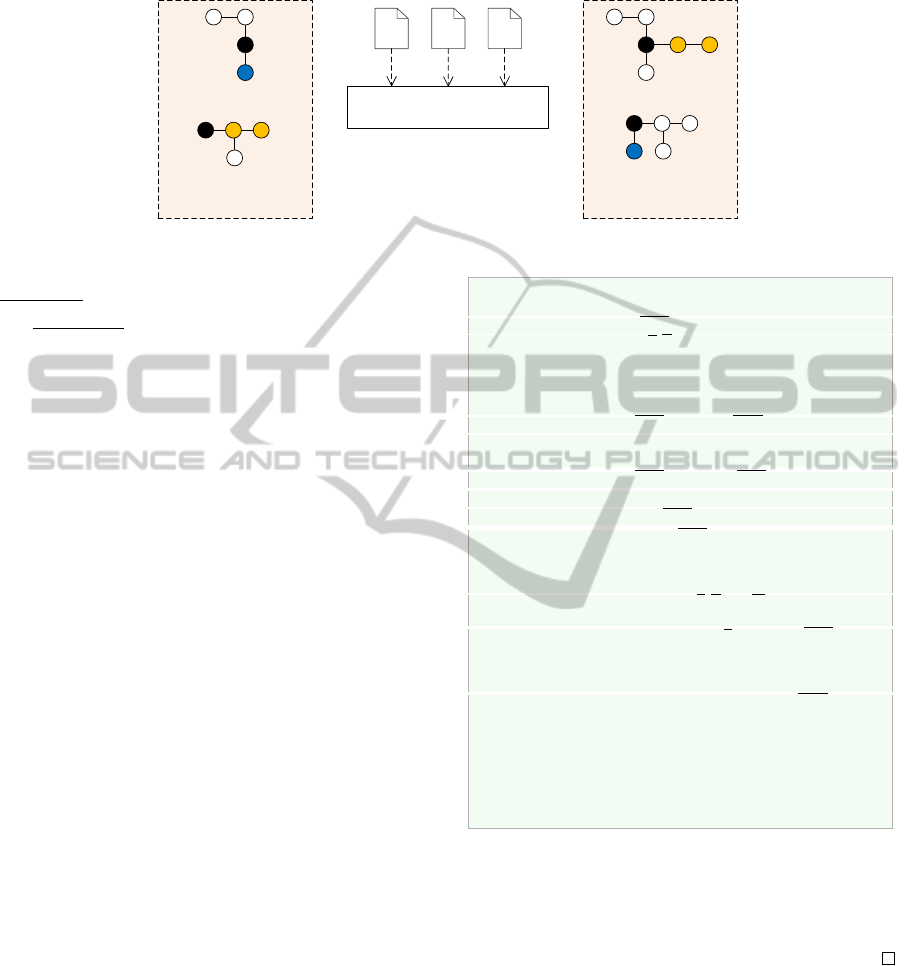
Framework : Conformance
σ
δ
name
mappings
object creation
specifications
M
a
: MM
1
M
b
: MM
2
M
a
: MM
1-2
M
b
: MM
1-2
φ
adaptation
strategy
Model Repository’
Model Repository
Figure 12: Illustration of how conformance is re-established.
pro j
c
(σ
p
) return property mappings for class C, i.e.,
[N p
c
→ N p] and pro j
c
(δ) object creation specifications,
i.e. hC, N p, Nati. createObj produces objects as spec-
ified by δ. Object creation is only performed if the
containing object does not already contain/refer these
objects. A class may have a reference with a non-
zero lower bound that is typed with a class that con-
tains a reference with a non-zero lower bound to the
first class. That is, there are two references between
a pair of classes where both references have a non-
zero lower bound. In this case, and in similar more
comprehensive cases, the algorithm/function will not
terminate. This may be addressed by reusing already
created objects of the classes. update creates a new
version of the given object. We show an excerpt of
the function, the rest is defined in a similar manner.
Theorem 1. Let M M
1
and M M
2
be well-
typed metamodels, and let E contain all
classes in M M
1
and M M
2
, and M an arbi-
trary model such that conformsTo(M , M M
1
) or
conformsTo(M , M M
2
). Let Φ be an adaptation
strategy such that E,
/
0,
/
0 ` Φ hE
0
, σ, δi, then we have
conformsTo(transform(M , Φ, σ, δ), E
0
).
Proof sketch. The proof is by induction over the
length of the adaptation strategy Φ and then by
cases. By Lemma 1 we have conformsTo(M , E)
and show that if E,
/
0,
/
0 ` ϕ
o
··· ϕ
i
hE
0
, σ, δi
and conformsTo(transform(M , ϕ
o
··· ϕ
i
, σ, δ), E
0
)
then if E
0
, σ, δ ` ϕ
i+1
hE
00
, σ
0
, δ
0
i, then
conformsTo(transform(M , ϕ
o
··· ϕ
i+1
, σ
0
, δ
0
), E
00
). Let o
be an object in M and show that o remains a valid
instance of its class after each adaptation step that
modifies E. We show that properties and operations
are analysed which yields name mappings specified
in σs. The mappings are used to update affected
property name references (slots) in o. Hence, renam-
ings, as a consequence of resolving name conflicts,
are reflected upon the objects of these classes. Values
for properties with a non-zero lower bound need to be
transform(M , ϕ
0
·· ·ϕ
n
, σ, δ ) : M
let transform(ϕ
i
·· ·ϕ
n
)
for each object hoid : N, (P, v)i ∈ M do
if ϕ
i
== addClass(hC, ε, P, Oi) // No action − no objects exist
if ϕ
i
== merge(C, C’)
σ
0
= pro j
c
(σ
c
); pro j
c
0
(σ
c
)
if N == C then
update(M , hoid : [C]
pro j
c
(σ
c
)
,
createOb j((P, v), pro j
c
(δ));[(P, v)]
pro j
c
(σ
p
);σ
0
i)
else if N == C
0
then
update(M , hoid : [C
0
]
pro j
c
0
(σ
c
)
,
createOb j((P, v), pro j
c
0
(δ));[(P, v)]
pro j
c
0
(σ
p
);σ
0
i)
else if (C subClassOf N) or (C
0
subClassOf N) then
update(M , hoid : N, [(P, v)]
pro j
N
(σ
p
);σ
0
i
else update(M , hoid : N, [(P, v)]
σ
0
i)
[ϕ
i+1
·· ·ϕ
n
]
σ
0
if ϕ
i
== addInterfaceClass(hC, ε, P, Oi, (D, P
0
) ∪ R )
if N = D then
update(M , hoid : N, createOb j(P
0
, pro j
D
(δ));(P, v)i)
if ϕ
i
== addProp(C, P)
if N = C then
update(M , hoid : N, createOb j(P, pro j
N
(δ));(P, v)i)
...
endfor
tranform(ϕ
i+1
·· ·ϕ
n
)
in
transform(ϕ
0
·· ·ϕ
n
)
end
return M
Figure 13: The transform function.
created, and this is ensured by createInst, where the
required type of objects and their respective counts
are determined based on information in δs.
4.1 Example Revisited
In Section 3.3 we showed how the product/merchan-
dise metamodel and business context metamodel were
combined by applying a simple adaptation strategy
Φ involving merge and interfacing operations. Con-
sequently, all existing product and business context
models should now be considered as models of the
composite metamodel. In order to re-establish con-
formance between existing models and the composite
AFormalisationofAnalysis-basedModelMigration
95

metamodel, existing models must be updated as spec-
ified by the the mappings in σ
00
, and default object
specifications in δ
00
.
Figure 14 shows how two existing models of
the product and business context metamodels, re-
spectively, are updated to ensure conformance with
the composite metamodel. In particular, trans-
form(M , Φ, σ
00
, δ
00
) updates objects of M and BC to be
valid instances of MBC, values of the attribute id in
M to be values of #id, and creates a default value for
country in all objects that were previously instances
of class M, as well as default objects for PS and ROS
in all existing models. As the objects do not contain
any references to operations, no changes are required
for the renaming of the format operation in M. Clearly,
we are aware that the default values and objects may
have to be updated to reflect the domain, e.g. a correct
value of country has to be specified. However, such
considerations are outside the scope of our work.
5 RELATED WORK
One approach for automatic metamodel evolution is
discussed in (Wachsmuth, 2007). The work is in-
spired by object-oriented refactoring, and is based on
a stepwise adaptation of metamodels using transfor-
mations. Three different types of transformations are
used to achieve this: refactoring (e.g. renaming of
an element), construction (e.g. adding a new class or
property) and destruction (e.g. removing a class or
property). The paper also discusses how models may
be co-adapted by defining transformations that work
on models. The work of our paper resembles that of
(Wachsmuth, 2007). We have defined a set of basic
operations that can be combined arbitrarily to define
adaptation strategies. We take things a step further by
formally defining all operations and proving that con-
formance are preserved after adaptation. Also, our ap-
proach uses analysis as a prerequisite for supporting
parallel evolution of an arbitrary number of metamod-
els.
(Ruscio et al., 2012) discusses how artefacts in the
metamodelling ecosystem are impacted when meta-
models evolve. In particular, the paper discusses how
adaptation of artefacts should be facilitated inherently
by the metamodel definition. This way, artefacts
evolve directly as a consequence of metamodel evolu-
tion. It is argued that this perspective on co-evolution
is important in order for metamodels to freely evolve
without being constrained by required modifications
to other artefacts, which may be both complex and
expensive to perform. In our paper, we have seen
how the accumulated effects can be used to update
existing models. However, the effects are structured
in a way that supports co-adaptation of other artefacts
in the metamodelling ecosystem. Hence, our work
addresses the concerns put forward in (Ruscio et al.,
2012).
The proposed analysis of our paper can be sup-
ported by model migration processes such as the one
described in (Gruschko et al., 2007). The adapta-
tions to be analysed can be provided by a change
recorder (Gruschko et al., 2007) and model migra-
tions can be implemented using model transformation
languages such as QVT(ObjectManagementGroup,
2007), ATL(Jouault, 2005) and ETL(Kolovos et al.,
2006b)(Rose et al., 2010) where the analysis effects
give mappings/rules for how model elements from a
input model can be mapped to elements in a target
model. When creating an element, a transformation
may fail if a target metaclass is not defined (Gruschko
et al., 2007). Our static analysis prevents this and
ensures that execution of generated model transfor-
mations will succeed. Metamodel evolution can also
be described using visual languages such as the one
proposed in (Narayanan et al., 2009) where migration
rules are defined with a graphical syntax.
(Cicchetti et al., 2008b)(Herrmannsdoerfer et al.,
2009) discuss mechanisms for addressing co-
evolution using difference models and transactions,
respectively. The work of (Cicchetti et al., 2008a)
discusses how a difference model can be used to au-
tomatically create transformations that support co-
evolution of models. According to this work, a
difference model conforms to an extended KM3
meta-metamodel. Specifically, the KM3 meta-
metamodel has been revised with classes for express-
ing atomic modifications, e.g. reference added, at-
tribute changed or class added. By substracting one
metamodel from another it is possible to derive a dif-
ference model which gives all the changes required
to derive the one metamodel from the other. The
discussion differentiates between parallel indepen-
dent and parallel dependent modifications. Parallel
dependent modifications can, as the name suggests,
not be performed in parallel since the modifications
depend on each other. A difference model is de-
composed into breaking resolvable and unresolvable
changes. This in turn yields two types of transfor-
mations: transformations that can be automatically
generated and transformations that must be completed
with input from the user. An implementation is avail-
able for difference models containing parallel inde-
pendent changes, whereas a solution for parallel de-
pendent changes is sketched in the paper. The latter
is addressed by an iterative process that splits the dif-
ference models into submodels that only contain par-
MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
96

m
1
: M
id = "001"
p
1
: Product p
2
: Product
ros
1
: ROS ros
2
: ROS
ps
1
:
ProfitShare
m
1
: MBC
#id = "001"
country =
"Norway"
p
1
: Product p
2
: Product
ros
1
: ROS ros
2
: ROS
ros
3
: ROS
bc
1
: BC
country =
"Norway"
a
1
:
Availability
a
2
:
Availability
bc
1
: MBC
country =
"Norway"
a
1
:
Availability
a
2
:
Availability
ps
1
:
ProfitShare
ros
1
: ROS
conformsTo(M
M
, MM
M
) conformsTo(M
M+
, MM
MBC
)
conformsTo(M
BC
, MM
BC
)
conformsTo(M
BC+
, MM
MBC
)
transformation
transformation
Figure 14: Evolution of models to ensure conformance.
allel independent changes. Our approach resembles
that of (Cicchetti et al., 2008a). However, there are
some significant differences. First, our approach de-
rives effects directly from the analysis. The effects are
used as input for the transform function or for gen-
erating model-to-model transformations; instead of a
difference model. Second, we support adaptation op-
erations that create dependencies between an arbitrary
number of metamodels, yet ensure that conformance
is preserved for all existing models of all metamodels.
We have focused on breaking resolvable adaptations.
We support both parallel independent and parallel de-
pendent adaptation operations. The analysis verifies
that dependent operations are applied in an appropri-
ate sequence, as given by the user, which can be sup-
ported by an interactive editor.
The work of (Garcs et al., 2009) resembles that of
(Cicchetti et al., 2008a). The main difference is how
metamodels are matched using heuristics in order to
derive the difference model.
(Taentzer et al., 2012) and (Mantz et al., 2010) for-
malise metamodel evolution and model co-evolution
using category theory and graph transformations. In
contrast, we formalise the low-level operations that
typically emerge in metamodel/model co-evolution
senarios based on MOF-metamodels which are the
the most common metamodel formalisation used in
industry. Hence, our approach is closer to exist-
ing frameworks and tools. We have not found any
work that formalises metamodel/model co-evolution
and metamodel composition in a similar manner as
our approach.
6 CONCLUSION AND FUTURE
WORK
In this paper we have discussed a mechanism for
metamodel adaptation and showed how model con-
formance can be preserved when metamodels are
adapted and modified, e.g. composed. We formalised
metamodel adaptation operations and addressed co-
evolution of models. We also proved that confor-
mance can be re-established between models and their
altered metamodels.
In the proposed framework, conflicts during merg-
ing of classes are remedied by renaming and not re-
solved from an ontological perspective. We fore-
see that considering ontological knowledge as part of
the analysis would refine the adaptation mechanism,
where adaptation of metamodels can be tuned by util-
ising domain knowledge, e.g. classes representing the
same type of domain concepts may be merged, etc.
This way we would also address matching of classes
prior to merging.
We addressed how the accummulated effects can
be used to update models. These effects can also
be used to update existing tools and model-to-model
transformations that are defined according to the con-
stituent metamodels. This can be achieved by defin-
ing a similar algorithm as described for model co-
evolution by the transform function. We have fo-
cused on model structure, and not considered adap-
tation of language semantics, which we consider as
future work.
REFERENCES
Cicchetti, A., Di Ruscio, D., Eramo, R., and Pierantonio,
A. (2008a). Automating co-evolution in model-driven
AFormalisationofAnalysis-basedModelMigration
97

engineering. In Proc. of the Enterprise Distrubuted
Object Computing Conference (EDOC’08).
Cicchetti, A., Di Ruscio, D., Eramo, R., and Pierantonio,
A. (2008b). Meta-model differences for supporting
model co-evolution. In Proc. of the 2nd International
Workshop on Model-Driven Software Evolution.
Del Fabro, M. D. and Valduriez, P. (2007). Semi-automatic
model integration using matching transformations and
weaving models. In Proceedings of the 2007 ACM
Symposium on Applied Computing, pp.963-970. ACM.
Didonet Del Fabro, M., Bzivin, J., and Valduriez, P. (2006).
Weaving models with the eclipse amw plugin.
Favre, J.-M. (2004). Towards a basic theory to model model
driven engineering. In 3rd international workshop on
Software Model Engineering (WISME ’04).
Fleurey, F., Baudry, B., France, R., and Ghosh, S. (2008).
A generic approach for automatic model composition.
In Models in Software Engineering, LNCS vol. 5002,
pp.7-15. Springer.
Garcs, K., Jouault, F., Cointe, P., and Bzivin, J. (2009).
Managing model adaptatio by precise detection of
metamodel changes. In Proc. of the 5th European
Conference on Model Driven Architecture.
Gruschko, B., Kolovos, D., and Paige, R. (2007). Towards
synchronizing models with evolving metamodels. In
Workshop on Model-Driven Software Evolution.
Henderson-Sellers, B. (2012). On the Mathematics of
Modelling, Metamodelling, Ontologies and Modelling
Languages. Springer.
Herrmannsdoerfer, M., Benz, S., and Juergens, E. (2009).
Cope: Coupled evolution of metamodels and models
for the eclipse modeling framework. In ECOOP 2009
- Object-Oriented Programming. LNCS vol. 5653,
pp.52-76. Springer.
Herrmannsdoerfer, M., D. Vermolen, S., and Wachsmuth,
G. (2011). An extensive catalog of operators for the
coupled evolution of metamodels and models. In Soft-
ware Language Engineering, LNCS vol. 6563, pp.163-
182. Springer.
Jouault, F.and Kurtev, I. (2005). Transforming models with
atl. In Proc. of the Model Transformations in Practice
Workshop at MoDELS 2005. Springer-Verlag.
Kent, S. (2002). Model driven engineering. In Inte-
grated Formal Methods, LNCS vol. 2335, pp.286-298.
Springer.
Kolovos, D., Paige, R., and Polack, F. (2006a). Merging
models with the epsilon merging language (eml). In
Model Driven Engineering Languages and Systems,
LNCS vol. 4199, pp.215-229. Springer.
Kolovos, D. S., Paige, R. F., and Polack, F. A. C. (2006b).
Eclipse development tools for epsilon. In In Eclipse
Summit Europe, Eclipse Modeling Symposium.
Mantz, F., Rutle, A., Lamo, Y., Rossini, A., and Wolter, U.
(2010). Towards a formal approach to metamodel evo-
lution. In Nordic Workshop on Programming Theory.
Morin, B., Klein, J., and Barais, O. (2008). A generic
weaver for supporting product lines. In 13th interna-
tional workshop on Early Aspects (EA ’08), pp.11-18.
ACM Press.
Morin, B., Perrouin, G., Lahire, P., Barais, O., Van-
wormhoudt, G., and Jzquel, J.-M. (2009). Weav-
ing variability into domain metamodels. In Model
Driven Engineering Languages and Systems, LNCS
vol. 5795, pp.690-705. Springer.
Narayanan, A., Levendovszky, T., Balasubramanian, D.,
and Karsai, G. (2009). Automatic domain model mi-
gration to manage metamodel evolution. In Schrr,
A. and Selic, B., editors, MoDELS, volume 5795 of
LNCS. Springer.
ObjectManagementGroup (2007). MOF QVT Final
Adopted Specification. OMG.
ObjectManagementGroup (2014). Meta object facility
(mof) core specification.
Rose, L. M., Kolovos, D. S., Paige, R. F., and Polack, F.
A. C. (2010). Model migration with epsilon flock. In
Proc. of the Third International Conference on Theory
and Practice of Model Transformations, ICMT’10,
pages 184–198. Springer-Verlag.
Rose, L. M., Paige, R. F., Kolovos, D. S., and Polack, F.
A. C. (2009). An analysis of approaches to model mi-
gration. In Proceedings of the Models and Evolution
Workshop. ACM.
Ruscio, D. D., Iovino, L., and Pierantonio, A. (2012).
Evolutionary togetherness: How to manage cou-
pled evolution in metamodeling ecosystems. In In:
Graph Transformations. LNCS vol. 7562, pp.20-37.
Springer.
Seidewitz, E. (2003). What models mean. In IEEE Soft-
ware, vol. 20, no. 5, pp.26-32.
Steel, J. and Jzquel, J.-M. (2007). On model typing. In
Software and Systems Modeling, vol. 6, no. 4, pp.401-
413. Springer.
Taentzer, G., Mantz, F., and Lamo, Y. (2012). Co-
transformation of graphs and type graphs with appli-
cation to model co-evolution. In In: Graph Transfor-
mations, LNCS vol. 7562, pp.326-340. Springer.
TheEclipseFoundation (2014). Eclipse modeling frame-
work (emf).
Wachsmuth, G. (2007). Metamodel adaptation and model
co-adaptation. In ECOOP 2007 - Object-Oriented
Programming. LNCS vol. 4609, pp.600-624. Springer.
MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
98
