
Perceptually Weighted Compressed Sensing for Video Acquisition
Sawsan A. Elsayed and Maha M. Elsabrouty
Electronics and Communication Engineering, Egypt-Japan University of Science and Technology (EJUST),
New Borg El-Arab City, Alexandria, Egypt
Keywords: Compressed Sensing, Video Acquisition, Perceptual Weighting, Human Visual System (HVS).
Abstract: Efficient video acquisition and coding techniques have received increasing attention due to the wide spread
of multimedia telecommunication. Compressed Sensing (CS) is an emerging technology, which enables
acquiring video in a compressed manner. CS proves to be very powerful for energy constrained devices that
benefit from processing at lower sampling rates. In this paper, a framework for compressed video sensing
(CVS) that relies on an efficient fixed perceptual weighting strategy is adopted for acquisition and recovery.
The proposed compressed sensing strategy focuses the measurements on the most perceptually pronounced
coefficients. Three weighting schemes are developed and compared with standard CS. Simulation results
demonstrate that the proposed framework provides a significant improvement in its three different setups over
standard CS in terms of both standard and perceptual objective quality assessment metrics.
1 INTRODUCTION
Source coding techniques aim to reduce statistical
redundancies inherited in the signal under concern.
Traditional coding methods achieve this task by first
acquiring the full signal at Nyquist rate, then
transforming it to a suitable sparse domain, where the
highest values coefficients are to be entropy coded
and transmitted. In recent video coding standards,
perceptual properties of the human have played an
increasing role as an intrinsic measure of redundancy.
The aim of perceptual coding is to transmit only the
most important perceptual coefficients. One aspect of
Human Visual System (HVS) that is exploited in
recent coding standards such as H.264/MPEG-4 AVC
(ITU-T 2003), and H.265/HEVC (Sullivan et al.
2013) is that the sensitivity of human eyes to low
frequency components is larger than high frequency
ones. A survey and recent developments on
perceptual video coding techniques can be found in
literature (e.g., Lee and Ebrahimi 2012, Lin and
Zhang 2013).
Despite the efficiency of the legacy video coding
systems, they still suffer from the unresolved
obligation to sample the signal at the Nyquist rate.
This means that high storage capacity is required.
However, only small part of coefficients will be
transmitted. This rather high sampling rate represents
an obstacle for resource constrained acquisition
devices.
Compressed Sensing (CS), first proposed by
Donoho (2006), is an emerging theory that comes
with a non-conventional solution to this problem. CS
theory promotes accurate signal recovery using a
much lower sampling rate compared to the Nyquist
rate. This is guaranteed for signals that have sparse or
compressible representation in some domain. CS has
found a remarkable potential in many diverse fields
(Qaisar et al. 2013), especially for multimedia
acquisition and sampling. CS enables sensing directly
in a compressed manner. Hence, it proves to be very
beneficial for resource limited devices as mobile
cameras or sensor nodes in wireless sensors networks
(WSN).
Weighted
- minimization techniques are
proposed in literature (e.g., Candes et al. 2008,
Friedlander et al. 2011), to improve CS signal
recovery by assigning different weights to different
signal components according to their importance.
Mansour and Yilmaz (2012) proposed adaptive CS
system for video acquisition in which previously
reconstructed frames are utilized to draw an
estimation about the support of subsequent frames.
This estimated support is fed back from the decoder
to the encoder to focus the measurements of
subsequent frame on the most probable non-zero
coefficients. Then, weighted
- minimization
209
A. Elsayed S. and M. Elsabrouty M..
Perceptually Weighted Compressed Sensing for Video Acquisition.
DOI: 10.5220/0005243302090216
In Proceedings of the 5th International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2015), pages
209-216
ISBN: 978-989-758-084-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

recovery is used at the decoder to focus the recovery
on this estimated support components.
Perceptual-based CS system for images, utilizing
block-based 2D-DCT sparsity basis, has been
introduced recently (Yang et al. 2009). In that work,
the image is first transformed to the transform
domain. Then, JPEG quantization tables are utilized
to derive the weighting coefficient for the encoding
process. Other perceptual based CS work that utilize
wavelet transform as sparsity basis has been also
presented (Lee et al. 2013). In that work, authors
utilize wavelet layered structure by applying different
measurement matrices and different weights for each
wavelet block.
In this paper, we employ perceptual features
inspired by recent video coding systems into the CS
framework aiming to low complexity video
acquisition and encoding system with improved
perceived quality. To this end, simple perceptual
based weighting strategy is adopted and embedded in
the sensing matrix and/or recovery algorithm.
Embedding the proposed weighting strategy in the
sensing matrix enables the proposed system to
directly acquire the most important perceptual
information from the video signal. Our strategy
mainly differs from previous adaptive and perceptual
CS work in that, our perceptual weights are fixed.
Consequently, the proposed system does not involve
weighting updates or feedback. We propose three
perceptual setups: applying perceptual weighting at
decoder side, at encoder side, and at both encoder and
decoder sides.
The rest of the paper is organized as follows:
Section 2 presents a brief theoretical background for
CS theory, and its application for video signals. The
proposed system is presented in Section 3. Section 4
is dedicated for presenting our simulation results.
Conclusion and future work are drawn in Section 5.
2 BACKGROUND
2.1 Compressed Sensing
Traditional coding techniques are based on an
overwhelmingly high sampling acquisition of the full
signal. CS theory guarantees accurate and robust
recovery for signals having sparse or compressible
representation in some basis with much lower
sampling rate than Nyquist rate.
Suppose the signal ∈ℝ
is to be acquired, CS
involves obtaining a vector ∈ℝ
, ≪ such
that:
=
(1)
Where ∈ℝ
is the sensing matrix. For accurate
recovery, the sensing matrix should satisfy some
properties
such as Restricted Isometry Property (RIP)
and incoherence (Donoho 2006). Random matrices
are proved to satisfy RIP and universal incoherence
with any fixed orthonormal basis.
The signal should be sparse or compressible in
some basis:
=
(2)
Where ∈ℝ
is the sparse transform coefficients of
in basis . Consequently:
==
(3)
Where =. It is required at the decoder side to
recover from , which is under-determined system
of linear equations. Many results (e.g. Candes et al.
2006a, Donoho 2006) show that solving general
-
minimization problem defined in (4) can stably and
robustly recover k-sparse signals form only ≥
..log
i.i.d Gaussian random measurements.
∗
=argmin
∈
ℝ
‖
‖
s.t.
‖
−
‖
≤ϵ
(4)
Where
∗
∈ℝ
is the optimal reconstructed sparse
representation of the signal, and
‖
.
‖
is the p
th
order
norm. If the signal has best k-term approximation
defined by
, the recovery error of (4) is governed by
the following equation (Candes et al., 2006b):
‖
∗
−
‖
≤C
.ϵ+C
.
‖
−
‖
√
k
(5)
For well- behaved constants
and
.
This means that, for compressible signals, the
recovery error is proportional to
−norm of
unconsidered coefficients. Moreover, collecting
measurements
=
, can improve the recovery
error (Mansour and Yilmaz 2012) .
With availability of prior information about signal
support, weighted
-minimization has been proved to
be an efficient way for enhancing signal recovery
(Friedlander et al. 2011). Let T
⊂ {1,2,….}
represent support estimation, and T
is its
complement. The recovery problem can be defined
as:
∗
=argmin
∈
ℝ
‖
‖
,
s.t.
‖
−
‖
≤ϵ
(6)
Where
‖
‖
,
=
∑
|
|
and the weight
coefficients vector is defined by:
=
,i∈T
1,i∈T
(7)
Where 0≤≤1. By applying smaller weights for
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
210

the estimated support coefficients, the recovery
algorithm forces the solution to focus on these
coefficients (Candes et al. 2008). Define support
accuracy =
⋂
, which is the accuracy of the
estimated T
with respect to original support T
. The
reconstruction error in this case can be given as
(Friedlander et al. 2011) :
‖
∗
−
‖
≤C
(
γ
)
+C
(
γ
)k
(
∩
+
∩
)
(8)
Equation (8) indicates that the recovery error
depends on the weights and support accuracy. Using
an accurate estimate of T
and well-adjusted weights,
the estimation error can decrease. In this paper, we
propose using a support estimate based on the human
eye sensitivity to different coefficients. The proposed
compressed sensing strategy aims to focus the error
in the less perceived coefficients.
2.2 Compressed Video Sensing
Video signals, despite having a huge quantity of data
pixels, are characterized with high correlation
between different pixels both in spatial and temporal
directions. Theoretically speaking, video signals have
nearly sparse (compressible) representation in some
domain. As such, CS is very suitable for acquisition,
coding, and transmission of video signals.
Compressed video sensing (CVS) has been shown to
be a practical alternative to traditional image and
video coding techniques with respect to resources and
measurements (Wahidah et al. 2011). Many
sparsifying transforms are proposed in literature such
as FFT, DCT, and Wavelet transforms (Sharma et al.
2012). DCT is commonly used in recent image and
video standard coding techniques. It proves efficiency
in representing most of the signal energy by small
number of non-zero coefficients. For its efficacy, 2D-
DCT/IDCT is utilized in our work as a sparsifying
basis for individual frames.
3 PROPOSED SYSTEM
One of the main features of human eye perception is
frequency discrimination. 2D-DCT/IDCT is
exploited here as sparsity basis. DCT basis has
structured sparsity and energy compaction properties.
The most important coefficients for human
perception, which are the low frequency coefficients,
are located in predetermined locations at top left
corner of 2D-DCT transform matrix. In addition to its
perceptual importance, low frequency coefficients
tend to have the largest values. Consequently,
perceptual based support estimation goes beyond
being a good guess of the location of the largest
coefficients in the actual signal. Fig. 1 shows one
frame of widely used Container video sequence
(Arizona State University 2014) at the top and its 2D-
DCT representation at the bottom. It can be seen that
most of the energy concentrated in low frequency
components at top left corner.
In the proposed algorithm, we follow the suit of
Mansour and Yilmaz (2012) in using weighting
coefficients for compressible signals. However, we
choose the support estimate to conform to the eye
perception properties. This choice proves to improve
the perceived quality of video signal. Let T
⊂
{1,2,….} represent the set of indices of the most
visually important coefficients, we can term it as
“visual support”. Support accuracy plays an
important role in enhancing the recovery performance
(Friedlander et al. 2011). The higher the support
accuracy, the higher the improvements achieved in
the reconstructed signal.
For example, empirical results show that our
support accuracy for T
= 0.2 is in range of 0.6
and 0.7. This means that the visual support estimate
in this case intersects with the actual support of the
signal with a percentage 60%-70% over all the
frames.
Three different setups can be used to embed visual
weighting in the compressed sensing and recovery
process. The first setup embeds perceptual weighting
at the decoder side only, the second setup utilize
perceptual weighting at the encoder side only, while
the third setup applying perceptual weighting at both
the encoder and decoder sides. Fig. 2 shows the
framework for the proposed three setups. To fully
exploit the support accuracy, the weights and support
sizes for the three setups are adjusted statistically
from a set of model tests. Their optimal values are as
shown in Table 1. The details for measurements and
recovery for the three setups are explained below.
3.1 Setup 1: Standard CS with
Perceptual Weighted Recovery
In this setup, standard measurements are obtained at
the encoder side while perceptually weighted
recovery is used at the decoder side. The
measurements are acquired as in (1). Then the signal
can be recovered by solving weighted
-
minimization problem (6). The weighting strategy
can be defined as in (7) replacing T
with visual
support estimate T
.
PerceptuallyWeightedCompressedSensingforVideoAcquisition
211
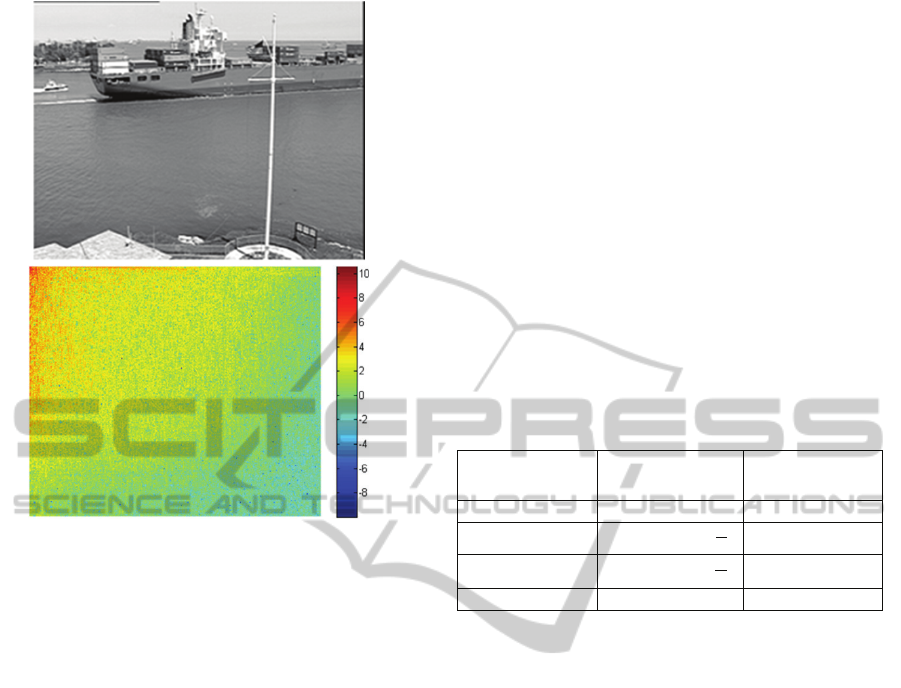
Figure 1: One video frame from Container sequence and its
2D-DCT transform coefficients.
3.2 Setup 2: Perceptual CS with
Standard Recovery
In this setup, the perceptual weighting is adopted at
the encoder side. While at the decoder side, standard
-minimization recovery is employed. The following
weighting strategy is adopted:
=
1,i∈T
,i ∈ T
(9)
According to (9), the coefficients related to the visual
support will be acquired fully. On the other hand, the
effect of the coefficients outside the visual support is
downplayed by factor . Define weight coefficients
matrix and perceptual weighting matrix as
follows:
=diag(
)
(10)
=
(11)
Hence the observation vector is represented as:
=
==
(12)
Where
= is the new sensing matrix, and
=
is visually weighted transform coefficients.
Then, the reconstructed signal can be obtained by
solving the following standard
- minimization
problem:
∗
=argmin
∈
ℝ
‖
‖
s.t.
‖
−
‖
≤ϵ
(13)
3.3 Setup 3: Perceptual CS with
Perceptual Weighted Recovery
In this setup, the observation vector is defined as in
(12):
=
. Then the recovery is done by solving
the following weighted
- minimization problem:
∗
=argmin
∈
ℝ
‖
‖
,
s.t.
‖
−
‖
≤ϵ
(14)
In this setup, the weighting strategy at the decoder
side is similar to Setup 1 which is defined by (7)
replacing T
with visual support estimate T
. While at
the encoder side, the weighting strategy is similar to
Setup 2 as defined by (9).
Table 1: List of different setups and optimal visual support
size and weights.
Sampling Scheme
Optimal visual
support size
Optimal weight
Standard Setup - -
Setup 1
0.085
.
0.3
Setup 2
0.058
.
0.1
Setup 3
0.85
0
4 SIMULATION RESULTS
The proposed perceptual compressed sensing setups
are applied to different test video sequences (Y
component of 4:2:0 sampling, 100 frames each). In
the following we present sample results. The video
sequences considered here are Container and News
(Arizona State University 2014), they are both CIF
resolution (352x288) with a frame rate of 30fps.
Random measurements are used for each individual
frame. Due to large scale nature for images, block
diagonal sensing matrix in which the diagonal is
populated with random sub-matrices is utilized (Park
et al. 2011). The dimension of each diagonal sub-
matrix is
x
, where
is block length, and
is
the number of measurements taken from each block.
Block length is selected in our system as
= 256.
2D-DCT for the full frame is utilized as sparsifying
transform. The recovery algorithm utilized here is
gradient projection for sparse reconstruction (GPSR)
(Figueiredo et al. 2007, 2009) with parameters
settings as: (initialization is done as
, debias
phase is on, continuation is on, and stopping criteria
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
212

(a)
(b)
(c)
Figure 2: Framework for different setups (a) standard CS with perceptual recovery, (b) Perceptual CS with standard recovery,
and (c) perceptual CS with perceptual recovery.
is when the relative change of objective function
reaches ToleranceA=0.001 for the first phase and
ToleranceD = 5x10
for debias phase). All
simulations are performed by MatlabR2013a
(MathWorks 2013). Two different quality assessment
metrics are used for performance evaluation, namely,
signal to noise ratio SNR and structural similarity
SSIM index. SNR is in dB and is defined by
(Friedlander et al. 2011):
SNR
(
,
∗
)
=10log
‖
‖
‖
−
∗
‖
(15)
Where is the original and
∗
is the recovered signal.
‖
‖
represents the energy of the original signal and
‖
−
∗
‖
represents the mean square error of the
recovered signal.
On the other hand, SSIM estimates the perceived
errors. It is consistent with human eye perception.
SSIM considers the perceived change in structural
information in the image (Wang et al. 2004a, 2004b).
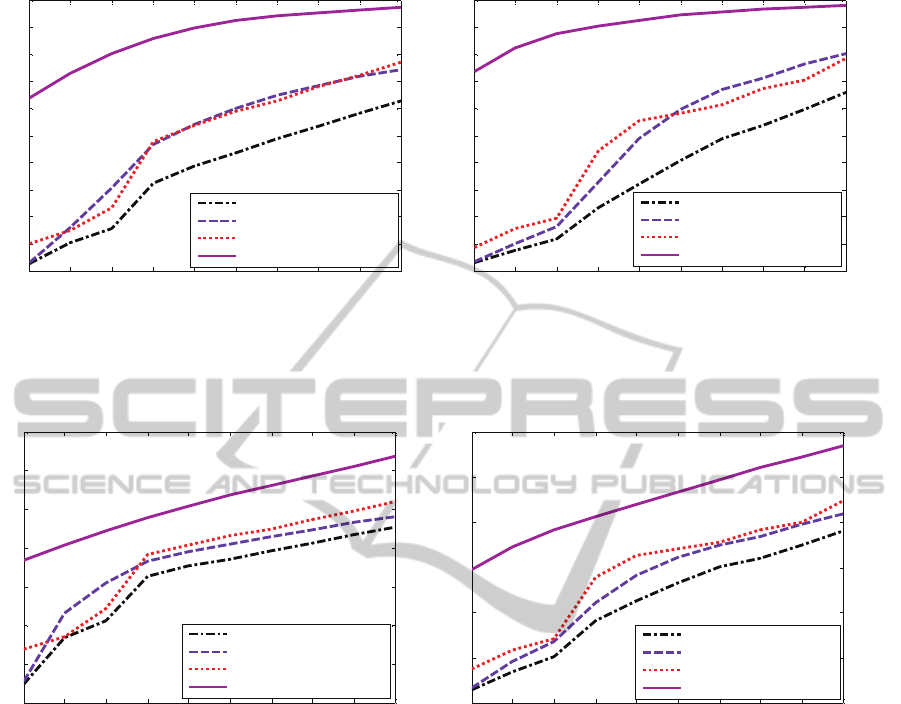
Fig. 3 and Fig. 4 show rate distortion (RD) curves in
terms of SSIM and SNR, respectively, for the
proposed three setups versus the standard CS for
Container and News video sequences. RD curves
show the performance of different systems with
different measurement rates (MRs).
The results show that applying perceptual weighting
at either the decoder side or the encoder side (Setups
1 and 2 respectively) improves the performance over
the standard CS scheme especially for higher
measurement rates. Moreover, applying perceptual
weighting at both the encoder and decoder sides
(Setup 3) has shown the best performance among all
setups with its most pronounced improvement at
lower measurement rates. Fig.3 shows that, at
MR=5% for example, while Setup 1 achieves no
SSIM gain over the standard CS for both video
sequences, Setup 2 achieves an SSIM gain of ~ 0.07
(7% of the full scale (FS)) for Container, and ~ 0.05
(5% of FS) for News. Moreover, Setup 3 achieves an
SSIM gain of ~ 0.61 (61% of FS) for Container and ~
0.7 (70% of FS) for News. Taking another point at
MR=25%, for example. For Container, both Setup 1
and 2 achieve an SSIM gain of ~ 0.15 (15% of FS)
and for News, Setup 1 and Setup 2 achieve an SSIM
gain of ~ 0.17 (17% of FS) and ~ 0.24 (24% of FS),
respectively. Moreover, at this sampling rate
(MR=25%), Setup 3 achieves an SSIM gain of ~ 0.51
(51% of FS) for Container and ~ 0.61 (61% of FS) for
News.
These results can be viewed from another angle.
Thinking of a system requiring a specified SSIM, the
PerceptuallyWeightedCompressedSensingforVideoAcquisition
213
(a) (b)
Figure 3: SSIM rate distortion curves for (a) Container sequence, and (b) News sequence, for different CS setups versus
standard CS scheme.
(a) (b)
Figure 4: SNR rate distortion curves for (a) Container sequence, and (b) News sequence, for different CS setups versus
standard CS scheme.
proposed setups are capable of achieving this SSIM
values with much lower measurement rates compared
to the standard CS scheme. For example, we can see
from Fig. 3 (a) that, for Container sequence, an SSIM
of 0.64 can be obtained using only 5% measurement
rate with Setup 3 and 32% for Setups 1 and 2, while
it requires more than 50% measurement rate for
standard CS to achieve the same SSIM value. Hence,
our proposed systems achieve better perceived video
quality using lower complexity acquisition devices.
In addition, proposed schemes also provide
significant improvements over the standard scheme in
terms of the SNR metric. Fig. 4 shows that, at
MR=5% for example, while Setup 1 achieves no SNR
improvement over standard CS for both video
sequences, Setup 2 achieves ~ 4.18 dB gain in case of
Container sequence and ~ 2.06 dB gain for News
sequence. Moreover, Setup 3 achieves ~ 15.62 dB
gain for Container sequence, and ~ 13.12 dB gain for
News sequence. For another point at MR=25% for
example, Setup 1 achieves gain of ~ 1.82 dB and ~
2.9 dB for Container and News sequences,
respectively. Setup 2 achieves gain of ~ 2.77 dB and
~ 5.06 dB for Container and News sequences,
respectively. Moreover, Setup 3 achieves gain of ~
7.77 dB and ~10.7 dB for Container and News
sequences, respectively.
In other terms, considering a system that require
certain SNR, our proposed setups are capable of
achieving this SNR values with much lower
measurement rates compared to the standard CS
scheme. For example, we can see from Fig. 4 (a) for
Container sequence that, an SNR of 18 dB can be
obtained using only MR=5% for Setup 3 and MR=
5 10 15 20 25 30 35 40 45 50
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Container video sequence
Measurements (%)
SSIM
StdCS-StdL1 (Standard CS)
StdCS-PercW L1 (Setup 1)
PercCS-StdL1 (Setup 2)
PercCS-PercWL1 (Setup 3)
5 10 15 20 25 30 35 40 45 50
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
News video sequence
Measurements (%)
SSIM
StdCS-StdL1 (Standard CS)
StdCS-PercWL1 (Setup 1)
PercCS-StdL1 (Setup 2)
PercCS-PercWL1 (Setup 3)
5 10 15 20 25 30 35 40 45 50
0
5
10
15
20
25
30
35
Container video sequence
Measurements (%)
SNR
StdCS-StdL1 (Standard CS)
StdCS-PercWL1 (Setup 1)
PercCS-StdL1 (Setup 2)
PercCS-PercWL1 (Setup 3)
5 10 15 20 25 30 35 40 45 50
0
5
10
15
20
25
30
News video sequence
Measurements (%)
S
NR
StdCS-StdL1(Standard CS)
StdCS-PercW L1 (Setup 1)
PercCS-StdL1 (Setup 2)
PercCS-PercWL1(Setup 3)
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
214

20% for Setups 1 and 2, while it requires 30% for the
standard CS scheme to achieve the same SNR value.
Consequently, our proposed systems can achieve
better video quality using lower complexity
acquisition devices.
5 CONCLUSION AND FUTURE
WORK
In this paper, an efficient perceptual weighting
strategy is adopted into CS framework for video
acquisition to improve the perceived quality of the
reconstructed signal. This goal has been achieved
through three different setups. The performance
evaluation for different setups demonstrates
remarkable improvements over standard CS in terms
of both SNR and SSIM metrics. While Setup 1 and 2
are competing, Setup3 shows the best performance
among all setups. Setup 3 can achieve a peak SSIM
gain of ~ 61% on FS for Container sequence and ~
70% on FS for News sequence. In addition, Setup 3
can achieve a peak SNR gain of ~ 15.62 dB for
Container sequence, and ~ 10.7 dB for News
sequence. The efficacy of our proposed systems for
low complexity acquisition devices has been
demonstrated.
This work is applied for single view video and
exploits only sparsity in spatial direction for separate
frames. As a future work, we aim to give attention to
inter-frame correlation to exploit the sparsity in the
temporal direction of the video rather than exploiting
only the sparsity in the spatial direction. This can
improve the compression order obtained through
compressed sensing. In addition, we aim to extend
our perceptual based system to multi-view video
coding. Quantization effects also can be considered
for future work.
ACKNOWLEDGEMENTS
This work has been supported by the Egyptian
Mission of Higher Education (MoHE). I am grateful
to Egypt-Japan University of Science and
Technology (E-JUST) for offering the tools and
equipment needed.
REFERENCES
Arizona State University, 2014. YUV video sequences
[online]. Available from: http://trace.eas.asu.edu/yuv/
[Accessed 26 Nov 2014].
Candes, E., Romberg, J., and Tao, T., 2006a. Robust
uncertainty principles: exact signal reconstruction from
highly incomplete frequency information. IEEE
transactions on information theory, 52 (2), 489 – 509.
Candes, E., Romberg, J., and Tao, T., 2006b. Stable signal
recovery from incomplete and inaccurate
measurements. Communications on pure and applied
mathematics, 59 (8), 1207–1223.
Candes, E., Wakin, M., and Boyd, S., 2008. Enhancing
sparsity by reweighted ℓ 1 minimization. Fourier
analysis and applications, special issue on sparsity, 14
(5), 877–905.
Donoho, D. L., 2006. Compressed sensing. IEEE
transactions on information theory, 52 (4), 1289–1306.
Figueiredo, M., Nowak, R. D., and Wright, S. J., 2009.
GPSR: Gradient Projection for Sparse Reconstruction:
Matlab source code [online]. Available from:
http://www.lx.it.pt/~mtf/GPSR/ [Accessed 22 Sep
2014].
Figueiredo, Má. a. T., Nowak, R. D., and Wright, S. J.,
2007. Gradient Projection for Sparse Reconstruction:
Application to Compressed Sensing and Other Inverse
Problems. IEEE Journal of Selected Topics in Signal
Processing, 1 (4), 586–597.
Friedlander, M. P., Mansour, H., Saab, R., and Yilmaz, O.,
2011. Recovering Compressively Sampled Signals
Using Partial Support Information. IEEE Transactions
on Information Theory, 58 (2), 1122–1134.
ITU-T, 2003. Advanced video coding for generic audio-
visual services. H.264 and ISO/IEC 14496-10 (AVC),
ITU-T and ISO/IEC JTC 1, May 2003 (and subsequent
editions).
Lee, H., Oh, H., Lee, S., and Bovik, A. C., 2013. Visually
weighted compressive sensing: measurement and
reconstruction. IEEE transactions on image processing,
22 (4), 1444–1455.
Lee, J. and Ebrahimi, T., 2012. Perceptual video
compression: a survey. IEEE Journal of selected topics
in signal processing, 6 (6), 684–697.
Lin, Y. and Zhang, X., 2013. Recent development in
perceptual video coding. In: International conference
on wavelet analysis and pattern recognition (ICWAPR).
Tianjin, 259–264.
Mansour, H. and Yilmaz, O., 2012. Adaptive compressed
sensing for video acquisition. In: IEEE international
conference on acoustics, speech and signal processing
(ICASSP). Kyoto, 3465 – 3468.
MathWorks, 2013. MATLAB - the Language of technical
computing [online]. Available from:
http://www.mathworks.com/products/matlab/.
Park, J.Y., Yap, H.L., Rozell, C.J., and Wakin, M.B., 2011.
Concentration of measure for block diagonal matrices
with applications to compressive sensing. IEEE
transaction on signal processing
, 5859 – 5875.
PerceptuallyWeightedCompressedSensingforVideoAcquisition
215

Qaisar, S., Bilal, R. M., Iqbal, W., Naureen, M., and Lee,
S., 2013. Compressive sensing : from theory to
applications , a survey. Communications and networks,
15 (5), 1–14.
Sharma, N., Garg, I., Sharma, P.K., and Sharma, D., 2012.
Analysis of transform techniques for 2D image
compression. International journal of engineering and
innovative technology (IJEIT), 1 (5), 78–82.
Sullivan, G. J., Wang, Y., and Wiegand, T., 2013. High
efficiency video coding (HEVC) text specification draft
10. ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG
11 12th Meeting: Geneva, CH.
Wahidah, I., Suksmono, A. B., and Mengko, T. L. R., 2011.
A comparative study on video coding techniques with
compressive sensing. In: International conference on
electrical engineering and informatics. Bandung,
Indonesia, 1–5.
Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E.
P., 2004a. Image quality assessment: from error
visibility to structural similarity. IEEE transactions on
image processing, 13 (4), 600–612.
Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E.
P., 2004b. The SSIM Index for image quality
assessment: Matlab source code [online]. Available
from:
https://ece.uwaterloo.ca/~z70wang/research/ssim/
[Accessed 1 Dec 2014].
Yang, Y., Au, O. C., Fang, L., Wen, X., and Tang, W.,
2009. Perceptual compressive sensing for image
signals. In: IEEE international conference on
multimedia and expo. (ICME). New York, NY, 89–92.
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
216
