Generative Training for 3D-Retrieval

Harald Grabner

, Torsten Ullrich

and Dieter W. Fellner

1,2

Institute of Computer Graphics and Knowledge Visualization (CGV), Technische Universit

at Graz, Graz, Austria

& Fraunhofer Austria Research GmbH, Visual Computing, Vienna, Austria

Technische Universit

at Darmstadt & Fraunhofer IGD, Darmstadt, Germany

Keywords:

Generative Modeling, Procedural Modeling, 3D-Retrieval, Machine Learning.

Abstract:

A digital library for non-textual, multimedia documents can be deﬁned by its functionality: markup, indexing,

and retrieval. For textual documents, the techniques and algorithms to perform these tasks are well studied.

For non-textual documents, these tasks are open research questions: How to markup a position on a digitized

statue? What is the index of a building? How to search and query for a CAD model? If no additional, textual

information is available, current approaches cluster, sort and classify non-textual documents using machine

learning techniques, which have a cold start problem: they either need a manually labeled, sufﬁciently large

training set or the (automatic) clustering / classiﬁcation result may not respect semantic similarity. We solve

this problem using procedural modeling techniques, which can generate arbitrary training sets without the

need of any “real” data.

The retrieval process itself can be performed with any method. In this article we describe the histogram

of inverted distances in detail and compare it to salient local visual features method. Both techniques are

evaluated using the Princeton Shape Benchmark (Shilane et al., 2004). Furthermore, we improve the retrieval

results by diffusion processes.

1 INTRODUCTION

Techniques for digitizing 3D shapes are currently be-

coming available to a wide audience. With more and

more data, questions of storage and archival arise –

especially for generalized documents (Fellner et al.,

2007). They should be treated analogue to ordinary

text documents, so that they can be inserted into a

digital library, which can be deﬁned by its main func-

tions: indexing and retrieval (Havemann et al., 2012).

This paper presents and combines three important

ideas for content-based retrieval:

1. a new 3D model retrieval meta approach based on

generative modeling techniques to eliminate the

cold start problem (Ullrich and Fellner, 2011);

2. the method histogram of inverted distances by

(Grabner et al., 2014) to measure the similarity

of two 3D models;

3. an approach to improve retrieval results using dif-

fusion processes (Donoser and Bischof, 2013).

All these ideas and techniques are described in detail

and are combined to one retrieval system for 3D mod-

els.

A generative model describes a family of shapes,

a so-called shape space. We use this shape space to

randomly draw a number of samples. These training

samples are passed to a machine learning based clas-

siﬁer. Without needing any “real” data, our method

uses solely generative 3D models in the training

phase. Consequently, it eliminates the cold start prob-

lem. The generative models themselves are repre-

sented as JavaScript code, which takes a number of

parameters and returns a 3D model.

The used classiﬁer is called histogram of inverted

distances. It is a geometry-based method that oper-

ates on volume models. In a preprocessing step, the

method converts the training samples to a voxel rep-

resentation, aligns their principal axes to the canon-

ical, Euclidean basis and calculates the inverted dis-

tance transformation of the volume model. The vol-

ume model is then split into a regular grid of cubes,

which we call cells. For each cell we determine

the histogram of inverted distances and learn a non-

parametric density function (Szeliski, 2010), (Bishop,

2007). The object class is represented by its genera-

tive model and its learned density function. In the

recognition phase the similarity is estimated using the

learned density function of the object class to test.

Grabner H., Ullrich T. and W. Fellner D..

Generative Training for 3D-Retrieval.

DOI: 10.5220/0005248300970105

In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 97-105

ISBN: 978-989-758-087-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

The similarity of the whole model is given by the

product of all cell similarities. This method is able

to ﬁnd similar objects. To illustrate its applicability,

we compare it to the established salient local visual

features method (Ohbuchi et al., 2008).

Using diffusion processes the retrieval results can

improved even further. The similarity between two

models can be calculated. If each model is compared

to each other, the resulting square matrix of differ-

ences/similarities is called the afﬁnity matrix. Re-

trieving 3D models similar to the i-th model using the

afﬁnity matrix only, is done by extracting the i-th row

and sorting this row by its values.

2 RELATED WORK

Our approach combines techniques of shape descrip-

tion and generative modeling with content-based re-

trieval and machine learning.

The main idea of generative modeling is the de-

scription of shapes using algorithms. An overview on

generative modeling techniques can be found in the

survey by Watson and Wonka (2008), in the overview

by Vanegas et al. (2010), as well as in the tutorial

notes “The Rules Behind – Tutorial on Generative

Modeling” (Krispel et al., 2014).

Concerning content-based retrieval, many meth-

ods for 3D models have been proposed recently.

Tangelder et al. (2008) and Bustos et al. (2007) have

both surveyed literature on content-based retrieval

methods. All methods can be classiﬁed according

to three categories: feature-based, graph-based and

geometry-based methods. Feature-based methods op-

erate on global (e.g. volume, area) or local (e.g. cur-

vature) properties. Graph-based methods calculate a

graph, such as a skeleton, based on the 3D model and

perform matching based on graphs. Geometry-based

methods operate directly on the models’ geometric

representation. For detailed explanation and repre-

sentative algorithms we refer the reader to the surveys

mentioned above.

For the training phase, the above mentioned meth-

ods need a given sample set. This introduces a cold

start problem: a sufﬁciently large data set has to be

tagged and classiﬁed manually (for training purposes)

or an unsupervised learning approach is used, which

may result in a classiﬁcation that does not correspond

to the objects’ semantics or the classiﬁcation used

in the respective ﬁeld of application. Ullrich and

Fellner (2011) circumvent this problem by ﬁtting gen-

erative models to the test data, so only the generative

models must be known in advance. We use the same

technique to span a shape space and to take a sample

set by random. This randomized subset is the input of

the training phase which uses histograms.

Shape histograms have previously been used by

Ankerst et al. (1999) to classify molecules; how-

ever their approach uses one global histogram per

molecule. Kriegel et al. (2003) also split their vox-

eled models into a regular grid of cells and calcu-

late features vectors per cell. In contrast to our ap-

proach, they do not use the histogram of inverted dis-

tances. The inverted distance transformation is used

by Dutagaci et al. (2005), and Kazhdan et al. (2003),

but they use discrete fourier transformation based de-

scriptors, radial cosine transformation based descrip-

tors or spherical harmonic representation based de-

scriptors for detection.

3 SHAPE DESCRIPTION

A possibility to describe a shape is realized by the

generative modeling paradigm (

Ozkar and Kotsopou-

los, 2008), (Ullrich et al., 2010). The key idea is to en-

code a shape with a sequence of shape-generating op-

erations, and not just with a list of low-level geometric

primitives. In its practical consequence, every shape

needs to be represented by a program, i.e., encoded

in some form of programming language, shape gram-

mar (M

uller et al., 2006), modeling language (Have-

mann, 2005) or modeling script (Autodesk, 2007).

Based on this idea each class of objects is repre-

sented by one algorithm M. Furthermore, each de-

scribed object is a set of high-level parameters x,

which reproduces the object, if an interpreter evalu-

ates M(x). As this kind of modeling resembles pro-

gramming rather than “designing”, it is obvious to

use software engineering techniques such as version-

ing and annotations. In this way, model M may con-

tain a human-readable description of the object class

it represents. In order to train a machine learning ap-

proach, the parameter domain D(M) is sampled ran-

domly using a uniform distribution. These random

models M(x

) are used in the training phase.

The generative models are implemented in

JavaScript and interpreted on-demand. The

scripts must implement the functions shapeName,

shapeDomain and shape. The ﬁrst function returns

the name of a model, for example “car”; the second

function returns an array that contains the lower and

the upper bounds for every model parameter; the

shape function takes an array containing numerical

values and returns concrete 3D geometry represented

by an indexed face set.

The generative models illustrated in Figure 1 rep-

resent the object classes “sedan car” (left) and “com-

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

Figure 1: The generative description of the “sedan car” model (left) has six degrees of freedom. These parameters (p

,..., p

)

deﬁne the outer shape of the car. The description of the “commercial airplane” takes ﬁve parameters (p

,..., p

), whose

effects are visualized in this construction plan (right). The implementations consist of 350 (car) and 250 (plane) lines of

JavaScript code.

mercial airplane” (right). The car model takes six pa-

rameters, whereas the plane model takes ﬁve param-

eters. Both models generate and return a 3D model

with a ﬁxed topology and varying geometry.

4 CONTENT-BASED RETRIEVAL

Histogram of Inverted Distances: For the training,

all training models are converted to a voxel repre-

sentation, scaled to a common size and aligned using

Principal Component Analysis (PCA) as illustrated in

Figure 2.

Afterwards, for each aligned training model T

the

inverted distance models are computed. The volume

Figure 2: Unaligned (left) and aligned (right) version of

a voxelized car model. The principal axes of the aligned

model are aligned to the canonical basis vectors and the

center of gravity of all aligned models is centered at





of the distance transformed training samples is de-

ﬁned by

v(T

,x,y,z) = max

cut−d(T

,x,y,z)

cut

with the Euclidean distance d(T

,x,y,z) of point

(x,y, z) to the model’s surface and a threshold value

cut. Due to the voxelization the inverted distances

can be calculated even for non-manifold and non-

watertight models. Any 3D geometry representa-

tion (point clouds, NURBS, etc.) can be used as

input data. Figure 3 shows the cross section of an

aligned voxeled training model (left) as well as its

corresponding inverted distance transformed version

(right).

In the next step several voxels are combined to one

cell C

and within each cell the histogram of inverted

distances with k bins is calculated. Having normal-

ized the histogram, it serves as a k-dimensional fea-

ture vector h

∈ [0,1]

of that cell. Based on the fea-

ture vectors h

we estimate a non-parametric density

function for each cell position (a,b,c) using Gaussian

kernel density estimation (Bishop, 2007). The density

Figure 3: The cross section of the aligned voxel model (top)

and the inverted distance model (bottom) of a car. The result

looks like a blurred image.

GenerativeTrainingfor3D-Retrieval

function for a cell at position (a,b,c) is

P(h

a,b,c

) =

∑

i=1

(2πσ

)

k/2

· exp



−

a,b,c

−h

2σ



where h

is the feature vector of a test model and σ

represents the standard deviation of the Gaussian ker-

nel. Usually the standard deviation can be estimated

easily using appropriate estimation methods (Jones

et al., 1996).

In the recognition phase, the model to test is pro-

cessed the same way each training sample has been

processed: it is voxelized, scaled, PCA-aligned, dis-

tance transformed, combined to cells, and converted

into a k-dimensional feature vectures (for each cell)

using normalized histograms.

Let X be a test model and h

(a,b,c)

denote the

feature vectors of the test model, then the joint

probability of model X belonging to the learned class

∏

(a,b,c)∈(1...p)

P(h

(a,b,c)

). We call this algorithm

the histogram of inverted distances (HID) algorithm.

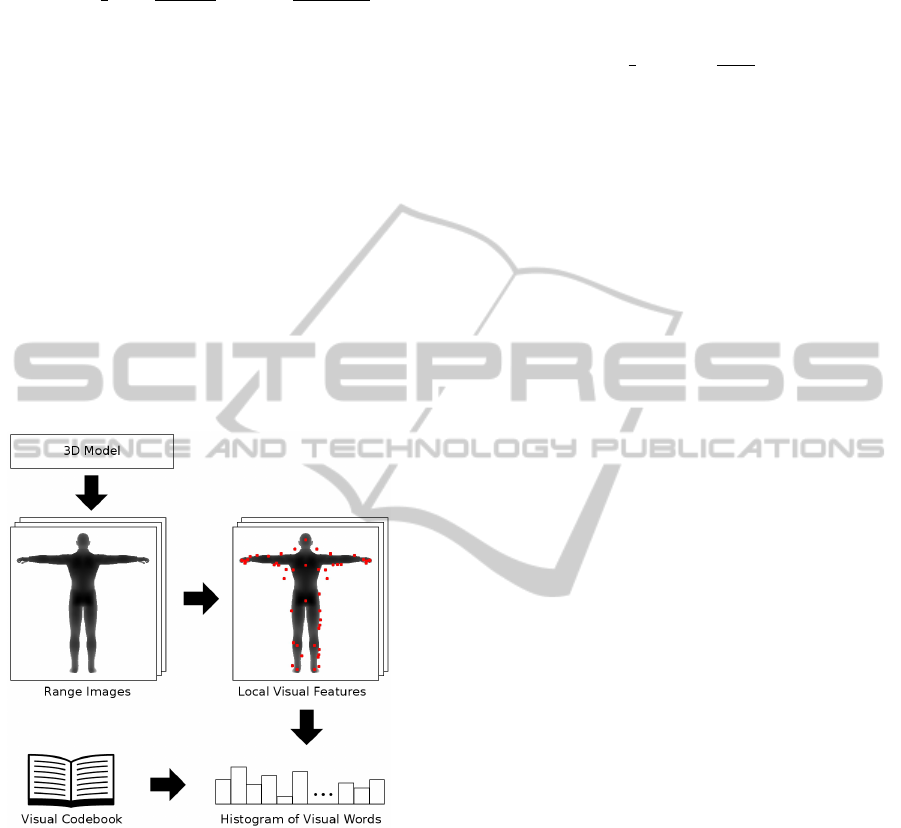
Figure 4: The salient local visual features method. A num-

ber of range images are rendered from various viewpoints.

Salient local visual features and their descriptors are ex-

tracted. The visual features can be quantized into visual

words using a precomputed visual codebook. By accumu-

lating the visual words into a histogram, a feature vector for

the 3D model is generated.

Salient Local Visual Features Method: To demon-

strate that the generative training approach presented

in the previous Section can be combined with differ-

ent retrieval techniques, we implemented the salient

local visual features method introduced by Ohbuchi

et al. (Ohbuchi et al., 2008). The method is depicted

schematically in Figure 4.

Like in the histogram of inverted distances, the vi-

sual word histogram is learned using kernel density

estimation. However, in this case Manhattan distance

is used as the kernel function. The similarity S for

the 3D model described by the visual word histogram

is given by:

S(l

) =

∑

i=1



−l

(i)



where n denotes the number of training samples and

σ represents the smoothing factor.

The visual codebook quantizes visual features into

visual words. The visual codebook is learned un-

supervised in a preprocessing step using k-means++

clustering (Arthur and Vassilvitskii, 2007). The set

of visual features that have to be clustered is selected

randomly from all views of the 3D models.

5 EVALUATION

We evaluated both retrieval methods with the Prince-

ton shape benchmark (Shilane et al., 2004) using the

two classes illustrated in Figure 1: “commercial air-

plane” and “sedan car”. The complete benchmark

consists of 907 test samples including 10 sedan cars

and 11 commercial airplanes. Both retrieval meth-

ods have been trained generatively without any “real-

world” data or any previously deﬁned or marked test

samples. The benchmark has been executed on a com-

puter with an Intel i7 950 CPU and 12 GB RAM. All

timings mentioned in this Section have been taken on

this reference system.

Sedan Car. The “sedan car” class was modeled us-

ing JavaScript taking six parameters. All other di-

mensions (e.g. length of the top) are derived com-

bining multiple parameters. The car consists of one

side (colored green in Figure 1 (left)). This side is ex-

truded twice using tapered extrusions with different

angles. The ﬁrst extrusion creates the blue parts and

the second one creates the red parts. By mirroring the

side and the two extrusions around its center plane

the whole car is created. The tires are modeled using

cylinders. The extrusion as well as the creation of a

cylinder are extracted JavaScript functions prepared

for reuse.

Commercial Airplane. The procedural model of the

“commercial airplane” has ﬁve parameters to control

the dimensions of the airplane (see Figure 1 (right)).

Dependent parameters – such as the length of the

wings – are combinations of free parameters. The

fuselage of the airplane is created using a rotational

surface which is then slightly deformed to model the

cockpit and the aft fuselage. The jet engines are sim-

ple cylinders. As this generative model can already

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

100

histogram of inverted distances salient local visual features

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Recall

Precision

Precision−Recall

Commercial Airplane

Sedan Car

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Recall

Precision

Precision−Recall

Commercial Airplane

Sedan Car

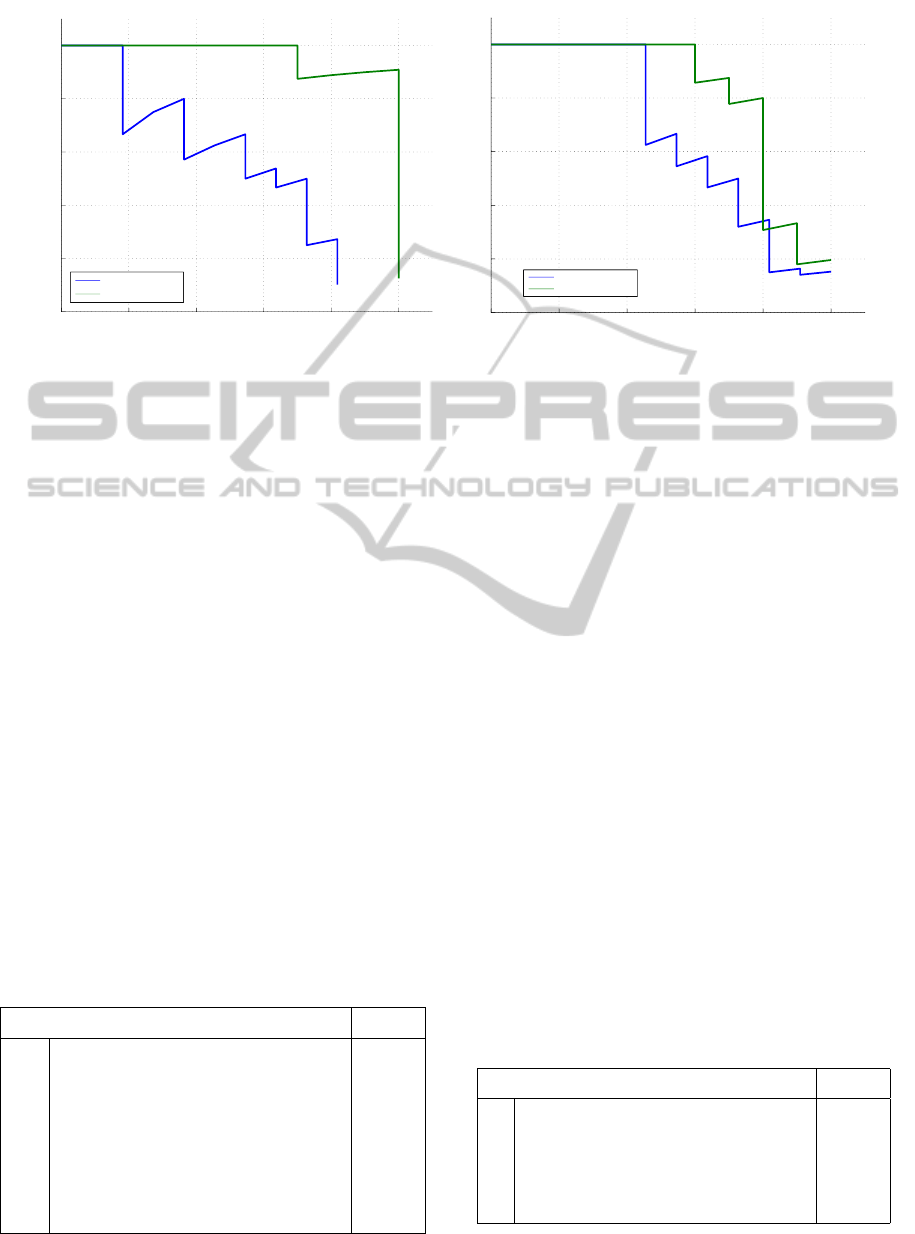
Figure 5: The evaluation of ranked retrieval results is commonly visualized by precision-recall graphs (Manning et al., 2008).

The corresponding visualizations show the benchmark results of the classes “sedan car” and “commercial airplane” using the

histogram of inverted distances method (left) and using the salient local visual features method (right).

reuse procedures needed for the sedan car, its code is

shorter than the car’s description.

Evaluation of the Histogram of Inverted Distances

Method. The values for the retrieval parameters were

evaluated empirically. All parameters and their cor-

responding values are displayed in Table 1. The gen-

eration and voxelization of 64 models for both model

classes took 103 seconds. The learning phase took

292 seconds. The actual retrieval process for both

classes took about 4.75 hours, respectively 9.41 sec-

onds per test model in average.

Figure 5 shows the precision-recall graphs (Man-

ning et al., 2008) for cars and airplanes using the his-

togram of inverted distances method (left) and using

the salient local visual features method (right).

The histogram of inverted distances method is

able to ﬁnd similar objects to the given generative

models. The retrieval results for the class “sedan car”

are almost perfect. However, the “commercial air-

plane” class performs signiﬁcantly worse. The main

Table 1: The parameters and their corresponding values

listed in this table have been used for benchmarking the his-

togram of inverted distances method.

Parameter Value

n Number of training samples 64

R Resolution of the voxel models 256

p Number of cells in one direction 16

σ Standard deviation for the Gaus-

sian kernel density estimation

cut Threshold in distance transforma-

tion

k Number of histogram bins 8

reason for this effect can be found in the genera-

tive model. It is not detailed enough to differentiate

between the benchmark’s different airplane classes

(commercial, ﬁghter, biplane, . . . ). Figure 6 shows

the top 16 retrieval results for both classes using in-

verted distances.

Evaluation of the Salient Local Visual Features

Method. The parameters for the salient local visual

features method are presented in Table 2.

Rendering of the range images, extraction of the

visual features and calculation of the visual word his-

togram took 15.5 seconds per 3D model on average.

The calculation of the visual codebook, which con-

sists of the extraction of 30000 visual features from

a random subset of the benchmark and the cluster-

ing of the features into 1024 clusters, took 72 min-

utes. The generation of 64 training models for both

model classes and the calculation of the visual word

histograms took 33 minutes. The actual retrieval pro-

cess took 0.55 seconds per class.

Figure 5 (right) shows the precision-recall graphs

Table 2: The parameters and their corresponding values

listed in this table have been used for benchmarking the

salient local visual features method in combination with the

generative training approach.

Parameter Value

n Number of training samples 64

R Resolution of the range images 256

σ Smoothing factor for the kernel

density estimation

w Number of visual words 1024

GenerativeTrainingfor3D-Retrieval

101

for both shape classes using the salient local visual

features method. The method is able to ﬁnd similar

objects to the given generative models. Again, the

“commercial airplane” class performs signiﬁcantly

worse than the “sedan car” class due to its generative

model, which is not detailed enough to differentiate

between the airplane classes “commercial”, “ﬁghter”,

etc. as can be seen in Figure 7. It shows the top 16

retrieval results for the classes “sedan car” and “com-

mercial airplane”.

6 IMPROVED RETRIEVAL VIA

DIFFUSION PROCESS

In order to improve retrieval results we use diffusion

processes. Using matching methods for 3D models,

the similarity or affnity between two models can be

calculated. Assuming that n is the number of 3D mod-

els, the so-called afﬁnity matrix (n×n) of all 3D mod-

els can be calculated. Retrieving 3D models similar

to the i-th model using the affnity matrix only, is done

by extracting the i-th row and sorting it by its affnity

values. However, doing so ignores the structure of

the underlying data manifold (Donoser and Bischof,

2013). Diffusion processes re-evaluate the affnities of

all models in the context of all other elements. This

is done by diffusing the affnity values through the

graph described by the affnity matrix. Donoser et al.

(2013) have recently surveyed diffusion processes for

retrieval.

One of the best known diffusion algorithm is the

Google page rank algorithm (Page et al., 1998). For

the page rank algorithm an affnity matrix A is needed,

which contains all pairwise affnity values. If each row

of A is divided by its sum, the result is a stochastic ma-

trix P, which can be interpreted as a transition matrix

for randomly walking on a complete graph of size n.

Assuming we want to retrieve 3D models similar

to the j-th model, the n-dimensional probability vec-

tor f

must be initialized with Kronecker δ

i j

. The

probability vector, which contains the ﬁnal affnities

for all other 3D models can be calculated iteratively

t+1

= f

·P. This update operation is performed until

convergence.

To apply diffusion processes in the ﬁeld of re-

trieval, n × n afﬁnity matrix containing all pairwise

similarities is needed. The pairwise similarities are

calculated by comparing the cell histograms of the

models. As described by (Johnson and Hebert, 1999),

the similarity between two cells is given by the corre-

lation coefﬁcient. The similarity between two models

is given by the sum of the cells similarity. The con-

struction of the affnity matrix for the whole Prince-

ton Shape Benchmark requires 18142 model compar-

isons. One comparison of two models took 0:34 sec-

onds on average, which results in ≈310 hours for the

whole benchmark. To speed up the calculation of the

affnity matrix, the workload has been distributed to

seven similar computers. Thereby, calculation time

was reduced to two days. From the affnity matrix for

the whole benchmark, the affnity matrix for the test

set was extracted. it is depicted in Figure 8 (left) us-

ing a the black body radiation color map. The result-

ing affnity matrix is depicted in Figure 8 (right).

The effect of the diffusion process reinforces re-

trieval effects; i.e. the precision slightly decreases at

lower recall values, but increases at recall values of

above 0.4.

7 CONCLUSION

This paper presents a new approach to perform

content-based retrieval of 3D shapes based on genera-

tive modeling techniques. The generative models are

used to describe 3D model classes, respectively, 3D

shape spaces. In the training phase, the shape spaces

are sampled randomly. In this way, no “real” training

data is needed a priori.

The big advantage of procedural modeling tech-

niques is the included expert knowledge within an

object description (Ullrich and Fellner, 2011); e.g.

the knowledge of an expert about the inner structure

and the semantics of an object class can be mapped

to procedures (Ullrich et al., 2013). Within the Cul-

tural Heritage (CH) project “Procedural Fitting Server

(ProFitS)” we incorporate this technique to index a

CH repository semantically using expert knowledge.

The approach of a generative training set, which does

not need any “real” data can be combined with various

retrieval algorithms. We have evaluated two retrieval

methods to illustrate this approach.

The ﬁrst method is called the histogram of in-

verted distances method by (Grabner et al., 2014).

The second method is called the salient local visual

features method based on the SIFT algorithm. Both

methods use feature vectors to learn a non-parametric

density function for each 3D model class. In the

recognition phase, the feature vector is calculated for

the test object and the similarity is estimated using the

learned non-parametric density function.

Furthermore, the retrieval results can be improved

using diffusion processes to take the underlying struc-

ture of the data manifold into account, similar to the

Google page rank algorithm.

Our contribution to 3D documents is a shape re-

trieval approach based on machine learning and gen-

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

102

search results for “sedan car” search results for “commercial airplane”

Figure 6: The top 16 retrieval results for the class “sedan car” using the histogram of inverted distances method (left) are

almost perfect. The ten car models of the benchmark are listed within the best 16 matches, whereas top 16 retrieval results for

the class “commercial airplane” using the same method have many false positives. Although all returned models are airplanes,

the Princeton Shape benchmark distinguishes between many different airplane classes (commercial, ﬁghter, biplane, . . . ).

search results for “sedan car” search results for “commercial airplane”

Figure 7: These top 16 retrieval results for the classes “sedan car” (left) and “commercial airplane” (right) have been generated

using the salient local visual features method. As the Princeton Shape benchmark distinguishes between many different

airplane classes, the results for “commercial airplane” have many false positives.

Figure 8: The affnity matrix before (left) and after (right) the application of the diffusion process. The values are mapped

using the black body radiation scheme. A black color indicates low similarity, whereas a white color indicates high similarity.

GenerativeTrainingfor3D-Retrieval

103

erative modeling. In this way, we provide a classiﬁ-

cation technique, which uses generative modeling to

encode expert knowledge in a way suitable for auto-

matic classiﬁcation and indexing of 3D repositories.

We have shown that it is possible to train a retrieval

method using generative models only. As a bene-

ﬁt (not only for users of our method), this technique

eliminates the cold start problem in the training phase.

A generative description implemented in a few lines

of code is sufﬁcient to generate a reasonable training

set.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge the support of

the European Commission within the project DU-

RAARK founded by the program “ICT-2011-4.3-

Digital Preservation” as well as the support of the

Austrian Research Promotion Agency (FFG) for the

project ProFitS.

REFERENCES

Ankerst, M., Kastenm

uller, G., Kriegel, H.-P., and Seidl, T.

(1999). 3D Shape Histograms for Similarity Search

and Classiﬁcation in Spatial Databases. Advances in

Spatial Databases (Lecture Notes in Computer Sci-

ence), 1651:207–226.

Arthur, D. and Vassilvitskii, S. (2007). k-means++: The

Advantages of Careful Seeding. Proceedings of

the annual ACM-SIAM symposium on discrete algo-

rithms, 18:1027–1035.

Autodesk (2007). Autodesk Maya API. White Paper, 1:1–

30.

Bishop, C. M. (2007). Pattern Recognition and Machine

Learning. Springer.

Bustos, B., Keim, D., Saupe, D., and Schreck, T. (2007).

Content-based 3D Object Retrieval. IEEE Computer

Graphics and Applications, 27(4):22–27.

Donoser, M. and Bischof, H. (2013). Diffusion Processes

for Retrieval Revisited. Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR), 29:1320–1327.

Dutagaci, H., Sankur, B., and Yemez, Y. (2005). Transform-

based methods for indexing and retrieval of 3D ob-

jects. Proceedings of the International Conference on

3-D Digital Imaging and Modeling, 5:188–195.

Fellner, D. W., Saupe, D., and Krottmaier, H. (2007). 3D

Documents. IEEE Computer Graphics and Applica-

tions, 27(4):20–21.

Grabner, H., Ullrich, T., and Fellner, D. W. (2014). Content-

based Retrieval of 3D Models using Generative Mod-

eling Techniques. Proceedings of EUROGRAPHICS

Workshop on Graphics and Cultural Heritage (Short

Papers / Posters), 12:9–12.

Havemann, S. (2005). Generative Mesh Modeling. PhD-

Thesis, Technische Universit

at Braunschweig, Ger-

many, 1:1–303.

Havemann, S., Ullrich, T., and Fellner, D. W. (2012). The

Meaning of Shape and some Techniques to Extract It.

Multimedia Information Extraction, 1:81–98.

Johnson, A. and Hebert, M. (1999). Using spin images

for efﬁcient object recognition in cluttered 3D scenes.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 21:433–449.

Jones, M. C., Marron, J. S., and Sheather, S. J. (1996). A

Brief Survey of Bandwidth Selection for Density Es-

timation. Journal of the American Statistical Associa-

tion, 91:401–407.

Kazhdan, M., Funkhouser, T. A., and Rusinkiewicz, S.

(2003). Rotation invariant spherical harmonic repre-

sentation of 3D shape descriptors. Proceedings of the

Eurographics/ACM SIGGRAPH Symposium on Ge-

ometry Processing, 1:156–164.

Kriegel, H.-P., Brecheisen, S., Kr

oger, P., Pfeiﬂe, M., and

Schubert, M. (2003). Using sets of feature vectors for

similarity search on voxelized CAD objects. Proceed-

ings of the ACM International Conference on Man-

agement of Data (SIGMOD), 29:587–598.

Krispel, U., Schinko, C., and Ullrich, T. (2014). The Rules

Behind – Tutorial on Generative Modeling. Proceed-

ings of Symposium on Geometry Processing / Gradu-

ate School, 12:2:1–2:49.

Manning, C. D., Raghavan, P., and Sch

utze, H. (2008). In-

troduction to Information Retrieval. Cambridge Uni-

versity Press.

uller, P., Wonka, P., Haegler, S., Andreas, U., and

Van Gool, L. (2006). Procedural Modeling of Build-

ings. Proceedings of 2006 ACM Siggraph, 25(3):614–

623.

Ohbuchi, R., Osada, K., Furuya, T., and Banno, T. (2008).

Salient local visual features for shape-based 3D model

retrieval. Proceeding of the IEEE International Con-

ference on Shape Modeling and Applications, 8:93–

102.

Ozkar, M. and Kotsopoulos, S. (2008). Introduction to

shape grammars. International Conference on Com-

puter Graphics and Interactive Techniques ACM SIG-

GRAPH 2008 (course notes), 36:1–175.

Page, L., Brin, S., Motwani, R., and Winograd, T. (1998).

The PageRank Citation Ranking: Bringing Order to

the Web. online:.

Shilane, P., Min, P., Kazhdan, M., and Funkhouser, T. A.

(2004). The Princeton Shape Benchmark. Shape Mod-

eling International, 8:1–12.

Szeliski, R. (2010). Computer Vision: Algorithms and Ap-

plications. Microsoft Research.

Tangelder, J. W. H. and Veltkamp, R. C. (2008). A survey of

content based 3D shape retrieval methods. Multimedia

Tools and Applications, 39:441–471.

Ullrich, T. and Fellner, D. W. (2011). Generative Object

Deﬁnition and Semantic Recognition. Proceedings of

the Eurographics Workshop on 3D Object Retrieval,

4:1–8.

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

104

Ullrich, T., Schinko, C., and Fellner, D. W. (2010). Proce-

dural Modeling in Theory and Practice. Poster Pro-

ceedings of the 18th WSCG International Conference

on Computer Graphics, Visualization and Computer

Vision, 18:5–8.

Ullrich, T., Schinko, C., Schiffer, T., and Fellner, D. W.

(2013). Procedural Descriptions for Analyzing Dig-

itized Artifacts. Applied Geomatics, 5(3):185–192.

Vanegas, C. A., Aliaga, D. G., Wonka, P., M

uller, P., Wad-

dell, P., and Watson, B. (2010). Modelling the Ap-

pearance and Behaviour of Urban Spaces. Computer

Graphics Forum, 29:25–42.

Watson, B. and Wonka, P. (2008). Procedural Methods for

Urban Modeling. IEEE Computer Graphics and Ap-

plications, 28(3):16–17.

GenerativeTrainingfor3D-Retrieval

105