
Discrete Optimal View Path Planning
Sebastian Haner and Anders Heyden
Centre for Mathematical Sciences, Lund University, Lund, Sweden
Keywords:
Path Planning, Next Best View Planning, Active Vision, Discrete Optimization, Semidefinite Programming,
Genetic Algorithm.
Abstract:
This paper presents a discrete model of a sensor path planning problem, with a long-term planning horizon.
The goal is to minimize the covariance of the reconstructed structures while meeting constraints on the length
of the traversed path of the sensor. The sensor is restricted to move on a graph representing a discrete set
of configurations, and additional constraints can be incorporated by altering the graph connectivity. This
combinatorial problem is formulated as an integer semi-definite program, the relaxation of which provides
both a lower bound on the objective cost and input to a proposed genetic algorithm for solving the original
problem. An evaluation on synthetic data indicates good performance.
1 INTRODUCTION
As an experimental design problem, camera network
design has been studied extensively in the photogram-
metry literature. The goal is to obtain the most accu-
rate reconstruction of a scene or object given a limited
number of observations, and the task is to find the op-
timal set of camera poses or sensor configurations. In
robotics, the next best view problem is similarly con-
cerned with finding the next sensor position to most
improve a sequential reconstruction of the environ-
ment. Both problems are hard due to the non-convex,
multi-modal costs arising (cf. (Fraser, 1984)), but also
to the sometimes high computational burden of eval-
uating the cost function. Recent research has mostly
focused on the latter problem of accurately and effi-
ciently evaluating the expected information gain of a
potential sensor configuration (Low and Lastra, 2006;
Vasquez-Gomez et al., 2013; Foix et al., 2012) and
on achieving coverage of the scene (Blaer and Allen,
2007), while other works tackle minimizing the re-
sulting cost functions to find one or a series of opti-
mal sensor configurations. As the name implies, next
best view planning usually employs a myopic plan-
ning horizon of only one step ahead, mainly due to
these difficulties. Camera network optimization, on
the other hand, can be seen as a long horizon plan-
ning problem, but without constraints on the order in
which observations are made.
Problems of this type have mainly been addressed
using stochastic optimization algorithms or by solv-
ing a relaxed, easier version. For example, in (Dunn
et al., 2006) the camera network problem is solved
using a genetic optimization algorithm searching the
high-dimensional parameter space of camera place-
ments. In (Wenhardt et al., 2006) the authors recon-
struct objects using a camera mounted on a robotic
arm. The object geometry is estimated using a
Kalman filter, and the next imaging location is deter-
mined by searching a discrete parameter space and
evaluating the expected information gain in the fil-
ter at each position. A different approach is taken in
(Trummer et al., 2010) where the next imaging loca-
tion is decided based only on the single currently least
well-determined feature, allowing a simple closed
form solution. In (Dunn et al., 2009) the path of a
robot moving in the plane is planned based on the
expected reconstruction accuracy of an observed ob-
ject. An approximation of the geometry is given and
the expected information gain from observing the ob-
ject from a particular vantage point is determined on
a discrete grid of camera locations. Each grid cell
is assigned a cost proportional to the inverse of the
information gain, and a minimum cost path is found
between the starting point and the global minimum
grid cell. This does not take into account the fact that
an observation may be more or less valuable depend-
ing on what other observations are available, and thus
does not optimize the desired objective. In (Haner and
Heyden, 2011) a continuous optimization approach is
used to solve the similar problem of finding the best
reconstruction while also reaching a predefined desti-
nation as quickly as possible, and while taking all fu-
ture observations into account, this method can only
411
Haner S. and Heyden A..
Discrete Optimal View Path Planning.
DOI: 10.5220/0005252104110419
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 411-419
ISBN: 978-989-758-091-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

guarantee locally optimal solutions using gradient de-
scent. In this paper, we formulate discrete analogs
of the problem formulation of (Haner and Heyden,
2011) and cast them as integer semi-definite programs
(SDPs). The relaxations to continuous SDPs may be
used in a branch-and-bound scheme to find optimal
solutions, or as input to a stochastic optimization al-
gorithm proposed below in Section 4.
Related discrete approaches include (Englot and
Hover, 2010) where a shortest path linear program
formulation similar to this work is used, but only con-
siders view coverage and not uncertainty. (Hollinger
et al., 2012) uses a two-stage approach where good
views are selected based on uncertainty, and then con-
nected by solving a traveling salesman problem.
In (Singh et al., 2009; Golovin and Krause, 2010)
approximation algorithms for the constrained path
problem using greedy strategies are shown to provide
solutions within a constant factor of the optimum,
given that the underlying cost function is submodu-
lar. Unfortunately, the maximum eigenvalue metric
used in this paper is not submodular and such guaran-
tees cannot be given; however, an optimality gap can
always be computed.
2 PROBLEM DESCRIPTION
Assume that the goal of a moving sensor is to reach
a predefined target destination, while simultaneously
reconstructing its surroundings as accurately as pos-
sible, based on observations taken along the path to
the destination. There is a trade-off between reach-
ing the destination quickly, and reducing the recon-
struction uncertainty; for a bearing-only sensor such
as a camera, a longer path can accommodate more ob-
servations with greater parallax, thus improving tri-
angulation accuracy. Given a trade-off preference,
or a bound on the path length, an optimal path can
be found by solving a discrete optimization problem.
The space between and around the start and destina-
tion positions is discretized into a finite number of
possible sensor positions, and these positions consti-
tute the nodes of a graph. The edges of the graph
encode a neighborhood connectivity, i.e. the possible
motions between the fixed positions. Thus a path in
the graph corresponds to a physical path. With each
node is also associated an information matrix encod-
ing how much information about the environment we
can expect to gain, if performing a measurement at
that node’s location.
The problem formulations in this paper are agnos-
tic to the graph geometry and topology, and to how
the information matrices are generated. Thus there
are no restrictions such as continuity or smoothness
on the function used to evaluate the information con-
tent of a proposed sensor configuration, but which
are typically required by continuous optimization ap-
proaches. Furthermore, the information of each view
can be computed in parallel to leverage modern multi-
core processors and GPU:s.
3 PROBLEM FORMULATION
Define a directed graph G = (V,E) and a set of pos-
itive semi-definite information matrices {I
i
∈ S
n
+
|i =
0,... , |V|}. For a given trade-off parameter λ, define
the optimization problem
min.
p∈P
length(p) +
1
λ
F
I
0
+
∑
i∈p
I
i
−1
(P1)
where P is the set of all simple paths in G from the
source node to the destination node. I
0
is the ini-
tially available information matrix of the environment
structure, and I
i
the expected information to be gained
at node i. The inverse of the information matrix is
the covariance matrix of the reconstructed structure,
so the second term measures the variance using the
scalarizing function F. This function is typically the
trace or maximum eigenvalue, corresponding to A-
and E-optimality in the experiment design literature
(Montgomery, 2000). For these choices of F, we note
that the second term is always decreasing as a func-
tion of the number of nodes on the path
1
. We now
make two observations: if λ is large enough, the prob-
lem is equivalent to finding the shortest path through
the graph, and may be solved efficiently using stan-
dard algorithms. If λ is sufficiently small, it is op-
timal to include all (non-zero) information matrices
in the sum, while still minimizing the distance trav-
eled, thus the problem is equivalent to the traveling
salesman problem (TSP). Since TSP is known to be
NP-hard, an efficient exact algorithm for the general
case is out of reach. Also, the recognition version of
TSP (“Is there a tour of length less than L?”) is NP-
complete, so we should not expect even to be able to
verify if a given solution is optimal. This is true even
for graphs with nodes of degree at most four, e.g. pla-
nar grids (Papadimitriou and Steiglitz, 1998).
In the above formulation (P1) the parameter λ is
used to control the trade-off between a short path and
a more accurate reconstruction of the surroundings.
It is however not obvious how to select this parame-
ter, or even its suitable range, without some trial-and-
error. In fact, another problem formulation may be
1
This follows from the Courant-Fischer theorem.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
412

more natural: given a time or distance budget, what
is the best reconstruction obtainable? In other words,
given an upper bound on the length of the path trav-
eled, minimize the reconstruction error, i.e.
min. F
I
0
+
∑
i∈p
I
i
−1
s.t. length(p) ≤ L .
(P2)
Note that with this formulation, as the allowed path
length grows we no longer approach TSP. Instead, for
L large enough, any Hamiltonian path on the graph
will be optimal, and for the types of graphs consid-
ered here, these are usually easily generated. Unfor-
tunately, the problem still appears difficult for length
limits of practical interest. There are several other
variations on the problem formulation, for example
one could minimize the path length under the con-
straint that the covariance is reduced by a certain
amount. However, all of them appear equally hard
to solve.
Below, we derive convex relaxations of (P1) and
(P2) and show how these can be used to solve the
original problems in a branch-and-bound scheme, or
more practically as guides for more local optimiza-
tion methods. The convex relaxation and optimiza-
tion methods presented are easily adapted to alterna-
tive problem formulations.
3.1 Shortest Path as a Linear Program
The problem of finding the shortest path between two
nodes in a graph with positive edge weights is often
solved using Dijkstra’s algorithm. It can be shown
that this algorithm is equivalent to applying a primal-
dual solver to the following linear program (Papadim-
itriou and Steiglitz, 1998):
min.
∑
(i, j)∈E
c
ij
x
ij
s.t.
∑
j: (i, j)∈E
x
ij
=
∑
j: (i, j)∈E
x
ji
, i ∈ {1,. ..,|V| \ s,t}
∑
j: (s, j)∈E
x
sj
= 1,
∑
j: ( j,t)∈E
x
jt
= 1
0 ≤ x
ij
≤ 1.
(LP)
Here x
ij
is a variable indicating if the edge between
node i and j is part of the path or not, and c
ij
the asso-
ciated non-negative edge weight. The constraints ex-
press flow conservation, so that the number of edges
incident on a node equal the number exiting, ex-
cept for the source (s) and terminal (t) nodes which
have one outgoing and one incident edge respectively.
These constraints can be summarized into A
G
x = b
where A
G
is the |V|-by-|E| edge incidence matrix of
G with entries
a
ij
=
−1 if edge j leaves node i
+1 if edge j enters node i
0 otherwise
, (1)
and x are the edge indicator variables suitably stacked.
It is easily shown that (LP) must have an integer opti-
mal solution. Note that this formulation does not ex-
plicitly forbid solutions consisting of a path between
the source and terminal, plus any number of closed
loops; these are only eliminated by virtue of not be-
ing optimal.
3.2 View Planning as a Semidefinite
Program
We adapt the shortest path problem formulation above
to the planning problem (P1). For convenience, intro-
duce binary variables α
i
for each node of the graph,
indicating whether that node is on the path or not. We
form the relaxed optimization problem
min.
∑
(i, j)∈E
c
ij
x
ij
+
1
λ
F
I
0
+
|V|
∑
i=1
α
i
I
i
−1
s.t. A
G
x = b
α
i
=
∑
j: ( j,i)∈E
x
ji
, i 6= s
α
s
= 1, 0 ≤ α
i
≤ 1,
(P3)
where α and x are not required to be binary. The cost
functions used in next best view planning are gen-
erally non-smooth and multi-modal, and difficult to
optimize. However, due to the discretization, the ar-
gument to the second term of the objective above is
affine in α. Both the trace-of-inverse and maximum
eigenvalue-of-inversefunctions are convex,and using
the epigraph trick the second term may be formulated
as a convex semidefinite constraint (see e.g. (Boyd
and Vandenberghe, 2004)). As one would expect, this
semidefinite program no longer has all the desirable
properties of the linear program; integrality of x or α
is no longer guaranteed, and a solution with disjoint
loops may in fact be optimal.
The corresponding convex relaxation of (P2) is
the same as (P3), except that the first term of the
objective is transformed into a linear inequality:
min. F
I
0
+
|V|
∑
i=1
α
i
I
i
−1
s.t. A
G
x = b
∑
(i, j)∈ E
c
ij
x
ij
≤ L
α
i
=
∑
j: ( j,i)∈E
x
ji
, i 6= s
α
s
= 1, 0 ≤ α
i
≤ 1.
(P4)
DiscreteOptimalViewPathPlanning
413

Selecting L is more intuitive than choosing λ; one
must only be careful not to produce an infeasible
problem by selecting L too low, but the lower limit
is readily obtained using a standard shortest path al-
gorithm.
It is possible to find an optimal integer solution
to (P3) or (P4) using a standard branch-and-bound
search, but this is also known to be NP-hard and
may take a large number of iterations, each involv-
ing solving a potentially quite large SDP. If a solu-
tion is found, it may also contain unwanted disjoint
loops. While it is easy to include linear constraints
forbidding any particular loop in the SDP, since there
are exponentially many possible loops in the graph,
adding constraints against them all at the outset is in-
feasible. But, they can be added on an as-needed ba-
sis; if loops are present in the solution, add constraints
against them and solve again until no loops remain.
As it turns out, 2-cycles are quite common in the so-
lutions, and as their number is typically linear in the
number of nodes, it is feasible to remove them at the
outset which may lead to faster convergence to a loop-
free solution.
Obviously, the above procedure may be very time
consuming or completely intractable for all but the
smallest problem instances. However, we also noted
above that depending on the trade-off parameter λ,
the original problem (P1) should vary in difficulty
between simple shortest path (typically O (|E|log|V|)
for Dijkstra’s) up to exponential complexity. Em-
pirically, it turns out that many instances are in fact
“easy”, in that very few steps of branch-and-bound
are required and few or no loops are included in the
solution. Yet, many other instances are indeed diffi-
cult and not amenable to this approach.
4 APPROXIMATE SOLUTION
Despite the problems of tractability in finding optimal
solutions described above, it can be noted that the re-
laxed SDP formulations (P3) and (P4) provide lower
bounds on the optimal objective values of (P1) and
(P2). This may be used to verify the performance of
approximation algorithms. Also, if the problem in-
stance at hand is “easy enough”, the relaxed solution
x
∗
may be quite close to a valid integer, loop-free so-
lution. In these cases it is possible to construct a valid
solution to (P1) using a simple shortest path search
on the graph G with edge weights c
ij
= 1− x
∗
ij
. This
solution may be good enough, or can serve as initial-
ization for local or stochastic optimization algorithms.
For the formulation (P2) a slightly different approach
is needed, which will not be explored here.
4.1 A Simplified Formulation
Given the hardness of (P1) and (P2), it is natural to
seek a simplified problem formulation which might
admit faster solution algorithms. Part of the difficulty
is the nonlinearity of the interaction between the in-
formation matrices when taking the inverse to obtain
the covariance; the value of any particular contribu-
tion to the information depends on all the others. For-
going this interaction, instead of minimizing the co-
variance, one can maximize the trace of the informa-
tion matrix, yielding the problem
min.
p∈P
length(p) −
1
λ
trace
I
0
+
∑
i∈p
I
i
.
(P5)
Since the trace is linear, this results in a shortest
path problem on G with modified weights (subtract
trace(I
i
)/λ from each edge incident on node i). As
long as this does not result in any negative cycles,
this may be efficiently solved using e.g. the Bellman-
Ford algorithm, or even Dijkstra’s if all weights are
non-negative. If negative cycles are present, the prob-
lem again becomes much more difficult. In the ex-
treme where all edge weights are negative, the prob-
lem is equivalent to the longest simple path problem
on −G, which is known to be NP-hard (Schrijver,
2004). Unfortunately, for many scenarios and reason-
able choices of λ negative cycles will be present, and
in these cases (P5) can be formulated as (LP) but with
binary constraints on x. While this ILP may be signif-
icantly faster to solve than (P3), the complexity is the
same and no-loop constraints must also be introduced
incrementally. However, in some scenarios it may be
reasonable to restrict the graph G to be acyclic, and
then the shortest path problem can always be solved
in linear time. A general graph may be reduced to a
directed acyclic graph by ordering the nodes by de-
creasing distance to the target node, and only keeping
edges reducing the distance, thus forcing the sensor
to move monotonically towards the destination. This
will of course not work for purely exploratory scenar-
ios where the start and end points may be near.
Even with this significantly simplified formulation
sacrificing the interdependence of measurements, the
problem is still not easy in general. We therefore in-
troduce a stochastic genetic algorithm applicable to
all problem formulations.
4.2 A Genetic Algorithm
Genetic algorithms (GA) are a class of evolutionary
optimization algorithms which emulate the process of
natural selection. A population of candidate solutions
is maintained, and in every iteration of the algorithm,
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
414

a new population is generated by mutation and cross-
ings of individuals of the previous generation. The
chance of an individual producing offspring in the
next generation is proportional to that individual’s fit-
ness, calculated from the corresponding value of the
function being minimized. Genetic algorithms have
been found to be quite efficient in providing good so-
lutions to many combinatorial optimization problems,
including TSP (Choi et al., 2003; Schmitt and Amini,
1998) and path planning (Davoodi et al., 2013), which
motivates the use here.
To use a genetic algorithm, one must choose a rep-
resentation for a candidate solution, and define unary
mutation and binary crossover operators. In this work,
each individual is described simply as a sequence of
vertices constituting the path. The GA framework
used is completely standard; for brevity we describe
only the important steps below.
Initialization The first step is to generate candidate
solutions, in this case paths in G from the source to
the terminal node. Unless we have some a priori in-
formation on the characteristics of the optimal solu-
tion, these should be spread out uniformly across the
space of all feasible paths. Unfortunately, truly uni-
form sampling of simple paths on a general graph ap-
pears to be a difficult problem. Reasonably random
paths, however, may be obtained using random order
depth-first search (DFS), loop-erased random walk
(Lawler, 2012), or for undirected graphs by comput-
ing the minimum cost spanning tree with randomized
edge weights, and extracting the unique path in the
tree. If candidate solutions have been obtained using
any of the heuristic methods based on the SDP relax-
ation, these can be included in the initial population
and will then be refined.
Mutation Operators A mutation operator should
introduce “noise” or randomnessinto an existing path,
while preserving its main features. In practice, sev-
eral mutation operators are often employed, exploit-
ing problem-specificheuristics. To modify a path, just
randomly replacing vertices is not possible, since not
every sequence of vertices is a valid path in the graph
G. Instead, our first operator selects two random cut
points along the path, and replaces the path in be-
tween with a random one generated using either ran-
domized DFS or loop-erased random walk. A second
operator instead replaces the section with the short-
est path between the cut points. This is motivated by
the fact that optimal paths are often quite regular, so
it makes sense to smooth out kinks. Both these oper-
ators are comparatively slow, so we also use a much
faster but more local operator which simply selects a
random vertex on the path, and replaces it with one
picked from the intersection of nodes reachable from
the preceding node with those with outgoing edges
incident on the next node on the path.
Crossover Operator The crossover operator takes
two existing paths as input and producesa mixed path,
containing parts of both, assuming they cross at some
point. This is accomplished by selecting a random
simple path on the graph obtained from G consisting
only of the edges on the two paths.
Local refinement To speed up convergence to a lo-
cally optimal solution, paths may be optimized by
systematically applying the fast local mutation oper-
ator described above in a deterministic fashion. Each
node on the path, visited in random order, is re-
placed with the neighbor which minimizes the objec-
tive function.
With the formulation (P2), we run the risk of gen-
erating infeasible paths in the course of the genetic
algorithm. A simple solution is to reject any infeasi-
ble path obtained and repeat the mutation or crossover
operation until a feasible realization is produced. It is
easy to verify that if the inputs are feasible, the oper-
ators defined above will eventually produce feasible
output. However, depending on how close L is to the
lower bound of feasibility, this may take an unreason-
able amount of time. The very simplest solution is to
transform the length constraint to a hard penalty term
in the objective, e.g.
min. F
I
0
+
∑
i∈p
I
i
−1
+ B
{p : length(p)≤L}
(2)
where B
S
is the barrier function for the set S s.t.
B(x) = 0 if x ∈ S and ∞ otherwise.
5 STRATIFIED SOLUTION
STRATEGY
The genetic algorithm will quickly find good solu-
tions if the search space is not too large. For large
grids with many hundreds of nodes and large neigh-
borhood connectivities, the algorithm risks getting
stuck in local optima, often producing implausible-
looking paths. We therefore propose to reduce the
search space by substituting a smaller graph, based on
the solution of the SDP relaxation of the problem, to
obtain a good initialization which can then be refined
on the full graph.
DiscreteOptimalViewPathPlanning
415

5.1 Reducing the Graph
The idea is to keep only a subset of the N most impor-
tant nodes, as indicated by the fractional SDP solu-
tion α
∗
. Interpreting these values as probabilities, we
draw N nodes without replacement, selecting nodes in
proportion to their α
∗
-value. The reduction in the co-
variance achieved using only these nodes is computed
and maximized through repeated random sampling of
the subset.
Once a subset has been chosen, a new fully con-
nected graph is formed, where edges between the
nodes represent the shortest path between them in the
original graph. This allows the mapping of paths on
the reduced graph to the full graph where they can
be evaluated. The genetic algorithm can now be run
without modification on the reduced graph, where the
parameter N can be chosen to trade fidelity for con-
vergence speed.
6 EXPERIMENTS
Due to the general formulation of the basic problem,
many different scenarios can be accommodated by
adapting the graph G and edge weights c
ij
, which
do not need to fulfill geometric constraints such as
the triangle inequality. For example, each node can
represent a camera position and an orientation, and
the connectivity between poses can be defined so as
to constrain angular velocity on the path. Purely ex-
ploratory behavior can be achieved by selecting start
and/or destination nodes as “super-nodes” connected
to every other node with zero weight, thus effectively
permitting arbitrary start and destination points. Typi-
cally, we know less about the scene further away from
the starting point, so the predictions of what will be
seen, or what obstacles lay ahead, may be incorrect.
Therefore one should plan with caution; by weight-
ing the information matrices based on distance to the
starting node, such behavior can be incorporated.
In the synthetic experiments below, each node
(except super-nodes) has an associated camera pose
defining position and orientation. The environment
structure is represented by 3D points, each consid-
ered independently estimated such that the initial
information matrix I
0
is block diagonal (in fact we
let it be the identity matrix so that the uncertainty
is on the order of the scene scale). To compute the
information gained from acquiring an image at a
certain pose, the standard pinhole camera model is
used, so that the relation ˆx = f(P,X) between a world
point X and its projection ˆx is given by
Figure 1: Cameras looking at a point cloud are placed on an
8-connected unit grid. Top left, the greenness and thickness
of edges is proportional to x
∗
ij
, the corresponding variable
of the solution to the relaxed SDP (P3), using the maxi-
mum eigenvalue scalarizing function and λ = 2. Due to the
symmetry of the problem, both a left and right path seem
to be given equal consideration. The lower bound obtained
is 61.1. Top right, the same problem with the path (green)
found by the genetic algorithm among possible positions
(blue), with a cost of 67.3. The third plot shows the same
problem but with λ = 40 and final cost 32.6, as compared
to the lower bound of 23.0. Depending on problem charac-
teristics, bounds may be more or less tight.
f(P,X) =
P
1
X + P
13
P
3
X + P
33
,
P
2
X + P
23
P
3
X + P
33
⊤
(3)
where P
i
is the i:th row of the camera matrix. Given
a point
¯
X, the corresponding block of I
i
is computed
as J
⊤
Σ
−1
J, where J =
d f
dX
(P
i
,
¯
X)
is the projection Ja-
cobian and Σ the assumed measurement error covari-
ance on the image plane. However, if
¯
X is out of the
camera’s field of view or too far away, the block is set
to zero. In Fig. 1–5 different experiments are shown
2
;
the details of the setup and results are in the figure
captions. Note that in these experiments, the online
nature of the problem is not demonstrated; in real use,
as the sensor moves and new information becomes
available, the structure and uncertainties need to be
updated and the path re-planned. By seeding the op-
timizer at each stage with the previous solution, rapid
convergence is possible.
6.1 Practical Considerations
The choice of scalarizing function F can have a large
impact on the solution time of the SDP, depending on
2
Many of the plots in the PDF version of this paper are embed-
ded 3D models which may be viewed on-screen in recent versions
of Adobe Reader.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
416

Figure 2: The same situation as in Fig. 1, now solving prob-
lem (P2) with L = 30. Top left, the solution obtained by
solving the analog of the simpler problem (P5), giving a
cost of 92.3 compared to the SDP lower bound of 67.7. Top
right, the red nodes indicate the reduced graph obtained by
sampling the SDP solution with N = 20, and applying the
GA gives a path with cost 88.7. In the bottom plot, the GA
run on the full graph with cost 86.36. The simplified formu-
lation is qualitatively different from the others and focuses
on getting as close to the structure as possible while ne-
glecting the parallax effects. It is therefore not a suitable
approximation in many situations.
Figure 3: In this example, two nodes each are placed in
every point of an 8-connected unit grid. The two nodes rep-
resent a camera looking at either of two objects/obstacles.
Top left, the solution to the relaxed SDP (P4), using the
trace scalarizing function and L = 22. Nodes of the original
square grid whose combined shortest distance to the start
and destination nodes is greater than L have been removed,
since they cannot be part of a feasible solution. As in Fig. 1,
there appears to be two competing paths, with edge values
x
∗
ij
≈ 1/2. Top right, the path obtained from the simplified
formulation (P5), which works reasonably for this problem
instance. In the bottom plot, the solution obtained using the
proposed genetic algorithm. The corresponding objective
values are 192.1, 271.8 and 262.1. The gap between the
final objective and the lower bound given by the SDP is rel-
atively large, but the path obtained directly from the SDP
solution is still quite reasonable.
the dimension of the information matrices. To mini-
mize the trace of the covariance matrix, one variable
per eigenvalue is required, while the maximum eigen-
value cost only needs one. On the other hand, eval-
uating the trace cost function is typically faster. Fur-
thermore, the maximum eigenvalue is vulnerable to
outliers e.g. features which are not seen in any or too
few views. If such features are not removed in a pre-
processing step, the cost function can never decrease
below the initial uncertainty.
The algorithms were implemented in Matlab with
core functions in MEX C++. SDPs were set up us-
ing YALMIP (L¨ofberg, 2004) and solved using the
MOSEK interior-point optimizer (Dahl, 2012). For
the experiment in Fig. 4, solving the SDP with the
trace cost took 8.7 s as opposed to 4.2 s for the max-
imum eigenvalue, while the genetic algorithm (on the
full problem) runs at about 10 iterations per second on
the same Core 2 Duo 3.0 GHz computer, with a pop-
ulation of 60 individuals. With parallel processing of
individuals, speed can likely be increased manyfold.
Figure 4: In this experiment, we simulate an omnidirec-
tional camera by adding the information matrices of four
cameras at each location. Each cluster thus corresponds to
only one node of the graph. Top left, the SDP (P4) with
L = 43 gives a lower bound at 4.11. Top right, the solution
using the stratified approach, with cost 5.47. In the last plot,
the graph has been reduced to a DAG such that the observer
must move towards the target at every step. This limits the
search space making branch-and-bound tractable, the opti-
mal solution with cost 17.98 is shown next to the solution
of the simplified problem (P5) (pale green) with cost 30.81.
DiscreteOptimalViewPathPlanning
417
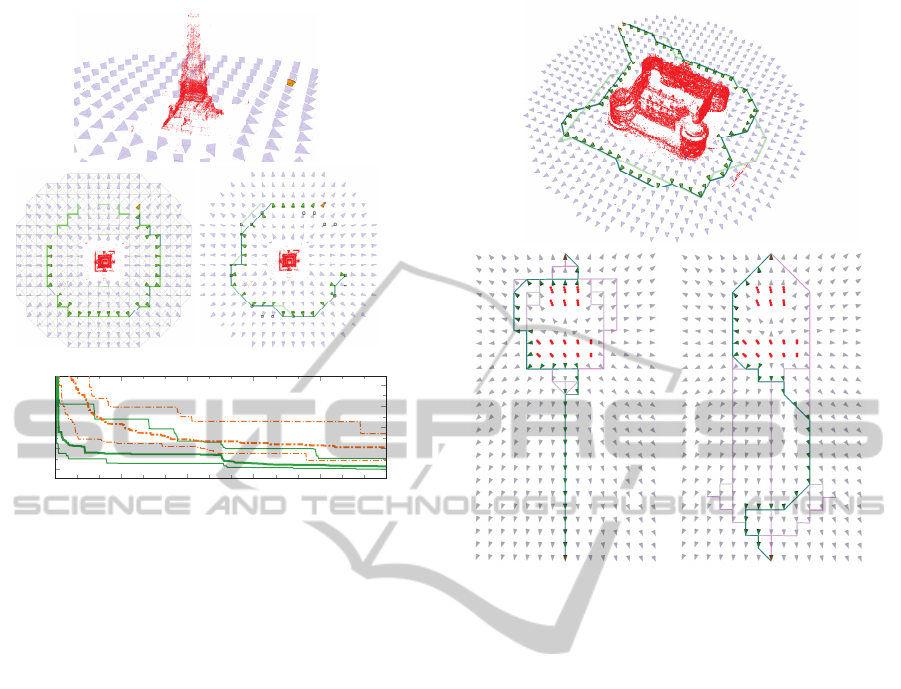
0 100 200 300 400
500
2.5
3
3.5
4
4.5
Iteration number
Φ(p)
Figure 5: Exploratory scenario with fixed start and free end
point. The point cloud of the monument has been reduced
to a few hundred representative points (by random sam-
pling) to constrain the information matrix dimension. In
the middle left plot, the SDP solution giving lower bound
1.76 along with the “filled in” path found as the shortest
path on the graph with weights 1− x
∗
(see Section 4), hav-
ing cost 3.18. Middle right, the GA solution on the reduced
graph obtained by sampling the SDP solution, with nodes
marked with black squares, shown in light green with cost
2.78. The dark green path is the result of the GA on the
full graph, seeded with the reduced solution, with cost 2.57.
Achieving similar cost using random initialization takes sig-
nificantly longer; the bottom graph shows the progression of
the objective value (Φ) over iterations of the proposed ge-
netic algorithms. The orange dashed curves show the max-
imum, minimum and median over 20 runs of the GA on
the full graph with random initialization. The green curves
show the same for the stratified approach, first running 250
iterations on the reduced graph, then switching to refine-
ment on the full graph. It is clear that the stratified scheme
converges much faster.
7 CONCLUSIONS
While the general problems considered in this paper
are demonstrably hard, satisfactory solutions can be
found sometimes directly from the SDP relaxation,
and often by the proposed genetic algorithm. In many
scenarios, the SDP solution gives hints as to what a
good path might look like, while in others it consists
of seemingly random, disconnected edges only. In
those cases the lower bound obtained is usually not
Figure 6: Top: stratified algorithm run on castle dataset, re-
duced to one hundred representative points using random
sampling. Bottom right: same scenario as on the left, but
here the information matrix at each node has been down-
weighted by the distance from the start node, to signify re-
duced confidence in future measurements. The pale purple
lines indicate the SDP solution, the green path the GA solu-
tion.
very tight and it is difficult to draw any conclusions
about the optimality of any path. This is of course to
be expected given the hardness of the problem. Nev-
ertheless, the SDP solution can always be used to seed
the GA optimizer in the proposed three-stage strati-
fied algorithm.
The linearized approximation (P5) sometimes
gives reasonable solutions, as in Fig. 3, but most
often does not show any proper long-term planning
behavior, as in Fig. 2. On a directed acyclic graph
(Fig. 4 right) it does have the advantage of being
extremely fast compared to the other methods.
For computational tractability, structure points
must be considered independent, and real point cloud
data need to be subsampled. How to best subsample
while preserving data characteristics has not yet
been considered. As the graph size and connectivity
increases, computational complexity also rises and
the quality of solutions attainable in reasonable time
drops. This limits the resolution of the discretization,
particularly in the orientation space, which means
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
418

local, continuous refinement may be a desirable
second step. This we leave to future work.
Full source code to replicate the exper-
iments in this paper are available at http://
github.com/sebhaner/nbv
discrete.
REFERENCES
Blaer, P. and Allen, P. (2007). Data acquisition and view
planning for 3-d modeling tasks. In Intelligent Robots
and Systems, 2007. IROS 2007. IEEE/RSJ Interna-
tional Conference on, pages 417–422.
Boyd, S. and Vandenberghe, L. (2004). Convex Optimiza-
tion. Cambridge University Press, New York, NY,
USA.
Choi, I.-C., Kim, S.-I., and Kim, H.-S. (2003). A genetic
algorithm with a mixed region search for the asym-
metric traveling salesman problem. Computers & Op-
erations Research, 30(5):773 – 786.
Dahl, J. (2012). Semidefinite optimization using MOSEK.
In 21st International Symposium on Mathematical
Programming.
Davoodi, M., Panahi, F., Mohades, A., and Hashemi, S. N.
(2013). Multi-objective path planning in discrete
space. Applied Soft Computing, 13(1):709 – 720.
Dunn, E., Olague, G., and Lutton, E. (2006). Parisian cam-
era placement for vision metrology. Pattern Recogni-
tion Letters, 27(11):1209–1219.
Dunn, E., van den Berg, J., and Frahm, J.-M. (2009). Devel-
oping visual sensing strategies through next best view
planning. In Intelligent Robots and Systems, 2009.
IROS 2009. IEEE/RSJ International Conference on,
pages 4001–4008.
Englot, B. and Hover, F. (2010). Inspection planning for
sensor coverage of 3d marine structures. In IROS,
pages 4412–4417. IEEE.
Foix, S., Kriegel, S., Fuchs, S., Aleny, G., and Torras, C.
(2012). Information-gain view planning for free-form
object reconstruction with a 3d tof camera. In Ad-
vanced Concepts for Intelligent Vision Systems, vol-
ume 7517 of Lecture Notes in Computer Science,
pages 36–47. Springer Berlin Heidelberg.
Fraser, C. S. (1984). Network Design Considerations for
Non-Topographic Photogrammetry. Photo Eng. and
Remote Sensing, 50(8):1115–1126.
Golovin, D. and Krause, A. (2010). Adaptive submodular-
ity: A new approach to active learning and stochastic
optimization. In 23rd Annual Conference on Learning
Theory, pages 333–345.
Haner, S. and Heyden, A. (2011). Optimal view path plan-
ning for visual SLAM. In Heyden, A. and Kahl, F., ed-
itors, Image Analysis, volume 6688 of Lecture Notes
in Computer Science, pages 370–380. Springer Berlin
/ Heidelberg.
Hollinger, G. A., Englot, B., Hover, F., Mitra, U., and
Sukhatme, G. S. (2012). Uncertainty-driven view
planning for underwater inspection. In ICRA, pages
4884–4891. IEEE.
Lawler, G. (2012). Intersections of Random Walks. Modern
Birkh¨auser Classics. Springer-Verlag New York.
L¨ofberg, J. (2004). Yalmip : A toolbox for modeling and
optimization in MATLAB. In Proceedings of the
CACSD Conference, Taipei, Taiwan.
Low, K.-L. and Lastra, A. (2006). An adaptive hierarchi-
cal next-best-view algorithm for 3d reconstruction of
indoor scenes. 14th Pacific Conference on Computer
Graphics and Applications, Taipei, Taiwan.
Montgomery, D. C. (2000). Design and Analysis of Exper-
iments. John Wiley & Sons Canada, Ltd., 5th edition.
Papadimitriou, C. H. and Steiglitz, K. (1998). Combinato-
rial Optimization: Algorithms and Complexity. Dover
Publications.
Schmitt, L. J. and Amini, M. M. (1998). Performance
characteristics of alternative genetic algorithmic ap-
proaches to the traveling salesman problem using path
representation: An empirical study. European Journal
of Operational Research, 108(3):551 – 570.
Schrijver, A. (2004). Combinatorial Optimization : Polyhe-
dra and Efficiency (Algorithms and Combinatorics).
Springer.
Singh, A., Krause, A., Guestrin, C., and Kaiser, W. J.
(2009). Efficient informative sensing using multiple
robots. J. Artif. Intell. Res. (JAIR), 34:707–755.
Trummer, M., Munkelt, C., and Denzler, J. (2010). Online
Next-Best-View Planning for Accuracy Optimization
Using an Extended E-Criterion. In Proc. International
Conference on Pattern Recognition (ICPR’10), vol-
ume 0, pages 1642–1645. IEEE Computer Society.
Vasquez-Gomez, J. I., Sucar, L. E., and Murrieta-Cid, R.
(2013). Hierarchical ray tracing for fast volumetric
next-best-view planning. 2013 International Confer-
ence on Computer and Robot Vision, 0:181–187.
Wenhardt, S., Deutsch, B., Hornegger, J., Niemann, H., and
Denzler, J. (2006). An Information Theoretic Ap-
proach for Next Best View Planning in 3-D Recon-
struction. In Proc. International Conference on Pat-
tern Recognition (ICPR’06), volume 1, pages 103–
106. IEEE Computer Society.
DiscreteOptimalViewPathPlanning
419
