Specific Electrodynamic Features of a Plasma Channel Created in

Gas by Powerful Femtosecond UV Laser Pulse

Application to the Problem of Guiding and Amplification of Microwave Radiation

A. V. Bogatskaya

1,2,3

, A. M. Popov

1,2,3

and E. A. Volkova

Department of Physics, Moscow State University, Moscow, 119991, Russia

D. V. Skobeltsyn Institute of Nuclear Physics, Moscow State University, Moscow, 119991, Russia

P. N. Lebedev Physical Institute, RAS, Moscow, 119991, Russia

Keywords: Laser and Microwave Radiation, Plasma Waveguide, Amplification of the Electromagnetic Radiation,

Electron Energy Distribution Function, Boltzmann Equation, Wave Equation in Paraxial Approximation.

Abstract: The evolution of strongly non-equilibrium plasma in a channel created in xenon by powerful KrF -

femtosecond laser pulse is studied. It is demonstrated that such a plasma channel can be used as a

waveguide for both transportation and amplification of the microwave radiation. The specific features of

such a plasma waveguide are studied on the basis of the self-consistent solution of the kinetic Boltzmann

equation for the electron energy distribution function in different spatial points of the gas media and the

wave equation in paraxial approximation for the microwave radiation guided and amplified in the channel.

The amplification factor in dependence on plasma channel radius, intensity and frequency of the input RF

radiation is analyzed.

1 INTRODUCTION

Recent technological progress in photonics and

materials science make it possible to obtain different

type of sources of radiation in terahertz (THz) or

subterahertz frequency range. Such sources of

radiation are of significant interest in a number of

research fields, such as chemistry (Skinner, 2010),

molecular biology (Meister, et al, 2013), medicine

(Titova, et al., 2013) and materials science (Grady,

et al., 2013). The continuously increasing interest for

terahertz and subterahertz radiation and its possible

applications is caused by its ability to penetrate

through a lot of materials (Jepsen, et al., 2011),

which are usually opaque in the infrared and visible.

Also, a number of physical and chemical processes

(vibrational dynamics of macromolecules and

crystalline lattices, reconstruction of hydrogen

bounds, etc.) can be controlled and governed by this

low frequency radiation.

The goal of our paper is to study the process of

transportation of focused microwave pulses in

subterahertz frequency band with low divergence

and possibility of their amplification in a plasma

channel at distances of order of 100 cm.

It is known, that if the electron energy distribution

function (EEDF) in a plasma is characterized by the

energy intervals with the inverse population, such

situation can be used for amplification of the

electromagnetic radiation (Bekefi, et al, 1961;

Bunkin, et al, 1973). Such EEDF can be easily

obtained in the process of multiphoton ionization of

a gas by a high-intensity laser pulse under the

conditions when the pulse duration is comparable or

even less than the average time interval between the

electron - atomic collisions. To realize the regime of

amplification one needs the gas of atoms or

molecules characterized by the transport cross

section increment with the energy where the peak of

photoelectrons is found to exist. Bogatskaya and

Popov (2013) had demonstrated that such a regime

of amplification of electromagnetic radiation can be

obtained in a xenon plasma created by powerful

(10

- 10

W/cm

) excimer KrF laser pulse

(



eV) of femtosecond duration in

subterahertz frequency band (

νω

< ,

is the

transport frequency) at time duration up to 100 ns. In

(Bogatskaya, et al, 2013) the possibility to amplify

the subtrerahertz radiation in different gases was

analyzed. The amplification regime in the air plasma

was studied in (Bogatskaya, et al, 2014a). It was

found that amplification in air plasma created by the

149

Bogatskaya A., Popov A. and Volkova E..

Speciﬁc Electrodynamical Features of a Plasma Channel Created in Gas by Powerful Femtosecond UV Laser Pulse - Application to the Problem of

Guiding and Ampliﬁcation of Microwave Radiation.

DOI: 10.5220/0005252801490156

In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 149-156

ISBN: 978-989-758-093-2

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

third harmonic of the Ti:Sa laser is also possible, but

positive value of a gain factor is found to exist only

for rather short durations ~ 20 ps. Hence there is a

possibility to amplify only extremely short radio-

frequency pulses of 2-3 cycles duration.

Bogatskaya, et al (2014b) demonstrated also

anomalous refractive properties of the strongly-

nonequilibrium plasma produced by the short UV

laser pulse. Such a plasma channel in the case of

low-frequency radiation (

νω

< ) will be optically

more dense in comparison with unionized gas, in

contrast to the typical situation when plasma is an

optically less dense medium. Just such a situation is

of interest in respect to creation of a sliding-mode

plasma waveguide (Zvorykin, et al., 2010). In the

present paper we develop the self-consistent

approach to the problem of transportation of the

radio-frequency (RF) pulse in the non-equilibrium

plasma channel. This approach is based on joint

solution of the Boltzmann equation for the EEDF

evolution in the strongly non-equilibrium plasma

and the wave equation in the paraxial approximation

for the transported through the channel RF pulse.

The process of guiding and simultaneous

amplification of the RF radiation in the plasma

channel formed by a powerful KrF laser

femtosecond pulse in xenon is studied in dependence

of plasma channel radius and different parameters of

the input RF pulse.

2 ELECTRODYNAMIC FEATU-

RES OF A NONEQUILIBRIUM

PLASMA CHANNEL

For the radiation with frequency

electrodynamic

features of a plasma channel are determined by

complex permittivity

'''

ωωω

ξξξ

i+= or complex

conductivity

'''

ωωω

σσσ

i+= which are related with

each other by the expression

πσ

i+=

(1)

The general expression for the complex conductivity

in a relatively weak electromagnetic field when the

two-term expansion for the EEDF

),( tn

is valid

can be written in a form (Ginzburg and Gurevich,

1960; Raizer, 1977):

),(

)(

))((



∞













∂

−

ενω

ωενε

(2)

Here

mne

πω

= is the plasma frequency

squared,

n is the electron density and

trtr

εεσεν

2)()( = is the transport frequency

of electron-atomic collisions,

)(

εσ

is the transport

cross section and

is the gas density. We should

also mention that the evolution of the EEDF is rather

slow in time and external electromagnetic field of

frequency

can be considered as the

quasimonochromatic one. The EEDF in eq. (2) is

normalized according to the condition

1),( =



εεε

dtn

If the transport frequency does not depend on energy

the complex refractive index is the same for an any

EEDF and for the case of weakly ionized plasma

(

trp

) can be written in the well-known

form

)(2)(2

'''

ωνω

νω

ωωω

trp

ninn

−

=+=

(3)

In particular, one derives from (3) that plasma is

optically less dense medium in comparison with the

unionized gas. Imaginary part of (3) determines the

absorption coefficient of the electromagnetic

radiation with frequency

in plasma (Raizer,

1977):

)(

''''2

trp

νω

ωω

ωωω

=×=×=

(4)

For an arbitrary dependence

)(

εν

the definite

expression for the EEDF is of importance. In this

case more general expressions for refractive index

should be used:



∞













∂

−













∂

−

−=−=

''2

νω

νε

πσ

νω

πσ

(5)

Typically the EEDF decreases with the increase of

energy, i.e.

∂∂n is negative and both of integrals

in (5) are positive. Hence, for such a more general

case plasma channel also appears to be optically less

dense in comparison with unionized media and the

absorption coefficient is positive,

However, as the energy intervals with positive

derivative

∂∂n contribute negatively to the

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

150

integrals (5), both of them may become negative.

Hence, plasma turns out to be an amplifying

medium. Also it can be optically more dense than

the neutral gas. The conditions, when integrals in (5)

can become negative are discussed in detail by

Bogatskaya, et al., (2014b). In particular, in the

energy range of inverse population in continuum for

low frequencies (

νω

<< ) the condition

0)( <

εσε

(6)

should be satisfied to obtain the positive gain factor

in a plasma, i.e. transport cross section should grow

up rapidly than the linear dependence. If the

condition

σε

(7)

is fulfilled plasma will be optically more dense

medium as compared with the neutral gas. The latter

condition is much softer than the previous one and is

fulfilled for a lot of atoms and molecules. If both of

inequalities (6) and (7) are satisfied a plasma

channel can be used as the waveguide for both

transportation and amplification of the microwave

radiation. For the xenon plasma at an atmospheric

pressure such a guiding regime with amplification

can be realized up to subterahertz frequency band.

To study temporal evolution of real and

imaginary parts of plasma conductivity or

permittivity in plasma channel the Boltzmann

kinetic equation for the EEDF in two-term

expansion was solved numerically taking influence

of the transported RF field and electron – electron

collisions into account. The details of the numerical

procedure as well as the information on the set of

cross sections used can be found in (Bogatskaya, et

al., 2013).

For the case of multiphoton ionization of xenon

by KrF laser radiation inelastic processes do not

contribute to the evolution of the EEDF as the

excitation potentials exceed the value of 8.31 eV

while the position of the lowest photoionization peak

is approximately 2.87 eV. At Fig.1 we present the

calculations of temporal evolution of the gain factor

per one electron and the real part of plasma

permittivity for the RF frequency

105 ×=

-1

and for different electronic densities. First, we note

that for rather low electronic densities both values

are found to increase in time while photoelectron

peak gradually shifts in time due to elastic collisions

towards lower energies but still locates in the range

where inequalities (6) and (7) are satisfied. Also it

can be seen that for rather small time intervals the

gain factor is proportional to the electronic density.

As about the real part of plasma permittivity

1Re −

, for small time intervals this value

increases even faster than electronic density (see

Fig.1b). On the other hand, the increment of the

electron density leads to faster maxwellization of the

EEDF which results in the rapid decrement of the

time interval during which the gain factor is still

positive and the real part of plasma permittivity is

greater than unity.

Figure 1: The gain factor (a) and the real part of plasma

permittivity (b) per one electron in xenon plasma for

different electronic concentrations (cm-3): 1 - 1010, 2 -

1011, 3 - 1012, 4 - 1013, 5 - 1014. Negative values

correspond to absorption of a RF radiation in plasma.

Results of calculations of the gain factor for

different values of radiation intensity with a

frequency

105 ×=

-1

are presented at Fig. 2 and

demonstrate that the time interval during which the

gain factor is positive reduces from 20 to 2 ns with

increase of RF intensity from zero to 10

W/cm

. For

the RF field intensity of 10 kW/cm

amplification in

a plasma channel is possible for very short times

about ~ 0.1 ns. From practical point of view it means

that microwave pulses of 2 ns duration can be

amplified up to the intensity of ~ 1 kW/cm

. We also

note that the amplification of RF pulse in the plasma

channel results in a decrement of electron energy,

i.e. an external electric field of a RF pulse leads to

the cooling of the plasma electron component.

SpecificElectrodynamicalFeaturesofaPlasmaChannelCreatedinGasbyPowerfulFemtosecondUVLaserPulse-

ApplicationtotheProblemofGuidingandAmplificationofMicrowaveRadiation

151

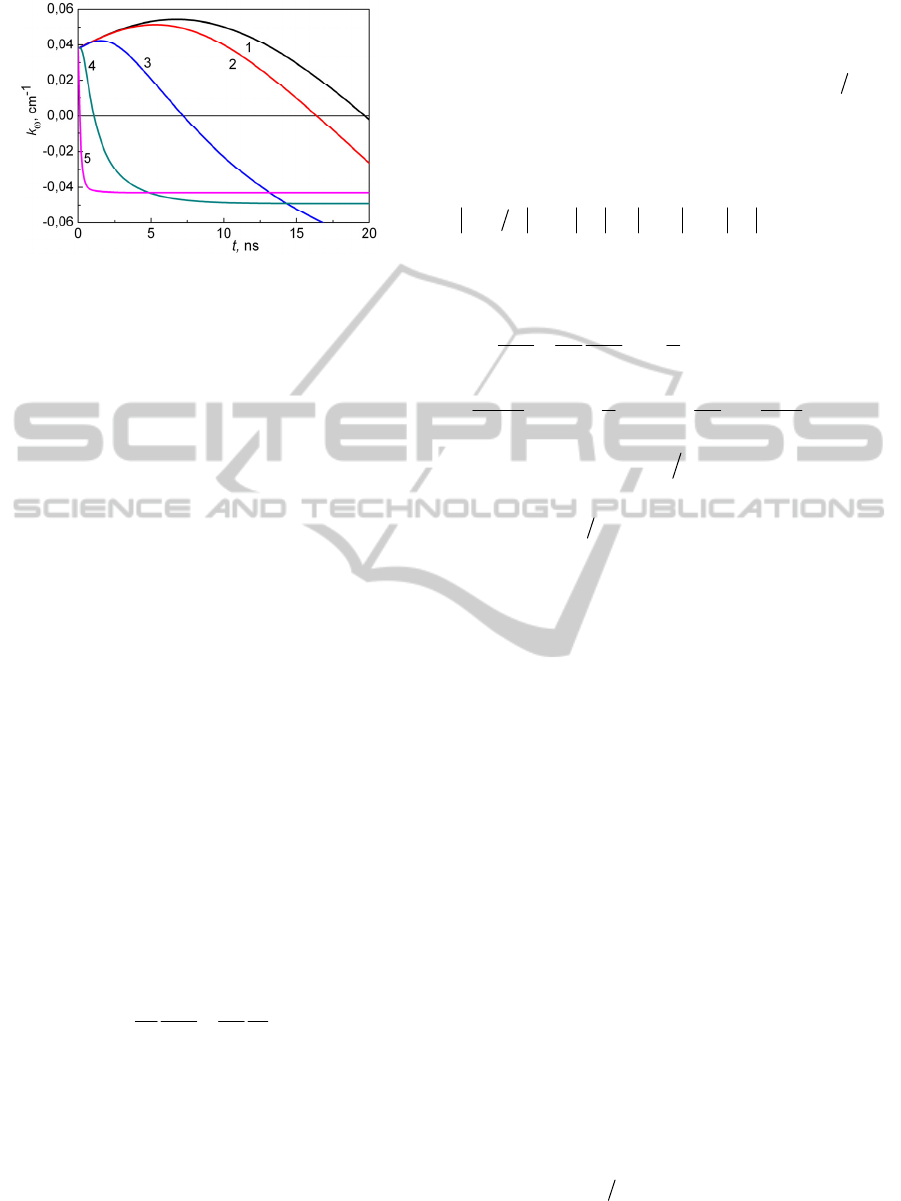
Figure 2: Time dependence of the gain factor of

electromagnetic radiation for different intensities of the

RF radiation (W/cm

): I=0 (1), 10 (2), 10

(3), 10

(4), 10

(5). The data obtained for electronic density

103 ×=

-3

and

105 ×=

-1

3 PROPAGATION AND AMPLI-

FICATION OF THE RF PULSES

IN A PLASMA WAVEGUIDE

In this chapter we will discuss propagation of a short

RF pulse in a plasma channel created in xenon by a

femtosecond KrF laser pulse. Our analysis is based

on the self-consistent solution of the wave equation

for the RF pulse and the Boltzmann equation for the

EEDF in a plasma channel in different spatial points.

If the RF field is weak enough and do not influence

on plasma parameters the set of Boltzmann

equations can be solved independently from the

wave equation. In this case the RF pulse propagates

in a channel with given plasma properties slow

varying in time. Much more complicated is the

situation when the RF pulse is strong enough and

produces significant effect on evolution of the

EEDF. In this case the self-consistent analysis of the

equations is mandatory.

As it is known, propagation of the electromagnetic

radiation in the medium is described by the wave

equation:

∂

−∇



(8)

Here



is an electric field strength and



is a

density of electric current in a plasma. Further we

will suppose the field to be linearly polarized. To

analyze the process of microwave pulse propagation

qualitatively we use paraxial approximation for the

solution of eq. (8) (for details see the monograph of

Akhmanov and Nikitin (1997)). According to this

approximation for the pulse propagation along

direction electric field

E should be represented as,

()()

.exp),,(),(

tkzitzEtrE

ωρ

−⋅=



(9)

Here

E is the envelope of the RF pulse, ck

= is

the wave number and

is the perpendicular spatial

coordinate. If we neglect temporal dispersion, the

expression for the current density can be written in a

simple form

),(),( trEtrj



= . Assuming that

ωω

σωσ

<<∂∂ t

ωω

σσ

k<<∇

, i.e. plasma

conductivity is a slow-varying function in time and

space, one derives from (8) the following equation

for RF pulse envelope in the paraxial approximation













∂

+∇−=













∂

⊥

EkkiEk

πσ

(10)

where

ωωω

πσμ

=−=

is the plasma gain

factor (if

k plasma absorbs the radiation), and

ωπσ

ωω

21 in += is the complex refractive index.

The first term in the right part in Eq. (10) stands for

the diffraction divergence of the electromagnetic

field, the second one describes plasma focusing

(defocusing) features and the third term represents

the absorption (amplification) process. The last term

in the right part of (10) is small in comparison with

previous ones and gives some corrections to the

focusing/defocusing and amplification/absorption of

the wave field.

The case of our study is the situation when

k and

. Such a situation is of interest

with respect to creation of the plasma waveguide

being capable to amplify the transported radiation.

Actually, the amplification duration

ampl

corresponds to the amplification distance of about

ampl

(

ampl

is the time interval of the positive

gain factor existence) which equals to tens of

centimetres. The same is for focusing properties of

the plasma, but the guiding length is typically

several times longer. So, a laser pulse creates the

plasma channel characterized by an amplifying and a

guiding «trails» (see Fig. 3). If we launch a laser

pulse and a RF pulse just one after another

simultaneously, the last one will continually locate

in the amplifying and guiding zones of a laser pulse.

It can be seen from Eq. (10) that in the case

1''21Re >−=

ωπσ

ωω

n the plasma channel can

partly suppress the diffraction divergence of the RF

radiation. If the condition

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

152

1)1(Re

>− Rkn

(11)

(here

is the plasma channel radius) is satisfied

the channel will look like the waveguide and can

transport the radiation without divergence. For

105⋅=

-1

and 7.16≈= ck

-1

and

001.0~1Re −=

ωω

nn (see Fig. 1b) the guiding

regime of propagation will be realized for

2>R

cm. It means a laser pulse in order to create such a

plasma channel with electron density

10~

-3

should have the power at least in sub-Terawatt level.

Figure 3: Spatial structure of radio (1) and laser (2) pulses

for a given instant of time. Dash curves are spatial profiles

of the gain factor and the refractive index.

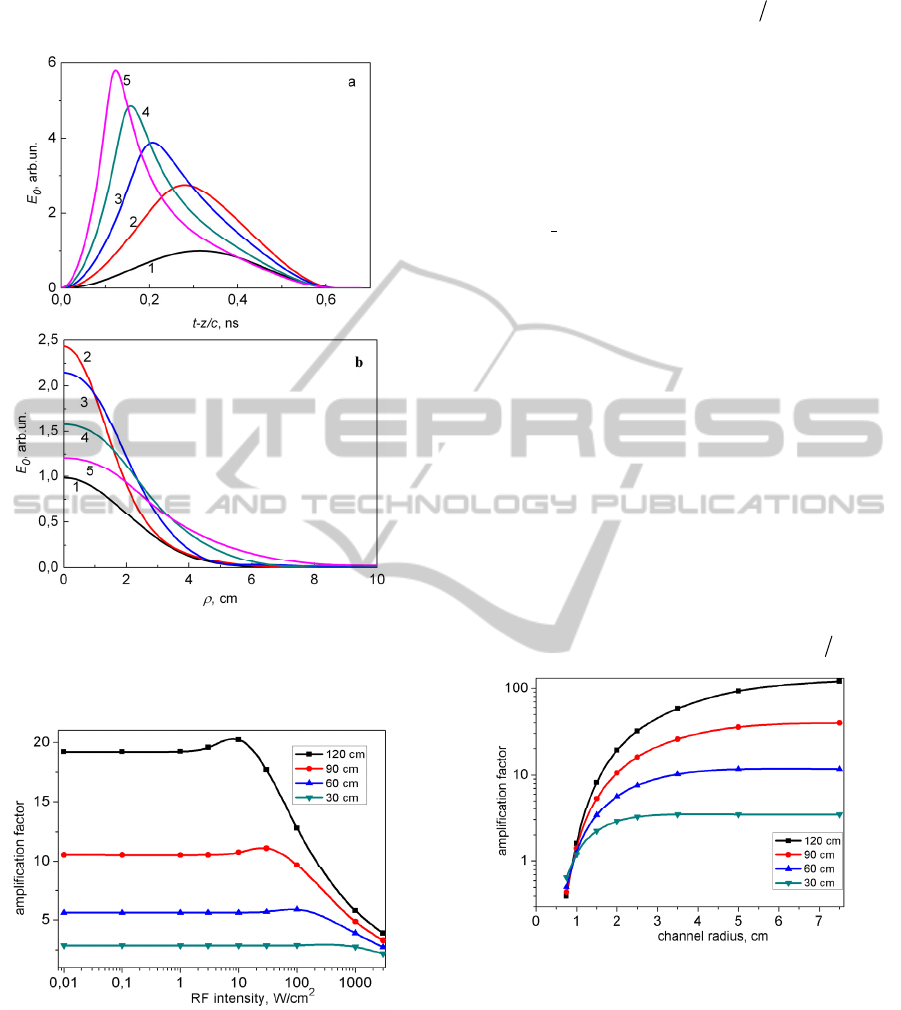
Figure 4: Temporal (1) and radial (2) profiles of the

electric field envelope of the amplifying pulse at different

propagation distances z: 1 – 0 cm, 2 – 30 cm, 3 – 60 cm, 4

– 90 cm, 5 – 120 cm. Initial peak intensity is 0.1 W/cm

First, we discuss the results of numerical integration

of the wave equation (10) for the case of weak field

when the contribution of the amplified RF pulse to

the EEDF evolution in the plasma channel can be

neglected. We assume that the RF pulse is

characterized by the sine-squared temporal envelope

)(sin~)(

0 p

ttE

τπ

, where

50=

)2(

ωπ

is the pulse duration. Typical distributions of the

electric field envelope

),,(

τρ

cztE −

for the

initial RF field and electron density distribution in

plasma channel Gaussian profiles, characterized by

the radius

cm versus the variable czt −=

(for

) and the radial variable

(for

that corresponds to the maximum of the envelope of

the initial pulse) are presented at Fig. 4. The first of

these distributions can be considered as the temporal

envelope of the pulse at different fixed values of z or

as a distribution over z - coordinate at a fixed instant

of time. For the RF pulse duration

50=

the

spatial length of the pulse is equal to

9.1≈

cm.

For such a pulse

04.0≈

k см

-1

and can be

considered to be nearly constant during the all

propagation time (see Fig. 2). The electric field

increases with propagation length approximately

exponentially

)exp(~

hzE with 024.0≈h cm

-1

This value is even little larger than

019.02 ≈

-1

, this difference arises from the partial focusing

effect during the propagation of the RF pulse in the

plasma waveguide. As about the radial distribution

(see Fig. 4b) it is nearly Gaussian one for all instants

of time.

The case of the initial RF pulse with relatively

high intensity when the guiding RF field contributes

significantly to the evolution of the EEDF in the

plasma channel is more interesting. The results of

such calculations for the initial RF intensity

10=I

W/cm

are presented at Fig. 5. It can be

seen for the same propagation length 120 cm there is

an increase in the peak intensity of the RF pulse just

only approximately six times. The pulse shape is

found to be distorted significantly, mainly because

of the dominant enhancement at the leading edge of

the pulse. As about the trailing edge of the pulse it

can be seen at fig.6a that for the propagation

distances of 60 cm and more the significant

absorption of the RF intensity is observed due to

dramatic reconstruction of the EEDF by the RF

pulse. As a result, the shorter RF pulse with leading

SpecificElectrodynamicalFeaturesofaPlasmaChannelCreatedinGasbyPowerfulFemtosecondUVLaserPulse-

ApplicationtotheProblemofGuidingandAmplificationofMicrowaveRadiation

153

peak and broader spectrum is formed in such a

propagation regime.

Figure 5. Temporal (1) and radial (2) profiles of the

electric field envelope of the amplifying pulse at different

propagation distances z: 1 – 0 cm, 2 – 30 cm, 3 – 60 cm, 4

– 90 cm, 5 – 120 cm. Initial peak intensity is 10

W/cm

Figure 6: Field amplification factor in dependence of the

input RF intensity for different propagation lengths (30,

60, 90 and 120 cm). Electronic density is

103×=

and

5.0=

THz, channel radius is 2 cm.

Let us now discuss the results of simulation

obtained for different initial parameters of an input

RF pulse (its peak intensity and frequency) and the

radius of the plasma channel. The dependence of the

field amplification factor

)0()(

== zEzEg for

different propagation lengths in dependence on peak

input RF intensity is presented at Fig. 6. In low

intensity limit the amplification factor do not depend

on the input intensity and reaches the value

20≈g

for the propagation length

120=L

cm. It means that

output intensity increases ~400 times in comparison

with the input one. In the range of input intensities

above 100 W/cm

the g-factor drops dramatically.

This results due to the rapid relaxation of the EEDF

in the presence of RF field and decrement of the

gain factor in the plasma channel. We also note the

local maximum which is well pronounced at the

input intensity 10 W/cm

for the L=120 cm. This

maximum appears to exist due to the additional

focusing effect of a plasma arising in the process of

EEDF relaxation at moderate intensities.

The dependence of the field amplification factor

on radius of a plasma channel is presented at Fig. 7.

The most important is the fact that in agreement with

(11) effective amplification of the RF pulse takes

place only for plasma channels of radius

2≥R

cm.

For

1<R

cm both effects of amplification and

plasma focusing cannot compensate the diffraction

divergence of the pulse and its intensity decreases

along the propagation length. The increment of the

channel radius above 2-4 cm leads to the saturation

of amplification factor at a level

)2exp( Lkg

= .

Figure 7: Field amplification factor in dependence of the

plasma channel radius for different propagation lengths

(30, 60, 90 and 120 cm). Electronic density is

103 ×=

-3

5.0=

THz and input RF intensity is

0.01 W/cm

It should be mentioned that there is an existence

of the optimal value of frequency for effective RF

pulse amplification for a given channel radius (see

data at Fig. 8). For R=2 cm this frequency is rather

close to

105 ×=

-1

. The decrement of the

frequency and, hence, increment of the microwave

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

154

radiation wavelength leads to the violation of the

inequality (11) determining realization of the

guiding regime. On the other hand, the amplification

factor also falls down for high frequencies. When

the condition

νω

≥ is fulfilled the gain factor

becomes negative and amplification regime is

impossible for any radius of the plasma channel. In

the situation under study the regime of amplification

can be realized for microwave frequencies

8.1≤

THz.

Figure 8: Field amplification factor in dependence of RF

pulse frequency for different channel radius R. Electronic

density is

103 ×=

-3

, input RF intensity is 0.01

W/cm

and propagation length is L=90 cm.

Figure 9: Field amplification factor in dependence of the

time delay between laser and RF pulses for different

propagation lengths (30, 60, 90 and 120 cm). Electronic

density is

103 ×=

-3

, input RF intensity is 0.01

W/cm

and R=2 cm.

All discussed above data were obtained for the

zero delay between optical and RF pulses. On the

other hand, the data presented at Fig. 1 lead to the

conclusion that in order to increase the amplification

factor we should introduce the time delay between

laser and microwave pulses. The value of this delay

depends on the electronic density in the channel and

for

103 ×=

-3

this delay should be of order of

10 ns. The data presented at Fig. 9 confirm the

above conclusion. The optimal delay in our situation

is ~7.5 ns. Due to increment of the gain factor and

refractive index during the initial period of the

EEDF evolution (see Fig. 1) such a delay value

allows to increase the amplification factor

approximately five times.

4 CONCLUSIONS

Thus, in this paper it is shown that the

nonequilibrium plasma channel created in xenon by

powerful femtosecond KrF laser can be used to

guide and amplify the RF pulses till subterahertz

frequency band. There is an opportunity to reach

significant amplification by the launching of the

laser and RF pulses, so that the RF pulse is

continually located in the guiding and amplification

zones of the laser pulse. Optimal parameters of

radio-frequency pulse for guiding and amplification

are discussed.

ACKNOWLEDGEMENTS

This work was supported by the Russian Foundation

for Basic Research (projects no. 14-02-31114, 15-

02-00373), by the noncommercial “Dynasty”

Foundation (program for support of students) and

the Educational Complex of the P.N.Lebedev

Physical Institute within the framework of the

Program of the Presidium of the Russian Academy

of Sciences for Young Researchers. Numerical

modeling was performed on the SKIF-MSU

Chebyshev supercomputer.

REFERENCES

Akhmanov, S. A. and Nikitin, S. Yu., 1997. Physical

Optics, Oxford.

Bekefi G., Hirshfield Y.L. and Brown S.C., 1961. Phys.

Fluids, 4, 173.

Bogatskaya, A. V. and Popov, A. M., 2013. JETP Lett.,

97, 388.

Bogatskaya, A. V., Volkova, E. A. and Popov, A. M.,

2013. Quantum Electronics, 43, 1110.

Bogatskaya, A. V., Volkova, E. A. and Popov, A. M., (a)

2014. In Proceedings of 2nd International Conference

on Photonics, Optics and Laser Technology, Lisbon,

Portugal, p. 199-204.

Bogatskaya, A. V., Smetanin, I. V., Popov, A. M., (b)

2014. J. Russian Laser Res., 35, 205.

Bunkin, F. V., Kazakov, A. A. and Fedorov, M. V., 1973.

Sov. Phys. Usp., 15, 416.

SpecificElectrodynamicalFeaturesofaPlasmaChannelCreatedinGasbyPowerfulFemtosecondUVLaserPulse-

ApplicationtotheProblemofGuidingandAmplificationofMicrowaveRadiation

155

Ginzburg, V. L. and Gurevich, A. V., 1960. Sov. Phys.

Usp. 3, 115.

Grady, N. K., et al., 2013. Science, 340, 1304.

Jepsen, P. U., Cooke, D. G. and Koch, M., 2011. Laser

Photonics Rev., 5, 124.

Meister, R., et al., 2013. PNAS, 110, 1617.

Raizer, Yu. P., 1977. Laser - Induced Discharge

Phenomena, Consultants Bureau, New York.

Skinner, J. L., 2010. Science, 328, 985.

Titova, V. T., et al., 2013. Scientific Reports, 3.

Zvorykin, V. D., Levchenko, A. O., Smetanin, I. V., and

Ustinovski, N. N., 2010. JETP Lett., 91, 226.

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

156