Adaptive Segmentation based on a Learned Quality Metric

Iuri Frosio

and Ed R. Ratner

Senior Research Scientist, NVIDIA, 2701 San Tomas Expressway, Santa Clara, CA 95050, U.S.A.

CTO, Lyrical Labs, 332 South Linn St. Suite 32, Iowa City, IA 52240, U.S.A.

Keywords: Superpixel, Adaptive Segmentation, Machine Learning, Segmentation Quality Metric.

Abstract: We introduce here a model for the evaluation of the segmentation quality of a color image. The model

parameters were learned from a set of examples. To this aim, we first segmented a set of images using a

traditional graph-cut algorithm, for different values of the scale parameter. A human observer classified

these images into three classes: under-, well- and over-segmented. This classification was employed to learn

the parameters of the segmentation quality model. This was used to automatically optimize the scale

parameter of the graph-cut segmentation algorithm, even at a local scale. Experimental results show an

improved segmentation quality for the adaptive algorithm based on our segmentation quality model, which

can be easily applied to a wide class of segmentation algorithms.

1 INTRODUCTION

Segmentation represents a key processing step in

many applications, ranging from medical imaging

(Sun, 2013; Frosio, 2006; Achanta, 2012) to

machine vision (Sungwoong, 2013; Alpert, 2012)

and video compression (Bosch, 2011). Segmentation

algorithms aggregate sets of perceptually similar

pixels in an image (Achanta, 2012; Kaufhold, 2004).

These sets capture image redundancy, they are used

to compute image characteristics and simplify

subsequent image processing.

In the recent past, graph-cut segmentation

algorithms attracted lot of attention because of their

computational efficiency and capability to adhere to

the image boundaries (Achanta, 2012). Most of these

are based on the seminal paper by Felzenszwalb and

Huttenlocher, (Felzenszwalb, 2004), that assert that

a segmentation algorithm should “capture

perceptually important groupings or regions, which

often reflect global aspects of the image.” The

graph-cut algorithm:

(i) builds an undirected graph G = (V, E), where

∈

V is the set of pixels of the image that has to be

segmented and (v

, v

)

∈

E is the set of edges that

connects pairs of neighboring pixels;

(ii) associates a non-negative weight w(v

, v

) to

each edge with a magnitude proportional to the

difference between v

and v

;

(iii) performs image segmentation by finding a

partition of V such that each component is

connected, the internal difference between the

elements of each component is minimal and the

difference between elements of different

components is maximal.

Figure 1: Panel (a) shows a 640x480 image; panels (b-d)

show the segmentation obtained with the algorithm in

(Felzenszwalb, 2004), with

= 0.5, min size = 5 and k = 3,

100 and 10,000 respectively.

A predicate determines if there is a boundary

between two adjacent components C

and C

, that is:

()

() ()







otherwisefalse

CCMIntCCDififtrue

CCD

2121

, (1)

where Dif(C

, C

) is the difference between the two

components, defined as the minimum weight of the

283

Frosio I. and Ratner E..

Adaptive Segmentation based on a Learned Quality Metric.

DOI: 10.5220/0005257202830292

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 283-292

ISBN: 978-989-758-089-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

set of edges that connects C

and C

; Mint(C

, C

) is

the minimum internal difference, defined as:

( ) () () () ()

[]

221121

,min, CCIntCCIntCCMInt

ττ

++=

, (2)

where Int(C) is the largest weight in the minimum

spanning tree of the component C (and it describes

therefore the internal difference between the

elements of C) and

to establish whether there is evidence for a boundary

between two components (it forces two small

segments not to fuse if there is strong evidence of

difference between them).

In practice, k is the most significant parameter of

the algorithm, as it sets the scale of observation

(Felzenszwalb, 2004). The authors demonstrated that

the algorithm generates a segmentation that is

neither too fine nor too coarse, but the definition of

fineness and coarseness essentially depends on k that

has to be carefully set to obtain a perceptually

reasonable result. Small k values lead to over-

segmentation (Fig. 1b), whereas a large k may

introduce under-segmentation (Fig. 1d). It is worth

noticing that the definition of a scale parameter is

common in many other superpixel algorithms like

SLIC (Achanta, 2012), where this parameter is

generally referred to as the size of the superpixel.

Assuming that an optimal segmentation algorithm

should extract “perceptually important groupings or

regions”, finding the optimal k for the graph-cut

algorithm (Felzenszwalb, 2004) remains up to now

an open issue. An analogue problem is the selection

of the threshold value used to identify the edges in

edge-based segmentation (Canny, 1986;

Senthilkumaran, 2009). Furthermore, even recently

proposed, efficient superpixel algorithms like SLIC

require a-prori definition of the typical scale of the

segments.

As an attempt to overcome this limitation, we

developed a heuristic model that quantifies the

segmentation quality for a color image. The

parameters of the model were learned from a set of

examples, classified by a human observer into three

classes: under-, well- and over-segmented. We

employed this model to automatically and adaptively

modulate k in graph-cut segmentation, such that a

human observer ideally classifies each part of the

image as well-segmented. We compared then the

segmentation obtained with the proposed method

with the original graph-cut algorithm and with the

recently proposed SLIC, showing that our model

furnishes a reasonable heuristic which can be used to

effectively improve and automate existing

segmentation algorithms.

2 METHOD

2.1 Preliminaries

Fig. 2 shows the block of 160x120 pixels

highlighted in Fig. 1a and segmented with graph-cut

for different values of k. For 1 ≤ k ≤ 50, over-

segmentation occurs: areas that are perceptually

homogeneous are divided into several segments. The

segmentation looks fine for 75 ≤ k ≤ 200, whereas

for 350 ≤ k ≤ 10,000 only few segments are present

(under-segmentation). To derive our segmentation

quality model we need to turn such qualitative

evaluations into a measurable, quantitative index.

To this end, we consider the information in the

original image, img, that is captured by the

segmentation process. We define the color image,

seg, obtained by assigning to each pixel the average

RGB value of the corresponding segment. For each

color channel, {R, G, B}, we compute the symmetric

uncertainty U of img and seg as (Witten, 2002):

{}

{} {}

()

{}{}

seg

BGR

img

BGR

BGRBGR

BGR

segimgI

,,,,

, (3)

where S

indicates the Shannon’s entropy (Witten,

2002), in bits, of the channel i of the image j,

whereas I(u,v) is the mutual information, in bits, of

the images u and v. The symmetric uncertainty

expresses the percentage of bits shared by img and

seg for each color channel; it is zero when the

segmentation is uncorrelated with the original color

image channel, whereas it is one when the

segmentation represents any fine detail (including

noise) in the corresponding channel of img. Since

Figure 2: Weighted uncertainty, U

, as a function of k, for

the 160x120 block highlighted in Fig. 1a, segmented with

the graph-cut algorithm in (Felzenszwalb, 2004), for

0.5, min size = 5 and k ranging from 1 to 10,000. The

classification into under-, well- or over-segmented class

operated by a human observe is also reported.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

284

different images have different information in each

color channel (for instance, the image in Fig. 1 has

lot of information in the green channel), we define

the following weighted uncertainty index:

seg

SSS

SUSUSU

⋅+⋅+⋅

. (4)

The index U

is in the interval [0, 1], and it is

represented in Fig. 2 as a function of k, for the

160x120 block in Fig. 1a. This curve empirically

demonstrates the strict relation between the

segmentation quality and U

, which we observed on

a large number of images: U

decreases

(approximately monotonically) for increasing k,

passing from over-segmentation to well- and under-

segmentation.

2.2 Segmentation Quality Model

The curve depicted in Fig. 2 represents the specific

case of the 160x120 block in Fig. 1a: U

values

Figure 3: Classification of segmented 160x120 sub-images

in the available dataset, performed by a human observer,

represented in the (log(k), U

) plane, for image resolutions

of 320x240 (panel (a)) and 640x480 (panel (b)) pixels.

The magenta and red lines represent the boundaries of the

area including the well-segmented sub-images (see text for

details); the green line is the ideal line for segmentation.

associated to a reasonable segmentation in this

specific case may not be adequate for other images.

An image with a lot of small details requires for

instance high U

values to represent them all. On the

other hand, small U

values are associated to a

reasonable segmentation quality in homogenous

areas, where most of the image information comes

from the image noise and not from image details that

are perceptually important.

To derive a general segmentation quality model,

we have therefore considered a set of 12 images

including flowers, portraits, landscapes and sport

images at 320x240 and 640x480 resolutions. We

divided each image into sub-images of 160x120

pixels and segmented each sub-image with the

graph-cut algorithm in (Felzenszwalb, 2004), for

0.5, min size = 5 and k ranging from 1 to 10,000.

Each segmented sub-image was classified by a

human observer as over-, well- or under-segmented

and for each of them we computed U

as in Eq. (4).

Fig. 3 shows the results of this classification

procedure. A single value of k cannot be used to

identify well- segmented blocks at a given

resolution, but an area in the (log(k), U

) can be

defined for this purpose (notice we used log(k)

instead of k to better highlight the difference along

the horizontal direction). We have therefore divided

the (log(k), U

) space into three different regions

representing under-, well- or over-segmented

images, by means of a classifier partially inspired to

Support Vector Machines (Shawe-Taylor, 2004). In

particular, let us consider two classes of points in the

(log(k), U

) space, for instance the under- and well-

segmented cases. To estimate the (m, b) parameters

of the curve U

= m·log(k) + b that divides these

two regions, we minimized the following cost

function (through the Nelder-Mead simplex):

()



⋅

+−⋅

+⋅

+−⋅

iWE

iWi

iUS

iWi

bUkm

bmE

log

, (5)

where N

and N

are respectively the number of

under- and well-segmented points and

US,i

and

WE,i

are 0 if the point is correctly classified (i.e., for any

under-segmentation point that does not lie under the

= m·log(k) + b curve) and 1 otherwise. The cost

function in Eq. (5) is the sum of the distances from

the line U

= m·log(k) + b of all the points that are

misclassified. The estimate of the two lines that

divide the (log(k), U

) is performed independently.

Finally, the average line between these two (in green

in Fig. 3) is assumed to be the optimal line for

AdaptiveSegmentationbasedonaLearnedQualityMetric

285

segmentation in the (log(k), U

) plane.

In the next section, we will detail how this learned

model can be used to automatically identify the

optimal k and to subsequently develop a spatially

adaptive segmentation algorithm. With this aim, it is

important to remember that we have experimentally

observed an approximately monotonic, S-shaped

curve U

= U

[log(k)] in the (log(k), U

) space for

each sub-image (Figs. 2 and 3): for small k values,

is constant and over-segmentation occurs;

increasing k, U

decreases rapidly and well-

segmented data are observed in this area; finally, for

large k, under-segmentation occurs and a new

plateau is observed on the curve. Given the shape of

the typical U

= U

[log(k)] curve in the (log(k),

), a point of intersection between the optimal line

for segmentation and the U

= U

[log(k)] curve can

always be identified. This observation represents the

key idea for the development of the estimate of the

optimal k parameter described in the next Section.

3 RESULTS

3.1 Automatic Identification of K

Figure 4: Iterative estimate of k for a 160x120 sub-image.

The iterative process is shown in the (log(k), U

) plane in

the upper panel. The lower panels show the corresponding

segmentations. Convergence is reached after 5 iterations.

The optimal line for segmentation, m·log(k) + b,

constitutes a set of points in the (log(k), U

) that are

associated to well-segmented sub-images by a

human observer. Given a 160x120 sub-image, the

optimal k is defined here as the one that generates a

segmentation whose weighted symmetric

uncertainty U

is as close as possible to m·log(k)+ b.

Such value is computed iteratively through a

bisection approach: at iteration 0, the sub-image is

segmented for k

Left

= 1 and k

Right

= 10,000 and the

corresponding values of U

W,Left

and U

W,Right

are

computed. At the next iteration, the mean log value

(k = exp{[log(k

Left

)+log(k

Right

)]/2}) is used to

segment the sub-image, the corresponding U

computed and k

Left

or k

Right

are substituted to k,

depending on the fact that (log(k

Left

), U

W,Left

), (log(k),

), and (log(k

Right

), U

W,Right

) lie under or above the

optimal segmentation line. Fig. 4 illustrates this

iterative procedure: the initial values of k clearly

lead to strong under- or over-segmentation, but after

5 iterations the image segmentation appears

reasonable and the corresponding point in the

(log(k), U

) space lies close to the optimal

segmentation line.

3.2 Adaptive Selection of K

To segment a 320x240 or 640x480, a set of adjacent

sub-images has to be considered. Nevertheless,

putting together the independent segmentations of

each sub-image does not produce a satisfying

segmentation, since segments across the borders of

the sub-images are divided into multiple segments.

We have therefore modified the original graph-cut

segmentation algorithm in (Felzenszwalb, 2004) to

obtain an iterative algorithm that makes use of an

adaptive scale factor k(x, y), instead of the constant

parameter used in the original algorithm (the

threshold function in Eq. (2), thus becomes

(C, x, y)

= k(x, y)/|C|).

The scale map k(x, y) was obtained with the

following procedure; first, the image was segmented

using k(x, y) =1 and k(x, y) =10,000 for all the image

pixels. Then, for each 160x120 sub-image and

independently from the other sub-images, the value

of k was updated through the iterative procedure

detailed in Section 3.1 and assigned to all the pixels

of the sub image; the adaptive scale factor k(x, y)

was finally smoothed through a low pass filter to

avoid sharp transition of k(x, y) along the image.

3.3 Results on Real Images

For the proposed adaptive graph-cut algorithm, the

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

286

original graph-cut in (Felzenszwalb, 2004) (using

= 0.5, min size = 5 in both cases)

and SLIC

(Achanta, 2012), we computed three indexes to

quantify the quality of the segmentation algorithms

on a set of 36 images at 320x240 and 640x480. It is

worthy to notice that the authors of SLIC consider

the graph-cut segmentation algorithm by

Felzenszwalb and Huttenlocher one of the first

superpixel algorithm, thus making this comparison

particularly significant.

Notice that multiple indexes are necessary to

evaluate the quality of segmentation, because of the

different aspects to be considered at the same time

(Chabrier, 2004; Gelasca, 2004; Beghdad, 2007).

The three indexes considered here are the Inter-class

contrast, Intra-class uniformity (Chabrier, 2004), and

their ratio. The first index measures the average

contrast between the different segments, and it is

generally higher for high quality segmentation

(although the contrast between different segments

can be lower if the segmentation contains textures).

The Intra-class uniformity measures the sum of the

normalized standard deviations of the segments and

it should be low for high quality segmentation

(although it also increases when the image contains

a lot of texture and/or noise). We also used the ratio

between these two indexes to obtain a first,

normalized index that depends less on the presence

of texture and noise.

During the testing, we first segmented the images

using the proposed, adaptive graph-cut algorithm,

which does not require any additional input

parameter. For the original graph-cut algorithm, we

set k to obtain the same number of segments

obtained with the proposed adaptive version of the

same algorithm. The number of superpixels in SLIC

was set following the same principle, whereas the

compactness parameter was fixed to 20.

The indexes measured over all the images of our

dataset, together with their average and median

value, are reported in table 1 and 2 for the 320x240

and 640x480 resolutions, respectively. The proposed

method has the higher Inter-class contrast at both

resolutions, thus suggesting that it separates different

object better than the original graph-cut algorithm

and SLIC. When Intra-class uniformity is

considered, SLIC achieves the best result for

320x240 resolution, but at 640x480 resolution the

proposed adaptive graph-cut algorithm has the

lowest Intra-class uniformity. These results are

overall consistent with the recent literature (Achanta,

2012), reporting that SLIC is characterized by lower

boundary recall with respect to the graph-cut

algorithm: it produces a set of regular, uniform

superpixels, but it also possibly includes in the same

segments areas occupied by different objects in the

image. This issue is however less evident at the low

320x240 resolution, where object boundaries are less

to SLIC further confirm that, when these quality

indexes are considered, the segmentation obtained

with the proposed method is qualitatively superior

with respect to that produced by SLIC.

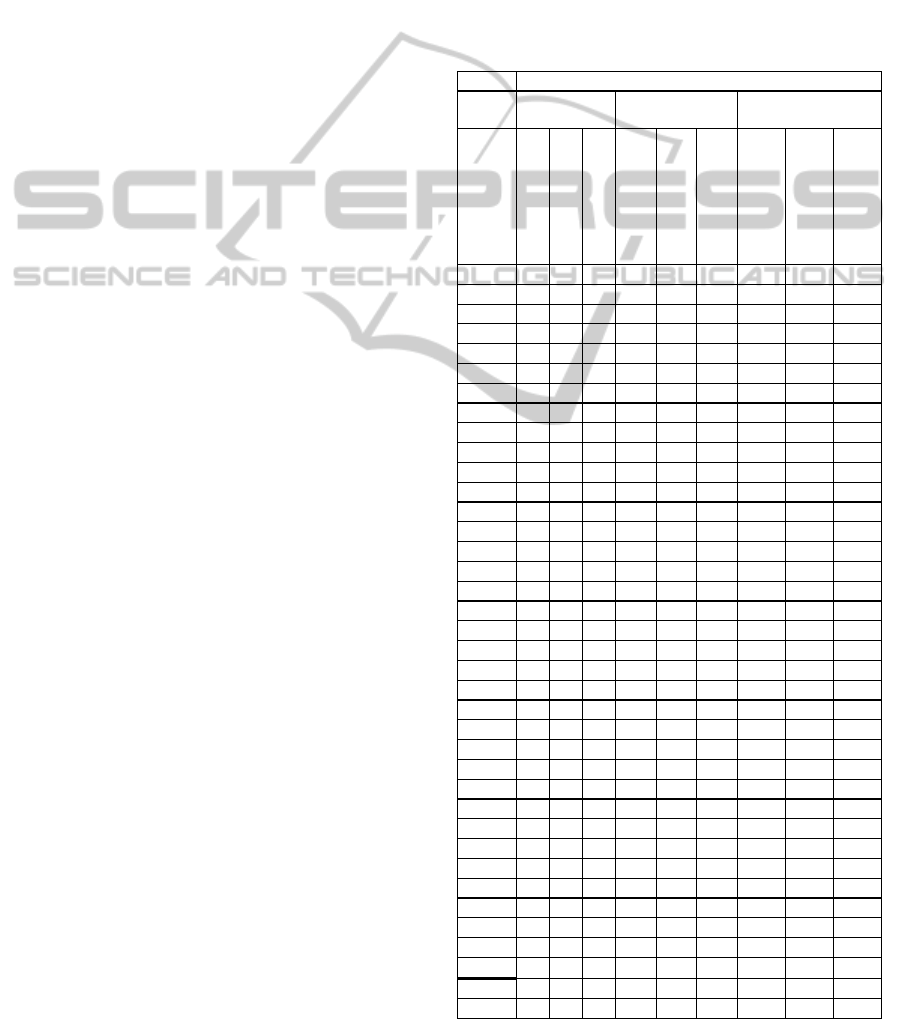
Table 1: Inter-class contrast, Intra-class uniformity and

their ratio for the graph-cut algorithm in (Felzenszwalb,

2004), its adaptive version developed here and SLIC, for

our testing set of images at 320x240 resolution.

# image

Adaptive Graph-Cut

Graph-Cut

SLIC

Adaptive Graph-Cut

Graph-Cut

SLIC

Adaptive Graph-Cut

Graph-Cut

SLIC

10.410.41 0.33 11.58 12.72 7.45 35.80 32.01 44.81

2 0.16 0.16 0.17 7.25 7.47 7.14 21.45 20.95 24.42

3 0.18 0.18 0.18 5.01 5.42 4.02 35.71 32.74 45.99

4 0.23 0.23 0.21 15.49 15.57 18.02 14.64 14.86 11.45

50.270.25 0.20 17.96 19.84 18.16 15.21 12.68 11.21

6 0.15 0.15 0.14 5.07 5.41 5.53 29.11 27.83 25.13

70.320.29 0.22 6.19 5.98 4.02 51.65 48.18 54.63

80.250.23 0.20 13.56 13.35 18.04 18.66 17.34 11.09

90.150.14 0.11 2.10 2.34 2.32 70.78 59.36 46.76

10 0.11 0.11 0.10 6.52 6.92 5.48 16.19 15.21 18.34

11 0.26 0.26 0.18 23.17 22.52 15.22 11.42 11.73 11.89

12 0.37 0.38 0.27 2.55 2.65 1.90 146.25 143.87 143.39

13 0.04 0.04 0.03 0.15 0.14 0.15 244.01 261.14 162.06

14 0.11 0.10 0.08 6.12 5.84 5.69 17.48 16.84 14.82

15 0.06 0.05 0.05 6.44 6.66 6.67 8.68 8.10 6.83

16 0.20 0.19 0.15 17.33 19.48 10.85 11.33 9.76 14.03

17 0.27 0.26 0.22 13.58 13.89 14.17 19.84 18.83 15.43

18 0.16 0.14 0.12 7.23 7.59 5.41 22.22 18.01 21.28

19 0.09 0.09 0.07 3.45 3.72 0.99 24.88 24.64 66.31

20 0.18 0.12 0.10 15.76 16.89 17.97 11.53 7.09 5.79

21 0.14 0.13 0.10 13.19 13.71 11.34 10.87 9.73 9.04

22 0.07 0.06 0.04 6.88 6.91 6.40 10.48 9.23 6.87

23 0.11 0.10 0.07 9.96 9.70 9.45 11.07 10.26 7.55

24 0.21 0.22 0.18 7.44 7.42 8.63 28.72 29.02 20.41

25 0.17 0.17 0.15 25.09 25.81 26.82 6.97 6.56 5.77

26 0.19 0.18 0.15 16.10 16.36 14.44 11.71 11.27 10.27

27 0.15 0.15 0.11 8.78 9.10 8.50 17.13 16.56 13.25

28 0.14 0.14 0.12 20.27 20.64 17.36 6.90 6.95 7.06

29 0.14 0.13 0.12 2.38 2.42 2.17 58.45 55.37 57.26

30 0.26 0.24 0.24 10.95 10.66 7.91 23.45 22.56 30.43

31 0.20 0.20 0.20 9.40 9.81 10.42 21.62 20.59 18.83

32 0.17 0.17 0.16 17.13 18.59 16.83 9.82 9.04 9.40

33 0.28 0.24 0.20 20.09 21.21 19.03 13.81 11.51 10.32

34 0.24 0.24 0.21 38.56 38.62 39.46 6.28 6.23 5.24

35 0.30 0.25 0.16 12.34 13.64 12.89 24.58 18.42 12.12

36 0.20 0.20 0.15 34.96 36.41 40.91 5.77 5.49 3.73

Average 0.19 0.18 0.15 12.22 12.65 11.72 30.40 29.17 27.31

Median 0.18 0.17 0.15 10.45 10.23 9.04 17.30 16.70 13.64

320x240

Inter-class

contrast

Intra-class

uniformity 1000 * Inter /Intra

AdaptiveSegmentationbasedonaLearnedQualityMetric

287

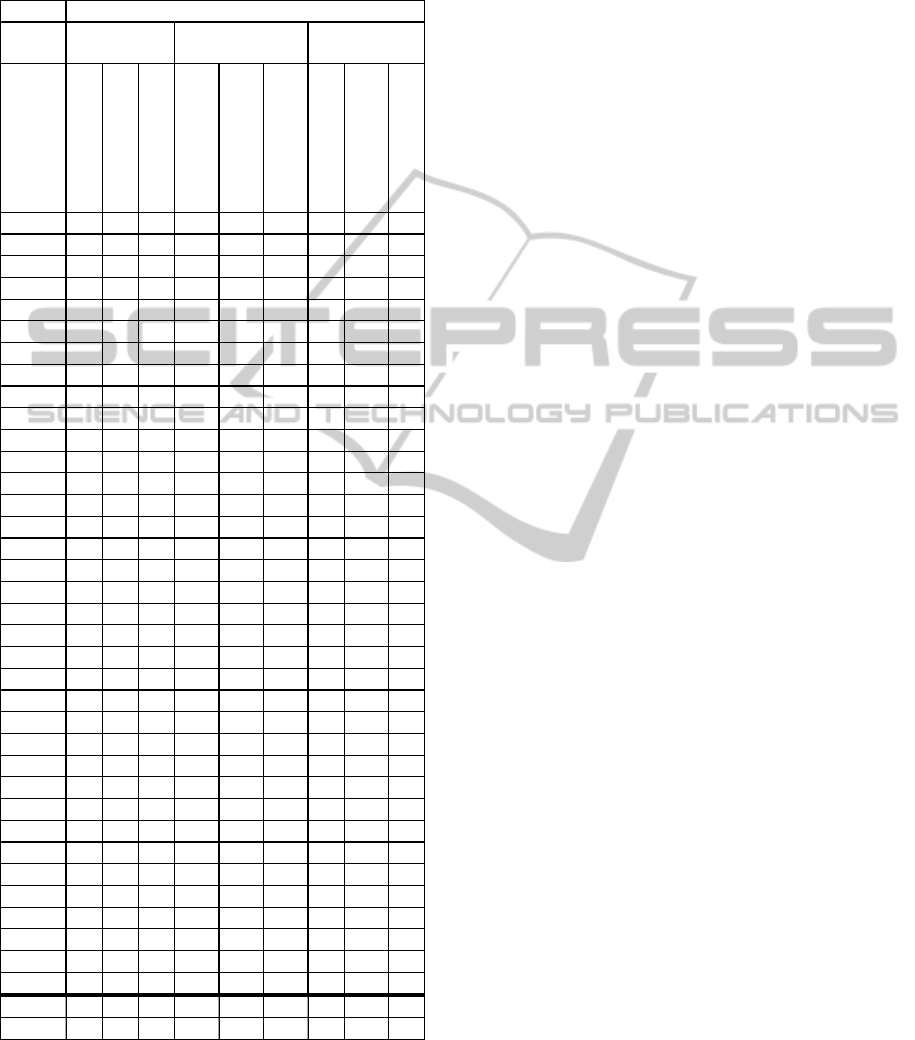
Table 2: Inter-class contrast, Intra-class uniformity and

their ratio for the graph-cut algorithm in (Felzenszwalb,

2004), its adaptive version developed here and SLIC, for

our testing set of images at 640x480 resolution.

precisely defined because of the low number of

pixels. The average and median value of the of Inter-

class contrast/Intra-class uniformity ratio of the

proposed adaptive graph-cut algorithm with respect

to SLIC further confirm that, when these quality

indexes are considered, the segmentation obtained

with the proposed method is qualitatively superior

with respect to that produced by SLIC.

It can also be noticed that the average and

median quality indexes are better for the adaptive

version of the graph-cut algorithm compared to its

original formulation. The only exception is the

average of Inter-class contrast / Intra-class

uniformity ratio. However, this fact is explained

considering that, for image #13 in our dataset, this

algorithm achieves a very large Inter/Intra ratio. This

is not surprising given that the Intra-class uniformity

measure does a poor job of evaluating segmentation

quality in cases of highly textured segments or

segments with smooth color gradients (like in the

case of image #3, see Fig. 6), though it is a very

useful measure in many other cases. Thus with truly

better segmentation, we would, in general, expect a

smaller Intra-class value, but we would expect

notable exceptions. This is, exactly, what we

observe.

Fig. 5 shows two typical segmentation results

obtained on 640x480 images; the same figure shows

the corresponding scale maps k(x, y) and the

segmentation achieved with the original graph-cut

algorithm (Felzenszwalb, 2004) and with SLIC.

When the segmentation quality model derived in

Section 2 is used to adaptively set k(x, y), large

segments are used in the uniform areas of the image,

like the sky in Fig. 5b as well as the road and the

grass areas in Fig. 5f. These areas are on the other

hand over-segmented when the original graph-cut

algorithm is used. The scale map in Fig. 5a,

associated to the segmented image in Fig. 5b, shows

how the quality segmentation model tends to favor a

large scale in the homogeneous area of the sky and

skyscrapers, thus preventing over-segmentation in

the sky area, which is on the other hand present in

the upper right area of Fig. 5c. The proposed

adaptive segmentation procedure also leads to a finer

segmentation in the upper right area of the second

image in Fig. 5, where many small leaves are present

(Fig. 5f-g).

Fig. 6 shows the segmentation of images #2, #4,

and #13 in the testing set obtained with the different

algorithms considered here. SLIC achieves the best

inter-class contrast and intra-class uniformity for

image #2, since lots of details in the image

background match the scale of the superpixels. This

does not happen for image #4, where the adaptive

algorithm proposed here is capable to adapt the size

of the segments at best (and it also identifies the

boundary between the roof and the sky better than

# image

Adaptive Graph-Cut

Graph-Cut

SLIC

Adaptive Graph-Cut

Graph-Cut

SLIC

Adaptive Graph-Cut

Graph-Cut

SLIC

10.360.36 0.28 22.9 25.6 16.0 15.9 14.0 17.2

2 0.15 0.15 0.15 14.0 14.3 13.3 10.7 10.4 11.6

30.170.16 0.16 11.0 12.2 8.6 15.0 13.3 18.5

40.210.20 0.17 40.7 42.0 43.8 5.1 4.8 3.9

50.220.20 0.17 60.6 68.3 62.7 3.7 2.9 2.7

60.140.13 0.11 7.1 8.0 9.0 19.4 15.7 12.4

70.230.21 0.16 17.9 20.3 9.4 12.8 10.3 17.4

80.230.17 0.16 38.0 42.7 44.3 5.9 4.0 3.6

90.130.12 0.08 5.3 5.8 4.7 24.5 20.2 17.4

10 0.09 0.10 0.09 12.1 13.0 9.6 7.8 7.5 9.1

11 0.19 0.19 0.15 56.0 57.5 40.8 3.5 3.2 3.6

12 0.25 0.31 0.21 5.4 5.7 3.5 45.5 53.8 60.6

13 0.03 0.03 0.02 0.3 0.2 0.3 85.1 142.2 59.3

14 0.09 0.08 0.07 29.7 29.9 30.0 3.2 2.6 2.2

15 0.05 0.05 0.04 21.3 22.6 25.3 2.3 2.1 1.7

16 0.17 0.16 0.13 47.3 58.5 32.3 3.6 2.8 4.1

17 0.24 0.24 0.20 45.1 47.6 48.3 5.3 5.0 4.2

18 0.13

0.11 0.09 23.4 25.1 17.8 5.6 4.4 5.3

19 0.06 0.06 0.05 4.7 9.2 3.1 12.3 6.9 14.5

20 0.15 0.13 0.11 89.2 89.6 128.3 1.7 1.4 0.9

21 0.14 0.12 0.10 65.9 66.6 75.5 2.1 1.9 1.3

22 0.07 0.06 0.05 36.3 36.2 39.1 1.9 1.7 1.3

23 0.10 0.09 0.07 44.8 44.8 52.1 2.2 2.1 1.3

24 0.18 0.17 0.14 18.7 20.4 18.4 9.7 8.5 7.7

25 0.16 0.15 0.13 93.0 95.1 119.8 1.7 1.6 1.1

26 0.16 0.15 0.14 47.0 49.0 49.0 3.5 3.1 2.8

27 0.14 0.12 0.10 31.8 32.9 43.3 4.4 3.5 2.3

28 0.12 0.11 0.11 48.7 51.4 43.9 2.5 2.2 2.5

29 0.13 0.13 0.09 3.3 3.6 3.9 39.2 35.1 24.3

30 0.22 0.22 0.19 18.8 23.1 14.8 11.6 9.5 12.7

31 0.18 0.18 0.16 19.9 21.0 23.8 9.3 8.4 6.5

32 0.14 0.14 0.13 37.9 39.5 37.5 3.8 3.5 3.5

33 0.19 0.18 0.17 44.8 47.5 43.0 4.3 3.7 4.0

34 0.24 0.23 0.21 123.8 129.9 139.5 2.0 1.8 1.5

35 0.18 0.17 0.13 26.6 26.7 33.9 6.9 6.4 3.9

36 0.17 0.17

0.15 69.9 72.5 91.1 2.4 2.4 1.7

Average 0.16 0.15 0.13 35.6 37.7 38.3 11.0 11.8 9.7

Median 0.16 0.15 0.13 30.7 31.4 33.1 5.2 4.2 3.9

640x480

Inter-class

contrast

Intra-class

uniformity

1000 * Inter

/Intra

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

288

Figure 5: Panels (b-d) and (f-h) show images #16 (first row) and #28 (second row) in our 640x480 resolution testing set,

segmented with the adaptive graph-cut algorithm, the original graph-cut algorithm (Felzenszwalb, 2004) and SLIC

(Achanta, 2012). Panels (a) and (e) show the scale maps k(x, y) for the adaptive graph-cut algorithm.

Figure 6: Segmentation of images #2, #4, and #13 in our 640x480 resolution testing set, obtained with different algorithms.

the original graph-cut algorithm) and therefore

achieves the best inter-class contrast and intra-class

uniformity. Finally, graph-cut work at best for these

indexes on the almost homogeneous image #13,

although the superiority of graph the proposed

adaptive graph-cut is questionable at visual

inspection in this case (see for instance how the

proposed approach uses a smaller number of

segments in the sky area and better fits the boundary

of the clouds, Fig. 6g-h).

A final remark is to be made about the

computational costs of the segmentation algorithms

considered here. SLIC is the fastest algorithm, with

a linear complexity with respect to the number N of

AdaptiveSegmentationbasedonaLearnedQualityMetric

289

superpixels, whereas graph-cut has N·logN

complexity. The complexity of the proposed method

is the highest: it is N·logN and it increases linearly

with the number of iterations required to reach the

convergence, which we experimentally observed to

occur typically in less than 7 iterations.

4 DISCUSSION

A wide array of literature on segmentation

algorithms exists based on the main idea expressed

in (Felzenszwalb, 2004) that any segmentation

algorithm should “capture perceptually important

groupings or regions”. Many authors have implicitly

defined the perceptive saliency of an image feature

on the basis of some well-established mathematical

rule: for instance the k parameter in (Felzenszwalb,

2004) defines the typical scale of the image

segments. In SLIC, a similar role is played by the

approximate number of desired segments which is

passed as input parameter, as the superpixels are

spread uniformly across the entire image. A trial-

and-error procedure is however required to set these

parameters such that the segments are perceptually

significant for a human observer. The same issue is

in common with many other segmentation

algorithms, whose output critically depends on the

choice of the input parameters (Sun, 2013;

Sungwoong, 2013; Alpert, 2012; Bosch, 2011).

To overcome this problem, we have developed a

segmentation quality model whose parameters were

learned from a set of segmentation data classified by

a human observer. The resulting segmentation

quality is therefore related to the fact that regions or

objects that are perceptually important for a human

observer are grouped in a same segment. The

segmentation quality model is particularly suited for

applications like medical imaging and video

compression, where the segmented images (or the

compressed video stream) are intended for human

observers.

Based on the proposed segmentation quality

model, we developed a parameter-free algorithm,

which constitutes a significant improvement with

respect to more traditional algorithms requiring

input parameters, whose adequacy has to be verified

a posteriori. The procedure adopted to learn the

model parameters has been applied here specifically

to the graph-based segmentation algorithm in

(Felzenszwalb, 2004). Nevertheless, such procedure

is far more general and ideas detailed in this paper

can be easily applied to other segmentation

algorithms requiring one or more input parameters,

like (Senthilkumaran, 2009; Prakash, 2004). We

have for instance developed and tested a similar

segmentation quality model for edge thresholding

segmentation in the YUV space (Canny, 1986),

achieving similar results (not shown here for reason

of space). We are also going to investigate the

application of the same procedure to develop a

parameter-free version of SLIC (Achanta, 2012) and

to automatically adapt the scale parameter from

region to region within the same image. Notice that,

in this case, two parameters (number of superpixels

and compactness) should be adapted: the optimal

segmentation line becomes in this case a plane (and

more generally, for algorithms with a higher number

of input parameters, an hyper-plane).

It is worthy noticing that the optimal

segmentation line in the (log(k), U

) space for the

320x240 resolution (Fig. 3a) is lower than the

optimal line for 640x480 images (Fig. 3b). Thus,

although we considered sub-images of 160x120

pixels for both resolutions, the parameters of the

segmentation quality model change with the image

resolution. This seems reasonable, since at higher

resolution more details are generally visible in the

image, thus requiring a finer segmentation (i.e.,

higher U

). The application of the segmentation

quality model to other image resolutions requires

therefore re-classifying segmented sub-images of

160x120 pixels for the given resolution. Another

approach would interpolate the model parameters.

The choice of sub-images of this particular size

was made as a compromise between the need to

include a significant set of image features in the sub-

image (sub-images that are too small could in fact

contain a unique segment and in this case their

classification in under-, well- or over-segmented is

meaningless) and the need to obtain a significantly

high number of sub-images. This last need has two-

fold advantages: first, it is well known that using a

large amount of data significantly improves the

training process in machine learning (Witten, 2002);

this principle is used here to reliably learn the

parameters of the segmentation quality model. As a

second point, optimizing the segmentation

parameters on small 160x120 sub-images allowed us

to develop an adaptive segmentation algorithm by

dividing a full resolution image in a set of sub-

images and computing the optimal scale parameter

for each of them. We were therefore able to develop

an adaptive algorithm, which is intrinsically more

robust and accurate than other procedures using a

single parameter for the entire image (Felzenszwalb,

2004; Isa, 2009).

The results reported in Tables 1 and 2

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

290

demonstrate that the adoption of the proposed

adaptive strategy for the computation of k(x, y) leads

to segments that have more contrast one with respect

to the other and that are more uniform, thus

demonstrating an overall increase in segmentation

quality. Comparison with SLIC shows that

optimizing the segmentation quality using the

proposed model generally leads to a semantic

segmentation, where large objects perceptually

recognized as a single class are effectively described

by a unique segment; this however requires a higher

computational time. On the other hand, SLIC

produces in a short a regular grid of superpixels,

which is more suited for further processing by other

algorithms.

Figs. 5 and 6 show that the proposed method

generally identifies the scale of the objects that are

important for a human observer: for instance

segments are larger close to people in Fig. 5f or in

the homogeneous sky area in Fig. 5b. Nevertheless,

we have also noticed that the proposed algorithm

sometimes produces sets of segments that are too

fine, such as in the left river area in Fig. 5b. Such

sub-optimal behavior has to be investigated more in

detail in the future. To this aim, we are planning to

use the Berkeley segmentation dataset (Martin,

2001) to build a large training set including

hundreds of images semantically segmented by

several human observers, so to significantly improve

the training of the segmentation quality model.

To summarize, the proposed segmentation

quality model can be used to perform segmentation

with no supervision, using an algorithm that

automatically adapts its parameter along the image

to generate a segmentation map that is perceptually

reasonable for a human observer. This is

particularly important in applications like video-

encoding; in this case, it can also be noticed that the

computational cost of the proposed method can be

significantly reduced. In fact, when applied to a

unique frame, the proposed method performs a

search for the optimal k value for each sub-image

considering the entire valid range for k. On the other

hand, since adjacent frames are highly correlated in

video, the range for k can be significantly reduced

considering the estimates obtained at previous

frames for the same sub-image.

REFERENCES

R. Achanta, A. Shaji, K. Smith, A. Lucchi, P. Fua, S.

Süsstrunk, SLIC Superpixels Compared to State-of-

the-art Superpixel Methods, IEEE TPAMI, 2012.

S. Alpert, M. Galun; A. Brandt, R. Basri, Image

Segmentation by Probabilistic Bottom-Up

Aggregation and Cue Integration, IEEE TPAMI, 2012.

A. Beghdad, S. Souidene, An HVS-inspired approach for

image segmentation evaluation, IEEE ISSPA, 2007.

M. Bosch, Z. Fengqing, E. J. Delp, Segmentation-Based

Video Compression Using Texture and Motion

Models, IEEE Journ. Sel. Topics in Sig. Proc., 2011.

J. Canny, A Computational Approach to Edge Detection,

IEEE TPAMI, 1986.

S. Chabrier, B. Emile, H. Laurent, C. Rosenberger, P.

Marché, Unsupervised Evaluation of Image

Segmentation: Application to multi-spectral images,

ICPR, 2004.

P. F. Felzenszwalb, D. P. Huttenlocher, Efficient Graph-

Based Image Segmentation, IJCV, 2004.

E. D. Gelasca, et al., Towards Perceptually Driven

Segmentation Evaluation Metrics, in CVPRW, 2004.

I. Frosio, G. Ferrigno, N. A. Borghese, Enhancing Digital

Cephalic Radiography with Mixture Model and Local

Gamma Correction, IEEE TMI, 2006.

J. Kaufhold, and A. Hoogs, Learning to segment images

using region-based perceptual features, in CVPR,

2004.

N. A. M. Isa, S. A. Salamah, U. K. Ngah, Adaptive fuzzy

AdaptiveSegmentationbasedonaLearnedQualityMetric

291

moving K-means clustering algorithm for image

segmentation, IEEE TCE, 2009.

D. Martin, C. Fowlkes, D. Tal, J. Malik, A Database of

Human Segmented Natural Images and its Application

to Evaluating Segmentation Algorithms and

Measuring Ecological Statistics, ICCV, 2001.

A. Prakash, E. R. Ratner, J. S. Chen, D. L. Cook. Method

and apparatus for digital image segmentation. U.S.

Patent 6,778,698, 2004.

R. Raina, A. Madhavan, A. Y. Ng., Large-scale deep

unsupervised learning using graphics processors,

ICML, 2009.

N. Senthilkumaran, R. Rajesh, Edge detection techniques

for image segmentation–a survey of soft computing

approaches, Int. Journ. Recent Trends in Eng., 2009.

J. Shawe-Taylor, N. Cristianini, Kernel Methods for

Pattern Analysis, 2004.

S. Sun, M. Sonka, R. R. Beichel, Graph-Based IVUS

Segmentation With Efficient Computer-Aided

Refinement, IEEE TMI, 2013.

K. Sungwoong, S. Nowozin, P. Kohli, C. D. Yoo, Task-

Specific Image Partitioning, IEEE TIP, 2013.

I. H. Witten, F. Eibe, Data Mining: Practical Machine

Learning Tools and Techniques, 2002.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

292