LDA Combined Depth Similarity and Gradient Features for Human

Detection using a Time-of-Flight Sensor

Alexandros Gavriilidis, Carsten Stahlschmidt, J

org Velten and Anton Kummert

Faculty of Electrical Engineering and Media Technologies, University of Wuppertal, D-42119 Wuppertal, Germany

Keywords:

Human Detection, Depth Image Features, LDA Feature Combination, Video Processing.

Abstract:

Visual object detection is an important task for many research areas like driver assistance systems (DASs),

industrial automation and various safety applications with human interaction. Since detection of pedestrians is

a growing research area, different kinds of visual methods and sensors have been introduced to overcome this

problem. This paper introduces new relational depth similarity features (RDSF) for the pedestrian detection

using a Time-of-Flight (ToF) camera sensor. The new features are based on mean, variance, skewness and

kurtosis values of local regions inside the depth image generated by the Time-of-Flight sensor. An evaluation

between these new features, already existing relational depth similarity features using depth histograms of

local regions and the well known histogram of oriented gradients (HOGs), which deliver very good results

in the topic of pedestrian detection, will be presented. To incorporate more dimensional feature spaces, an

existing AdaBoost algorithm, which uses linear discriminant analysis (LDA) for feature space reduction and

new combination of already extracted features in the training procedure, will be presented too.

1 INTRODUCTION

Conventional camera systems capturing only avail-

able light of the surrounding area have many bene-

ﬁts as well as drawbacks for the task of visual pedes-

trian detection. Beneﬁts of passive camera systems

are, beside the ﬁnancial point, the usability for many

different tasks, like pattern recognition, object detec-

tion and image registration. The lighting conditions

are the strongest limitation factors for conventional

camera systems. Relating to pedestrian detection, the

appearance, e.g. color of clothes, and the contrast of

the pedestrian to the background are typical problems

for conventional monocular (Enzweiler and Gavrila,

2009) or stereo (Keller et al., 2011) camera systems.

Besides cues for detection of pedestrians which are

exhaustive evaluated in (Doll

ar et al., 2012), informa-

tion about the distance to a detected object are essen-

tial for many assistance systems. The estimation of

a distance to a detected object based on camera cali-

bration and conventional monocular camera systems

is a typical problem too. To overcome such prob-

lems, sensors like Time-of-Flight (ToF) cameras, also

called RGB-D cameras, can be used. In (Ikemura

and Fujiyoshi, 2010) relational depth similarity fea-

tures (RDSFs) for the detection of pedestrians have

been introduced, which are extracted from a depth

image captured by a TOF camera. Based on a max-

imum range resolution of 7.5m of the TOF camera,

a depth image will be quantized into 25 bins, where-

upon each bin has a range resolution of 0.3m. For a

rectangular region, the depth histogram will be cre-

ated using the occurrence of pixel inside each bin of

the 25 quantization steps. After normalization of the

histogram, the Bhattacharyya distance between two

different rectangular regions inside the image will be

calculated and the scalar result will be used as feature

for an AdaBoost classiﬁer. The time of computing

the 25 integral images, as well as the evaluation of the

Bhattacharyya distance over two 25-dimensional his-

tograms for many different rectangular region combi-

nations can be very expensive.

Another approach like (Mattheij et al., 2012) eval-

uates the well known Haar-like features from (Viola

and Jones, 2001b) on depth images and shows that

Haar-like features can deliver accurate results com-

bined with a fast calculation time using integral im-

ages. Histogram of Depth Differences (HDD) de-

veloped in (Wu et al., 2011) and derived from the

Histogram of Oriented Gradients (HOGs) (Dalal and

Triggs, 2005) is nearly the same. The only difference

is the use of the whole 360 degrees of the possible ori-

entations and not just the 180 degrees as described in

(Dalal and Triggs, 2005) of the HOG feature.

349

Gavriilidis A., Stahlschmidt C., Velten J. and Kummert A..

LDA Combined Depth Similarity and Gradient Features for Human Detection using a Time-of-Flight Sensor.

DOI: 10.5220/0005257403490356

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 349-356

ISBN: 978-989-758-089-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

In (Spinello and Arras, 2011) the Histogram of

Oriented Depths (HOD) feature will be introduced,

that has been also derived from the HOG feature. The

HOD will be calculated in the depth image and used

by a soft linear support vector machine (SVM) to de-

tect pedestrians. To improve the decision of the HOD,

a so called Combo-HOD will be introduced that uses

two detectors trained each on either the depth image

with HOD features or the intensity (grayscale) image

with HOG features and combines in that case the sen-

sor cues of each image. The Combo-HOD promises

more accurate precision than the single detectors on

either the depth or the RGB image.

Based on the idea of local binary pattern (LBP),

in (Wang et al., 2012) so called pyramid depth self-

similarities (PDSS) are introduced, which will be

used with a depth image. The core part is to com-

pare local areas in the manner of LBP features, e.g. to

compare a cell (an image area) of a detection window

with its neighbouring cells, by use of histogram inter-

section methods. To concatenate the histograms by a

spatial pyramid over the depth image is a time con-

suming task too. To be as fast and accurate as pos-

sible, the presented approach of this paper is based

on features which are also comparing the relation in

depth of two different areas, but can be computed very

fast, like Haar-like features. Time consuming features

can be used to increase the performance in addition to

the weak features, which will be introduced later in

this paper.

The remainder of the paper is structured as fol-

lows, the next section gives an overview of the used

sensor, the available sensor data and other basic re-

ﬂections regarding the difference between intensity

and depth images. The available features for pedes-

trian detection in 2.5D (RGB-D) data will be de-

scribed in section three. Section four describes the

used classiﬁer and the usage of high dimensional fea-

tures by linear discriminant analysis (LDA) transfor-

mation. The following section show up the results of

the paper and in the last section, a summary and con-

clusions will be given.

2 PRELIMINARY

CONSIDERATIONS

The used ToF camera is the CamCube 3.0 from PMD

Technologies GmbH with a maximum measurement

range of up to 7.5m for the available depth image.

Field of view of the ToF camera is 40 degrees in both

directions with a pixel resolution of (200 × 200) by

a possible frame rate of over 30 frames per second

(fps). A general image can be described by pixel val-

ues g = f (n) with f : n → g, g ∈ R, n ∈ M , where

M =

{

n ∈ Z

|0 ≤ n < N

}

(1)

and N ∈ Z

describing the number of values in all

dimensions of an image f (n), 0 is a vector con-

taining only zeros. The used ToF camera delivers

three important two dimensional (2D) images with

n = [n

, n

]

including an intensity image I (n

, n

) ∈

[0, 255], a depth image D(n

, n

) ∈ R

≥0

and an ampli-

tudes image A(n

, n

) ∈ N\

{

}

, whereupon each im-

age has the same pixel resolution of N = [200, 200]

pixel. In other words, one great property of the Pho-

tonic Mixer Device (PMD) sensor is, there are three

images available and each pixel has three represen-

tations, which can be used for new feature combi-

nations. The amplitudes image, which will be not

presented in this scope, includes information about

the signal strength of the measured reﬂected light.

It could be used as indicator for accurate measured

depth information. In Figure 1 the intensity and the

Figure 1: On the left hand side the intensity image and the

corresponding magnitude image of the gradient calculation,

as described in section 3, are shown. On the right hand side,

the depth image is presented as well as the corresponding

magnitudes image.

depth image can be seen. The intensity image of the

PMD camera can be badly scaled, based on poor re-

ﬂected light. Because of this, some areas will deliver

very poor gradient information, like it can be seen in

the lower part of the intensity image of Figure 1. In

contrast to this, the depth image will deliver small gra-

dients, if all observed objects are close to the same

plane, e.g. an object close to a wall. Additionally,

a huge problem of the depth image of the ToF cam-

era is the ambiguity in the distance resolution, which

causes gradients in the depth image that are not in-

duced by real objects. But for objects up to 7.5m, the

depth image can deliver accurate gradients along the

borders of objects segmented by the surrounding area.

This illumination resistant property of the ToF camera

and the information about the measured distance of an

object to the sensor in the real world can be used to

create new features by combination of existing ones

to improve the object detection task.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

350

3 FAST DEPTH RELATIONAL

SIMILARITY FEATURES

Based on the work of (Ikemura and Fujiyoshi, 2010)

new fast features, which are described in the follow-

ing subsections, will be inspired to detect humans in

a depth image of a ToF camera. Since, the RDSFs

developed in (Ikemura and Fujiyoshi, 2010) describe

how two rectangular regions inside the depth image

are similar to each other based on a quantized depth

histogram, it is also possible to describe such a re-

lation based on the idea of (Mattheij et al., 2012).

The idea is to remove the bottlenecks of the RDSF

calculation, which are based on the calculation of

25 integral images and the calculation of the Bhat-

tacharyya distance between two 25-dimensional fea-

ture vectors, but to keep the smart combination of

two different local regions inside the image plane.

Based on the training size of an image of (64 × 128)

pixel, the smallest size of a region (cell) is assumed

as (8 × 8) pixel, like described in (Ikemura and Fu-

jiyoshi, 2010), and each region can grow along one

image dimension about its smallest cell size. Since, a

region should not reach the size of the whole training

window, the largest size of one region will be lim-

ited to (48 × 96) pixel. Each region between (8 × 8)

pixel and (48 × 96) pixel, including the extremal val-

ues (48 × 8) pixel and (8 × 96) pixel, will be shifted

by one pixel inside the training image. Since, the

number of all possible combinations between two dif-

ferent regions shifted pixel by pixel will be too large,

one of both regions will not change the size and posi-

tion. The choice of this assumption will be discussed

in the next sections. The remaining number of possi-

ble features is now 49248, whereupon one region will

not be changed. In contrast to this, the regions de-

scribed in (Ikemura and Fujiyoshi, 2010) are growing

in both image directions with the smallest cell size

at the same time, in other words quadratically, and

only regions on the current grid, which is deﬁned by

the smallest cell size, are used. Each combination be-

tween two regions on this grid leads to a total number

of 120.786 possible features, as described in (Ikemura

and Fujiyoshi, 2010).

3.1 Mean and Variance Features

(MV-RDSF)

Inspired by the idea of (Ikemura and Fujiyoshi, 2010)

to compare the depth information between two rectan-

gular regions inside of the depth image and due to a

pedestrian will have distances which are close to one

plane, the comparison of mean and variance values

of two regions can be used as feature to ﬁnd char-

acteristics of a pedestrian. Because of each combi-

nation between two different regions in an image of

(64 × 128) pixel resolution will lead to an exorbitant

number of possible features, as described at the be-

ginning of this section, the following assumption will

be preferred. Based on an empirical evaluation of all

possible combinations of two rectangular regions, a

region on the upper part of the body is one of the

best choices for one of both rectangular regions which

should not be changed anymore. This ﬁrst rectangular

region is placed on the left upper corner n = [24, 32]

with a width of 16 pixel and a height of 32 pixel. In

Figure 2, three different selected feature combinations

can be seen, whereupon the green (middle) rectangle

Figure 2: Three different selected mean and variance fea-

tures which has been selected during the AdaBoost training.

The green rectangle (each time on the torso of the human)

is the same feature in each boosting iteration.

does not change its size or position, only by scaling,

as all the other rectangles too. The integral image rep-

resentation can be used to be more efﬁcient by calcu-

lating the local mean

µ(u, v, w, h) =

w · h

∑

i=u

∑

j=v

D(i, j), (2)

and the local variance

(X −µ)

= σ(u, v, w,h)

w · h

∑

i=u

∑

j=v

D(i, j)

− µ

(3)

as deﬁned in (Shafait et al., 2008), where (u, v, w, h)

are the image coordinates, width and height of a rect-

angular region. In other words, two integral images,

one over the normal depth image and one over the

squared depth image, can be used to calculate the

mean and the variance of a rectangular region using

the integral image representation. The two dimen-

sional feature vector will be the difference

x =



− µ



− σ





(4)

of the means (µ

, µ

) and the variances (σ

, σ

) of the

two regions. This simple 2D feature can be used to

LDACombinedDepthSimilarityandGradientFeaturesforHumanDetectionusingaTime-of-FlightSensor

351

describe the difference of depth between two rectan-

gular regions.

3.2 Mean, Variance, Skewness and

Kurtosis Features (MVSK-RDSF)

Besides the mean and variance of depth image infor-

mation between two rectangular regions, it is possible

to extend the feature vector of the last subsection by

the two values skewness and kurtosis. The skewness

(



X −µ



)

= skew(u, v, w, h) =

w · h

∑

i=u

∑

j=v

D(i, j)

−

3µ

w · h

∑

i=u

∑

j=v

D(i, j)

+ 2µ

(5)

and the kurtosis

(



X −µ



)

= kurt(u, v, w,h) =

w · h

∑

i=u

∑

j=v

D(i, j)

−

4µ

w · h

∑

i=u

∑

j=v

D(i, j)

6µ

w · h

∑

i=u

∑

j=v

D(i, j)

− 3µ

(6)

can be used in this representation also with integral

images. The combined four dimensional feature vec-

tor is then based on

x =







− µ



− σ



skew

− skew

kurt

− kurt







(7)

and includes some more information about the distri-

butions of depth values between the both regions.

3.3 Mean, Variance and HOG Features

(MV-HOG-RDSF)

Since, the MV-RDSF and MVSK-RDSF representa-

tions might not be efﬁcient enough to distinguish a

pedestrian from all other objects, the combination of

the relation of depth and depth gradients can be used.

Therefore, the idea of the HOG feature representation

can be used applied on the depth image. Since, one

of both rectangular regions (green region of Figure 3)

does not include any gradient in the depth image, if a

pedestrian is visible like shown in Figure 2, the gradi-

ent calculation will only be used on the second region

(red region). Because of, only one region is available,

the original HOG representation with one cell will

be used as the whole HOG block. The HOG feature

will be calculated with the integral image representa-

tion based on the gradient images, calculated by con-

volving the depth image with the masks [1, 0, −1] and

[−1, 0, 1]

, and the magnitude between the gradients

in both image directions. Finally, each HOG block

will be normalized using the L1-norm. For the evalu-

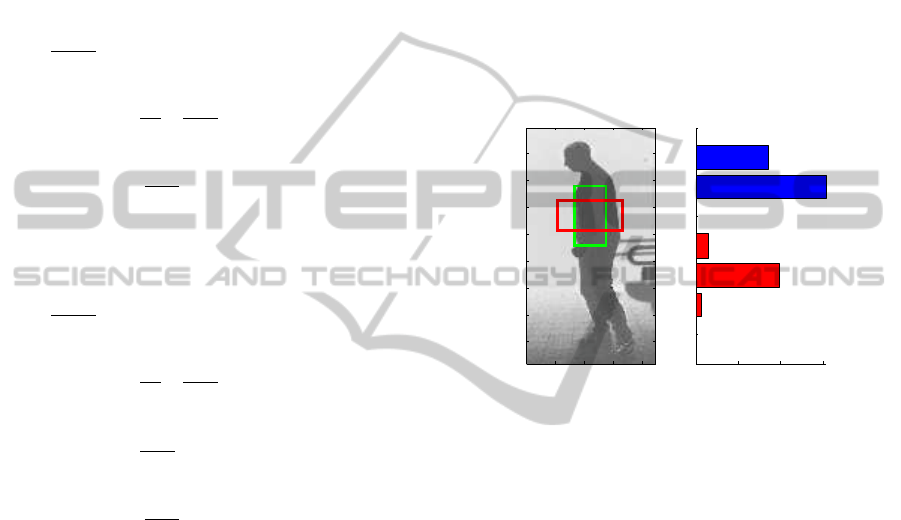
Figure 3: One feature combination between two rectangles

can be seen on the left hand side. On the right hand side,

the corresponding feature vector with concatenated mean,

variance and HOG values. The ﬁrst two bars (coloured in

blue) are the mean and variance differences, the values from

three to seven are the histogram values of the red coloured

rectangle, which can change in size and position, as shown

in Figure 2.

ation, ﬁve bins have been used for one HOG feature,

which can be seen in Figure 3. The ﬁnal MV-HOG-

RDSF is a concatenation of the two dimensional MV-

RDSF and the HOG feature, as it can be seen on the

right hand side of Figure 3. This new feature repre-

sentation includes the relation in depth direction be-

tween two rectangular regions and the gradient infor-

mation in depth direction from the rectangular region,

which is changing its size and position (red rectangle).

4 CLASSIFIER

Fast and accurate detection of objects depends on the

underlying feature space and the used classiﬁer. As

classiﬁer for pedestrian detection, the SVM will be

used in many applications due to the usage of high

dimensional feature spaces. Because of the feature

space of a pedestrian classiﬁer can be highly non-

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

352

linear, the classes pedestrian and non-pedestrian may

not be sufﬁciently dividable by a linear SVM kernel.

Therefore, boosting classiﬁers such as AdaBoost (Vi-

ola and Jones, 2001a) or non-linear kernels with a

SVM can be used. Non-linear SVM evaluation is very

expensive, but on the other side also very accurate.

Based on the property of fast detection, the asymmet-

ric cascaded AdaBoost will be used in this paper as

described in (Viola and Jones, 2001a).

To improve the usage of presented features of the

last section, the combination and extraction of fea-

tures based on the linear discriminant analysis (LDA)

will be used as presented in (Nunn et al., 2009). A

training set can be deﬁned like

, x

), . . . , (y

, x

)

| {z }

positive examples

, (y

, x

), . . . , (y

, x

)

| {z }

negative examples

with M

, M ∈ N\{0} and label information y

∈

{

−1, 1

}

, where i = 1, . . . , M, for positive (y

= +1)

and for negative (y

= −1) training examples. For

each example of the training set with a feature vec-

tor

= (x

, . . . , x

)

, m ∈ N\{0} (8)

the AdaBoost algorithm uses weights

t+1

(i) =

(i)e

(−α

, f ,p,Θ))

, (9)

with t ∈ N\

{

}

, D

(i) =

and Z

as normalization

factor to keep D

t+1

as a distribution for all training

examples. The value α

will be calculated using the

minimum error

= min

f ,p,Θ

∑

(i)

, f , p, Θ) − y

(10)

of the weak classiﬁers

, f , p, Θ) =



1 if p f (x

) < pΘ

−1 otherwise

(11)

where p is a sign for the inequality, f (x

) is the result

of the feature evaluation and Θ is a threshold value,

which has to be determined. Based on the error ε

which will be evaluated for each round of boosting in

the training phase, the value

= log



1 − ε



(12)

can be calculated. Each feature vector can be trans-

formed into one linear dimension by

˜x

= w

· x

(13)

where w is the transformation vector determined from

w = Σ

−1

(µ

− µ

) (14)

with (µ

, µ

) as the means of the class one and class

two in a two class problem. The matrix Σ

Σ is the co-

variance matrix of both classes as deﬁned in (Nunn

et al., 2009) and (Izenman, 2008). All AdaBoost

weights D

(i) have to be considered in the calculation

of the covariance matrix Σ

Σ. Therefore, the means

∑

i=1

(i)

∑

i=1

(i) · x

, (15)

∑

i=N

(i)

∑

i=N

(i) · x

(16)

will be used to calculate the covariance matrices of

the different classes

∑

i=1

(i)

∑

i=1

(i) · (x

− µ

)(x

− µ

)

, (17)

∑

i=N

(i)

∑

i=N

(i) · (x

− µ

)(x

− µ

)

(18)

and the combined covariance matrix

Σ = Σ

+ Σ

, (19)

respectively.

Each of the features, described in the last sec-

tion 3, will be transformed by the LDA transforma-

tion to calculate the result of the weak classiﬁers for

the AdaBoost training. It is worthwhile to know, that

with this LDA transformation it is possible to com-

bine the MV-RDSF and the classical HOG features

into one new feature space. The transformation vec-

tor w, which transforms the current feature, will be

selected in the training procedure. The combination

of selected transformation vectors and features will be

used to classify in the online procedure an unknown

feature vector for the AdaBoost classiﬁer.

5 EVALUATION

5.1 Database

The RDSF of (Ikemura and Fujiyoshi, 2010), the new

MV-RDSF, MVSK-RDSF, the combined MV-HOG-

RDSF and the classic HOG features will be trained

with an asymmetric AdaBoost algorithm and evalu-

ated over a generated dataset including 8400, 3600

positive and 6650, 2850 negative examples for train-

ing and testing, respectively. Some positive and neg-

ative examples of depth images can be seen in Figure

4. Due to the detection of occluded humans, as it is

LDACombinedDepthSimilarityandGradientFeaturesforHumanDetectionusingaTime-of-FlightSensor

353

Figure 4: The upper part of the ﬁgure includes negative ex-

amples of the training and test set and the lower part of the

ﬁgure shows some positive examples.

described in (Ikemura and Fujiyoshi, 2010), is not in

focus of this evaluation, the positive examples include

only small partial occlusion from the foreground and a

large variation of the background, including also am-

biguities in the depth caused by the time of ﬂight prin-

ciple.

5.2 Feature Performance Comparison

The evaluated classical HOG features contain one cell

((8 × 8) pixel) per block to be comparable to the new

combined MV-HOG-RDSF. Each possible rectangu-

lar region from (8 × 8) pixel up to (56 × 112) pixel

with an increasing factor of 8 pixel in each dimension

of the block will be considered. Additionally, each

possible HOG block will be shifted by one pixel over

the whole training window, as described also in sec-

tion 3, and not by the smallest cell size as it will be

done by the RDSFs. This results in a total number of

48510 classical HOG features.

Figure 5 shows the results of the trained classi-

ﬁers with the new features based on mean, variance,

skewness and kurtosis. The mean and variance fea-

tures (MV-RDSF) deliver the worst performance. By

extending the MV-RDSF with skewness and kurtosis

properties, it is possible to increase the performance

of the classiﬁer only slightly. However, both features,

the MV-RDSF and the MVSK-RDSF, cannot reach

the performance of the original RDSF, because the

feature space is strongly limited for a good separa-

tion. Strong noise involved by the depth ambiguity

and the sensor hardware cannot be considered just by

the mean and variance of depth information.

The comparison between the classical HOG fea-

ture and the RDSF of (Ikemura and Fujiyoshi, 2010)

is shown in Figure 6. The classical HOG feature

has similar results as the RDSF of (Ikemura and Fu-

Figure 5: The receiver operating characteristics (ROCs) of

the MV-RDSF and MVSK-RDSF trained with the asym-

metric AdaBoost procedure.

jiyoshi, 2010). Again, it is mentionable that in (Ike-

mura and Fujiyoshi, 2010) it is not described which

version of a HOG feature has been used. Here, as

described in section 3, one HOG block consists of

one cell with the size of (8 × 8) pixel and has only

5 orientations. The concatenation of the MV-RDSF

and the HOG features, the MV-HOG-RDSF, uses a

combination of similarity in depth and depth gradi-

ents for shape characterization and delivers the best

results in the experiments, as it can be seen in Figure

6. Based on the LDA transformation of the combined

Figure 6: The receiver operating characteristics (ROCs) of

the classical HOG feature, the RDSF and the MV-HOG-

RDSF trained with the asymmetric AdaBoost procedure.

depth relation and depth gradients, more information

for the separation of positive and negative examples

are available. On the other hand, the computation of

the integral images for the orientations of the classical

HOG feature and the integral images over the mean

and variance of the depth image is still faster than the

generation of 25 integral images to quantize the depth

image as used by (Ikemura and Fujiyoshi, 2010). Fur-

thermore, the calculation of the MV-HOG-RDSF in

the online detection phase is still faster than the com-

putation of the RDSF, because for each RDSF the

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

354

Bhattacharyya distance of two 25 dimensional vec-

tors has to be determined. This improvement in speed

and the better performance in detection favour the us-

age of the MV-HOG-RDSF for the human detection

in depth images, where strong occlusion of the hu-

mans has not to be considered.

Each classiﬁer has been trained with a ﬁnal false

positive rate of 1%. To compare the performance of

the different features, the 1% false positive point on

the ROC curves will be used. Table 1 includes the re-

sults of the ROC curves in this point for each feature

used with the asymmetric AdaBoost classiﬁer. The

Table 1: The table inlcudes the results of the different fea-

tures at the 1% false positive point on the ROC curves. The

last column shows the number of selected features of the

ﬁnal classiﬁer which has been selected during the training

phase.

Feature True Positive Rate Number of Features

MV-RDSF 0.9703 73

MVSK-RDSF 0.9703 103

MV-HOG-RDSF 0.9867 24

Classic HOG 0.9811 33

RDSF 0.9828 41

MV-RDSF and MVSK-RDSF are signiﬁcantly infe-

rior to the RDSF, but the combination of gradients

features and depth features deliver an improved de-

tection accuracy.

5.3 Relative Time Performance

However, the gap in the performance is not so large,

but the time complexity of the feature and integral im-

age calculation between the RDSF and the MV-HOG-

RDSF is huge. The calculation of the integral im-

ages of the MV-HOG-RDSF is twice as fast as of the

RDSF, without pronouncing the absolute time values,

which are hardware dependent. It is worthwhile to

know, no parallelization has been used for each com-

putation. Additionally, the single feature calculation

of the MV-HOG-RDSF is also still faster than the cal-

culation of the Bhattacharyya distance between two

25 dimensional feature vectors.

Furthermore, the computational costs of the ﬁnal

classiﬁers are directly dependent from the number of

selected features in the training procedure. As it can

be seen in Table 1, the MV-RDSF and MVSK-RDSF

have many selected features in the ﬁnal classiﬁer, but

are still very fast due to the simplicity of the used fea-

tures. The new MV-HOG-RDSF have just almost half

of the number of selected features for the ﬁnal classi-

ﬁer as the RDSF and also less selected features than

the classical HOG features. The reduced number of

selected features and the low computational complex-

ity of the MV-HOG-RDSF in relation to the RDSF

(a) True positive examples hallway

(b) True positive example room

Figure 7: Subﬁgure 7(a) shows some true positive results

of the MV-HOG-RDSF classiﬁer in a hallway, where depth

ambiguities can occur. Subﬁgure 7(b) includes a true posi-

tive example in a room without the presence of depth ambi-

guities and in subﬁgure 7(c) are a true positive and a false

positive example visible, where the false positive example

is inﬂuenced by depth ambiguity.

LDACombinedDepthSimilarityandGradientFeaturesforHumanDetectionusingaTime-of-FlightSensor

355

shows the excellent usage of the LDA combination of

depth similarity and gradient features for human de-

tection in depth images.

6 CONCLUSIONS

To reduce the complexity of the RDSF calculation

and to keep the performance just by usage of mean

and variance features on the depth image, delivers not

sufﬁciently accurate results. The computational time

of the MV-RDSF is very fast, but the accuracy of the

original RDSF cannot be reached. Since, the feature

space of the MV-RDSF is not signiﬁcantly enough to

separate the dataset, a LDA combination between the

classical HOG feature and the MV-RDSF shows very

good attributes to solve the problem. The time com-

plexity of the MV-HOG-RDSF is better than of the

RDSF (Ikemura and Fujiyoshi, 2010) and less fea-

tures are selected (needed) in the training to separate

the positive examples from the negative ones. Fur-

thermore, just the depth image, and not the intensity

or the RGB image, is needed, for a good classiﬁca-

tion result. The complexity of computing the inte-

gral images and features add up to a fast classiﬁcation.

Based on the LDA combination, just one classiﬁer is

needed and not a decision fusion of different classi-

ﬁers, which are using just one of both feature types,

as it has been done in (Wang et al., 2012).

Further research could try to combine other depth

features with each other to reach more and more

the best possible classiﬁcation result. Still on focus

should be the time complexity of the used features to

produce as fast as possible classiﬁers for real time ap-

plications, where real time means to ensure the com-

putation of all methods inside the frame rate of the

underlying sensor, in this case 33ms.

ACKNOWLEDGEMENT

The research of the project ”Move and See” leading

to these results has received funding from the Min-

istry of Health, Equalities, Care and Ageing of North

Rhine-Westphalia (MGEPA), Germany and the Euro-

pean Union.

REFERENCES

Dalal, N. and Triggs, B. (2005). Histograms of Oriented

Gradients for Human Detection. In Proceedings of

the IEEE Computer Society Conference on Computer

Vision and Pattern Recognition (CVPR’05), volume 1,

pages 886–893, San Diego,California,USA.

Doll

ar, P., Wojek, C., Schiele, B., and Perona, P. (2012).

Pedestrian Detection: An Evaluation of the State of

the Art. IEEE Transactions on Pattern Analysis and

Machine Learning, 34(4):743 – 761.

Enzweiler, M. and Gavrila, D. M. (2009). Monocular

Pedestrian Detection: Survey and Experiments. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 31(12):2179 – 2195.

Ikemura, S. and Fujiyoshi, H. (2010). Real-Time Hu-

man Detection using Relational Depth Similarity Fea-

tures. In Proceedings of the 10th Asian Conference on

Computer Vision (ACCV’10), pages 25 – 38, Queen-

stown,New Zealand.

Izenman, A. J. (2008). Modern Multivariate Statistical

Techniques - Regression, Classiﬁcation, and Manifold

Learning. Springer New York.

Keller, C. G., Enzweiler, M., and Gavrila, D. M. (2011). A

New Benchmark for Stereo-Based Pedestrian Detec-

tion. In IEEE Intelligent Vehicles Symposium (IV’11),

pages 691 – 696, Baden-Baden,Germany.

Mattheij, R., Postma, E., van den Hurk, Y., and Spronck,

P. (2012). Depth-based detection using haar-like fea-

tures. In Proceedings of the 24th BENELUX Confer-

ence on Artiﬁcial Intelligence (BNAIC’12), pages 162

– 169, Maastricht,Netherlands.

Nunn, C., M

uller, D., Meuter, M., M

uller-Schneiders,

S., and Kummert, A. (2009). An Improved Ad-

aboost Learning Scheme using Lda Features for Ob-

ject Recognition. In Proceedings of the 12th In-

ternational IEEE Conference on Intelligent Trans-

portation Systems (ITSC’09), pages 486 – 491, St.

Louis,MO,USA.

Shafait, F., Keysers, D., and Breuel, T. M. (2008). Efﬁ-

cient Implementation of Local Adaptive Threshold-

ing Techniques Using Integral Images. In Yanikoglu,

B. A. and Berkner, K., editors, Proceedings SPIE

6815,Document Recognition and Retrieval XV.

Spinello, L. and Arras, K. O. (2011). People detection

in RGB-D data. In Proceedings of the IEEE/RSJ

International Conference on Intelligent Robots and

Systems (IROS’11), pages 3838 – 3843, San Fran-

cisco,CA,USA.

Viola, P. and Jones, M. (2001a). Fast and Robust Classi-

ﬁcation using Asymmetric AdaBoost and a Detector

Cascade. In Advances in Neural Information Process-

ing System 14, pages 1311 – 1318. MIT Press.

Viola, P. and Jones, M. (2001b). Rapid Object Detection

Using a Boosted Cascade of Simple Features. In Pro-

ceedings of the IEEE Computer Society Conference on

Computer Vision and Pattern Recognition (CVPR’01),

volume 1, pages 511 – 518, Kauai,HI,USA.

Wang, N., Gong, X., and Liu, J. (2012). A New Depth

Descriptor for Pedestrian Detection in RGB-D Im-

ages. In Proceedings of the 21st International Confer-

ence on Pattern Recognition (ICPR’12), pages 3688 –

3691, Tsukuba,Japan.

Wu, S., Yu, S., and Chen, W. (2011). An attempt to pedes-

trian detection in depth images. In Proccedings of the

3rd Chinese Conference on Intelligent Visual Surveil-

lance (IVS’11), pages 97 – 100, Beijing,China.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

356