
Identifying Strong Statistical Bias in the Local Structure of Metabolic
Networks
The Metabolic Network of Saccharomyces Cerevisiae as a Test Case
Paulo A. N. Dias
1
, Marco Seabra dos Reis
1
, Pedro Martins
2,3
and Armindo Salvador
4,5
1
CIEPQPF, Department of Chemical Engineering, University of Coimbra, Rua Sílvio Lima, 3030-790, Coimbra, Portugal
2
Polytechnic Institute of Coimbra - ISCAC, Quinta Agrícola - Bencanta, 3040-316, Coimbra, Portugal
3
Operations Research Center (CIO), Faculty of Sciences, University of Lisbon, Lisbon, Portugal
4
Center for Neuroscience and Cell Biology, University of Coimbra, 3004-517 Coimbra, Portugal
5
Chemistry Department FCTUC, Largo D. Dinis, Rua Larga, 3004-535 Coimbra, Portugal
Keywords: Metabolic Networks, Network Motifs, Network Analysis.
Abstract: The detection of strong statistical bias in metabolic networks is of much interest for highlighting potential
selective preferences. However, previous approaches to this problem have relied on ambiguous
representations of the coupling among chemical reactions or in physically unrealizable null models, which
raise interpretation problems. Here we present an approach that avoids these problems. It relies in a
bipartite-graph representation of chemical reactions, and it prompts a near-comprehensive examination of
statistical bias in the relative frequencies of topologically related metabolic structures within a predefined
scope. It also lends naturally to a comprehensive visualization of such statistical relationships. The approach
was applied to the metabolic network of Saccharomyces cerevisiae, where it highlighted a preference for
sparse local structures and flagged strong context-dependences of the reversibility of reactions and of the
presence/absence of some types of reactions.
1 INTRODUCTION
The detection of over- or under-represented local
structures (motifs and anti-motifs, respectively) in
biological networks has attracted much interest as a
way of detecting potential selective constraints
(Milo et al., 2002, Aittokallio and Schwikowski,
2006, Barabasi and Oltvai, 2004). The implicit
rationale is that over-representation with respect to
expectation from a prescribed null model is likely to
be a consequence of natural selection for
maintenance of the motif, driven by functional
advantages provided by its dynamic properties.
However, it is hard to conceive physically realizable
and biologically plausible null models of metabolic
networks. Null models generated by the
randomization procedures considered in previous
publications (Shellman et al., 2013) are not
physically realizable, as they violate atom
conservation. The meaningfulness of statistical over-
representation with respect to such unrealistic null
models is therefore questionable (Artzy-Randrup et
al., 2004). As a more reasonable alternative, Milo et
al. (Noor et al., 2010) consider randomly generated
networks such that all the allowed reactions could in
principle be catalyzed by known enzyme activities
considered at the third level of the E.C.
classification. However, the extent to which
networks generated in this way are legitimate “no-
selection” null models is debatable. Enzymes are
products of natural selection and expensive to
maintain. So, the fact that an enzyme exists to
catalyze a given reaction is already an indication that
such a reaction has selective advantages for at least
some organisms. Further, this procedure is liable to
knowledge bias.
The representation of metabolic connectivity
structures in motif analysis can also be problematic.
Previous analyses (Shellman et al., 2013) defined
structures as graphs where each metabolite A is
connected to another one B by a directed edge if
there is a reaction converting A to B. However, such
metabolite connectivity structures are ambiguous
and difficult to interpret and relate to dynamics and
function. This is so because the same structure may
correspond to very different reaction structures.
207
A. N. Dias P., Seabra dos Reis M., Martins P. and Salvador A..
Identifying Strong Statistical Bias in the Local Structure of Metabolic Networks - The Metabolic Network of Saccharomyces Cerevisiae as a Test Case.
DOI: 10.5220/0005258102070212
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2015), pages 207-212
ISBN: 978-989-758-070-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Here we present an approach to systematically
highlight and visualize strong statistic preferences in
local metabolic connectivity structures without
requiring an artificial null model. In order to avoid
the ambiguity problems discussed in the previous
paragraph, structures are represented as directed
bipartite graphs, with reaction and metabolite nodes
(Aittokallio and Schwikowski, 2006). The approach
consists in first constructing a topological hierarchy
of structures of increasing complexity. Then,
comparisons among the frequencies of structures
differing by a single structural element (one reactant
or product of one reaction, a reaction connecting two
metabolites, or the reversibility of one reaction) can
be properly performed using such framework. We
illustrate its application to the set of structures
formed by 3 metabolites and 2 or 3 reactions in the
metabolic network of Saccharomyces cerevisiae.
2 METHODS
2.1 Definitions
We denote by “topological structure”, abbreviatedly
“structure”, a specific pattern of interconnections
between the two types of nodes of the metabolic
network: metabolites and reactions. Isomorphic
representations obtained from each other by
relabeling metabolites and/or reactions are
considered as the same structure.
Two structures are said to be directly related if
the most complex one can be obtained from the
simplest one by addition of just one of the following
structural components: (i) a reactant or product to a
reaction; (ii) the reverse of a reaction; (iii) a third
reaction converting one metabolite into one other.
The simplest of two directly related structures is
denoted as “parent”, and the other, derived from it
by the addition of a structural element, is referred as
its “child”. Each structure may have multiple parents
and children. We denote by “offspring” of a
structure the set of all of its children, grand-children,
etc.
We denote by “instance” any concrete realization
of a given structure in a metabolic network, i.e., an
actual set of metabolites and reactions connected as
defined in the structure.
2.2 Scope
All the structures considered in the present paper are
formed by three metabolites connected through two
or three (possibly reversible) reactions. Further, the
third reaction must connect a reactant-product pair
not connected by any of the other reactions (Figure
1). Reactions in instances of each structure may
have additional reactants or products not represented
in the structure, but reversibility in the structure
implies reversibility of a corresponding reaction in
the instances.
A)
B)
Figure 1: Examples of structures of three metabolites and
two or three reactions: (A) considered in this work, (B)
excluded.
2.3 Structure Enumeration
The three simplest structures include two reactions,
each with a reactant and a product. All other
structures were iteratively constructed from these
three seed structures through the stepwise addition
of any of the following three structural components:
(i) a new reactant or product (from the structure) to a
pre-existing reaction; (ii) the reverse of a pre-
existing reaction; (iii) a third reaction converting one
metabolite in the structure into another. At each step,
structures were checked for isomorphism and
inclusion in the structural scope defined in section
2.2.
The procedure above generates a layered
network of topological relationships among
structures (Figure 2). The nodes in this network are
the 149 non-isomorphic topological structures,
arranged in 8 generations, from the sparsest (i.e.,
with the fewest structural components) structures to
the densest. The edges join directly related structures
as defined in section 2.1.
Importantly, the topology of this network is
uniquely determined by the topological relationships
of the structures and independent of the properties of
concrete metabolic networks. It therefore provides a
19)
60)
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
208

convenient and sound reference to represent the
local-topology characteristics of the metabolism of
different microorganisms and assess their affinities
and particularities through topological oriented
statistical descriptors.
2.4 Instance Counting in a Metabolic
Network
The approach was applied to a reconstruction
(Forster et al., 2003) of the S. cerevisiae metabolic
network, which includes 1058 reactions (335
reversible and 723 irreversible) and 991 metabolites.
Each reversible reaction was replaced by a pair of
unidirectional reactions, making a total of 1393
unidirectional reactions.
We determined the following statistics in this
metabolic network.
2.4.1 Naked Frequency
We define the naked frequency of structure i,
,
as the number of instances matching the structure
but not any of its offspring.
2.4.2 Embedded Frequency
We define the embedded frequency of structure i,
, as the total number of instances of the
structure, whether or not embedded in any of its
offspring. The value of
is obtained by adding
and the naked frequencies of all of structure i’s
offspring.
The embedding ratio of structure i into its child j,
,
=
/
measures the propensity of
structure i to be embedded into its child j and
respective offspring.
The independence ratio
=
/
measures the tendency of structure i to appear in its
“naked” form, rather than embedded in any of its
offspring structures.
2.4.3 Metabolite Coverage
We define the metabolite coverage of structure i,
, as the fraction of metabolites in the network
that appear as nodes in all instances of structure i,
considering only exact matches as for the
computation of naked frequencies.
2.4.4 Children Information
We define the children information of structure n,
∆
,as (eq. 1):
∆
=
−
=
=−
1
−−
,∀∈ℎ
(1)
where ℎ
is the set of all the children of structure
. The value of ∆
is null if all children are
equally frequent, and high if the distribution of
children frequencies is very uneven.
3 RESULTS AND DISCUSSION
Some of the statistics above were graphically
represented in Figures 2 and 3. The analysis of these
statistics highlights the following remarkable
features about the local structure of the metabolic
network:
1. Although most structures have instances in the
network, 22 of the 149 structures do not (e.g.,
76, 92, 110). The latter are usually very dense
(Figure 2).
2. Sparse structures tend to be more frequent
than denser ones (Figures 2, 3). This is
expected for embedded frequencies because
simpler structures can a priori be matched by
more instances than more complex structures
for combinatorial reasons. However, sparser
structures also tend to have higher naked
frequencies, which may highlight a selective
preference. The avoidance of denser structures
may stem from the fact that maintaining
multiple enzymes for converting among
similar substrates (other than metabolic
currencies) would spend cellular biosynthetic
resources without bringing significant
advantages.
Most structures that have high values are
dense. This is in part because these structures
can have few denser offspring. However, some
sparse structures have high (e.g., B
→ C + A,
B → A + C), and some relatively dense structures
(e.g., A Φ C + B, B Φ C, C + B Φ A) have very
low R. Although there is a significant negative
correlation between and the number of
offspring of the structures (ρ
Spearman
= –0.20, p<
0.02) this correlation is low. Therefore, the
number of offspring explains only a minor
portion of the variation in .
High values of
may stem from the following two
distinct situations. First, there may be many disjoint
instances of the structure. Second, there may
IdentifyingStrongStatisticalBiasintheLocalStructureofMetabolicNetworks-TheMetabolicNetworkof
SaccharomycesCerevisiaeasaTestCase
209
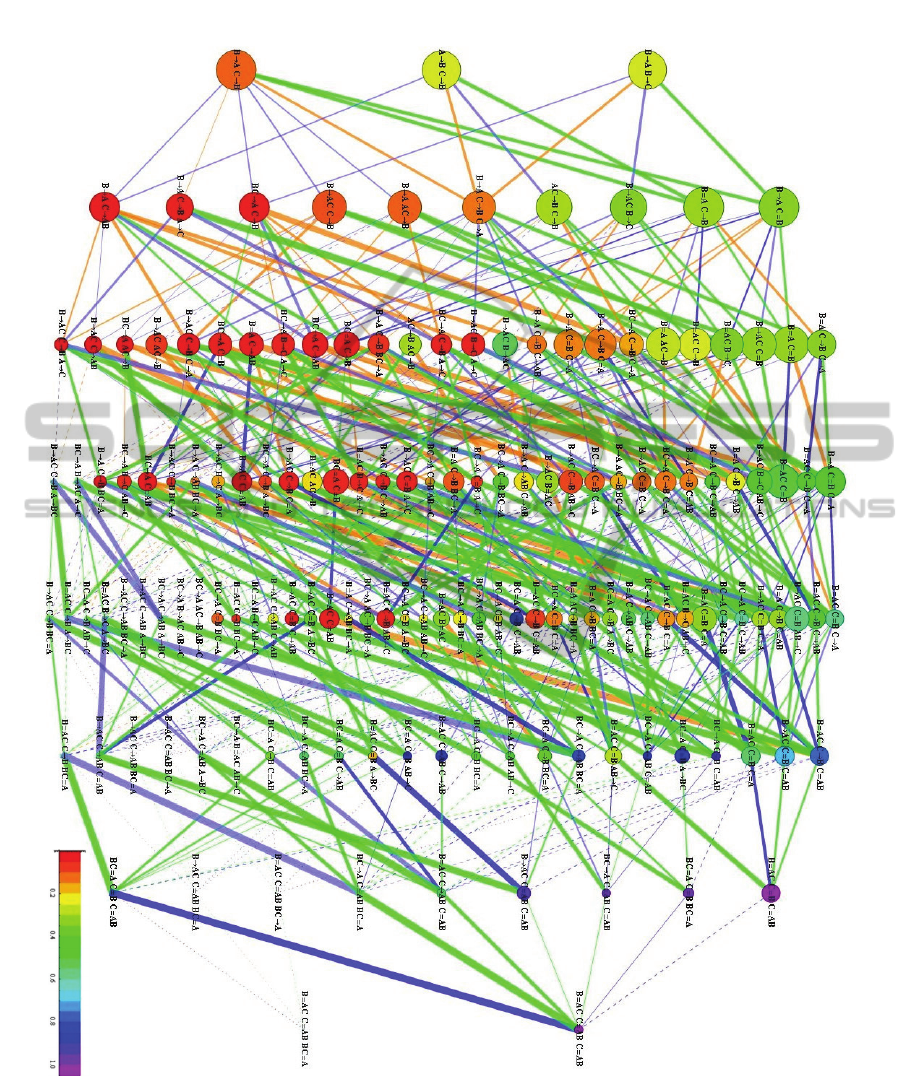
Figure 2: Network of topological relationships among the structures, and statistics for the metabolic network of S.
cerevisiae. Nodes at each generation are ordered by naked frequency. Node diameter is proportional to
. Node
hue represents
(scale at the bottom right corner). Edge colours represent relationships: blue, addition of
reactant/product to unidirectional (dark) or bidirectional (light) reaction; orange, addition of reaction; green, addition of
reverse reaction. Edge thicknesses are proportional to
,
. Dashed edges:
,
0.05. Dotted edges connect to
structures that lack instances in the metabolic network.
/
122)
133)
62)
84)
125)
119)
121)
137)
132)
131)
70)
61)
59)
47)
66)
97)
124)
101)
135)
83)
142)
82)
120)
105)
93)
69)
136)
68)
145)
140)
130)
129)
118)
78)
46)
60)
99)
55)
43)
65)
64)
39)
112)
45)
123)
116)
96)
74)
147)
51)
57)
67)
103)
134)
80)
25)
141)
95)
100)
148)
127)
20)
91)
58)
117)
114)
77)
81)
149)
144)
139)
138)
128)
110)
104)
92)
76)
37)
44)
8)
111)
54)
63)
53)
49)
42)
146)
50)
98)
24)
115)
79)
89)
73)
102)
87)
56)
107)
12)
29)
41)
94)
19)
109)
126)
75)
22)
113)
72)
143)
90)
38)
4)
6)
15)
7)
27)
48)
35)
36)
52)
23)
106)
88)
33)
71)
11)
21)
108)
17)
10)
40)
28)
30)
18)
86)
2)
3)
14)
32)
34)
26)
5)
9)
85)
16)
13)
31)
1)
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
210

Figure 3: Relationship between naked frequency,
embedded frequency and relative structure density.
Relative structure density was computed as
, with
N
Edges
the number of edges connecting metabolite and
reaction nodes. Structures to the left of the dashed line
have a ratio
≤0.1and
>1000. These
structures are frequent and occur preferentially embedded
in offspring structures.
be a combinatorial explosion such that part of the
metabolites and reactions forming the structure are
shared among many of the instances and the rest of
the structure can be matched by many other
metabolites and reactions in the metabolic network.
The very high
values of most instances are due to
the second factor. Thus, when only overlaps by up to
one metabolite (and no reactions) are allowed,
structure 16 (B
→ A, C → A + B), which ranks 12
th
in terms of
, becomes the one with highest naked
frequency (12). However, the embedded frequencies
with overlaps restricted to no more than one
metabolite are strongly correlated to
(ρ
Spearman
=
0.90), which is simpler to compute.
There is also a strong correlation between
and
(ρ
Spearman
= 0.91). But remarkably, although
seed structures 13 (B → A, B → C) and 31 (A → B,
C → B) have higher embedded frequency, their
respective children 2 and 3, resulting from addition
of one reverse reaction have higher metabolite
coverage. This is explained by a greater overlap
among instances for structures 13 and 31 than for
structures 2 and 3.
Structures with low R and high
are those that
occur frequently when embedded in more complex
structures but not in isolation. A more detailed
analysis of the statistics for some of these structures
highlights the following remarkable features of the
local structure of the metabolic network in point.
1. In 96% of the (total) instances of structure 18
(B → A + C, C → A + B) the latter reaction is
reversible (structure 19 and offspring), and in
95% of the instances there is also a C → B
reaction (structure 56 and offspring). On the
other hand, structure 18 is rarely embedded in
offspring that also contain a B → A or a A →
B reaction.
2. In turn, in 96% of the instances of structure 56
the reaction C → A + B is reversible (structure
60 and offspring), but structure 56 is rarely
embedded in offspring containing either a
reaction of the form C + A → B or a second
reaction of the form C → A + B.
3. In 93% (51%) of its occurrences, structure 19
is associated to a B → C (respectively C → B)
reaction, but it is rarely associated to reactions
A → B, B → A, A → C or C → A.
4. 91% of the instances of structure 17 (A → B +
C, B Φ C) contain also a A → B reaction.
5. In 93% of the occurrences of the cycle A → B
→ C → A (structure 85 and offspring) at least
one of the steps is reversible.
The computation and ranking of children
information provide another means of flagging
unexpected bias. The analysis of the results allowed
determining interesting features of the local structure
of the metabolic network:
1. Structure 40 (A → B + C, C → B, C → A) has
∆= 2.0 bit. The structure has seven
children, three of which are obtained by
adding a reversible reaction. The child with
the first reaction reversible, structure 44, is
clearly dominant, representing 85% of the
instances of all children.
2.
Structure 11 (A Φ B + C, C → B) has ∆=
1.9 bit. Of its seven children, four are obtained
by adding a 3
rd
reaction: C → A, A → C, A →
B or B → A. Structure 44 is obtained by
adding the first reaction and comprises 82% of
the instances of all the children.
3. Structure 21 (B + C → A, C → A) has ∆=
1.8 bit. Of its 8 children, six are obtained by
adding a new reaction. Adding the reaction C
→ B leads to structure 111, which comprises
72% of the children’s instances.
4 CONCLUSIONS
The approach to characterize statistical trends in the
1
23
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
6
2
7
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
7
7
78
79
80
81
82
83
84
85
86
87
88
89
9
0
91
92
93
94
95
96
97
98
99
100
101
102
103
10
4
105
106
107
108
109
110
111
112
113114
115
116
117 118119
120
121
122
12
3
124
125
126
127
1 2 3 4 5
1
2
3
4
5
Relative structure density
1
2 3 4 5
1
2
3
4
5
IdentifyingStrongStatisticalBiasintheLocalStructureofMetabolicNetworks-TheMetabolicNetworkof
SaccharomycesCerevisiaeasaTestCase
211

local structure of metabolic networks presented in
this article shows several desirable features.
First, it represents local topological structures as
bipartite and directed graphs, which permits an
unambiguous description of the chemical reaction
patterns involved.
Second, it presents a comprehensive enumeration
of the structures within a prescribed scope and
highlights the topological relationships among
structures, facilitating a comprehensive examination
of statistical trends.
Third, it prompts a comprehensive visualization
of structure statistics and of statistic relationships
among topologically related structures (e.g. Figure
2). This will facilitate direct comparisons among the
local-topological characteristics of the metabolic
networks of distinct organisms and organelles,
which can be put in relation to their environments
and functions.
Fourth, the approach to detecting potential
selective constraints does not hinge on null models
based on physically meaningless random networks.
It emphasises not so much the absolute frequencies
of the structures as the relative frequencies among
topologically related structures. Therefore it puts in
relief the local-context dependence of the
presence/absence of additional reactions,
reversibility, etc. We presented above several
statistics that help detecting strong bias.
Applied to the S. cerevisiae metabolic network,
the approach highlights a preference for sparse
structures. It also highlights some very strong
context-dependence of the reversibility of reactions
and of the presence/absence of some types of
reactions. The underpinnings of these trends deserve
further investigation as a way to reveal functional
(e.g. dynamic) properties underlying an evolutionary
preference for some reaction-coupling
configurations, with the potential to guide synthetic
biology and metabolic engineering approaches.
Ongoing algorithmic developments include the
expansion of the topological scope of the analysis
and strategies to efficiently navigate the network of
topologically related structures towards highly
represented complex structures.
ACKNOWLEDGEMENTS
We acknowledge grants PEst-C/SAU/LA0001/2013-
2014, PEst-OE/MAT/UI0152 and FCOMP-01-0124-
FEDER-020978 financed by FEDER through the
“Programa Operacional Factores de
Competitividade, COMPETE” and by national funds
through “FCT, Fundação para a Ciência e a
Tecnologia” (project PTDC/QUI-
BIQ/119657/2010).
REFERENCES
Aittokallio, T. & Schwikowski, B. 2006. Graph-based
methods for analysing networks in cell biology.
Briefings in Bioinformatics, 7, 243-255.
Artzy-Randrup, Y., Fleishman, S. J., Ben-Tal, N. & Stone,
L. 2004. Comment on "Network motifs: simple
building blocks of complex networks" and
"Superfamilies of evolved and designed networks".
Science (New York, N.Y.), 305, 1107; author reply
1107.
Barabasi, A. L. & Oltvai, Z. N. 2004. Network biology:
Understanding the cell's functional organization.
Nature Reviews Genetics, 5, 101-U15.
Forster, J., Famili, I., Fu, P., Palsson, B. O. & Nielsen, J.
2003. Genome-scale reconstruction of the
Saccharomyces cerevisiae metabolic network. Genome
Research, 13, 244-253.
Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N.,
Chklovskii, D. & Alon, U. 2002. Network Motifs:
Simple Building Blocks of Complex Networks.
Science, 298, 824-827.
Noor, E., Eden, E., Milo, R. & Alon, U. 2010. Central
Carbon Metabolism as a Minimal Biochemical Walk
between Precursors for Biomass and Energy.
Molecular Cell, 39, 809-820.
Shellman, E. R., Burant, C. F. & Schnell, S. 2013.
Network motifs provide signatures that characterize
metabolism. Molecular BioSystems, 9, 352-360.
BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
212
