Edge-stacked Timelines for Visualizing Dynamic Weighted Digraphs

Michael Burch, Tanja Munz and Daniel Weiskopf

VISUS, University of Stuttgart, Stuttgart, Germany

Keywords:

Dynamic Graph Visualization.

Abstract:

We investigate the problem of visually encoding time-varying weighted digraphs to provide an overview about

dynamic graphs. Starting from a rough overview of dynamic relational data an analyst can subsequently

explore the data in more detail to gain further insights. To reach this goal we ﬁrst map the graph vertices in the

graph sequence to a common horizontal axis. Edges between vertices are represented as stacked horizontal

and color-coded links starting and ending at their corresponding start and end vertex positions. The direction

of each edge is indicated by placing it either above or below the horizontal vertex line. We attach a vertically

aligned timeline to each link to show the weight evolution for those links. The order of the vertices and stacked

edges is important for the readability of the visualization. We support interactive reordering and sorting in the

vertex, edge, and timeline representations. The usefulness of our edge-stacked timelines is illustrated in a case

study showing dynamic call graph data from software development.

1 INTRODUCTION

The visual encoding of dynamic graphs is challeng-

ing (Beck et al., 2014a) compared to the visualiza-

tion of static graphs. Using node-link diagrams in a

two-dimensional layout as well as matrix representa-

tions either in a time-to-time (animation) or time-to-

space mapping either leads to cognitive efforts due to

the preservation of the viewer’s mental map or to vi-

sual scalability problems due to showing a number of

graphs in a small multiples or stacked fashion. This

gets even more challenging when the focus is on ﬁnd-

ing time-varying patterns among the edge weights.

We introduce a novel dynamic graph visualization

that avoids explicit link crossings and supports the

preservation of a viewer’s mental map. To achieve

these goals we use a time-to-space mapping of the

graph sequence by visually encoding the vertices oc-

curing in the graph sequence to a horizontal centered

line to equidistant positions. The edges are placed

in a vertex-aligned manner as color coded parallel

and stacked straight links each starting and ending

at their corresponding vertex positions. The time-

varying weights of each edge are displayed by stacked

and link-aligned timelines to the left hand side with-

out overlap of the graph view.

This technique provides an overview for a time-

varying weighted digraph with an additional hierar-

chical vertex organization. As a second step the tech-

nique supports interactively zooming into any rectan-

gular region in the graph view. Filtering in the ver-

tex, edge, and time dimensions can be used to further

reduce the vast amounts of displayed data. Finally,

details-on-demand features are also integrated which

might be used to display a selected graph in another

representation (Shneiderman, 1996).

The technique supports two ordering techniques

for the vertices or the edges: Interactive reorder-

ing of vertices is applied to reduce link lengths as

also proposed in the work of (van den Elzen et al.,

2013) and edge stacking ordering to put edges close

to each other that are required to ﬁnd graph structures.

In combination, these ordering strategies can reveal

common trends among edge groups between hierar-

chically organized vertex groups.

2 RELATED WORK

Dynamic graph visualization has become a growing

discipline due to many application domains (Beck

et al., 2014a). Several aesthetic graph drawing cri-

teria (Beck et al., 2009, 2013) play a crucial role in

order to make ﬁrst static diagrams readable and aes-

thetically pleasing and second, allow to visually an-

alyze the dynamics of the graph. For the dynamics,

criteria such as dynamic stability leading to a preser-

vation of a viewer’s mental map (Archambault et al.,

Burch M., Munz T. and Weiskopf D..

Edge-stacked Timelines for Visualizing Dynamic Weighted Digraphs.

DOI: 10.5220/0005259200930100

In Proceedings of the 6th International Conference on Information Visualization Theory and Applications (IVAPP-2015), pages 93-100

ISBN: 978-989-758-088-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

2011; Purchase et al., 2007) are of special interest to

reduce the cognitive efforts for a viewer when making

comparisons among the single graphs in a sequence.

There are two lines of research: Graph anima-

tion (Diehl and G

org, 2002; Frishman and Tal, 2007),

on the one hand, has become an approach to visually

map the dynamic graph data. But when the graphs be-

come dense, the node-link metaphor which is mainly

used for displaying animated graph sequences, suffers

from visual clutter (Rosenholtz et al., 2007) making

even a single diagram hard to read. For animation,

sophisticated layout algorithms are needed which fo-

cus on producing aesthetically pleasing diagrams on

the one hand but also follow rules such as dynamic

stability. Even when many of these design principles

are followed in an animated diagram it still remains

hard to analyze the data for temporal patterns and to

apply interactive features as well as a hierarchical or-

ganization of the vertices if one exists (Burch et al.,

2010; Beck et al., 2014b).

In our design we are more in favour of a non-

animated diagram for showing the graph evolution

over time. Such non-animated time-to-space ap-

proaches are for example the parallel edge splatting

technique (Burch et al., 2011) that uses a small mul-

tiples representation by mapping the graphs in a se-

quence to side-by-side vertical stripes similar to par-

allel coordinates. Although, this is a useful idea,

by making a graph artiﬁcially bipartite and by map-

ping the vertices to one-dimensional vertical lines, the

probability of link crossings increases.

In our approach, instead, we apply a more clutter-

free visualization strategy by stacking the links and

the aligned timelines for the edges. In this tech-

nique, links are not crossing each other. Moreover, the

graphs are not made artiﬁcially bipartite which intro-

duces additional representatives (as also in adjacency

matrix visualizations) making path-related tasks in a

graph difﬁcult to solve. Another concept apart from

using small multiples is by directly integrating the

graphs in a stacked manner into one static diagram

by using aligned planes (Brandes and Corman, 2003).

Also matrix representations have been introduced

for dynamic graph visualization where each cell of the

matrix includes some timeline showing the evolution

of a single edge, for instance, based on pixel repre-

sentations (Stein et al., 2010), line angles (Brandes

and Nick, 2011), or bar charts (Burch et al., 2013).

Also radial matrix-based approaches have been de-

signed (Burch and Diehl, 2008; Vehlow et al., 2013)

which suffer from visual scalability problems for ver-

tices and edges. Moreover, visual comparisons over

time are difﬁcult to solve due to the mapping to circu-

lar shapes.

Our novel technique is in some way related to

the approach proposed by (van den Elzen et al.,

2013) which is based on the Massive Sequence

Views (MSV) introduced by (Jerding and Stasko,

1995, 1998) as Execution Mural and later adapted to

software visualization by (Cornelissen et al., 2007;

Holten et al., 2007). Van den Elzen et al. investigate

the ordering problem of vertices as well as the optimal

linear arrangement problem (OLA) (Garey and John-

son, 1979) with the goal to make the diagrams more

readable and understandable. This algorithmic strat-

egy focuses on trends, countertrends, and anomalies

in the graph dynamics but also on static graph pat-

terns such as community or star patterns.

3 DATA MODEL

We model a directed weighted graph as G = (V, E

)

where V := {v

, . . . , v

} denotes the ﬁnite set of n ∈ N

vertices and E

⊆ V ×V := {e

, . . . , e

} the ﬁnite set

of m ∈ N directed adjacency edges. Each edge e

∈

, 1 ≤ j ≤ m is attached by a weight w(e

) where

w : E −→ R denotes a weight function giving each

edge a speciﬁc real-valued number.

A dynamic graph Γ of length k ∈ N is denoted

as a sequence of single graphs Γ := {G

, . . . , G

}

where each graph G

, 1 ≤ i ≤ k is a static directed and

weighted graph in the sense described above with a

vertex set V

and an edge set E

The hierarchical organization among the graph

vertices is modeled as another graph, i.e. a hierar-

chy, H = (

i=1

, E

). The hierarchical organization

is hence composed of the set of all vertices occuring

in the graph sequence and another set of relations, the

inclusion edges E

expressing parent-child relation-

ships among the hierarchy vertices. It may be noted

that E

and E

are disjoint sets, i.e. E

∩ E

3.1 Vertex and Edge Ordering

Our novel visualization technique places graph ver-

tices equidistantly on a one-dimensional line. For

this, all vertices from the set V :=

i=1

are taken

into account, i.e. all vertices that occur in all graphs

in the sequence. If a hierarchy H exists among the

vertices V this must be maintained when laying out

the graph vertices, i.e. the hierarchical organization

must also be mapped to a one-dimensional line.

The traversal of the graph vertices plays a deciding

role for the edges E

. The Optimal Linear Arrange-

ment Problem (Garey and Johnson, 1979) which is

NP-hard can be algorithmically solved by a heuristics

as also described in the work of (van den Elzen et al.,

IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications

2013) when reordering Massive Sequence Views but

we additionally have to deal with a hierarchical orga-

nization of the vertices which makes the problem even

harder.

In our work we do not focus on an effective

and efﬁcient automatic reordering of the graph ver-

tices focusing on the reduction of link lengths or

the sum of overlaps since our novel contribution is

more on showing a dynamic weighted graph with ex-

plicit timelines attached to the graph links in an edge-

aligned manner. Moreover, the graph edges should be

aligned to their corresponding timeline to better ex-

plore the time-series weights for dynamic patterns as

described in the work of (Burch and Weiskopf, 2011).

Also the ordering of the edges E

, i.e. the stack-

ing order, plays an important role when discover-

ing temporal trends. The vertical order of the edges

directly inﬂuences the order of the timelines in the

same way. This again helps to ﬁnd groups of simi-

lar time-varying patterns and can directly be explored

for matching a group of relations coming from simi-

lar subhierarchies and targeting to other or the same

subhierarchies. For the edge order we achieve more

freeness than in the approach of (van den Elzen et al.,

2013) because in their work the edge stacking di-

mension is ﬁxed since it is used as time axis. The

edge ordering also plays a deciding role when detect-

ing graph patterns such as star patterns, clusters, or

graph symmetries. For this reason we support several

edge stacking strategies in our technique which are

described in more detail in Section 4.1 such as order-

ing by shortest edges, oldest edges, youngest edges,

edges with the smallest start vertex index, edges with

the shortest path through a given hierarchy and the

like.

3.2 Data Aggregation

We live in a data-driven era, i.e. datasets become

larger and larger due to the progress in hardware tech-

nologies. The growing of datasets has also an impact

on dynamic graph data. Todays dynamic graph visu-

alization techniques must keep up with the ﬂood of

relations. Graphs can grow in either the vertex, edge,

or time dimension. Also additional attributes such as

edge weights or a hierarchical organization among the

graph vertices is present in many scenarios which is

also of interest for a graph analyst.

As (Tufte, 1992) puts it ”Above all else show the

data”, we follow a similar concept in our approach.

We display as much of the graph data in a com-

pressed and aggregated way. This means we display

as many vertices, edges, and time steps as are given

in a dataset. Since we have a limited display capac-

ity this data should be aggregated in an effective and

efﬁcient way in all three dimensions.

Generally, spatially neigbored vertices must be

represented in a single pixel when the screen resolu-

tion is not large enough to display all of them sepa-

rately. The same holds for neighbored links as well

as timelines. To achieve a good overview of the dy-

namic graph data in all three dimensions, aggregation

in both horizontal and vertical direction is required.

To this end we support simple aggregation tech-

niques that take either the sum, the average, or the

maximum of the edge weights into account. The ag-

gregated weights are displayed as color-coded pixels.

Moreover, the color coding can be displayed linearly

or logarithmically.

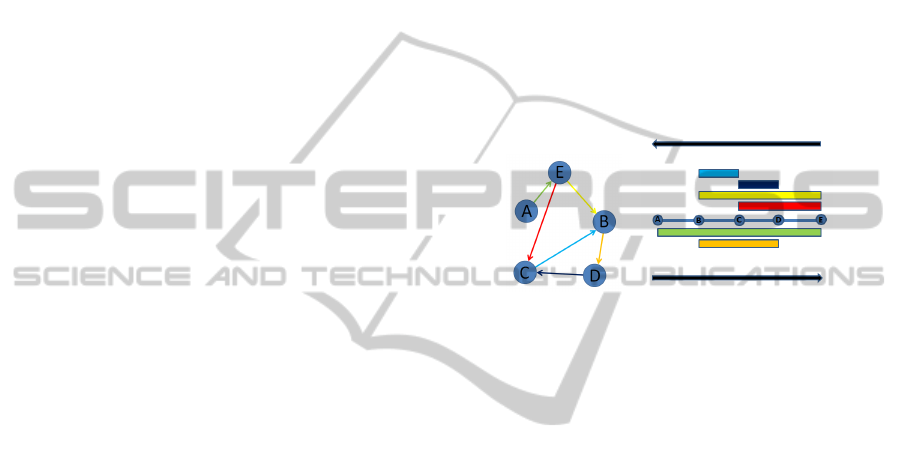
(a) (b)

Figure 1: A weighted and directed graph: (a) Standard

node-link representation with color-coded links and arrow

heads. (b) Edge-stacked visualization of the same static

graph as in (a) but with color-coded stacked lines.

4 VISUALIZATION TECHNIQUE

Our novel visualization technique has to deal with

three data dimensions as well as additional attached

and inherent data. The contribution of this work is

that the vertex, edge, and time dimension of a dy-

namic graph should be displayable in a scalable way.

Time-varying edge weights, structural graph proper-

ties, symmetries, the direction of the edges, or the hi-

erarchical organization of the graph vertices will also

be visually encoded in the diagram. Apart from using

a time-to-space mapping for the dynamic data also vi-

sual clutter should be reduced, i.e. the static diagram

should not suffer from link crossings as typically oc-

curing in node-link diagrams. Runtime complexities

should be reduced allowing an interactive visualiza-

tion technique. This is problematic for graph anima-

tion when generating stable graph layouts.

Another advantage, in particular compared to ma-

trix visualizations, is the fact that only one representa-

tive element is displayed for each graph vertex which

makes path-related tasks easier to solve. Moreover,

both absolute as well as relative time can be displayed

in the aligned and stacked time axes which allows

Edge-stackedTimelinesforVisualizingDynamicWeightedDigraphs

comparisons between time intervals, also on different

time axis granularities.

4.1 Static Graph Visualization

We ﬁrst show how a static directed and weighted

graph is visualized as an edge-stacked visualization.

First the vertices of a graph are mapped equidistantly

to a horizontal line. The edges are mapped as parallel

stacked lines (or rectangles) where the horizontal po-

sitions of the start and target vertices indicate the line

ends. Depending on the direction of an edge, the cor-

responding line is placed either above or below the

horizontal separation line. Self-edges are displayed

on both sides to give a correct impression on the sym-

metries in a graph. Color coding is used to visually

map the edge weights of a static graph. Also cate-

gorical edge attributes instead of quantitative weights

might be visually encoded by color.

Figure 1 (a) illustrates a weighted directed graph

consisting of ﬁve vertices and six edges. The directed

links are color-coded to demonstrate different weights

in a graph. The mapping of this static graph to an

edge-stacked visualization is shown in Figure 1 (b).

The hierarchical organization among the graph

vertices (if one exists) is displayed as a layered ici-

cle plot (Kruskal and Landwehr, 1983) oriented to

the top and to the bottom. This hierarchical organiza-

tion can be used to collapse or expand subhierarchies.

Moreover, if it is present in the dataset it allows to de-

rive graph patterns between subhierarchies and also

on different levels of hierarchical granularity.

(a) (b)

Figure 2: A weighted and directed graph with an additional

hierarchical organization of the vertices: (a) Standard node-

link diagram with hierarchy indicated by dashed lines. (b)

Edge-stacked visualization with attached layered icicle plot

to display the hierarchy.

Figure 2 (a) illustrates a static weighted and di-

rected graph with an additional hierarchical organiza-

tion of the graph vertices. This is indicated by the

dashed lines showing a small hierarchy H consisting

of subhierarchies H1 (leaf vertices A, B, and C) and

H2 (leaf vertices D and E). Figure 2 (b) visualizes this

static graph with an additional hierarchy as an edge-

stacked representation.

It may be noted that the reordering of the vertices,

i.e. a traversal of the hierarchy does not inﬂuence the

order of the stacked edges. It can have an impact on

single line lengths and the sum of line lengths as well

as their overlap. The reduction of this overlap is ref-

ered to as the Optimal Linear Arrangement Problem

(OLA) which is NP-hard.

Based on a given vertex order we apply different

strategies for the graph edge stacking as ordering by

shortest edges, by oldest edges, by youngest edges,

by edges with the smallest start vertex indices, by the

shortest path through a given hierarchy, or by edges

of graph-theoretic problem solutions.

4.2 Time Mapping

A dynamic graph Γ := {G

, . . . , G

} consists of a se-

quence of k static graphs. One solution to display

the graph sequence would be a small multiples rep-

resentation which shows each graph of the sequence

in the visualization technique described above in Sec-

tion 4.1. Following this concept would lead to visual

scalability issues and problems when comparing the

evolution of weights of longer sequences.

In our approach we apply a different visualization

strategy. We integrate the graph sequence into a static

diagram by displaying all graph vertices and edges oc-

curing in the sequence as an edge-stacked visualiza-

tion. Moreover, each edge is attached by an aligned

timeline on the left hand side to indicate the evolution

of its weight over time. Doing this supports not only

to explore the graph for structural properties but also

for time-varying patterns on different levels of hierar-

chical as well as temporal granularity.

Moreover, single graphs or longer subsequences

can be selected which has an inﬂuence on the color

coding of the stacked edges. If only one graph is se-

lected, all edges in the edge-stacked visualization oc-

curing in this selected graph are color coded by the

same color as used for the weights in this graph. If

more than one graph is selected we color code all

edges occuring in at least one of the graphs. If the

same edge occurs in more than one selected graph

we support edge weight aggregation by either show-

ing the maximum, minimum, average, or sum of the

weights in the color coding. The edges in the edge-

stacked visualization which are not occuring in se-

lected graphs are displayed as grayed out lines. This

helps to provide context information and to support

mental map preservation when a viewer wants to click

through the graph sequence one-by-one in order to an-

alyze the graph sequence for changes (see for example

Figures 5 (a) to (f)).

IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications

(a)

(b)

Figure 3: A sequence of three weighted digraphs is shown:

(a) As a side-by-side representation of traditional node-link

diagrams. (b) As an edge-stacked timeline visualization.

Figure 3 (a) illustrates a sequence of three directed

and weighted graphs as node-link diagrams with color

coded links. The edge-stacked timeline visualization

with graph G

selected for this dynamic graph is rep-

resented in Figure 3 (b). We can easily recognize that

there are two edges which show a constant behavior,

i.e. the edge starting at vertex D and ending at ver-

tex C has always the same color (dark blue). Also

the edge starting at vertex A and ending at vertex E

shows a constant behavior (green color). Also weight

changes over time can be found for example for the

edge from E to C which changes from green to red

color over time. If edges are added or deleted over

time this can be recognized by inspecting the gaps in

the timeline view.

Following all these design principles leads to a

representation of dynamic weighted digraphs with-

out showing any explicit link crossing in the result-

ing dynamic graph diagram. Sorting algorithms and

aggregation techniques can further be used to achieve

a more pattern-indicating visualization. For example,

clusters among the vertices might be of interest mean-

ing a reordering of the horizontal vertex positions.

Dynamic patterns might also be of interest meaning

the vertical stacking order of the links (attached by

timelines) must be reordered. It may be noted that

any reordering will not introduce any link crossings

which is typically the case for traditional layout al-

gorithms in two-dimensional layouts for static graphs

due to aesthetic graph drawing criteria.

We show the dynamic graph data in a static (time-

to-space) mapping which allows to integrate sev-

eral interaction techniques to explore the dynamic

graph data in the vertex, edge, and time dimensions.

The most prominent ones are zooming and distor-

tion, ﬁltering, brushing and linking, region expansion

and collapse, vertex and edge orderings, solutions to

graph-theoretic problems, a difference functionality

for graph directions, and computation of differences

or commonalities between subsequent graphs.

5 DYNAMIC CALL RELATIONS

We inspect dynamic graph data from the open source

software project PMD which supports the analysis of

source code implemented in the JAVA programming

language. With PMD one is able to ﬁnd inefﬁcient

code structures like local variables not used during

program execution, package imports occuring several

times, or empty try/catch blocks. The graph to be an-

alyzed contains 1,851 vertices, 28,748 edges and 7

timesteps which are the revisions for this project.

The edge-stacked timeline visualization for the

complete dataset is represented in Figure 4 in which

graph G

is selected from the sequence. For the edge

stacking we use the shortest edge stacking strategy,

i.e. the shorter an edge the closer it is placed to the

horizontal separation line. We use a vegetation color

scale, mapping low values to blue color and high val-

ues to red. Values in-between are mapped to green to

yellow color, see Figure 4.

From this diagram we can make interesting ob-

servations: If we inspect all relations in the edge-

stacked view (color coded and grayed out edges) we

see graph structures which refer to call clusters. This

insight can be derived from the short stacked edges

(blocks) which express call relations inside a direc-

tory. Only a fraction of the edges are very long, cross-

ing the complete horizontal display area. In general,

the longer edges refer to calls between functions lo-

cated far away in the hierarchy. Such inter-package

calls might be problematic for software engineering.

In Figure 4 graph G

is selected and only the edges

are color coded in the edge-stacked view which are

present in G

. Here we can detect two clusters lo-

cated to the left and to the right and also some longer

edges to the top (and to the bottom due to symmetries)

which connect elements from both clusters. Hover-

ing over the hierarchy shows that the leftmost clus-

ter is caused by relations from the ast and cpd direc-

tories whereas the rightmost cluster contains calls of

swingui and rules directories.

Looking at Figures 5 (a) to (f) one can see that the

clusters with the short edges persist for the ﬁrst ﬁve

revisions, whereas the cluster with the longer edges

persists over the complete time interval.

Edge-stackedTimelinesforVisualizingDynamicWeightedDigraphs

Figure 4: The dynamic call relations of the PMD Open Source software project. 1,851 vertices, 28,748 weighted edges, and

7 timesteps are displayed. In this example graph G

is selected and the links are color coded as in G

. All other existing

relations in the graph sequence are grayed out to provide context information.

Applying interaction techniques uncovers that the

methods of the subdirectories java, dfa, jsp, ec-

mascript, ast, and cpp as well as several methods of

the directory sourceforge/pmd/lang are not related to

any other method during the ﬁrst ﬁve time steps.

6 LIMITATIONS

Although we proposed a scalable visualization tech-

nique for dynamic weighted digraphs we are aware

of the fact that there are also several limitations of

our approach. Also various improvements might be

added to the existing technique, some of them have

been described in the paper.

Visual scalability is achieved by data aggregation

which means that several data points are summarized

into one single data point. By this operation insights

are lost which might be important to derive other not

apparent visual patterns and consequently, patterns in

the data. For this reason, we allow several aggregation

techniques which can be switched on users’ demand.

Pattern detection can be difﬁcult if the vertex,

edge, or timeline order strategy is not suitable for the

dataset under exploration. To mitigate this situation

we provide several ordering techniques which must

also be tested for their suitability.

The network topology is not derivable that eas-

ily as in node-link diagrams in the two-dimensional

space. In our work we plot the vertices to a one-

dimensional horizontal line to only use one represen-

tative element for each vertex but clusters and outliers

may be harder to identify.

Also the computational scalability plays a decid-

ing role in our work. As sophisticated layout algo-

rithms must be applied in traditional node-link dia-

grams also in our edge-stacked timelines visualiza-

tion, reordering techniques should be applied to make

the diagrams more readable. But the reordering is also

proved to be an NP-hard problem.

7 CONCLUSION

In this paper we introduced a visualization technique

for dynamic weighted and directed graphs based on

edge-stacked timelines. The approach is able to dis-

play graphs with many vertices, edges, and long time

sequences by using an aggregated pixel-based repre-

sentation. Interaction techniques for vertex and edge

ordering are proposed and tested for suitability. By

using our technique we were able to detect time-

varying patterns in real-world graph data for both the

evolution of edge weights and the structural proper-

ties of the graph. Apart from inspecting the static dia-

gram, which already shows several visual patterns and

serves as an overview, our visualization tool supports

interaction techniques also for ﬁnding graph-speciﬁc

properties.

Since this visualization is designed to be scalable

for large graphs, limitations for path-related tasks can

be regarded as a drawback which can be solved by

interaction techniques. A better exploration of sin-

gle graphs is focus of future work. Additional graph

views in form of traditional node-link diagrams or

adjacency matrices might be integrated combined by

IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications

(a) (b)

(e) (f)

Figure 5: Call graphs G

to G

of the PMD project displayed as edge-stacked timeline visualizations in a side-by-side small

multiples representation. In each of the ﬁgures, one graph is selected and the occuring edges are color coded accordingly.

brushing and linking features to give an analyst a way

to inspect the data from different perspectives. A user

study should be conducted with the goal to ﬁnd out

if our novel visualization technique can keep up with

existing dynamic graph visualizations.

Edge-stackedTimelinesforVisualizingDynamicWeightedDigraphs

REFERENCES

Archambault, D., Purchase, H., and Pinaud, B. (2011). An-

imation, small multiples, and the effect of mental map

preservation in dynamic graphs. IEEE Transactions

on Visualization and Computer Graphics, 17(4):539–

552.

Beck, F., Burch, M., and Diehl, S. (2009). Towards an aes-

thetic dimensions framework for dynamic graph visu-

alisations. In Proceedings of International Conference

on Information Visualisation (IV), pages 592–597.

Beck, F., Burch, M., and Diehl, S. (2013). Matching appli-

cation requirements with dynamic graph visualization

proﬁles. In Proceedings of International Conference

on Information Visualisation (IV), pages 12–18.

Beck, F., Burch, M., Diehl, S., and Weiskopf, D. (2014a).

The state of the art in visualizing dynamic graphs. In

EuroVis State-of-the-Art Reports, EuroVis STAR.

Beck, F., Burch, M., Munz, T., Silvestro, L. D., and

Weiskopf, D. (2014b). Generalized Pythagoras trees

for visualizing hierarchies. In Proceedings of the In-

ternational Conference on Information Visualization

Theory and Applications, pages 17–28.

Brandes, U. and Corman, S. R. (2003). Visual unrolling

of network evolution and the analysis of dynamic dis-

course. Information Visualization, 2(1):40–50.

Brandes, U. and Nick, B. (2011). Asymmetric relations in

longitudinal social networks. IEEE Transactions on

Visualization and Computer Graphics, 17(12):2283–

2290.

Burch, M. and Diehl, S. (2008). TimeRadarTrees: Visualiz-

ing dynamic compound digraphs. Computer Graphics

Forum, 27(3):823–830.

Burch, M., Raschke, M., and Weiskopf, D. (2010). Indented

Pixel Tree Plots. In Proceedings of the International

Symposium on Advances in Visual Computing, pages

338–349.

Burch, M., Schmidt, B., and Weiskopf, D. (2013). A matrix-

based visualization for exploring dynamic compound

digraphs. In Proceedings of International Conference

on Information Visualisation (IV), pages 66–73.

Burch, M., Vehlow, C., Beck, F., Diehl, S., and Weiskopf,

D. (2011). Parallel edge splatting for scalable dynamic

graph visualization. IEEE Transactions on Visualiza-

tion and Computer Graphics, 17(12):2344–2353.

Burch, M. and Weiskopf, D. (2011). Visualizing dynamic

quantitative data in hierarchies - TimeEdgeTrees: At-

taching dynamic weights to tree edges. In Proceedings

of the International Conference on Information Visu-

alization Theory and Applications, pages 177–186.

Cornelissen, B., Holten, D., Zaidman, A., Moonen, L., van

Wijk, J. J., and van Deursen, A. (2007). Understand-

ing execution traces using massive sequence and cir-

cular bundle views. In Proceedings of International

Conference on Program Comprehension, pages 49–

58.

Diehl, S. and G

org, C. (2002). Graphs, they are changing.

In Proceedings of Graph Drawing, pages 23–30.

Frishman, Y. and Tal, A. (2007). Online dynamic graph

drawing. In Proceedings of EuroVis, pages 75–82.

Garey, M. R. and Johnson, D. S. (1979). Computers

and Intractability: A Guide to the Theory of NP-

Completeness. W. H. Freeman.

Holten, D., Cornelissen, B., and van Wijk, J. J. (2007).

Trace visualization using hierarchical edge bundles

and massive sequence views. In Proceedings of VIS-

SOFT, pages 47–54.

Jerding, D. F. and Stasko, J. T. (1995). The information mu-

ral: a technique for displaying and navigating large in-

formation spaces. In Proceedings of INFOVIS, pages

43–50.

Jerding, D. F. and Stasko, J. T. (1998). The information mu-

ral: A technique for displaying and navigating large

information spaces. IEEE Transactions on Visualiza-

tion and Computer Graphics, 4(3):257–271.

Kruskal, J. and Landwehr, J. (1983). Icicle plots: Better

displays for hierarchical clustering. American Statis-

tician, 37(2):162–168.

Purchase, H. C., Hoggan, E., and G

org, C. (2007). How

important is the “mental map”? – An empirical in-

vestigation of a dynamic graph layout algorithm. In

Proceedings of Graph Drawing, pages 184–195.

Rosenholtz, R., Li, Y., and Nakano, L. (2007). Measuring

visual clutter. Journal of Vision, 7(2):1–22.

Shneiderman, B. (1996). The eyes have it: A task by

data type taxonomy for information visualizations. In

Proceedings of the IEEE Symposium on Visual Lan-

guages, pages 336–343.

Stein, K., Wegener, R., and Schlieder, C. (2010). Pixel-

oriented visualization of change in social networks.

In Proceedings of the International Conference on Ad-

vances in Social Networks Analysis and Mining, pages

233–240.

Tufte, E. R. (1992). The visual display of quantitative in-

formation. Graphics Press.

van den Elzen, S., Holten, D., Blaas, J., and van Wijk,

J. (2013). Reordering massive sequence views: En-

abling temporal and structural analysis of dynamic

networks. In Proceedings of IEEE Paciﬁc Visualiza-

tion Symposium, pages 33–40.

Vehlow, C., Burch, M., Schmauder, H., and Weiskopf, D.

(2013). Radial layered matrix visualization of dy-

namic graphs. In Proceedings of International Con-

ference on Information Visualisation, pages 51–58.

IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications

100