Performance Evaluation of Bit-plane Slicing based Stereo Matching

Techniques

Chung-Chien Kao

and Huei-Yung Lin

Department of Electrical Engineering, National Chung Cheng University, 168 University Rd., Chiayi 621, Taiwan

Department of Electrical Engineering, Advanced Institute of Manufacturing with High-Tech Innovation,

National Chung Cheng University, 168 University Rd., Chiayi 621, Taiwan

Keywords:

Stereo Matching, Bit-plane Slicing, Hierarchical Processing.

Abstract:

In this paper, we propose a hierarchical framework for stereo matching. Similar to the conventional image

pyramids, a series of images with less and less information is constructed. The objective is to use bit-plane

slicing technique to investigate the feasibility of correspondence matching with less bits of intensity informa-

tion. In the experiments, stereo matching with various bit-rate image pairs are carried out using graph cut,

semi-global matching, and non-local aggregation methods. The results are submitted to Middlebury stereo

page for performance evaluation.

1 INTRODUCTION

Stereo matching is one of the most active research

areas in computer vision. In the existing stereo al-

gorithms, block matching techniques exploiting lo-

cal constraints and energy minimization for global

optimization have been extensively studied (Min and

Sohn, 2008; Chen et al., 2001; Szeliski et al., 2008;

Sun et al., 2003). While a large number of al-

gorithms for stereo correspondence matching have

been developed (Brown et al., 2003), relatively lit-

tle work has been done on characterizing their per-

formance (Hirschmuller and Scharstein, 2007). Since

Scharstein and Szeliski published a paper regarding

the taxonomy and evaluation of stereo correspon-

dence algorithms (Scharstein and Szeliski, 2002b),

many authors used various methods and algorithms to

participate in an on-line evaluation platform which is

known as Middlebury Stereo Evaluation (Scharstein

and Szeliski, 2002a). This on-line evaluation website

provides many stereo data sets to evaluate the perfor-

mance of stereo matching algorithms. Furthermore,

because the progress in stereo algorithm performance

is quickly outpacing the ability of existing stereo data

sets to discriminate among the best-performing algo-

rithms, (Scharstein and Szeliski, 2003) present new

stereo data sets to the on-line evaluation website,

which act as the four stereo data sets for the new Mid-

dlebury’s Stereo Evaluation - Version 2.

In this work, we address the feasibility of hierar-

chical stereo matching in the intensity domain (Lin

and Lin, 2013). Similar to the conventional image

pyramids, a series of images with less and less in-

formation is constructed hierarchically. They are cre-

ated with different intensity quantization levels. In

this kind of image presentation, more bits per pixel

will contain more detailed texture for stereo match-

ing. However, processing the low intensity quanti-

zation images generally requires less memory usage.

Thus, obtaining good disparity results without using

the full intensity depth of the images is an important

advantage for stereo matching algorithms (Humen-

berger et al., 2010; Lu et al., 2009).

Based on the previous investigation of stereo

matching on low intensity quantization images (Lin

and Chou, 2012), this paper evaluate the bit-plane

slicing techniques with recent well-known stereo al-

gorithms. The objective is to integrate the hierar-

chical framework with the high-performance stereo

matching techniques (Yang, 2012; Akhavan et al.,

2013), and report the improvement over the Mid-

dlebury Stereo Vision Page for on-line evaluation.

In the experiments, stereo matching on various bit-

rate image pairs is implemented using graph cut

(Kolmogorov and Zabin, 2004), semi-global match-

ing (Hirschmuller, 2008), and non-local aggregation

(Yang, 2012). The results demonstrate an alternative

for the development of stereo matching algorithms,

especially for the high intensity depth images.

365

Kao C. and Lin H..

Performance Evaluation of Bit-plane Slicing based Stereo Matching Techniques.

DOI: 10.5220/0005260203650370

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 365-370

ISBN: 978-989-758-089-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: The pixel values in bit-plane representation with binary format.

Bit-Plane Bit Preserved Slice Value Binary Value

0 Bit 0 (LSB) (0000 0000)

(0)

1 Bit 1 (0000 0010)

(1)

2 Bit 2 (0000 0000)

(0)

3 Bit 3 (0000 1000)

(1)

4 Bit 4 (0000 0000)

(0)

5 Bit 5 (0010 0000)

(1)

6 Bit 6 (0000 0000)

(0)

7 Bit 7 (MSB) (1000 0000)

(1)

2 THEORETICAL BACKGROUND

ON BIT-PLANE SLICING

We start by looking into a bit-plane sliced image, pre-

serving one bit per bit-plane while masking out all

other bits on each bit-plane. Given an 8-bit grayscale

image, we can slice an image into the following bit-

planes: Bit-plane 0 preserves only the least signiﬁ-

cant bit (LSB) while Bit-plane 7 preserves only the

most signiﬁcant bit (MSB). Adding all 8 bit-planes to-

gether will result in the 8-bit pixel value for the orig-

inal image. For easier understanding, a pixel’s bit-

plane sliced result is illustrated in Table 1.

For demonstration purposes, if the masked re-

maining bit is 1, we convert it to a binary image set-

ting that pixel to 1. On the other hand, if after mask-

ing a certain pixel results in a 0 value, we will show

it as 0 in the binary image. We do this to show how

much detail exists in each bit position for all 8 bits vi-

sually. The bit-layer slicing visual results are shown

in Fig. 1. We can clearly see that the bit-planes closer

to the MSB seem to preserve more important infor-

mation about the objects in the image. From this ob-

servation, if we could use fewer bits to calculate dense

stereo disparity maps, it would greatly reduce the total

bit-rate required, and thus reduce the memory usage,

communication bandwidth, etc.

To implement this idea, we combine the bit-planes

and form a “bit-plane pyramid”. The top-most plane

of the pyramid is the same as the bit-layer No. 7 in Ta-

ble 1. Stepping down in the pyramid each time we add

an extra bit-plane to the pyramid, and thus increase

the bit-rate while preserving more data from the orig-

inal image. The proposed “bit-plane pyramid” is il-

lustrated in Fig. 1. The goal is to use the least amount

of bits to achieve certain image quality requirement.

We implement and derive results from this bit-plane

pyramid used in dense stereo disparity map calcula-

tion.

In our proposed bit-plane pyramid, the lower lay-

ers (the bottom layers in the pyramid) in the hierar-

chy preserves more detailed information than the top

layers in the original image (Gong and Yang, 2001).

Note that the information reduced is in terms of the

representation using the image intensity, instead of

the image resolution. With less information needed

to be processed, stereo algorithms which originally

require a large amount of memory space may be re-

duced dramatically while maintaining good quality

stereo image disparity estimation output.

3 FRAMEWORK FOR EXISTING

STEREO MATCHING

ALGORITHMS

The proposed stereo matching framework is ﬁrst car-

ried out on a low bit-rate image pair (Bit-layer 1 of the

bit-plane pyramid). If the resulting disparity meets

some quality requirements, the stereo matching algo-

rithms terminates. The process continues until the

disparity estimate is satisfactory or the ﬁnest level

(bit-layer 8 of the bit-plane pyramid) in the hierar-

chy is reached. While using the ﬁnest level may give

the best disparity result, the proposed technique min-

imizes the amount of data required to achieve certain

quality thresholds for disparity computation. Further-

more, in the experiments we sometimes ﬁnd less bits

give better disparity results.

The chosen stereo matching algorithms are sep-

arated to two categories for performance evaluation.

The ﬁrst category is for the ones which use 8-bit

grayscale stereo images as the input, and the second

category use 3-channel RGB color stereo image pair

as the input. These two implementations only differ

in the bit-slicing stage.

While the grayscale stereo image input is bit-plane

sliced hierarchically as described previously, 24-bit

RGB color stereo images need to be bit-plane sliced

by each of the three color channels simultaneously

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

366

Figure 1: The image pyramid constructed with bit-plane slicing. Top layers contain less information and lower layers contain

more information, in terms of image intensity depth.

in the same way as grayscale images separately. For

instance, the top-most bit-plane (layer 1) of the bit-

plane pyramid for the color stereo images preserves

the most signiﬁcant bit (MSB) from each of the 3

color channels forming a bit-plane sliced stereo im-

age pair. Layer 2 preserves top-most 2 bits of each

color channel (bit-plane 8 + bit-plane 7), and so on.

Fig. 2 shows the original image and all 8 layers of the

bit-plane pyramid. We can clearly see that using only

a few bits we still can show most details in an image.

To implement the bit-plane pyramid stereo match-

ing technique, we adopt the existing dense stereo al-

gorithms and integrate with our framework. The pro-

posed bit-plane slicing pyramid is tested with the al-

gorithms which the authors provided source code for

others to use. First we look into the OpenCV li-

brary and ﬁnd that it provides 2 methods to calculate

a dense disparity map. Second, we survey the top per-

forming algorithms on the Middlebury Stereo Evalua-

tion site. In all submissions to the Middlebury Stereo

Evaluation website in the past 10 years, many authors

have provided source code for their stereo algorithms.

We’ve gathered a couple of submissions who also pro-

vided the source codes for testing.

OpenCV provides 3 implementations to com-

pute a disparity map for input rectiﬁed stereo im-

age pairs; all of these algorithms use single chan-

nel 8-bit grayscale stereo images as input. The ﬁrst

one is a faster method called “block matching” by

Kurt Konolige (Konolige, 1997). It is a fast one-

pass stereo matching algorithm that uses sliding sums

of absolute differences between pixels in the left im-

age and the right image. It is fast but the results are

not so good unless the parameters are tuned accord-

ing to the input images. The second one is called

“semi-global block matching”, which is a variation to

(Hirschmuller, 2008). Since we match blocks rather

than individual pixels, the results are often better than

the ﬁrst method. The third one is a “Kolmogorov’s

graph cuts-based” stereo correspondence algorithm

(Kolmogorov and Zabin, 2004). It gives the best re-

sults of all.

Middlebury stereo evaluation site provides the

evaluation of algorithms submitted to their web site

using speciﬁc data sets with ground-truth disparities.

There is also an on-line submission script to allow

evaluation of the stereo algorithm comparing it to

other existing submissions. In hundreds of submis-

sions, we choose a high ranked method “NonLocal-

Filter” (Yang, 2012) for testing. This algorithm and

many top performing methods takes color stereo im-

ages as input rather than grayscale to take advantage

of the additional color intensity data to compute ag-

gregation costs.

4 EXPERIMENTAL RESULTS

In the experiments, we use semi-global block match-

ing, graph cut based, and Non-local ﬁlter stereo algo-

rithms to test the bit-plane slicing method. The dis-

parity map results are shown in Figure 3. We then

submit the results to Middlebury stereo page for eval-

uation. The website provides online submission and

evaluation for provided disparity maps for stereo im-

age pairs, Tsukuba, Venus, Teddy and Cones. Sub-

mitted results will be compared with disparity map

ground truth, getting average percent of bad pixels

for each image pair. One thing worth noting is the

website evaluates disparities for the whole image (ex-

cept for a border region in the Tsukuba and Venus

stereo image pairs). So if the stereo algorithm does

not produce the disparity in occlusion and border ar-

eas, the stereo algorithm must extrapolate the dispar-

ities in those regions or else they will be seen as bad

pixels.

PerformanceEvaluationofBit-planeSlicingbasedStereoMatchingTechniques

367

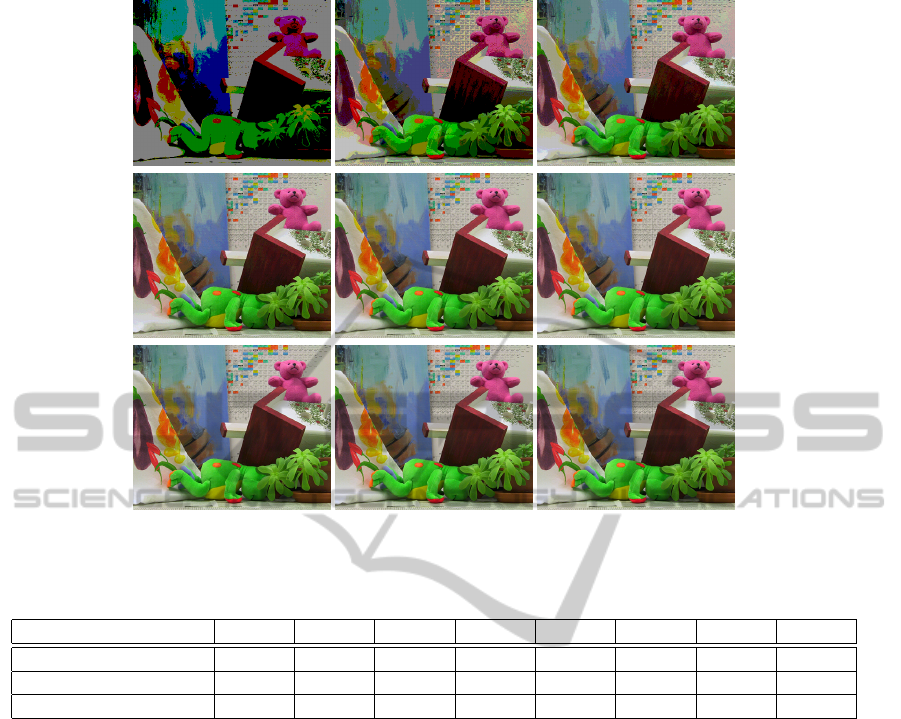
Figure 2: 24-bit RGB color image bit-plane sliced into 8 layers. From top-left to bottom-right: layer 1, layer 2, ..., layer 8,

and the original image.

Table 2: The averages of bad matching pixels (in percentage) obtained using SG, GC and NL algorithms.

Algorithm 8-bit 7-bit 6-bit 5-bit 4-bit 3-bit 2-bit 1-bit

Semi-global matching 20.6 % 20.7 % 21.0 % 21.5 % 22.8 % 24.8 % 30.6 % 38.8 %

Graph cut 14.4 % 14.7 % 14.5 % 15.1 % 16.0 % 17.9 % 41.8 % 52.2 %

Non-local aggregation 5.48 % 5.31 % 6.00 % 7.40 % 11.9 % 15.7 % 21.2 % 40.8 %

The evaluation with average percentage of bad

pixels and average rank is shown in Tables 2 and 3.

For semi-global matching, although the bad-pixel rate

and the average rank are not so good, it reduces only 1

percent of bad pixels with half of the image data (with

a 4-bit image). Graph cut method from OpenCV also

shows good results, losing only 2 - 3% of the aver-

age bad pixels compared to the one using all 8 bits.

Note that these two dense stereo algorithms use 8-bit

grayscale stereo images as input. On the other hand,

NonLocalFilter uses 24-bit RGB color stereo image

pairs as input (8 bits for each color channel). Bit-

plane slicing color stereo input images is done sim-

ilar to the 8-bit grayscale stereo pairs, but it is done

in each of the three color channels simultaneously. It

seems that taking the advantage of color stereo input

images gains the ability to calculate the aggregation

costs better. This results in having the best perfor-

mance when using all stereo pairs input data or even

when masking out lower-bits in each color channel.

It is noted that if we compare the disparity pre-

serving only top-most 2 bits and top-most 3 bits re-

sults, NonLocalFilter’s disparity map seems capable

of estimating objects in the foreground such as the

lamp (white shape in the disparity map) and the head

sculpture’s disparity still can be seen. Items with

larger disparities seems to vanish from disparity map.

This may have something to do with the color lumi-

nance existing in each 3 RGB color channels. On

the other hand, Graph cut’s disparity estimation per-

formance for foreground and background objects de-

grade evenly while masking input stereo image pair

bits.

5 CONCLUSIONS

In this work, a hierarchical stereo matching frame-

work is presented. A pyramid image representa-

tion is used to combine with existing stereo match-

ing algorithms for disparity computation. Graph-

cut, semi-global matching and non-local aggregation

methods are tested in our framework with various

bit-rate image pairs. The disparity computation for

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

368

(a) Semi-global matching (b) Graph-cut (c) Non-local ﬁlter

Figure 3: The disparity maps computed using the stereo matching algorithms, semi-global matching, graph-cut and non-local

aggregation.

PerformanceEvaluationofBit-planeSlicingbasedStereoMatchingTechniques

369

Table 3: The averages rank obtained by performing stereo matching using SG, GC and NL algorithms.

Algorithm 8-bit 7-bit 6-bit 5-bit 4-bit 3-bit 2-bit 1-bit

Semi-global matching 148.2 148.3 148.8 149.6 150.8 151.2 151.8 152

Graph cut 121.7 124 131.4 130.3 135.8 140.4 151.5 152

Non-local aggregation 45.4 43.2 65.5 89 117.2 137 149.3 151.9

stereo datasets are submitted to Middlebury stereo site

for performance evaluation. The results have demon-

strated the feasibility of our bit-plane slicing based

stereo matching framework.

ACKNOWLEDGEMENTS

The support of this work in part by the National Sci-

ence Council of Taiwan under Grant NSC-102-2221-

E-194-019 is gratefully acknowledged.

REFERENCES

Akhavan, T., Yoo, H., and Gelautz, M. (2013). A frame-

work for hdr stereo matching using multi-exposed im-

ages. In Proceedings of HDRi2013 - First Interna-

tional Conference and SME Workshop on HDR imag-

ing (2013).

Brown, M. Z., Burschka, D., and Hager, G. D. (2003). Ad-

vances in computational stereo. IEEE Trans. Pattern

Anal. Mach. Intell., 25(8):993–1008.

Chen, Y.-S., Hung, Y.-P., and Fuh, C.-S. (2001). Fast

block matching algorithm based on the winner-update

strategy. IEEE Transactions on Image Processing,

10(8):1212 –1222.

Gong, M. and Yang, Y.-H. (2001). Multi-resolution stereo

matching using genetic algorithm. In SMBV ’01: Pro-

ceedings of the IEEE Workshop on Stereo and Multi-

Baseline Vision (SMBV’01), page 21.

Hirschmuller, H. (2008). Stereo processing by semiglobal

matching and mutual information. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

30(2):328–341.

Hirschmuller, H. and Scharstein, D. (2007). Evaluation of

cost functions for stereo matching. In Computer Vi-

sion and Pattern Recognition, 2007. CVPR ’07. IEEE

Conference on, pages 1–8.

Humenberger, M., Zinner, C., Weber, M., Kubinger, W.,

and Vincze, M. (2010). A fast stereo matching algo-

rithm suitable for embedded real-time systems. Com-

puter Vision and Image Understanding, 114(11):1180

– 1202. Special issue on Embedded Vision.

Kolmogorov, V. and Zabin, R. (2004). What energy func-

tions can be minimized via graph cuts? Pattern Anal-

ysis and Machine Intelligence, IEEE Transactions on,

26(2):147–159.

Konolige, K. (1997). Small vision systems: hardware and

implementation. In Eighth International Symposium

on Robotics Research, page 111–116.

Lin, H.-Y. and Chou, X.-H. (2012). Stereo matching on low

intensity quantization images. In Pattern Recognition

(ICPR), 2012 21st International Conference on, pages

2618–2621.

Lin, H.-Y. and Lin, P.-Z. (2013). Hierarchical stereo match-

ing with image bit-plane slicing. Mach. Vision Appl.,

24(5):883–898.

Lu, J., Rogmans, S., Lafruit, G., and Catthoor, F. (2009).

Stream-centric stereo matching and view synthesis:

A high-speed approach on gpus. IEEE Transac-

tions on Circuits and Systems for Video Technology,

19(11):1598 –1611.

Min, D. and Sohn, K. (2008). Cost aggregation and oc-

clusion handling with wls in stereo matching. IEEE

Transactions on Image Processing, 17(8):1431 –1442.

Scharstein, D. and Szeliski, R. (2002a). Middlebury stereo

vision page. http://vision.middlebury.edu/stereo.

Scharstein, D. and Szeliski, R. (2002b). A taxonomy and

evaluation of dense two-frame stereo correspondence

algorithms. Int. J. Comput. Vision, 47(1-3):7–42.

Scharstein, D. and Szeliski, R. (2003). High-accuracy

stereo depth maps using structured light. In Com-

puter Vision and Pattern Recognition, 2003. Proceed-

ings. 2003 IEEE Computer Society Conference on,

volume 1, pages I–195–I–202 vol.1.

Sun, J., Zheng, N.-N., and Shum, H.-Y. (2003). Stereo

matching using belief propagation. IEEE Trans. Pat-

tern Anal. Mach. Intell., 25(7):787–800.

Szeliski, R., Zabih, R., Scharstein, D., Veksler, O., Kol-

mogorov, V., Agarwala, A., Tappen, M., and Rother,

C. (2008). A comparative study of energy min-

imization methods for markov random ﬁelds with

smoothness-based priors. IEEE Trans. Pattern Anal.

Mach. Intell., 30(6):1068–1080.

Yang, Q. (2012). A non-local cost aggregation method

for stereo matching. In Computer Vision and Pat-

tern Recognition (CVPR), 2012 IEEE Conference on,

pages 1402–1409.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

370