
Medial Width of Polygonal and Circular Figures
Approach via Line Segment Voronoi Diagram
L. M. Mestetskiy
Faculty Computational Mathematics and Cybernetics,Moscow State University, Moscow, Russia
Keywords: Medial Width Function, Skeleton, Bicircle, Voronoi Diagram, Polygonal Figure, Circular Figure.
Abstract: The paper proposes the concept of building the so-called medial width function - integral shape descriptor of
figures used in image recognition tasks. Medial width function is determined based on the skeleton of the
shape and the radial function. An algorithm to compute the medial width function for polygonal figures based
on the line segment Voronoi diagram is also presented here. Generalized solution to the circular figures
obtained by rounding corners in a polygonal figure is presented. Computational experiment demonstrates the
efficiency and effectiveness of the approach to the problem of palm shapes comparing for personal
identification.
1 INTRODUCTION
Features generation for classification of objects of
variable shape, such as a human figure or an animal
is to build shape descriptors which remain invariant
during object deformation.
A useful tool for object shape classification is a
skeleton or medial axis of the figure. Skeleton of
figure is defined as the set of points-centers of the
circles inscribed in the figure. Skeleton looks like flat
geometric graph and analysis of this graph gives the
ability to generate multiple topological and metric
features of the object's shape.
Another source for shape features generating is
the width of the object with respect to medial axis.
Width of the object is described by the radial
function, which establishes a correspondence
between the points of the skeleton and the radii of the
inscribed circles with centers at these points. Medial
axis and radial function together form a medial
representation of figures (Siddiqi, 2008).
Radial function gives a local description of the
width of the figures at the points of the skeleton. This
width is tied to the skeleton and allows us to compare
objects that have isomorphic skeletons. To use these
widths for the classification of objects having
different skeletal structure, we need to construct an
integral descriptor of the object width. As an example
of such descriptor pattern spectrum (Maragos, 1989)
with the disk structuring element can be used.
Calculation of the pattern spectrum is based on the
operations of mathematical morphology that are
associated with the transformation of discrete raster
images. The limitation of these methods is the high
computational complexity. For example, in the
problem of biometric identification by hand geometry
pattern spectrum shows good results (Ramirez-cortes,
2008). But because of the slow work allows you to
work only with images of small size with low
resolution. The time consumed to compute the pattern
spectrum precludes its use in processing of video
sequences and the analysis of complex high-
resolution images.
We propose an alternative approach that can
significantly reduce the time required for the
calculation of the integral shape descriptors based on
the width of objects. A new descriptor, called the
medial width, the calculation of which is performed
by means of efficient algorithms of computational
geometry is proposed. The approach is based on the
following principles.
1. Introduce the concept of the medial width
of figure at a point on the basis of the medial
representation.
2. In the figure, define the region of given
width as the set of points at which the
medial width does not exceed a
predetermined value.
3. Define the medial width function of figure
describing the area ofthe region of given
width as a function of the width parameter.
379
Mestetskiy L..
Medial Width of Polygonal and Circular Figures - Approach via Line Segment Voronoi Diagram.
DOI: 10.5220/0005261903790386
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 379-386
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

The paper proposes a method for direct calculation of
the medial width function of polygonal figure
(polygon with polygonal holes). The method is based
on Voronoi diagram of line segments formed by the
boundary of a polygonal figure. On the one hand,
efficient algorithms for constructing such Voronoi
diagrams are known (Held, 2011, Karavelas, 2004 ,
Mestetskiy, 2013). On the other hand, figures that
have non-linear boundary, as well as figures from the
bitmaps can be easily approximated by polygonal
figures.
For a more adequate approximation of such
shapes, we introduced the circular figures. Circular
figure is obtained by the process of skeleton pruning,
leading to "rounding" corners of the polygonal figure
by circular arcs. The proposed method of direct
calculation of the medial width function for polygonal
figures allows us to calculate the same ones for
circular figures as well.
Implementation and experimental evaluation of
the proposed approach is made with respect to the
problem of personal identification through the hand
geometry. We compute the medial width function for
circular figures approximating the shape of palm in
bitmap. Later we construct a measure of difference of
palm shapes based on the comparison of these
functions.
2 MEDIAL REPRESENTATION
AND MEDIAL WIDTH OF
FIGURES
We consider medial representation of bound closed
regions in Euclidean plane and name them figures.
The skeleton of figure is a locus of centers of
maximum empty circles in this region. The circle is
considered to be empty if all its internal points are
internal points of the region and the maximum empty
circle which is not contained in any other empty circle
is called inscribed circle. Radial function is defined
in a point of skeleton and is equal to the radius of
inscribed circle centered at this point.
Definition 1. A spoke is a line segment from the
skeleton point to any nearest boundary point.
Spokes have important properties (Mestetskiy,
2014):
1) Each point in figure belongs to at least one
spoke, hence spokes cover the entire figure.
2) If the point of figure does not belong to the
skeleton, then it is incident on one spoke only.
Definition 2. Medial width of figure in an internal
point is equal to the length of its incidence spoke.
All spokes of a point of skeleton have the same
length. Therefore medial width for points of skeleton
is equal to the radial function. The incidence spoke of
the non-skeletal internal point is unique. Hence
medial width in this point is well defined too.
Boundary points of the figure may have several
incident spokes of different length. But the total area
of the boundary is 0. Consequently, these points do
not contribute to the area calculation of the region of
given width. Therefore, medial width at the boundary
points can be set arbitrarily, for example, put it equal
to zero.
We will use the following notation:
– Euclidean plane,
– figure, bound closed region⊂
,
– boundary of figure ,
– internal open region of figure ,
=∖,
() – inscribed circle centered in the point ∈,
– skeleton of figure .
We denote
(
)
,∈′ – medial width of the
figure at the points ,
=
∈
,()≤
– the
region of given width ≥0.
Definition 3. Medial width function ℱ
(
)
of figure
is an area of given width ≥0 ℱ
(
)
=
(
′
)
.
3 POLYGONAL AND CIRCULAR
FIGURES AND THEIR MEDIAL
WIDTH
Polygonal figure is closed bounded region with
boundary consisting of polygons. Polygonal figures
can be used as convenient continuous models for
approximating binary bitmap objects.
The boundary of the polygonal figure can be
represented as the set of point-sites (vertices of a
figure) and segment-sites (sides of boundary
polygons). Voronoi diagram (VD) of line segments is
defined for these set of sites. The part of this VD,
lying inside the figure is termed as VD of polygonal
figure, which is a geometric graph whose edges are of
straight line segments and quadratic parabola
segments.
Let is a polygonal figure,
(
)
=
〈
,
〉
is
VD of figure . Here – the set of vertices, – set
of VD edges. Each edge of is associated with a pair
of sites to which this edge is the bisector – the
common boundary of their Voronoi cells. Consider
the VD subgraph
〈
,
〉
, formed from
(
)
by
cutting of some terminal vertices and edges incident
to these vertices. If cut vertices and edges of
(
)
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
380
which incident to concave vertices of polygonal
figure, then the union of the edges of the VD subgraph
〈
,
〉
is the skeleton of figure, i.e. =
〈
,
〉
,
⊆,
⊆. Therefore, the skeleton of a
polygonal figure can be considered as a subgraph of
VD =
〈
,
〉
,
⊆,
⊆.
Let be a polygonal skeleton of . Pruning, a
process of sequential cutting of some terminal
vertices and their incident edges helps in the
construction of subgraphs
,
,…,
such that
=
〈
,
〉
,
=
〈
,
〉
,
=
\
,
=
\
,
∈
,
∈
, and the vertex
is
terminal in the subgraph
, and
is its incident edge.
Definition 4. Subgraphs of VD resulting from
pruning process are called skeletal subgraphs.
Definition 5. Union ′=
⋃
()
∈
of
inscribed circles centered on skeletal subgraph ⊆
, is called a circular figure.
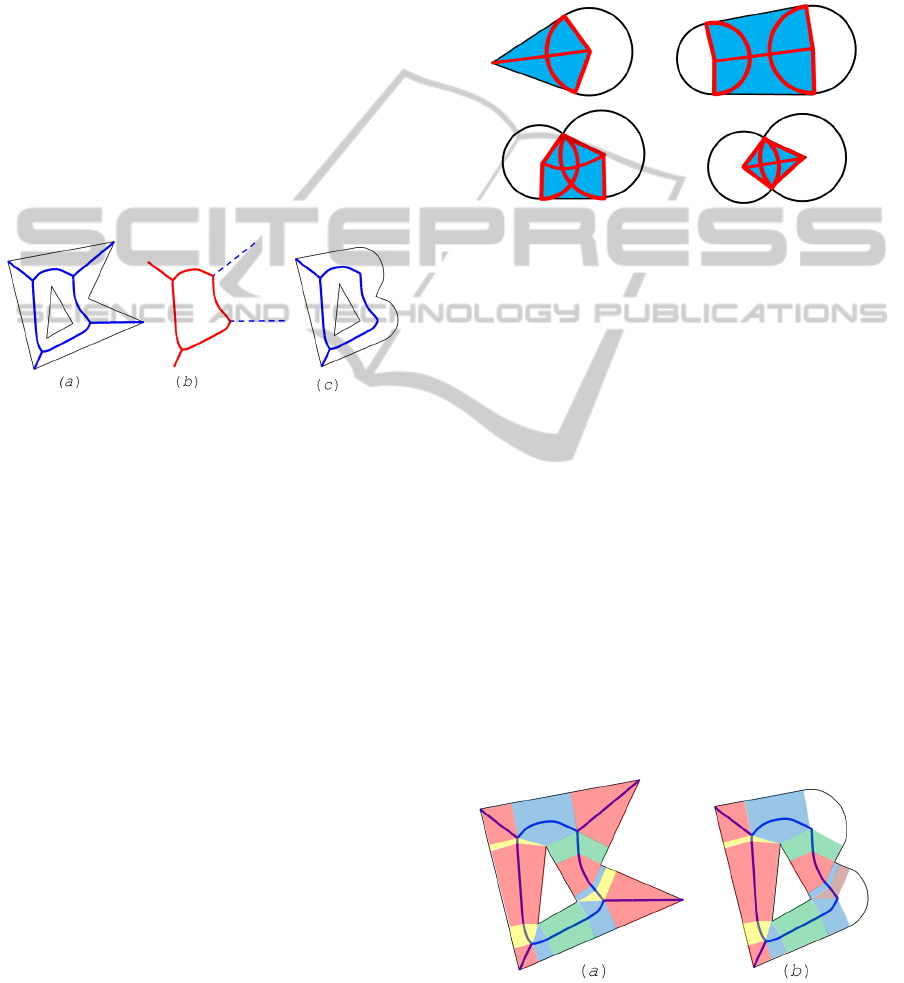
Figure 1: (a) the polygonal figure and the skeleton, (b) the
skeleton subgraph resulting from pruning, (c) the circular
figure corresponding skeleton subgraph.
Polygonal figure can be represented as the
union of all the inscribed circles which are centered
at the skeleton points =
⋃
()
∈
, i.e., it is a
particular case of circular figure. The example in
Fig.1 presents a polygonal figure, its skeleton,
skeletal subgraph, and circular figure formed by
circles of this subgraph.
4 BICIRCLES IN THE
POLYGONAL AND CIRCULAR
FIGURES
An edge ∈ of the skeletal subgraph is a segment
of a straight line or a parabola. This segment has two
endpoints at the graph vertices. The remaining points
of the edge will be named as internal.
Definition 6. A bicircle of the edge ∈ is the
union of all inscribed circles centered on . The edge
is called axes of bicircle.
Definition 7. Proper region of bicircle of edge
is the closure of the union of all the spokes incident
to an interior point of .
Proper region of bicircle is included to bicircle.
Boundary of proper region includes two spokes. Two
circles with centers at the edge endpoints are end
circles of bicircle. Couple spokes divides end circle
into two sectors – external and internal. External
sector includes a part of the border of bicircle whereas
the internal sector comprises the remainder of the end
circle (Fig.2).
Figure 2: Bicircles, proper regions, internal and external
sectors of end circles.
Let
– a proper region of the bicircle
of edge
.
Definition 8. The subset
⊆
of bicircle
=
∈
,()≤
, in which the medial width
does not exceed ≥0, be called the region of width
.
Denote
(
)
– area of
.
Definition 9. Medial width function of bicircle
is ℱ
(
)
=
(
)
.
Proper regions of two bicircles may have
intersection over the boundary spokes only. The area
of this intersection is zero. On the other hand proper
regions of bicircles cover the entire polygonal figure
completely. Therefore, the medial width function of
the polygonal figure is equal to the sum of the medial
width functions of bicircles
ℱ
(
)
=
ℱ
(
)
∈
(1)
Figure 3: (a) Coverage of the polygonal figure by proper
regions of bicircles, (b) coverage of the circular figure by
proper regions and border sectors.
MedialWidthofPolygonalandCircularFigures-ApproachviaLineSegmentVoronoiDiagram
381

The circular figure is the union of all bicircles of its
skeletal graph. But proper regions of these bicircles
do not cover the entire circular figure. Therefore, the
remaining portion of the circular figure is covered by
the external sectors of bicircles (Fig. 3).
Definition 10. In the circular figure the part of the
inscribed circle () centered in the skeleton vertex
∈, which is not covered by proper regions of
bicircles, is called the border sector.
The inscribed circle () exists for every
skeleton vertex ∈. Let () is the area of the
border sector of (). Denote
⊆ the set of
vertices of the skeleton, which radii of the inscribed
circles
(
)
≤.
Then the medial width function of the circular
figure is
ℱ
(
)
=
∑
ℱ
(
)
∈
+
∑
(
)
∈
. (2)
The first term is the area of proper regions of
bicircles, and the second term is the area of the
external sectors of vertices.
5 MEDIAL WIDTH OF
BICIRCLES
Each edge of the skeleton has two site generators.
Couple sites “point-segment” forms a parabolic edge
and the corresponding bicircle is said to be parabolic.
Couples “point-point” and “segment-segment” form
linear edges. In these cases graphs of the dependence
of the inscribed circle radius with the position of the
circle center on the edge are a straight line (for a pair
“segment-segment”) or hyperbola (for a pair “point-
point”). For convenience, corresponding bicircle are
said to be linear and hyperbolic.
We wish to obtain an explicit formula for the
calculation of the medial width functions: ℱ
() –
for linear bicircle, ℱ
() – for parabolic bicircle,
ℱ
() – for hyperbolic bicircle as a function of the
width parameter .
The formulas for calculating these functions are
provided below. Detailed formation of these formulas
performed on the basis of the geometric analysis and
was described in (Mestetskiy, 2014).
Denote
, – radii of bicircle’s end circles, ≤,
– distance between end circle centers,
=
−(−)
– length of the bicircle axis
projection on the segment-site in linear and parabolic
bicircles.
5.1 Medial Width of a Linear Bicircle
Medial width function of linear bicircle can be
computed as
ℱ
(
)
=
0i
f
<
+ i
f
≤≤
(
+
)
>
where
=
0if=
−
if<
=
2 if=
−
if<
.
5.2 Medial Width of a Parabolic
Bicircle
Parabolic bicircle axis is a segment of a parabola. To
calculate the medial width of the bicircle, it is
necessary to determine the position of the vertex of
the parabola with respect to the axis of the bicircle.
Position of the vertex of the parabola defined by the
parameters of the parabolic bicycle.
Let where
∗
=2
(−).
The variants of the parabola vertices are:
(a) if =
∗
then the vertex of the parabola is the
endpoint of axis,
(b) if >
∗
then the vertex of the parabola is an
interior point of the axis,
(c) if <
∗
then the vertex of the parabola lies
outside the axis.
Definition 11. Parabolic bicircle having vertex of
the parabola coinciding with the endpoint of axis is
called as root parabolic bicircle.
Position of the parabola vertex is defined by the
relation: at =
∗
option (a), >
∗
option (b), <
∗
option (c), where
∗
=2
(−).
Parabola parameter for parabolic bicircle is
=
++
(+)
−
.
Area of proper region of root parabolic bicircle with
parameter and the end circle radius is
φ()=(+)
−
.
Medial width function of root parabolic bicircle
with parameter and end circle radius is
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
382

Φ(,,)=
0if≤
φ() if
<≤
φ() if>
.
Now the medial width function of the parabolic
bicircle can be calculated through areas of 2 root
bicircles:
if the vertex of the parabola lies on the axis, then
ℱ
(
)
=Φ
(
,,
)
+Φ
(
,,
)
if the vertex of the parabola lies outside the axis,
then
ℱ
(
)
=Φ
(
,,
)
−Φ
(
,,
)
5.3 Medial Width of a Hyperbolic
Bicircle
Definition 12. Midpoint of the segment connecting
the point-sites of hyperbolic bicircle, called the center
of hyperbolic bicircle.
The position of the center relative to the axis of
the hyperbolic bicircle is also important for
calculating of the medial width function. Depending
on the values of ,, the center lies on the axis of
the bicircle, or outside the axis.
(a) if
+
=
then the center coincides
with the endpoint of axis,
(b) if
+
>
then the center is an interior
point of the axis,
(c) if
+
<
then the center lies outside
the axis.
Let is the distance between point-sites of
hyperbolic bicircle. We name it as the parameter of
hyperbolic bicircle.
The parameter is calculated by the formula
=
[(
+
)
−
]
∙[
−
(
−
)
] .
Definition 13. Hyperbolic bicircle is called as the
root bicircle, if the center of the bicircle coincides
with the endpoint of axis.
Area of proper region of root hyperbolic bicircle
with parameter and the end circle radius is
ψ()=
−
.
Medial width function of root hyperbolic bicircle
with parameter and end circle radius is
Ψ(,,)=
0if≤
ψ() if
<≤
ψ() if>
.
Medial width function of the hyperbolic bicircle
can now be calculated through areas of 2 root
hyperbolic bicircles:
if the center of the bicircle lies on the axis
ℱ
()=Ψ(,,)+Ψ(,,)
if the center of the bicircle lies outside the axis
ℱ
(
)
=Ψ
(
,,
)
−Ψ(,,)
5.4 Medial Width of End Sectors
To evaluate the medial width function of the circular
figure, we must calculate the areas of border sectors
of vertices, which are not covered by bicircle proper
regions.
Suppose that a skeleton vertex ∈, has incident
edges
,
,…,
, ≥1 and bicircles of these edges
have a common end circle centered at .
The border sector is the intersection of external
sectors of all incident bicircle, whereas the internal
sectors in these bicircles do not overlap. Therefore, if
the angular size of the internal sectors are
,
,…,
, then their sum does not exceed 2, i.e.,
+
+⋯+
≤2.
If a vertex preserved all incident edges after
pruning, then
+
+⋯+
=2. But, if some
edges have been removed during the pruning, then
+
+⋯+
<2. Thus, the angular size of
the border sector of the vertex is
(
)
=2−(
+
+⋯+
).
If
is the radius of the inscribed circle ()
centered at vertex , then the area of the border sector
is
(
)
=
(
)
∙
(
)
.
Thus, to calculate the area of border sectors
(
)
for all vertices ∈, there is a need to find the
angular size of all internal sectors of bicircles. These
sizes are calculated depending on the type of bicircle
(linear, parabolic, or hyperbolic).
In linear bicircle the size of internal arc of small
end circle is =+2∙
, and of large
end circle is =−2∙
.
Internal arc of a large end circle of the parabolic
bicircle with the parameter is
=1−
.
An internal arc of a small circle is
=1−
in the case where the parabola
MedialWidthofPolygonalandCircularFigures-ApproachviaLineSegmentVoronoiDiagram
383

vertex lies on the axis of the bicircle, and
=2−1−
, if it lies outside axis.
Internal arc of a large end circle of the hyperbolic
bicircle with the parameter has a size =
. If the center lies on the axis of the
bicircle then the internal arc of the small circle has the
size =
, and if it lies outside the axis,
=2−
.
Formulas (1), (2) allow us to calculate the value
of the medial width function ℱ
(
)
for a fixed value
of the argument . As can be seen from the formulas
obtained, the calculation of the medial width function
of one bicycle ℱ
(
)
is (1). Hence, the
computational complexity for the sum
∑
ℱ
(
)
∈
is
(
|
|
), where
|
|
- is the number of edges in skeletal
graph of figure. Calculation of the areas of border
sectors
(
)
for all vertices ∈ is carried in a
single pass over the edges of the skeletal graph, i.e.
has the complexity (
|
|
). Calculating the sum
∑
(
)
∈
adds to this (
|
|
). Thus, the calculation
of ℱ
(
)
has complexity (
|
|
+
|
|
). Since skeletal
graph is planar, single complexity of computing ℱ
(
)
can be written as (), where - is the number of
vertices in the skeletal graph.
For feature generation it is necessary to calculate
the medial width function for the argument =
,
,…,
, where - the dimension of the feature
vector. Thus, the total computational complexity of
constructing the feature vector based on the medial
width function will be () in the worst case.
6 APLICATION TO PALM SHAPE
COMPARING
Our example is intended to demonstrate the utility of
the medial width function and effectiveness of the
method of its calculation. We consider an application
for biometric identification by hand geometry. The
task is to construct a measure of distinction palm
shapes, presented in the form of binary images. We
use our method of circular approximation and
constructing a continuous skeleton of a binary bitmap
image (Mestetskiy, 2008). It contains the following
steps.
1. We model binary bitmap as an integer lattice
points in the plane. First, we construct a polygonal
figure approximating a binary raster image. The
boundary of figure consists of separating polygons of
the minimum perimeter.
2. Construct the VD of line segments formed from
approximating polygonal figure boundaries. Extract
the internal part of the VD of the figure.
3. To obtain an approximating circular figure,
pruning of internal Voronoi diagram is performed.
4. Calculate the medial width function of circular
figure using the algorithm discussed in this article.
Figure 4: (a) binary raster image, (b) approximating
polygonal figure and continuous skeleton, (c) skeleton after
pruning, (d) medial representation of image.
Fig.4 illustrates an example for the described
scheme. Original binary image is the 640×480 bitmap
(Fig.4a). The resulting polygonal figure is the simple
polygon with 346 vertices. Skeletal graph (VD) has
689 edges (Fig. 4b). Simple pruning (regularization
by parameter 1) leaves 435 edges in the skeletal graph
(Fig. 4c).
The resulting sub-graph generates circular figure
that approximates the original bitmap image with
accuracy ε in the Hausdorff metric. In our example, ε
= 1. Further semantic segmentation leaves in the
skeletal graph only significant part which describes a
hand (removes wrist).
The result is a graph with the edges 382. This
graph gives a circular shape consisting of 382
bicircles (Fig. 4d), among them are 182 linear, 152
parabolic and 48 hyperbolic bicircles.
We consider three measures of palm differences
based on different features: line of hand geometric
points, the curvature of the fingers and the medial
width.
Line of hand geometric points is a polyline whose
vertices are the singular points on the boundary
contour of the palm: 5 tips and 4 valleys points
(Fig.5). The method of allocation of these points in
the image is described in (Mestetskiy, 2011).
Let
,
,⋯,
– sequential vertices of the
polyline, and
=
|
|
,=1,…,8 – the length of
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
384

Figure 5: Line of hand geometric points.
segments, =
∑
– total length. Feature vector
is defined as Γ=
,
,…,
. Measure of the
difference of two palms Γ
()
and Γ
()
is calculated
as the Euclidean distance μ
(Γ
()
,Γ
()
)between
these vectors.
Measure the curvature of the fingers is
constructed as follows (Fig. 6). For each finger, =
1,…,5 in the continuous skeleton find centers of the
inscribed circles: the tip
and a base
. The method
of obtaining these points is described in (Mestetskiy,
2011). Then, on a skeleton branch
find most
distant points from straight line
to the right
(point
) and to the left (point
). Let
– distance
from
to
,
– distance from
to
, and
=
|
|
– segment length. Feature vector Δ=
,
,
,
,…,
,
is a vector of curvature of
fingers. Measure differences of palms Δ
()
and Δ
()
is calculated as the Euclidean distance μ
(Δ
()
,Δ
()
).
Figure 6: Curvature of the fingers.
Feature vector of palm width is calculated using the
normalized of the medial width function of the
circular figure. Normalization is necessary for
compare images of different sizes, obtained under
various shooting conditions. Let the radius of the
maximum inscribed circle of palm image is
.
Scale the virtual circular figure so that the radius of
its maximum inscribed circle became
. For this
set of scaling coefficient =
⁄
. Then we
obtain the normalized function of the medial
widthℱ
(
)
=
ℱ
(
)
. In our experiments we used
=100. Feature vector describing the medial
width of the palm has the form Ω=(
,
,…,
),
=
,
=ℱ
(
)
, =0,1,…,. The
difference of palms Ω
()
and Ω
()
on the medial width
is calculated as the Euclidean distance μ
(Ω
()
,Ω
()
).
General measure of differences for pairs of
images of palms I
()
=Γ
()
,Δ
()
,Ω
()
and I
()
=
Γ
()
,Δ
()
,Ω
()
, combining all three measures, is
μ(
(
)
,
(
)
)=
μ
(Γ
(
)
,Γ
(
)
)+
+
μ
(Δ
(
)
,Δ
()
)+
μ
(Ω
(
)
,Ω
()
).
To prove the efficacy of proposed approach, we
conducted the experiments including 160 binary 640
× 480 images of palms of 35 people, 4-5 samples for
each person. Based on a comparison of the distances
between samples with a threshold occurs
classification of a pair as their "own" or "alien". The
threshold is set so that rates FAR and FRR are equal.
The value obtained Equal Error Rate (EER) is
considered by us as a quality criterion for the
construction of the metric. The values of the
coefficients
,
,
are obtained by minimizing
the EER.
The table 1 shows the EER values for different
formations of μ(
(
)
,
(
)
) by combining measures
Hand Geometric Points (HGP), Finger Curvature
(FC), Palm Width (PW).
Table 1: Efficiency of the medial width for measuring the
of palm shape similarities.
Measure EER
FC (
=
=0)
15.9%
PW (
=
=0)
11.8%
HGP (
=
=0)
8.5%
HGP & FC (
=0)
7.7%
FC & PW (
=0)
6.7%
HGP & PW (
=0)
5.1%
HGP & FC & PW 4.0%
MedialWidthofPolygonalandCircularFigures-ApproachviaLineSegmentVoronoiDiagram
385

The experiment shows that the medial width (PW)
substantially improves the classification level in
comparison with features based on the use of only the
boundary (HGP) and skeleton (FC).
The table 2 shows the computation time (in
millisecond) for the processor Intel® Core™ i5-
3210M CPU @ 2.50GHz. Operation "Calculation of
the medial width
function" includes the construction
of approximating polygonal figure, the calculation of
the medial representation, regularization of the
skeleton, as well as a direct computation of three
measures based on medial representation.
Table 2: Expenses of time for the palm medial width
calculating.
Operation Amount Time spent Time per step
Medial width function 160 images 2325 ms 14.53 ms
Comparisons 12720 3200 ms 0.25 ms
High computational efficiency of our approach
enables the use of the medial width for image
recognition in real-time computer vision systems.
7 CONCLUSION
The proposed method opens up new possibilities for
the application of high-performance computational
geometry algorithms in the analysis and recognition
of discrete raster images. Known approaches to the
calculation of descriptors for the width of the figures
on the basis of pattern spectrum is not suitable for use
in real-time computer vision systems, as they have
high computational complexity. The proposed
transition to a continuous model based on polygonal
and circular figures, as well as a highly effective
method of calculating the medial width function for
these figures allow us to overcome this short coming.
Medial width is a universal feature, it does not
include structural analysis of shapes, therefore, its use
requires a combination with other features, such as
the image skeleton. Future work should build such
combined classification methods.
ACKNOWLEDGEMENTS
The author thanks the Russian Foundation for Basic
Research for the support on this study (grant 14-01-
00716).
REFERENCES
Siddiqi, K., Pizer, S., 2008. Medial Representations:
Mathematics, Algorithms and Applications, Springer.
Maragos, P., 1989. Pattern Spectrum and Multiscale Shape
Representation. In IEEE Tran. on Pattern Analysis and
Machine Intelligence, vol.11, Issue 7, pp. 701-716.
Ramirez-cortes, J.M., Gomez-gil, P., Sanchez-perez, G.,
Baez-lopez, D., 2008. A Feature Extraction Method
Based on the Pattern Spectrum for Hand Shape
Biometry. In Proc. World Congress on Engineering
and Computer Science.
Held, M., 2011. Vroni and ArcVroni: Software for and
Applications of Voronoi Diagrams in Science and
Engineering. In Proc. 8th Int. Symp. on Voronoi
Diagrams in Science and Engineering (ISVD), pp. 3-
12.
Karavelas, M., 2004. A robust and efficient implementation
for the segment Voronoi diagram. In Proc. 1st Int.
Symp. on Voronoi Diagrams in Science and
Engineering (ISVD), pp. 51-62.
Mestetskiy, L., Semenov, A., 2008. Binary image skeleton
- continuous approach. In Proc. 3rd Int. Conf. on
computer vision theory and applications (VISAPP),
Vol. 1, Funchal, Madeira, Portugal, pp.251-258.
Mestetskiy, L., Bakina, I., Kurakin, A., 2011. Hand
geometry analysis by continuous skeletons. In Lecture
Notes in Computer Science, Vol. 6754, Part 2, pp. 130-
139.
Mestetskiy, L., 2014. Medial width of a figure - an image
shape descriptor. Machine Learning and Data Analysis.
Vol. 1, № 9, pp. 1291 - 1318. (in Russian).
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
386
