
A Qualitative Representation of a Figure and
Construction of Its Planar Class
Kazuko Takahashi, Mizuki Goto and Hiroyoshi Miwa
School of Science&Technology, Kwansei Gakuin University, 2-1, Gakuen, Sanda, 669-1337, Japan
Keywords:
Qualitative Spatial Reasoning, Formalization, PLCA, Planarity.
Abstract:
PLCA is a framework for qualitative spatial reasoning. It provides a symbolic expression of spatial entities
and allows reasoning on this expression. A figure is represented using the objects used to construct it, that is,
points, lines, circuits and areas, as well as the relationships between them without numerical data. The figure
is identified by the patterns of connection between the objects. For a given PLCA expression, the conditions
for planarity, that is, an existence of the corresponding figure on a two-dimensional plane, have been shown;
however, the construction of such a PLCA expression has not been discussed. In this paper, we describe a
method of constructing such expressions inductively, and prove that the resulting class coincides with that of
the planar PCLA. The part of the proof is implemented using a proof assistant Coq.
1 INTRODUCTION
There are many areas in which spatial data are en-
countered, including image data and video data. As
part of image recognition or analysis, we typically
extract pertinent aspects of image data, such as di-
mensions, position, and direction, depending on our
purpose. For example, we may focus on the rel-
ative positional relationships of the objects, that is,
whether the objects are connected and the relative
spatial location, as well as changes in these relation-
ships for moving objects. Using this information, we
can create an abstract description of moving objects
or find a path that describes the trajectory. Qualita-
tive spatial reasoning is a method of representing spa-
tial data by extracting the topological, mereological,
or geometric properties without requiring numerical
data, which may depend on the application (Stock,
1997; Cohn and Renz, 2007; Ligozat, 2011; Haz-
arika, 2012). This reflects human cognition and rea-
soning of common-sense knowledge. Logical expres-
sions are typically adopted in such a representation.
Logical expressions for a figure enable us to perform
mechanical reasoning on symbols, which reduces the
computational complexity. There are various promis-
ing practical applications of qualitativespatial reason-
ing: simulation on Geographic Information System,
query-answering system on spatial database, naviga-
tion on mobile robots, and so on.
To certify a system on qualitative spatial reason-
ing, we must prove that an expression correctly repre-
sents the properties of the image data and that there is
a corresponding image for a given expression. Al-
though there have been lots of works of qualita-
tive spatial reasoning in the field of artificial intelli-
gence (Randell et al, 1992; Egenhofer, 1995; Freksa,
1991; Borgo, 2013), little work has been carried out
from the viewpoint of the computational model.
On representation, most research claim expres-
sive power for spatial knowledge but do not refer to
the class the expression stands for. We do not know
whether a proposed expression is valid or reliable. It
is necessary to clarify to what extent the expression is
effective, if we implement a system based on the ex-
pression. On reasoning, most research focus on con-
sistency check, that is, whether there exists a space
that can satisfy all the given relationships among spa-
tial objects, and efficient algorithms for solving this
problem (Renz, 2002). However, they do not discuss
how to construct such a consistent set.
In this paper, we describe a computational model
for a qualitative representation.
Takahashi et al. have proposed a framework for
qualitative spatial reasoning, PLCA
1
(Takahashi and
Sumitomo, 2007; Takahashi, 2012), which focuses on
the patterns of connections between regions. This
method distinguishes patterns in which regions are
1
The name of PLCA is originated from an acronym for
Point(P), Line(L), Circuit(C) and Area(A).
204
Takahashi K., Goto M. and Miwa H..
A Qualitative Representation of a Figure and Construction of Its Planar Class.
DOI: 10.5220/0005263102040212
In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART-2015), pages 204-212
ISBN: 978-989-758-074-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

connected in different ways, for example, by a sin-
gle point, by two points, by a line and so on. For
example, in Figure 1, (a),(b) and (c) are regarded as
the same, while (d),(e) and these figures are regarded
to be different.
PLCA expressions represent the properties of spa-
tial data by describing the constituent objects, and the
relationships between them, without considering at-
tributes such as the size, direction, or shape.
(a)
(b)
(c)
(d) (e)
Figure 1: Classification of figures in PLCA. (a)-(c) Regions
connected by a line, (d) regions connected by a point, and
(e) regions that are not connected.
Takahashi et al. have described the conditions for
planarity of a given PLCA expression (Takahashi et
al, 2008), that is, an existence of the corresponding
figure on a two-dimensional plane, and given a proof
for this; however, they have not discussed the con-
struction of such a planar PLCA expression. In this
paper, we describe the construction of a planar PLCA
expression inductively, and prove that the resulting
class coincides with that of the planar PLCA. The part
of this proof is implemented using a proof assistant
Coq (Bertot and Cast´ran, 1998).
The remainder of this paper is organized as fol-
lows. In Section 2, we describe a PLCA expression.
In Section 3, we describe the inductiveconstruction of
a PLCA expression. In Section 4, we prove that the
constructed class coincides with that of planar PLCA.
In Section 5 we compare our work with the related
work, and Section 6 concludes the paper.
2 PLCA
2.1 Target Figure
The target figure of PLCA is considered as a region
segmentation of a finite space. In addition, PLCA ad-
mits regions with holes, and regards a hole itself to be
a region. It does not admit isolated lines or points, be-
cause a region cannot be properly defined. Here, we
describe a target figure using a simple closed curve
(Kosniowski, 1980).
Definition 2.1. (simple closed curve) A non-self-
intersecting continuous loop in a plane is called a
simple closed curve or a Jordan curve.
The following is the well-known theorem on Jor-
dan curve.
Theorem 2.1. Every Jordan curve divides the plane
into an interior region bounded by the curve and an
exterior region containing all of the nearby and far
away exterior points.
Formally, our target figure is a finite region on
a two-dimensional plane, divided into a finite set of
subregions of which each boundary is a simple closed
curve. In Figure 2, (a) and (b) are target figures,
whereas (c) and (d) are not.
(b) (c) (d)(a)
Figure 2: Examples of (a) and (b) target figures, and (c) and
(d) non-target figures.
2.2 PLCA Expression
A PLCA expression is defined as a five-tuple,
hP, L, C, A, outermosti, where P is a set of points, L ⊆
P
2
, C ⊆ L
n
(n ≥ 3), A ⊆ C
m
(m ≥ 1), outermost ∈ C.
In PLCA, there are four basic types of object:
points P, lines L, circuits C and areas A. An element
l ∈ L is defined as a pair of points p
1
and p
2
, and
denoted by l. points = [p
1
, p
2
], where p
1
and p
2
are
distinct. Intuitively, a line is an edge between points.
No two lines are allowed to cross. A line has an in-
herent orientation. When l. points = [p
1
, p
2
], l
+
and
l
−
mean [p
1
, p
2
] and [p
2
, p
1
], respectively. They are
called directed lines. l
∗
denotes either l
+
or l
−
and
l
∗re
denotes the line with the inverse orientation of l
∗
.
An element c ∈ C is defined as a list of directed
lines and denoted by c.lines = [l
∗
1
, . . . , l
∗
n
], where l
∗
i
6=
l
∗
j
if i 6= j (0 ≤ i, j ≤ n), l
∗
i
= [p
i−1
, p
i
](1 ≤ i ≤ n)
and p
n
= p
0
. If p ∈ l. points ∧ l
∗
∈ c.lines, it is said
that p is on c. A circuit has a cyclic structure, that
is, [l
∗
0
, . . . , l
∗
n
] and [l
∗
j
, . . . , l
∗
n
, l
∗
0
, . . . , l
∗
j−1
] represent the
same circuit for any j (1 ≤ j ≤ n). Intuitively, a cir-
cuit is the boundary between an area and its adjacent
areas.
An element a ∈ A is defined as a set of circuits and
denoted by a.circuits = {c
0
, . . . , c
n
}, where any pair
of circuits c
i
and c
j
(0 ≤ i 6= j ≤ n) cannot share a
point. Intuitively, an area is a connected region which
consists of exactly one piece.
In addition, outermost is a specific circuit in the
outermost side of the figure.
Example 2.1. (PLCA Expression)
A PLCA expression hP, L, C, A, outermosti corre-
sponding to the example target figure shown in Fig-
ure 3 is given below.
AQualitativeRepresentationofaFigureandConstructionofItsPlanarClass
205

p
1
p
0
p
2
p
3
p
4
p
5
c
0
a
0
a
1
c
1
c
2
l
0
l
1
l
5
l
4
l
2
l
3
l
6
Figure 3: An example of a target figure.
P = {p
0
, p
1
, p
2
, p
3
, p
4
, p
5
, p
5
}
L = {l
0
, l
1
, l
2
, l
3
, l
4
, l
5
, l
6
}
C = {c
0
, c
1
, c
2
}
A = {a
0
, a
1
}
outermost = c
2
l
0
. points = [p
0
, p
1
]
l
1
. points = [p
1
, p
2
]
l
2
. points = [p
2
, p
3
]
l
3
. points = [p
3
, p
4
]
l
4
. points = [p
4
, p
5
]
l
5
. points = [p
5
, p
0
]
l
6
. points = [p
1
, p
4
]
c
0
.lines = [l
−
0
, l
−
5
, l
−
4
, l
−
6
]
c
1
.lines = [l
−
1
, l
+
6
, l
−
3
, l
−
2
]
c
2
.lines = [l
+
0
, l
+
1
, l
+
2
, l
+
3
, l
+
4
, l
+
5
]
a
0
.circuits = {c
0
}
a
1
.circuits = {c
1
}
2.3 Basic Concepts of PLCA
Expressions
For c
1
, c
2
∈ C, we introduce two new predicates lc
and pc to indicate that two circuits share line(s) and
point(s), respectively.
lc(c
1
, c
2
)
def
= ∃l ∈ L;(l
∗
∈ c
1
.lines) ∧ (l
∗re
∈
c
2
.lines)
pc(c
1
, c
2
)
def
= ∃p ∈ P;(p ∈ l
1
. points) ∧ (p ∈
l
2
. points)∧ (l
+
1
∈ c
1
.lines) ∧ (l
−
2
∈
c
2
.lines).
If lc(c
1
, c
2
), then either pc(c
1
, c
2
) or pc(c
2
, c
1
)
holds. For any pair of circuits c
1
, c
2
∈ C, if c
1
, c
2
∈
a.circuits, then ¬pc(c
1
, c
2
) holds from the definition
of Area.
For a circuit c, we define a corresponding circuit-
segment.
Definition 2.2. (circuit-segment) Let c.lines =
[l
∗
0
, . . . , l
∗
n
]. A sequence cs = [m
∗
0
, . . . , m
∗
k
] (0 ≤ k ≤ n),
where m
∗
i
= l
∗
(i+ j) mod n
(0 ≤ j ≤ n− 1) is said to be a
circuit-segment of c, and denoted by cs ⊑ c.
For a circuit-segment cs = [m
∗
0
, . . . , m
∗
k
], we define
its inverse as inv(cs) = [m
∗re
k
, . . . , m
∗re
0
].
Example 2.2. (circuit-segments) In Example 2.1,
[l
−
0
, l
−
5
], [l
−
4
, l
−
6
, l
−
0
], [l
−
0
, l
−
5
, l
−
4
, l
−
6
] are some circuit-
segments of c
0
. Furthermore, inv([l
−
0
, l
−
5
]) is [l
+
5
, l
+
0
].
For a pair of circuits c
1
and c
2
, S
scs
(c
1
, c
2
) rep-
resents a set of their shared circuit-segments, that is,
S
scs
(c
1
, c
2
) = {cs |cs ⊑ c
1
, inv(cs) ⊑ c
2
}. For any
cs ∈ S
scs
(c
1
, c
2
), inv(cs) ∈ S
scs
(c
2
, c
1
) holds.
Definition 2.3. (MSCS) An element cs ∈ S
scs
(c
1
, c
2
)
is said to be a maximal shared circuit-segment of c
1
and c
2
if there does not exist cs
′
∈ S
scs
(c
1
, c
2
) such
that cs is a subsequence of cs
′
. A set of maximal
shared circuit-segments of c
1
and c
2
is denoted by
S
MSCS
(c
1
, c
2
).
When c.lines is contained in S
MSCS
(c
1
, c
2
), c
1
and
c
2
are the inner and the outer circuits of a simple
closed curve, respectively.
Example 2.3. (shared circuit-segments) In Figure 4,
S
scs
(c
0
, c
1
) = {[], [l
+
0
], [l
+
1
], [l
+
2
], [l
+
3
], [l
+
0
, l
+
1
], [l
+
2
, l
+
3
]}.
Furthermore, S
MSCS
(c
0
, c
1
) = {[l
+
0
, l
+
1
], [l
+
2
, l
+
3
]} and
S
MSCS
(c
1
, c
0
) = {[l
−
1
, l
−
0
], [l
−
3
, l
−
2
]}.
l
3
l
2
l
1
l
0
0
c
1
c
Figure 4: Shared circuit-segments of c
0
and c
1
.
Here, we introduce a new type Path. An instance
path of type Path is defined as a list of directed
lines and used to construct a new circuit. For path,
start(path), end(path) and inner
lines(path) show
the starting point, ending point and list of directed
lines, respectively. The length of inner
lines(path),
which may be 0, is said to be the length of the path.
Clearly, any circuit-segment is a Path.
2.4 Consistency
A consistent PLCA expression does not allow an iso-
lated point or an isolated line, and all of the objects
should be correctly defined by the incidence relations.
For any point, there exists at least one line that con-
tains it. For any line, there exist exactly two distinct
circuits that contain it and its inverse direction, re-
spectively. For any circuit, there exists exactly one
area that contains it. The outermost is not included
in any area. The consistency is formally defined as
follows.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
206

Definition 2.4. (PLCA consistency)
• [Consistency of Point-Line]
∀p ∈ P(∃l ∈ L; p ∈ l. points)
∀l ∈ L(∀p ∈ l. points; p ∈ P)
• [Consistency of Line-Circuit]
∀l ∈ L(∃c, c
′
∈ C;l
+
∈ c.lines∧ l
−
∈ c
′
.lines)
∀c ∈ C(∀l
∗
∈ c.lines;l ∈ L)
∀l ∈ L(l
∗
∈ c
1
.lines, l
∗
∈ c
2
.lines → c
1
= c
2
)
• [Consistency of Circuit-Area]
∀c ∈ C(∃a ∈ A;c ∈ a.circuits)
∀a ∈ A(∀c ∈ a.areas;c ∈ C)
∀c ∈ C(c ∈ a
1
.circuits, c ∈ a
2
.circuits → a
1
=
a
2
)
• [Independence of outermost]
¬∃a ∈ A;outermost ∈ a.cuicuit.
2.5 PLCA-connectedness
Intuitively, PLCA-connectedness guarantees that no
objects are separated, including the outermost. In
other words, for any pair of objects, there exists a trail
from one object to the other via further objects.
Definition 2.5. (d-pcon) Let e =
hP, L, C, A, outermosti be a PLCA expression.
For a pair of objects of e, the binary relation d-pcon
on P∪ L∪C∪ A is defined as follows.
1. d-pcon(p, l) iff p ∈ l. points.
2. d-pcon(l, c) iff l ∈ c.lines.
3. d-pcon(c, a) iff c ∈ a.circuits.
Definition 2.6. (pcon) Let α, β and γ be objects of a
PLCA expression.
1. If d-pcon(α, β), then pcon(α, β).
2. If pcon(α, β), then pcon(β, α).
3. If pcon(α, β) and pcon(β, γ), then pcon(α, γ).
Definition 2.7. (PLCA-connected) A PLCA expres-
sion e is said to be PLCA-connected iff pcon(α, β)
holds for any pair of objects α and β of e.
2.6 Planar PLCA Expression
Intuitively, PLCA-Euler guarantees that a PLCA ex-
pression can be embedded in a two-dimensional plane
so that the orientation of each circuit can be correctly
defined.
Definition 2.8. (PLCA-Euler) For a PLCA expression
hP, L, C, A, outermosti, if |P| − |L| − |C| + 2|A| = 0,
then it is said to be PLCA-Euler.
Takahashi et al. have given a proof of the follow-
ing theorem on the planarity of a PLCA expression
(Takahashi et al, 2008).
Theorem 2.2. For a consistent, connected PLCA ex-
pression, it is PLCA-Euler iff there exists a corre-
sponding target figure on a two-dimensional plane.
Planar PLCA is defined as follows.
Definition 2.9. (planar PLCA) For a PLCA expres-
sion, if it is consistent, PLCA-connected and PLCA-
Euler, then it is said to be planar PLCA
2
.
For example, the PLCA expression in Exam-
ple 2.1 is planar.
The following lemmas hold for a planer PLCA ex-
pression, and are used in the subsequent proof for the
realizability of an inductively constructed PLCA.
Lemma 2.1. For a planar PLCA expression, there ex-
ists an area that has a single circuit.
Proof. Let hP, L, C, A, outermosti be a planar PLCA
expression. Assume that for any area a ∈ A,
|a.circuits| ≥ 2 holds. Set k = 0 and c
0
be outermost.
Take c such that lc(c
k
, c) holds. Take an area a
k
such that c ∈ a
k
.circuits holds. Let a
k
.circuits be
{c, c
k
1
, . . . , c
k
n
}. Note that ¬pc(c, c
k
i
) holds for all
i from the definition of Area. Take an arbitrary c
k
i
(c
k
i
6= c) and let c
k+1
be c
k
i
Increment k and repeat
this procedure, then we can take an infinite sequence
of circuits SeqC = c
0
, c
1
, . . ..
Figure 5 illustrates each step of this procedure.
Take c
0
as an outermost and c such that lc(c
0
, c) holds.
Take an area a
0
such that c ∈ a
0
.circuits holds (Fig-
ure 5(a)). There are three circuits in a
0
.circuits other
than c. Take an arbitrary circuit among them and set it
as c
1
; take c such that lc(c
1
, c) holds. Take an area a
1
such that c ∈ a
1
.circuits holds. (Figure 5(b)). There
is one circuit in a
1
.circuits other than c. Take this cir-
cuit and set it as c
2
; take c such that lc(c
2
, c) holds.
Take an area a
2
such that c ∈ a
2
.circuits holds. (Fig-
ure 5(c)). We continue this procedure.
Each circuit is a simple closed curve.
¬pc(c
i
, c
i+2
) holds for each i, from Theorem 2.1,
since c
i
and c
i+2
are circuits in the exterior region and
interior region of c
i
, respectively. On the other hand,
the number of circuits is finite. Therefore, we cannot
take an infinite sequence of circuits SeqC. Hence,
there exists an area a ∈ A such that |a.circuits| = 1.
Lemma 2.2. For any circuit c of a planar PLCA ex-
pression, there exists a circuit that has only one max-
imal shared circuit-segment with c.
2
Strictly, the original PLCA admits a curved line, and
multiple lines between the same pair of points. If we admit
only straight lines, we convert a PLCA expression in the
original definition by adding the same number of points and
lines, and this conversion does not affect the condition for
planarity or the proof thereof.
AQualitativeRepresentationofaFigureandConstructionofItsPlanarClass
207

c
a
0
c
0
(a) step1: take a
0
c
1
c
a
1
(b) step2: take a
1
a
2
c
2
c
(c) step3: take a
2
Figure 5: Existence of an area with a single circuit.
Proof. Let hP, L, C, A, outermosti be a planar PLCA,
and c ∈ C be an arbitrary circuit. Assume that for
all circuits c
′
∈ C, |S
MSCS
(c, c
′
)| 6= 1 holds. For a
circuit c
′
such that ¬lc(c, c
′
) holds, |S
MSCS
(c, c
′
)| =
0 holds. Therefore, we take a circuit c
′
such that
lc(c, c
′
) holds. Let S
MSCS
(c, c
′
) = {cs
1
, cs
2
}. Circuit-
segments cs
1
and cs
2
do not share a point. Since
cs
1
and cs
2
are considered to be paths, we can take
their starting points and ending points: start(cs
1
) =
p, end(cs
1
) = q, start(cs
2
) = r, end(cs
2
) = s. Then
there exists cs ⊑ c such that start(cs) = q, end(cs) =
r, and each line in cs is not included in c
′
.lines. Since
c
′
is a circuit, there exists cs
′
; cs
′
⊑ c
′
, start(cs
′
) =
r, end(cs
′
) = q. On the other hand, from the consis-
tency of Line-Circuit, there exists c
0
; inv(cs) ⊑ c
0
,
start(inv(cs)) = r, end(inv(cs)) = q. Then, circuit c
0
is defined by appending two circuit-segments inv(cs
′
)
and inv(cs). Therefore, S
scs
(c, c
0
) = {cs}. It follows
that |S
MSCS
(c, c
0
)| = 1, which is a contradiction (Fig-
ure 6).
cs
p
q
r
s
cs’
c
c’
c
0
cs
1
cs
2
Figure 6: Existence of an area with a single maximal
shared circuit-segments. (Relationships of circuit-
segments: cs
1
, cs
2
, cs ⊑ c, inv(cs
1
), inv(cs
2
), cs
′
⊑ c
′
inv(cs), inv(cs
′
) ⊑ c
0
, start(cs
1
) = p, end(cs
1
) = q,
start(cs
2
) = r, end(cs
2
) = s. start(cs) = q, end(cs) = r,
start(cs
′
) = r, end(cs
′
) = q.)
3 CONSTRUCTION OF PLCA
Theorem 2.2 gives the conditions for planarity of a
given PLCA expression. The next issue to address is
how to construct such an expression.
We can construct a PLCA expression of elements
P, L, C and A in this order, for example. In this ap-
proach, we must check all of the constraints on the
objects carefully during each stage. For example, we
must make a circuit so that there exist exactly two dis-
tinct circuits: one that contains a line, and one the
line in the inverse direction. If this is not satisfied, we
must backtrack to construct these lines. This not only
requires time, but it is also very difficult to prove that
the resulting structure is a planar PLCA expression.
Therefore, we take a different approach, in which
we begin with outermost and construct a PLCA ex-
pression inductively.
We define a class for PLCA expressions using the
following three constructors: single
loop, add loop
and add
path. A constructor single loop corresponds
to the base case, and the other two correspond to op-
erations that construct a new PLCA expression by di-
viding an existing area in a current PLCA expression
using a path. An arbitrary path, the length of which is
more than one is introduced, makes a new circuit us-
ing it. Points and lines contained in the path are added
simultaneously, and the area is divided into two areas.
We must add objects of four different types simul-
taneously during an induction step because the objects
of a PLCA expression are mutually related. We take
the number of areas as a measure of induction, and
the number of other objects increases following the
application of each constructor. We cannot take the
number of points or lines as such a measure, because
the expression that is obtained as a result of adding
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
208

a single point or a single line to a PLCA expression
may not be a PLCA expression.
An alternative method of generating a new area
is to add a path to the outer part of the outermost.
That is, we take two points on the current outermost
and combine these with a path in the exterior region
of outermost. In this case, outermost changes during
each step where a constructor is applied. Because the
construction of a new outermost is the base case in
an inductive definition, we cannot succeed in a proof
if we change the definition of outermost during each
step. Therefore, we do not adopt this method.
We now describe the construction. The idea of
construction is based on drawing a figure. Although
we demonstrate the construction process on a figure to
provide an intuitive discussion, the construction itself
is performed symbolically.
A constructor single
loop is for a base case,
and corresponds to the simplest target figure with
one area. There are only two circuits: the outer-
most circuit and the inner side thereof. Consider
an arbitrary path path, such that start(path) = x,
end(path) = y, and inner
lines(path) = [l
+
0
, . . . , l
+
n
].
Then we create new circuits outermost such that
outermost.lines = [l
+
, l
+
0
, . . . , l
+
n
] and c such that
c.lines = [l
−
n
, . . . , l
−
0
, l
−
], where l. points = [y, x] (Fig-
ure 7).
x y
c
outermost
a
l
Figure 7: The constructor single loop.
We now define add
loop. Consider an arbi-
trary area a (Figure 8(a)). Take an arbitrary path
path, such that start(path) = x, end(path) = y and
inner
lines(path) = [l
+
0
, . . . , l
+
n
]. Make a line l such
that l. points = [y, x] (Figure 8(b)). Then make new
circuits c
1
and c
2
such that c
1
.lines = [l
+
, l
+
0
, . . . , l
+
n
],
and c
2
.lines = [l
−
n
, . . . , l
−
0
, l
−
]. Add c
1
to a
1
.circuits
and c
2
to a
2
.circuits (Figure 8(c)). As a result, a is
divided into two areas, a
1
and a
2
(the hatched part).
The points and lines contained in path are added ac-
cordingly. If a contains more than one circuit, all of
them remain in a
1
, and a
2
contains none.
Now we define add path. Consider a circuit c
such that c ∈ a.circuits, and two points y, z on c.
Here y and z may be identical. Because a circuit-
segment is a path, consider a circuit-segment cs ⊑ c
such that start(cs) = y, end(cs) = z. Then c is
divided into two circuit-segments: cs and cs
′
. Let
c.lines = [ll
+
0
. . . , ll
+
m
], cs = [ll
+
0
. . . , ll
+
k
] (0 ≤ k ≤ m)
and cs
′
= [ll
+
k+1
. . . , ll
+
m
] (Figure 9(a)). Take an
arbitrary path path, such that start(path) = s,
end(path) = e and inner
lines(path) = [l
+
0
, . . . , l
+
n
].
Make lines l
s
and l
e
such that l
s
. points = [s, y]
and l
e
. points = [z, e], respectively (Figure 9(b)).
Then make new circuits c
1
and c
2
such that
c
1
.lines = [l
−
s
, l
+
0
, . . . , l
+
n
, l
−
e
, ll
+
k+1
. . . , ll
+
m
] and
c
2
.lines = [l
+
e
, l
−
n
, . . . , l
−
0
, l
+
s
, ll
+
0
. . . , ll
+
k
]. Add c
1
to
a
1
.circuits and add c
2
to a
2
.circuits (Figure 8(c)). As
a result, a is divided into two areas, a
1
and a
2
(the
hatched part), c is eliminated, and two new circuits
are created. The points and lines contained in path
are added and the objects are changed. If a contains
circuits other than c, all of them remain in a
1
, and a
2
contains none.
Note that add
loop is applied to a specific area,
whereas add
path is applied to a specific circuit and
two points on it.
Definition 3.1. (IPLCA) PLCA expressions con-
structed by the above three constructors are said to
be Inductive PLCA (IPLCA).
4 PROOF OF FORMALIZATION
Here we prove that IPLCA coincides with planar
PLCA.
4.1 Proof of Planarity
We first prove that IPLCA is planar. From Theo-
rem 2.2, we prove the following theorem.
Theorem 4.1. (planarity for IPLCA) If e is IPLCA, e
is (i) consistent, (ii) PLCA-connected, and (iii) PLCA-
Euler.
We implement IPLCA and prove these three prop-
erties using the proof assistant Coq (Bertot and
Cast´ran, 1998). Coq is based on typed logic adopted
for higher-order functions. The data types and func-
tions are defined in recursive form, and the proof pro-
ceeds by connecting suitable tactics. The definition
of IPLCA and the proof of Theorem 4.1 required ap-
proximately 5500 lines of code in total The advantage
of using Coq is to certify the correctness of the for-
malization. We do not show the detail of the proof
here, since it is out of the focus of this paper. The
entire code is shown in (Goto, 2014).
4.2 Proof of Realizability
We prove that a planar PLCA is IPLCA. This means
that any target figure can be drawn by applying the
AQualitativeRepresentationofaFigureandConstructionofItsPlanarClass
209
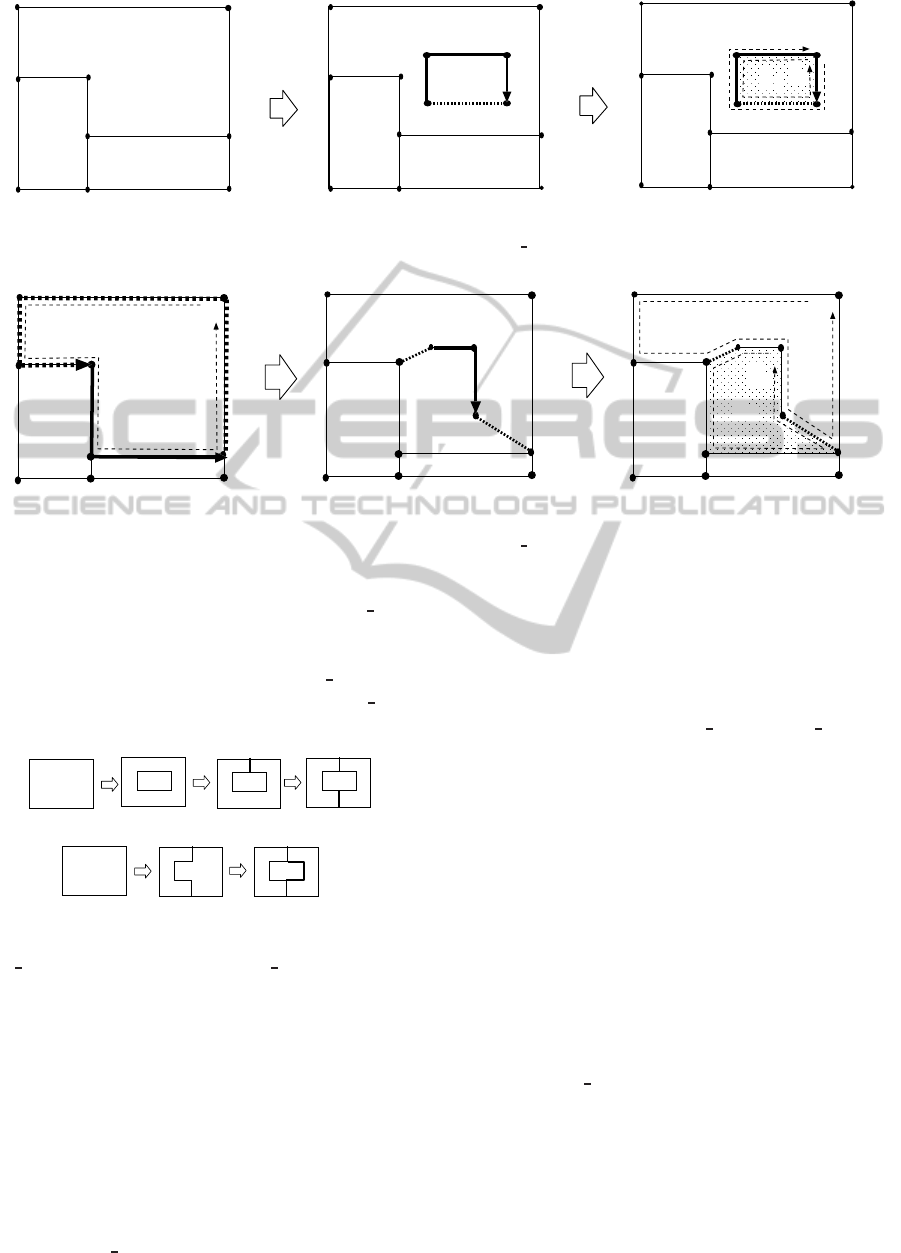
(a)
(b)
(c)
a
x
y
c
1
2
c
a
1
a
2
x
y
l
Figure 8: The constructor add loop.
(a)
(b)
(c)
cs’
y
z
2
c
e
s
c
1
y
z
e
s
l
s
e
l
cs
y
z
a
c
a
1
a
2
Figure 9: The constructor add path.
constructors of IPLCA in a suitable order. For ex-
ample, consider Figure 10. If we apply add
loop
first, we cannot successively apply constructors, be-
cause any intermediate figure is not the target figure
(Figure 10(a)). However, if we apply add
path first,
we can successively add areas by applying add
path
again (Figure 10(b)).
(a)
(b)
add_loop
add_path
Figure 10: Constructing figures (a) by first applying
add
loop, and (b) by first applying add path.
Theorem 4.2. (Realizability for IPLCA) A planar
PLCA is IPLCA.
Proof. Let F be a target figure. We prove the theorem
using induction on the number of areas of F.
(Base case) The number of areas is 1.
F consists of only a simple closed curve. This is
clearly a base case of IPLCA, and is constructed by
applying single loop.
(Induction step) The number of areas is n+ 1.
The principle of our proof via induction is as fol-
lows. For a planar PLCA e, of which the number of
areas is n+ 1, we remove a suitable area a such that
we can form a planar PLCA e
′
, where the number of
areas is n. Because e
′
is IPLCA from the induction
hypothesis, we can apply add
loop or add path to
obtain e. We proceed the proof based on this princi-
ple.
We can take an area a with a single circuit c
from Lemma 2.1. Then, there exists c
′
such that
|S
MSCS
(c, c
′
)| = 1, from Lemma 2.2. Assume that
c
′
= outermost. Since the number of areas is more
than one, a contains more than one circuit, which is a
contradiction. Therefore, c
′
6= outermost.
Case 1. S
MSCS
(c, c
′
) = {c.lines}.
In this case, we remove a, c, c
′
, and all objects
on c and c
′
to obtain a planar PLCA e
′
such that
|e
′
.areas| = n. Note that since c
′
6= outermost, e
′
has
an outermost. Here e
′
is IPLCA from the induction
hypothesis. Then we can construct e by applying the
constructor add
loop on a
′
(Figure 11).
Case 2. S
MSCS
(c, c
′
) 6= {c.lines}.
Let S
MSCS
(c, c
′
) = {cs}. In this case, c is divided
into two circuit-segments cs and cs
1
, and c
′
is divided
into two circuit-segments inv(cs) and cs
2
(Figure 12).
We remove a, c, c
′
, and all objects on c and c
′
, and add
a circuit newC by appending cs
1
and cs
2
. We obtain
a planar PLCA expression e
′
such that |e
′
.areas| = n.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
210
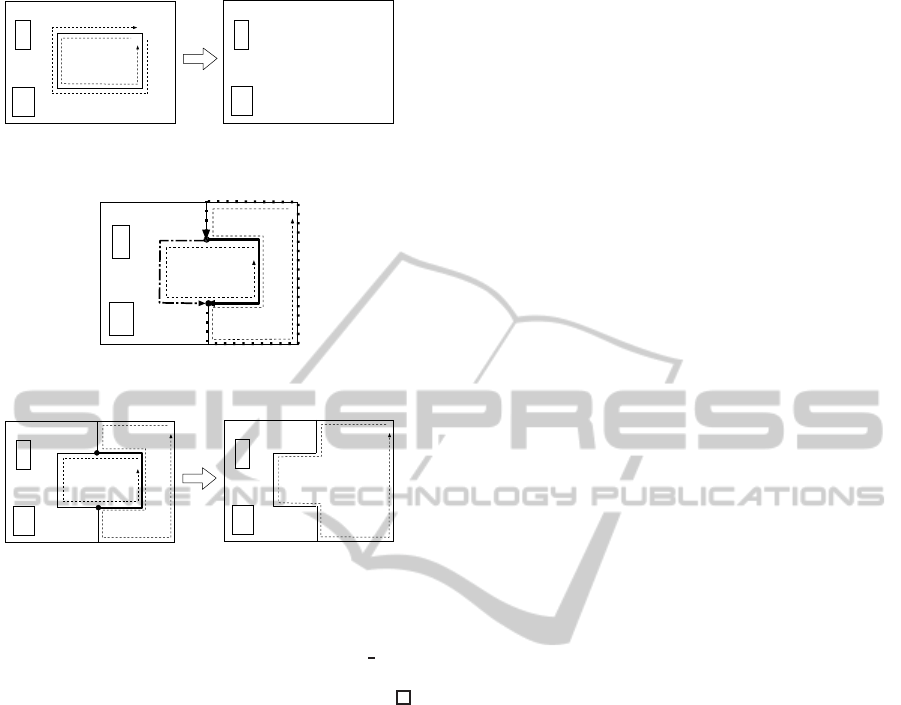
a’
c
a
c’
a’
e
e’
Figure 11: Removing an area with case 1.
cs
2
cs
1
cs
c
c’
Figure 12: Circuit-segments in case 2. Circuit c is divided
into cs and cs
1
, and circuit c
′
is divided into inv(cs) and cs
2
.
a’
newC
e e’
a’
c
a
c’
Figure 13: Removing an area with case 2.
e
′
is IPLCA from the induction hypothesis. Then we
can construct e by applying the constructor add
path
on newC, start(cs
1
) and end(cs
1
) (Figure 13).
5 RELATED WORK
There exist several symbolic expressions other than
qualitative spatial representations for a figure on
a two-dimensional plane, including computational
geometry (de Berg et al, 1997) and graph the-
ory (Harary, 1969). Different from qualitative spatial
representations, the main objective of computational
geometry is to analyze the complexity of algorithms
for problems expressed in terms of geometry and to
develop efficient ones, rather than to recognize or to
analyze the characteristics of a figure. Graph theory
can be used to provide symbolic expressions of spa-
tial data. The topological structure of spatial data can
be represented as a graph by treating spatial objects,
such as points and lines, as nodes and the relation-
ships between them as edges. There exists a condition
to determine the planarity of a given graph; however,
in general, a graph does not contain any information
on an area, and therefore we only know that we can
embed a graph by locating areas properly. In contrast,
a PLCA expression places constraints on the locations
of areas. In this respect, a PLCA expression is more
specific than a graph.
One of the challenges for symbolic expressions of
a figure on a two-dimensional plane is the concept
of a hypermap. A hypermap is an algebraic struc-
ture that represents objects and relationships between
them, and can be used to distinguish the topological
and geometric aspects. There are several works that
use a hypermap and give a formalization and a proof
of the properties of these aspects using proof assis-
tants. Gonthier et al. formalized and proved the four-
color theorem and showed a proof (Gonthier, 2008).
In this work, planar subdivisions are described by a
hypermap. Dufourd applied a hypermap to formal-
ize and to prove a Jordan curve theorem (Dufourd,
2009). He also showed a treatment of surface subdi-
vision and planarity based on a hypermap (Dufourd,
2010). Brun et al. showed a derivation of a program
to compute a convex-hull for a given set of points
from their specification using a hypermap (Brun et al,
2012). They specified the algorithm and proved its
correctness using a structural induction. Hypermap is
a strong method for providing a mechanical proof of
the topological or geometric properties in a symbolic
form; however, the representation is too complicated
to understand intuitively.
6 CONCLUSION
We have described a method of constructing a PLCA
expression inductively, and have proved that the de-
fined class coincides with that of planar PCLA. For-
malization and part of the proof was implemented us-
ing the proof assistant Coq. Our main contribution
is giving a computational model to a qualitative spa-
tial representation, which is the first attempt in the re-
search field on qualitative spatial reasoning.
Mechanical proof using a proof assistant provides
a rigorous proof of correctness of the formalization.
In future, we will complete the mechanical proof of
the part currently done manually.
ACKNOWLEDGEMENTS
This work is supported by JSPS KAKENHI Grant
Number 25330274.
AQualitativeRepresentationofaFigureandConstructionofItsPlanarClass
211

REFERENCES
de Berg, M., M. van Kreveld, M. Overmars and
O. Schwarzkopf (1997). Computational Geometry.
Springer-Verlag.
Bertot, Y. and P. Cast´ran (1998). Interactive Theorem Prov-
ing and Program Development - Coq’Art: The Calcu-
lus of Inductive Constructions. Springer Verlag.
Borgo, S. (2013). RCC and the theory of simple re-
gions R
2
. Conference On Spatial Information Theory
(COSIT13), pp.457-474.
Brun, C., J. -F. Dufourd and N. Magaud (2012). Designing
and proving correct a convex hull algorithm with hy-
permaps in Coq. Computational Geometry : Theory
and Applications, 45(8):436-457.
Cohn, A. G. and J. Renz (2007). Qualitative spatial rea-
soning. in Handbook of Knowledge Representation.
F. Harmelen, V. Lifschitz and B. Porter(eds.), Chapt
13, pp.551-596, Elsevier.
Dufourd, J. -F. (2009). An intuitionistic proof of a discrete
form of the Jordan curve theorem formalized in Coq
with combinatorial hypermaps. Journal of Automated
Reasoning, 43(1):19-51.
Dufourd, J. -F. and Y. Bertot (2010). Formal study of plane
Delaunay triangulation. Interactive Theorem Proving,
pp.211-226, LNCS 6172, Springer-Verlag.
Egenhofer, M. and J. Herring (1995). Categorizing bi-
nary topological relations between regions, lines, and
points in geographic databases. Department of Sur-
veying Engineering, University of Maine.
Freksa, C. (1991). Conceptual neighborhood and its role
in temporal and spatial reasoning. Proceedings of the
IMACS Workshop on Decision Support Systems and
Qualitative Reasoning, pp.181-187.
Gonthier, G. (2008). Formal proof - The four color theorem.
Notices of the AMS, 55(11):1382-1393.
Goto, M. and K. Takahashi (2014). http://ist.ksc.kwansei.
ac.jp/∼ktaka/IPLCA/
Harary, F. (1969). Graph Theory. Reading, MA, Addison-
Wesley.
Hazarika, S. (2012). Qualitative Spatio-Temporal Repre-
sentation and Reasoning: Trends and Future Direc-
tions. IGI Publishers.
Kosniowski, C. (1980). A First Course in Algebraic Topol-
ogy. Cambridge University Press.
Ligozat, G. (2011). Qualitative Spatial and Temporal Rea-
soning. Wiley.
Randell, D. A., Z. Cui and A. G. Cohn (1992). A spatial
logic based on regions and connection. Proceedings
of the Third International Conference on Principles
of Knowledge Representation and Reasoning (KR92),
pp.165-176.
Renz, J. (2002). Qualitative Spatial Reasoning with Topo-
logical Information. LNAI 2293, Springer-Verlag.
Stock, O. (Ed.) (1997). Spatial and Temporal Reasoning,
Kluwer Academic Publishers.
Takahashi, K. (2012). PLCA: A framework for qualitative
spatial reasoning based on connection patterns of re-
gions. in (Hazarika, 2012), Chapt 2, pp.63-96.
Takahashi, K. and T. Sumitomo (2007). The qualitative
treatment of spatial data. International Journal on Ar-
tificial Intelligent Tools,16(4):661-682.
Takahashi, K., T. Sumitomo and I. Takeuti (2008). On
embedding a qualitative representation in a two-
dimensional plane. Spatial Cognition and Computa-
tion, 8(1-2):4-26.
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
212
