Automatic Variable-timing Animation Transition based on Hierarchical

Interpolation Method

Yumeng Wang

1,2

, Fubo Lang

, Zheng Wang

1,2

and Bo Xu

Interactive Digital Media Technology Research Center, Institute of Automation,

Chinese Academy of Sciences, Beijing, China

Zhejiang Institute of Digital Media of Chinese Academy of Sciences, ShaoXing, China

Keywords:

Animation Transition, Interpolation, Variable Timing, Character Animation.

Abstract:

Character animation has been used in many ﬁelds, such as ﬁlm making, virtual reality interaction and video

games. Video game needs a large set of character animations for users to trigger. However, it is a complex and

tedious work for animators to manufacture all the transition animations between each pair of character anima-

tions. In this paper, a novel rapid method is presented to generate transition animation automatically. Firstly,

animations in the game animation set are classiﬁed. Secondly, the time length during motion interpolation is

calculated automatically, which is decided by the angle velocity of character’s joints. The method is called

variable timing method. Lastly, by using hierarchical interpolation method, postures interpolate between dif-

ferent animations. The transition animation can be quickly acquired, according with human dynamics. In this

way, we can get a natural movement by connecting animations together. Experimental results demonstrate

that our method can be effectively and efﬁciently applied to generate transition animations between various

character animations.

1 INTRODUCTION

Interactive entertainment is a signiﬁcant application

of virtual character animation. There are two stan-

dards to evaluate the quality of interactive games,

the reality of immersion and the real-time response.

Nowadays, there are a large number of role-play video

games, they need to create a lot of character anima-

tions for virtual characters.

When a user trigger an animation, the player in

game will respond accordingly. The character needs a

period of transition animation, while its motion trans-

forms from one to another. There are several solutions

for transition animation as follows.

The ﬁrst approach is to connect two animations

directly, without any transition animation. This is the

most convenient and efﬁcient way, however,the worst

user experience. This approach directly connect the

last frame of former animation and the ﬁrst frame of

next animation on the spot. This movement is very

stiff and unreal.

The second approach is the most common method

in the video game industry nowadays. The game will

have a large animation set for users to invoke while

playing the game. The animation set includes all the

character animation, as well as all the transition an-

imation between each animation, which is made by

animators. This approach brings animators a lot of

work, especially when story line of the game is com-

plex. It is also impossible for animators to make all

the transition animation between each two frames. In

this case, the animation will run until one frame there

has a transition animation, leading to time delay.

The third approach is to set a precise time length

for animation blending. In this way, the anima-

tion transition will generate automatically by blend-

ing some keys to overlap these two animations. The

blend time is set previously, it uses the same transition

method for different animation, other than according

to the varied degree of complexity between two dif-

ferent postures.

In this paper, a novel method is presented to solve

these problems above. Firstly, the time length of tran-

sition will be calculated according to the differences

between postures. We call it variable timing method

for the time length is variable. It is a priori to adapt

to the speed of every joint’s movement. And then,

animation transition is generated by rotation interpo-

lation and position prediction according to animation

trend. Different from other methods, this is a hier-

309

Wang Y., Lang F., Wang Z. and Xu B..

Automatic Variable-timing Animation Transition based on Hierarchical Interpolation Method.

DOI: 10.5220/0005264703090316

In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 309-316

ISBN: 978-989-758-087-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Present

animation

Animation

Classification

Interpolation

method

Hierarchical

interpolation

input

Transition

animation

output

Figure 1: The pipeline of our method.

archical interpolation method, which is based on the

classiﬁcation of animations and joints. Different in-

terpolation method is used for different joints. At

the same time, according to animation classiﬁcation,

different interpolation parameter is used for different

types of movement. In the premise of smoothness, it

can improve the calculation speed, by using the hi-

erarchical interpolation method. The pipeline of our

method is show in Figure 1. This paper will explain

all these in detail in later section.

2 RELATED WORK

Common interpolation method of character animation

is described in (Smith, 2013). There are some exten-

sions for interpolation method. (Patil and Chai, 2014)

was used for interactive real time applications and

predeﬁned animations. (Chakra and Li, 2009) pre-

sented a level of details technique applicable to artic-

ulated characters in real-time graphical interpolation

simulation. (Kong et al., 2011) presented the inter-

polation method showed more motion details, which

was based on key frame classiﬁcation and the synthe-

sis of animations.

Motion interpolation allows constraints to be sat-

isﬁed. The constraints of (Chai and Hodgins, 2007)

were user-deﬁned, it synthesised the constraints with

motion. (Safonova and Hodgins, 2007) combined

interpolation and motion graphs. (Moulard et al.,

2013) integrated spatial and dynamic constraints for

humanoid character. (O’Brien et al., 2011) showed

space-time vertex constraints to adapt the animation,

the motion adaptation describes constraints of dynam-

ics and kinetics. (Yumeng et al., 2014) provided the

method to optimize the control of motion trajectory.

The posture of character involves the descriptions

of the orientation and position of each segment (Ben-

itez, 2007). An approach for motion simulation which

is driven by data was introduced by (Wang et al.,

2008), which was based on Gaussian process models

for motion generation. (Sok et al., 2010) described a

method of editing motions by interacting directly with

the momentum along particular axes. (Kuznetsova et

al., 2013) generated completely new meshes and mo-

tion and a speciﬁc motion for a given mesh or a spe-

ciﬁc shape using an existing motion. (Shapiro and

Feng, 2013) associated physical properties with char-

acter’s joint to visualize explicitly a number of proper-

ties that can help animators develop high-quality ani-

mation.

There are some researches about proper duration

of transition. (Wang and Bodenheimer, 2003) ad-

dressed what kind of cost function should be used to

assure smooth transitions between primitives. They

also studied the optimal duration for a transition given

a previously learned distance measure (Wang and Bo-

denheimer, 2004) . (Shum et al., 2009) developed

a method to determine appropriate timings for mo-

tion transition by considering momentum preserva-

tion. (McCann and Pollard, 2007) could pre-compute

optimal transitions based on character state for kine-

matic controllers.

3 DATA PREPARATION

Animation set includes a mass of character anima-

tions, which has already been provided by animators.

Players can trigger different animations during the

video game. In order to get prepared for the creation

of transition, all these animations need to be classi-

ﬁed.

When a new character input into the interface of

video game, the ﬁrst thing is to traverse all the joints.

Based on the character structure, pivotal joints are

recognized and marked, especially the joints of hip

and feet. These joints will be set as basis of anima-

tion classiﬁcation.

XOY plane is deﬁned as the ground plane, charac-

ters will play on this plane. Axis Z is deﬁned as the

world up vector, which is perpendicular to the ground.

All these animations can be classiﬁed into three

parts.

1. Animation on the spot. The change of the dis-

placement of feet in Axis X and Axis Y is not above

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

310

Figure 2: The example of animation classiﬁcation.

a certain threshold. It can be recorded as ∆X

foot

→ 0

and ∆Y

foot

→ 0. Many motions such as squat, stand

up, applause, shoot and so on, can fall into this cate-

gory.

2. Plane motion. These animations have appar-

ent movement on the XOY plane, as well as the hip’s

value of the Axis Z is no more than original value. It

can be recorded as ∆Z

hip

< δ. Such as walking and

running.

3. Space ﬂight. These animations include the sit-

uations that both feet leave the ground, such as danc-

ing and jumping. These motion would constrained by

the physical properties of anthropometric kinematics.

These animations is classiﬁed by the position of feet,

which are both off the ground for a period of time. It

is recorded as Z

foot

> 0.

As show in Figure 2, the left picture shows the

character stands on the ground and shakes his head

proudly, this belongs to the animation on the spot.

The middle picture shows the character walk along

in a direction, this is a walk cycle along Axis X di-

rection, which represents as plane motion. The right

picture is a complicated dance movement, which has

a lot of jumps and ﬂight parts, belonging to the third

category, space ﬂight.

All the animation data has already been classiﬁed

before the on-the-ﬂy generation of transition anima-

tions. The transformation between different move-

ments is distinct.

4 AUTOMATICALLY SET THE

TRANSITION TIME LENGTH

For the stability of interactive entertainment, and

good user experience, our method not only need

smooth animation transition, but also the real-time re-

sponse. The transition animation needs to generate

rapidly and smoothly during a tiny time that user does

not perceive.

The time length of the transition animation in our

method can be automatically set. The variable time

length is calculated in real-time automatically. It is

decided by the angular velocity of every joint and the

movement of the character.

The animation transition between two animations

should be smooth. Sudden changes in movement and

appearance would make users edgy and reduce users’

experience.

Some transition method sets an exact blend time.

If there are huge differences between two postures

and the blend time is improper, the method may also

generate a sudden change.

In our research, a variable timing method is raised

to solve the problem of cohesive movement is not

smooth. This method automatically generate a time

length, neither present sudden change, nor take too

long time.

For a biped character, the motion of legs and feet

plays a decisive role in character motion rhythm. To

simplify the calculational complexity, we only take

joints of legs and feet to calculate transition time

length. In addition, hip is the root joint, the rota-

tion of hip is also need to be calculated. These joints

are marked through the traversal of character skeleton

structure. They are numbered with i, and N is the total

number.

As show in Eq. 1, angular acceleration of every

joint is calculated. i represents different joints, n rep-

resents different segmentation of animation. To gen-

erate the transition animation, n = 1 is the present

movement, n = 2 is the next movement.

ω is the an-

gular acceleration,

P is a unit vector of rotation axis,

θ is the second derivative of rotation angle θ.

(1)

During the transition animation, angular accelera-

tion is set as a constant, as show in Eq. 2.

is the

angular acceleration of the last frame of the present

animation. ω

is not the last frame of the whole an-

imation, it is the present frame that user triggers the

next movement of the character.

is the angular ac-

celeration of the ﬁrst frame of the next animation.

is a vector to sum these two.

(2)

The time length could be calculate as Eq. 3.

The duration of time length is to divide rotation an-

gle by angular velocity. ∆θ

can be obtained from

Eq. 4, which is the joint’s rotation angle between two

frames. θ

is the angle of last frame of the present

animation, θ

is the angle of ﬁrst frame of the next

animation. ω

can be obtained from Eq. 2.

= ∆θ

· ω

−1

(3)

∆θ

= arccos(θ

· θ

) (4)

The methods to calculate the time length of every

joint, ensuring the velocity of each joint can adapt to

AutomaticVariable-timingAnimationTransitionbasedonHierarchicalInterpolationMethod

311

the movement rhythm of the whole body. As we get

all the possible time length of the joints’ movement,

proper time length for the transition animation needs

to be chose. The maximum value of t

is chose as

the time length T, as show in Eq. 5, every joint needs

to display an appropriate movement. We do not ex-

pect the time length leads to an inappropriate sudden

change of any joint.

T = max{t

|i ∈ N} (5)

In this way, the time length of the transition can be

automatically obtained in real-time. The time length

T will be used in the interpolation between anima-

tions.

5 HIERARCHICAL

INTERPOLATION METHOD

The motion offers by animators is based on data, we

call it data-driven key frame animation. The inter-

polation between key frames can provides real-time

character animation.

The key pose contains the rotation data of each

joint and the position data of the root node. Different

interpolation methods is used between rotation data

and position data. The transition frame is triggered

by the users, whenever they want, and whatever the

pose is. All the interpolation method and interpola-

tion parameter is chose hierarchically.

5.1 Rotation Interpolation Method

Rotation data is expressed as quaternions, the most

widely used method is Linear Quaternion interpola-

tion (Lerp). the interpolation curve can be stated as

Eq. 6.

Lerp(q

;h) = q

(1− h) + q

h (6)

In the equation, q

is the quaternion of the current

frame, q

is the quaternion of the ﬁrst frame of the

next movement, h ∈ [0,1] is interpolation parameter.

This is a linear combination of the two quaternions.

Even though the interpolation curve of Lerp can

be quickly and easily used, the velocity graph is not

intuitively satisﬁed. During the middle part of the in-

terpolation, the curve do not match the unit sphere

very well. On the other hand, the projection of the

interpolation onto the hyper sphere does not generate

constant speed, resulting non-constant angular veloc-

ity. The interpolation function has larger velocity in

the middle of the curve.

To solve this problem, the interpolation method

should yield constant angular velocity. It is called

Spherical Linear Quaternion interpolation (Slerp), as

show in Eq. 7. The interpolation path can be proved to

be the shortest path between two points over the hyper

sphere. Since the angle between the two quaternions

is linearly interpolated, Slerp provides constant angu-

lar velocity.

SLerp(q

;h) =

sin(1 − h)θ

sinθ

sinhθ

sinθ

(7)

As show in Eq. 7, θ = arccos(q

· q

) is the angu-

lar separation of the two quaternions, h ∈ [0, 1] is the

interpolation parameter.

When interpolating between two rotation data, the

Slerp is optimal, however, when interpolating be-

tween a series of rotation, there emerge some prob-

lems. The interpolation curve may not smooth at the

control points, and the angular velocity is not contin-

uous at the control points.

Even though our interpolation is between two key

frames, the ﬁnal animation should be smooth during

the whole path. Therefore, the movement of present

animation and next animation need to be considered.

Not only the frame before the present frame, but also

the frame after the end frame of transition need to be

used.

When interpolating between a series of control

points, the curve can be constructed by Bezier curves.

As show in Eq. 8, it is the Spherical Spline Quaternion

interpolation (Squad), i is the present frame, i+ 1 is

the next frame, i − 1 is the frame before the present

frame, s can be calculated by Eq. 9.

Squad (q

+ 1, s

+ 1;h) = SLerp(SLerp

i+1

;h), SLerp(s

i+1

;h);2h(1− h))

(8)

= q

·exp

−

log



−1

i+1



+ log



−1

i−1



(9)

Squad is similar to Bezier curve, but involves

spherical linear interpolation instead of simple linear

interpolation. As it shows that, Squad is derived from

Slerp. In this way, the interpolation is under inﬂuence

of the previous movement and the next movement.

Figure 3 compares all these interpolation methods.

The data-based character animation contains rota-

tion data of all the joints. The rotation interpolation is

used in every joint of the skeleton structure, including

the hip, which is the root node of the skeleton. The

root node is also an important joints in rotation inter-

polation.

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

312

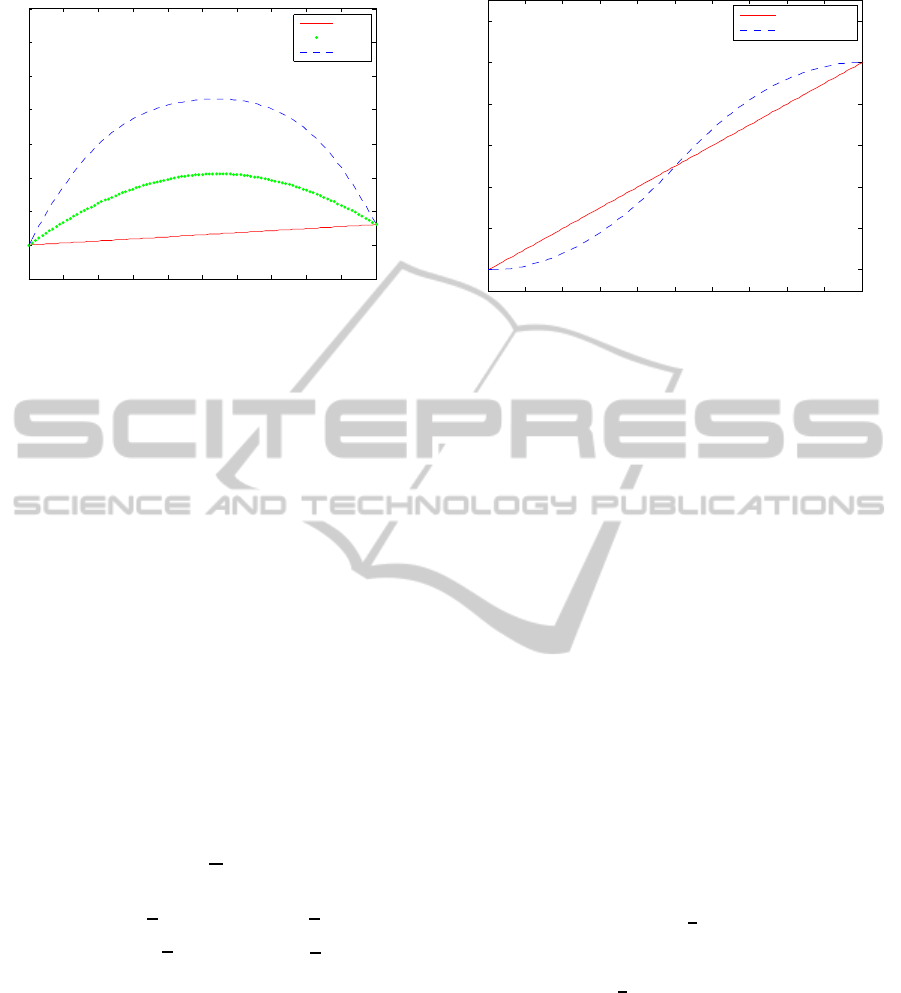
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

100

110

timeline

Lerp

Slerp

Squad

Figure 3: The comparison of different interpolation method.

5.2 Interpolation Parameter

The interpolation parameter h needs to be set. the key

frames can be separate into two categories by the vari-

able motion of joints. We call it common key frames

and variable speed key frames.

The common key frames are mainly used for pre-

sentation of joint movement as a constant speed. The

variable speed key frames are used as non-constant

speed. The difference of the two interpolation param-

eter is show in Figure 4.

Some transformation angle of key frames in the

motion sequence is large . The process of transforma-

tion is speed up ﬁrst and then slow down again, which

is in accordance with normal human body kinematic

law, and laws of physics. Any transformation from

one state to another requires a force process that is a

process from acceleration to deceleration. The main

function of variable speed key frames is to enhance

the details of velocity change.

h =

(10)

h =

(





−2



− 1



+ 1 t

≥

(11)

For the common key frames, the interpolation pa-

rameter h shows as Eq. 10; for the variable speed key

frames, the interpolation parameter h shows as Eq. 11.

is the current time, T is the total interpolation time

as calculate in Eq. 5.

5.3 Hierarchical Interpolation Method

Based on Motion Classiﬁcation

To express more detail information, our method uses

different interpolation algorithm for different anima-

tion. This is the hierarchical interpolation method

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.2

0.4

0.6

0.8

1.2

common

variable speed

Figure 4: The comparison of interpolation parameter.

based on motion classiﬁcation. Each joint is inter-

polated separately, which can realize different kinds

of animation interpolation respectively and enhance

details of movement.

To generate transition animation rapidly, our hier-

archical interpolation method learned from the level

of detail technique. With the classiﬁcation of joints

and animations, different interpolation methods are

used.

5.3.1 Interpolation Method Selection

As a couple of similar movements, the transition

needs not to use complexityinterpolation method. For

the transition time will be calculate really small, it is

really difﬁcult to distinguish the transition is good or

bad. In this case, we prefer to use the simple interpo-

lation method to save time.

On the other hand, for a complex movement, in-

terpolation method needs to present better motion de-

tails. Since the transition movementhas a longer tran-

sition duration, the motion details could be easier to

unfold before the eyes of users.

As we discussed, angle offset ∆θ of all joints need

to be calculated. We choose

as the threshold value,

they can be separated into normal rotation and large

angle rotation. If a joint needs to rotate a large angle,

which means ∆θ ≥

, we call it large angle rotation.

For large angle rotation, we use Squad interpolation

method, and for normal rotation, we use Slerp inter-

polation method.

All the joints discussed above do not include the

joints of ﬁngers. By traversing the character skele-

ton structure, the joints of ﬁngers have been marked.

the movement of the ﬁngers is tiny to the whole body

movement, therefore, we use the simple Lerp inter-

polation method with the simple linear interpolation

parameter as Eq. 6, to save time.

AutomaticVariable-timingAnimationTransitionbasedonHierarchicalInterpolationMethod

313

5.3.2 Interpolation Parameter Selection

The classiﬁcation of the animation set is described in

section 3. All the animations have already separated

into three parts, animation on the spot, plane motion

and space ﬂight.

Transition animation between animations on the

spot needs to be simply and quickly generated. We

just use common key frames interpolation parameter,

as Eq. 10.

Except for the transition between two animations

on the spot, all the other animation transition can be

classiﬁed as complex transition animations, such as

the transition between space ﬂight, transition between

plane motion, transition between plane motion and

space ﬂight, transition from animation on the spot to

space ﬂight and so on. In order to satisfy the behaviors

and kinematics of human beings, the variable speed

key frame interpolation parameter is used for all these

movement, as show in Eq. 11.

5.4 Position Interpolation

Only the root node has the position data, which de-

cides the global position of the character. According

with human dynamics and motion trend, the trans-

formation of the root node is essential to generate a

proper transition animation .

Animators could not know the current character

global position while playing a video game. There-

fore, animator provides character animations based on

local displacement coordinates. For this reason, the

character’s start frame of next animation needs to set

global position ﬁrstly. The position of the character

movement trajectory should conforms to the charac-

ter motion trend and physical properties.

Except for animations on the spot, the character

may have a movetrend, while the character is moving.

Therefore, the position of the last frame of present

animation and the position of the ﬁrst frame of next

animation should not be simply set as the same point.

The global position of the next animation should be

set as the position after transition animation.

The movement trajectory should be physically

correct. For an transition animation between plane

motions, the position could be calculate as Eq. 12. p

is the position of start frame, v is the velocity of start

frame of transition,

v is the acceleration of the start

frame of transition, t

is the current time during the

total time T.

p(t

) = p

+ t

v (12)

For a transition animation involving space ﬂight

animation, we not only need to consider the plane mo-

tion trend, but also the acceleration of gravity. The

position could be calculate as Eq. 13, g is the gravity,

is the parameter of gravitational acceleration.

p(t

) = p

+ t

v+ k

g (13)

6 RESULTS

By applying our method onto the animation set to ob-

tain the animation transition. The process of transfor-

mation from one movement to another could start at

any frame.

As show in Figure 5, it is the transition animation

from walk to stand. While the character is walking

along, the user can trigger to stand pose at any time,

we choose four different movements during walking

arbitrarily. The animation ﬁnally transform to the

stand pose with his hands on his waist, as the right-

most picture of each row in Figure 5.

Our method is not only suitable for simple anima-

tion transition, but also suitable for complex anima-

tion transition. As show in Figure 6, it is the transi-

tion animation from dance to run. While the virtual

character is dancing, the user could trigger to the next

animation, such as running, at any frame. There is

no need to wait the ﬁnish of the dance movement, a

smooth transition animation to the next animation is

generated automatically. We choose four frames from

dancing animation arbitrarily, as show in the four left-

most picture of each row in Figure 6. The dancing

animation we choose for experiment is complex, in-

cluding running, jumping, rotating and so on. The

ﬁrst frame of next animation can be seen as the ﬁnal

posture of the transition animation, which is the right-

most picture of each row in Figure 6. Even though

the movement shows in different perspective in the

screenshot, they are the same movement. The creation

of transition animations between all these animations

are proved to be available.

It is proved by experiments, our method could ap-

ply on all the animations to generate transition anima-

tion at any time. The transition can generate quickly

and automatically. Meanwhile, the transition anima-

tion conforms to human body dynamics, and adapts

to the previous and the next animation trend. This al-

lows users to get more realistic experiences.

7 CONCLUSIONS

In this paper, we have presented a novel method

to generate the transition animation rapidly and

smoothly. It can calculate transition time length by

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

314

Figure 5: The transition animation from walk to stand.

Figure 6: The transition animation from dance to run.

AutomaticVariable-timingAnimationTransitionbasedonHierarchicalInterpolationMethod

315

using variable-timing method. Therefore, the time

length can be obtained automatically according to dif-

ferent motion complexity. We use the hierarchical

interpolation method to generate a transition in the

shortest possible time with the precondition of proper

movement. This method uses different interpolation

method based on the classiﬁcation of joints, and it

uses different interpolation parameter based on the

classiﬁcation of animations. The generated transition

animation is ﬂexibility and changeability for different

animation conditions. The ﬁnal experimental result

shows perfect result of generating transition anima-

tion.

There are also some limitations in our work. In

order to make our generated animation more realis-

tic and reliable, some extra constraints need to be

added. Such as rotation angle constraint, collision

constraint and center of mass constraint. As our tran-

sition method is generated automatically, the trajec-

tory of the joints and the bones could not avoid col-

lision themselves, therefore, we need collision detec-

tion. It also needs to keep the character’s balance dur-

ing animation. We cannot control the trajectory of ev-

ery joint without additional constraints, and the move-

ment without constraints and error feedback may lead

to an unreal animation presentation. We will solve

this problem in our future work

ACKNOWLEDGEMENTS

The authors thank the 863 Plan (No. 2013AA013803)

and the National Science Foundation of China (No.

61103153/F020503) for ﬁnancially supporting this

study. We also thank Shaohua Hu, Xingzhang Long

and Zhengyuan Chen from Zhejiang Institute of Dig-

ital Media of Chinese Academy of Sciences, for the

great help of providing us the model and animation

set of the virtual character.

REFERENCES

Benitez, A. (2007). Forward Kinematics for Virtual Agents.

agents. Eng. Lett. 15(2), 225233 (2007)

Chai, J. and Hodgins, J. K (2007). Constraint-based mo-

tion optimization using a statistical dynamic model. In

ACM Transactions on Graphics (TOG) (Vol. 26, No. 3,

p. 8). ACM.

Chakra, A. A., and Li, X. (2009). Priority-Based Level of

Detail Approach for Animation Interpolation of Artic-

ulated Objects. In ASTEC’2010 (pp.69-76).

Dam, E. B., Koch, M., and Lillholm, M. (1998). Quater-

nions, interpolation and animation. Datalogisk Insti-

tut, Kbenhavns Universitet.

Kong, D. H., Wang, L. C., and Zheng, C. Y. (2011). A

Key Frame Interpolation Method Enhancing Motion

Details of Skeletal Animation. In Journal of Beijing

University of Technology, 8, 023.

Kuznetsova, A., Troje, N. F., and Rosenhahn, B. (2013). A

Statistical Model for Coupled Human Shape and Mo-

tion Synthesis. In GRAPP/IVAPP (pp. 227-236).

McCann, J., and Pollard, N. (2007, August). Responsive

characters from motion fragments. In ACM Transac-

tions on Graphics (TOG) (Vol. 26, No. 3, p. 6). ACM.

Moulard, T., Yoshida, E., and Nakaoka, S. I. (2013, Oc-

tober). Optimization-based motion retargeting inte-

grating spatial and dynamic constraints for humanoid.

In Robotics (ISR), 2013 44th International Symposium

on (pp. 1-6).IEEE.

O’Brien, C., Dingliana, J., and Collins, S. (2011, August).

Spacetime vertex constraints for dynamically-based

adaptation of motion-captured animation. In Proceed-

ings of the 2011 ACM SIGGRAPH/Eurographics Sym-

posium on Computer Animation (pp. 277-286).ACM.

Patil, S., and Chai, Y. H. (2014). Affordance Gesture Input

Motion Interpolation. ASTL Volume 46, 2014: Con-

vergence Research Trend I.

Safonova, A. and Hodgins, J. K. (2007). Construction and

optimal search of interpolated motion graphs. In ACM

Transactions on Graphics (TOG) (Vol. 26, No. 3, p.

106). ACM.

Shapiro, A., and Feng, A. W. (2013). The Case for

Physics Visualization in an Animator’s Toolset. In

GRAPP/IVAPP (pp. 247-253).

Shum, H. P., Komura, T., and Yadav, P. (2009). Angular mo-

mentum guided motion concatenation. In Computer

Animation and Virtual Worlds, 20(23), 385-394.

Smith, M. (2013). Applications of Dual Quaternions in

Three Dimensional Transformation and Interpolation.

Sok, K. W., Yamane, K., Lee, J., and Hodgins, J. (2010,

July). Editing dynamic human motions via momen-

tum and force. In Proceedings of the 2010 ACM SIG-

GRAPH/Eurographics Symposium on Computer Ani-

mation (pp. 11-20).Eurographics Association.

Wang, J., and Bodenheimer, B. (2003, August) An eval-

uation of a cost metric for selecting transitions be-

tween motion segments. In Proceedings of the 2003

ACM SIGGRAPH/Eurographics symposium on Com-

puter animation (pp. 232-238).Eurographics Associa-

tion.

Wang, J., and Bodenheimer, B. (2004, August) Comput-

ing the duration of motion transitions: an empirical

approach. In Proceedings of the 2004 ACM SIG-

GRAPH/Eurographics symposium on Computer ani-

mation (pp. 335-344). Eurographics Association.

Wang, J. M., Fleet, D. J., and Hertzmann, A. (2008). Gaus-

sian process dynamical models for human motion.

In Pattern Analysis and Machine Intelligence, IEEE

Transactions on, 30(2), 283-298.

Yumeng, W., Zheng, W., Guanbo, B., and Bo, X. (2014).

Optimization Control for Biped Motion Trajectory.

In 2014 4th International Conference on Audio, Lan-

guage, and Image Processing (ICALIP).

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

316